黑体辐射出射度曲线绘制
黑体辐射实验-学生讲义

近代物理实验 黑体辐射任何物体都有辐射和吸收电磁波的本领。
物体所辐射电磁波的强度按波长的分布与温度有关,称为热辐射。
处于热平衡状态物体的热辐射光谱为连续谱。
一切温度高于0K 的物体都能产生热辐射。
黑体是一种完全的温度辐射体,能吸收投入到其面上的所有热辐射能,黑体的辐射能力仅与温度有关。
任何普通物体所发射的辐射通量都小于同温度下的黑体发射的辐射通量;其辐射能力不仅与温度有关,还与表面的材料的性质有关。
所有黑体在相同温度下的热辐射都有相同的光谱,这种热辐射特性称为黑体辐射。
黑体辐射的研究对天文学、红外线探测等有着重要的意义。
黑体是一种理想模型,现实生活中是不存在的,但却可以人工制造出近似的人工黑体。
辐射能力小于黑体,但辐射的光谱分布与黑体相同的温度辐射体称为灰体。
[实验目的]1. 理解黑体辐射的概念。
2. 验证普朗克辐射定律。
3. 验证斯特藩一玻耳兹曼定律。
4. 验证维恩位移定律。
5. 学会测量一般发光光源的辐射能量曲线。
[实验原理]1. 黑体辐射的光谱分布—普朗克辐射定律德国物理学家普朗克1900年为了克服经典物理学对黑体辐射现象解释上的困难, 推导出一个与实验结果相符合的黑体辐射公式,他创立了物质辐射(或吸收)的能量只能是某一最小能量单位(能量量子)的整数倍的假说,即量子假说,对量子论的发展有重大影响。
他利用内插法将适用于短波的维恩公式和适用于长波的瑞利—金斯公式衔接,提出了关于黑体辐射度的新的公式—普朗克辐射定律,解决了“紫外灾难”的问题。
在一定温度下,单位面积的黑体在单位时间、单位立体角内和单位波长间隔内辐射出的能量定义为单色辐射度,普朗克黑体辐射定律为:式中:第一辐射常数)(1074.3221621m W hc C •⨯==-π 第二辐射常数)(104398.122K m k hc C •⨯==- 其中,h 为普朗克常数,c 为光速,k 为玻耳兹曼常数。
黑体光谱辐射亮度由下式给出:图1-1给出了T L λ随波长变化的图形。
ht黑体辐射出射度曲线绘制实验报告..

黑体辐射出射度曲线绘制实验报告姓名:学号:班级:黑体辐射出射度曲线绘制一、 实验目的:学习和巩固黑体辐射定律,验证普朗克辐射定律、斯蒂芬—玻尔兹曼定律、维恩位移定律;了解单色仪的工作原理及基本结构。
二、 实验内容:按照实验指导书的要求和步骤操作仿真黑体实验的装置,验证黑体相关定律。
三、 实验设备:WHS-型黑体实验装置,计算机,打印机等。
四、 实验原理:黑体是一个能完全吸收并向外完全辐射入射在它上面的辐射能的理想物体。
黑体的光谱辐射量和温度之间存在精确的定量关系,确定了黑体的温度,就可以确定其他的辐射量,因此黑体辐射定律在辐射度学中起了基准作用,占据十分重要的地位。
自然界中不存在绝对黑体,用人工的的方法可以制成尽可能接近绝对黑体的辐射源。
钨的熔点约为3695K ,充气钨灯丝的光谱辐射分布和黑体十分相近,因此可以用来仿真黑体。
CIE 规定分布温度2856K 的充气钨丝灯作为标准A 光源,以此实现绝对温度为2856K 的完全辐射题的辐射,即标准照明体A 。
本次试验所用的WHS-1黑体实验装置就是以溴钨灯模拟黑体的辐射源,通过改变灯丝的电流来模拟改变黑体的色温。
描述黑体辐射定律的普朗克公式以波长表示的形式为:1)exp(1),(2510-=Tc c T M λλλ (1) 其中第一辐射常数21621m W 107418.32⋅⨯==-hc c π;第二辐射常数K m 104388.122⋅⨯==-khc c ,k 为玻尔兹曼常数,c 为光速。
由于黑体是朗伯辐射体,因此可以得到黑体的光谱辐亮度表示式如下:1)e x p (1),(2510-=T c c T L λπλλ (2)斯蒂芬—玻尔兹曼定律描述的是黑体的辐射出射度与温度之间的关系:)m W()(240T T M σ= (3) 式(3)中,)K m W (106696.5154-2-84241⋅⋅⨯==-c c πσ称为斯蒂芬—玻尔兹曼常数。
黑体光谱辐射是单峰函数,其峰值波长满足维恩位移定律:)K m (⋅=μλb T m (4) 式(4)中,常数K m 28989651.42⋅==μc b 。
2 实验二 黑体辐射实验

实验二黑体辐射实验概述WGH-10型黑体实验装置专门用于进行黑体辐射能量的测量和任意发射光源的辐射能量的测量。
可以记录出发光源的辐射能量曲线。
在实验时,通过改变光源的温度,分别进行扫描,可以从记录的光谱辐射曲线直接看到维恩位移定律的现象,并能够对普朗克定律、斯忒藩-波尔兹曼定律进行较精确的验证。
WGH-10型黑体实验装置的控制系统采用WINDOWS界面,在WINDOWS 95/98系统下均能适用,功能强大、操作简便。
控制软件中,根据普朗克公式可以计算出任意温度下的绝对黑体的理论曲线,用户可以根据需要提取。
WGH-10型黑体实验装置所配的光源是溴钨灯,溴钨灯的谱线大致类似于黑体,但是由于钨的发射系数不是1,所以需要进行修正。
软件可以对不同温度下溴钨灯的曲线进行发射系数 (仅限于溴钨灯)的修正。
此外WGH-10型黑体实验装置还可作为光谱区间在800-2500nm范围的光栅光谱仪使用,进行其它实验。
1.规格与主要技术指标1.1 规格、参数:相对孔径 D/F=1/7焦距 302.5 mm色散元件 300L光栅狭缝 0-2 mm连续可调,示值精度0.01mm/格,最大高度20mm主机尺寸 360×300×160mm1.2 主要技术指标:波长范围 800—2500nm波长精度±6 nm波长重复性 3 nm杂散光≤0.3%T2.黑体的基本理论2.1 黑体辐射任何物体,只要其温度在绝对零度以上,就向周围发射辐射,这称为温度辐射。
黑体是一种完全的温度辐射体,即,任何非黑体所发射的辐射通量都小于同温度下的黑体发射的辐射通量;并且,非黑体的辐射能力不仅与温度有关,而且与表面的材料的性质有关。
而黑体的辐射能力则仅与温度有关。
黑体的辐射亮度在各个方向都相同,即黑体是一个完全的余弦辐射体。
辐射能力小于黑体,但辐射的光谱分布与黑体相同的温度辐射体称为灰体。
2.2黑体辐射定律2.2.1 黑体辐射的光谱分布——普朗克辐射定律此定律用光谱辐射度表示,其形式为:)1(251-=TC e C E T λλλ(瓦特/米3)式中:第一辐射常数C 1 = 3.74×10-16 (瓦×米2)第二辐射常数C 2 = 1.4398⨯10-2(米×开尔文)黑体光谱辐射亮度由下式给出:πλλT T E L =(瓦特/米3.球面角)图2-1 给出了T L λ随波长变化的图形。
黑体辐射实验
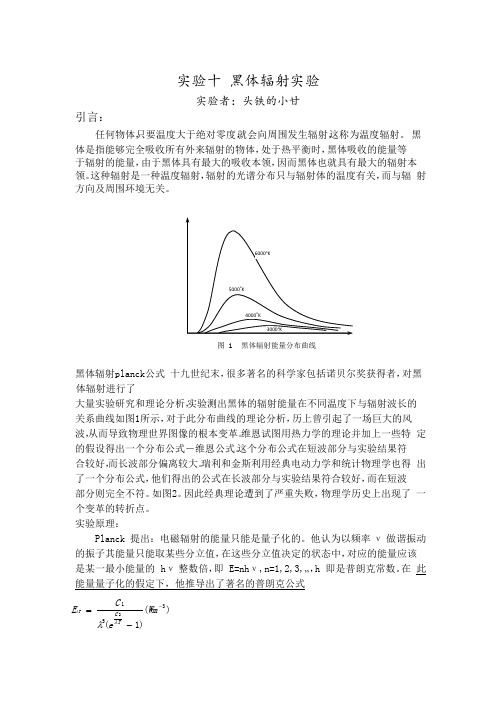
实验十 黑体辐射实验实验者:头铁的小甘引言:任何物体,只要温度大于绝对零度,就会向周围发生辐射,这称为温度辐射。
黑体是指能够完全吸收所有外来辐射的物体,处于热平衡时,黑体吸收的能量等 于辐射的能量,由于黑体具有最大的吸收本领,因而黑体也就具有最大的辐射本 领。
这种辐射是一种温度辐射,辐射的光谱分布只与辐射体的温度有关,而与辐 射方向及周围环境无关。
6000o K5000o K4000o K3000o K图 1 黑体辐射能量分布曲线黑体辐射 p lanck 公式 十九世纪末,很多著名的科学家包括诺贝尔奖获得者,对黑体辐射进行了大量实验研究和理论分析,实验测出黑体的辐射能量在不同温度下与辐射波长的 关系曲线如图 1 所示,对于此分布曲线的理论分析,历上曾引起了一场巨大的风 波,从而导致物理世界图像的根本变革。
维恩试图用热力学的理论并加上一些特 定的假设得出一个分布公式-维恩公式。
这个分布公式在短波部分与实验结果符 合较好,而长波部分偏离较大。
瑞利和金斯利用经典电动力学和统计物理学也得 出了一个分布公式,他们得出的公式在长波部分与实验结果符合较好,而在短波 部分则完全不符。
如图 2。
因此经典理论遭到了严重失败,物理学历史上出现了 一个变革的转折点。
实验原理:Planck 提出:电磁辐射的能量只能是量子化的。
他认为以频率ν做谐振动 的振子其能量只能取某些分立值,在这些分立值决定的状态中,对应的能量应该 是某一最小能量的 h ν整数倍,即 E=nh ν,n=1,2,3,…,h 即是普朗克常数。
在 此能量量子化的假定下,他推导出了著名的普朗克公式)()1(3512--=Wm eC E TC T λλλπ第一辐射常数C 1=8πhc =3.74×10-16(Wm 2),第二辐射常数C 2=1.4388×10-2(mK )。
它与实验结果符合得很好。
Planck 提出的能量量子假说具 有划时代的意义,标志了量子物理学的诞生。
实验七 黑体辐射

实验七 黑体辐射Black-body Radiation任何物体,只要其温度在绝对零度以上,就向周围发射辐射,这称为温度辐射;只要其温度在绝对零度以上,也要从外界吸收辐射的能量。
处在不同温度和环境下的物体,都以电磁辐射形式发出能量,而黑体是一种完全的温度辐射体,即任何非黑体所发射的辐射通量都小于同温度下的黑体发射的辐射通量;并且,非黑体的辐射能力不仅与温度有关,而且与表面的材料的性质有关,而黑体的辐射能力则仅与温度有关。
在黑体辐射中,存在各种波长的电磁波,其能量按波长的分布与黑体的温度有关。
实验目的(experimental purpose)1.了解黑体实验的发展历史,明确光谱辐射曲线的广泛应用;2.了解黑体实验仪器组件,明确测量过程与分析要素;3.明确黑体实验设计思想,掌握黑体辐射原理与定律。
实验原理(experimental principle)任何物体都具有不断辐射、吸收、发射电磁波的本领。
辐射出去的电磁波在各个波段是不同的,也就是具有一定的谱分布。
这种谱分布与物体本身的特性及其温度有关,因而被称之为热辐射。
为了研究不依赖于物质具体物性的热辐射规律,物理学家们定义了一种理想物体——黑体(black body),以此作为热辐射研究的标准物体。
所谓黑体是指入射的电磁波全部被吸收,既没有反射,也没有透射( 当然黑体仍然要向外辐射)。
显然自然界不存在真正的黑体,但许多地物是较好的黑体近似( 在某些波段上)。
黑体不仅仅能全部吸收外来的电磁辐射,且发射电磁辐 射的能力比同温度下的任何其它物体强。
黑体辐射指黑体发出的电磁辐射。
黑体辐射能量按波长的分布仅与温度有关。
对于黑体的研究,使得自然现象中的量子效应被发现。
我们换一个角度来说:所谓黑体辐射其实就是当地的状态光和物质达到平衡所表现出的现象:物质达到平衡,所以可以用一个温度来描述物质的状态,而光和物质的交互作用很强,而如此光和光之间也可以用一个温度来描述(光和光之间本身不会有交互作用,但光和物质的交互作用很强)。
黑体辐射

中国石油大学近代物理实验实验报告成绩:班级:姓名:同组者:教师:黑体辐射实验【实验目的】1、了解黑体辐射实验现象,掌握辐射研究方法。
2、学会仪器调整与参数选择,提高物理数量关系与建模能力。
3、通过验证定律,充实物理假说与思想实验能力。
【实验原理】黑体是指能够完全吸收所有外来辐射的物体,处于热平衡时,黑体吸收的能量等于辐射的能量,由于黑体具有最大的吸收本领,因而黑体也就具有最大的辐射本领。
这种辐射是一种温度辐射,辐射的光谱分布只与辐射体的温度有关,而与辐射方向及周围环境无关。
事实上当然不存在绝对黑体,但有些物体可以近似地作为黑体来处理,比如,一束光一旦从狭缝射入空腔体内,就很难再通过该狭缝反射回来,那么,这个开着的狭缝空腔体就可以看作是黑体。
1、黑体辐射的光谱分析实验测出黑体的辐射强度在不同温度下与辐射波长的关系曲线。
维恩假定辐射能量按频率的分布类似于麦克斯韦的分子速率分布,导出如下公式E(λ,T)=bλ−5e−a/λT(1)式中E(λ,T)称为单色辐出度,它表示单位时间内,在黑体的单位面积上单位波长间隔内所辐射出的的能量,单位是瓦特/米2 ,T表示绝对温度,a,b是与波长和温度无关的常数。
这个分布在短波部分与实验结果符合较好,而长波部分偏离较大。
瑞利和金斯利用经典电动力学和统计物理学推导得到单色辐出度E(λ,T)=2πCλ4kT(2)式中,C为真空中的光速,k为玻尔兹曼常量。
它在波长很长,温度较高时与实验结果相符合,但在短波段偏离非常大,当频率趋于无穷大时引起发散,这就是当时有名的“紫外灾难”。
普朗克提出:电磁辐射的能量只能是量子化的。
他认为黑体是由多个带点谐振子组成,这些谐振子处于热平衡状态,每个振子具有一个固有的谐振频率ν,可以发出与吸收相同频率的电磁波,每个谐振子只能吸收或发射不连续的一份一份的能量,这个能量是一个最小能量ε0 =hν的整数倍,即谐振子能量为E=nhν,n为正整数,h为普朗克常量。
实验七 黑体辐射

实验七 黑体辐射Black-body Radiation任何物体,只要其温度在绝对零度以上,就向周围发射辐射,这称为温度辐射;只要其温度在绝对零度以上,也要从外界吸收辐射的能量。
处在不同温度和环境下的物体,都以电磁辐射形式发出能量,而黑体是一种完全的温度辐射体,即任何非黑体所发射的辐射通量都小于同温度下的黑体发射的辐射通量;并且,非黑体的辐射能力不仅与温度有关,而且与表面的材料的性质有关,而黑体的辐射能力则仅与温度有关。
在黑体辐射中,存在各种波长的电磁波,其能量按波长的分布与黑体的温度有关。
实验目的(experimental purpose)1.了解黑体实验的发展历史,明确光谱辐射曲线的广泛应用;2.了解黑体实验仪器组件,明确测量过程与分析要素;3.明确黑体实验设计思想,掌握黑体辐射原理与定律。
实验原理(experimental principle)任何物体都具有不断辐射、吸收、发射电磁波的本领。
辐射出去的电磁波在各个波段是不同的,也就是具有一定的谱分布。
这种谱分布与物体本身的特性及其温度有关,因而被称之为热辐射。
为了研究不依赖于物质具体物性的热辐射规律,物理学家们定义了一种理想物体——黑体(black body),以此作为热辐射研究的标准物体。
所谓黑体是指入射的电磁波全部被吸收,既没有反射,也没有透射( 当然黑体仍然要向外辐射)。
显然自然界不存在真正的黑体,但许多地物是较好的黑体近似( 在某些波段上)。
黑体不仅仅能全部吸收外来的电磁辐射,且发射电磁辐 射的能力比同温度下的任何其它物体强。
黑体辐射指黑体发出的电磁辐射。
黑体辐射能量按波长的分布仅与温度有关。
对于黑体的研究,使得自然现象中的量子效应被发现。
我们换一个角度来说:所谓黑体辐射其实就是当地的状态光和物质达到平衡所表现出的现象:物质达到平衡,所以可以用一个温度来描述物质的状态,而光和物质的交互作用很强,而如此光和光之间也可以用一个温度来描述(光和光之间本身不会有交互作用,但光和物质的交互作用很强)。
黑体辐射实验

黑体辐射1900年普朗克发表的黑体辐射公式在物理学上是一项划时代的成就。
在此以前黑体辐射的波长分布虽然已经有了相当可靠的实验数据,但经典物理学的理论解释却导致了非常尖锐的矛盾。
这一问题在经典物理学的范畴内是无法合理地解决的,普朗克引进了量子化的假设,推导出黑体辐射波长分布公式。
量子化假设已成为当代物理学的基石,对当代科学技术的发展产生了深远的影响。
【实验目的】1、研究物体的辐射面、辐射体温度对物体辐射能力的影响,并分析原因。
2、测量改变测试点与辐射体距离时,物体辐射能量W 和距离L 以及距离的平方的关系,并描绘W -2L 曲线。
3、依据维恩位移定律,测绘物体辐射能量与波长的关系图。
【实验原理】热辐射的真正研究是从基尔霍夫开始的。
1859年他从理论上引入了辐射本领、吸收本领和黑体概念,他利用热力学第二定律证明了一切物体的热辐射本领r (ν,T )与吸收本领α(ν,T )成正比,比值仅与频率ν和温度T 有关,其数学表达式为:),(),(),(T F T T r νναν= (1) 式中F (ν,T )是一个与物质无关的普适函数。
1861年他进一步指出,在一定温度下用不透光的壁包围起来的空腔中的热辐射等同于黑体的热辐射。
1879年,斯特藩从实验中总结出了黑体辐射的辐射本领R 与物体绝对温度T 四次方成正比的结论;1884年,玻耳兹曼对上述结论给出了严格的理论证明,其数学表达式为:4T R T σ= (2)即斯特藩-玻耳兹曼定律,其中4212/10673.5K cm w -⨯=σ为玻耳兹曼常数。
1888年,韦伯提出了波长与绝对温度之积是一定的。
1893年维恩从理论上进行了证明,其数学表达式为:b T =max λ (3)式中b =2.8978×10-3( m.K )为一普适常数,随温度的升高,绝对黑体光谱亮度的最大值的波长向短波方向移动,即维恩位移定律。
1图 1 辐射能量与波长的关系图 l 显示了黑体不同色温的辐射能量随波长的变化曲线,峰值波长λmax与它的绝对温度T成反比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黑体辐射出射度曲线绘制
一、目的:学习和巩固黑体辐射定律,验证普朗克辐射定律、斯蒂芬-玻尔兹曼
等定律;了解单色仪的工作原理及基本结构。
二、内容:按照实验指导书的要求和步骤操作仿真黑体实验装置,验证黑体相关
定律。
三、设备:WHS-型黑体实验装置,计算机,打印机等。
四、原理:
黑体是一个能完全吸收并向外完全辐射入射在它上面的辐射能的理想物体。
黑体的光谱辐射量和温度之间存在精确的定量关系,确定了黑体的温度,就可以确定其他的辐射量,因此黑体辐射定律在辐射度学中起了基准的作用,占据十分重要的地位。
自然界不存在绝对黑体,用人工的方法可以制成尽可能接近绝对黑体的辐射源。
钨的熔点约为3695K,充气钨丝灯的光谱辐射分布和黑体十分接近,因此可以用来仿真黑体。
CIE规定分布温度2856K的充气钨丝灯作为标准A光源,以此实现绝对温度为2856K的完全辐射体的辐射,即标准照明体A。
本次实验所用的WHS-1黑体实验装置就是以溴钨灯模拟黑体的辐射源,通过改变灯丝的电流来模拟改变黑体的色温。
描述黑体辐射定律的普朗克公式以波长表示的形式为:
(1)式(1)中,第一辐射常数;第二辐射常数
;;为光速。
由于黑体是朗伯辐射体,因此可以得到黑体的光谱辐亮度表示式如下:
(2)
斯蒂芬-玻尔兹曼定律描述的是黑体的辐射出射度与温度之间的关系:
(3)
式(3)中,称为斯蒂芬-玻尔兹曼常数。
黑体光谱辐射是单峰函数,其峰值波长满足维恩位移定律:
(4)
式(4)中,常数。
实验就是要验证黑体辐射的上述定律。
WHS-1型黑体实验装置的工作过程为:调整灯丝电流为某一数值,如1.7A,停留几分钟待光源稳定;单色仪光栅机构复位,从800nm至2500nm以一定的间隔(如1nm)进行扫描,将数据存进内存(即软件中所指“寄存器_1”等),显示的
辐出度数值为:。
为保证显示值不偏离理论值太多,除了要保证光栅扫描机构的精度外,溴钨灯的稳定性也十分重要。
因此溴钨灯的预热,以及调整电流后,应有充足的稳定时间。
五、实验步骤:
1.正确连接计算机、单色仪、接收单元、电控箱、溴钨灯电源、溴钨灯;
2.打开计算机、电控箱及溴钨灯电源,使机器预热20分钟;
3.按照软件的提示,确认反射镜拨杆的位置置于位置“1”,即把拨杆拨向
出射狭缝方向(拨向相反方向用于“观察窗查看二级谱线”实验);
4.将溴钨灯电源的电流调节为1.7A(即对应黑体色温2999K)扫描一条从
800~2500nm的曲线,得到在色温2999K时的黑体辐射曲线;
注意:测试完一条曲线后,可以点击主菜单的“验证热辐射定律”下的“普朗克辐射定律 (W)”进行验证。
输入800~2500nm之间不同的波长值,验证测量值和理论值的符合程度。
如果相差太大,此时应点击“工作”下的“修正黑体辐射系数参数 (Y)”的“选择计算 (Z)”进行标定。
标定步骤参照“使用说明书”20~22页的说明进行。
5.依次改变溴钨灯的电源为1.6A(对应2889K),1.5A(对应2674K),1.4A
(对应2548K),1.3A(对应2544K),1.2A(对应2303K),1.1A(对应
2208K),1.0A(对应2101K),0.9A(对应2001K),可得到相应色温的
黑体辐射曲线,分别存入各寄存器,最多可以存9条曲线。
6.实验结果如下:
进行完步骤5,且每次验证普朗克定律误差较小,则可以验证斯蒂芬-玻尔兹曼定律和维恩位移定律。
实验结果如下:
图4. 维恩位移定律验证界面
注意事项
图4. 维恩位移定律验证界面
六、注意事项:
1.日常使用时黑体辐射系数参数已标定好,因此一般情况下不要调整入射
和出射狭缝的大小;
2.如果因测试环境发生变化(狭缝大小变化)或实验数据误差过大,则需
要参照软件提示和“使用说明书”20~22页的说明对黑体辐射系数参数进行修正。
七、参考文献:
[1]. 金伟其,胡威捷. 辐射度、光度与色度及其测量[M]. 北京理工大学出版社.
2006
[2]. 吴继宗,叶关荣. 光辐射测量[M]. 机械工业出版社. 1992
(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
可复制、编制,期待你的好评与关注)。
