人教版九年级数学下册28.2 :解直角三角形 精练题(含答案)
人教版九年级数学下册第28章锐角三角函数28.2解直角三角形及其应用复习练习及答案

第28章锐角三角函数28.2 解直角三角形及其应用1. 在厶ABC中,/ A=120° AB=4 AC=2 贝卩sinB 的值是()A. 口B .-i C .2 D14 5 7 142. 在Rt△ ABC中,/ C=90 ,若AB=4 sinA=?,则斜边上的高等于()5A. 64 B .兰C . 16 D . 1225 25 5 53. 如图,在Rt△ ABO中,斜边AB= 1,若OC/ BA / AOC= 36°,贝S ()A. 点B到AO的距离为sin 54B. 点B到AO的距离为tan 36 °C. 点A到OC的距离为sin 36 ° sin 54D. 点A到OC的距离为cos 36 sin 544. 如图是教学用直角三角尺,边AC= 30 cm,/ C= 90° tan / BAC=则边BC的长为()A. 30 3 cm B . 20 3 cm C . 10 3 cm D . 5 3 cm\[2 35. 如图,在△ ABC中,cos B= ,sin C= , AC= 5,则厶ABC的面积是()2 5A.fB. 12C. 14D. 21 6•河堤横断面如图所示,堤高BC= 6 m,迎水坡AB的坡比为1 : 3,则AB的长为()A. 12 m B . 4 3 m C . 5 3 m D . 6 3 m7. 如图,在两建筑物之间有一旗杆,高15 m,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角a为60°,又从A点测得D点的俯角B为30°,若旗杆底部G为BC的中点,则矮建筑物的高CD为()A. 20 m B . 10 3 m C . 15 3 m D . 5 6 m8. 一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20 n mile,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20 min 后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为()A. 10:3 n mile/h B .30 n mile/h C . 20 ';3 n mile/h D . 30 : 3n mile/h9. 从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是(A. (6+2 .3) 米B (6+3 .3) 米C (6+6 .3 )米D . 12 米10. 如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30° 则B、C两地之间的距离为()3A. 100 3 m B 50 2m C. 50 3m D .咛11. 在Rt△ ABC中,CA= CB AB=込/2,点D在BC边上,连接AD 若tan1/ CAD= 3,贝y BD的长为 _____ .12. 在平面直角坐标系中,点A的坐标为(3 , 0),点B为y轴正半轴上的一点,点C是第一象限内一点,且AC= 2,设tan / BOC= m则m的取值范围是________ .13. 在等腰三角形ABC中,/ A= 30°, AB= 8,贝S AB边上的高CD的长是14. 在Rt△ ABC中,/ C=90 , tanA = 4, BC=8 则厶ABC的面积为.315. 等腰三角形的一腰长为6cm,底边长为673cm则其顶角为___________ .16. 在Rt△ ABC中,/ ACB=90 , CDLAB于点D.已知AC=5 , BC=2 那么sin / ACD= _____17. 如图,在Rt△ ABC中,/ C=90°, D为BC上一点,/ DAC=30 , BD=2 AB= 2怎,贝S AC的长是_______ .18. 如图,从地面上点A处测得山顶上铁塔BD的塔顶和塔底的仰角分别为B =60°和a =45°,已知塔高BD=100m那么山高CD= m .(结果保留根号)19. 如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C 点处的俯角为45°.则海底C点处距离海面DF的深度为________ 米(结果精确到个位,参考数据:2〜1.414 , . 3〜1.732 , 〜2.236 )…字二…一/产'即~~时•、\I 、20. 如图,一幢大楼的顶部竖有一块写有“校训”的宣传牌CD小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45° .已知山坡AB垂直于视线AD AB=20米,AE=30米,则这块宣传牌CD的高度为________________ 米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:2〜1.414 , 3〜1.732 ).21. 如图,在△ ABC中,CDLAB 垂足为D.若AB=12 CD=6 tanA=?,求2 sinB+cosB 的值.22. 已知:如图,Rt△ AOB中,/ 0=90,以0A为半径作O Q BC切OO于点C,连接AC交QB于点P.(1) 求证:BP=BC(2) 若sin / PAQ= 1,且PC=7 求OO 的半径.323. 如图,已知某小区的两幢10层住宅楼间的距离为AC= 30 m,由地面向上依次为第1层、第2层,…,第10层,每层高度为3 m假设某一时刻甲楼在乙楼侧面的影长h m.(1)用含a的式子表示h;(不必指出a的取值范围)⑵当a= 30°时,甲楼楼顶B点的影子落在乙楼的第几层?若a每小时增加15°,从此时起几小时后,甲楼的影子刚好不影响乙楼采光?24. 如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红眼睛与地面的距离(CD是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、ND 在同一条直线上).求出旗杆MN勺高度.(参考数据:2〜1.4…3〜1.7 , 结果保留整数.)26.如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角a为45° .从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角B为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号)[Um答案:1 —10 DBCCA AADCA 11.612.5 m^-2"13.^3^或4 或4 314.2415. 120°16.二3 17. 318. 50 ( 3+1)19. 260020. 5.421. 解:在 Rt △ ACD 中,T/ADC=90,二 tanA 二 CD - 3,二 AD=4 AD AD 2••• BD=AB -AD=12-4=8 在 Rt △BCD 中,BDC=90 , BD=8 CD=6 BC= BD 2 CD 2 =10, • sinB 二 CD 3 , cosB=BD - , • sinB+cosB=3+« =7 . BC 5BC5 5 5 5 22. (1)证明:连接 OC T BC 是O O 切线,•/0(B=90°,「./OCA / BCA=90 , T OA=O , •/ OCA / OAC / BOA=90,•/ OAC+APO=90,T / APO / BPC •/ OAC / BPC=90,•/ BPC / BCA 二 BC=BP(2)解:延长 AO 交O O 于点 E ,连接 CE 在 Rt △ AOP 中, T sin / PAO=,3设 OP=x AP=3x 贝y AO=22x ,T AO=OE 二 OE=22x ,「. AE=^2x , 解得:x=3,・ AO=6 2 .23. 解:(1)如图,过点E 作EF ±AB 于点F.由题意可知,四边形 ACEF 为矩形,• EF = AC= 30, AF = CE= h ,Z BEF= T AB= 3X 10= 30,・ BF = AB- AF = 30- h.T sin / PAO=,3CE = 1 AE 3 AC 2一2 . 3x 7= .・ --------- - AE 3 '3「• h = 30— 30tan a .⑵ 当 a = 30° 时,h = 30 — 30tan 30 ° = 30 — 30^3〜12.7.3T 12.7 — 3~4.2,二当a= 30°时,B 点的影子落在乙楼的第五层.当 h = 0 时,30 — 30ta n a= 0,得 a= 45 °,Ta 每小时增加15°,二从此时起1小时后,甲楼的影子刚好不影响乙楼采光.24. 解:过点A 作AE± MN 于 E ,过点C 作CF 丄MN 于 F ,则 EF=AB-CD=1.7-1.5=0.2 (m ),在 Rt △ AEM 中, v/ AEM=90 , / MAE=45 , • AE=ME 设 AE=ME=xm 贝S MF=(x+0.2 ) m , FC= (28-x ) m在 Rt △ MFC 中, v/ MFC=90,/ MCF=30,二 MF=CF?ta / MCF• x+0.2二乜 (28-x ),解得 9.7,二 MN 二ME+EN=9.7+1.711 米.又•••在 Rt △ BEF 中,tan / BEF = ||, ••• tan a= 30—1,即 30— h = 30tan a, 30答:旗杆MN 的高度约为11米.解:由题意可知/ BAD W ADB=45,二 FD 二EF 二米,在 Rt △ PEH 中, tan B =CG ,二CG=( 5 3+6)?二=5+2 3,:. CD=( 6+2.3 ) 米. PG 326. tan B =EH PHBF ,八 BF =: 5 3,二 PG=BD=BF+FD=35+6, 在 RT A PCG K。
人教版九年级下《28.2解直角三角形及其应用》《解直角三角形》训练有答案

《解直角三角形》基础训练知识点1已知两边解直角三角形1.在Rt△ABC 中,AB=4,的度数为( ) A.30° B.40° C.45° D.60°2.在Rt△ABC 中,∠A,∠B,∠C 所对的边分别为a ,b ,c ,∠C=90°,a=5,则∠B=____,b=____.3.在Rt△ABC 中,∠C=90°,∠A ,∠B,∠C 所对的边分别为a ,b ,c ,且求这个三角形的其他元素.知识点2已知一边及一锐角解直角三角形4.如图,在Rt△ABC 中,∠C =90°,∠B=30°,AB=8,则BC 的长是( )A.335.[2018河南信阳羊山中学期中]如图,三角形ABC 中,∠C =90°,AC=3,∠B =30°,P 是BC 边上的动点,则AP 的长不可能是( ) A.3.5 B.4.2 C.5.8 D.6.56.在Rt△ABC 中,∠C=90°,a ,b ,c 分别是∠A,∠B,∠C 的对边.求下列直角三角形中的未知量.(1)∠B=60°,c=25;(2)∠A=30°,知识点3解直角三角形的综合运用7.[2018黑龙江哈尔滨香坊区期末]在△ABC 中,∠A ,∠B 均为锐角,且sinA=12,cosB=2,AC=40,则△ABC 的面积是( )8.如图,已知在△A BC 中,AD 是边BC 上的高,BC=14,AD=12,sinB=45,则线段DC 的长为( )A.3B.4C.5D.69.如图,平面直角坐标系中有正方形ABCD ,B(0,∠BA0=60°,那么点C 的坐标为____.10.在△ABC 中,AC=6,BC=5,sinA=23,∠A,∠B 为锐角,求tanB 的值.11.如图,已知四边形ABCD 中,∠ABC =90°,∠ADC=90°,AB=6,CD=4,BC 的延长线与AD 的延长线交于点E(1)若∠A=60°,求BC 的长;若sinA=45,求AD 的长.(注意:本题中的计算过程和结果均保留根号)参考答案1.C 【解析】在R t△ABC 中,∵AB=4,AC AB =4=2,∴∠A=45°.故选C.2.45° 5【解析】因为sinA=ac 5∠B =∠A,所以b=a=5.归纳总结:(1)解直角三角形要注意每个三角形都有6个元素,即3个角和3条边.(2)解直角三角形时要注意发现已知和未知之间的联系,充分利用三角函数的定义来列式求值,正弦、余弦、正切三种函数都涉及两边一角,要正确选择,不能将它们弄混.(3)直角三角形中两锐角互余,三边之间满足勾股定理.3.【解析】在Rt△ABC 中,∵∠C=90°,∴tanA=a b ∴∠A=60°,∴∠B=90°-∠A=30°,∴5故.4.D 【解析】在Rt△ABC 中,∵∠C=90°,∠B=30°,AB=8,∴BC=ABcos 33故选D. 5.D 【解析】根据垂线段最短,可知AP 的长不可能小于3.在三角形ABC 中,∠C=90°,AC=3,∠B=30°,∴AB=6,∴AP 的长不可能大于6.故选D.6.【解析】(1)在Rt△ABC 中,∠C=90°,∠B=60°,∴∠A=30°,∴sinA=a c =12, ∵c=25,∴a=252.∵cos A=b c =2,c=25,∴b=2.综上a=252, b=2,∠A=30°. (2)∵∠C=90°,∠A=30°,∴∠B=60°.在Rt△ABC 中,cosA=b c c=2,∴a=12c=1.综上,a=l ,c=2,∠B=60°.名师点睛:解直角三角形的过程,就是把所有未知元素求出来的过程,不是只求单独的一条未知边或一个未知角.7.D 【解析】∴sinA=12,如图,过点C 作CD ⊥AB 于点D ,则CD=12AC=20,S △ABC =12故选D.8.C 【解析】∵AD 是边BC 上的高,∴AD⊥BC.在Rt△BDA 中,∠BDA=90°,AD=12,sinB=AD AB =45,∴AB=15,DC=BC -BD=14-9=5.故选C.9.(1)【解析】过点C 作CE ⊥y 轴于点E ,则易证Rt△CEB≌Rt△BOA,BE=AO=BOtan ∠BAO=l ,所以OE=OB +1因此点C 的坐标为(1) .10.【解析】如图,过点C 作CD ⊥AB 于点D ,则sinA=CD AC =23,∴CD=23AC=4. 在Rt△BCD,BC=5,CD=4,∴BD=3,∴tanB=CD BD =43. 11.【解析】(1)∵∠A=60O ,∠AB E =90°,∴∠E=30°. 在Rt△AB E 中,∵AB=6,tanA=BEAB,∴BE=AB·tan 3∵∠CDE=90°,CD=4,sinE=CD CE ,∴CE=CDsin E =412=8,BC=BE -38. (2)∵∠ABE=90°,AB=6,sinA=BE AE =45,∴设BE=4x ,AE=5x ,则AB=3x ,∴3x=6,得x=2,∴BE=8,AE=10,∴tanE=AB BE =68=CD DE =4DE ,解得DE=163,∴AD=AE-DE=lO -163=143.归纳总结:本题考查解直角三角形,解题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数进行解答.《解直角三角形》提升训练1.[2018陕西延安市实验中学课时作业]如图,在菱形ABCD中,AE⊥BC于点E,EC=4,sinB=45,则菱形ABCD的周长是( )A.10B.20C.40D.282.[2018河南省第二实验中学课时作业]如图,在△ABC中,点D,E分别是边AB,AC的中点,AF ⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )3.[2017贵州安顺中考]如图,⊙O的直径AB=4,BC切⊙0于点B,OC平行于弦AD,0C=5,则AD 的长为( )A. 65B. 85C.4.[2017贵州铜仁中考]如图,在Rt△ABC 中,∠C=90°,点D 是AB 的中点,ED ⊥AB 交AC 于点E.设∠A=a ,且tana=13,则tan2a=____.5.[2018河北邯郸二十三中课时作]如图,在等腰直角三角形ABC 中,∠C=90°,AC=6,D 是AC上一点,若tan ∠DBA=15,则AD 的长是____.6.[2017上海中考]如图,一座钢结构桥梁的框架是△ABC ,水平横梁BC 长18米,中柱AD 高6米.其中D 是BC 的中点,且AD ⊥BC. (1)求sinB 的值;(2)现需要加装支架DE ,EF ,点E 在AB 上,BE=2AE.且EF ⊥BC ,垂足为点F ,求支架DE 的长.7.[2018吉林九中课时作业]如图,在四边形ABCD 中,对角线AC ,BD 交于点0,∠BCD 是钝角,AB=AD ,BD 平分∠ABC ,若CD=3,,sin∠DBC=3,求对角线AC 的长.8.[2018广东深圳中学课时作业]如图,在四边形ABCD中,对角线AC,BD交于点E,∠BA C=90°,∠CED=45°,∠DCE=30°,CD的长和四边形ABCD的面积.参考答案1.C【解析】由sinB=45,易知cosB=35.∵在菱形ABCD中,AE⊥BC于点E,EC=4,cosB=BEAB=BC ECBC-=35,∴BC=10,则菱形ABCD的周长为4BC=40.故选C.2.D【解析】∵点D,E分别是边AB,AC的中点,∴DE是△ABC的中位线,∴DE∥BC,∴∠ABC=∠ADE=30°,∵AF⊥BC,∴∠AFB=90°.在Rt△AFB中,∵DF是斜边AB上的中线,∴AB=2DF=8,∵∠ABC=30°,∴BF=A B cos故选D.3.B【解析】如图,连接BD.∵AB是⊙O的直径,∴∠ADB=90°.∵OC∥AD,∴∠A=∠BOC,∴cos∠A=cos∠BOC.∵BC切⊙0于点B,∴OB⊥BC,∴cos∠BOC=OBOC=25,∴cos∠A= cos∠BOC=25.又cos∠A=ADAB,AB=4,∴AD=85.故选B.4.34【解析】如图,连接BE,∵点D是AB的中点,ED⊥AB,∴ED是AB的垂直平分线,∴EB=EA,∴∠EBA=∠A=a,∴∠BEC=2a.∴tana=DEAD=13,∴设DE=a,AD=3a,则a,AB=6a.设BC=x,CE=y,则222222x+yx+(y)=36a=ìïïíïïîBCCE34=.5.2【解析】过点D作DE⊥AB于点E,∵tan∠DBA=15=DEBE,∴B E=5DE.∵△ABC为等腰直角三角形,∠C=90°,∴∠A=45°,∴AE=DE ,∴BE=5AE.∵AC=6BE=AE +∴在等腰直角三角形ADE 中,由勾股定理,得6.【解析】(1)∵点D 是BC 的中点,∴BD=12BC=9米.∵AD⊥BC ,∴△ABD 是直角三角形,∴米),∴sinB=ADAB 6. (2)∵EF ⊥BC ,AD ⊥BC ,∴EF∥AD,∴△BEF∽△BAD,∴EF BF BE 2AD BD AB 3===,∴EF=23AD=4米,BF=23BD=6米,则DF=BD -BF=9-6=3(米).在Rt△DEF 中,米).7.【解析】如图,过点D 作DE ⊥BC 交BC 的延长线于点E ,则∠E=90°,∵sin∠DBC=DE BD =3,2在Rt△CD E 中,∵CD=3,2E=CD 2-DE 2=1,在Rt△BDE 6222BD -DE =4,∴BC=3,BC=CD ,∴∠CBD=∠CDB, ∵BD 平分∠ABC,∴∠ABD=∠DBC,∴∠ABD=∠CDB,∴AB∥CD. 同理AD∥BC,∴四边形ABCD 是菱形.∴AC ⊥BD ,A0=CO ,622BC -BO 223-(6)338.【解析】如图,过点D 作DH ∥⊥AC 于点H.∵∠CED=45°,EH=DEcos45°,∴DH=1.又∠DCE=30°,∴HC=DH tan 30︒CD=DHsin 30︒=2.∵∠AEB=∠CED=45°,∠BAC=90°,∴AB=AE=2,∴AC=AE +EH +HC=2+1∴S 四边形ABCD =S △ABC +S △ADC =12+12.。
2021-2022学年人教版九年级数学下册《28-2解直角三角形及其应用》知识点分类训练(附答案)

2021-2022学年人教版九年级数学下册《28.2解直角三角形及其应用》知识点分类训练(附答案)一.解直角三角形1.如图,在平面直角坐标系中,AB=3,连接AB并延长至C,连接OC,若满足OC2=BC•AC,tanα=2,则点C的坐标为.二.解直角三角形的应用2.图1是挂墙式淋浴花洒的实物图,图2是抽象出来的几何图形.为使身高175cm的人能方便地淋浴,应当使旋转头固定在墙上的某个位置O,花洒的最高点B与人的头顶的铅垂距离为15cm,已知龙头手柄OA长为10cm,花洒直径AB是8cm,龙头手柄与墙面的较小夹角∠COA=26°,∠OAB=146°,则安装时,旋转头的固定点O与地面的距离应为多少?(计算结果精确到1cm,参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)3.图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.(1)求∠ABC的度数;(2)测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,≈1.414)4.如图1,是一辆小汽车与墙平行停放的实物图片,图2是它的俯视图.汽车靠墙一侧OB 与墙MN平行且距离为0.8米,已知小汽车车门宽AO为1.2米.(参考数据:sin40°≈0.6428,cos40°≈0.7660,sin41°≈0.6561,cos41°≈0.7547,sin42°≈0.6691,cos42°≈0.7431)(1)当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(2)若车停在原地不动,靠墙一侧的车门能打开的最大角度约为多少?5.图①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图,托板长AB=115mm,支撑板长CD=70mm,板AB固定在支撑板顶点C处,且CB=35mm,托板AB可绕点C转动,支撑板CD可绕点D转动.(1)当∠CDE=60°时,①求点C到直线DE的距离(计算结果保留根号);②若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);(2)为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在直线DE上即可,则CD旋转的角度为.(直接写出结果)(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,≈1.7)三.解直角三角形的应用-坡度坡角问题6.如图,某超市的自动扶梯高为h(m),坡角为θ,那么扶梯长l(m)为()A.h cosθB.C.h tanθD.7.如图,AB是斜靠在墙上的长梯,AB与地面夹角为α,当梯顶A下滑1m到A′时,梯脚B滑到B′,A'B'与地面的夹角为β,若tanα=,BB'=1m,则cosβ=()A.B.C.D.8.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AB的长度为()A.6m B.3m C.9m D.6m9.一架5米长的梯子斜靠在墙上,测得它与地面的夹角为40°,则梯子底端到墙角的距离为()A.5cos40°米B.5sin40°米C.米D.米10.如图所示,建筑物AB坐落在一斜坡的坡顶的平地上,当太阳光线与水平线夹角成60°时,测得建筑物AB在坡顶平地上的一部分影子BC=15米,在斜坡CE上的另一部分影子CD=5米,且斜坡CE的坡度为i(即tanα)=1:,求建筑物AB的高度.(结果保留根号)四.解直角三角形的应用-仰角俯角问题11.许昌市旅游服务中心由广场和“一门四阙”主题建筑组成,如图1.广场为迎宾广场一门”为“许昌之门”,“四闕”为广场四角的汉阙,是许昌的标志性建筑.某数学兴趣小组在迎宾广场测量旅游服务中心的高度,图2为测量示意图,MN为服务中心的对称轴,在地面的AB处架设测角仪,测得旅游服务中心的最高点D的仰角45°,利用无人机在点B的正上方57.8米处的点C处测得点D的俯角为32°,测角仪的高度AB=1.6米,FH=17.2米,DE=19.8米.(1)求旅游服务中心的高度为多少米?(结果精确到0.1m.参考数据:sin32°≈0.530,cos32°≈0.848,tan32°≈0.625,≈1.414)(2)兴趣小组测量后到旅游服务中心参观,发现讲解员讲解的高度为36.8m,请用物理知识解释测量值与实际值出现差距的原因,如何避免或者减小差距?12.大汉雄风坐落于河南省永城市芒砀山主峰,是为纪念刘邦在芒砀山斩蛇起义创建四百年大汉王朝而建,某数学兴趣小组想测量底座之上部分雕像AB的高度,如图在和雕塑底座上端水平的山坡C处测得雕塑顶端B的仰角为58.5°,沿山坡上行10米到达点D,测得雕塑顶端B的仰角为45°,已知山坡的坡度i=1:3,且A,C在同一水平地面上,求塑像AB的高度.(测倾器高度忽略不计,结果精确到0.1米,参考数据:sin58.5°≈0.85,cos58.5°≈0.52,tan58.5°≈1.63,≈1.4,≈1.7,≈3.2.)13.九年级数学兴趣小组的实践课题是“测量物体高度”.小组成员小明与小红分别采用不同的方案测量同一个底座为正方体的旗杆的高度.以下是他们研究报告的部分记录内容:课题:测量旗杆高度小明的研究报告小红的研究报告测量示意图测量方案与测量数据在点D处用距离地面高度为1.6m的测角仪测出旗杆顶端A的仰角α=55°,再用皮尺测得测角仪底部所在点D处用距离地面高度为1.6m的测角仪测出旗杆顶端A的仰角α=29°,然后沿DF方向走20m到达点F处,在位置与旗杆底座正方体边缘的最短距离为10m.测出旗杆顶端A的仰角β=60°.参考数据sin55°≈0.82,cos55°=0.57,tan55°≈1.43,sin29°≈0.48,cos29°≈0.87,tan29°≈0.55,≈1.73计算旗杆高度10×tan55°+1.6≈15.9(m)(1)写出小红研究报告中“计算旗杆高度”的解答过程(结果精确到0.1m);(2)数学老师说小明的测量结果与旗杆实际高度偏差较大,超出了误差允许范围,请你针对小明的测量方案分析测量偏差较大的原因.14.某校一初三学生在学习了“锐角三角函数”的应用后,来到“孔子圣像”的雕像前,如图,想要用所学知识解决“孔子圣像”雕像AB的高度,他在雕像前C处用自制测角仪测得顶端A的仰角为60°,底端B的俯角为45°;又在同一水平线上的E处用自制测角仪测得顶端A的仰角为30°,已知DE=6m,求雕像AB的高度.(结果保留根号)15.2020年6月23日,北斗卫星最后一颗全球组网卫星发射成功.运载火箭从地面A处(忽略发射塔高度)竖直向上发射,当运载火箭到达点B处时,地面D处的雷达站测得B处仰角为37°,BD=50km.10秒后,运载火箭直线上升到达点C处,此时地面E处一观测点测得C处的仰角为56°,已知点A,D,E在同一条直线上,并且D,E两处相距15km,求运载火箭从B处到C处时的平均速度(单位:km/s).(参考数值:sin37°≈,cos37°≈,tan37°≈,sin56°≈,cos56°≈,tan56°≈)五.解直角三角形的应用-仰角俯角问题16.中原福塔,又名“河南广播电视塔”,是郑州市著名地标之一.小明和小亮利用卷尺和自制的测角仪测量福塔的高度.如图,小明站在点A处测得福塔顶端D的仰角为60°,小亮站在点B处测得福塔顶端D的仰角为72.3°.已知测角仪高度为1m,两人相距100m (点A,B,C在一条直线上).(1)求中原福塔CD的高度;(结果精确到0.1m.参考数据:sin72.3≈0.95,cos72.3≈0.30,tan72.3≈3.13,)(2)“景点简介”显示,中原福塔总高388m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.六.解直角三角形的应用-方向角问题17.如图,一艘渔船以40海里/小时的速度由西向东追赶鱼群,在A处测得小岛C在渔船的北偏东60°方向;半小时后,渔船到达B处,此时测得小岛C在渔船的北偏东30°方向.已知以小岛C为中心,周围18海里以内为军事演习着弹危险区.如果这艘渔船继续向东追赶鱼群,是否有着弹危险?18.如图,一艘海轮船位于灯塔P北偏东60°方向,与灯塔距离为80nmile的A处,它沿正南方向航行一段时间后,到达位于灯塔P南偏东37°方向的B处,求此时轮船所在B 处与灯塔P的距离.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,≈1.7,结果取整数)19.为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习.如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向(30+30)km处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是40km/h,第二组乘公交车,速度是35km/h.(1)求学校到红色文化基地A的距离?(2)哪组同学先到达目的地?请说明理由(结果保留根号).参考答案一.解直角三角形1.解:∵∠C=∠C,∵OC2=BC•AC,即,∴△OBC∽△OAC,∴∠A=∠COB,∵α+∠COB=90°,∠A+∠ABO=90°,∴∠ABO=α,∵tanα=2,∴tan∠ABO=,∴OA=2OB,∵AB=3,由勾股定理可得:OA2+OB2=AB2,即,解得:OB=3,∴OA=6.∴tan A=.如图,过点C作CD⊥x轴于点D,∵tanα=2,∴设C(﹣m,2m),m>0,∴AD=6+m,∵tan∠A=,∴,∴,解得:m=2,经检验,m=2是原方程的解.∴点C坐标为:(﹣2,4).故答案为:(﹣2,4).二.解直角三角形的应用2.解:如图,过点B作地面的垂线,垂足为D,过点A作地面GD的平行线,交OC于点E,交BD于点F,在Rt△AOE中,∠AOE=26°,OA=10cm,则OE=OA•cos∠AOE≈10×0.90=9cm,在Rt△ABF中,∠BAF=146°﹣90°﹣26°=30°,AB=8cm,则BF=AB•sin∠BAF=8×=4cm,∴OG=BD﹣BF﹣OE=(175+15)﹣4﹣9=177cm,答:旋转头的固定点O与地面的距离约为177cm.3.解:(1)过点B作BH⊥MP,垂足为H,过点M作MI⊥FG,垂足为I,过点P作PK ⊥DE,垂足为K,∵MP=25.3cm,BA=HP=8.5cm,∴MH=MP﹣HP=25.3﹣8.5=16.8(cm),在Rt△BMH中,cos∠BMH===0.4,∴∠BMH=66.4°,∵AB∥MP,∴∠BMH+∠ABC=180°,∴∠ABC=180°﹣66.4°=113.6°;(2)∵∠BMN=68.6°,∠BMH=66.4°,∴∠NMI=180°﹣∠BMN﹣∠BMH=180°﹣68.6°﹣66.4°=45°,∵MN=28cm,∴cos45°==,∴MI≈19.80cm,∵KI=50cm,∴PK=KI﹣MI﹣MP=50﹣19.80﹣25.3=4.90≈4.9(cm),∴此时枪身端点A与小红额头的距离是在规定范围内.4.解:(1)过点A作AC⊥OB,垂足为点C,在Rt△ACO中,∵∠AOC=40°,AO=1.2米,∴AC=sin∠AOC•AO≈0.6428×1.2≈0.77米,∵汽车靠墙一侧OB与墙MN平行且距离为0.8米,∴车门不会碰到墙.(2)当靠墙一侧的车门能打开的最大角度时,AC=0.8米,∵sin∠AOC==≈0.67,∴∠AOC≈42°.答:靠墙一侧的车门能打开的最大角度约为42°.5.解:(1)①过点C作CG∥DE,过点A作AH⊥CG于H,过点C作CF⊥DE于点F,则点C到直线DE的距离为CF,在Rt△CDF中,∵sin∠CDE=,∴CF=CD•sin60°=70×=35(mm).②由图可知,点A到直线DE的距离为:AH+CF.∵∠DCB=70°,∴∠ACD=180°﹣∠DCB=110°,∵CG∥DE,∴∠GCD=∠CDE=60°.∴∠ACH=∠ACD﹣∠DCG=50°.在Rt△ACH中,∵sin∠ACH=,∴AH=AC•sin∠ACH=(115﹣35)×sin50°≈80×0.8=64(mm),∴点A到直线DE的距离为AH+CF=35+64=123.5≈124(mm).(2)如下图所示,虚线部分为旋转后的位置,B的对应点为B′,C的对应点为C′,则B′C′=BC=35mm,DC′=DC=70mm.在Rt△B′C′D中,∵tan∠B′DC′===0.5,tan26.6°≈0.5,∴∠B′DC′=26.6°.∴CD旋转的角度为∠CDC′=∠CDE﹣∠B′DC′=60°﹣26.6°=33.4°.故答案为:33.4°.三.解直角三角形的应用-坡度坡角问题6.解:因为sinθ=,所以l=.故选:B.7.解:如图.∵在Rt△ABC中,∠ACB=90°,tanα=,∴可设AC=4xm,那么BC=3xm,∴AB==5xm,∴A′B′=AB=5x(m).∵在Rt△A′B′C中,∠A′CB′=90°,A′C=(4x﹣1)m,B′C=(3x+1)m,∴(4x﹣1)2+(3x+1)2=(5x)2,解得x=1,∴A′C=3m,B′C=4m,A′B′=5m,∴cosβ=.故选:A.8.解:∵迎水坡AB的坡比为1:,∴=,即=,解得,AC=3,由勾股定理得,AB==6(m),故选:A.9.解:在Rt△ABC中,cos A=,则梯子底端到墙角的距离AC=AB•cos A=5cos40°,故选:A.10.解:如图,延长BC交AD于F,过F作FG⊥CD于G,∵斜坡CE的坡度为i(即tanα)=1:,∴α=30°.∵BF∥EM,∴∠FCD=∠E=30°.∵∠AFB=60°.∴∠CDF=∠AFB﹣∠FCD=30°.∴∠ECD=∠FDC=30°.∴FC=FD.∴CG=CD=.∴CF===5(米).∴BF=BC+CF=15+5=20(米).∴AB=BF•tan60°=20(米).答:建筑物AB的高度是20米.四.解直角三角形的应用-仰角俯角问题11.解:(1)作DG⊥AC于点G,由题意可得,∠1=32°,∠2=45°,∴∠CDG=32°,∠ADG=45°,∴∠ADG=∠DAG=45°,∴GD=GA,设CG=x米,则AG=BC﹣BA﹣CG=57.8﹣1.6﹣x=(56.2﹣x)米,则GD=(56.2﹣x)米,∵tan∠CGD=,∴tan32°=,解得x≈21.6,∴BG=BC﹣GC≈57.8﹣21.6=36.2(米),∴MN=BG=36.2米,答:旅游服务中心的高度约为36.2米;(2)造成误差的主要原因有系统误差和随机误差,比如误读、误算、视差、刻度误差等,避免或者减小差距可以通过多次测量,求平均值.12.解:过点PD作DE⊥AC交AC于点E,DF⊥AB交AB于点F,∵i=1:3,CD=10,设DE=xm,则CE=3xm,在Rt△CED中,x2+(3x)2=102,解得:x=或x=﹣(舍),∴DE=m,则CE=3m,∵∠BDF=∠DBF=45°,∴BF=DF,设BF=DF=m米,则AB=(m+)米,AC=(m﹣3)米,在Rt△CAB中,,解得:m≈29.9,∴AB=29.9+≈33.1(米),答:塑像的高度约为33.1米.13.解:(1)如图,延长CE交AB于点G,则四边形CDFE和四边形EFBG是矩形,根据题意可知:α=29°,β=60°.CD=EF=GB=1.6m,DF=20m,设FG=x,在Rt△AEG中,∵∠AEG=β=60°,∴∠EAG=30°,∴AG=x,在Rt△ACG中,∵tanα=,∴≈0.55,∴x≈9.3,∴AG≈9.3(m),∴AB=AG+GB=9.3+1.6=10.9(m),答:旗杆高度为10.9m;(2)原因:小明测量的只是测角器所在位置与旗杆底座正方体边缘的最短距离,不是测量测角器所在位置与底座中心的最短距离.14.解:设CD=xm,∵∠ACD=60°,∠BCD=45°,∴AD=x•tan60=x(m),DB=x•tan45°=x(m),∵∠AED=30°,DE=6m,∴AD=DE•tan30°=6×=2(m),∴x=2,解得x=2(m),∴AB=AD+DB=x+x=(2+2)m.答:雕像AB的高度为(2+2)m.15.解:由题意得,BD=50km,∠ADB=37°,DE=15km,∠AEC=56°,在Rt△ABD中,∵BD=50km,∠ADB=37°,∴AB=sin37°×BD≈×50=30(km),AD=cos37°×BD≈×50=40(km),∴AE=AD﹣DE=40﹣15=25(km),在Rt△AEC中,∠AEC=56°,∴AC=tan56°×AE≈×25=37(km),∴BC=AC﹣AB=37﹣20≈17(km),∴火箭的速度为17÷10≈1.7(km/s),答:运载火箭从B处到C处时的平均速度约为1.7km/s.五.解直角三角形的应用-仰角俯角问题16.解:(1)如图,延长EF交CD于点G.由题意知,四边形ABFE和四边形BCGF均为矩形.∴EF=AB=100m,BC=FG,AE=BF=CG=1m,设BC=FG=xm,则EG=(100+x)m.在Rt△DEG中,∵∠DEG=60°,∴DG=EG•tan60°=(100+x)≈1.73(100+x)m.在Rt△DFG中,∵∠DFG=72.3°,∴DG=FG•tan72.3°≈3.13x(m),∴1.73(100+x)=3.13x,解得x=123.57.∴CD=DG+CG≈3.13×123.57+1≈387.8(m).答:中原福塔CD的高度约为387.8m.(注:解法不同,答案会有误差,合理即可).(2)误差为388﹣387.8=0.2(m).减小误差可多次测量,去测量数据的平均值(答案不唯一,合理即可).六.解直角三角形的应用-方向角问题17.解:过点C作CD⊥AB交AB的延长线于D,由题意得,AB=40×=20,∠CAB=30°,∠CBD=60°,∴∠ACB=∠CBD﹣∠CAB=30°,∴∠ACB=∠CAB,∴CB=AB=20,在Rt△CBD中,sin∠CBD=,∴CD=BC•sin∠CBD=20×=10,∵10<18,∴这艘渔船继续向东追赶鱼群,有着弹危险.18.解:过点P作PD⊥AB于D点,由题意知,AB∥EF,∠ADP=∠BDP=90°,AP=80nmile,∴∠A=∠EP A=60°,∠B=∠BPF=37°,Rt△ADP中,∵sin A=,∴PD=AP•sin A=AP•sin60°=(nmile),Rt△BDP中,∵sin B=,∴(nmile),答:轮船所在B处与灯塔P的距离约为113nmile.19.解:(1)作BD⊥AC于D.依题意得,∠BAE=45°,∠ABC=105°,∠CAE=15°,∴∠BAC=30°,∴∠ACB=45°.在Rt△BCD中,∠BDC=90°,∠ACB=45°,∴∠CBD=45°,∴∠CBD=∠DCB,∴BD=CD,设BD=xkm,则CD=xkm,在Rt△ABD中,∠BAC=30°,∴AB=2BD=2xkm,tan30°=,∴=,∴AD=x,在Rt△BDC中,∠BDC=90°,∠DCB=45°,∴sin∠DCB==,∴BC=x,∵CD+AD=30+30,∴x+x=30+30,∴x=30,∴AB=2x=60(km);(2)第二组先到达目的地,理由:∵BD=30km,∴BC=x=30km,第一组用时:60÷40=1.5(h);第二组用时:30÷35=(h),∵<1.5,∴第二组先到达目的地,答:第二组先到达目的地.。
九年级数学下册28.2 解直角三角形同步练习4 新人教版 (含答案)

28.2解直角三角形专题一利用解直角三角形测河宽与山高1.如图,小丽想知道自家门前小河的宽度,于是她按以下办法测出了如下数据:小丽在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°;小丽沿河岸向前走30 m选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮助小丽计算小河的宽度.2.在一次暑假旅游中,小亮在仙岛湖的游船上(A处),测得湖西岸的山峰太婆尖(C处)和湖东岸的山峰老君岭(D处)的仰角都是45°,游船向东航行100米后(B处),测得太婆尖、老君岭的仰角分别为30°、60°.试问太婆尖、老君岭的高度为多少米?(3≈1.732,结果精确到1米)专题二利用解直角三角形测坝宽与坡面距离3.如图,一段河坝的横断面为梯形ABCD,试根据图中的数据,求出坝底宽AD.(i=CE:ED,单位:m)专题三利用解直角三角形解决太阳能问题4.某市规划局计划在一坡角为16°的斜坡AB上安装一球形雕塑,其横截面示意图如图所示.已知支架AC与斜坡AB的夹角为28°,支架BD⊥AB于点B,且AC、BD的延长线均过⊙O的圆心,AB=12 m,⊙O的半径为1.5 m,求雕塑最顶端到水平地面的垂直距离.(结果精确到0.01 m)(参考数据:cos28°≈0.9,sin62°≈0.9,sin44°≈0.7,cos46°≈0.7)【知识要点】1.解直角三角形的几种基本图形:图形1:tan30°=33=+a x x , ∠ABD =∠A ,BD =AD =a , tan60°=xx a + , x a x 333=+,2360sin =︒=a x , x a x +=3, 213+=x a . a x 23= . a a x 21313+=-= . 图形2:tan30°=33=-x a x , tan60°=3=-xa x , a a x 21313-=+=. a a x 233133-=+= .图形3:AC =CD =a +x , AC =BE =DE =x , ∠BAD =∠BDA =30°,tan30°=33=+a x x , tan60°=3=+x x a , AB =BD =a ,a a x 21313+=-= . a a x 21313+=-= . x =21BD =21a . 【温馨提示】1.解直角三角形的基本思想是“化斜为直”,在转化过程中,尽量保证已知度数的角的完整性.2.当一个三角形是钝角三角形,且其钝角的补角是30、45、60度时,常常从该钝角顶点向对边作垂线构造“双直角三角形”.【方法技巧】1.双直角三角形中,公共直角边是“桥梁”,通过它建立起两直角三角形的联系.2.如果条件中给出参考数据,结合原始数据,构造直角三角形.当计算过程中用到了参考数据,你的思路一定是正确的.参考答案1.解:示意图如下:连接AC ,B C ,过点C 作CE ⊥AD 于E .由题意得,∠ACB =∠CBE -∠CAD =60°-30°=30°, ∴∠CAD =∠ACB ,∴BC =AB =30.在Rt △BEC 中,CE =BC sin60°=30×23=153(m ). 答:小河的宽度为153m.2.解:设太婆尖高h 1米,老君岭高h 2米,依题意,有1122100tan 30tan 45100.tan 45tan 60h h h h ⎧-=⎪⎪⎨⎪-=⎪⎩,解得11)137h =≈(米),2h 50(3237=≈(米). 答:太婆尖的高度约为137米,老君岭的高度约为237米 .3.解:如图所示,过点B 作BF ⊥AD 于F ,可得矩形BCEF , ∴EF =BC =4,BF =CE =4.在Rt △ABF 中,∠AFB =90°,AB =5,BF =4,由勾股定理可得3AF ==.∵Rt △CED 中,12CE i ED ==, ∴ED =2CE =2×4=8.∴AD =AF +FE +ED =3+4+8=15(m).4.解:过点O 作水平地面的垂线,垂足为E . 在Rt△AOB 中,cos∠OAB =OA AB,即cos28°=OA 12,∴OA =121213.333cos 280.9≈≈︒.∵∠BAE =16°,∴∠OAE =28°+16°=44°.在Rt△AOE 中,sin∠OAE =OA OE,即s in44°333.13OE≈, ∴OE 333.97.0333.13≈⨯≈,9.333+1.5≈10.83(m).∴雕塑最顶端到水平地面的垂直距离约为10.83 m .。
人教版九年级数学下册28.2 解直角三角形 同步练习3 含答案

28.2解直角三角形(3)一、选择题1. 一个人从山下沿30°角的坡路登上山顶,共走了500m,那么这山的高度是[ ]m.A.230B.240C.250D.2602. 一个人从A点出发向北偏东60°方向走了一段距离到达B点,再从B点出发向南偏东15°方向走了一段距离到C点,则∠ABC的度数为 [ ]A.15°B.75°C.105°D.45°3. 为了求河对岸建筑物AB的高,在地平面上测得基线CD=180米,在C点测得A点的仰角为30°,在地平面上测得∠BCD=∠BDC=45°,那么AB的高是[ ]米.4. 如图,一船向正北航行,看见正东有两个相距10海里的灯塔,船航行半小时后,一个灯塔在船的东南,另一个灯塔在船的东22°30′南,则船的速度(精确到0.1米)是[ ]米/时(tg22°30′=0.4142)A.12.1B.13.1C.14.1D.15.15. 一只船向正东航行,上午7时在灯塔A的正北C处,上午9时到达塔的北偏东60°B处,已知船的速度为每小时20千米,那么AB的距离是[ ]千米.6. 如图:B处有一船,向东航行,上午9时在灯塔A的西南58.4千米的B上午11时到达灯塔的南C处,那么这船航行的速度是[ ]千米/时.A.19.65B.20.65C.21.65D.22.657. 如图:一只船以每小时20千米的速度向正东航行,起初船在A处看见一灯塔B在船的北偏东60°,2小时后,船在C处看见这个灯塔在船的北偏东45°,则灯塔B到船的航海线AC的距离是 [ ]千米.二、填空题一只船向东航行,上午9点到一座灯塔的西南68海里处,上午11点到达这座灯塔的正南,这只船航行的速度是_____________.(答案可带根号)三、解答题1. 如图:已知一船以每小时20海里的速度向正南行驶,上午10时在A 处见灯塔P 在正东,1小时后行至B 处,观察灯塔P 的方向是北60°东.求正午12时船行驶至C 处距灯塔P 的距离.(答案可带根号)2.如图:东西方向的海岸线上有A 、B 两码头,相距100 )13(-千米,由码头A 测得海上船K 在北偏东30°,由码头B 测得船K 在北偏西15°,求船K 距海岸线AB 的距离(已知tan75°=32+-)参考答案一、选择题1. C2. B3. C4. C5. D6. B7. C二、填空题时海里/217三、解答题1.米7202.350千米。
【九年级】九年级数学下28.2解直角三角形及其应用(二)同步练习(人教版附答

【九年级】九年级数学下28.2解直角三角形及其应用(二)同步练习(人教版附答28.2解直角三角形及其应用同步练习(二)一、单选题(本大题共15个子题,每个子题得3分,共计45分)一、一人乘雪撬沿坡度为的斜坡滑下距离(米)与时间(秒)之间的关系为.若滑动时间为秒,则他下降的垂直高度为().a、仪表b.米c、仪表d.米2.如图所示,有人站在楼顶观察对面的直旗杆。
已知观测点到旗杆的距离(长度),测量旗杆顶部的仰角,测量旗杆底部的俯角,则旗杆高度为()a.(b(c.(d(3、如图,在处测得旗杆的顶端的仰角为,向旗杆前进米到达处,在处测得的仰角为,则旗杆的高为()米A.b.Cd.4.在中学升国旗时,同学a站在旗杆底部以引起注意。
当国旗升到旗杆顶端时,同学视线的仰角为。
如果他的眼睛离开地面,旗杆的高度是()a.米b、仪表c.米d、仪表5、如图,一渔船在海岛南偏东方向的处遇险,测得海岛与的距离为海里,渔船将遇险情况报告给位于处的救援船后,沿北偏西方向向海岛靠近,同时,从处出发的救援船沿南偏西方向匀速航行,分钟后,救援船在海岛处恰好追上渔船,那么救援船航行的速度为()海里/小时.A.b.Cd.6.如图所示,为了测量一棵树垂直于地面的高度,在距树底m处测量的树顶仰角为,则树高为()a.米b、仪表c.米d、仪表7、如图,一艘海轮位于灯塔的北偏东方向,距离灯塔海里的点处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离长是()a、大海b.海里c、大海d.海里8.如图所示,该船沿正南方向以每小时海里的匀速航行。
据观察,灯塔位于该地点的西偏南方向。
航行数小时后,它到达了北。
据观察,灯塔的方向是西偏南。
如果船继续向南航行到离灯塔最近的位置,船与灯塔之间的距离约为(通过科学计算器,,)获得)9、小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为米,坡面上的影长为米.已知斜坡的坡角为,同一时刻,一根长为米、垂直于地面放置的标杆在地面上的影长为米,则树的高度为()a、仪表b.米c、仪表d.米10.为了如图所示测量上坡坡道的坡度,小明测量了如图所示的数据,则坡度角的正切值为()a.Bc.D11、如图,长的楼梯的倾斜角为,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角为,则调整后的楼梯的长为()12.如图所示,在,,,中,点是边的中点。
人教版九年级数学下册28.2解直角三角形同步练习4含答案

28.2 解直角三角形(4)1、测得某坡面垂直高度为2m,水平宽度为4m,则坡度为[]2、在 Rt △ ABC中,∠ C=90°,∠ A=30 °, b=103 ,则a=,c=;3、已知在直角梯形ABCD中,上底CD=4,下底AB=10,非直角腰BC=4 3 ,则底角∠B=;4.如图:铁路的路基的横截面是等腰梯形,斜坡AB的坡度为1∶ 3 ,BE为3 3 米,基面 AD宽 2 米,求路基的高AE,基底的宽BEC及坡角 B 的度数 . (答案可带根号)5.水坝横断面为等腰梯形,尺寸如图,(单位:米)坡度I=AE=1,求坡面倾斜角(坡DE角),并计算修筑长1000 米的水坝约需要多少土方?6.如图,上午 9 时,一条船从A处出发,以 20 节的速度向正北航行, 11 时抵达B处,从A,B望灯塔 C,测得∠ NAC=36°,∠ NBC=72°,那么从 B 处到灯塔 C的距离是多少海里?7.如图,王聪同学拿一把∠ACB=30°的小型直角三角尺ABC目测河流在市里河段的宽度.他先在岸边的点 A 顺着30°角的邻边AC的方向确立河对岸岸边的一棵树M.而后,沿30°角的对边 AB 的方向行进到点 B′,顺着斜边B C的方向看见 M,并测得AB=100 m,那么他目测的宽大概为多少? ( 结果精准到 1m)8.海中有一个小岛A,它的四周8 海里内有暗礁,渔船追踪鱼群由西向东航行,在 B 点测得小岛 A 在北偏东60°,航行12 海里抵达D点,这时测得小岛 A 在北偏东30°.假如渔船不改变航向,持续向东捕捞,有没有触礁的危险?思虑· 探究·沟通1.如图,MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东 60°的方向上有一点A,以 A 为圆心、500 m为半径的圆形地区为居民区.取MN上另一点 B,测得 BA的方向为南偏东75°.已知 MB=400 m,经过计算回答,假如不改变方向,输水道线能否会穿过居民区?答案: 1、 D 2 、 10, 20 3、30°AE14.解:∵3 33∴AE=3(米)BC=( 2+63 )(米)∠B=30°5. 45 ° ,444000 土方6. 40 海里.7.河宽约173 m .8.渔船没有触礁的危险.思虑·探究·沟通答案:1.输水道线不会穿过居民区.提示:过点 A 作 MN的垂线,垂足为C,求 AC.。
人教版九年级数学下册28.2: 解直角三角形及其应 用同步练习(附答案)
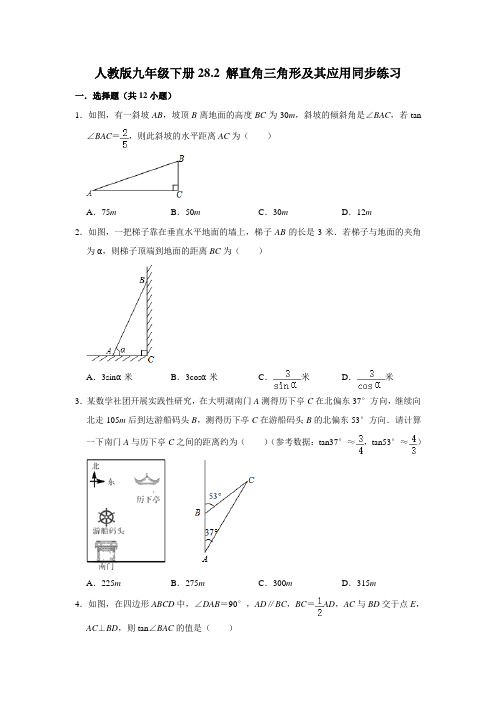
人教版九年级下册28.2 解直角三角形及其应用同步练习一.选择题(共12小题)1.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若tan ∠BAC=,则此斜坡的水平距离AC为()A.75m B.50m C.30m D.12m2.如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米.若梯子与地面的夹角为α,则梯子顶端到地面的距离BC为()A.3sinα米B.3cosα米C.米D.米3.某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为()(参考数据:tan37°≈,tan53°≈)A.225m B.275m C.300m D.315m4.如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是()A.B.C.D.5.如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A处看乙楼楼顶B处仰角为30°,则甲楼高度为()A.11米B.(36﹣15)米C.15米D.(36﹣10)米6.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是()A.10B.8C.4D.27.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为()A.B.C.D.8.小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高AB为1.5米,她先站在A处看路灯顶端O的仰角为35°,再往前走3米站在C处,看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为(已知sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)()A.3.2米B.3.9米C.4.7米D.5.4米9.如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60nmile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是()A.30nmile B.60nmileC.120nmile D.(30+30)nmile10.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为()A.米B.米C.米D.米11.如图,在△ABC中,CA=CB=4,cos C=,则sin B的值为()A.B.C.D.12.如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1:2.4,那么建筑物AB的高度约为()(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)A.65.8米B.71.8米C.73.8米D.119.8米二.填空题(共7小题)13.如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则CD的长为米.(结果保留根号)14.如图,河的两岸a,b互相平行,点A,B,C是河岸b上的三点,点P是河岸a上的一个建筑物,某人在河岸b上的A处测得∠P AB=30°,在B处测得∠PBC=75°,若AB =80米,则河两岸之间的距离约为米.(≈1.73,结果精确到0.1米)15.某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车(填“超速”或“没有超速”)(参考数据:≈1.732)16.如图,建筑物C上有一杆AB.从与BC相距10m的D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则旗杆AB的高度约为m(结果取整数,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33).17.如图,无人机于空中A处测得某建筑顶部B处的仰角为45°,测得该建筑底部C处的俯角为17°.若无人机的飞行高度AD为62m,则该建筑的高度BC为m.(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)18.如图,某校教学楼AC与实验楼BD的水平间距CD=15米,在实验楼顶部B点测得教学楼顶部A点的仰角是30°,底部C点的俯角是45°,则教学楼AC的高度是米(结果保留根号).19.如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB约为米.(精确到1米,参考数据:≈1.414,≈1.732)三.解答题(共3小题)20.小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为60°,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为30°.已知山坡坡度i=3:4,即tanθ=,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据:≈1.732)21.如图,学校教学楼上悬挂一块长为3m的标语牌,即CD=3m.数学活动课上,小明和小红要测量标语牌的底部点D到地面的距离.测角仪支架高AE=BF=1.2m,小明在E 处测得标语牌底部点D的仰角为31°,小红在F处测得标语牌顶部点C的仰角为45°,AB=5m,依据他们测量的数据能否求出标语牌底部点D到地面的距离DH的长?若能,请计算;若不能,请说明理由(图中点A,B,C,D,E,F,H在同一平面内)(参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)22.如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上,求旗杆AB的高度.(结果精确到0.1m,参考数据:≈1.41,=1.73)参考答案一.选择题(共12小题)1.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若tan ∠BAC=,则此斜坡的水平距离AC为()A.75m B.50m C.30m D.12m【解答】解:∵∠BCA=90°,tan∠BAC=,BC=30m,∴tan∠BAC=,解得,AC=75,故选:A.2.如图,一把梯子靠在垂直水平地面的墙上,梯子AB的长是3米.若梯子与地面的夹角为α,则梯子顶端到地面的距离BC为()A.3sinα米B.3cosα米C.米D.米【解答】解:由题意可得:sinα==,故BC=3sinα(m).故选:A.3.某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为()(参考数据:tan37°≈,tan53°≈)A.225m B.275m C.300m D.315m【解答】解:如图,作CE⊥BA于E.设EC=xm,BE=ym.在Rt△ECB中,tan53°=,即=,在Rt△AEC中,tan37°=,即=,解得x=180,y=135,∴AC===300(m),故选:C.4.如图,在四边形ABCD中,∠DAB=90°,AD∥BC,BC=AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是()A.B.C.D.【解答】解:∵AD∥BC,∠DAB=90°,∴∠ABC=180°﹣∠DAB=90°,∠BAC+∠EAD=90°,∵AC⊥BD,∴∠AED=90°,∴∠ADB+∠EAD=90°,∴∠BAC=∠ADB,∴△ABC∽△DAB,∴=,∵BC=AD,∴AD=2BC,∴AB2=BC×AD=BC×2BC=2BC2,∴AB=BC,在Rt△ABC中,tan∠BAC===;故选:C.5.如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A处看乙楼楼顶B处仰角为30°,则甲楼高度为()A.11米B.(36﹣15)米C.15米D.(36﹣10)米【解答】解:过点A作AE⊥BD,交BD于点E,在Rt△ABE中,AE=30米,∠BAE=30°,∴BE=30×tan30°=10(米),∴AC=ED=BD﹣BE=(36﹣10)(米).∴甲楼高为(36﹣10)米.故选:D.6.如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是()A.10B.8C.4D.2【解答】解:∵∠C=90°,cos∠BDC=,设CD=5x,BD=7x,∴BC=2x,∵AB的垂直平分线EF交AC于点D,∴AD=BD=7x,∴AC=12x,∵AC=12,∴x=1,∴BC=2;故选:D.7.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为()A.B.C.D.【解答】解:如图,过C作CD⊥AB于D,则∠ADC=90°,∴AC===5.∴sin∠BAC==.故选:D.8.小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高AB为1.5米,她先站在A处看路灯顶端O的仰角为35°,再往前走3米站在C处,看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为(已知sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1)()A.3.2米B.3.9米C.4.7米D.5.4米【解答】解:过点O作OE⊥AC于点F,延长BD交OE于点F,设DF=x,∵tan65°=,∴OF=x tan65°,∴BF=3+x,∵tan35°=,∴OF=(3+x)tan35°,∴2.1x=0.7(3+x),∴x=1.5,∴OF=1.5×2.1=3.15,∴OE=3.15+1.5=4.65,故选:C.9.如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60nmile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是()A.30nmile B.60nmileC.120nmile D.(30+30)nmile【解答】解:过C作CD⊥AB于D点,∴∠ACD=30°,∠BCD=45°,AC=60.在Rt△ACD中,cos∠ACD=,∴CD=AC•cos∠ACD=60×=30.在Rt△DCB中,∵∠BCD=∠B=45°,∴CD=BD=30,∴AB=AD+BD=30+30.答:此时轮船所在的B处与灯塔P的距离是(30+30)nmile.故选:D.10.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为()A.米B.米C.米D.米【解答】解:作AD⊥BC于点D,则BD=0.3=,∵cosα=,∴cosα=,解得,AB=米,故选:B.11.如图,在△ABC中,CA=CB=4,cos C=,则sin B的值为()A.B.C.D.【解答】解:过点A作AD⊥BC,垂足为D,如图所示.在Rt△ACD中,CD=CA•cos C=1,∴AD==;在Rt△ABD中,BD=CB﹣CD=3,AD=,∴AB==2,∴sin B==.故选:D.12.如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1:2.4,那么建筑物AB的高度约为()(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)A.65.8米B.71.8米C.73.8米D.119.8米【解答】解:过点E作EM⊥AB与点M,延长ED交BC于G,∵斜坡CD的坡度(或坡比)i=1:2.4,BC=CD=52米,∴设DG=x,则CG=2.4x.在Rt△CDG中,∵DG2+CG2=DC2,即x2+(2.4x)2=522,解得x=20,∴DG=20米,CG=48米,∴EG=20+0.8=20.8米,BG=52+48=100米.∵EM⊥AB,AB⊥BG,EG⊥BG,∴四边形EGBM是矩形,∴EM=BG=100米,BM=EG=20.8米.在Rt△AEM中,∵∠AEM=27°,∴AM=EM•tan27°≈100×0.51=51米,∴AB=AM+BM=51+20.8=71.8米.故选:B.二.填空题(共7小题)13.如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则CD的长为4﹣4米.(结果保留根号)【解答】解:在Rt△CMB中,∵∠CMB=90°,MB=AM+AB=12米,∠MBC=30°,∴CM=MB•tan30°=12×=4,在Rt△ADM中,∵∠AMD=90°,∠MAD=45°,∴∠MAD=∠MDA=45°,∴MD=AM=4米,∴CD=CM﹣DM=(4﹣4)米,故答案为:4﹣4.14.如图,河的两岸a,b互相平行,点A,B,C是河岸b上的三点,点P是河岸a上的一个建筑物,某人在河岸b上的A处测得∠P AB=30°,在B处测得∠PBC=75°,若AB =80米,则河两岸之间的距离约为54.6米.(≈1.73,结果精确到0.1米)【解答】解:过点A作AE⊥a于点E,过点B作BD⊥P A于点D,∵∠PBC=75°,∠P AB=30°,∴∠DPB=45°,∵AB=80,∴BD=40,AD=40,∴PD=DB=40,∴AP=AD+PD=40+40,∵a∥b,∴∠EP A=∠P AB=30°,∴AE=AP=20+20≈54.6,故答案为:54.615.某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车没有超速(填“超速”或“没有超速”)(参考数据:≈1.732)【解答】解:作AD⊥直线l于D,在Rt△ADB中,∠ABD=45°,∴BD=AD=100,在Rt△ADB中,tan∠ACD=,则CD==100≈173.2,∴BC=173.2﹣100=73.2(米),小汽车的速度为:0.0732÷=52.704(千米/小时),∵52.704千米/小时<速60千米/小时,∴小汽车没有超速,故答案为:没有超速.16.如图,建筑物C上有一杆AB.从与BC相距10m的D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则旗杆AB的高度约为3m(结果取整数,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33).【解答】解:在Rt△BCD中,tan∠BDC=,则BC=CD•tan∠BDC=10,在Rt△ACD中,tan∠ADC=,则AC=CD•tan∠ADC≈10×1.33=13.3,∴AB=AC﹣BC=3.3≈3(m),故答案为:3.17.如图,无人机于空中A处测得某建筑顶部B处的仰角为45°,测得该建筑底部C处的俯角为17°.若无人机的飞行高度AD为62m,则该建筑的高度BC为262m.(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)【解答】解:作AE⊥BC于E,则四边形ADCE为矩形,∴EC=AD=62,在Rt△AEC中,tan∠EAC=,则AE=≈=200,在Rt△AEB中,∠BAE=45°,∴BE=AE=200,∴BC=200+62=262(m),则该建筑的高度BC为262m,故答案为:262.18.如图,某校教学楼AC与实验楼BD的水平间距CD=15米,在实验楼顶部B点测得教学楼顶部A点的仰角是30°,底部C点的俯角是45°,则教学楼AC的高度是(15+15)米(结果保留根号).【解答】解:过点B作BE⊥AB于点E,在Rt△BEC中,∠CBE=45°,BE=15;可得CE=BE×tan45°=15米.在Rt△ABE中,∠ABE=30°,BE=15,可得AE=BE×tan30°=15米.故教学楼AC的高度是AC=15米.答:教学楼AC的高度是(15)米.19.如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB约为566米.(精确到1米,参考数据:≈1.414,≈1.732)【解答】解:如图,设线段AB交y轴于C,在直角△OAC中,∠ACO=∠CAO=45°,则AC=OC.∵OA=400米,∴OC=OA•cos45°=400×=200(米).∵在直角△OBC中,∠COB=60°,OC=200米,∴OB===400≈566(米)故答案是:566.三.解答题(共3小题)20.小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为60°,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为30°.已知山坡坡度i=3:4,即tanθ=,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据:≈1.732)【解答】解:作DC⊥EP交EP的延长线于C,作DF⊥ME于F,作PH⊥DF于H,则DC=PH=FE,DH=CP,HF=PE,设DC=3x,∵tanθ=,∴CP=4x,由勾股定理得,PD2=DC2+CP2,即252=(3x)2+(4x)2,解得,x=5,则DC=3x=15,CP=4x=20,∴DH=CP=20,PH=FE=DC=15,设MF=ym,则ME=(y+15)m,在Rt△MDF中,tan∠MDF=,则DF==y,在Rt△MPE中,tan∠MPE=,则PE==(y+15),∵DH=DF﹣HF,∴y﹣(y+15)=20,解得,y=7.5+10,∴ME=MF+FE=7.5+10+15≈39.8,答:古塔的高度ME约为39.8m.21.如图,学校教学楼上悬挂一块长为3m的标语牌,即CD=3m.数学活动课上,小明和小红要测量标语牌的底部点D到地面的距离.测角仪支架高AE=BF=1.2m,小明在E 处测得标语牌底部点D的仰角为31°,小红在F处测得标语牌顶部点C的仰角为45°,AB=5m,依据他们测量的数据能否求出标语牌底部点D到地面的距离DH的长?若能,请计算;若不能,请说明理由(图中点A,B,C,D,E,F,H在同一平面内)(参考数据:tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)【解答】解:能,理由如下:延长EF交CH于N,则∠CNF=90°,∵∠CFN=45°,∴CN=NF,设DN=xm,则NF=CN=(x+3)m,∴EN=5+(x+3)=x+8,在Rt△DEN中,tan∠DEN=,则DN=EN•tan∠DEN,∴x≈0.6(x+8),解得,x=12,则DH=DN+NH=12+1.2=13.2(m),答:点D到地面的距离DH的长约为13.2m.22.如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上,求旗杆AB的高度.(结果精确到0.1m,参考数据:≈1.41,=1.73)【解答】解:过点C作CE⊥AB于点E,∵CD=2,tan∠CMD=,∴MD=6,设BM=x,∴BD=x+6,∵∠AMB=60°,∴∠BAM=30°,∴AB=x,已知四边形CDBE是矩形,∴BE=CD=2,CE=BD=x+6,∴AE=x﹣2,在Rt△ACE中,∵tan30°=,∴=,解得:x=3+,∴AB=x=3+3≈8.2m。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
28.2解直角三角形(第一课时)精练题1.某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于 60°,否则就有危险,那么梯子的长至少为( ) A .8米B .83米C .83米 D .43米 分析:本题考查的是利用解直角三角形的有关知识解决实际问题。
它可以归结为: 在Rt ΔABC 中,已知∠A=60°,CB=4,求斜边AB 的长。
由ABBCA =sin 得:33860sin 4sin ===︒A BC AB 正确答案:C2、如图,自动扶梯AB 段的长度为20米,倾斜角A 为α,高度BC 为 米(结果用含α的三角比表示).分析:本题考查的是利用解直角三角形的有关知识解决实际问题,本题可以归结为在Rt ΔABC 中,已知∠A=α°,AB=20,求对边BC 的长由ABBC=αsin 得:ααsin 20sin ==AB BC 正确答案:αsin 203、如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:(1) 未开始收绳子的时候,图中绳子BC 的长度是多少米? (2) 收绳8秒后船向岸边移动了多少米?(结果保留根号) 思路分析:第一小题考查的内容是:在直角三角形的中, 已知锐角及对边,求斜边的问题。
在Rt ΔCAB,,BCACCBA =∠sin ∴10sin =∠=ABC AC BC 。
第二小题考查的勾股定理的应用:收绳8秒后,BC=6,AC=5,∴11562222=-=-=AC BC AB正确答案:解(1)如图,在Rt △ABC 中,BCAC=sin30° ∴ BC =︒sin305=10米(2)收绳8秒后,绳子BC 缩短了4米,只有6米,αACB第2题图这时,船到河岸的距离为1125365622=-=-米.4、如图,有一段斜坡BC 长为10米,坡角12CBD ︒∠=,为方便残疾人的轮椅车通行,现准备把坡角降为5°.(1)求坡高CD ;(2)求斜坡新起点A 与原起点B 的距离(精确到0.1米).分析:本题考查的是解直角三角形在实际生活中的具体应用。
在Rt ΔCDB 中,∠D=90°,BC=10米,利用BCCDCBD =∠sin ,得:︒=12sin BC CD 1.221.010=⨯≈米,当坡角 降为5°时,在Rt ΔCDA 中,AD CD CAD =∠tan ,可以求得:︒=5tan CD AD 2.123.330.09≈≈故:23.339.813.5313.5AB AD BD =-≈-=≈正确答案:(1)在BCD Rt ∆中,︒=12sin BC CD 1.221.010=⨯≈(米). (2)在BCD Rt ∆中,︒=12cos BC BD8.998.010=⨯≈(米); 在ACD Rt ∆中,︒=5tan CD AD 2.123.330.09≈≈(米), 23.339.813.5313.5AB AD BD =-≈-=≈(米). 答:坡高2.1米,斜坡新起点与原起点的距离为13.5米28.2解直角三角形(第二课时)精练题1如图所示,小华同学在距离某建筑物6米的点A 处测得︒=∠︒=∠35,52CAD BAD ,则广告牌的高度BC 为_____________米(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)思路分析:本题考查的知识是利用解直角三角形的知识解决生活中 的实际问题。
结合图形,知:BC=BD-CD 。
而在ACD Rt ∆中ADCDCAD =∠tan ,∴︒⨯=∠=35tan 6tan CAD AD CD ≈4.2 同理,在BAD Rt ∆中,BD ≈7.68 ∴BC ≈3.5 米 正确答案: 3.52、如图所示,一棵大树在一次强烈的地震中于C 处折断倒下,树顶落在地面B 处,测得B(第4题)DCBA51处与树的底端A 相距25米,∠ABC=24°. (1)求大树折断倒下部分BC 的长度;(精确到1米) (2)问大树在折断之前高多少米?(精确到1米)思路分析:本题可以化归为在直角三角形中,已知一锐角及邻边,求对边及斜边的问题。
由锐角三角函数的概念知:已知一锐角及邻边,求对边可以用正切,求斜边,即可以利用勾股定理,也可以用该锐角的余弦。
答案:解:如图,在Rt △ABC 中,∠CAB=90°,∠ABC=24°,AB=25米(1)∵cos ∠ABC=BCAB∴BC=ABC AB ∠cos =024cos 25≈27(米) 即大树折断倒下部分BC 的长度约为27米. (2)∵tan ∠ABC=ABAC∴AC=AB·tan ∠ABC=25·tan24°≈11.1(米) ∴BC+AC≈27+11.1≈38(米)即大树折断之前高约为38米.3、如图,两条笔直的公路AB 、CD 相交于点O ,∠AOC 为36°.指挥中心M 设在OA 路段上,与O 地的距离为18千米.一次行动中,王警官带队从O 地出发,沿OC 方向行进.王警官与指挥中心均配有对讲机,两部对讲机只能在10千米之内进行通话.通过计算判断王警官在行进过程中能否实现与指挥中心用对讲机通话.【参考数据:sin36°=0.59,cos36°=0.81,tan36°=0.73.】分析:要判断王警官在行进过程中能否实现与指挥中心用对讲机通话,只须计算出点M 到DC 的最近距离,因此,我们可以将这个问题转化为在直角三角形中,已知一锐角及斜边求对边问题来解决。
正确答案:过M 点作ME ⊥DC 于E 点 在Rt ΔOME 中,sin ∠MOE=OMME,ME=OMsin ∠MOE= 10.62 Θ ME=10.62>10 ∴不能通话 4、在一次课外实践活动中,同学们要测量某公园人工湖两侧A B ,两个凉亭之间的距离. (图1)现测得30AC =m ,70BC =m ,120CAB ∠=°,请计算A B ,两个凉亭之间的距离.思路分析:由已知的条件可以看出,ABC ∆不是特殊的三角形,因此要测出两凉亭之间的距离,必须将它转化为在直角三角形中求解,因此,我们可以通过添加如图所示的辅助线, 这样,AB=BD- AD ,而线段BD 和AD 的长就可以利用解直角三角形的有关知识来解决。
答案:解:如图,过C 点作CD 垂直于AB 交BA 的延长线于点D在Rt CDA △中,3018018012060AC CAD CAB =∠=-∠=︒-︒=︒,°CD AC ∴=·sin 30CAD ∠=·sin 60=°AD AC =·cos 30CAD ∠=·cos 60°=15. 又在Rt CDB △中,22270BC BD BC CD ==Q ,-,65BD ∴==.651550AB BD AD ∴=-=-=, 答:A B ,两个凉亭之间的距离为50m.28.2解直角三角形(第三课时)精练题1、王师傅在楼顶上的点A 处测得楼前一棵树CD 的顶端C 的俯角为60 o, 又知水平距离BD=10m ,楼高AB=24 m ,则树高CD 为( )A .mB.mC.m D.9m分析:解直角三角形在实际生活中的应用,是中考考查的重点,也是考查的热点,解决这种类型题目的关键是:(1)转化实际问题为数学问题(2)重点画出符合题意的几何图形(3)找出题目中每句话对应的是图中的哪个角,哪条边(包括已知的所求的),(4)做辅助线进而利用解直角三角形的正切函数知识解决问题。
此题CD=24-10tan60°=m 正确答案:A2、一根电线杆的接线柱部分AB 在阳光下的投影CD 的长为1米,太阳光线与地面的夹角60ACD ∠=°,则AB 的长为( )A .12米 BCD分析:此题是上一个题的延伸,在考查上述知识外,对题目的内涵进一步的挖掘,即太阳光线处处平行,由此可将CD 平移至AB 所在的直角三角形中, 再利用特殊角的正切即可算出AB=tan60°=米。
答案选B.3、如图,线段AB DC 、分别表示甲.乙两建筑物的高,AB BC DC BC ⊥,⊥,从B 点测得D 点的仰角α为60°从A 点测得D 点的仰角β为30°,已知甲建筑物高36AB =米. (1)求乙建筑物的高DC ;(2)求甲.乙两建筑物之间的距离BC (结果精确到0.01米).1.414 1.732)分析:此题是考查三角函数在实际生活中测物高的应用,在已有的草图中,涉及到仰角的有αβD乙CBA 甲关概念,做AE ⊥CD 于E ,进一步数形结合,此题不能只解一个直角三角形,而是对其所求的量进行分解,先在Rt AED ∆中用DE=x 和仰角正切值表示出AE ,再把此部分量归结在RT DCB ∆中,再用60°的仰角的正切的概念列出方程,并解方程,最后对其计算出来的结果按要求取近似值.正确答案:(1)过点A 作AE ⊥CD 于E ,根据题意,得60,30,DBC DAE αβ∠=∠=︒∠=∠=︒AE=BC ,EC=AB=36米,设DE=x ,则DC=DE+EC=X+36, 在RT AED ∆,tan tan 30DEDAE AE∠=︒=, ∴3AE x =,∴3BC AE x == 在RT DCB ∆中,tan tan 60DCDBC BC ∠=︒= , ∴33x=, ∴336,18,x x x =+= ∴DC=54(米) (2).∵3,18BC AE x x ===,∴31818 1.73231.18BC =⨯=⨯≈(米)4、铁岭某旅游区有一个景观奇异的望天洞,D 点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A 处观看旅游区风景,最后坐缆车沿索道AB 返回山脚下的B 处.在同一平面内,若测得斜坡BD 的长为100米,坡角10DBC ∠=°,在B 处测得A 的仰角40ABC ∠=°,在D 处测得A 的仰角85ADF ∠=°,过D 点作地面BE 的垂线,垂足为C .(1)求ADB ∠的度数;(2)求索道AB 的长.(结果保留根号)分析:正确理解仰角,坡角的概念是解决问题的关键,用数形结合的方法,尝试通过添加辅助线,构造直角三角形,恰当地选择锐角三角函数表示出边角关系并最终解决实际问题。
