切比雪夫I型数字带通滤波器要点
切比雪夫Ⅰ型滤波器和切比雪夫Ⅱ型滤波器的对比
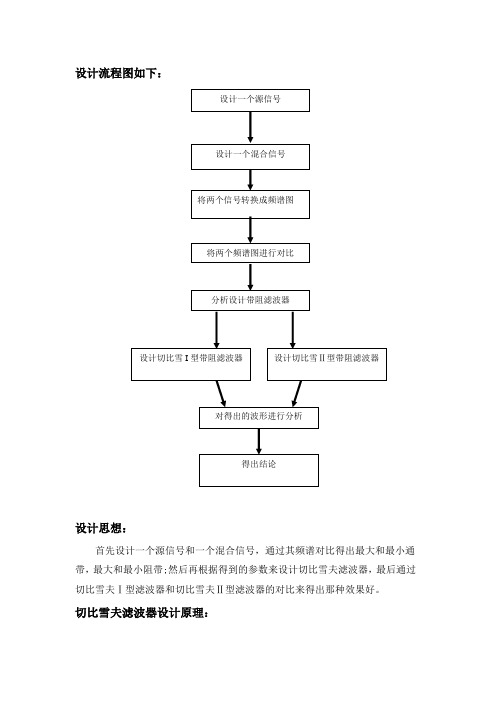
设计流程图如下:设计思想:首先设计一个源信号和一个混合信号,通过其频谱对比得出最大和最小通带,最大和最小阻带;然后再根据得到的参数来设计切比雪夫滤波器,最后通过切比雪夫Ⅰ型滤波器和切比雪夫Ⅱ型滤波器的对比来得出那种效果好。
切比雪夫滤波器设计原理:切比雪夫滤波器的振幅具有等波纹特性,它有两种形式:1)振幅特性在通带内是等波纹的、在阻带内是单调的切比雪夫I 型滤波器;2)振幅特性在通带内是单调的、在阻带内是等波纹的切比雪夫II型滤波器,采用何种形式的切比雪夫滤波器取决于实际用途.切比雪夫滤波器的设计方法就是将逼近精确度均匀分布在整个通带内,或者均匀分布在整个阻带内,或者均匀分布在两者之内,这样就可以使滤波器阶数大大降低。
切比雪夫I型滤波器平方幅度响应函数表示为:2)(ΩjG=[1+2εC2N(Ω)]2/1-其中ε<1(正数),它与通带波纹有关,ε越大,波纹也越大;CN(Ω) 是切比雪夫多项式,它被定义为:CN (Ω)=cos(Narccos(Ω)),Ω≤1, CN(Ω)=cosh(Narcosh(Ω)),Ω>1. 而切比雪夫II型滤波器平方幅度响应函数表示为:)(ΩjG2={1+2ε{ C2N(Ω)/[2N(Ω/cΩ)]2}}1-其中ε<1(正数),表示波纹变化情况;cΩ为截止频率;N为滤波器的阶次,也是CN (NΩΩ/)的阶次。
源信号编码及其图形:t=-1:0.01:1y=(cos(2*pi*10*t)+cos(2*pi*40*t)); N=length(y);fx=fft(y);df=100/N;n=0:N/2;f=n*df;subplot(2,1,1);plot(f,abs(fx(n+1))*2/N); grid;title('源波形频谱')图(一)混合信号编码及其图形:t=-1:0.01:1;X=(cos(2*pi*10*t)+cos(2*pi*25*t)+cos(2*pi*40*t));N=length(X);fx=fft(X);df=100/N;n=0:N/2;f=n*df;subplot(2,1,2);plot(f,abs(fx(n+1))*2/N); grid;title('混合波形频谱')图(二)从图(一)和图(二)对比可以得出:为了能达到和满足我们的要求,我们取以下的参数,最大通带wp2:0.5,最小通带wp1:0.05,最大阻带w s2:0.3,最小阻带ws1:0.1。
切比雪夫1型数字滤波器的设计及滤波过程

切比雪夫1型数字滤波器的设计及滤波过程切比雪夫1型低通模拟滤波器的幅度平方函数为:)(11)(2222|)(|ΩΩΩ+==ΩpNCj H Aa ε其中ε表示通带内幅度波动的程度,ε越大,波动幅度也越大。
1101.0-=Apε)(x CN称为N 阶切比雪夫多项式。
1、滤波器设计及结果如下IIR-DF 滤波器设计(切比雪夫1型)(1) 切比雪夫1型低通数字滤波器的损耗函数曲线、滤波分离出的DSB 信号的时域波形及其频谱如下:0.10.20.30.40.50.60.70.80.91-100-90-80-70-60-50-40-30-20-100w/π幅度/d B切比雪夫1型模拟低通滤波器的幅频响应曲线00.010.020.030.040.050.060.070.08-1-0.500.51t/sy 1(t )y1(t)的时域波形f/Hz幅度y1(t)的频谱其中阶数N=7(2) 切比雪夫1型带通数字滤波器的损耗函数曲线、滤波分离出的DSB 信号的时域波形及其频谱如下:0.10.20.30.40.50.60.70.80.91-100-90-80-70-60-50-40-30-20-100w/幅度/d B切比雪夫1型带通数字滤波器幅频响应曲线0.010.020.030.040.050.060.070.08-1-0.500.51t/sy 2(t )y2(t)的时域波形200400600800100012001400160018002000f/Hz幅度y2(t)的频谱其中阶数N=8(3)切比雪夫1型高通数字滤波器的损耗函数曲线、滤波分离出的DSB 信号的时域波形及其频谱如下:0.10.20.30.40.50.60.70.80.91-100-90-80-70-60-50-40-30-20-100w/幅度/d B切比雪夫1型高通数字滤波器幅频响应曲线0.010.020.030.040.050.060.070.08-1-0.500.51t/sy 3(t )y3(t)的时域波形f/Hz幅度y3(t)的频谱其中N=73、结果分析特点:误差值在规定的频段上等波纹变化。
切比雪夫I型带通数字滤波器设计

课程设计设计题目:切比雪夫I型带通数字滤波器设计学院:物理与电信工程学院专业班级:电信1301学号:1313034016姓名:钱红伟指导教师:王桂宝完成地点:博远楼c11092016年11月17日目录切比雪夫I型带通数字滤波器的设计 ............................................................ I II 摘要 .................................................................................. 错误!未定义书签。
引言 .................................................................................................................... I II 1 数字滤波器的发展现状及前景 . (1)1.1 数字滤波器的研究背景及意义 (1)1.2 数字滤波器的发展现状及前景 (1)2 数字滤波器的概述 (3)2.1 数字滤波器的概念 (3)2.2 数字滤波器的基本结构 (3)2.2.1 IIR滤波器的基本结构 (3)2.2.2 FIR滤波器的基本结构 (4)2.3 数字滤波器的分类 (5)2.4 带通数字滤波器 (7)2.4.1 带通数字滤波器的特点 (7)2.4.2 带通数字滤波器的作用 (7)2.5 带通数字滤波器的设计方法 (7)2.5.1 IIR数字滤波器的设计方法 (8)2.5.2 FIR数字滤波器的设计方法 (9)2.6 IIR数字滤波器与FIR数字滤波器的比较分析 (10)3 数字滤波器的设计 (10)3.1 双线性变换法设计滤波器 (10)3.1.1 双线性变换的基本知识 (10)3.1.2 用双线性变换法设计IIR 数字带通滤波 (10)3.2 脉冲响应不变法设计滤波器 (11)3.2.1 脉冲响应不变法的基本知识 (11)3.2.2 用脉冲响应不变法设计IIR数字带通滤波 (11)3.3 脉冲响应不变法与双线性变换法的比较 (12)3.4 数字滤波器的算法设计 (13)3.4.1 巴特奥兹滤波器 (13)3.4.2 切比雪夫滤波器 (14)3.4.2 椭圆滤波器 (16)4仿真过程 (17)4.1 用MATLAB设计滤波器的步骤 (17)4.2 设定系统的仿真对象 (18)4.3 系统对象滤波器设计方法 (18)4.4 MATLAB程序仿真设计 (18)4.4.1 产生一个含有50Hz、100Hz和150Hz的混合正弦波信号 194.4.2 对混合正弦波信号X进行滤波 (20)4.4.3 绘出信号滤波前、后的幅频图 (21)4.4.4 创建仿真模型图 (22)4.4.5 仿真模块参数设置 (23)4.5 系统仿真运行 (25)结论 (27)致谢 (27)参考文献 (28)切比雪夫I型带通数字滤波器的设计钱红伟(陕理工物理与电信工程学院电子信息科学与技术专业电信1301班,陕西汉中723001)指导教师:王桂宝[摘要]几乎在所有的工程技术领域中都会涉及到信号处理问题,滤波器作为信号处理的重要组成部分,已经发展的非常成熟。
切比雪夫I型数字滤波器的设计

数字信号处理原理及实现课程设计报告题目切比雪夫I型数字滤波器的设计专业电子信息工程学生姓名黄亚胜学号 090305041年级 2009级班级 5班指导教师邓凯设计时间 2011 年 12 月 21 日目录一、数字滤波器介绍 (1)二、数字滤波器的分类和设计方法 (1)1、FIR 滤波器的特点及设计方法 (1)2、IIR 滤波器的特点及设计方法 (2)三、设计内容介绍 (5)3.1.设计目的 (5)3.2.设计内容 (5)3.3.技术指标 (5)3.4.功能参数 (5)四、MATLAB编程实现 (6)五、总结 (7)一、数字滤波器的介绍数字滤波器处理模拟信号时,首先须对输入模拟信号进行限带、抽样和模数转换。
数字滤波器输入信号的抽样率应大于被处理信号带宽的两倍,其频率响应具有以抽样频率为间隔的周期重复特性,且以折叠频率即1/2抽样频率点呈镜像对称。
为得到模拟信号,数字滤波器处理的输出数字信号须经数模转换、平滑。
数字滤波器具有高精度、高可靠性、可程控改变特性或复用、便于集成等优点。
数字滤波器在语言信号处理、图像信号处理、医学生物信号处理以及其他应用领域都得到了广泛应用。
二、数字滤波器的分类和设计方法数字滤波器有低通、高通、带通、带阻和全通等类型。
它可以是时不变的或时变的、因果的或非因果的、线性的或非线性的。
应用最广的是线性、时不变数字滤波器,以及FIR 滤波器。
1、FIR 滤波器的特点及设计方法一个截止频率为c ω(rad/s)的理想数字低通滤波器,其传递函数的表达式:⎪⎩⎪⎨⎧≤≤≤=-πωωωωωτωc c j jd ee H ,0,)( 由上式可以看出,这个滤波器在物理上是不可实现的,因为冲激响应具有无限性和因果性。
为了产生有限长度的冲激响应函数,我们取样响应为)(n h ,长度为N ,其系数函数为)(z H :∑-=-=10)()(N n nz n h z H用)(n h 表示截取)(n h d 后冲激响应,即)()()(n h n n h d ω=,式子中)(n ω为窗函数,长度为N 。
切比雪夫带通滤波器的设计

切比雪夫带通滤波器的设计首先,确定滤波器的阶数。
滤波器的阶数决定了它的频率响应的陡峭程度。
一般来说,阶数越高,滤波器的陡峭程度越高,但计算复杂度也会变得更高。
在确定阶数时,需要考虑滤波器的设计要求和实际应用情况。
例如,如果要求滤波器的截止频率附近有较小的衰减,可以选择一个较高的阶数。
接下来,设计各个极点的位置。
切比雪夫带通滤波器的极点位置是通过在复平面上放置极点,并选择最佳的位置来实现所需的频率响应的。
极点的位置与滤波器的阶数和截止频率有关。
一般来说,极点应该分布在一个叫做单位圆的圆周上。
为了设计切比雪夫带通滤波器,需要采用以下步骤:1.确定滤波器的截止频率范围。
这个范围决定了希望保留的频率段。
2.根据所需的截止频率计算正规化的截止频率。
正规化的截止频率是指将实际的截止频率与采样频率归一化为单位圆的截止频率。
3.选择滤波器的阶数。
一般来说,选择较低的阶数可以实现较为平滑的频率响应,而选择较高的阶数可以实现更陡峭的截止频率。
4.使用切比雪夫滤波器的设计公式计算极点的位置。
具体的公式可以参考相关文献或使用专门的软件工具进行计算。
5. 根据计算得到的极点位置,可以进一步验证滤波器的频率响应是否符合设计要求。
可以使用工具如Matlab来绘制滤波器的幅频响应和相频响应。
6.根据设计结果,可以进一步调整滤波器的参数以满足具体应用的要求。
例如,可以调整滤波器的截止频率或增加滤波器的阶数来改变滤波器的性能。
总之,切比雪夫带通滤波器的设计需要确定滤波器的阶数和设计各个极点的位置。
通过合理选择滤波器的参数,可以实现所需的频率响应,并满足特定应用的要求。
设计一个高性能的切比雪夫带通滤波器需要对滤波器的理论和计算方法有一定的了解,并结合实际应用情况进行调整和优化。
切比雪夫

连环的脑筋急转弯大全加答案做脑筋急转弯的题目不能用通常的思路来回答问题,需要改变思维方式,还记得那些让人哭笑不得的奇葩答案吗?下面店铺为你分享连环的脑筋急转弯,希望对你有所帮助!连环的脑筋急转弯(精选篇)1. 美玲每晚都出去梦游,为什么她的丈夫不带她去医院治疗呢?答案:她每回梦游回来都带回来两千元2. 世界上哪一种鸭蛋不能吃,煮不熟,却打得破?答案:比赛成绩的鸭蛋.3. 老王是个酒鬼,有一天他去看医生,医生警告他喝酒一次不可超过杯,为什么老王还是不怕,一次喝了杯呢?答案:因为他连续看了两次医生4. 有一间屋子的北边有肥料厂,南边有酒厂,它有项优点,你知道是什么吗?答案:只要一开窗子就能知道什么风5. 小虎的机车既没有锁,也没有违规,但是仍然被锁上了,为什么?答案:不知道那个迷糊蛋锁错了6. 明明是个“错”字,为什么小华却偏偏说要“对”?答案:的确是个"错"字呀7. 三个人一起下田,但其中一个人却老站在那里不动手,为什么?答案:那是个稻草人8. 外国人问路,小明拼命有英语对他说,他却一点也听不懂,这是为什么?答案:因为他是法国人9. 福尔摩斯花了半天时间,却查不出命案现场有任何线索及目击者,但他随即就宣布破案了,为什么?答案:因为凶手自首了10. 气候突然转冷,一只鸵鸟决定南迁,请问它头向南,尾朝北,而爪子该朝向哪一方呢?答案:鸵鸟不会飞连环的脑筋急转弯(最新篇)1. 什么时候,我们会目中无人?答案:半夜我们一个人走在墓地2. 谁会连续摇头半个小时以上?答案:看球赛的3. 考一个亲戚称呼问题,如果你曾祖父的儿子,就是娶了你妈妈的那个人,你应该叫他什么?答案:喂乘儿子吃了没有4. 嫦娥为什么后悔上广寒宫?答案:因为月亮上没有赛月饼5. 人在做哪一件事的时候,最好能闭上眼睛?答案:死掉的时候省得吓人6. 除了司机以外,还有谁可以每天搭公车而不必给钱?答案:售票员7. 在机场办出境手续时,才想起忘了拿护照,怎么样才能在最短的时间里拿到护照呢?答案:打开皮包就可以拿到了8. 对一个打算把头发留到腰部的人来说,最重要的一件事是什么?答案:晚上不要穿着白衣服出门9. 为什么有人说:“情人眼里出西施”?答案:因为爱情使人盲目10. 超人看到有人在银行抢劫,为什么不去阻止?答案:找不到电话亭11. 什么地方物品售价愈高,客人愈高兴?答案:当铺12. 车子应该靠右行使才对,为什么杨先生靠左行使却没事?答案:因为他正行驶在靠左行驶的国家13. 老陈工作时一直闭着眼睛,从不睁开,他究竟是做什么工作的?答案:假装瞎子乞讨14. 在没有停电、跳电的情况下,为什么吴先生按了开关电灯却没有亮?答案:他接的是电视开关当然不会亮了15. 小呆一天写作文时,发现不会写“笨”字,于是他查字典,但是却查不到这个字,为什么?答案:她笨的去拿英文字典去查了16. 安妮的医师男友到外地出差一年,每两天会写一封情书给安妮,请问两个月之后,安妮会收到几封情书?答案:一封也没有,有,但他太懒了,一封也没有寄.17. 阿三死了,为什么大毛理直气壮的说:“凶手不是我,绝对另有其人!”答案:因为阿三是电视推理剧场中的18. 一名国中女生上了传说中闹鬼的厕所后,为什么昏倒在厕所里面?答案:他忘了厕所门是带拉的推半天推不开晕过去了19. 某人向枪靶射击了五发子弹,共得一百分,他射中了哪里?答案:只中一发正好一百20. 甲跟乙打赌:“我可以咬到自己的右眼。
切比雪夫带通滤波器的设计

切比雪夫带通滤波器的设计切比雪夫带通滤波器是一种数字滤波器,常用于信号处理中,用于滤除特定频率范围内的信号。
它在通带内具有较为平坦的频率响应,同时在阻带内有较高的抑制能力。
切比雪夫带通滤波器的设计基于切比雪夫多项式的性质,可以通过选择合适的阶数和通带抽样点来实现所需的滤波效果。
1.确定滤波器的通带和阻带范围以及所需的通带波动和阻带衰减。
这些参数通常由具体的应用需求决定。
2.根据通带和阻带的频率范围,选择合适的切比雪夫多项式的阶数。
阶数越高,滤波器的性能越好,但也会增加计算复杂度。
3.根据所选的阶数,计算切比雪夫多项式的系数。
切比雪夫多项式的系数可以通过递推关系式计算得到,也可以查阅切比雪夫多项式表格获得。
4.将切比雪夫多项式作为带通滤波器的传递函数,将其转化为巴特沃斯等效滤波器的传递函数。
巴特沃斯等效滤波器的传递函数可以通过对切比雪夫多项式进行相应的变换获得。
5.根据巴特沃斯等效滤波器的传递函数,使用频率变换方法得到带通滤波器的巴特沃斯等效滤波器的传递函数。
频率变换方法可以通过将巴特沃斯等效滤波器的传递函数中的标准正弦函数替换为带通滤波器的正弦函数来实现。
6.根据巴特沃斯等效滤波器的传递函数,计算带通滤波器的巴特沃斯等效滤波器的传递函数的系数。
7.根据带通滤波器的巴特沃斯等效滤波器的传递函数的系数,得到带通滤波器的巴特沃斯等效滤波器的巴特沃斯多项式系数。
8.利用巴特沃斯多项式系数,可以计算带通滤波器的巴特沃斯多项式的误差函数,进而得到最终的带通滤波器的巴特沃斯多项式系数。
9.将带通滤波器的巴特沃斯多项式系数转化为传输函数,从而可以在实际系统中进行实现。
总结起来,切比雪夫带通滤波器的设计可以通过选择适当的阶数和频率参数,并结合切比雪夫多项式的性质和频率变换方法,计算出最终的滤波器传递函数系数。
这样设计出的滤波器在通带内具有较为平坦的频率响应,并能在阻带内提供较高的抑制能力。
基于切比雪夫1的IIR低通滤波器

课程设计课程设计名称:DSP课程设计专业班级:电信1005班学生姓名:学号:指导教师:李相国课程设计时间:2013年6月数字信号处理专业课程设计任务书说明:本表由指导教师填写,由教研室主任审核后下达给选题学生,装订在设计(论文)首页填表说明1.“课题性质”一栏:A.工程设计;B.工程技术研究;C.软件工程(如CAI课题等);D.文献型综述;E.其它。
2.“课题来源”一栏:A.自然科学基金与部、省、市级以上科研课题;B.企、事业单位委托课题;C.校、院(系、部)级基金课题;D.自拟课题。
1 需求分析数字滤波器是指完成信号滤波处理功能的,用有限精度算法实现的离散时间线性非时变系统,其输入是一组数字量,其输出是经过变换的另一组数字量。
因此,它本身即可以是用数字硬件装配成的一台完成给定运算的专用数字计算机,也可以是将所需运算编成程序,让通用计算机来执行。
在本次课程设计中,我做的是基于双线性变换法设计 Chebyshev-I 型 IIR 数字低通滤波器,看到这个题目,我们很快就能联系到数字信号处理中的 IIR 数字滤波器的设计,根据以前学习的东西我们知道,要想设计一个数字低通滤波器,我们可以把所给的数字指标转换为模拟参数,通过设计一个模拟低通的滤波器,对设计好的模拟低通滤波器进行数字化就可以得到一个数字低通滤波器。
在本次实验中,我们首先将所给的滤波器数字指标转换为模拟指标,利用Chebyshev-I型函数设计一个 Chebyshev-I 型低通模拟滤波器,然后对所设计好的 Chebyshev-I型低通模拟滤波器进行参数分析,接下来利用双线性变化法将此模拟低通滤波器转变为数字低通滤波器。
2 概要设计3 运行环境PC 机,windows2000及其以上,matlab 软件。
4 开发工具和编程语言MATLAB 软件,编程语言为DSP 设计语言。
5 详细设计第一步:将数字低通滤波器的性能指标转化成模拟低通滤波器指标Chebyshev-I 型IIR 数字低通滤波器的性能指标:p ω=0.25π,s ω=0.4π,p δ=0.01,s δ=0.001程序模块: %转化成模拟量 rp=-20*log10(1-lp); rs=-20*log10(ls); Omgp=tan(wp/2) Omgs=tan(ws/2) Fs=0.5;第二步:利用切比学夫逼近法设计模拟滤波器切比雪夫1低通滤波器的原理:幅度平方函数为: 其中ε为小于1的正数,表示通带内幅度波动的程度,p Ω称为通带截止频率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计课程名称:数字信号处理题目编号: 0801题目名称:切比雪夫I型带通IIR数字滤波器专业名称:电子信息工程班级: 1203班学号:学生姓名:段超任课教师:陈忠泽2015年08月30日目 录1. 数字滤波器的设计任务及要求(编号0801) ................... 2 2. 数字滤波器的设计及仿真 .. (2)2.1数字滤波器(编号0801)的设计 ................................... 2 2.2数字滤波器(编号0801)的性能分析 . (4)3. 数字滤波器的实现结构对其性能影响的分析 (6)3.1数字滤波器的实现结构一(0801)及其幅频响应 ...................... 7 3.2数字滤波器的实现结构二(0801)及其幅频响应 ...................... 9 3.3 数字滤波器的实现结构对其性能影响的小结 (12)4. 数字滤波器的参数字长对其性能影响的分析 (12)4.1数字滤波器的实现结构一(0801)参数字长及幅频响应特性变化 ...... 14 4.2数字滤波器的实现结构二(0801)参数字长及幅频响应特性变化 ....... 17 4.3 数字滤波器的参数字长对其性能影响的小结 (20)5. 结论及体会 (20)5.1 滤波器设计、分析结论 .......................................... 21 5.2 我的体会 ...................................................... 21 5.3 展望 . (21)1. 数字滤波器的设计任务及要求(1)切比雪夫I 型带通IIR 数字滤波器各项指标如下: 阻带下截止频率1s ω=radi d π32)ln(;通带下截止频率1p ω=rad i i d d π⎪⎪⎭⎫ ⎝⎛+20)(32)ln(log 10;通带上截止频率2p ω=rad i i d d π⎪⎪⎭⎫ ⎝⎛-20)(32)ln(-1log 10;阻带上截止频率2s ω=radi d π⎪⎪⎭⎫ ⎝⎛32)ln(-1; 通带最大衰减p α=1dB; 阻带最小衰减s α=60dB.其中的i d 为抽到的题目的四位数编号,我的题目编号是0801,所以取 i d 为801. (2)滤波器的初始设计通过手工计算完成;(3)在计算机辅助计算基础上分析滤波器结构对其性能指标的影响(至少两种 合适的滤波器结构进行分析);(4)在计算机辅助计算基础上分析滤波器参数的字长对其性能指标的影响; (5)以上各项要有理论分析和推导、原程序以及表示计算结果的图表; (6)课程设计结束时提交说明书。
2. 数字滤波器的设计及仿真 2.1数字滤波器的设计(1)根据任务,确定性能指标:在设计带通滤波器之前,首先根据工程实际的需要确定滤波器的技术指标:(手工计算完成)通带下截止频率1p ω=0.354π 通带上截止频率2p ω=0.646π 阻带下截止频率1s ω=0.208π 阻带上截止频率2s ω=0.792π 阻带最小衰减 s α=60dB 通带最大衰减 p α=1dB 抽样频率s F =8kHz(2)有所给的技术参数可直接得到各模拟频率。
1p Ω=1p ω*s F ,2p Ω=2p ω*s F , 1s Ω=1s ω*s F , 2s Ω=2s ω*s F 1p Ω=2832π, 2p Ω=5168π, 1s Ω=1664π, 2s Ω=6336π(3) 根据教程表7.8的变换关系,设归一化(_Ωp )低通滤波器的阻带衰减用-Ω表示,则有 p B =2p Ω-1p Ω=2336π, 0p Ω=21p p ΩΩ=3825.6732π2st Ω=pst p st B 20222ΩΩ-Ω=1.723 1st Ω=pst p st B 10122ΩΩ-Ω =-3.053取 st _Ω=min (| 1st -Ω|,| 2st -Ωst2|)=1.723,可满足阻带衰减要求。
(4)求波纹系数εε=1101.0-pα=0.50885 (5)根据st _Ω及给定的p α,s αN ≥[]⎪⎭⎫ ⎝⎛ΩΩ---p st arcch arcch s /1102.01αε=)723.1()2147.1965(arcch arcch =1398.12765.8=26114.7取N=8.(6)查教程表7.5,可得N=8,p α=1dB 时的归一化原型切比雪夫I 型低通滤波器的系统函数)(-s H an)(-s H an =01723.01073.04478.08468.08369.16552.14230.29198.0123456782118++++++++---------s s s ss s s s ε(7)按教表7.8的相应变换关系,求出模拟带通滤波器系统函数为:(8)按冲激响应不变法的修正公式(7.78)式,求所需数字滤波器的系统 函数2.2 数字滤波器的性能分析MATLAB 程序如下:>> Rs=1;As=60;Fs=8000;T=1/Fs;wp1=0.354*pi; wp2=0.646*pi; ws1=0.208*pi; ws2=0.792*pi;>>Omegap1=wp1*Fs;Omegap2=wp2*Fs;Omegap=[Omegap1,Omegap2];Omegas1=ws1*Fs ;Omegas2=ws2*Fs;Omegas=[Omegas1,Omegas2];>> bw=Omegap2-Omegap1;w0=sqrt(Omegap1*Omegap2);>> [N,OmegaC]=cheb1ord(Omegap1,Omegas1,Rp,As,'s')N =8OmegaC=8.8970e+03>>[z0,p0,k0]=cheb1ap(N,Rp);ba1=k0*real(poly(z0));aa1=real(poly(p0)); >> [ba,aa]=lp2bp(ba1,aa1,w0,bw);[bd,ad]=impinvar(ba,aa,Fs);%(C,B,A)=dir2par(bd,ad)[H,w]=freqz(bd,ad);dbH=20*log10((abs(H)+eps)/max(abs(H)));>> subplot(2,2,1),plot(w/pi,abs(H));>> subplot(2,2,2),plot(w/pi,angle(H)/pi);>> subplot(2,2,3),plot(w/pi,dbH);>> subplot(2,2,4),zplane(ba,ad);相应的图形图1频率特性曲线和零极点图3. 数字滤波器的实现结构对其性能影响的分析在理想状态下,对于同一个传递函数几乎对应着无数种等效结构,然而这些结构却并不一定都能实现。
在无限参数字长的情况下,所有能实现传递函数的结构之间,其表现完全相同。
然而在实际中,由于参数字长有限的限制,各实现结构的表现不同。
下面我们就对比直接型和级联型两种结构在本设计中对性能指标的影响。
在MATLAB中可以利用FDATOOL工具箱建构不同类型的数字滤波器。
再次为了使对比效果明显,将上述初步设计的切比雪夫带通IRR数字滤波器的设计参数字长(即转移函数中分子分母各项前的系数)进行保留小数点后3位的进一步缩减。
缩减参数如下:Nun=[0 0 0 0 0 0.002 -0.002 -0.001 0.004 -0.002 -0.001 0.001 0 0 0 0] Den=[1 -0.532 5.791 -2.601 15.733 -5.983 26.035 -8.273 28.585 -7.37921.273 -4.232 10.469 -1.446 3.116 -0.228 0.430]将上述参数输入FDATOOL中的filter coefficients 工具中3.1数字滤波器的实现结构一及其幅频响应直接型结构滤波器的转移函数为:差分方程:直接一型的结构流图如下:选择filter structure 选项框中的Direct-Form I选项,点击窗口下方的Import Filter 按钮,构建直接1型结构的椭圆带通IRR 数字滤波器,结果如图所示。
图 3 Direct-Form I型结构滤波器幅频响应图表1 Direct-Form I 结构滤波器性能指标影响(1p ω,2p ω,1s ω,2s ω单位为rad/sample π;s α,p α,单位为dB )由图3和表1可以看出:(1)滤波器幅频曲线在通带和阻带内波动幅度不均匀; (2) 阻带最小衰减与通带最大衰减都存在误差; (3) wp 和ws 分别较初始设计变化了。
3.2数字滤波器的实现结构一及其幅频响应 级联型结构滤波器的转移函数:图4 级联型的结构流图图5级联型结构滤波器幅频响应图表2 级联型结构滤波器性能指标影响(1p ω,2p ω,1s ω,2s ω单位为rad/sample π;s α,p α,单位为dB )从上图和表2中可以看出,采用级联结构的滤波器 (1)滤波器幅频曲线在通带和阻带内波动较均匀;(2)出现了阻带最小衰减上升了0.45133dB,通带最大衰减下降了0.1324799dB 的误差;(3)wp1和ws2分别较初始设计减小-0.0026818和-0.0289624rad π/sample ,(4)wp2和ws1分别较初始设计增大了0.003292和0.0897295rad π/sample3.3 数字滤波器的实现结构对其性能影响的小结比较表1和表2发现:在参数字长仅保留了小数点后三位的情况下,两种结构的滤波器较初始设计在性能指标方面均有误差。
但是直接型误差比级联型更大,受有限参数字长影响更大,其各项性能指标与设计要求间的差的绝对值普遍大于级联型。
此外,直接型和级联型的幅频响应曲线的通带波动均不稳定,但是级联型的稳定性要好于直接型。
造成这一现象的原因是:直接型滤波器的系数不是直接决定单个零极点,因而不能很好的进行滤波器性能的控制;此外直接性滤波器对参数的变化过于敏感,从而使得系统的响应对参数的变化也特别敏感,对参数的有限字长运算过于灵敏,容易出现不稳定或产生较大误差。
而级联型滤波器每个二阶节系数单独控制一对零极点,有利于控制频率响应;此外级联结构中后面的网络输出不会再流到前面,运算误差的积累相对直接型就4.数字滤波器参数字长对其性能指标的影响的分析在实际的数字滤波器的设计中,由于计算机或DSP芯片字长和存储空间有限,所以也只能对设计参数取有限字长进行设计。
