有限元网格划分和收敛性
有限元网格划分

1网格数量网格数量的多少将影响计算结果的精度和计算规模的大小。
一般来讲,网格数量增加,计算精度会有所提高,但同时计算规模也会增加,所以在确定网格数量时应权衡两个因数综合考虑。
网格较少时增加网格数量可以使计算精度明显提高,而计算时间不会有大的增加。
当网格数量增加到一定程度后,再继续增加网格时精度提高甚微,而计算时间却有大幅度增加。
所以应注意增加网格的经济性。
实际应用时可以比较两种网格划分的计算结果,如果两次计算结果相差较大,可以继续增加网格,相反则停止计算。
在决定网格数量时应考虑分析数据的类型。
在静力分析时,如果仅仅是计算结构的变形,网格数量可以少一些。
如果需要计算应力,则在精度要求相同的情况下应取相对较多的网格。
同样在响应计算中,计算应力响应所取的网格数应比计算位移响应多。
在计算结构固有动力特性时,若仅仅是计算少数低阶模态,可以选择较少的网格,如果计算的模态阶次较高,则应选择较多的网格。
在热分析中,结构内部的温度梯度不大,不需要大量的内部单元,这时可划分较少的网格。
2网格疏密网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分布特点。
在计算数据变化梯度较大的部位(如应力集中处),为了较好地反映数据变化规律,需要采用比较密集的网格。
而在计算数据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。
这样,整个结构便表现出疏密不同的网格划分形式。
采用疏密不同的网格划分,既可以保持相当的计算精度,又可使网格数量减小。
因此,网格数量应增加到结构的关键部位,在次要部位增加网格是不必要的,也是不经济的。
划分疏密不同的网格主要用于应力分析(包括静应力和动应力),而计算固有特性时则趋于采用较均匀的钢格形式。
这是因为固有频率和振型主要取决于结构质量分布和刚度分布,不存在类似应力集中的现象,采用均匀网格可使结构刚度矩阵和质量矩阵的元素不致相差太大,可减小数值计算误差。
同样,在结构温度场计算中也趋于采用均匀网格。
第07讲-有限元网格划分的基本原则及技巧

7-6
网格疏密
• • 网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分 布特点。 在计算数据变化梯度较大的部位(如应力集中处、几何形状、材料、厚度变化的 位置),为了较好地反映数据变化规律,需要采用比较密集的网格。而在计算数 据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。这样,整 个结构便表现出疏密不同的网格划分形式。—— 网格数量应增加在结构的关键 部位,在次要部位增加网格是不必要的,也是不经济的。 边界上最好要在8个单元以上,至少不少于4个; 分析结果完成后,需要检查以下各项,误差较大的位置要进行细分: 单元应力的连续性,比较相邻单元应力值的差值; 应力偏差:结点上的单元结点应力和结点平均应力的差值的较大值; 当以上差值与其中的最大应力的比值较大时,该位置的网格需要细分。
精度 计算时间 精确解 1 2 O
7-4
•
•
P
网格数量
网格数量(续)
在决定网格数量时应考虑分析数据的类型。 实体单元:
• •
1、在静力分析时,如果仅仅是计算结构的变形,网格数量可以少一些。如 果需要计算应力,则在精度要求相同的情况下应取相对较多的网格。 2、在响应计算中,计算应力响应所取的网格数应比计算位移响应多。 3、在计算结构固有动力特性时,若仅仅是计算少数低阶模态,可以选择较 少的网格,如果计算的模态阶次较高,则应选择较多的网格。
左图中(a)、(b)改 变了结构质量的对称分 布,应避免。 (c)是 比较理想的结果。
(a)
7-8
(b)
(c)
单元的形状及评价
• 形状比(长边与短边距离之比) 一般实体单元的长宽比越大,分析误差也越大。 对于板壳单元,评价应力为主时不宜超过1:3,评价位移为主时不宜超过1:5; 对于块体单元,评价应力为主时不宜超过1:2,评价位移为主时不宜超过1:3; 在应力分布几乎没有变化的区域里使用的单元,适当放大也没问题。 倾角(表示单元偏离直角四边形的程度(Angular Deviation)) 四边形的内倾角最好是在45度~135度之间,不要超过15度~165度。 锥度(限于四边形) 用几何偏离(Geometric Deviation)表示四边形单元的变形程度。
有限元的网格划分技术

有限元的网格划分技术对于有限元分析来说,网格划分是其中最关键的一个步骤,网格划分的好坏直接影响到解算的精度和速度。
网格化有三个步骤:定义单元属性(包括实常数)、在几何模型上定义网格属性、划分网格。
定义网格的属性主要是定义单元的外形、大小。
单元大小基本上在线段上定义,可以用线段数目或长度大小来划分,可以在线段建立后立即声明,或整个实体模型完成后逐一声明。
采纳BottOm-UP方式建立模型时,采纳线段建立后立即声明比较便利且不易出错。
例如声明线段数目和大小后,叁制对象时其属性将会一•起夏制,完成上述操作后便可进行网格化命令。
网格化过程也可以逐步进行,即实体模型对象完成到某个阶段就进行网格话,如所得结果满足,则连续建立其他对象并网格化。
网格的划分可以分为自由网格(free meshing)、映射网格(mapped meshing)和扫略网格(SWeeP meshing)等。
一、自由网格划分自由网格划分是自动化程度最高的网格划分技术之一,它在面上可以自动生成三角形或四边形网格,在体上自动生成四周体网格。
通常状况下,可采用ANSYS的智能尺寸掌握技术(SMARTSIZE命令)来自动掌握网格的大小和疏密分布,也可进行人工设置网格的大小(AESIZE、LESIZE、KESIZE、ESIZE等系列命令)并掌握疏密分布以及选择分网算法等( MOPT 命令)。
对于简单几何模型而言,这种分网方法省时省力,但缺点是单元数量通常会很大,计算效率降低。
同时,由于这种方法对于三维简单模型只能生成四周体单元,为了获得较好的计算精度,建议采纳二次四周体单元(92号单元)。
假如选用的是六面体单元,则此方法自动将六面体单元退化为阶次全都的四周体单元,因此,最好不要选用线性(•阶次)的六面体单元(没有中间节点,比如45号单元),由于该单元退化后为线性的四周体单元,具有过大的刚度,计算精度较差;假如选用二次的六面体单元(比如95 号单元),由于其是退化形式,节点数与其六面体原型单元全都,只是有多个节点在同一位置而己,因此,可以采用TCHG命令将模型中的退化形式的四周体单元变化为非退化的四周体单元(如92号单元),削减每个单元的节点数量,提高求解效率。
结构有限元教程

结构有限元教程全文共四篇示例,供读者参考第一篇示例:结构有限元分析是工程领域中常用的结构分析方法之一,它在设计、优化和验证工程结构的过程中起着重要作用。
有限元方法将复杂的结构分析问题简化为离散的数学模型,通过有限元软件进行分析计算,得到结构的应力、应变、位移等重要信息,从而评估结构的安全性和稳定性。
本文将介绍结构有限元分析的基本原理、常用软件、建模方法以及常见问题的解决方案,帮助读者更好地理解和运用结构有限元分析。
一、有限元分析的基本原理有限元分析的本质是一种数值逼近方法,通过有限元剖分结构,将结构分解为有限个简单的单元,每个单元的行为可以通过一组节点的位移来描述。
有限元分析的基本原理是根据物理方程和边界条件建立有限元模型,通过数值计算得到结构的应力、位移等信息,从而评估结构的性能和安全性。
在有限元分析中,通常有以下几个步骤:1.建立有限元模型:根据实际结构的几何形状和材料性质,选择适当的有限元类型(如梁单元、壳单元、体单元等),剖分结构并建立节点和单元之间的连接关系。
2.确定边界条件:根据实际情况确定结构的边界条件,如支撑条件、受力条件等。
3.建立单元刚度矩阵:根据单元的几何形状和材料性质,计算单元的刚度矩阵,并根据节点和单元之间的连接关系组装成整体刚度矩阵。
4.施加载荷:根据实际需要,施加结构上的外部载荷,如集中力、分布力等。
5.求解方程组:通过数值计算方法求解整体刚度矩阵和载荷向量的方程组,得到结构的位移、应力等信息。
6.分析和优化:根据分析结果评估结构的性能和安全性,并进行结构优化设计。
二、结构有限元分析常用软件目前市面上有许多结构有限元分析软件,其中一些较为知名的软件包括ANSYS、ABAQUS、Nastran、SAP2000等。
这些软件在结构有限元分析领域有着广泛的应用和较高的声誉,具有良好的计算性能和强大的功能特点。
1.ANSYS:是一款功能强大的有限元分析软件,可用于结构、热、流体、电磁等多物理场耦合问题的分析计算。
有限元分析理论基础

有限元分析概念有限元法:把求解区域看作由许多小的在节点处相互连接的单元(子域)所构成,其模型给出基本方程的分片(子域)近似解,由于单元(子域)可以被分割成各种形状和大小不同的尺寸,所以它能很好地适应复杂的几何形状、复杂的材料特性和复杂的边界条件有限元模型:它是真实系统理想化的数学抽象。
由一些简单形状的单元组成,单元之间通过节点连接,并承受一定载荷。
有限元分析:是利用数学近似的方法对真实物理系统(几何和载荷工况)进行模拟。
并利用简单而又相互作用的元素,即单元,就可以用有限数量的未知量去逼近无限未知量的真实系统。
线弹性有限元是以理想弹性体为研究对象的,所考虑的变形建立在小变形假设的基础上。
在这类问题中,材料的应力与应变呈线性关系,满足广义胡克定律;应力与应变也是线性关系,线弹性问题可归结为求解线性方程问题,所以只需要较少的计算时间。
如果采用高效的代数方程组求解方法,也有助于降低有限元分析的时间。
线弹性有限元一般包括线弹性静力学分析与线弹性动力学分析两方面。
非线性问题与线弹性问题的区别:1)非线性问题的方程是非线性的,一般需要迭代求解;2)非线性问题不能采用叠加原理;3)非线性问题不总有一致解,有时甚至没有解。
有限元求解非线性问题可分为以下三类:1)材料非线性问题材料的应力和应变是非线性的,但应力与应变却很微小,此时应变与位移呈线性关系,这类问题属于材料的非线性问题。
由于从理论上还不能提供能普遍接受的本构关系,所以,一般材料的应力与应变之间的非线性关系要基于试验数据,有时非线性材料特性可用数学模型进行模拟,尽管这些模型总有他们的局限性。
在工程实际中较为重要的材料非线性问题有:非线性弹性(包括分段线弹性)、弹塑性、粘塑性及蠕变等。
2)几何非线性问题几何非线性问题是由于位移之间存在非线性关系引起的。
当物体的位移较大时,应变与位移的关系是非线性关系。
研究这类问题一般都是假定材料的应力和应变呈线性关系。
它包括大位移大应变及大位移小应变问题。
有限元网格划分和收敛性
一、基本有限元网格概念1.单元概述ﻫ几何体划分网格之前需要确定单元类型.单元类型的选择应该根据分析类型、形状特征、计算数据特点、精度要求和计算的硬件条件等因素综合考虑。
为适应特殊的分析对象和边界条件,一些问题需要采用多种单元进行组合建模。
ﻫ 2.单元分类选择单元首先需要明确单元的类型,在结构有限元分析中主要有以下一些单元类型:平面应力单元、平面应变单元、轴对称实体单元、空间实体单元、板单元、壳单元、轴对称壳单元、杆单元、梁单元、弹簧单元、间隙单元、质量单元、摩擦单元、刚体单元和约束单元等。
根据不同的分类方法,上述单元可以分成以下不同的形式。
ﻫ3。
按照维度进行单元分类根据单元的维数特征,单元可以分为一维单元、二维单元和三维单元。
ﻫ一维单元的网格为一条直线或者曲线。
直线表示由两个节点确定的线性单元。
曲线代表由两个以上的节点确定的高次单元,或者由具有确定形状的线性单元。
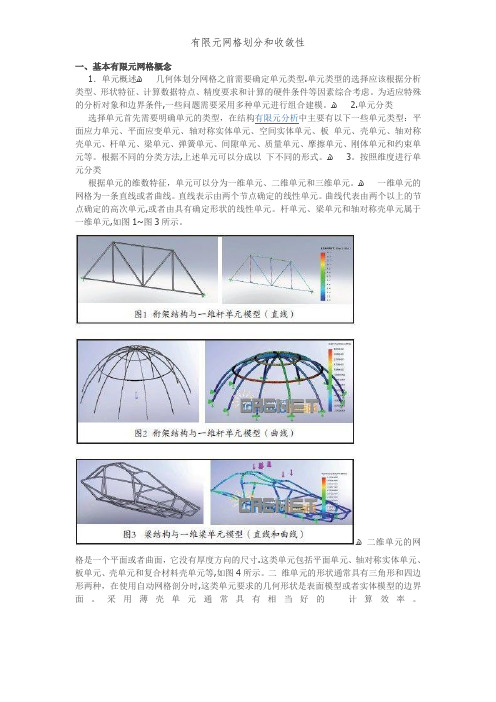
杆单元、梁单元和轴对称壳单元属于一维单元,如图1~图3所示。
ﻫ二维单元的网格是一个平面或者曲面,它没有厚度方向的尺寸.这类单元包括平面单元、轴对称实体单元、板单元、壳单元和复合材料壳单元等,如图4所示。
二维单元的形状通常具有三角形和四边形两种,在使用自动网格剖分时,这类单元要求的几何形状是表面模型或者实体模型的边界面。
采用薄壳单元通常具有相当好的计算效率。
ﻫﻫ三维单元的网格具有空间三个方向的尺寸,其形状具有四面体、五面体和六面体,这类单元包括空间实体单元和厚壳单元,如图5所示.在自动网格划分时,它要求的是几何模型是实体模型(厚壳单元是曲面也可以)。
ﻫ4.按照插值函数进行单元分类根据单元插值函数多项式的最高阶数多少,单元可以分为线性单元、二次单元、三次单元和更高次的单元。
线性单元具有线性形式的插值函数,其网格通常只具有角节点而无边节点,网格边界为直线或者平面.这类单元的优点是节点数量少,在精度要求不高或者结果数据梯度不太大的情况下,采用线性单元可以得到较小的模型规模.但是由于单元位移函数是线性的,单元内的位移呈线性变化,而应力是常数,因此会造成单元间的应力不连续,单元边界上存在着应力突变,如图6所示。
网格划分的原则

划分网格是建立有限元模型的一个重要环节,它要求考虑的问题较多,需要的工作量较大,所划分的网格形式对计算精度和计算规模将产生直接影响。
为建立正确、合理的有限元模型,这里介绍划分网格时应考虑的一些基本原则。
1网格数量网格数量的多少将影响计算结果的精度和计算规模的大小。
一般来讲,网格数量增加,计算精度会有所提高,但同时计算规模也会增加,所以在确定网格数量时应权衡两个因数综合考虑。
图1中的曲线1表示结构中的位移随网格数量收敛的一般曲线,曲线2代表计算时间随网格数量的变化。
可以看出,网格较少时增加网格数量可以使计算精度明显提高,而计算时间不会有大的增加。
当网格数量增加到一定程度后,再继续增加网格时精度提高甚微,而计算时间却有大幅度增加。
所以应注意增加网格的经济性。
实际应用时可以比较两种网格划分的计算结果,如果两次计算结果相差较大,可以继续增加网格,相反则停止计算。
图1位移精度和计算时间随网格数量的变化在决定网格数量时应考虑分析数据的类型。
在静力分析时,如果仅仅是计算结构的变形,网格数量可以少一些。
如果需要计算应力,则在精度要求相同的情况下应取相对较多的网格。
同样在响应计算中,计算应力响应所取的网格数应比计算位移响应多。
在计算结构固有动力特性时,若仅仅是计算少数低阶模态,可以选择较少的网格,如果计算的模态阶次较高,则应选择较多的网格。
在热分析中,结构内部的温度梯度不大,不需要大量的内部单元,这时可划分较少的网格。
2网格疏密网格疏密是指在结构不同部位采用大小不同的网格,这是为了适应计算数据的分布特点。
在计算数据变化梯度较大的部位(如应力集中处),为了较好地反映数据变化规律,需要采用比较密集的网格。
而在计算数据变化梯度较小的部位,为减小模型规模,则应划分相对稀疏的网格。
这样,整个结构便表现出疏密不同的网格划分形式。
图2是中心带圆孔方板的四分之一模型,其网格反映了疏密不同的划分原则。
小圆孔附近存在应力集中,采用了比较密的网格。
有限元的性质和收敛性

有限元的性质和收敛性一、有限元解的收敛准则有限单元法作为求解数学微分方程的一种数值方法可以认为是里兹法的一种特殊形式,不同在于有限单元法的试探函数是定义于单元(子域)而不是全域。
因此有限元解的收敛性可以与里兹法的收敛性对比进行讨论。
里兹法的收敛条件是要求试探函数具有完备性和连续性,也就是说,如果试探函数满足完备性和连续性要求,当试探函数的项数n--->∞时,则Ritz法的近似解将趋近于数学微分方程的精确解。
现在要研究什么是有限元解的收敛性提法?收敛的条件又是什么?在有限单元法中,场函数的总体泛函是由单元泛函集成的。
如果采用完全多项式作为单元的插值函数(即试探函数),则有限元解在一个有限尺寸的单元内可以精确地和真正解一致。
但是实际上有限元的试探函数只能取有限项多项式,因此有限元解只能是真正解的一个近似解答。
有限元解的收敛准则需要回答的是,在什么条件下当单元尺寸趋于零时,有限元解趋于真正解。
下面仍以含有一个待求的标量场函数为例,微分方程是:A(φ) = L(φ) + b = 0 (1.1)相应的泛函是:(1.2)假定泛函∏中包含φ和它的直至m阶的各阶导数,若m阶导数是非零的,则近似函数至少必须是m次多项式。
若取p次完全多项式为试探函数,则必须满足p≥m,这时及其各阶导数在一个单元内的表达式如下:......(1.3)由上式可见,由于是p次完全多项式,所以它的直至m阶导数的表达式中都包含有常数项。
但单元尺寸趋近于零时,在每一单元内及其直至m阶导数将趋近于它的精确值,即趋近于常数。
因此,每一个单元的泛函有可能趋于它的精确值。
如果试探函数还满足连续性要求,那么整个系统的泛函将趋近于它的精确值。
有限元解就趋近于精确解,也就是说解是收敛的。
从上述讨论可以得到下列收敛准则:准则1完备性要求。
如果出现在泛函中场函数的最高阶导数是m阶,则有限元解收敛的条件之一是单元内场函数的试探函数至少是m次完全多项式。
或者说试探函数中必须包括本身和直至m 阶导数为常数的项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、基本有限元网格概念1.单元概述几何体划分网格之前需要确定单元类型。
单元类型的选择应该根据分析类型、形状特征、计算数据特点、精度要求和计算的硬件条件等因素综合考虑。
为适应特殊的分析对象和边界条件,一些问题需要采用多种单元进行组合建模。
2•单元分类选择单元首先需要明确单元的类型,在结构中主要有以下一些单元类型: 平面应力单元、平面应变单元、轴对称实体单元、空间实体单元、板单元、壳单元、轴对称壳单元、杆单元、梁单元、弹簧单元、间隙单元、质量单元、摩擦单元、刚体单元和约束单元等。
根据不 同的分类方法,上述单元可以分成以下不同的形式。
3. 按照维度进行单元分类根据单元的维数特征,单元可以分为一维单元、二维单元和三维单元。
一维单元的网格为一条直线或者曲线。
直线表示由两个节点确定的线性单元。
曲线代表 由两个以上的节点确定的高次单元, 或者由具有确定形状的线性单元。
杆单元、梁单元和轴 对称壳单元属于一维单元,如图 1〜图3所示。
二维单元的网格是一个平面或者曲面,它没有厚度方向的尺寸。
这类单元包括平面单元、 轴对称实体单元、板单元、壳单元和复合材料壳单元等,如图 4所示。
二 维单元的形状通常具有三角形和四边形两种,在使用自动网格剖分时, 这类单元要求的几何形状是表面模型图1捋果詰柯与一维杆单无犠型(直豉)&2桁舉第构石一隼杆早死撲型(曲线)B3毀姑构与一纯梁单元除世(直疑和呦疚〕或者实体模型的边界面。
采用薄壳单元通常具有相当好的计算效率。
洞丨伍金哉钩和潯壳社电三维单元的网格具有空间三个方向的尺寸,其形状具有四面体、五面体和六面体,这类单元包括空间实体单元和厚壳单元,如图5所示。
在自动网格划分时,它要求的是几何模型是实体模型(厚壳单元是曲面也可以)。
图5三址乙勺久和父侬草无4. 按照插值函数进行单元分类根据单元插值函数多项式的最高阶数多少,单元可以分为线性单元、二次单元、三次单元和更高次的单元。
线性单元具有线性形式的插值函数,其网格通常只具有角节点而无边节点,网格边界为直线或者平面。
这类单元的优点是节点数量少,在精度要求不高或者结果数据梯度不太大的情况下,采用线性单元可以得到较小的模型规模。
但是由于单元位移函数是线性的,单元着应力突变,如图6所示。
S6錢41吕节点点单无fu节庖实体羊元二次单元的插值函数是二次多项式,其网格不仅在每个顶点处有角节点,而且在棱边上还存 在一个边节点,因此网格边界可以是二次曲线或者曲面。
这类单元的优点是几何和物理离散精度较高,单元内的位移呈二次变化, 应力呈线性变化,因此单元边界上的应力是连续的。
但是在单元数量相同的条件下二次单元的节点数比线性 单元的节点数多,模型的规模较大,如图7和图8所示。
三次单元的插值函数是三次多项式,其网格的每条边上存在两个节点,有些三次单元还具有内部节点。
这类单元的离散精度更高,但是由于单元节点数较多,网格划分较为困难,模型规模很大,一般用于具有特殊精度要求的场合,如图9所示。
97二尖G 节点三角形売单元和二次10节点曲面体单元图N 简单戀髻茱玻性单尤乖二衣单元应力比较对于一阶和二阶单元,我们通常也称其为单元。
三阶及以上的单元,我们也称其为P单元,高阶次的P单元可以更好地拟合变形形状,特别对于曲率或者应力梯度变化较大的区域会较为真实的模拟,但会比H-单元有较多的运算量,如图10所示。
5. 结构单元与非结构单元根据单元能否离散成实际结构,可以将单元分为结构单元和非结构单元。
能离散成实际结构的称为结构单元,如轴对称单元离散轴对称结构,杆、梁单元用于离散杆件结构,实体单元用于离散空间结构等,这些单元都属于结构单元。
除此之外,还有一类单元并不用于实际结构的离散,而是在模型中模拟一些特殊的结构和边界条件,如质量单元用于实际的物体质量效应,弹簧和阻尼单元用于模拟结构的弹性支承和减振吸能部件,间隙和接触单元拟节点之间的刚性连接等,这些单元称为非结构单元。
由于非结构单兀非常抽象,使用起来有一定的难度,在设计一体化分析里面通常会将其工程化,帮助使用者淡化其力学概念。
6.节点和单兀的重要力学概念针对前述的单兀分类,此处要澄清关于节点和单兀的一些非常有用的总结性概念。
此位移的准确性高于应变、应变高于应力;◎当结构静力平衡时计算变形的单兀是求得准确有限兀分析结果的关键,因此线性计算中单兀不可以变形过大,否则会造成求解失败;◎网格质量概括来说,初始网格必须可呈现初始模型的几何形状,而且要足够弹性”以符合静力平衡后的变形几何形状◎在预计会有应力梯度变化剧烈的位置上,为预测其准确变形情况,细小特征几何必须£9陌单悬臂翳二阮单元和三农羊元庖力比快要更精确符合,以利于准确计算这些位置上的应力值;◎在理想曲率边线与网格曲率边线之间的差距称之为离散误差。
二、有限元误差分析1.有限元误差有限元的误差主要来自两个方面,一是模型误差,一是计算误差。
有限元模型和实际问题之间的差异。
它包括有限元离散处理所固有的原理性误差,也可能包括几何模型处理、实际工况转化为模型边界条件时所带来的偶然性误差。
计算误差是指采用数值方法对有限元模型进行计算所产生的误差,误差的性质是舍入误差和截断误差。
、收敛性及自动收敛方法一般而言,网格拥有较多的单元,可得到较准确的结果。
会有更多的节点可供计算,所以结果会较准确。
较多的单元也就表示单元大小较小,所以物理离散误差可减小。
实际分析上也有极限,在收敛性分析过程中网格尺寸一再缩减也不一定会对精确结果有帮助。
对一给定几何而言,要达到收敛性的网格会与外部负载条件及边界约束条件有关(见图11)。
在线性静态分析中,载荷大小不是收敛性的系数。
F面以SolidWorks Simulation 的收敛性为例简单介绍收敛性的处理方法和技巧。
SolidWorks Simulati on提供三种收敛性的技术。
包括有手动控制收敛性和软件自动控制收敛性技术。
其中自动控制收敛性的方法我们也称之为自适应方法,如图12所示,包括自动H自适应方法(H-adaptive)、自动P自适应方法(P-adaptive)。
目适应aa/t?力述说明目适应万怯亠h-目适应.?-§iS应&\2收欽技栓制矣至1. 自动H自适应方法(H-adaptive)H方法的本质就是根据应力梯度的变化情况自动在应力梯度大的地方,根据预先规定的收敛准则,重新自动剖分网格,进行自动加密(见图13,原始网格与H自适应网格结果)。
图13原妊网密芍H方注石母成的网舞SolidWorks Simulation 的H方法具有以下特性。
1)适用于实体零件及装配体(仅支持实体单元)的静态分析研究;2)在应变能误差较高的区域使用较小网格尺寸;3)可以在应变能误差较低区域网格粗化(加大网格尺寸),便于在后面的优化计算中降低计算规模,大大提高优化效率;4)目标精度定义应变能量密度范数的精度等级默认值是98%,此处可以调整能量密度范数的精度等级,一般情况下默认的精度可以达到分析的要求;5)精度偏差设置(见图13);自适旺法0无強自融C十自适应谯项低高目折精度:..... 冏*本地輕〕整站的復傭差;量大潼环数曲)□阿格祖槌化图门H方法中的楕度倔基设置◎精度偏差设置有局部(本地)和全局(整体);◎滑动杆朝局部移动,指示程序以较少的单元取得精确的峰值应力结果]◎滑动杆朝全局移动,指示程序取得整体零件刚度精确的结果,而不是应力结果。
7)网格粗糙化的目的是对应力梯度变化不大的区域,加大此处的单元尺寸,可以使用较小的网格得到较好的结果,同时也便于后继的优化求解。
图14展示了某机械零件,采用一阶单元不同单元大小,并采用自适应方法进行分析。
方案1采用平均单元大小13.6mm 进行网格划分,然后采用H自适应网格划分,此时得到的最大应力点的应力是44MPa。
方案2采用平均单元大小为3.4mm进行网格划分,然后采用H自适应网格划分,此时得到的最大应力点的应力是75.6MPa,两者之间有42%的差异。
图14 一阶单无占H方法钛度分析同样的模型,不做任何修改采用二阶单元进行网格划分,如图15所示,然后采用H方法,得到的应力误差小于3%,说明采用较大的全局二阶单元,然后采用H方法可以得到相当准确的应力结杲。
说明采用线性单元,使用H方法得不到准确的结果。
2•自动P 自适应方法(P-adaptive )P 方法的本质就是根据约束条件 (如应变能)的变化情况自动在约束条件大的地方,根据 预先规定的收敛准则,调整该处的单元形函数的阶次,在单元大小不变的情况下提高单元内 部应力的精确性(见图16)。
1216卜{方法设蓋罕面1)适用于实体零件及装配体的静态分析研究,但装配体仅支持结合方式,不可以有其他接触存在;2)收敛准则有总应变能、均方根合位移、均方根 von Mises 应力;3)默认收敛准则是总应变能,均方根合位移及von Mises 应力准则并不常用;4)默认的设定通常就足够,由于系统通常会提前满足设定精度,因此最大 p-order 及最大循环数很少用到;5) 开始p-阶序起始于2,设为1会报错; 6)必须使用二阶单元为初始网格;◎一般而言初始的网格尺寸影响很小(见图17);旷目适便选坂 应匕时号止虑应壹需更靳带百过口丄情日M 应更龍错浜的卑无.凰大L 航序肋a 15二盼单元与H 汙块精嵐分祈■■更改討1板或更少 g 「ft 或更多◎ Jacobian (雅可比检查)对误差有较大的影响,在局部位置无法反馈结果。
建议将 Jacobian 检查设定在节点(见图18)。
岡格品履 O 草稿 雅可比点四、手动收敛性检查1.相对收敛性检查在大多数复杂情况下很难通过自适应方法得到好的结果, 必须通过相对收敛性检查得到收敛的结果(见图19),其操作步骤如下。
1)执行多个分析研究,逐步调整加密网格,检查应力值的变化情形 2)每次以2:1比例调整加细网格尺寸■ IV*•E —£ !■ H岡格盏类型◎标谁13.64ii m 3斗mmSS B MPaigi7干同的初姑肾搐丸小时结果秒怕不大图诃P 方法时邛可比点會査进賣---Br¥= S 匸£3)如果局部网格尺寸远小于整体网格尺寸,要留意扭曲失真的情况。
2. 等值线质量检查(见图20)1)节点解是临近单元的节点应力的平均值2)单元解是每个单元所有节点应力的平均值ISzt 範量范It 谯羞检鱼1)ERR 能量范数误差绘图可以显示出相邻元素之应力值差异,2)并非绝对是收敛性测试方法,但会显示出要特别注意的高误差区域3)最佳的应用方式是在比较不同的设计过程。
佳状况并维持一致,其分析结果的比较应该较具有实际意义。
结果,如果几何体光滑连续而结果呈锯齿状, 1)应力等值线应该和连续几何体一样连续,使用不连续选项可以 表明此处结果不好,3•误差估算方法1:能量范数值(见图21)” 10 mm J C K |Tinn4•误差估算方法2:节点和单元应力值比较(见图22) 单元轉 节点解圈22单元盛力狐节点应力相比校3)评定标准,理论上节点和单元应力值应该有较小的差异;4)一般情况下,节点应力和单元应力的误差不允许超过2)针对结合的装配体分析◎使用p-adaptive收敛方法,二阶质量单元及默认单元大小;◎如果有Jacobian误差发生,使用不同的初始网格尺寸执行可避免不正确的高应力值产生;'3)针对有连接接头或接触条件的装配体分析◎使用传统的手动H-单元收敛方法;◎使用二阶质量单元及默认单元大小;◎使用初始网格控制以确保符合未变形的几何体;◎使用局部网格控制在需要位置以达到收敛。
