线性定常系统非齐次状态方程的解
现代控制理论知识点汇总

现代控制理论知识点汇总Revised at 2 pm on December 25, 2020.第一章 控制系统的状态空间表达式1. 状态空间表达式 n 阶DuCx y Bu Ax x+=+= 1:⨯r u 1:⨯m y n n A ⨯: r n B ⨯: n m C ⨯:r m D ⨯:A 称为系统矩阵,描述系统内部状态之间的联系;B为输入(或控制)矩阵,表示输入对每个状态变量的作用情况;C 输出矩阵,表示输出与每个状态变量间的组成关系,D直接传递矩阵,表示输入对输出的直接传递关系。
2. 状态空间描述的特点①考虑了“输入-状态-输出”这一过程,它揭示了问题的本质,即输入引起了状态的变化,而状态决定了输出。
②状态方程和输出方程都是运动方程。
③状态变量个数等于系统包含的独立贮能元件的个数,n 阶系统有n 个状态变量可以选择。
④状态变量的选择不唯一。
⑤从便于控制系统的构成来说,把状态变量选为可测量或可观察的量更为合适。
⑥建立状态空间描述的步骤:a 选择状态变量;b 列写微分方程并化为状态变量的一阶微分方程组;c 将一阶微分方程组化为向量矩阵形式,即为状态空间描述。
⑦状态空间分析法是时域内的一种矩阵运算方法,特别适合于用计算机计算。
3. 模拟结构图(积分器 加法器 比例器)已知状态空间描述,绘制模拟结构图的步骤:积分器的数目应等于状态变量数,将他们画在适当的位置,每个积分器的输出表示相应的某个状态变量,然后根据状态空间表达式画出相应的加法器和比例器,最后用箭头将这些元件连接起来。
4. 状态空间表达式的建立① 由系统框图建立状态空间表达式:a 将各个环节(放大、积分、惯性等)变成相应的模拟结构图;b 每个积分器的输出选作i x ,输入则为i x;c 由模拟图写出状态方程和输出方程。
② 由系统的机理出发建立状态空间表达式:如电路系统。
通常选电容上的电压和电感上的电流作为状态变量。
利用KVL 和KCL 列微分方程,整理。
现代控制理论-状态方程的解

3、复频域上
非齐次状态方程的解
2、说明
e At 状态转移矩阵
一般用 t 表示,即 t e At
考虑初始条件拉氏变换
sX ( s ) X (0 ) AX ( s ) BU ( s ) 有 ( sI A) 1 X ( s ) X ( 0 ) BU ( s ) 即 1 X ( s ) ( sI A) X (0) ( sI A) 1 BU ( s ) 则
e
d At e Ae At e At A dt
At 1
e At
[5]、对于 n n的方阵 A、 B 当且仅当 AB BA时 有 e At e Bt e( A B)t , 而当AB BA, e At e Bt e( A B)t。
电气工程学院
几个特殊的矩阵指数eAt
设单变量系统的差分方程为:
y(k n) an1 y(k n 1) a0 y(k ) bnu(k n) bn1u(k n 1) b0u(k )
相应的系统脉冲传递函数为
bn z n bn 1 z n 1 b1 z b0 G( z ) n z an 1 z n 1 a1 z a0
有
d At At AX ] e X e [X dt e At Bu(t )
考虑初始条件 拉氏变换得 sX ( s ) X ( 0 ) AX ( s )
将上式积分有 t t X (t ) 1 ( sI A) 1 X (0) A d A e Bu( ) d d e X ( ) 0 0 d 1 显然 e At 1 t ( sI A) At A X ( 0 ) e X ( t ) e 可得 At Bu( )d
《自动控制原理》线性定常连续系统状态方程的解

2
k!
= P −1IP + P −1 APt + 1 P −1 A2 Pt 2 + + 1 P −1 Ak Pt k +
2
k!
= P −1 (I + At + 1 A2t 2 + + 1 Ak t k + )P = P −1e At P
2
k!
因而式(9-39)成立。
性质10: 两种常见的状态转移矩阵。设 A = diag[1, 2 ,,n ],
2. 拉普拉斯变换法。将式(9-22)取拉氏变换有
sX (s) = AX (s) + x(0)
则
(sI − A) X (s) = x(0)
X (s) = (sI − A)−1 x(0)
(9-27)
进行拉氏反变换有
x(t) = −1[(sI − A)−1]x(0)
(9-28)
与(9-25)相比有
e At = −1[(sI − A)−1 ]
进行拉氏反变换有 x(t) = −1(sI − A)−1 x(0) + −1[(sI − A)−1 BU (s)]
由拉氏变换卷积定理
−1[F1(s)F2 (s)] =
t
0 f1 (t − ) f2 ( )d
=
t
0 f1 ( ) f2 (t − )d
在此将(sI − A)−1 视为F1 (s),将BU (s) 视为 F2 (s) ,则有
x(t) = eA(t) x(0) + t eA(t− )Bu( )d 0 t = (t)x(0) + 0 (t − )Bu( )d
结果与式(9-43)相同。上式又可表示为
2-1 线性定常系统的解及转移矩阵

A(t t0 )
x(t0 )
(8)
将(8)式代入(1)式验证
x (t )
和
d x (t ) A e A(t t0 ) x (t0 ) Ax (t ) dt x (t ) t t e A(t0 t0 ) x (t0 ) x (t0 )
0
矩阵指数函数
e
A ( t t 0 )
即
(t ) A (t ) (t ) A
e A0 I
即
(0) I
3)可逆性 即 4)传递性
e
(t )
e
1
At 1
e At
1 (t ) (t )
A( t 2 t1 ) A( t1 t0 )
即
5)当且仅当
(t2 t1 ) (t1 t0 ) (t2 t0 )
根据凯莱-哈密顿定理
Δ( A) An an1 An1 a2 A2 a1 A a0 I 0 An an1 An1 a2 A2 a1 A - a0 I
例 解
3 9 用凯莱-哈密顿定理计算 2 6 λ 3 9 Δ( λ) det λ2 9λ 0 2 λ 6
1)A 的特征值互异 应用凯-哈定理, λi 和 A 都满足 A 的特征方程。因此, λi 也可以 满足(13)式。
e λit a0 (t ) a1 (t ) λi a2 (t ) λi2 an1 (t ) λin1
(其中,i 1,2,, n ) 写成矩阵形式 e λ1t 1 λ1 λ2t e 1 λ2 λnt e 1 λn 于是
2
100
线性定常连续系统状态方程的解

...
eAtI
AtA2t2
...Aktk
...
2!
k!
其中eAt称为时间t的矩阵指数函数,并有
L1[(sIA)1]L1Is
A s2
A2 s3
.
..
Ak1 sk
.
..
I AtA2t2 ...Aktk ...
2!
k!
eAt
❖ 因此,基于上述(sI-A)-1的拉氏反变换,该齐次方程的解为
x(t)=L-1[(sI-A)-1]x0 = eAt x0
sI A s2 3s 2 (s 1)(s 2)
(sI
A)1
adj(sI A) sI A
(s
1 1)(s
ห้องสมุดไป่ตู้
2)
s 3
2
1 s
2 s 1
1 s2
s
2
1
s
2
2
1 s 1
1 s2
s
1 1
s
2
2
(2) 计算矩阵指数函数eAt。
e At L1[( sI A)1]
L1
s
证明 由指数矩阵函数的展开式,有
eAetAsIA t A 2!2t2... A k!ktk...IAsA 2!2s2... A k!ksk...
IA(ts)A2(t22tss2)... Ak(ts)k...
2!
k!
eA(ts)
3) [Φ(t2-t1)]-1=Φ(t1-t2)
e A ( t 2 t 1 ) 1 e A ( t 2 t 1 ) e A ( t 1 t 2 )
2. 矩阵指数函数和状态转移矩阵的性质
❖ 由矩阵指数函数的展开式和状态转移矩阵的定义,可证明矩 阵指数函数和状态转移矩阵具有如下性质(Φ(t)为方阵A的状 态转移矩阵) 1) Φ(0)=eA0=I
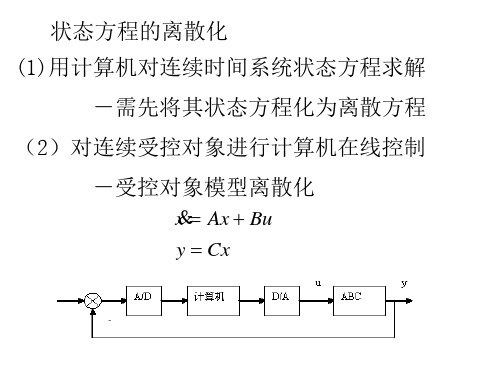
离散化的状态方程
T ∫0
I ⋅ B ⋅ dt = BT
结论:上式为近似计算方法 例2.6 已知时变系统
0 5(1 − e −5t ) 5 5e −5t u ɺ x= x + −5t −5t 0 5(e − 1) 0 5(1 − e )
试将它离散化,并求出输入和初始条件分别为
0, x(0) = 0时,方程在采样时刻的近似解 u (t ) = 0 1
1 (3)H(T) = ∫ 0 0
T T 1/ 2(1−e )0 1 dt= ∫0 −2t e 1 0 −2t −2t
x 1 [( k + 1)T] x 1 (kT ) (4) = [G (T)] x (kT ) + [H (kT) U (kT)] x 2 [( k + 1)T] 2
归纳:将连续状态方程离散化步骤
1、求Φ(t )=e = L [ SI − A] 2、G(T ) = Φ(T ) = Φ(t ) t = T T At 3、求H (T ) = ∫0 e Bdt 4、求x[(k + 1)T ] = G(T ) x(kT ) + H (T )u (kT )
At
−1
−1
例2.5已知控制对象满足 1 x + 0u,求其离散化方程 ɺ = 0 x 0 1 −2
系统离散状态方程(T=0.1) 可见T较小时, x1[(k + 1)T ] 0.9 0.1 x1(kT ) 0 = + r (kT ) 两种方法得 x2[(k + 1)T ] − 0.1 0.9 x2 (kT ) 0.1 状态空间表 x1(kT ) 达式近似相 输出y(kT ) = [1 0] 等。 x2 (kT ) 离散方程求解可按2.3递推法或Z变换求解
现代控制工程简答题

现代控制工程简答题1、控制系统的基本构成及特点。
2、现代控制理论的主要内容。
3、控制系统的状态空间描述及意义。
4、线性定常非齐次连续系统状态(方程解)的动态特性。
参考答案:1、控制系统主要由具有动态特性的被控对象系统、实现控制作用的控制机构、完成数据收集的检测机构,以及实现性能指标评价和信息处理的计算机构等部分构成。
控制系统的主要特点为:以动态系统为控制对象,通过施加必要的操作,实现对象系统状态按照指定的规律进行变化,达到某一特定功能;强调动态过程和动态行为的目的性、稳定性、能观测性、可控性、最优性以及时实性等;控制系统的数学模型主要用微分方程描述,设计方法为动态优化方法。
,2、主要包括五个方面:①线性系统理论(状态空间描述、能控性、能观测性和稳定性分析,状态反馈、状态观测器及补偿理论和设计方法),②建摸和系统辩识(模型结构及参数辩识方法论、参数估计理论),③最优滤波理论(卡尔曼滤波理论),④最优控制理论(经典变分法、最大值原理法、动态规划法),⑤自适应控制理论(模型参考自适应控制方法论、自校正控制方法论、鲁棒稳定自适应理论等)。
3、控制系统的状态空间描述:由状态方程和输出方程组成的状态空间表达式。
状态方程是一个一阶微分方程组,描述系统输入与系统状态的变化关系,即系统的内部描述;输出方程是一个代数方程,主要描述系统状态与系统输出的关系,即系统的外部描述。
意义:状态空间描述反映了控制系统的全部信息,是对系统特性的全部描述,是实现现代控制系统分析、设计的重要手段。
4、线性定常非齐次连续系统状态(方程解)的一般形式为:动态特性:系统状态的动态运动(随时间变化过程)受两部分作用,第一部分为系统初始状态的转移作用,即系统的自由运动项;第二部分为控制输入信号激励下的受控作用,即系统的强迫运动项。
适当选择控制输入,可使系统状态在状态空间中获得满足要求的最佳轨线。
1、控制工程理论(控制科学)的基本任务及广义定义。
线性系统的运动分析

A 有二种标准形式: 对角线矩阵、约当矩阵
(1)当A的特征值 1, 2,, n 为两两相异时:对角线标准型
e1t
0
e At Te AtT1 T
T 1
0
ent
其中: T为使A化为对角线标准型的非奇异变换矩阵。
求状态转移矩阵的步骤:
1) 先求得A阵的特征值 i 。
2) 求对应于 i 的特征向量 pi ,并得到T阵及T的逆阵。
j0
其中: a0(t), a1(t),, an1(t) 为t的标量函数,可按A的特 征值确定。
1) A的特征值 1, 2 ,, n 两两相异时,
注意求逆
a0(t)
1 1
12
n1 1
1
e 1t
a1 ( t )
1
1
22
n1 2
e
2t
an1 ( t )
1
1
2n
n1 n
e
nt
三、几个特殊的矩阵指数函数
(1)设 A diag 1 n ,即A为对角阵且具有互异元素时,
有
e1t
Φt
e2t
0
0
ent
(2)若A能通过非奇异变换为对角阵时,即
T -1AT Λ
e1t
ΦΦ(t)t
T
e2t
0
0
T
-1
(2-9)
ent
1
0
(3)设A为 (n n) 约当阵,即 A
a0
a1
(t (t
) )
1 1
1
1
e
1t
2
e
2t
在第3种方法中已经求得特征根,所以得:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(t 0)(0 ( )) (t ( )) (t )
(3)可逆性: Φ1(t) Φ(t)
由(1),(t t) I, 由(2),(t)(t) I.
可依此计算0时刻的状态值
x(t) Φ(t)x(0) x(0) Φ1(t)x(t) Φ(t)x(t)
x(t2) (t2 0)x(0)
(t2 ) (t2 t1)(t1 0)
2.2.2、状态转移矩阵的性质
(1)状态转移矩阵初始条件:
Φ(0) I
也即: (t t) I
意为状态向量从时刻 t 转移到t ,显然保持不变。
(2)组合性: (t)( )=(t )
dt
2!
k!
=A(I+At L 1 Akt k +L ) k!
x(t) eAtx0,t 0.
令:
eAt Φ(t)
e
A
(
t
t
0
)
Φ(t t0 )
则有:
状态转移矩阵
x(t) Φ(t)x(0) x(t) Φ(t t0 )x(t0 )
注1:对于线性定常系统来说,状态转移矩阵就是矩阵指数函数。
注2:状态转移矩阵的物理意义:
x(0)
ax(0)(t
t0 )
1 a2 x(0)(t 2!
t0 )2
L
1 ak k!
x(0)(t
t0
)k
L
x(t) Ax(t)
向量
仿照标量 x(t) b0 b1(t t0 ) b2 (t t0 )2 L bk (t t0 )k L 微分方程:
从时间角度看,状态转移矩阵使状态向量随着时间的推移不断地
在状态空间中作转移,故称为状态转移矩阵
x2
x(0)
x(t1 )
0
t1
x(t2 )
t t2
x1
(t1 0)
(t2 t1 )
x(t1) (t1 0)x(0)
x(t2) (t2 t1)x(t1)
x(t2) (t2 t1)(t1 0)x(0)
代入微分方程: x&(t) Ax(t) A(b0 b1(t t0 ) b2 (t t0 )2 L bk (t t0 )k L ) 对 x(t )求导: x&(t) b1 2b2 (t t0 ) 3b3 (t t0 )2 L kbk (t t0 )k 1 L
其解即为自由解。
x(t) |t t0 x(0)
非齐次状态方程:
x Ax Bu, x(t) |tt0 x(t0 )
其解为自由运动和强迫运动之和。
2.1.2、齐次状态方程的解:
状态方程
x(t) Ax(t)
求 x(t) ?
启发:一阶标量微分方程 x&(t) ax(t), x(t0 ) x(0)
u0
x
( A, B)
x& Ax , x(t) |t t0 x(0)
2)强迫运动(零初态响应):线性定常系统在只有输入作用而无初始状态作用
下的运动,称为强迫运动。 u
x
( A, B)
x& Ax Bu , x(t ) |tt0 x(t0 ) 0
齐次状态方程: x& Ax ,
(4) Φ&(t) AΦ(t) Φ(t)A Φ(0) A
eAt I At 1 A2t2 L 1 Aktk L
2!
k!
(5)
AB BA e(AB)t eAteBt eBteAt
d eAt A 2 A2t L k Akt k 1 L
L
1 k!
Ak
(t
t0
)k
L
)x(t0)
x(t) eA(tt0 )x(t0 )
eA(tt0 )
I
A(t
t0
)
1 2!
A2
(t
t0
)2
L
1 k!
A矩k (阵t 指t0数)k函L数
结论:考虑齐次状态方程 x(t) Ax(t),
若初始状态为x(t0 ) x0, 其解为:x(t) eA(tt0)x0,t t0,
dx ax dx a dt ln x ln x(0) a(t t0 )
dt
x
x(t) ea(t t0 ) x(0)
指数函数:
ea(t t0 )
1 a(t t0 )
1 a2 2!
(t
t0
)2
L
1 ak (t k!
t0 )k
L
x(t)
若 t0 0, 其解为x(t) eAtx0,t 0.
矩阵指数 eAt 把系统的状态 x(0)转移到 x(t),也把它称为 状态转移矩阵,记为 (t) 。 (t) 是一般的表示形式
2.2 状态转移矩阵
2.2.1、状态转移矩阵的含义
线性定常系统的齐次状态方程的解:
x(t) eA(tt0)x0,t t0,
b0
Ab0
(t
t0
)
1 2!
A2b0
(t
t0
)2
L
1 k!
Akb0
(t
t0
)k
L
(I
A(t
t0
)
1 2!
A2
(t
t0
)2
L
1 k!
Ak
(t
t0
)k
L
) b0
t t0 x(t0 ) b0
x(t) (I A(t
t0)
1 2!
A2
(t
t0
)2
第二章 控制系统状态空间表达式的解
本章主要内容:
• 线性定常齐次状态方程的解(自由解) • 矩阵指数函数——状态转移矩阵 • 线性定常系统非齐次状态方程的解
2.1 线性定常齐次状态方程的解
2.1.1 线性定常系统的运动
1)自由运动(零输入响应):线性定常系统在没有控制作用,即u=0时,
由初始状态引起的运动称自由运动。
比较以上两式系数有:
b1 Ab0
32bb32
Ab1 Ab2
kb k Abk 1
b1 Ab0
b
2
b 3
1312AA2131!bb!A21A23bb00
b k
1
k
Ab1k k!
A1
k
b0
x(t) b0 b1 (t t0 ) b2 (t t0 )2 L bk (t t0 )k L
