Network Simplex Method网络单纯形法
运筹学单纯形法
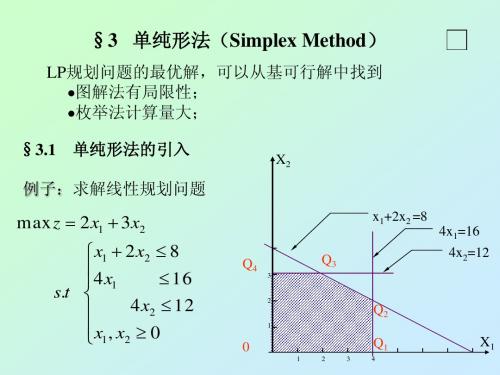
只要取 x5=min{-,8/2,12}=4 就有上式成立。 x5=4时, x4=0,故决定用x5换x4 x1 =4- 1/4 x4 x5 =4-1/2 x4 +2 x3 x2 =2+1/8 x4–1/2 x3 代入得 z=14-3/2 x3 –1/8 x4 ,令x3 ,x4=0得z=14。新基可 行解为 X(3) =(4,2,0,0,4) T –为最优解,新顶点Q2 最优目标值z=14 。
§3.4 最优性检验和判别定理
线性规划解的四种可能: 1、有唯一解; 2、无穷多最优解; 3、无界解; 4、无可行解。 何时达最优解, 何种最优解?
将基本可行解X(0)和X(1)分别代入目标函数得
z z
(0)
= ∑ ci xi0
i =1 m
mቤተ መጻሕፍቲ ባይዱ
(1)
= ∑ ci [ xi0 − θ aij ] + θ ci
§3.3 从初始基可行解转换为另一基可行解
0 0 记初始基可行解为X(0),有 X ( 0 ) = (x10 x 2 L x m 0 L 0
)
Pi xi0 = b 该解满足约束方程, 即 ∑
i =1
m
(1)
非基向量可以用基向量的线性组合表示
Pj = ∑ aij Pj
i =1 m
m
(2) (3)
Pj − ∑ aij Pj = 0
从实际例子中分析单纯形法原理的基本框架为 •第一步:将LP线性规划变标准型,确定一个初始可行解 (顶点)。 •第二步:对初始基可行解最优性判别,若最优,停止;否 则转下一步。 •第三步:从初始基可行解向相邻的基可行解(顶点)转 换,且使目标值有所改善—目标函数值增加,重复第二和 第三步直到找到最优解。
单纯形方法(SimplexMethod)

单纯形⽅法(SimplexMethod)最近在上最优理论这门课,刚开始是线性规划部分,主要的⽅法就是单纯形⽅法,学完之后做了⼀下⼤M算法和分段法的仿真,拿出来与⼤家分享⼀下。
单纯形⽅法是求解线性规划问题的⼀种基本⽅法。
线性规划就是在⼀系列不等式约束下求⽬标函数最⼤值或最⼩值的问题,要把数学中的线性规划问题⽤计算机来解决,⾸先要确定⼀个标准形式。
将所给的线性规划问题化为标准形式:s.t.是英⽂subject to 的简写,意思是受约束,也就是说第⼀个⽅程受到后⾯两个⽅程的约束。
对于求最⼤值问题可以将⽬标函数加负号转换为最⼩值问题。
对于求最⼤值问题可以将⽬标函数加负号转换为最⼩值问题。
其他的问题就是将实际问题中的不等式约束改为等式约束,主要⽅法是引进松弛变量和剩余变量,以及将⾃有变量转换为⾮负变量。
①对于不等式,引⼊松弛变量将其变为等式形式如下:②对于不等式,引⼊剩余变量将其变为等式形式如下:③若变量为⾃有变量(可取正、负或零,符号⽆限制),则引⼊两个⾮负变量将其表⽰如下:关于线性规划问题的解:确定了标准形式,我们就针对这个标准形式讨论⼀下线性规划问题的解。
线性规划问题的解能满⾜标准形式中约束条件的向量X的值,但只有最优解才能使⽬标函数值最⼩。
对于上⽂中的标准形式,约束矩阵A是⼀个m*n维矩阵,且m<n,所以⼀定可以从A中找到⼀个满秩m*m矩阵。
这个矩阵就称作矩阵A的⼀个基阵,矩阵A就可以写作 [B N] , 相应的解 x 也可以写成 x=(xB,xN)’,那么 Ax=b 就变为,左式两端同乘B矩阵的逆,得到。
由此引出下列名词:基阵:⾮奇异矩阵(满秩矩阵、可逆矩阵)B基向量:基阵B由m个线性⽆关的向量组成,称之为基向量基变量:向量xB各分量,与基向量对应的xB中的m个分量成为基变量⾮基变量:向量xN各分量基本解:令xN各分量为0,由得到的解称为基阵B对应的基本解基本可⾏解:当成⽴时,称基本解为基本可⾏解,因为只有满⾜所有分量不⼩于0,才符合标准形式中的约束条件(最后⼀条)。
单纯形法

cj 基 解
3 5 000 x1 x2 x3 x4 x5
0 x3 8 1 0
5 x2 6 0 1
第 0 x5 12 3 0
二
次
30 -3 0
迭 代
0
x3
4
5 x2 6
00 01
3 x1 4
10
1 00 0 1/2 0 0 -2 1
0 5/2 0 1 2/3 -1/3 0 1/2 0 0 -2/3 1/3
Simplex Method 第二章 单纯形法
SM
第2章 单纯形法
2.1 单纯形法的基本思想 2.2 单纯形法的计算过程 2.3 人工变量法 2.4 单纯形法补遗
2
第2章 单纯形法
2.1 单纯形法的基本思想
单纯形法有三种形式: ① 方程组形式 ② 表格形式 ③ 矩阵形式
2.1.1 方程组形式的单纯形法
2x2 0 +1x4 0 = 12 ②
3x1 + 4x2 0 0 +1x5 = 36 ③
条典
⑴ 当前基:m阶排列阵 ⑵ 目标方程中:一切基变量
的系数 σj = 0
满足条典的方程组称为典式(方程组)。 初始基本可行解
排列阵:
每行每列有且仅有一个元素 为1,其余元素全为0 的方阵。
X0 = (0, 0, 8, 12, 36)T z0 = 0
2.3 人工变量法
考虑标准型 (M): 分别给每个约束方程硬性加入一个非负变量
a11x1 +a12x2+…+a1nxn +xn+1
a12x1 +a22x2+…+a2nxn
+xn+2
… … ………
单纯形法

单纯形法simplex method求解线性规划问题的通用方法。
单纯形是美国数学家G.B.丹齐克于1947年首先提出来的。
它的理论根据是:线性规划问题的可行域是n维向量空间Rn中的多面凸集,其最优值如果存在必在该凸集的某顶点处达到。
顶点所对应的可行解称为基本可行解。
单纯形法的基本思想是:先找出一个基本可行解,对它进行鉴别,看是否是最优解;若不是,则按照一定法则转换到另一改进的基本可行解,再鉴别;若仍不是,则再转换,按此重复进行。
因基本可行解的个数有限,故经有限次转换必能得出问题的最优解。
如果问题无最优解也可用此法判别。
根据单纯形法的原理,在线性规划问题中,决策变量(控制变量)x1,x2,…x n的值称为一个解,满足所有的约束条件的解称为可行解。
使目标函数达到最大值(或最小值)的可行解称为最优解。
这样,一个最优解能在整个由约束条件所确定的可行区域内使目标函数达到最大值(或最小值)。
求解线性规划问题的目的就是要找出最优解。
最优解可能出现下列情况之一:①存在着一个最优解;②存在着无穷多个最优解;③不存在最优解,这只在两种情况下发生,即没有可行解或各项约束条件不阻止目标函数的值无限增大(或向负的方向无限增大)。
单纯形法的一般解题步骤可归纳如下:①把线性规划问题的约束方程组表达成典范型方程组,找出基本可行解作为初始基本可行解。
②若基本可行解不存在,即约束条件有矛盾,则问题无解。
③若基本可行解存在,从初始基本可行解作为起点,根据最优性条件和可行性条件,引入非基变量取代某一基变量,找出目标函数值更优的另一基本可行解。
④按步骤3进行迭代,直到对应检验数满足最优性条件(这时目标函数值不能再改善),即得到问题的最优解。
⑤若迭代过程中发现问题的目标函数值无界,则终止迭代。
用单纯形法求解线性规划问题所需的迭代次数主要取决于约束条件的个数。
现在一般的线性规划问题都是应用单纯形法标准软件在计算机上求解,对于具有106个决策变量和104个约束条件的线性规划问题已能在计算机上解得。
单纯形法——精选推荐

单纯形法单纯形法的基本思想(Simplex method )简要地讲就是,每次从单纯形上的⼀个顶点⾛到⼀个更好的顶点直到找到最⼩(⼤)值。
线性规划是由两部分组成的:线性的⽬标函数和线性的限制条件。
限制条件由等式和不等式组成。
每⼀个线性的等式在⼏何上就限制了可⾏解必须在⼀个超平⾯上。
每⼀个线性的不等式在⼏何上就限制了可⾏解必须在⼀个超平⾯的⼀边。
于是这些限制条件就限制了可⾏解必须在某个单纯形上,所谓单纯形就是很多超平⾯围成的区域。
由于⽬标函数也是线性的,所以如果最优解存在,⼀定有⼀个最优解是单纯形上的⼀个顶点。
所以⽬标变成了找单纯形上最好的顶点。
最好的顶点怎么找?最直接的办法就是逐个找。
聪明⼀点的办法是,每次找到的新的顶点都⽐原来的好。
单纯形法就是这类⽅法。
问题描述min z =CXs.t.AX =b X ≥0单纯形法基本思路:从⼀个初始的基本可⾏解出发,选中⼀条达到最优基本可⾏解的最佳途径。
确定初始的基本可⾏解约束⽅程AX =b 表⽰为:AX =(B N )X B X N=BX B +NX N =b得:X B =B −1b −B −1NX N 若令所有⾮基变量X N =0,则基变量X B =B −1b由此可得初始的基本可⾏解X =B −1b 0判断现⾏的基本可⾏解是否最优假如已经求得⼀个基本可⾏解X =B −1b 0将其代⼊⽬标函数,可求得相应的⽬标函数值z =CX =C B C NB −1b 0=C B B −1b其中,C B 和C N 分别表⽰基变量和⾮基变量所对应的⽬标函数系数⼦向量.怎么判断C B B −1b 是否已经达到最⼩值?min z =C BB −1b+(C N −C BB −1N )XN s.t.X B =B −1b −B −1NX N X B ,X N ≥0定理1 (最优化准则)如果σN ≥0,则基可⾏解x =B −1b 0为原问题的最优解.其中,σN =C N −C B B −1N =(σm +1,σm +2,⋯,σn )称为⾮基变量X N 的检验向量,它的各个分量称为检验数.若σN 的每⼀个检验数均⼤于等于0,即σN ≥0,则⽬前的基本可⾏解就是最优解.()()()()()()基本可⾏解的改建— 基变换先从检验数为负的⾮基变量中确定⼀个换⼊变量,使它从⾮基变量变成基变量,再从原来的基变量中确定⼀个换出变量,试它从基变量变成⾮基变量,由此可得到⼀个新的基本可⾏解.换⼊变量的确定—最⼤减⼩原则选取最⼩负检验数所对应的⾮基变量为换⼊变量,即若min {σj |σj <0,m +1≤j ≤n }=σm +k则选取对应的x m +k 为换⼊变量.由于σm +k <0且为最⼩,因此当x m +k 由零增⾄正值时,可使⽬标函数值最⼤限度的减⼩.换出变量的确定—最⼩⽐值原则如果确定确定x m +k 为换⼊变量,设p m +k 为A 中与x m +k 对应的系数列向量.现在需要在X B 中确定⼀个基变量为换出变量. 当x m +k 由零慢慢增加到某个值时,为保持解的⾮负性,可以按最⼩⽐值原则确定换出变量:θ=min {(B −1b )i(B −1p m +k )i|(B−1p m +k )i >0,1≤i ≤m }=(B −1b )l(B −1p m +k )l则选取对应的基变量x l 为换出变量.例⼦min z =−5x 1−2x 2−3x 3+x 4−x 5s.t.x 1+2x 2+2x 3+x 4=83x 1+4x 2+x 3+x 5=7x 1,x 2,x 3,x 4,x 5≥0解:已知A =1221034101,b =87,C =(−5,−2,−3,1,−1)1. 确定初始基本可⾏解基变量x 4,x 5,B =P 4P 5=1001,X B =x 4x 5T ,X N =x 1x 2x 3T ,B =1001,N =122341,C B =1−1,X N =−5−2−3b =87T令X N =0,则X B =B −1b =87T ,X =00087Tz =C B B −1b =11. 检验X 是否最优检验向量σN =C N −C B B −1N =(−3,0,−4)因为σ1和σ3均⼩于0,所以X =00087T 不是最优解.1. 基本可⾏解的改进(1)选取换⼊变量{[][]()[]()()[][]()()()()()()因为min {−3,−4}=−4,选取x 3为换⼊变量(2)选取换出变量B −1b =87T ,B −1P 3=21T >0,因为min {82,71}=82,选取x 4为换出变量.1. 求解改进了的基本可⾏解— 旋转运算对约束⽅程组的增⼴矩阵A b 施以初等⾏变换,使换⼊变量x 3所对应的系数向量P 2变换成换出向量x 4所对应的单位向量P 4,保持x 5的系数向量P 5为单位向量不变.122108341017⇒121112045230−1213基变量x 3,x 5,B =P 3P 5=1001,X B =x 3x 5T ,X N =x 1x 2x 4T ,B =1001,N =12112523−12,C B =−3−1,X N =−5−2−1b =43T令X N =0,则X B =B −1b =43T ,X =00403Tz =C B B −1b =−151. 转2,检验X 是否最优检验向量σN =C N −C B B −1N =(−1,4,2)因为σ1⼩于0,所以X =00403T 不是最优解.1. 转3,基本可⾏解的改进(1)选取换⼊变量因为σ1=−1,选取x 1为换⼊变量(2)选取换出变量B −1b =43T ,B −1P 3=1252T>0,因为min {41/2,35/2}=35/2,选取x5为换出变量.1. 转4,求解改进了的基本可⾏解对约束⽅程组的增⼴矩阵施以初等⾏变换,使换⼊变量x 1所对应的系数向量P 1变换成换出向量x 5所对应的单位向量P 5,保持x 3的系数向量P 3为单位向量不变.()()[]()()()[]()()[][]()()()()()()()()121112045230−1213⇒25135−151751650−152565基变量x3,x1,B=P3P1=10 01,X B=x3x1T,X N=x2x4x5T,B=1001,N=2535−1565−1525,C B=−3−5,X N=−21−1b=17565T令X N=0,则X B=B−1b=17565T,X=65017500Tz=C B B−1b=−8151. 转2,检验X是否最优检验向量σN=C N−C B B−1N=(265,95,25)因为所有检验系数均⼩于0,所以X=65017500T是最优解.参考资料()() ()[]()()[][]()()()()()()Processing math: 100%。
第二章 单纯形法

最小比值规则
当确定进基变量后, 当确定进基变量后,以进基变量的系数列向量 中的正数为分母, 中的正数为分母,以相应的方程右端常数为分子求 最小比值,所得到的最小比值的分母就是主元 主元. 最小比值,所得到的最小比值的分母就是主元.主 元所在的方程中的基变量就是离基变量 离基变量. 元所在的方程中的基变量就是离基变量.即:
bi bl min α ik > 0 = a ik a lk
令新的非基变量 x3 = x 4 = 0 ,得到新的 基本可行解: 基本可行解: T 经济含义—— 经济含义—— 分别生产甲,乙产品20 20个 分别生产甲,乙产品20个,此时可获得 利润200百元. 200百元 利润200百元.
几个名词
进基, 进基,进基变量 离基, 离基,离基变量 最大检验数规则 最小比值规则 主元/ 主元/主方程 迭代(旋转运算) 迭代(旋转运算)
增加单位产品甲比乙对目标函数 的贡献值大(600>400),故先把非 的贡献值大(600>400),故先把非 ), 变成基变量, 基变量 x1 变成基变量,称为让 x1 进基, 进基变量. 进基,同时称 x1 为进基变量.
R( A) = R( A, b ) = 3 < 5
则该函数约束等式方程组有无穷多组解. 则该函数约束等式方程组有无穷多组解.
分析目标函数表达式
max z = 6 x1 + 4 x 2 + 0 x3 + 0 x 4
非基变量的系数都是正数,若将它们转换 非基变量的系数都是正数, 为基变量,目标函数值则就会可能增加. 为基变量,目标函数值则就会可能增加. 经济含义:每分别多生产一个单位产品甲, 经济含义:每分别多生产一个单位产品甲, 目标函数值分别增加6 乙,目标函数值分别增加6,4,即利润分 别增加600 600元 400元 别增加600元, 400元.
单纯形法

定理2.2 定理
在已知一个基本可行 初始基本可行解)的前提下, 解(初始基本可行解)的前提下, 使用单纯形法求解线性规划时, 使用单纯形法求解线性规划时,若 每次迭代得出的基本可行解的基变 量均大于零(称为非退化), ),则算 量均大于零(称为非退化),则算 法必有限步终止。 法必有限步终止。
P22
min z = 9 10 x1 +27 x3 s.t. x2 = 5 + x1 3x3 x4 = 6 2 x1 + 4 x3 x1 , x2 , x3 , x4 ≥ 0 T 是否为(2.9)的最优解 判断 (0,5,0,6) 是否为(2.9)的最优解
1 0 0 0 1 0
T
(2.9)
-2 1 7
0 0 1 0 -1/5 2/5 3/5 1/5
4 2 5 16 3 4 3 17
从表中知( , , , , ) 从表中知(4,3,3,0,0)T为最优 略去松弛变量, 解,略去松弛变量,得:
x = (4,3)
T
——最优解 最优解Fra bibliotekz = 17
——最优值 最优值
§2.5
大M法 法
引入:问题提出, 引入:问题提出,当初始 基本可行解不知道时, 基本可行解不知道时,如何 求解? 求解? 先利用容许的运算使右列 为非负, 为非负,然后在中心部位人 工地添加一个单位子块。 工地添加一个单位子块。
最优解的读法: 最优解的读法: 单位子块中1所对应的变量取相应右列的值, 单位子块中 所对应的变量取相应右列的值,不在 所对应的变量取相应右列的值 单位子块位置中的变量取值为0。 单位子块位置中的变量取值为 。而右下端元素变号 即为LP的最优值 的最优值。 即为 的最优值。 单纯形法的步骤: 单纯形法的步骤:
运筹学术语(新版11)

翻译以下英文术语,并深入了解术语的含义。
1.optimal solution:最优解,使目标函数取得最大值的可行解。
P352.objective function:目标函数,指需优化的量,即欲达的目标,用决策变量的表达式表示。
P123.feasible region:可行域,指所有可行解的集合。
P284. simplex method:单纯形法:是一种迭代的算法,其核心思想是不仅将取值范围限制在顶点上,而且保证每换一个顶点,目标函数值都有所改善.P1175. BF solutions:基可行解,满足变量非负约束条件的基解称为基可行解。
P1816. sensitivity analysis:敏感性分析:指对系统或事物因周围条件变化显示出来的敏感程度的分析。
P1467. algorithm:算法,指系统的求解过程。
p1078. spanning tree:生成树,若有限图的生成子图是一棵树,则称为该图的生成树。
树指不含有圈的连通网。
P3799. states:状态,各阶段开始时的客观条件. P44510.directed arc:有向弧,指通过一条弧的流只有一个方向的弧。
P37611. unbounded:无界,指约束条件不能阻止目标函数值在有利的方向上(正的或者负的)增长。
P3512. CPF solution:顶点(角点)可行解,指位于可行域顶点的解。
P3713. functional constraints:约束条件,指决策变量取值时受到的各种资源条件的限制,通常表达为含决策变量的等式或不等式。
P3414 multiple optimal solutions:多个最优解的问题,指有无穷多解,每一个解都有相同的目标函数值的问题。
P12215. slack variable:松弛变量,添加x i到约束条件的不等式中使其变为等式的变量P10816. augmented solution:增广解,指原始变量(决策变量)取值再加入相应的松弛变量取值后而形成的解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fatme Elmoukaddem Jignesh Patel Martin Porcelli
Outline
• Definitions • Economic Interpretation • Algebraic Explanation • Initialization • Termination
Network
• A network is a collection of nodes connected by arcs
• Each node has a demand for the commodity
– Nodes that are sources of the commodity have a negative demand
i
LP Formulation (2)
• Let A be the matrix indexed by the set of nodes x the set of arcs
– Ai,jk is either
• -1 if i=j • 1 if i=k • 0 otherwise
• A is known as the incidence matrix of the network
3
Algebraic Description (Step 1)
• We define c’ = c – yA. • c’ is the difference between the cost of an arc
and the value difference across the arc. • If ij T then c’ij = cij + yi – yj = 0. • If ij T and if c’ij < 0 then ij is candidate for
Transshipment Problem
• Find the cheapest way to ship prescribed amounts of a commodity from specified origins to specified destinations through a transportation network
• Let b be a column vector indexed by the set of nodes
– bi is the demand at i
Example
-5 1
4 5
3
12
7
43
33 1
9
5 5 -2
c 54739 1 5
x 12
x 13
x
entering arc. • Also if ij T then xij = 0, combining with above
we get c’x = 0 ( ij, either c’ij = 0 or xij=0).
Algebraic Description (Step 1)
-5 1
7
3
• If no such arc exists then c’ ≥ 0 and so c’x’ ≥ 0.
• Hence equation (1) implies cx’ ≥ cx for every feasible solution x’, and so x’ is optimal.
• If we find such an arc e, we it to the tree T.
x x
14 23
x 25
x 35
x 54
b 5133 2
LP Formulation
minimize cx cij xij subject to
ij
ij
xij 0
i
x ji xij bi
ji
ij
bi 0
3 1
0
12
1 43
33 0
0
2 5 -2
LP Formulation
• Let c be a row vector and x a column vector indexed by the set of arcs
– cij is the cost of shipping over ij – xij is the amount to ship over ij
• c is the cost (row) vector, b is the demand (column) vector, and A is the incidence matrix.
Algebraic Description (Step 1)
-5 1
7
3
4
-5 1
3
3
4
G: 1
3
5
T: 2
0
0
2 0
3
9
2
2
0
2
A
x
12 14 23 24 34
2
y
0 1 10 7
1 1 1 0 0 0
2
1
0
1 1
0
3 0 0 1 0 1
4
0
1
0
1
1
3 2 0 0
c 1 7 9 3 5
3 2
b
5
0
2
52
Optimality
• If no arc like ki exists, then your prices can not be undercut
– A competitor could break even at best
Algebraic Description (Step 1)
• Each step begins with a feasible tree solution x defined by a tree T.
– The sum of all the demands is zero
• Each arc has a cost to ship a unit of commodity over it
Example
-5 1
4 5
3
12
7 43
33 1
9
5 5 -2
Schedule
• A schedule describes how much of the commodity is shipped over each arc
0
2
3
1 7 9 3 5 c' 0 0 0 -3 8
Algebraic Description (Step 1)
• For any feasible solution x’ (i.e. Ax’ = b,
x’ ≥ 0), its cost is
cx’ = (c’ + yA)x’
– You want to ship as much as possible – You must also adjust the rest of your
schedule to conform with demand
Example
01
4 5
3
52
7 38
47 01
4
5
5
7 34
5 2 52
47 5
• A feasible tree solution x associated with a spanning tree T is a feasible solution with
– xij = 0 if ij is not an arc of T
Network Simplex Method
• Search through feasible tree solutions to find the optimal solution
cx’ = cx + c’x’
(1)
• So if c’x’ < 0 then x’ is a better solution than x.
Algebraic Description (Step 2)
• In step 2 we find an arc e = uv such that yu + cuv < yv (i.e. c’uv < 0).
• Has a nice economic interpretation
Economic Interpretation
• Given a spanning tree T and an associated feasible tree solution x
• Imagine you are the only company that produces the commodity
• What price should you sell the commodity for at each node?
– Assume that you ship according to x
Price Setting
• You want to set the price yi at node i
• Requirements
– The amount entering a node minus the amount leaving it is equal to its demand
– The amount shipped over any arc is nonnegative
