【新课标】2018年最新沪教版(五四制)八年级数学下册同步练习:梯形
【新课标】2018年最新沪教版(五四制)八年级数学下册同步练习:平行四边形

2017-2018学年(新课标)沪教版五四制八年级下册22.2 平行四边形一、课本巩固练习1、如图所示,ABCD中,M,N,P,Q分别为AB,BC,CD,DA上的点,且AM=BN=CP=DQ,求证四边形MNPQ 为平行四边形。
2、如图,在□ABCD中,∠DAB=60°,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB.求证:四边形AFCE是平行四边形。
思考:若去掉已知条件的“∠DAB=60°,上述的结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.二、基础过关一、判断题1.一组对边平行,另一组对边相等的四边形一定是平行四边形。
( )2.在四边形ABCD 中,如果AB=BC ,CD=AD,那么四边形ABCD 一定是平行四边形。
( )3.如果在四边形中,有一组对边平行且相等,那么这个四边形一定是平行四边形。
( )4.若在四边形中,一组对边相等,另一组对角相等,那么此四边形一定是平行四边形。
( )5.如果四边形的一条对角线把四边形分成两个全等的三角形,那么此四边形一定是平行四边形。
( )6. 有两组内角分别相等的四边形一定是平行四边形。
( )7.如图,在ABCD 中,AC 为对角线,BE ⊥AC ,DF ⊥AC ,E 、F 为垂足, 求证:BE =DF .8、已知如图,O 为平行四边形ABCD 的对角线AC 的中点,EF 经过点O ,且与AB 交于E ,与CD 交于F 。
求证:四边形AECF 是平行四边形。
9. 如图,在Rt △ABC 中, ∠BAC=90°,延长BA 到D ,使AD=AB 21,点E,F 分别为边BC ,AC 的中点。
1)求证:四边形AEFD 是平行四边形。
2)若BC=10cm,求DF 的长。
3)若BC=10cm ,且∠C=30°,求四边形AEFD 的面积。
10、已知:如图43-1,在□ABCD中,AE⊥BC于E,AF⊥DC于F,∠EAF=60°,BE=2cm,DF=3cm。
上海数学八年级下梯形件
A
D
等腰梯形
B
C
A
D
直角梯形
B
C
第5页/共15页
思考:
D
如图:DE//BC分别交△ABC的
边AB、AC于D,E
B
得△ADE与四边形DECB
那么:四边形DECB是梯形吗?
A
E
C A
D
E
满足什么条件时,
B
C
四边形DECB是直角梯形?
A
满足什么条件时,四边形DECB
D
E
是等腰梯形?
B
C
第6页/共15页
例题1:
第14页/共15页
感谢您的观看。
第15页/共15页
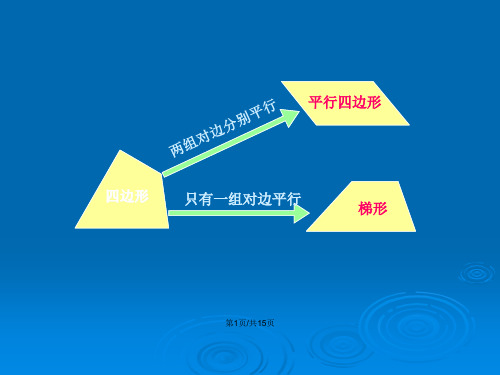
平行四边形
四边形 只有一组对边平行
梯形
第1页/共15页
定义: 一组对边平行而另一组对 边不平行的四边形叫做梯形.
第2页/共15页
想一想
下列四边形一定是梯形吗?
1. 一组对边平行;
A
D
2. 一组对边平行且不相等;
3. 一组对边平行另组对边不平行;
4. 一组对边平行另组对边不相等. B
C
梯形ABCD中,AD∥BC,
A
D
B
C
第8页/共15页
梯形中常用的辅助线:
第9页/共15页
小试牛刀1:
在直角梯形ABCD中,AD//BC,∠A=90°,
A D AD=10cm, DC=13cm,BC=15cm,求AB的长。
B
C
第10页/共15页
小试牛刀2:
如图:有一块四边形土地ABCD,测得AD=26m, CD=10m,BC=5m,顶点D、C到AB的距离分别是 10m,4m;求这块地的面积。
沪教版八年级 梯形,带答案

1.掌握等腰梯形的性质定理、判定定理,并能应用这些定理进行计算和证明;2.会添加适当的辅助线,将等腰梯形问题转化成三角形、平行四边形等熟知的几何图形来解决问题.(此环节设计时间在10-15分钟)教法说明:首先回顾上次课的预习思考内容,归纳总结梯形的性质与判定. 1.在箭头上填上适当的条件2.回顾等腰梯形的性质与判定,完成下表:边 角 对角线 对称性等腰梯形 两底平行 两腰相等同底上的两底角相等对角线相等轴对称等腰梯形的判定方法 边 两腰相等的梯形 角 同底上两底角相等的梯形 对角线对角线相等的梯形练习一组对边平行,另一组对边不平行有一个角是直角两腰相等四边形梯形直角梯形等腰梯形1.如图,在等腰梯形ABCD 中,AD ∥BC ,对角线AC ,BD 相交于点O ,有如下四个结论:①AC =BD ; ②AC ⊥BD ; ③等腰梯形ABCD 是中心对称图形; ④△AOB ≌△DOC .则正确的结论是( ) A 、①④ B 、②③ C 、①②③ D 、①②③④2.在梯形ABCD 中,AD ∥BC ,∠B =65°,∠C =75°,则∠D =________,∠A =_______.3.如图,在梯形ABCD 中,如果AD ∥BC ,AB =CD ,∠B =60°,AC ⊥AB ,那么∠ACD = ___ ___.参考答案:1.A ; 2.105°,115°; 3.30°.(此环节设计时间在50-60分钟)例题1:已知:如图,AM 是△ABC 的中线,D 是线段AM 的中点,AM =AC ,AE ∥BC . 求证:四边形EBCA 是等腰梯形.证明:∵AE ∥BC ,∴∠AED =∠MCD ,∠EAD =∠CMD .∵AD =MD ,∴△AED ≌△MCD . ∴AE =CM .∵BM =CM ,∴AE =BM .∴四边形AEBM 是平行四边形. ∴EB =AM .而AM =AC ,∴EB =AC .∵AE ∥BC ,EB 与AC 不平行,∴四边形EBCA 是梯形. ∴梯形EBCA 是等腰梯形.例题2:(1)在梯形ABCD 中,AD ∥BC ,其中AB =4,CB =8,AD =2,则腰CD 的取值范围是__________.参考答案:210CD <<(平移一条腰,构造平行四边形和三角形)(2)如图,梯形ABCD 中,AD ∥BC ,且∠B +∠C =90°,E 、F 分别是两底的中点,联结EF ,若AB =8,ODABCCDABD B ACEDBAC DMAEBC参考答案:(1)点B 坐标为(4,8), ()()108041022=-+-=AB由28410105+++=+t ,得t =11 ;此时点P 在CB 上(2)证法一:作OF ⊥AB 于F ,BE ⊥OA 于E ,DH ⊥AB 于H ,则 BE =OC =8.∵ OF AB BE OA ⋅=⋅,∴ 8==BE OF ,DH =4. ∴ t t S 2421=⨯⨯=(0≤t ≤10) (3)点P 只能在AB 或OC 上,(ⅰ)当点P 在AB 上时,设点P 的坐标为(x ,y )由COAB APD S S 梯形41=∆; 得 14521=⨯⨯y ,得y =528由 142=t ,得t =7; 由 ()495281022=⎪⎭⎫⎝⎛+-x ,得529=x . 即在7秒时有点)535,545(1P ;(ⅱ)当点P 在OC 上时,设点P 的坐标为(0,y )由COAB OPD S S 梯形41=∆; 得 14521=⨯⨯y ,得y =528此时t =5216)5288(14=-+; 即在1652秒时,有点)535,0(2P .故在7秒时有点)535,545(1P 、在1652秒时,有点)535,0(2P 使PD 将梯形COAB 的面积分成1:3的两部分.此环节设计时间在30分钟左右(20分钟练习+10分钟互动讲解)。
沪教版(五四制)八年级数学下册 第六讲 梯形 讲义(无答案)

(一) 梯形定义:一组对边平行而另一组对边不平行的四边形叫做梯形。
在梯形中,平行的两边叫做梯形的底(通常把较短的底叫做上底,较长的底叫做下底);不平行的两边叫做梯形的腰;两底之间的距离叫做梯形的高。
(二) 直角梯形定义:有一个角是直角的梯形叫做直角梯形。
(三) 等腰梯形定义:两腰相等的梯形叫做等腰梯形。
(四) 等腰梯形性质定理1:等腰梯形在同一底上的两个内角相等。
等腰梯形性质定理2:等腰梯形的两条对角线相等。
等腰梯形性质定理3:等腰梯形是轴对称图形,经过两底中点的直线是它的对称轴。
(五) 等腰梯形判定定理1:在同一底边上的两个内角相等的梯形是等腰梯形。
等腰梯形判定定理2:对角线相等的梯形是等腰梯形。
直角梯形等腰梯形梯形有一个角是直角梯形中几种常见的添加辅助线方法:梯形本身的性质并不多,所以实际解梯形的问题时,往往通过添加辅助线将梯形分成三角形或平行四边形,三角形是最简单的直线形,而平行四边形具有很好的对称性质。
⑴作梯形的高:一般是过梯形的一个顶点作高,其好处是将梯形分成一个直角三角形和一个直角梯形,从而可以用勾股定理。
如果过梯形的两个顶点分别作高,则会出现矩形,使问题更便于解决。
⑵过梯形的一个顶点作另一腰的平行线:这样便将梯形分成了一个平行四边形和一个三角形,这样做的好处是可以将两腰拉到同一三角形中,并且三角形的另一边恰好是梯形的两底之差,从而将问题集中到三角形中。
⑶延长梯形两腰交于一点:这样做同样可以使梯形问题转化为三角形的问题。
⑷过梯形一腰的中点作另一腰的平行线:可以将梯形等积变换成一个平行四边形。
⑸连结梯形一个顶点和另一腰上的中点并延长交另一底边:可以将梯形等积变换成一个三角形。
第六讲梯形与梯形有关的计算【例题1】【基础】在等腰梯形中,上底:腰:下底1:2:3=,则下底的度数是多少?【提高、尖子】(2000年3月19日第十一届“希望杯”全国数学邀请赛初二第1试第5题)用四条线段:14d=作为四条边构成一个梯形,则在所构成的梯形c=,7b=,9a=,13中,中位线的长的最大值为()。
八年级数学(下)《梯形》同步测试题含答案

八年级数学(下)《梯形》同步测试题一、选择题1.等腰梯形上、下底差等于一腰的长,那么腰长与下底的夹角是( ).A.5°B.60° .45° D.30°2.等腰梯形的高是腰长的一半,则底角为( ).A.30°B.45°C.60°D.90°3.下列命题中,真命题是( ).A.有一组对边平行,另一组对边相等的梯形是等腰梯形B.有一组对角互补的梯形是等腰梯形C.有一组邻角相等的四边形是等腰梯形D.有两组邻角分别相等的四边形是等腰梯形4.如图1,在等腰梯形ABCD 中,AD=6cm,BD=9cm,AB=8cm,E 、F 、G 、H 分别是AD 、BD 、BC 、AC 的中点,那么四边形EFGH 的周长是( ).A.14cmB.15cmC.16cmD.17cm图1 图2 图35.如图2,等腰梯形ABCD,周长为40,∠BAD=60°,BD 平分∠ABC,则CD 的长为( ).A.4B.5C.8D.106.下列四边形中,两条对角线一定不相..等.的是( ). A.正方形 B.矩形 C.等腰梯形 D.直角梯形7.如图3,等腰梯形ABCD 中,AB ∥DC ,AD=BC=8,AB=10,CD=6,则梯形ABCD 的面积是( ). A.1516 B.516 C.1532 D.17168.在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形,又能拼成三角形和梯形的是 ( ).A B C D9.在梯形ABCD 中,AB ∥CD ,AB>CD ,如果∠D>∠C ,那么AD 和BC 的关系是( )A .AD>BCB .AD=BC C .AD<BCD .不能确定10.腰梯形两底之差的一半等于它的高,那么此梯形的一个底角是( )A .30°B .45°C .60°D .75°二、填空题11.直角梯形两底之差等于高,则其最大角等于_______.12.如图4,四边形ABCD是等腰梯形,AD//BC,AB=CD,则AC=_______,∠BAD=_____,∠BCD=_____,等腰梯形这个性质用文字语言可表述为_______.ADB C图413.等腰梯形ABCD中,对角线AC、BD相交于点O,那么图中的全等三角形最多有________对.14.在四边形ABCD中AD∥BC,但AD≠BC,若使它成为等腰梯形,则需添加的条件是_____(填一个正确的条件即可)15.如图5,梯形ABCD中,AB//CD,∠ABC=90°,AB=9cm,BC=8cm,CD=7cm,M是AD的中点,过M作AD的垂线交BC于N,则BN等于_____cm.2图5 图616.如图6,梯形ABCD中,AD∥BC,若∠B=60°,AC⊥AB,那么∠DAC= .3017.如图7,在等腰梯形ABCD中AD//BC,AB=DC,CD=BC,E是BA、CD延长线的交点,∠E=40°,则∠ACD=____________度.15图7 图818.如图8,在等腰梯形ABCD中,AD//BC,AC、BD相交于点O,有如下结论:①∠DAC=∠DCA;②梯形ABCD是轴对称图形;③△AOB≌△AOD;④AC=BD.请把其中正确结论的序号填写在横线上__________.19.等腰梯形ABCD中,AD∥BC,AD=AB,BC=BD,则∠A= .20.等腰梯形ABCD中,AB∥CD,AC平分∠DAB,∠DAB=60°,若梯形周长为8㎝,则AD= .三、解答题21.(12分)如图9,等腰梯形的上下底分别是3cm和5cm,一个角是45°,求等腰梯形的面积.图922.(12分) 如图10,等腰梯形ABCD中,AB//CD,DC=AD=BC,且对角线AC垂直于腰BC,求梯形的各个内角.图1023.(14分) 如图11,梯形ABCD中,AB//CD,AD=BC,延长AB到E,使BE=DC,连结AC、CE.求证AC=CE.图1124.(14分)如图12,等腰梯形ABCD中,AD//BC,AD=3,AB=4,BC=7,求∠B的度数.4.图1225.如图13(尺寸单位:㎜)所示甲、乙两种直角梯形零件,且使两种零件的数量相等,有两种面积相等的矩形铝板可供选用.第一种长500㎜,宽300㎜;第二种长600㎜,宽250㎜.为了充分利用材料,应选第种铝板,这时一块铝板最多能剪甲、乙零件共个.2答案一、1.B 2.A 3.B 4.C 5.C 6.D 7.B 8.D 9. A 10.B二、11. 135°; 12. BD ,∠CDA ,∠ABC ,等腰梯形的对角线相等,等腰梯形同一底上的两个角相等; 13. 3; 14. ∠B=∠C 等; 15.2; 16.30°; 17.15; 18.②④. 19.108°; 20.85㎝ 三、21. 解:因为ABCD 是等腰梯形,AD=3cm,BC=5cm,过点A 作AE ⊥BC 于E, 因为∠B=45°,∠BAE=45°,所以BE=AE,BE=21(5-3)=1,所以AE=1,所以 S 梯形ABCD =21(5+3)×1=4(cm 2). 22. 解:因为AB//CD ,DC=AD=BC ,所以∠1=∠2,∠1=∠3,∠DAB=∠B , 所以∠1=∠2=∠3,所以∠B=∠DAB=∠2+∠3=2∠2,又AC ⊥BC ,所以∠2+∠B=90°,所以∠B=60°,所以∠DAB=60°,∠ADC=∠BCD=120°.23. 证明:因为AB//CD,BE=DC,且BE 在AB 的延长线上,所以CD//BE,CD=BE,所以四边形DBEC 是平行四边形,所以CE=DB,因为AD=BC,所以梯形ABCD 是等腰梯形,所以AC=BD,所以AC=CE.24.过点A 作AE//DC 交BC 与E,]∵AD//BC ,四边形AEDC 是平行四边形.∴EC=AD=3,DC=AE ,∴BE=BC-CE=7-3=4.∵等腰梯形两腰相等,∴AB=CD=4,∴AE=AB=BE=4,∴△ABE 是等边三角形,∴∠B=60º.25.选第一种铝板,最多能剪甲、乙两种零件2个,共计4个.剩余边角料面积=500×300-(100+300)×200-(100+300)×150=10000㎜2。
沪科版数学八年级下册1《等腰梯形》-课件

∴ ∠ B= ∠EAD ∠ C = ∠EDA
又∵ ∠ B= ∠ C
B
C
∴∠EAD = ∠EDA(等量代换)
∴EA = ED(等角对等边)
即 △ EAD是等腰三角形
如图:已知在等腰梯形ABCD中, AD ∥ BC, AB=DC =4,AD =3,BC =7,求∠ B的度数。
A
3D
4
4
4
B4
E3
C
如图:已知在等腰梯形ABCD中, AD ∥ BC, AB=DC =4,AD =3,BC =7,求∠ B的度数。
D E
1
C
等腰梯形的性质定理:
等腰梯形同一底边上的两个内角相等
已知:在等腰梯形ABCD中,AD∥ BC,AB=DC 求证: ∠ B= ∠ C ∠ A = ∠ D 证明:分别过点A、D作AE⊥ BC于E,DF⊥ BC于F
A
D
B E
C F
性质定理 等腰梯形的对角线相等
A B1
已知:在等腰梯形ABCD中,AD ∥ BC,AB=DC 求证: AC=BD
D 证明: ∵ ABCD是等腰梯形
O
∴ ∠ ABC= ∠ DCB
2
C (等腰梯形同一条底边上的两个内角相等)
又∵ AB=DC BC=CB
∴ △ ABC≌△DCB(SAS) ∴AC=BD(全等三角形的对应边相等)
(OB = OC OA = OD)
判定定理 同一底上的两个内角相等的
梯 形是等腰梯形
已知:在梯形ABCD中, AD∥BC,∠B= ∠C .
∴ ∠ B= ∠C(---) 又∵ ∠ A 与∠ B、∠ C与 ∠ ADC互补
∴ ∠ A = ∠ ADC
A B
【新课标】2018—2019年最新沪教版(五四制)八年级数学下册期中考试模拟试题及答案解析

2017-2018学年(新课标)沪教版五四制八年级下册期中试卷八年级数学(满分100分,时间90分钟)题号一二三四五总分得分一、选择. 1. 下列函数中,是一次函数的是()A.y=x2+2 B.C.y=kx+b(k、b是常数)D.y=x﹣12. 对于一次函数y=﹣3x+1,下列结论正确的是()A.点(﹣1,3)在此函数图象上B. y的值随x值的增大而增大C.图象经过第一、二、三象限D.图象与x轴、y轴的交点分别为(,0),(0,1)3. 下列说法正确的是()A.x2+3x=0是二项方程B.xy﹣2y=2是二元二次方程C.是分式方程D.是无理方程4. 下列方程中,有实数解的是()A.=﹣1 B.=﹣x C.D.=0=05. 一次函数y=kx﹣k(k<0)的图象大致是()A .B .C .D .6. 如图,在四边形ABCD 中,若已知AB ∥CD ,再添加下列条件之一,能使四边形ABCD 成为平行四边形的条件是( )A . ∠DAC=∠BCAB . ∠DCB+∠ABC=180°C . ∠ABD=∠BDCD . ∠BAC=∠ACD二、填空7. 当x=时,一次函数y=2x ﹣1的值为0.8. 已知一次函数y=(1﹣m )x+m ﹣2,当m 时,y 随x 的增大而增大. 9. 六边形ABCDEF 的内角和等于 .10. 平行四边形ABCD 中,∠A :∠B=2:1,则∠B 的度数为 . 11. 解方程﹣=,设y=,那么原方程化为关于y 的整式方程是 .12. 一次函数的图象过点(0,3)且与直线y=﹣x 平行,那么函数解析式是 . 13. 方程的根是 .14. 解关于x 的方程:b(x-1)=x+1 (b ≠1) ,可得x=________. 15. 已知关于x 的方程出现增根,则a 的值等于 .16. 如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是.17. 一次函数y1=kx+b与y2=x+a的图象如图,则不等式kx+b>x+a的解集是.18.一次函数y=﹣x+3的图象分别与x轴、y轴交于点A、B,将线段AB绕点A顺时针旋转90°得到线段AC.则过B、C两点直线的解析式为___________三、简答19. 画出函数y=x﹣4的图像,求出该图像与坐标轴交点的坐标;并写出其向上平移3个单位后的图像的解析式.20. 解方程:.21. 解方程组:.22. 马小虎的家距离学校1800米,一天马小虎从家去上学,出发10分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,在距离学校200米的地方追上了他,已知爸爸的速度是马小虎速度的2倍,求马小虎的速度.四、解答23. 如图,已知E、F分别为▱ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,求证:EF与MN互相平分.24. 小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即按原路匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.(1)图中a= ,b= ;(2)求小明的爸爸下山所用的时间.25. 如图,在平面直角坐标系中,函数y=﹣2x+12的图象分别交x轴、y轴于A、B两点,过点A的直线交y 正半轴于点M,且点M为线段OB的中点.(1)求直线AM的函数解析式.(2)试在直线AM上找一点P,使得S△ABP=S△AOM,求P坐标.(3)在坐标平面内是否存在点C,使以A、B、M、C为顶点的四边形是平行四边形?若存在,请直接写出点C的坐标;若不存在,请说明理由.八年级数学答案一、选择1. B2. D3. B4. C5. A6. A二、 填空7.8. m <1 9. 720° 10. 60° 11. 3y 2﹣4y ﹣3=0 12. y=﹣x+3 13. 214.11-+b b15. 16. 1 17. x <﹣2 18. 371+=x y 三、简答19.图准确2分,与x 轴交点(4,0) 与y 轴交点(0.-4)2分,平移后解析式:1-=x y 2分20. 解方程:.解答:解:方程化为, 1’ 两边平方得:, 1’∴,x 2﹣6x+9=15﹣x ,即x 2﹣5x ﹣6=0 2’ x=﹣1或x=6 1’ 经检验,x=﹣1是增根,所以原方程的根为x=6 1’21. 解方程组:.解答:解:由方程②得:(x+y)2=1,x+y=1,x+y=﹣1,2’即组成方程组或,2’解这个两个方程得:或,即原方程组的解为:或.2’22. 马小虎的家距离学校1800米,一天马小虎从家去上学,出发10分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,在距离学校200米的地方追上了他,已知爸爸的速度是马小虎速度的2倍,求马小虎的速度.解答:解:设马小虎的速度为x米/分,则爸爸的速度是2x米/分,依题意得1’-- +10,3’解得x=80.2经检验,x=80是原方程的根.1’答:马小虎的速度是80米/分.1’23. 如图,已知E、F分别为▱ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,求证:EF与MN互相平分.解答:证明:连接EN、FM,∵EM⊥AC,FN⊥AC,∴∠AME=∠EMN=∠FNC=∠FNM=90°,∴EM∥FN,1’∵四边形ABCD是平行四边形,1’∴AD∥BC,AD=BC,∴∠EAM=∠FCN,1’∵DE=BF,∴AE=CF,1’在△AEM和△CFN中∴△AEM≌△CFN(AAS),3’∴EM=FN,∵EM∥FN,∴四边形EMFN是平行四边形,2’∴EF与MN互相平分.124. 小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即按原路匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.(1)图中a= 8 ,b= 280 ;2’+2’(2)求小明的爸爸下山所用的时间.解答:解:(1)由图象可以看出图中a=8,b=280,故答案为:8,280.(2)由图象可以得出爸爸上山的速度是:280÷8=35米/分,小明下山的速度是:400÷(24﹣8)=25米/分,2’∴小明从下山到与爸爸相遇用的时间是:(400﹣280)÷(35+25)=2分,∴2分爸爸行的路程:35×2=70米,2’∵小明与爸爸相遇后,和爸爸一起以原下山速度返回出发地.∴小明和爸爸下山所用的时间:(280+70)÷25=14分.2’. 如图,在平面直角坐标系中,函数y=﹣2x+12的图象分别交x轴、y轴于A、B两点,过点A 的直线交y 正半轴于点M,且点M为线段OB的中点.(1)求直线AM的函数解析式.(2)试在直线AM上找一点P,使得S△ABP=S△AOM,请直接写出点P的坐标.(3)在坐标平面内是否存在点C,使以A、B、M、C为顶点的四边形是平行四边形?若存在,请直接写出点C的坐标;若不存在,请说明理由.解答:解:(1)∵直线AB的函数解析式y=﹣2x+12,∴A(6,0),B(0,12).2又∵M为线段OB的中点,∴M(0,6).1’设直线AM的解析式为:y=kx+b,则,解得:,故直线AM的解析式y=﹣x+6;2’(2)设点P的坐标为:(x,﹣x+6),∴AP==|x﹣6|,过点B作BH⊥AM于点H,∵OA=OM,∠AOM=90°,∴∠AMO=45°,∴∠BMH=45°,∴BH= 6×=3,1’∵S△ABM=S△AOM,S△AOM=OA•OM=×6×6=18,S△ABP=AP•BH=×|x﹣6|×3,1’∴×|x﹣6|×3=18,解得:x=0或12,2’故点P的坐标为:(0,6)或(12,﹣6).(3) (6,-6)、(6,6)、(-6,18)每个点1分。
八年级数学下册 22.4 梯形教案 沪教版五四制

让学生认识到过上底两顶点作下底的垂线段得到高的常用方法.
等腰梯形、直角梯形是常见的特殊梯形,给出明确的定义,加强学生的认识.
由梯形长底边向短底边延长两腰能够得到三角形的常用添辅助线方法.
梯形可由三角形截得,指三角形被平行于一直角边的直线分割成一个直角三角形和一个直角梯形;等腰三角形被平行于底边的直线分割成一个等腰三角形和一个等腰梯形
课外
作业
练习册
预习
要求
22.5(1)等腰梯形
1、理解并掌握等腰梯形的性质,能初步运用解决问题;
2、理解梯形中常用四种添辅助线的方法.
教学后记与反思
1、课堂时间消耗:教师活动15分钟;学生活动25分钟)
2、本课时实际教学效果自评(满分10分):分
3、本课成功与不足及其改进措施:
将梯形分解成三角形,是解决梯形的基本思路,而通过平行线得到平行四边形与三角形则是常用方法.
引导学生认识到该题的实质是通过“腰的平移”将梯形分解成平行四边形与三角形.
通过作高将梯形分解为矩形与三角形,是另一种常用方法.
等高同底是梯形中的常见面积问题,正确理解并熟悉图形中三角形的面积相等有利于帮助学生迅速找到类似问题的解题思路.
两腰相等的梯形叫做等腰梯形.
有一个角是直角的梯形叫做直角梯形.
等腰梯形的表示方法:
在梯形ABCD中,AB∥CD,AD=BC.
新课探索二
操作任意画一个三角形EBC,再画一条直线,使它与边BC平行,且与边BE,CE分别相交于点A和D(与点E不重合),得△EAD和四边形ABCD.
思考
1.四边形ABCD是一个梯形吗?
新课探索四
例题2如图,梯形ABCD是一座大坝的横截面,其中AD∥BC,∠B=30°,∠C=45°,AD(坝顶)=6m,CD=20m.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年(新课标)沪教版五四制八年级下册
22.4 梯形
一、课本巩固练习
1、.如图在Rt△ABC中,∠BAC=900,BD=BA,M为BC中点,MN//AD交AB于N。
求证:DN=BC。
2、已知如图,梯形ABCD中,AD//BC,AC⊥BD,BD=5cm,高DE=4cm。
求:S梯形。
ABCD
3、.已知:梯形ABCD中,DC//AB,AC=CB,∠ACB=900,BD=AB,AC、BD相交于E。
求证:△ADE是等腰三角形。
二、基础过关
1、等腰梯形两底长为4cm和10cm,一底角为450,求:它的面积。
2、.梯形ABCD中,AB//CD,CD=4,BC=4,AD=8,∠C=1350,求梯形面积。
3、已知:如图,梯形ABCD中,AD//BC,∠B+∠C=900,M、N分别是AD,BC的中点。
求证:MN=0.5 (BC-AD)
4、如图,已知梯形ABCD,AD//BC,AB⊥AC,AB=AC,BD=BC,求∠DBC的度数。
5、如图,已知在梯形ABCD 中,AB ∥DC ,∠D=60°,∠C=45°,AB=2,AD=4,求梯形ABCD 的面积.
6、在梯形ABCD 中,AD//BC ,AB=DC=AD=2, BC=4,求∠B 的度数及AC 的长。
7、如图所示,已知等腰梯形ABCD 中,AD ∥BC ,∠B =60°,AD =2,BC =8,求等腰梯形的周长。
8、 如图所示,AB ∥CD ,AE ⊥DC ,AE =12,BD =20,AC =15,求梯形ABCD 的面积。
A
B C D
A B C D A B C D E
9、 如图所示,已知等腰梯形的锐角等于60°,它的两底分别为15cm 和49cm ,求它的腰长.
10、 如图所示,已知等腰梯形ABCD 中,AD ∥BC ,AC ⊥BD ,AD +BC =10,DE ⊥BC 于E ,求DE 的长.
11、已知:如图,梯形ABCD 中,AD ∥BC ,AB=DC ,∠BAD 、∠CDA 的平分线AE 、DF 分别交直线BC 于点E 、F .
求证: CE=BF .
12、如图,在梯形ABCD 中,AD BC ∥,9038BD CD BDC AD BC =∠===,°,,.求
AB 的长. A B C D A B C D E。
