安徽省振阳公学2017届高三上学期第四次月考数学(文)试题
【月考试卷】安徽省四校2017届高三10月联考数学(文)试题 Word版含答案

十月联考数学(文科)试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.计算:cos 210= ( )A .12-B. C .12 D2.若集合2{|10}A x R ax ax =∈++=其中只有一个元素,则a =( ) A .4 B .2 C .0 D .0或43.设2:,40p x R x x m ∀∈-+>,:q 函数321()213f x x x mx =-+--在R 上是减函数,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要 4.若'0()3f x =-,则000()()limh f x h f x h h→+--=( )A .-3B .-6C .-9D .-125.函数2233(2)()log (1)(2)x x f x x x -⎧<⎪=⎨-≥⎪⎩,若()1f a =,则a 的值为( ) A .2 B .1 C .1或2 D .1或-26. 定义在R 上的偶函数()f x 满足:对任意的1212,(,0)()x x x x ∈-∞≠,都有1212()()0f x f x x x -<-,则下列结论正确的是( )A .20.32(0.3)(2)(log 5)f f f <<B .0.322(log 5)(2)(0.3)f f f <<C .20.32(log 5)(0.3)(2)f f f <<D .20.32(0.3)(log 5)(2)f f f <<7.已知函数322()f x x ax bx a =+++在1x =处有极值10,则(2)f 等于( ) A .11或18 B .11 C .18 D .17或188.函数sin(2)3y x π=-与2cos(2)3y x π=+的图象关于直线x a =对称,则a 可能是( ) A .24π B .12π C .8π D .1124π 9.已知函数()f x 的定义域为R ,当0x <时,3()1f x x =-;当11x -≤≤时,()()f x f x -=-,当12x >时,11()()22f x f x +=-,则(6)f =( ) A .-2 B .-1 C .0 D .210.在ABC ∆中,若3sin 4cos 6A B +=,4sin 3cos 1B A +=,则角C 为( ) A .30 B .30 或150 C .150 D .6011.3sin x =的根的个数是( ) A .3 B .4 C .5 D .612.已知集合{|(31)(1)220}A l m x m y m =++---=直线直线的方程是,集合3{|}B l y x ==直线直线是的切线,则A B = ( )A .{(,)|320}x y x y --=B .{(1,1)}C .{(,)|3410}x y x y -+=D .{(,)|0}x y x y -=第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知命题:p x 满足220x x --<,命题:q x 满足1m x m ≤≤+,若p 是q 的必要条件,则m 的取值范围是 .14.过点(2,4)作函数32y x x =-的切线,则切线方程是 . 15.在三角形ABC 中,则tantan tan tan tan tan 222222A B B C A C++的值是 . 16.设定义在R 上的函数()f x 满足()(2)2016f x f x +=,若(1)2f =,则(99)f = .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分10分)已知2:7100p x x -+<,22:430q x mx m -+<,其中0m >. (1)若4m =且p q ∧为真,求x 的取值范围;(2)若q ⌝是p ⌝的充分不必要条件,求实数m 的取值范围. 18. (本小题满分12分)已知函数32()39f x x x x a =-+++. (1)求()f x 的单调递减区间;(2)若()f x 在区间[2,2]-上的最大值为20,求它在该区间上的最小值. 19. (本小题满分12分)已知函数21()cos cos 2f x x x x =-可以化为()sin()(0,0,(0,))f x A x A ωϕωϕπ=+>>∈.(1)求出,,A ωϕ的值并求函数()f x 的单调增区间; (2)若等腰ABC ∆中,A ϕ=,2a =,求角B ,边c . 20. (本小题满分12分) 在ABC ∆中,已知6C π=,向量(sin ,1)m A = ,(1,cos )n B =,且n m ⊥ .(1)求角A 的值;(2)若点D 在BC 边上,且3BD BC =,AD =ABC ∆的面积.21. (本小题满分12分)定义在非零实数集上的函数()f x 满足()()()f xy f x f y =+,且()f x 是区间(0,)+∞上的递增函数.(1)求(1),(1)f f -的值; (2)求证:()()f x f x -=; (3)解不等式1(2)()02f f x +-≤. 22.(本小题满分12分)已知函数()()x f x x ae a R =+∈. (1)讨论函数()f x 的单调性;(2)当0,1x a <≤时,证明:2'(1)()x a x xf x ++>.参考答案一、选择题BAABA ACADA CC 二、填空题13. 11m -<< 14. 1016y x =-或2y x =+ 15. 1 16.1008 三、解答题17.解:(1)由27100x x -+<,解得25x <<,所以:25p x <<又22430x mx m -+<,因为0m >,解得3m x m <<,所以:3q m x m <<.当4m =时,:412q x <<,又p q ∧为真,,p q 都为真,所以45x <<.18.解:(1)'2()369f x x x =-++ 令'()0f x <,解得1x <-或3x >∴函数()f x 的单调递减区间为(,1)-∞-和(3,)+∞. (2)∵(2)812182f a a -=+-+=+(2)8121822f a a =-+++=+,∴(2)(2)f f >-.∵在(1,3)-上'()0f x >,∴()f x 在(1,2]-上单调递增.又由于()f x 在[2,1]--上单调递减,因此(2)f 和(1)f -分别是()f x 在区间[2,2]-上的最大值和最小值.于是有2220a +=,解得2a =-, ∴32()392f x x x x =-++-.∴(1)13927f -=+--=-,即函数()f x 在区间[2,2]-上的最小值为-719.解:(1)21()cos cos 2f x x x x =-1cos 2122x x x +=-15cos 22sin(2)sin(2)2266x x x x ππ=-=-=+ 所以1A =,2ω=,56πϕ=.(2)12B π=,c =20.解:(1)由题意知:sin cos 0m n A B ∙=+=又6C π=,A B C π++=,所以5sin cos()06A A π+-=即1sin sin 02A A A +=,即sin()06A π-=,又506A π<<,所以2(,)663A πππ-∈-,所以06A π-=,即6A π=. (2)设||BD x = ,由3BD BC = ,得||3BC x =,由(1)知,6A C π==,所以||3BA x = ,23B π=,在ABD ∆中,由余弦定理,得2222(3)23cos3x x x x π=+-⨯⨯, 解得1x =,所以3AB BC ==,所以112sin 33sin 2234ABC S BA BC B π∆=∙∙=⨯⨯⨯=. 21.解:(1)令1x y ==,则(1)(1)(1)f f f =+∴(1)0f =令1x y ==-,则(1)(1)(1)f f f =-+-,∴(1)0f -=(2)令1y =-,则()()(1)()f x f x f f x -=+-=,∴()()f x f x -= (3)据题意可知,函数图象大致如下:1(2)()(21)02f f x f x +-=-≤∴1210x -≤-<或0211x <-≤ ∴102x ≤<或112x <≤ 22.解:(1)由()x f x x ae =+,可得'()1x f x ae =+当0a ≥时,'()0f x >,则函数()f x 在(,)-∞+∞上为增函数当0a <时,由'()0f x >可得1ln()x a <-,由'()0f x <可得1ln()x a>-则函数()f x 在1(,ln())a -∞-上为增函数,在1(ln(),)a-+∞上为减函数 (2)证明:令2'()(1)()F x x a x xf x =+--则2'2()(1)()()x xF x x a x xf x x ax axe x x a ae =++-=+-=+- 令()x H x x a ae =+-,则'()1xH x ae =-∵0x <,∴01x e <<,又1a ≤,∴110x xae e -≥->∴()H x 在(,0)-∞上为增函数,则()(0)0H x H <=,即0xx a ae +-<由0x <可得()()0x F x x x a ae =+->,所以2'(1)()x a x xf x ++>.。
2017届高三上学期第四次月考数学(文)试题Word(无答案)

2016-2017学年第一学期第四次月考高三数学(文科)试卷(请在答题卡上作答)一、选择题(每题5分,共60分)1.已知集合{}2>=x x A ,{}31<<=x x B ,则=B A ( )..{|2}A x x > .{|1}B x x > .{|23}C x x << .{|13}D x x <<2.若复数z 满足i iz =-1,其中i 为虚数单位,则=z ( ) . A .i -1 B .i +1 C .i --1 D .i +-13. “1<x <2”是“x <2”成立的( ).A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.设7log 3=a ,1.12=b ,1.38.0=c 则( ).A.c a b <<B.b a c <<C.a b c <<D.b c a <<5.如果等差数列{}n a 中,12543=++a a a ,那么=+++721a a a ( ).A .14B .21C .28D .356.若点()9,a 在函数x y 3=的图象上,则6tanπa 的值为( ) . A .0 B .33 C .1 D .3 7.若变量x 、y 满足约束条件⎪⎩⎪⎨⎧≥≥≤-≤+0,024y x y x y x ,则y x +2的最大值是( ).A. 2B. 4C. 7D. 88.不等式021<+-x x 的解集为( ) . A .(1,+∞) B .(-∞,-2)C .(-2,1)D .(-∞,-2)∪(1,+∞)9.已知向量)1,1(-=a ,),2(x =.若1=⋅,则=x ( ).A .1-B .21-C .21 D .1 10.已知m ,n 表示两条不同直线, α表示平面,下列说法正确的是( ).A .若αα//,//n m ,则n m //B .若m α⊥,n α⊂,则m n ⊥C .若m α⊥,m n ⊥,则α//nD .若α//m ,m n ⊥,则n α⊥11.若圆1:221=+y x C 与圆086:222=+--+m y x y x C 外切,则=m ( ).A . 9B . 19C .21D .11-12.定义运算“⊗”:xyy x y x 22-=⊗ (0,,≠∈xy R y x ).当0,0>>y x 时,x y y x ⊗+⊗)2(的最小值是 ( ).A .0B .22 C .1 D .2 二.填空题:(每小题5分,计20分)13.若等比数列{}n a 满足2142=a a ,则=5231a a a _________. 14.若△ABC 的面积为3,BC=2, C=︒60,则边AB 的长度等于_________.15.已知单位向量21,e e 的夹角为α,且31cos =α,若向量2123e e -==_______. 16.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积为_______.三.解答题:(共70分)17.(本小题满分12分)已知等比数列{}n a 中,311=a ,31=q . (1)n S 为数列{}n a 前n 项的和,证明:21n n a S -=; (2)设n n a a a b 32313log log log +++= ,求数列{}n b 的通项公式.18.(本小题满分12分)在锐角△ABC 中,内角C B A ,,的对边分别为c b a ,,, 且b B a 3sin 2=.(1)求角A 的大小;(2)若8,6=+=c b a ,求△ABC 的面积.19.(本小题满分12分)如图,四棱锥P-ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,点E 在线段AD 上,且CE ∥AB .(1)求证:CE ⊥平面PAD ;(2),若PA=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P-ABCD 的体积.20.(本小题满分12分)已知以点P 为圆心的圆经过点A(-1,0)和B(3,4),线段AB 的垂直平分线交圆P 于点C 和D ,且CD =410.(1) 求直线CD 的方程;(2) 求圆P 的方程.21.(本小题满分12分)已知函数bx ax x x f --=233)(,其中a 、b 为实数.(1)若)(x f 在1=x 处取得的极值为2,求a 、b 的值;(2)若)(x f 在区间[]2,1-上为减函数,且a b 9=,求a 的取值范围.22.(本小题满分10分)选修4-4:坐标系与参数方程在极坐标系中,已知圆θρcos 2=与直线0sin 4cos 3=++a θρθρ相切, 将圆与直线方程化为直角坐标方程并求实数a 的值.。
(优辅资源)安徽省淮南高三上学期第四次月考(12月)数学(文)试题 Word版含答案

淮南二中2016-2017学年第一学期高三年级第四次月考数学试题(文科)请注意:所有答案都要写在答题卡上,2B 铅笔填涂 一.选择题(每题5分,共12题60分)1.设i 是虚数单位,计算=+++432i i i i ( )A .-1B .0C .1D .22.若0,0>>b a ,则“1>+b a ”是“1>ab ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 3.集合{}4,3,2,1=A ,{}0))(2(<--=a x x x B ,若集合{}4,3=B A ,则实数错误!未找到引用源。
的范围是( )A .54<<aB .54<≤aC .54≤<aD .4>a4.若向量a ,b 满足|a |=|b |=1,23)(=⋅+b b a ,则向量a 与b 的夹角为( )A . 30B . 45C . 60D . 905. 顶点在原点,对称轴为坐标轴,且过点)2,4(--P 的抛物线的标准方程是( ) A .x y -=2B .y x 82-= C .x y 82-= 或y x -=2D .x y -=2或y x 82-= 6.已知直线02:1=+-a y ax l 与0)32(:2=++-a ay x a l 互相垂直,则a 的值是( )A .2或0B .-2或0C . -2D .07.如图所示的程序框图中,若,log ,)161(2421==b a log log a b c b a =⨯,则输出的x =( )A. 0.25B.0.5C.1D.28.已知圆0128:22=+-+x y x C 与2+=kx y 相切,则k 的值是( )A .34-B .0C .034或D .034或- 9.将函数)62sin(2)(π+=x x f 的图象向左平移6π个单位,再向上平移1个单位,得到)(x g的图象.则)(x g 的解析式为( )A .12cos 2+xB .12cos 2+-xC .1)32sin(2++πx D .12sin 2+x10.已知函数2()(1)xf x e x =-+(e 为自然对数的底),则()f x 的大致图象是( )11. 已知{}n a 满足()*21102,4n n a a a n n N +=-=∈,则数列n a n ⎧⎫⎨⎬⎩⎭最小项的值为( ) A .25 B .26 C .27 D .2812.已知函数2()3ln f x x ax bx =-++(0a >,b R ∈),若对任意0x >都有()(3)f x f ≥成立,则( )A .ln 1a b >--B .ln 1a b ≥--C .ln 1a b ≤--D .ln 1a b <--二.填空题(每题5分,共4题20分)13.若双曲线11622=-my x 的离心率2=e ,则=m . 14.已知正项等比数列}{n a ,满足211=a ,)1(4342-=⋅a a a ,则=7a . 15. 定义在R 上的偶函数)(x f 满足对任意∈x R ,都有)()8(x f x f =+,且]4,0[∈x 时,x x f -=4)(,则)13(f = ..______415)0(,20,.16的最小值为则,的最大值为若目标函数满足已知变量ba ab by ax z x y x y y y x +>>+=⎪⎩⎪⎨⎧-≤≤≥三、解答题(17-21题12分,22-23题10分)17.在△ABC 中,c b a ,,是角C B A ,,对应的边,向量),(),,(c b a c b a +=-+=,且ab )32(+=⋅(1)求角C ;(2)函数212sin )cos(cos )sin(2)(2-+-+=x B A x B A x f ,求)(x f 在R 上的单调递增区间.18.如图,从参加环保知识竞赛的学生中抽出40名,将其成绩(均为整数....)整理后画出的频率分布直方图如下,观察图形,回答下列问题: (1)80~90这一组的频率是多少?(2)估计这次环保知识竞赛成绩的众数、中位数.(不要求写过程)(3)从成绩是80分以上(包括80分)的学生中选两人,求他们在同一分数段的概率.19.如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60BAD ∠=,已知2,PB PD PA ==(1)证明:PC BD ⊥(2)若E 为PA 的中点,求三棱锥P BCE -的体积.20.如图,椭圆C :22221(0)x y a b a b +=>>的右焦点为F ,右顶点、上顶点分别为点A 、B,且||||2AB BF =. (1)求椭圆C 的离心率;(2)若斜率为2的直线l 过点(0,2),且l 交椭圆C 于P 、Q 两点,OP OQ ⊥. 求椭圆C 的方程.21.设函数x k x k x x f ln )1(2)(2--+= ,其中0≠k . (Ⅰ)讨论)(x f 的单调性;(Ⅱ)若k 为正数,且存在0x 使得2023)(k x f -<,求k 的取值范围.请考生在第22、23题中任选一题解答,并把题号填涂在答题卡上!如果多做,则按所做的第一题计分。
高三数学上学期第四次月考试题文2

南阳一中2017届高三上期第四次月考文数试题考试时间:一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.函数()()234lg1x xf xx--+=+的定义域为A.()1,0(0,1]-B.(1,1]-C.(4,1]--D.()4,0(0,1]-2.复数22izi=-(i为虚数单位)的共轭复数所对应的的点位于复平面内A.第一象限B.第二象限C.第三象限D.第四象限3.将正三棱柱截去三个角如图1所示,A、B、C分别是△GHI三边的中点,得到几何体如图2,则该几何体按图2所示方向的侧视图为4.设,a b R∈,则“22log loga b>”是“21a b->”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.已知函数()()()21sin,02f x xωω=->的周期为π,若将其图象沿x轴向右平移a个单位()0a>,所得图象关于原点对称,则实数a的最小值为A.π B.34πC.2πD.4π6.已知实数x,y满足不等式组21,0,10,xx y mx y≤⎧⎪-+≥⎨⎪+-≥⎩若目标函数2z x y=-+的最大值不超过4,则实数m的取值范围是A.()3,3-B.[0,3] C.[3,0]- D.[3,3]-7.已知函数()sin3cosf x x x=+,当[]0,xπ∈时,()1f x≥的概率为A.13B.14C.15D.128.已知ABC∆的外接圆半径为1,圆心为点O,且3450OA OB OC++=,则ABC∆的面积为A.85B.75C .65D.459.设函数2()f x ax bx c=++(),,,a b c R∈,若函数()xy f x e=在1x=-处取得极值,则下列图象不可能为()y f x=的图象是A B C D10.已知在正项等比数列{}n a中,存在两项m a,n a满足14m na a a=,且6542a a a=+,则14m n+的最小值是A.32B.2 C.73D.25611.已知函数()2ln,041,0x xf xx x x⎧>⎪=⎨++≤⎪⎩,若方程()()f x a a R=∈有四个不同的实数根1234,,,x x x x(其中1234x x x x<<<),则12431x x xx+++的取值范围是A.(]2,24e-- B.(]1,22e-- C.(]2,24e+ D.不确定12.已知函数()f x是R上的单调函数,且对任意实数x都有()21213xf f x⎛⎫+=⎪+⎝⎭,则2(log3)f=A.1 B.45C.12D.0二、填空题:本大题共4小题,每小题5分,共20分.13.执行如图所示的程序框图,若输出的结果是8,则输入的数是.14.已知当11a-≤≤时,2(4)420x a x a+-+->恒成立,则实数x的取值范围是15.已知P为抛物线24y x=上一个动点,Q为圆()2241x y+-=上一个动点,当点P到点Q的距离与点P到抛物线的准线的距离之和最小时,点P的横坐标为16.已知AC,BD 为圆22:8O x y +=的两条相互垂直的弦,垂足为()1,2M ,则四边形ABCD 的面积的最大值为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17.(12分)已知各项均不相等的等差数列{}n a 的前五项和520S =,且1a ,3a ,7a 成等比数列.(1)求数列{}n a 的通项公式;(2)若n T 为数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和,且存在*n N ∈,使得10n n T a λ+-≥成立,求实数λ的取值范围. 18.(12分)为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:平均每天喝500ml 以上为常喝,体重超过50kg 为肥胖.常喝 不常喝 合计 肥胖 2 不肥胖 18 合计30已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为415. (1)请将上面的列联表补充完整;(2)是否有99%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;(3)已知常喝碳酸饮料且肥胖的学生中有2名女生,现从常喝碳酸饮料且肥胖的学生抽取2人参加电视节目,则正好抽到一男一女的概率是多少?参考数据:2()P K k ≥k(参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++)19.(12分)如图,已知三棱锥A —BPC 中,AP⊥PC,AC⊥BC,M 为AB 中点,D 为PB 中点,且△PMB 为正三角形.(1)求 证:BC⊥平面APC ;(2)若BC=6,AB=20,求三棱锥D —BCM 的体积. 20. (本小题满分12分)如图,已知点(1,2)A 是离心率为22的椭圆C :12222=+b x a y (0)a b >>上的一点,斜率为2的直线BD 交椭圆C 于B 、D 两点,且A 、B 、D 三点互不重合.(1)求椭圆C 的方程;(2)求证:直线AB ,AD 的斜率之和为定值. 21. (本小题满分12分)已知函数ln ()a xf x x+=在点()(),e f e 处的切线与直线20e x y e -+=垂直. (1)若函数()f x 在区间(),1m m +上存在极值,求实数m 的取值范围;(2)求证:当1x >时,()()()12111x x f x e e x xe ->+++.选考题:请考生在22,23两题中任选一题作答,如果多做,按所做的第一题计分。
高三数学(文科)第四次月考试题.doc
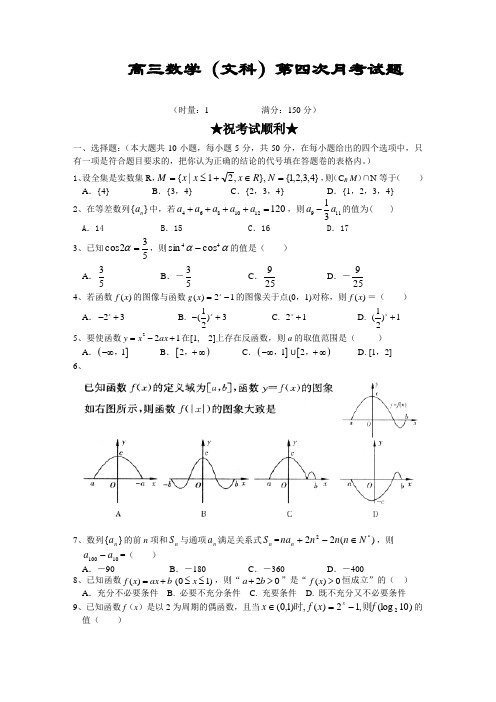
高三数学(文科)第四次月考试题(时量:1 满分:150分)★祝考试顺利★一、选择题:(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的,把你认为正确的结论的代号填在答题卷的表格内。
)1、设全集是实数集R ,}4,3,2,1{},,21|{=∈+≤=N R x x x M ,则(C R M )∩N 等于( )A .{4}B .{3,4}C .{2,3,4}D .{1,2,3,4}2、在等差数列{}n a 中,若4681012120a a a a a ++++=,则91113a a -的值为( ) A .14 B .15 C .16D .173、已知532cos =α,则αα44cos sin -的值是( ) A .53 B .-53 C .259D .-2594、若函数()f x 的图像与函数()21xg x =-的图像关于点(0,1)对称,则()f x =( )A .23x-+B. 1()32x -+ C. 21x+ D. 1()12x +5、要使函数221y x ax =-+在[1, 2]上存在反函数,则a 的取值范围是( )A .(]1-∞,B .[)2+∞,C .(]1-∞,[)2+∞, D. [1,2]6、7、数列}{n a 的前n 项和n S 与通项n a 满足关系式n S =)(22*2N n n n na n ∈-+,则10100a a -=( )A .-90B .-180C .-360D .-4008、已知函数()f x ax b =+(01)x ≤≤,则“20a b +>”是“()0f x >恒成立”的( ) A .充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件 9、已知函数f (x )是以2为周期的偶函数,且当)10(log ,12)(,)1,0(2f x f x x则时-=∈的值( )A .53 B .58 C .85- D .35-10.有限数列12(,,,)n A a a a =,n S 为前n 项和,定义12nS S S n+++为A 的“凯森和”如有99项的数列1299(,,,)a a a 的“凯森和”为1000,则有100项的数列1299,,,a a a (1,)的“凯森和”为( )A 、1001B 、991C 、999D 、990 二、填空题:本大题共5小题,每小题5分,共25分。
安徽省2017届高三模拟考试含答案

安徽省2017届高三模拟考试含答案数学(文)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{N |24}A x x =∈-<<,1{|24}2x B x =≤≤,则A B =( ) A .{|12}x x -≤≤ B .{1,0,1,2}- C .{1,2} D .{0,1,2}2.已知i 为虚数单位,若复数11ti z i-=+在复平面内对应的点在第四象限,则t 的取值范围为( ) A .[1,1]- B .(1,1)- C .(,1)-∞-D .(1,)+∞ 3.下列函数中,与函数3y x =的单调性和奇偶性一致的函数是( )A.y =.tan y x = C.1y x x=+ D .e e x x y -=- 4.已知双曲线1C :22143x y -=与双曲线2C :22143x y -=-,给出下列说法,其中错误的是( ) A.它们的焦距相等 B .它们的焦点在同一个圆上C.它们的渐近线方程相同 D .它们的离心率相等5.某学校上午安排上四节课,每节课时间为40分钟,第一节课上课时间为8:00~8:40,课间休息10分钟.某学生因故迟到,若他在9:10~10:00之间到达教室,则他听第二节课的时间不少于10分钟的概率为( )A .15B .310C .25D .456.若倾斜角为α的直线l 与曲线4y x =相切于点()1,1,则2cos sin 2αα-的值为( )A .12-B .1C .35-D .717- 7.在等比数列{}n a 中,“4a ,12a 是方程2310x x ++=的两根”是“81a =±”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8.执行如图所示的程序框图,则输出的S 值为( )A.1009 B .-1009 C.-1007 D .10089.已知一几何体的三视图如图所示,则该几何体的体积为( )A .163π+B .112π+C .1123π+D .143π+ 10.已知函数()sin()f x A x ωϕ=+(0,0,||)A ωϕπ>><的部分图象如图所示,则函数()cos()g x A x ϕω=+图象的一个对称中心可能为( )A .5(,0)2-B .1(,0)6 C.1(,0)2- D .11(,0)6- 11.《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F 在半圆O 上,点C 在直径AB 上,且OF AB ⊥,设AC a =,BC b =,则该图形可以完成的无字证明为( )A.2a b +≥(0,0)a b >> B .222a b ab +≥(0,0)a b >>C.2ab a b ≤+(0,0)a b >> D .2a b +≤(0,0)a b >> 12.已知球O 是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A BCD -的外接球,3BC =,AB =E 在线段BD 上,且3BD BE =,过点E 作圆O 的截面,则所得截面圆面积的取值范围是( )A .[],4ππB .[]2,4ππC .[]3,4ππD .(]0,4π第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 已知(1,)a λ= ,(2,1)b = ,若向量2a b + 与(8,6)c = 共线,则a = .14.已知实数x ,y 满足不等式组20,250,20,x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩目标函数422log log z y x =-,则z 的最大值为 .15.在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,cos c B -是cos b B 与cos a A的等差中项且8a =,ABC ∆的面积为b c +的值为 .16.已知抛物线C :24y x =的焦点是F ,直线1l :1y x =-交抛物线于A ,B 两点,分别从A ,B 两点向直线2l :2x =-作垂线,垂足是D ,C ,则四边形ABCD 的周长为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知函数()212f x x mx =+(0m >),数列{}n a 的前n 项和为n S ,点(),n n S 在()f x 图象上,且()f x 的最小值为18-. (1)求数列{}n a 的通项公式;(2)数列{}n b 满足12(21)(21)nn n a n a a b +=--,记数列{}n b 的前n 项和为n T ,求证:1n T <. 18.如图,点C 在以AB 为直径的圆O 上,PA 垂直与圆O 所在平面,G 为AOC ∆的垂心.(1)求证:平面OPG ⊥平面PAC ;(2)若22PA AB AC ===,点Q 在线段PA 上,且2PQ QA =,求三棱锥P QGC -的体积.19.2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[)50,60,[)60,70,…,[]90,100分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).(1)求频率分布直方图中的x 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;(3)若在样本中,利用分层抽样的方法从成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求[)[]80,90,90,100两组中至少有1人被抽到的概率.20.已知椭圆C :22221(0)x y a b a b+=>>的长轴长为,且椭圆C 与圆M :221(1)2x y -+=的公共(1)求椭圆C 的方程.(2)经过原点作直线l (不与坐标轴重合)交椭圆于A ,B 两点,AD x ⊥轴于点D ,点E 在椭圆C 上,且()()0AB EB DB AD -⋅+=uu u r uu r uu u r uuu r ,求证:B ,D ,E 三点共线.. 21.已知函数()2ln f x m x x =-,()23e 3x g x x -=(R m ∈,e 为自然对数的底数). (1)试讨论函数()f x 的极值情况;(2)证明:当1m >且0x >时,总有()()30g x f x '+>.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.已知直线l的参数方程为4,x y ⎧=+⎪⎪⎨⎪=⎪⎩(t为参数),以坐标原点为极点,x 轴的非负半轴为极轴建立极坐标系,圆C 的极坐标方程为4cos ρθ=,直线l 与圆C 交于A ,B 两点.(1)求圆C 的直角坐标方程及弦AB 的长;(2)动点P 在圆C 上(不与A ,B 重合),试求ABP ∆的面积的最大值.23.已知函数()|21||1|f x x x =-++.(1)求函数()f x 的值域M ;(2)若a M ∈,试比较|1||1|a a -++,32a ,722a -的大小.试 卷 答 案一、选择题1-5:D B D D A 6-10:D A B C C 11 D 、12: B二、填空题13.1 15..18+三、解答题17.(1)解:()()22122m f x x m =+-, 故()f x 的最小值为2128m -=-. 又0m >,所以12m =,即21122n S n n =+. 所以当2n ≥时,1n n n a S S n -=-=;当1n =时,11a =也适合上式,所以数列{}n a 的通项公式为n a n =.(2)证明:由(1)知12(21)(21)nn n n b +==--1112121n n +---, 所以11111113372121n n n T +=-+-++--- 11121n +=--, 所以1n T <.18.(1)证明:如图,延长OG 交AC 于点M .因为G 为AOC ∆的重心,所以M 为AC 的中点.因为O 为AB 的中点,所以//OM BC .因为AB 是圆O 的直径,所以BC AC ⊥,所以OM AC ⊥.因为PA ⊥平面ABC ,OM ⊂平面ABC ,所以PA OM ⊥.又PA ⊂平面PAC ,AC ⊂平面PAC ,PA AC A = ,所以OM ⊥平面PAC ,即OG ⊥平面PAC .又OG ⊂平面OPG ,所以平面OPG ⊥平面PAC .(2)解:由(1)知OM ⊥平面PAC ,所以GM 就是点G 到平面PAC 的距离.由已知可得,1OA OC AC ===,所以AOC V 为正三角形,所以2OM =.又点G 为AOC V 的重心,所以136GM OM ==.故点G 到平面PQC所以13P QGC G PQC PQC V V S --==V 1233PAC GM S GM ⋅=⨯⋅V 212192=⨯⨯⨯=19.解:(1)由频率分布直方图可得第4组的频率为10.10.30.3---0.10.2-=,故0.02x =.故可估计所抽取的50名学生成绩的平均数为(550.01650.03⨯+⨯750.03850.02+⨯+⨯+)950.011074⨯⨯=(分).由于前两组的频率之和为0.10.30.4+=,前三组的频率之和为0.10.30.30.7++=,故中位数在第3组中. 设中位数为t 分,则有()700.030.1t -⨯=,所以1733t =, 即所求的中位数为1733分. (2)由(1)可知,50名学生中成绩不低于70分的频率为0.30.20.10.6++=,由以上样本的频率,可以估计高三年级2000名学生中成绩不低于70分的人数为20000.61200⨯=.(3)由(1)可知,后三组中的人数分别为15,10,5,故这三组中所抽取的人数分别为3,2,1.记成绩在[)70,80这组的3名学生分别为a ,b ,c ,成绩在[)80,90这组的2名学生分别为d ,e ,成绩在[]90,100这组的1名学生为f ,则从中任抽取3人的所有可能结果为(),,a b c ,(),,a b d ,(),,a b e ,(),,a b f ,(),,a c d ,(),,a c e ,(),,a c f ,(),,a d e ,(),,a d f ,(),,a e f ,(),,b c d ,(),,b c e ,(),,b c f ,(),,b d e ,(),,b d f ,(),,b e f ,(),,c d e ,(),,c d f ,(),,c e f ,(),,d e f 共20种.其中[)[]80,90,90,100两组中没有人被抽到的可能结果为(),,a b c ,只有1种, 故[)[]80,90,90,100两组中至少有1人被抽到的概率为11912020P =-=. 20.(1)解:由题意得2a =a =由椭圆C 与圆M :()22112x y -+=其长度等于圆M 的直径,可得椭圆C经过点1,⎛ ⎝⎭, 所以211212b+=,解得1b =. 所以椭圆C 的方程为2212x y +=. (2)证明:设()11,A x y ,()22,E x y ,则()11,B x y --,()1,0D x .因为点A ,E 都在椭圆C 上,所以2211222222,22,x y x y ⎧+=⎪⎨+=⎪⎩ 所以()()1212x x x x -++()()121220y y y y -+=, 即()121212122y y x x x x y y -+=--+. 又()()AB EB DB AD -⋅+uu u r uu r uu u r uuu r 0AE AB =⋅=uu u r uu u r , 所以1AB AE k k ⋅=-, 即1121121y y y x x x -⋅=--, 所以()11211212y x x x y y +⋅=+ 所以()1211122y y y x x x +=+ 又1211212BE BD y y y k k x x x +-=-=+121212120y y y y x x x x ++-=++, 所以BE BD k k =,所以B ,D ,E 三点共线.21.(1)解:()f x 的定义域为()0,+∞,()21m f x x '=-=2x m x--. ①当0m ≤时,()0f x '<,故()f x 在()0,+∞内单调递减,()f x 无极值;②当0m >时,令()0f x '>,得02x m <<;令()0f x '<,得2x m >.故()f x 在2x m =处取得极大值,且极大值为()()22ln 22f m m m m =-,()f x 无极小值.(2)证法一:当0x >时,()()30g x f x '+>⇔23e 3630x m x x-+->⇔23e 3630x x mx -+->. 设函数()23e 3x u x x =-63mx +-,则()()3e 22x u x x m '=-+.记()e 22x v x x m =-+, 则()e 2xv x '=-. 当x 变化时,()v x ',()v x 的变化情况如下表:由上表可知()()ln 2v x v ≥,而()ln2ln 2e 2ln 22v m =-+=22ln 22m -+=()2ln 21m -+,由1m >,知ln 21m >-,所以()ln 20v >,所以()0v x >,即()0u x '>.所以()u x 在()0,+∞内为单调递增函数.所以当0x >时,()()00u x u >=.即当1m >且0x >时,23e 3x x -630mx +->.所以当1m >且0x >时,总有()()30g x f x '+>.证法二:当0x >时,()()30g x f x '+>⇔23e 3630x m x x-+->⇔23e 3630x x mx -+->. 因为1m >且0x >,故只需证()22211x e x x x >-+=-.当01x <<时,()21x e x >1>-成立;当1x ≥时,()221xx e x e x >-⇔>-1,即证2x e x >-1.令()2x x e x ϕ=-+1,则由()212x x e ϕ'=-1=0,得2ln 2x =. 在()1,2ln 2内,()0x ϕ'<;在()2ln 2,+∞内,()0x ϕ'>,所以()()2ln 222ln 210x ϕϕ≥=-+>.故当1x ≥时,()21x e x >-成立.综上得原不等式成立.22.解:(1)由4cos ρθ=得24cos ρρθ=,所以2240x y x +-=,所以圆C 的直角坐标方程为22(2)4x y -+=.将直线l 的参数方程代入圆:C 22(2)4x y -+=,并整理得20t +=, 解得10t =,2t =-.所以直线l 被圆C截得的弦长为12||t t -=(2)直线l 的普通方程为40x y --=.圆C 的参数方程为22cos ,2sin ,x y θθ=+⎧⎨=⎩(θ为参数), 可设圆C 上的动点(22cos ,2sin )P θθ+,则点P 到直线l的距离d=|2cos()4πθ=+. 当cos()14πθ+=-时,d 取最大值,且d的最大值为2所以12ABP S ∆≤⨯(22=+ 即ABP ∆的面积的最大值为223. 解:(1)3,1,1()2,1,213,.2x x f x x x x x ⎧⎪-<-⎪⎪=--≤≤⎨⎪⎪>⎪⎩ 根据函数()f x 的单调性可知, 当12x =时,min 13()()22f x f ==. 所以函数()f x 的值域3[,)2M =+∞.(2)因为a M ∈,所以32a ≥,所以3012a <≤. 因为|1||1|1a a a -++=-123a a ++=≥, 所以3|1||1|2a a a-++> 因为37222a a ⎛⎫--= ⎪⎝⎭24732a a a -+=()()1432a a a -- 又由32a ≥,知10a ->,430a ->, 所以(1)(43)02a a a-->, 所以37222a a >-, 所以|1||1|a a -++>37222a a >-.。
高三数学上学期第四次月考试题文重点班
ON = gOM+gOP 值线MP 不过点O),则%等于()A. 15 B ・ I 。
C. 40 D . 20 /⑴在P+S )上为减函数,心)一°,则不 ()B. (3,+s)(;J)U(3,+s) D. 3 二、填空题:(本大题共5小题,每小题5分,满分20分.其中14〜15题是选做题,考生只能 选做一题,两题全答的,只计算前一题得分•)11・若椭圆经过点(2, 3),且焦点为片(-2,0),巧ao ),则这个椭圆的离心率等于■_______________ •12. 一个正方体的全而积为於,它的「顶点全郁在一个球而上,则这个球的表面积为 ______________ :“、,1 1t (X )~+ --------- x -----13. 若xv°,则函数"一 疋’x 的最小值是 ____________________ .14. 等差数列仏}中,如<°,如>°,且如>|如,若{%}的前”项和S”v0,则“的最大值是 _____________________ . -15. 一船自西向东匀速航行,上午10时到达一座灯塔P 的南偏西75°距塔64海里的M 处,下午2时 到达这座灯塔的东南方向的N 处,则这只船的航行速度为 ______________________________ 海里/小 时.三、解答题:(本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.)16. (本小题满分12分)已知 f (^) = -2cos 2 x- 2V2 sinx + 2 泄义域为 R,(1) 求/(x)的值域;(2在区间f(a) = 3 ,求sin(2a + -)) 2 2317. (本小题满分14分) 10.已知/(X )是左义R 在上的偶函数,/(log j A )<0等式 ° 的解集为 (0,:)U(3,+s) C. 3如图,在四棱锥P - ABCD中,底而ABCD是正方形,侧棱他丄底而ABCD,皿=眈,E是PC的中点,作防丄RS交PB于点F:(I)iiE明曲R平而EDE :仃I)证明PB丄平而EFD:18(本小题满分14分)甲乙二人用4张扑克牌(分别是红桃2,红桃3,红桃4,方片4)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌而上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.(I)设(jj)分别表示甲、乙抽到的牌的数字"写出甲乙二人抽到的牌的所有情况.(1【)若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?(III)甲乙约泄:若甲抽到的牌的牌面数字比乙大,则甲胜,反之,则乙胜.你认为此游戏是否公平,说明你的理由.19甲.(14分)如图,平而必2?丄平而救刀,△砸是等边三角形,個②是矩形,AB: AD= ^2 :1,尸是曲的中点.(1)求农与平面如?所成的角:(2)求二而角片F0B的度数;(3)当7到平面月万G?的距离是3时,求万到平而疔C的距离.20.(12分)商学院为推进后勤社会化改革,与桃园新区商左:由该区向建设银行贷款500万元在桃园新区为学院建一栋可容纳一千人的学生公寓,工程于2002年初动工,年底竣工并交付使用,公寓管理处采用收费还贷偿还建行贷款(年利率5%,按复利计算),公寓所收费用除去物业管理费和水电费18万元.其余部分全部在年底还建行贷款.(1)若公寓收费标准定为每生每年800元,问到哪一年可偿还建行全部贷款;(2)若公寓管理处要在2010年底把贷款全部还淸,则每生每年的最低收费标准是多少元(精确到元).(参考数据:lgl. 7343 = 0. 2391, Igl. 05 = 0. 0212, 1.0^=1.4774)21 (14分).数列{山}的前"项和记为以,5=:,点(»山心)在直线y = 2x+1上,neN\(1)当实数'为何值时,数列{©}是等比数列?⑵在(1)的结论下,设"=呃昭,且人是数列"% 的前"项和,求©H2的值. 数学(文科)参考答案一选择题:CABDC DADBC二填空题:12- T13. 4 , 14. 19 , 15. 8x/6三解答题:16.解:(1) /(x) = -2(1-sin2 x)-2V2sinx + 2 = 2(siii x-^-)2 -1 x e R^sinx e[-1,1]值域[-L2 + 2\/2J5 .(2)由(1)得,/(a) = 2(sina—宁尸一1 = 3L p.・.(sin —#)2=2, 乂* 417. (I)证明:连结AC, AC交BD于0。
安徽省枞阳县高三数学上学期第四次月考试题 文 新人教A版
一、选择题:本大题共10小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是 符合题目要求的。
1. 设i 为虚数单位,则复数34ii +=( )()A 43i -- ()B 43i -+ ()C i 4+3 ()D i 4-3【解析】选D 依题意:234(34)43i i ii i i ++==-2.设全集R U =,=A (2){|21},{|ln(1)}x x x B x y x -<==-,则图中阴影部分表示的集合为( )A .{|1}x x ≥B .{|01}x x <≤C .{|12}x x ≤<D .{|1}x x ≤分析:根据所给的文恩图,看出阴影部分所表达的是要求B 集合的补集与A 集合的交集,整理两个集合,求出B 的补集,再求出交集解答:解:由文恩图知阴影部分表示的是A∩C U B∵A={x|2x (x-2)<1}={x|0<x <2},B={x|y=ln (1-x )}={x|x <1}, ∴阴影部分对应的集合是{x|1≤x<2} 故选C . 3. 若向量(1,2),(3,4)AB BC ==;则AC =( )()A (4,6)-- ()B (4,6) ()C (,)-2-2 ()D (,)22【解析】选B (4,6)AC AB BC =+=4.定义运算a bc d ,ad bc =-则函数()f x =2sin 12cos x x -图像的一条对称轴方程是( )A .4x π=B .2x π=C .x π=D .0x =4.【解析】()2sin cos 2sin 22f x x x x =+=+. 当4x π=时()f x 取最值.选A.5. 已知变量,x y 满足约束条件1101x y x x y +≤⎧⎪+≥⎨⎪-≤⎩,则2z x y =+的最小值为( )()A 3 ()B 1 ()C 6- ()D 5-【解析】选D 约束条件对应ABC ∆边际及内的区域:(1,0),(1,2),1,2)A B C --- 则2[5,3]z x y =+∈-6. 在ABC ∆中,若60,45,32A B BC ︒︒∠=∠==,则AC =( )()A 43 ()B 3 ()C 23 ()D 32【解析】选C由正弦定理得:3223sin sin sin 60sin 45BC AC ACAC A B ︒︒=⇔=⇔=7.某几何体的三视图如图1所示,它的体积为( )()A 72π ()B π30 ()C 48π ()D π24【解析】选C 几何体是半球与圆锥叠加而成它的体积为3222141335330 233Vπππ=⨯⨯+⨯⨯⨯-=8. 在平面直角坐标系xOy中,直线3450x y+-=与圆224x y+=相交于,A B两点,则弦AB的长等于( )()A23()B33()C3()D1【解析】选A圆224x y+=的圆心(0,0)O到直线3450x y+-=的距离515d-==弦AB的长22223 AB r d=-=9. 执行如图2所示的程序框图,若输入n的值为6,则输出s的值为()A105()B16()C15()D1【解析】选Cs11315i135710. 对任意两个非零的平面向量α和β,定义βββαβα••=•;若两个非零的平面向量,a b满足a与b的夹角(,)42ππθ∈,且αββα••,都在集合}2nn Z⎧∈⎨⎩中,则βα•( )()A 12()B1()C32()D52【解析】选A21cos 0,cos 0()()cos (0,)2a ba b b a a b b a baθθθ=>=>⇒⨯=∈,a b b a 都在集合}2n n Z ⎧∈⎨⎩中得:*12121()()(,)42n n a b b a n n N a b ⨯=∈⇒=二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
高三第四次月考数学试题(文科).doc
高三第四次月考数学试题(文科)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
共150分。
考试时间120分钟。
第Ⅰ卷(选择题 共60分)参考公式:如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B )如果事件A 、B 相互独立,那么P (A ·B )=P (A )·P (B )如果事件A 在一次试验中发生的概率是P ,那么它n 次独立重复试验中恰好发生k 次的概率k n k kn n P P C k P --=)1()(正棱锥、圆锥的侧面积公式S 棱锥=cl 21其中c 表示底面周长,l 表示斜高或母线长。
球的体积公式V 球= 334R π 其中R 表示球的半径一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设P={3,4,5},Q={4,5,6,7},定义P ※Q=},|),{(Q b P a b a ∈∈,则P ※Q 中元素的个数为( )A .3B .4C .7D .122.1-=a 是直线03301)12(=++=+-+ay x y a ax 和直线垂直( )A .充分而不必要的条件B .必要而不充分的条件C .充要条件D .既不充分又不必要的条件3.某学生离家去学校,一开始跑步前进,跑累了再走余下的路程。
下列图中纵轴表示离校 的距离,横轴表示出发后的时间,则较符合学生走法的是 ( )x A B C D4.准线方程为3=x 的抛物线的标准方程为 ( )A .x y 62-=B .x y 122-=C .x y 62=D .x y 122=5.已知直线a 、b 与平面α,给出下列四个命题①若a ∥b ,b ⊂α,则a ∥α; ②若a ∥α,b ⊂α,则a ∥b ; ③若a ∥α,b ∥α,则a ∥b; ④a ⊥α,b ∥α,则a ⊥b. 其中正确的命题是 ( ) A .1个 B .2个 C .3个 D .4个6.如果命题“ (p 或q)”为假命题,则 ( )A .p 、q 均为真命题B .p 、q 均为假命题C .p 、q 中至少有一个为真命题D .p 、q 中至多有一个为真命题 7.若把一个函数的图象按a =(-3π,-2)平移后得到函数y=cos x 的图象,则原图象的函数解析式为 ( )A .y=cos(x +3π)-2; B .y=cos(x -3π)-2; C .y=cos(x+3π)+2; D .y=cos(x -3π)+28.已知一个简单多面体的各个顶点处都有三条棱,则顶点数V 与面数F 满足的关系式是( )A .2F+V=4;B .2F -V=4;C .2F+V=2;D .2F -V=2;9.在正方体ABCD —A 1B 1C 1D 1中,B 1C 与对角面DD 1B 1B 所成的角的大小是A .15°B .30°C .45°D .60° ( )10.点P 是曲线323+-=x x y 上移动,设点P 处切线倾斜角为α,则α的取值范围是( ) A .]2,0[πB .))πππ,43[2,0[⋃C .)ππ,43[D .]43,2(ππ11.设F 1,F 2是双曲线1422=-y x 的两个焦点,点P 在双曲线上,且021=⋅PF PF , 则||||21PF PF ⋅的值等于 ( )A .2B .22C .4D .812.在今年公务员录用中,某市农业局准备录用文秘人员二名,农业企业管理人员和农业法宣传人员各一名,报考农业公务员的考生有10人,则可能出现的录用情况种数是( )A.5040B.2520C.1260D.210第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题4分,共16分. 把答案填在题中横线上)13.已知x 、y 满足约束条件⎪⎩⎪⎨⎧-≥≤+≤11y y x x y ,则z=2x+y 的最大值是 。
安徽省巢湖市2017届高三上学期第四次月考数学文试题
巢湖市柘皋中学2016-2017年高三上第四次月考数 学 试 卷(文)考试时间:120分钟 满分:150分 命题人:梁小跃 审题人:王军一、选择题:本大题共12小题,每小题5分,满分60分.在每题的四个选项中,只有一项是符合要求的.1.集合{}223M x x x =-≥,集合{}2680N x x x =-+<,则M N ⋂=( ) A .(]2,3 B .[)3,4C .()1,2-D .(]1,3-2.已知命题:p 对于x R ∈恒有222xx-+≥成立;命题:q 奇函数()f x 的图像必过原点,则下列结论正确的是( ) A .p q ∧为真B .()p q ⌝∨为真C .()q ⌝为假D .()p q ∧⌝为真3.复数1-i2-i的共轭复数对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限4.在等差数列{a n }中,已知a 4=7,a 3+a 6=16,a n =31,则n 为( ) A .13 B .14 C .16D .155..曲线y =sinx + e x 在点(0,1)处的切线方程是( )A .x-3y +3=0B .x -2y +2=0C .2x -y +1=0D .3x -y +1=0 6.函数y =A sin(ωx +φ)(ω>0,|φ|≤π2)的部分图象如图所示,则函数的一个表达式为( )A .y =4sin(π8x -π4)B .y =-4sin(π8x +π4)C .y =-4sin(π8x -π4)D .y =4sin(π8x +π4)7.若圆O 的半径为3,直径AB 上一点D 使3AB AD =,E F 、为另一直径的两个端点,则DE DF ⋅=( ) A .3-B .4-C . 6-D .8-8.设F 1、F 2分别是椭圆E :x 2+y 2b 2=1(0<b <1)的左、右焦点,过F 1的直线l 与椭圆相交于A 、B 两点,且|AF 2|,|AB |,|BF 2|成等差数列,则|AB |的长为( ) B .19.已知A ,B 是球O 的球面上两点,∠AOB =900,C 为该球面上的动点,若三棱锥O -ABC 体积的最大值为36,则球O 的体积为( )A .72πB .144πC .288πD .576π10.若某空间几何体的三视图如图所示, 则该几何体的表面积是( )A .23B .2+2+ 6C .2+22+ 6D .2+322+ 6 11.已知函数的定义域为R ,当x <0时,f (x )=x 3-1;当-1≤x ≤1时,f (-x )=-f (x );当x>12时,11()()22f x f x +=-.则f (6)=( )A .-2B .-1C . 2D .012.已知变量a ,b 满足b =-12a 2+3lna (a >0),若点Q (m ,n )在直线y =2x +12上, 则(a -m )2+(b -n )2的最小值为( ) A .9B .553 C .3 D .59 二、填空题:本大题共4小题,每小题5分.13.设x , y 满足1010330x y x y x y +-≥⎧⎪--≤⎨⎪-+≥⎩,则z =x +2y 的最大值为_________.14.若双曲线1422=-y m x 的右焦点与抛物线x y 162=的焦点重合,则m = 15.已知圆C 过点(1,0),且圆心在x 轴的正半轴上,直线l :1y x =-被该圆所截得的弦长为22C 的标准方程为.16.已知函数f (x )=2|54|,x 02|2|,0x x x x ⎧++≤⎨->⎩.若函数y =f (x )-a |x |恰有4个零点,则实数a 的取值范围为_______.三、解答题:本大题共6小题,共70分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽省振阳公学2017届高三上学期第四次月考数学(文)试题(时间:120分钟 分值:150分)第I 卷(满分60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{|1}M x x =>,2{|20}N x x x =-≥,则M N = ( )A .(,0](1,)-∞+∞B .(1,2]C .(1,)+∞D .[2,)+∞ 2.复数()21i +的虚部是( )A .0B .2-C .2D .i 23.已知向量(2,1),(1,)a b x ==,若a b + 与a b - 平行,则实数x 的值是( )A .-2B .12C .1D .24.已知条件:0p a <,条件2:q a a >,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5. 设函数⎩⎨⎧+∞∈-∞∈=),2(,log ]2,(,2)(2x x x x f x ,则满足()3f x =的x 的值是 ( )A .2log 3B .8C . 2log 3或8D .8或6 6.已知等差数列{}n a 中8,0102==a a ,则=2018a ( )A .2015B .2016C .2017D .20187. 在ABC ∆中,2,4a b A π===,则角B =( )A .6πB .6π或56πC .3πD .56π8.将函数()R x x y ∈⎪⎭⎫⎝⎛+=3sin π的图像向左平移)0(>m m 个单位长度后,所得到的图像关于y轴对称,则m 的最小值是( ) A.12π B.6π C.3πD.65π 9.函数21ln ||12y x x =-+的图象大致为( )10.已知点)1,0(A ,曲线x a y C ln :=上点()0,1B ,P 为曲线C 上的动点且⋅的最小值为2,则=a ( )A .2-B .1-C .2D .111.已知正实数,a b 满足8=+b a ,则ba 41+的最小值为 ( ) A .1 B .78 C .98D .212.已知()x x x x f ln 86212-+-=在[]1,+m m 上不单调,则实数m 的取值范围是 ( )A .()()3,41,2B .(][)4,32,1C . ()3,4D .()1,2第Ⅱ卷(满分90分)二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上 13.已知数列{a n }的首项21=a ,且()11+=+n n na a n ,则4a 的值为_____________14.设x 、y 满足约束条件010,30y x y x y ≥⎧⎪-+≥⎨⎪+-≤⎩则22--=y x z 的最小值为_____________15.第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如下图会标是由四个全等的直角三角形与一个小正方形拼 成的一个大正方形,如果小正方形的面积为1,大 正方形的面积为25,直角三角形中较大的锐角为θ,那么=⎪⎭⎫ ⎝⎛+3sin πθ_____________.16.若函数()y f x =满足()()2f a x f a x b ++-=(其中a ,b 不同时为0),则称函数()y f x =为“准奇函数”,称点(,)a b 为函数()f x 的“中心点”.现有如下命题: ①函数()sin 1f x x =+是准奇函数;②若准奇函数()y f x =在R 上的“中心点”为(,())a f a ,则函数()()()F x f x a f a =+-为R 上的奇函数;③已知函数()232sin +⎪⎭⎫ ⎝⎛-=πx x f 是准奇函数,则它的“中心点”为⎪⎭⎫⎝⎛+2,3ππk④已知函数32()362f x x x x =-+-是准奇函数,则它的“中心点”为(1,2); 其中正确的命题是_____________.(写出所有正确命题的序号)三.解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(本题满分10分)已知函数()sin f x a x x =(a ∈R )的图象经过点(,0)3π.(Ⅰ)求()f x 的最小正周期;(Ⅱ)若3[,]22x ππ∈,求()f x 的取值范围.18.(本题满分12分)在公差不为0的等差数列{}n a 中,已知11=a ,且1452,,a a a 成等比数列.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)令n n n a b ⋅=2,求数列{}n b 的前n 项和n T .19.(本题满分12分)设向量()()x x x x sin ,cos 3,sin ,sin ==,(Ⅰ)设函数()f x a b =⋅,求()f x 的单调递增区间;(Ⅱ)在△ABC 中,锐角A 满足()23=A f ,7,4==+a c b ,求△ABC 的面积.20.(本题满分12分)设△ΑΒC 的内角C B A ,,所对的边分别为c b a ,,,且b c C a 2c o s 2=+.(Ⅰ)求角A 的大小;(Ⅱ)若1=a ,求△ΑΒC 的周长的取值范围.21.(本题满分12分)在等比数列{}n a 中公比1≠q ,等差数列{}n b 满足3132411,,3a b a b a b ==== (I )求数列{}n a 与{}n b 的通项公式;(II )记()n n n a b c +-=n1,求数列{}n c 的前n 2项和n S 2.22. (本小题满分12分)已知函数1()(1)ln ,f x ax a x a x=--+∈R .(I )若2a =-,求函数()f x 在21=x 处的切线方程;(Ⅱ)若1a ≥,且()1f x >在区间1[,e]e上恒成立,求a 的取值范围;安徽省振阳公学2017届高三上学期第四次月考数学(文)试题答案一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有13.8 14.4- 15.10334+ 16.①②④ 三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(本题满分10分)解:(Ⅰ)因为函数()sin f x a x x =的图象经过点(,0)3π,所以()0.322f π== 解得 1a = .所以()sin 2sin()3f x x x x π==-.所以()f x 最小正周期为2π.(Ⅱ)因为322x ππ≤≤,所以7.636x πππ≤-≤ 所以当32x ππ-=,即56x π=时,()f x 取得最大值,最大值是2;当736x ππ-=,即32x π=时,()f x 取得最小值,最小值是 1.-所以()f x 的取值范围是[1,2]-.18.(本题满分12分)19.(本题满分12分)解:(Ⅰ)21()cos sin sin(2)62f x a b x x x x π=⋅=+=-+由222262k x k πππππ-≤-≤+得增区间为:,()63k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦;(Ⅱ)由3()2f A =,得3A π=;又因为4,b c a +==由余弦定理2222cos a b c bc A =+-得:3bc =;所以1sin 2ABC S bc A ∆==20.(本题满分12分)解:(1)由b c C a 2cos 2=+,即B C C A sin 2sin cos sin 2=+, 又sin sin()sin cos cos sin B A C A C A C =+=+,1sin cos sin 2C A C =∴.1sin 0cos 2C A ≠=∵,∴.又(0π)A ∈∵,,π3A =∴.(2)由正弦定理得sin sin a B b B c C A ===,,1sin )1sin()]l a b c B C B A B =++=+=++∴1π12cos 12sin 26B B B ⎫⎛⎫=++=++⎪ ⎪⎪⎝⎭⎝⎭.π3A =∵,2πππ5π03666B B ⎛⎫⎛⎫∈+∈ ⎪ ⎪⎝⎭⎝⎭∴,,,,π1sin 162B ⎛⎫⎛⎤+∈ ⎪ ⎥⎝⎭⎝⎦∴,.故△ΑΒC 的周长的取值范围是(23],.21. (本题满分12分)(Ⅰ) 设等比数列{}n a 的公比为q ,1≠q ,等差数列{}n b 的公差为d .由已知得:()d d d q d q q d q d 4114113123333222+=+⇒⎩⎨⎧+=+=⇒⎩⎨⎧=+=+解得⎩⎨⎧==32q d 或⎩⎨⎧==10q d (舍去)..n n n a 3331=⨯=∴-, ()12213+=-+=n n b n(Ⅱ) 由题意得:()()nn n n c 3121++-=,()()()[]14149753333222++---+-+-++++=n n S n n.()()()()()()[]14147935313132--+++-+-+--=n n n n n 223312+-=+22. (本题满分12分)解:(Ⅰ)若2a =-,则1()2ln f x x x x =--+,(0,)x ∈+∞ 421`=⎪⎭⎫ ⎝⎛f ,2ln 321--=⎪⎭⎫ ⎝⎛f ∴⎪⎭⎫ ⎝⎛-=++2142ln 3x y 即052ln 4=---y x .(Ⅱ)依题意,在区间1[,e]e 上min ()1f x >. 222(1)1(1)(1)()ax a x ax x f x x x-++--'==,1a ≥. 令()0f x '=得,1x =或1x a =.若e a ≥,则由()0f x '>得,1e x <≤;由()0f x '<得,11ex ≤<.所以min ()(1)11f x f a ==->,满足条件; 若1e a <<,则由()0f x '>得,11e x a≤<或1e x <≤;由()0f x '<得,11x a <<.min 1()min{(),(1)}e f x f f =,依题意1()1e (1)1f f ⎧>⎪⎨⎪>⎩ ,即2e e 12a a ⎧>⎪+⎨⎪>⎩,所以2e a <<.若1a =,则()0f x '≥.所以()f x 在区间1[,e]e 上单调递增,min 1()()1ef x f =<,不满足条件; 综上,2a >.。
