2023高考数学复习专项训练《等比数列》(含答案)
辽宁省2023届高考数学复习:近年真题模拟题专项(数列综合题)练习(附答案)

辽宁省2023届高考数学复习:近年真题模拟题专项(数列综合题)练习1.(2022•新高考Ⅱ)已知{}n a 是等差数列,{}n b 是公比为2的等比数列,且223344a b a b b a -=-=-. (1)证明:11a b =;(2)求集合1{|k m k b a a =+,1500}m 剟中元素的个数.2.(2021•新高考Ⅱ)记n S 是公差不为0的等差数列{}n a 的前n 项和,若35a S =,244a a S =. (Ⅰ)求数列{}n a 的通项公式n a ; (Ⅱ)求使n n S a >成立的n 的最小值.3.(2022•沈阳一模)等差数列{}n a 和等比数列{}n b 满足111a b ==,2414a a +=,246b b a =,且0n b >. (1)求数列{}n b 的通项公式;(2)已知:①1000n b <;②m N +∃∈,使m n a b =.设S 为数列{}n b 中同时满足条件①和②的所有的项的和,求S 的值.4.(2022•沈阳一模)已知等差数列{}n a 和正项等比数列{}n b 满足14a =,12b =,212n n n b b b ++=+,332a b =+. (1)求{}n a 和{}n b 的通项公式;(2)对于集合B ,定义集合{A B x A -=∈且}x B ∈∉,设数列{}n a 和{}n b 中的所有项分别构成集合A ,B ,将集合A B -的所有元素按从小到大依次排列构成一个新数列{}n c ,求数列{}n c 的前30项和30S .5.(2022•沈河区校级二模)已知等差数列{}n a 满足59a =,4822a a +=. (1)求{}n a 的通项公式;(2)等比数列{}n b 的前n 项和为n S ,且11b a =,再从下面①②③中选取两个作为条件,求满足2021n S <的n 的最大值.①312b a a =+; ②37S =; ③1n n b b +>.6.(2022•大连模拟)已知等差数列{}n a 的公差为正实数,满足14a =,且1a ,3a ,54a +成等比数列. (1)求数列{}n a 的通项公式;(2)设数列{}n b 的前n 项和为n S ,若11b =,且 ______,求数列{}n n a b +的前n 项和为n T ,以下有三个条件:①21n n S =-,*n N ∈; ②21n n S b =-,*n N ∈; ③121n n S S +=-,*n N ∈.从中选一个合适的条件,填入上面横线处,使得数列{}n b 为等比数列,并根据题意解决问题.7.(2022•辽宁一模)已知{}n a 是等差数列,36a =,612a =,且1,2,nn n a a n b n +⎧=⎨⎩为偶数为奇数. (1)求{}n a 的通项公式; (2)求{}n b 的前2n 项和.8.(2022•辽宁模拟)已知等差数列{}n a 的前n 项和为n S ,满足11a =,7210126S a a -=+. (1)求数列{}n a 的通项公式;(2)记数列1{2}n a n a +⋅的前n 项和为n T ,求满足920409665n T n ->-的正整数n 的最小值.9.(2022•沙河口区校级模拟)已知单调递增的等比数列{}n a ,满足23428a a a ++=,且32a +是2a ,4a 的等差中项.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若n n b na =-,12n n S b b b =++⋯+,对任意正整数n ,总有1()0n n S n m a +++<成立,试求实数m 的取值范围.10.(2022•辽宁模拟)已知n S 为数列{}n a 的前n 项和,13a =,114n n S a ++=. (1)求数列{}n a 的通项公式;(2)从下面两个条件中选择一个,求数列{}n b 的前n 项和n T . ①211(1)n n n n a b S a +++=+;②242221(1)(21013)2n n n n n n n b a a -+-⋅++⋅=⋅.11.(2022•大东区模拟)已知数列{}n a 的前n 项和为n S .从下面①②③中选择其中一个作为条件解答试题,若选择不同条件分别解答,则按第一个解答计分. ①数列{}n a 是等比数列,26S =,且24a ,32a ,4a 成等差数列; ②数列{}n a 是递增的等比数列,1432a a =,2312a a +=; ③22n n S a =-.(1)求数列{}n a 的通项公式;(2)已知数列{}n b 的前n 项的和为n T ,且2212211(log )(log )n n n b a a -+=,证明:12n T <.12.(2022•辽宁模拟)已知数列{}n a 的前n 项和为n S ,满足:*21()nn S a n N n=+∈. (Ⅰ)求证:数列{}n a 为等差数列; (Ⅱ)若25a =,令1n nb a =,数列{}n b 的前n 项和为n T ,若不等式22145()5n n T T m m +--…对任意*n N ∈恒成立,求实数m 的取值范围.13.(2022•辽宁一模)记数列{}n a 的前n 项和为n S ,17a =-,26a =-,11(n n a ka n N ++=+∈,)k R ∈. (1)证明数列{}n a 为等差数列,并求通项公式n a ; (2)记123||||||||n n T a a a a =++++ ,求n T .14.(2022•辽宁模拟)记正项等差数列{}n a 的前n 项和为n S ,已知11a =,235a a S =. (1)求数列{}n a 的通项公式;(2)已知等比数列{}n b 满足11b a =,22b a =,若782m b a =,求数列{}n b 前m 项的和m T .15.(2022•抚顺一模)已知等差数列{}n a 的前n 项和为n S ,又对任意的正整数n ,m ,都有2n ma a n m-=--,且530S =.(1)求数列{}n a 的通项公式; (2)设||22na nb =,求数列{}n b 的前n 项和n T .16.(2022•丹东模拟)数列{}n a 中,2112,2(2)n n n a a a ++=-=-.(1)计算2a ,3a ,猜想{}n a 的通项公式并加以证明;(2)设n S 为数列{}n a 的前n 项和,证明:数列{}n S 中任意连续三项按适当顺序排列后,可以组成等差数列.17.(2022•铁东区校级模拟)已知n S 是等差数列{}n a 的前n 项和,0n a >,315S =,公差1d >,且从①21a -为11a -与31a +等比中项,②等比数列{}n b 的公比为3q =,11b a =,24b a =这两个条件中,选择一个补充在上面问题的横线上,使得符合条件的数列{}n a 存在并作答. (1)求数列{}n a 的通项公式; (2)设数列11{}n n a a +的前n 项和为n T ,求证:16n T <.18.(2022•沈河区校级四模)已知数列{}n a 满足11a =,23a =,*2132()n n n a a a n N ++=-∈, (Ⅰ)证明:数列1{}n n a a +-是等比数列; (Ⅱ)求数列{}n a 的通项公式.19.(2022•锦州模拟)已知等比数列{}n a 的公比1q >,且22a =,135a a +=. (1)求数列{}n a 的通项公式;(2)在①11b =,n n S nb =,②231n n S b =-这两个条件中任选一个,补充在下面问题中,若问题中的k 存在,求k 的最小值;若k 不存在,说明理由.问题:设数列{}n b 的前n 项和为n S ,_____,数列{}n n a b -的前n 项和为n T ,是否存在正整数k ,使得100k T >?20.(2022•大连二模)已知数列{}n a 是首项11a =的正项等比数列,{}n b 是公差2d =的等差数列,且满足322b a =,341a b =+.(Ⅰ)求数列{}n a ,{}n b 的通项公式; (Ⅱ)若n c =____,求{}n c 的前n 项和n S . 请在①3(1)n n n c a b =+-;②13n n nb c a -=.这两个条件中任选一个,补充在上面的横线中,并加以解答.21.(2022•辽宁模拟)记n S 为数列{}n a 的前n 项和,已知22n n S a n =+. (1)证明:数列1{}n n a a ++为等差数列; (2)求{}n a 的通项公式.22.(2022•辽宁二模)已知数列{}n a 满足11a =,22a =,对于任意正整数n ,有2132n n n a a a ++=-.若12n n n b a a +=-.(1)判断数列{}n b 是等差数列还是等比数列,并求数列{}n a 的通项公式; (2)设21log n n n c a a +=⋅,求数列{}n c 的前n 项和n S .23.(2022•辽宁模拟)已知等比数列{}n b 和递增的等差数列{}n a 满足112a =,11b =,225a b =,332a b =. (1)求数列{}n a 和数列{}n b 的通项公式;(2)数列{}n a 和数列{}n b 中的所有项分别构成集合A 和B ,将A B 的所有元素按从小到大依次排列构成一个新数列{}n c ,求数列{}n c 前63项和63S .24.(2022•鞍山模拟)在①231n n S n =--,②123n n a a +=+,12a =-,这两个条件中任选一个,补充在下面的问题中,并作答.设数列{}n a 的前n 项和为n S ,且____(只需填入序号). (1)求数列{}n a 的通项公式;(2)若(3)n n b n a =⋅+,求数列{}n b 的n 项和n T .25.(2022•辽宁三模)已知数列{}n a 中,满足1a a =,2a b =,12()n n n a k a a ++=+对任意*n N ∈都成立,数列{}n a 的前n 项和为n S .(1)若{}n a 是等差数列,求k 的值;(2)若1a b ==,且1{}n n a a ++是等比数列,求k 的值,并求n S .26.(2022•沈阳模拟)已知公差大于1的等差数列{}n a 中,23a =,且11a +,31a -,63a -成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设数列11{}n n a a +的前n 项和为n S ,求证:1132n S <….27.(2022•辽宁模拟)已知数列{}n a 中,132a =且*1241()n n a a n n N +=+-∈. (1)求证:数列2n n a ⎧⎫+⎨⎩⎭为等比数列;(2)求数列{}n a 的前n 项和n S .28.(2022•辽阳二模)①{2}n n a 为等差数列,且358a =;②{}21n a n -为等比数列,且234a =.从①②两个条件中任选一个,补充在下面的问题中,并解答在数列{}n a 中,112a =,_______. (1)求{}n a 的通项公式;(2)已知{}n a 的前n 项和为n S ,试问是否存在正整数p ,q ,r ,使得n n r S p qa +=-?若存在p ,q ,r 的值;若不存在,说明理由.29.(2022•葫芦岛二模)已知数列{}n a 是等差数列,且101a -,122a +,1444a +分别是公比为2的等比数列{}n b 中的第3,4,6项.(1)求数列{}n a 和{}n b 的通项公式;(2)若数列{}n c 通项公式为sin()n n n c b a π=,求{}n c 的前100项和100S .30.(2022•中山区校级一模)已知等差敉列{}n a 和等比数列{}n b 满足11a =,213a b ==. (1)求{}n a 的通项公式;(2)在①312b =;②211b a =;③22323a b a +=这三个条件中选择一个作为已知条件,使得{}n b 存在且唯一,并求数列{}n a b 的前n 项和n S .31.(2022•沈阳模拟)设各项为正数的数列{}n a 的前n 项和为n S ,数列{}n S 的前n 项积为n T ,且21n n S T +=. (1)求证:数列1n T ⎧⎫⎨⎬⎩⎭是等差数列;(2)求数列{}n a 的通项公式.32.(2022•辽宁模拟)已知公比为q 的等比数列{}n a 的前n 项和为n S ,且满足2128a a -=,384S =,*q N ∈. (1)求数列{}n a 的通项公式;(2)若112222log log log log n nnn a a n a a b ++=+,求数列{}n b 的前n 项和n T .33.(2022•沙河口区校级一模)在下面①和②这两个条件中任选一个补充在下面横线中,并加以解答.已知数列{}n a 满足16a =,23a =-.____.①若*122()n n n a a a n N +++=∈.设1n n n b a a +=-,求证:数列{}n b 是等比数列,若数列{}n a 的前n 项和n S 满足*()n S m n N ∈…,求实数m 的最小值;②若数列{}n a 的奇数项与偶数项分别成等差数列,且*1()n n a a n N +>∈,3433a a +=-,求数列{}n a 的通项公式.若数列{}n a 的前n 项和n S ,求||n S .34.(2022•辽宁三模)已知{8}n a +是公比为2的等比数列,n S 为数列{}n a 的前n 项和,且32S S =. (1)求{}n a 的通项公式; (2)求数列{||}n a 的前n 项和n T .35.(2022•沈河区校级模拟)已知等差数列{}n a ,其前n 项和为n S ,等比数列{}n b 的各项均为正数,公比是q ,且满足:13a =,11b =,2212b S +=,22S b q =. (Ⅰ)求n a 与n b ;(Ⅱ)设332n a n n b λ=- ð,()R λ∈,若数列{}n ð是递增数列,求λ的取值范围.36.(2022•和平区校级模拟)已知数列{}n a 满足12a =,112(*)n na n N a +=-∈. (1)设11n n b a =-,求证数列{}n b 为等差数列,并求数列{}n a 的通项公式; (2)设21n n a c n =+,数列1{}n n c c +的前n 项和为n T ,是否存在正整数m ,使得213n m m T c c +<对任意的*n N ∈都成立?若存在,求出m 的最小值;若不存在,试说明理由.37.(2022•葫芦岛一模)记n S 为等差数列{}n a 的前n 项和,已知1310a a +=,80S =. (1)求{}n a 的通项公式; (2)求n S ,并求n S 的最大值.38.(2022•丹东模拟)已知等差数列{}n a 的前n 项和为n S ,公差为2,1a ,2a ,5a 成等比数列. (1)证明:(1)n S n n >-; (2)证明:12311112nS S S S ++++<39.(2022•望花区校级模拟)已知数列{}n a 满足11a λ=-,且12(0)n n a a λλ+=+≠,且数列{1}n a +是等比数列.(1)求λ的值;(2)若(2)n n n b a a =+,求123n b b b b +++⋯+.参考答案1.(2022•新高考Ⅱ)已知{}n a 是等差数列,{}n b 是公比为2的等比数列,且223344a b a b b a -=-=-. (1)证明:11a b =;(2)求集合1{|k m k b a a =+,1500}m 剟中元素的个数. 【答案】(1)见解析;(2)9【过程详解】(1)证明:设等差数列{}n a 的公差为d , 由2233a b a b -=-,得1111224a d b a d b +-=+-,则12d b =, 由2244a b b a -=-,得111128(3)a d b b a d +-=-+, 即11124(3)a d b d a d +-=-+, 11a b ∴=.(2)由(1)知,1122d b a ==,由1k m b a a =+知,11112(1)k b a m d a -⋅=+-+, ∴111112(1)2k b b m b b -⋅=+-⋅+,即122k m -=,又1500m 剟,故1221000k -剟,则210k 剟, 故集合1{|k m k b a a =+,1500}m 剟中元素个数为9个.2.(2021•新高考Ⅱ)记n S 是公差不为0的等差数列{}n a 的前n 项和,若35a S =,244a a S =. (Ⅰ)求数列{}n a 的通项公式n a ; (Ⅱ)求使n n S a >成立的n 的最小值. 【答案】(Ⅰ)26n a n =-;(Ⅱ)7 【过程详解】(Ⅰ)数列n S 是公差d 不为0的等差数列{}n a 的前n 项和,若35a S =,244a a S =. 根据等差数列的性质,3535a S a ==,故30a =,根据244a a S =可得333333()()(2)()()a d a d a d a d a a d -+=-+-+++, 整理得22d d -=-,可得2(0d d ==不合题意), 故3(3)26n a a n d n =+-=-. (Ⅱ)26n a n =-,14a =-, 2(1)4252n n n S n n n -=-+⨯=-, n n S a >,即2526n n n ->-,整理可得2760n n -+>, 当6n >或1n <时,n n S a >成立, 由于n 为正整数, 故n 的最小正值为7.3.(2022•沈阳一模)等差数列{}n a 和等比数列{}n b 满足111a b ==,2414a a +=,246b b a =,且0n b >. (1)求数列{}n b 的通项公式;(2)已知:①1000n b <;②m N +∃∈,使m n a b =.设S 为数列{}n b 中同时满足条件①和②的所有的项的和,求S 的值.【答案】(1)12n n b -=;(2)见解析【过程详解】(1)设等差数列{}n a 的公差为d 和等比数列{}n b 的公比为q ,0q >, 由111a b ==,2414a a +=,246b b a =,可得11314d d +++=,315q q d ⋅=+, 解得3d =,2q =,则13(1)32n a n n =+-=-,12n n b -=;(2)①1000n b <,即121000n -<,解得1n =,2,3,...,10; ②m N +∃∈,使m n a b =,即1322n m --=,可得1m =,1n =;2m =,3n =;6m =,5n =;22m =,7n =;86m =,9n =. 所以141664256341S =++++=.4.(2022•沈阳一模)已知等差数列{}n a 和正项等比数列{}n b 满足14a =,12b =,212n n n b b b ++=+,332a b =+. (1)求{}n a 和{}n b 的通项公式;(2)对于集合B ,定义集合{A B x A -=∈且}x B ∈∉,设数列{}n a 和{}n b 中的所有项分别构成集合A ,B ,将集合A B -的所有元素按从小到大依次排列构成一个新数列{}n c ,求数列{}n c 的前30项和30S . 【答案】(1)31n a n =+,2n n b =;(2)1632【过程详解】(1)设等差数列{}n a 的公差为d ,设正项等比数列{}n b 的公比为q , 由于满足14a =,12b =,212n n n b b b ++=+,332a b =+, 所以22q q =+,解得2q =或1-(负值舍去), 故2n n b =,所以332a b =+,所以31331a a d -==-, 整理得31n a n =+;(2)由于3091a =,6764121128b b =<<=, 所以30S 中要去掉数列{}n b 的项最多6项, 数列{}n b 的前6项分别为2,4,8,16,32,64; 其中4,16,64三项是数列{}n a 和{}n b 的公共项;所以数列{}n c 前30项由数列{}n a 的前33项再去掉{}n b 的24b =,416b =,664b =这三项构成, 所以30123324633(43331)(...)()(41664)16322S a a a b b b ⨯+⨯+=+++-++=-++=.5.(2022•沈河区校级二模)已知等差数列{}n a 满足59a =,4822a a +=. (1)求{}n a 的通项公式;(2)等比数列{}n b 的前n 项和为n S ,且11b a =,再从下面①②③中选取两个作为条件,求满足2021n S <的n 的最大值.①312b a a =+; ②37S =; ③1n n b b +>.【答案】(1)21n a n =-;(2)见解析 【过程详解】(1)设等差数列{}n a 的首项为1a ,公差为d , 因为4822a a +=,所以6222a =,所以611a =,又59a =, 所以651192d a a =-=-=,154981a a d =-=-=, 所以1(1)221n a n n =+-⨯=-.(2)若选择①②:设等比数列{}n b 的公比为q , 因为11b a =,312b a a =+,所以11b =,34b =, 因为37S =,所以23132b S b b =--=,所以212b q b ==, 所以1(1)211n n n b q S q -==--, 因为2021n S <,所以212021n -<, 所以10n …,即n 的最大值为10.若选择①③:设等比数列{}n b 的公比为q , 因为11b a =,312b a a =+,所以11b =,34b =, 所以2314b q b ==,2q =±, 因为1n n b b +>,所以2q =,所以1(1)211n n n b q S q -==--, 因为2021n S <,所以212021n -<, 所以10n …,即n 的最大值为10.若选择②③:设等比数列{}n b 的公比为q , 因为37S =,11b =,所以217q q ++=, 所以2q =或3q =-, 因为1n n b b +>,所以2q =,所以1(1)211n n n b q S q -==--, 因为2021n S <,所以212021n -<, 所以10n …,即n 的最大值为10.6.(2022•大连模拟)已知等差数列{}n a 的公差为正实数,满足14a =,且1a ,3a ,54a +成等比数列. (1)求数列{}n a 的通项公式;(2)设数列{}n b 的前n 项和为n S ,若11b =,且 ______,求数列{}n n a b +的前n 项和为n T ,以下有三个条件:①21n n S =-,*n N ∈; ②21n n S b =-,*n N ∈; ③121n n S S +=-,*n N ∈.从中选一个合适的条件,填入上面横线处,使得数列{}n b 为等比数列,并根据题意解决问题. 【答案】(1)22n a n =+;(2)见解析 【过程详解】(1)设等差数列{}n a 的公差为d ,则0d >.由14a =得342a d =+,5484a d +=+,由1a ,3a ,54a +成等比数列得2(42)4(84)d d +=+. 所以2d =±,由0d >知2d =,从而1(1)42(1)22n a a n d n n =+-=+-=+.(2)若选①:21n n S =-,*n N ∈,则当1n =时,11211b S ==-=;当2n …,*n N ∈时,111(21)(21)2n n n n n n b S S ---=-=---=. 当1n =时,也满足上式,所以12n n b -=,*n N ∈.所以11222nn n n b b +-==,所以数列{}n b 为首项为1,公比为2的等比数列. 所以数列{}n n a b +的前n 项和为2(422)(21)2312n n n n n T n n ++=+-=++-.若选②:21()n n S b i =-,当1n =时,11121S b b ==-,*n N ∈,11b =;当2n …时,1121()n n S b ii --=-, ()()i ii 两式相减得:122n n n b b b -=-,即12n n b b -=,2n …,*n N ∈,所以12nn b b -=. 所以数列{}n b 为首项11b =,公比2q =的等比数列,所以12n n b -=,*n N ∈. 所以数列{}n n a b +的前n 项和为2(422)(21)2312n n n n n T n n ++=+-=++-.若选③:121()n n S S i +=-, 2121()n n S S ii ++=-,()()ii i -得:212n n b b ++=,*n N ∈, 所以12nn b b -=,数列{}n b 是公比为2q =的等比数列,且1n =时12121a a a +=-, 解得11a =,所以12n n b -=,*n N ∈. 所以数列{}n n a b +的前n 项和为2(422)(21)2312n n n n n T n n ++=+-=++-.7.(2022•辽宁一模)已知{}n a 是等差数列,36a =,612a =,且1,2,nn n a a n b n +⎧=⎨⎩为偶数为奇数. (1)求{}n a 的通项公式;(2)求{}n b 的前2n 项和.【答案】(1)2n a n =;(2)224(161)2315n n T n n ⨯-=++ 【过程详解】(1)由于{}n a 是等差数列,36a =,612a =,设首项为1a .公差为d , 所以1126512a d a d +=⎧⎨+=⎩,整理得122a d =⎧⎨=⎩,所以22(1)2n a n n =+-=,(2)由(1)得:21,4,n n n n b n +⎧=⎨⎩为偶数为奇数,所以13212224(161)(541)4(161)(44 (4))(59...41)2341215n n n n n n T n n n --++⨯-=++++++++=+=++-. 8.(2022•辽宁模拟)已知等差数列{}n a 的前n 项和为n S ,满足11a =,7210126S a a -=+. (1)求数列{}n a 的通项公式;(2)记数列1{2}n a n a +⋅的前n 项和为n T ,求满足920409665n T n ->-的正整数n 的最小值.【答案】(1)21n a n =-,*n N ∈;(2)6【过程详解】(1)由题意,设等差数列{}n a 的公差为d , 则7721S d =+,21a d =+,1019a d =+, 7210126S a a -=+ ,721126(1)(19)d d d ∴+-=+++, 解得2d =,12(1)21n a n n ∴=+-=-,*n N ∈.(2)由(1),可知122(21)2n a n n a n +⋅=-⋅, 则2462123252(21)2n n T n =⋅+⋅+⋅+⋅⋅⋅+-⋅,24622221232(23)2(21)2n n n T n n +=⋅+⋅+⋅⋅⋅+-⋅+-⋅,两式相减,可得246222312222222(21)2n n n T n +-=⋅+⋅+⋅+⋅⋅⋅+⋅--⋅4222222242(21)212n n n ++-=+⋅--⋅- 226520233n n +-=-⋅-,226520299n n n T +-∴=⋅+, 2222920(65)22020(65)2n n n T n n ++∴-=-⋅+-=-⋅,故22920265n n T n +-=-,1240962= , ∴不等式920409665n T n ->-即为221222n +>,即2212n +>,解得5n >, ∴满足920409665n T n ->-的正整数n 的最小值为6.9.(2022•沙河口区校级模拟)已知单调递增的等比数列{}n a ,满足23428a a a ++=,且32a +是2a ,4a 的等差中项.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若n n b na =-,12n n S b b b =++⋯+,对任意正整数n ,总有1()0n n S n m a +++<成立,试求实数m 的取值范围.【答案】(Ⅰ)2n n a =;(Ⅱ)(-∞,1]- 【过程详解】(Ⅰ)设等比数列{}n a 的首项为1a ,公比为q . 依题意32a +是2a ,4a 的等差中项, 有3242(2)a a a +=+, 代入23428a a a ++=, 得38a =. 2420a a ∴+=.∴31121208a q a q a q ⎧+=⎪⎨=⎪⎩, 解之得12a q ==或132a =,12q =, 又{}n a 单调递增, 2q ∴=,12a =,2n n a ∴=;(Ⅱ)2n n n b na n =-=-⋅,23122232...2n n S n ∴-=⨯+⨯+⨯++⨯① 23121222(1)22n n n S n n +-=⨯+⨯++-+⋅②①-②得,231222...22n n n S n +=++++-⋅12(12)212n n n +-=-⋅-11222n n n ++=--⋅, 由1()0n n S n m a +++<,即1111222220n n n n n n m ++++--⋅+⋅+⋅<对任意正整数n 恒成立, 11222n n m ++∴⋅<-. 对任意正整数n , 112nm <-恒成立.1112n->-,1m ∴-…. 即m 的取值范围是(-∞,1]-.10.(2022•辽宁模拟)已知n S 为数列{}n a 的前n 项和,13a =,114n n S a ++=. (1)求数列{}n a 的通项公式;(2)从下面两个条件中选择一个,求数列{}n b 的前n 项和n T . ①211(1)n n n n a b S a +++=+;②242221(1)(21013)2n n n n n n n b a a -+-⋅++⋅=⋅.【答案】(1)1(2)2n n a n -=+⋅;(2)见解析 【过程详解】(1)13a =,114n n S a ++=,所以2n …时,114n n S a -+=, 11144n n n n n a S S a a ++-=-=-,转换为1122(2)n n n n a a a a +--=-, 即1122(2)2n nn n a a n a a +--=-…,当2n =时,23112a ++=,解得28a =;当3n =时,338132a +++=,解得320a =, 322122(2)a a a a -=-,所以数列1{2}n n a a --是从第二项2122a a -=为首项,2为公比的等比数列,所以1122(2)n n n a a n ---=…, 可得111222n n n n a a ---=, 所以数列{}2n na 是以2为首项,12为公差的等差数列, 所以122(2)222n n a n n +=+-=, 即有1(2)2(2)n n a n n -=+⋅…, 上式对1n =也成立, 故1(2)2n n a n -=+⋅; (2)若选择①,1114(2)2n n n S a n +++==+⋅,121111(4)2411(1)(2)2(3)2(2)(3)2(2)2(3)2n n n n n n n n n n a n n b S a n n n n n n +++++++⋅+====-++⋅⋅+⋅++⋅+⋅+⋅,所以数列{}n b 的前n 项和1111111111...6161640(2)2(3)26(3)2n n n n T n n n ++=-+-++-=-+⋅+⋅+⋅; 若选择②.②242242222224222221(1)(21013)2(1)(21013)22101311(1)(1)[](2)(3)2(2)(3)(2)(3)n n n n n n n n n n n n n n n n b a a n n n n n n ---+-⋅++⋅-⋅++⋅++===-⋅=-+⋅++⋅++++, 可得122221*********((()...(1)[](1)[]91616252536(1)(2)(2)(3)n nn T n n n n -=-+++-+++-++-+++++ 211(1)9(3)n n =-+-⋅+.11.(2022•大东区模拟)已知数列{}n a 的前n 项和为n S .从下面①②③中选择其中一个作为条件解答试题,若选择不同条件分别解答,则按第一个解答计分. ①数列{}n a 是等比数列,26S =,且24a ,32a ,4a 成等差数列; ②数列{}n a 是递增的等比数列,1432a a =,2312a a +=; ③22n n S a =-.(1)求数列{}n a 的通项公式;(2)已知数列{}n b 的前n 项的和为n T ,且2212211(log )(log )n n n b a a -+=,证明:12n T <.【答案】见解析【过程详解】(1)解:若选①数列{}n a 是等比数列,26S =,且24a ,32a ,4a 成等差数列; 所以1(1)6a q +=,32444a a a =+,即22244a q a q =+, 解得,2q =,12a =, 故2n n a =;若选②数列{}n a 是递增的等比数列,1432a a =,2312a a +=; 所以142332a a a a ==,2312a a +=, 所以24a =,38a =,2q =, 故222422n n n n a a q --=⋅=⨯=; 若选③22n n S a =-, 当1n >时,1122n n S a --=-,两式相减得,122n n n a a a -=-,即12n n a a -=, 当1n =时,1122S a =-,即12a =,所以数列{}n a 是以2为首项,2为公比的等比数列, 故2n n a =;(2)证明:由(1)得22122111111((log )(log )(21)(21)22121n n n b a a n n n n -+===--+-+,所以111111111(1)(1)233521212212n T n n n =-+-+⋅⋅⋅+-=-<-++.12.(2022•辽宁模拟)已知数列{}n a 的前n 项和为n S ,满足:*21()nn S a n N n=+∈. (Ⅰ)求证:数列{}n a 为等差数列; (Ⅱ)若25a =,令1n nb a =,数列{}n b 的前n 项和为n T ,若不等式22145()5n n T T m m +--…对任意*n N ∈恒成立,求实数m 的取值范围.【答案】(Ⅰ)见解析;(Ⅱ)(-∞,2][7- ,)+∞ 【过程详解】(Ⅰ)证明:依题意,由21n n S a n =+,可得(1)2n n n a S +=, 当1n =时,11112a a S +==,解得11a =, 当2n …时,111(1)(1)(1)(1)1222n n n n n n n n a n a na n a a S S ---+-+--+=-=-=, 即12(1)1n n n a na n a -=--+,整理,可得11(1)()n n n a n a a --=--,构造数列{}n b ,令1n n n b a a -=-,设数列{}n b 的前n 项和为n T , 因为11a =,即11n n a a a -=-,而12132112()()()n n n n a a a a a a a a b b b --=-+-+⋅⋅⋅+-=++⋅⋅⋅+, 所以1n n a T -=, 即(1)n n T n b =-, 同理,11(2)n n T n b --=-,两式相减,可得11(1)(2)n n n n n b T T n b n b --=-=---, 整理,得1n n b b -=,所以数列{}n b 是一个常数列,当2n …时,1n n a a --的值为一个固定的常数, 所以数列{}n a 为等差数列.(Ⅱ)若25a =,则21514d a a =-=-=,所以14(1)43n a n n =+-=-, 1143n n b a n ==-,数列{}n b 的前n 项和12...n n T b b b =+++, 21121221......n n n n n T b b b b b b +++=+++++++,可设211221111 (414581)n n n n n n M T T b b b n n n +++=-=+++=++++++, 11111 (45498189)n M n n n n +=++++++++, 1114808941(89)(41)n n n M M n n n n +---=-=<++++, 可得{}n M 为递减数列, 所以111145945n M M =+=…, 若不等式22145()5n n T T m m +--…对任意*n N ∈恒成立, 可得21454545m m -⨯…,解得7m …或2m -…, 则m 的取值范围是(-∞,2][7- ,)+∞.13.(2022•辽宁一模)记数列{}n a 的前n 项和为n S ,17a =-,26a =-,11(n n a ka n N ++=+∈,)k R ∈. (1)证明数列{}n a 为等差数列,并求通项公式n a ; (2)记123||||||||n n T a a a a =++++ ,求n T .【答案】(1)见解析;(2)2(15),07211556,822n n n n T n n n -⎧-<⎪⎪=⎨⎪-+⎪⎩……【过程详解】(1)证明:当1n =时,有211a ka =+,即671k -=-+,解得1k =, 所以11n n a a +-=,即数列{}n a 是公差为1的等差数列, 故7(1)18n a n n =-+-⨯=-. (2)解:由(1)知,8n a n =-,当07n <…时,0n a <;当8n …时,0n a …,所以当07n <…时,1212(78)(15)||||||()22n n n n n n n T a a a a a a -+--=+++=-+++=-=-; 当8n …时,12312789||||||||()()n n n T a a a a a a a a a a =++++=-+++++++ 2777(15)7(715)115()22562222n n n n S S S S S n n -⨯-=-+-=-=-⨯=-+, 故2(15),07211556,822n n n n T n n n -⎧-<⎪⎪=⎨⎪-+⎪⎩……. 14.(2022•辽宁模拟)记正项等差数列{}n a 的前n 项和为n S ,已知11a =,235a a S =. (1)求数列{}n a 的通项公式;(2)已知等比数列{}n b 满足11b a =,22b a =,若782m b a =,求数列{}n b 前m 项的和m T . 【答案】(1)43n a n =-;(2)3906 【过程详解】(1)设正项等差数列{}n a 的公差为0d …,11a = ,235a a S =, 54(1)(12)52d d d ⨯∴++=+,解得4d =. 14(1)43n a n n ∴=+-=-.(2) 等比数列{}n b 满足11b a =,22b a =, 111b a ∴==,225b a ==, ∴公比5q =,15n n b -∴=,782m b a = ,1547823m -∴=⨯-,解得6m =,∴数列{}n b 前6项的和6651390651T -==-.15.(2022•抚顺一模)已知等差数列{}n a 的前n 项和为n S ,又对任意的正整数n ,m ,都有2n ma a n m-=--,且530S =.(1)求数列{}n a 的通项公式; (2)设||22n a n b =,求数列{}n b 的前n 项和n T .【答案】(1)122n a n =-;(2)65642,16612,7n n n n T n --⎧-=⎨+⎩剟…【过程详解】(1)由已知对任意的正整数m ,m ,都有2n ma a n m-=--, 可得等差数列{}n a 的公差2d =-, 又530S =,即1545(2)302a ⨯+⨯-=,解得110a =, 122n a n ∴=-.(2)由(1)知122n a n =-,令602na n =-…,得6n …, 当6n …时,0n a …, 从而126222122264[1()]6422n a a a n n n T -=+++=⋅-=- ,当6n >时,671252222222222612na a a a a n n T ---=++++++=+ ,综上得65642,16612,7n n n n T n --⎧-=⎨+⎩剟…. 16.(2022•丹东模拟)数列{}n a 中,2112,2(2)n n n a a a ++=-=-. (1)计算2a ,3a ,猜想{}n a 的通项公式并加以证明;(2)设n S 为数列{}n a 的前n 项和,证明:数列{}n S 中任意连续三项按适当顺序排列后,可以组成等差数列. 【答案】见解析【过程详解】(1)解:24a =-,38a =,猜想12(2)n n a -=-. 式子212(2)n n n a a ++-=-可化为112(1)22nn n n na a ++-=-. 所以当2n …时, 111213112121213212(1)2(1)(1)()(()12(1)2(1)2(1)1(1)222222221(1)n n n n n n n n n a a a a a a a a --------=+-+-++-=+-+-++-=+=---- 当1n =时,111(1)2a --=,所以(1)2n n n a =--.于是因此{}n a 的通项公式(2)n n a =--. (2)证明:由(1)可得12n na a +=-,所以{}n a 是以为2首项,2-为公比的等比数列. 从而2[1(2)]2[1(2)]1(2)3n n n S --==----于是121222[1(2)],[1(2)]33n n n n S S ++++=--=--因为124[1(2)]23n n n n S S S +++=--=.故1n S +,n S ,2n S +或2n S +,n S ,1n S +成等差数列.于是数列{}n S 中任意连续三项n S ,1n S +,2n S +按适当排列后,可以组成等差数列.17.(2022•铁东区校级模拟)已知n S 是等差数列{}n a 的前n 项和,0n a >,315S =,公差1d >,且从①21a -为11a -与31a +等比中项,②等比数列{}n b 的公比为3q =,11b a =,24b a =这两个条件中,选择一个补充在上面问题的横线上,使得符合条件的数列{}n a 存在并作答. (1)求数列{}n a 的通项公式; (2)设数列11{}n n a a +的前n 项和为n T ,求证:16n T <. 【答案】见解析 【过程详解】选①,(1)由n S 是等差数列{}n a 的前n 项和,0n a >,315S =,公差1d >, 得2315a =,即25a =,又21a -为11a -与31a +等比中项, 则2213(1)(1)(1)a a a -=-+, 即16(4)(6)d d =-+, 又1d >, 则2d =,则52(2)21n a n n =+-=+, (2)证明:由(1)得111111()(21)(23)22123n n a a n n n n +==-++++, 则1111111111[()()...(2355721236466n T n n n =-+-++-=-<+++,命题得证. 选②,(1)由n S 是等差数列{}n a 的前n 项和,0n a >,315S =,公差1d >, 得2315a =,即25a =,又等比数列{}n b 的公比为3q =,11b a =,24b a =, 由21b q b =,得413aa =, 则523(5)d d +=-, 解得2d =,则52(2)21n a n n =+-=+, (2)证明:由(1)得111111()(21)(23)22123n n a a n n n n +==-++++, 则1111111111[()()...(2355721236466n T n n n =-+-++-=-<+++, 命题得证.18.(2022•沈河区校级四模)已知数列{}n a 满足11a =,23a =,*2132()n n n a a a n N ++=-∈, (Ⅰ)证明:数列1{}n n a a +-是等比数列; (Ⅱ)求数列{}n a 的通项公式.【答案】(Ⅰ)见解析;(Ⅱ)n a *21()n n N =-∈ 【过程详解】(Ⅰ)证明:2132n n n a a a ++=- , 2112()n n n n a a a a +++∴-=-, ∴*2112()n n n na a n N a a +++-=∈-,11a = ,23a =,∴数列1{}n n a a +-是以212a a -=为首项,2为公比的等比数列,(Ⅱ)解:由(Ⅰ)得*12()n n n a a n N +-=∈, 112211()()()n n n n n a a a a a a a a ---∴=-+-+⋯+-+122221n n --=++⋯++*21()n n N =-∈.19.(2022•锦州模拟)已知等比数列{}n a 的公比1q >,且22a =,135a a +=. (1)求数列{}n a 的通项公式;(2)在①11b =,n n S nb =,②231n n S b =-这两个条件中任选一个,补充在下面问题中,若问题中的k 存在,求k 的最小值;若k 不存在,说明理由.问题:设数列{}n b 的前n 项和为n S ,_____,数列{}n n a b -的前n 项和为n T ,是否存在正整数k ,使得100k T >?【答案】(1)12n n a -=;(2)见解析【过程详解】(1)在等比数列{}n a 中,1q >且22a =,135a a +=, 则121125a q a a q =⎧⎨+=⎩, 解得112a q =⎧⎨=⎩或1412a q =⎧⎪⎨=⎪⎩(舍). ∴12n n a -=.(2)选择条件①,11b =,n n S nb =,当2n …时,11(1)n n S n b --=-, 可得11(1)n n n n n b S S nb n b --=-=--,整理得1n n b b -=, ∴数列{}n b 为常数列,又11b =,所以1n b =,121n n n a b --=-,211(12)(1222)2112n n n n T n n n -⨯-=+++⋅⋅⋅+-=-=---,令()21x g x x =--,则()2210x g x ln '=->在[1,)+∞上恒成立, 则()g x 在[1,)+∞上单调递增,即21n n T n =--在[1,)+∞上单调递增, 又657100T =<,7120100T =>,∴存在k ,使得100k T >,k 的最小值为7;选择条件②,231n n S b =-,当1n =时,1112231S b b ==-,得11b =,当2n …时,11231n n S b --=-, 可得112()3(3)n n n n S S b b ---=-,即1233n n n b b b -=-,得13n n b b -=,∴数列{}n b 是首项为1,公比为3的等比数列,则13n n b -=,1123n n n n a b ---=-,因为1n …时,1123n n --<,所以0n n a b -<, 故不存在正整数k ,使得100k T >.20.(2022•大连二模)已知数列{}n a 是首项11a =的正项等比数列,{}n b 是公差2d =的等差数列,且满足322b a =,341a b =+.(Ⅰ)求数列{}n a ,{}n b 的通项公式; (Ⅱ)若n c =____,求{}n c 的前n 项和n S . 请在①3(1)n n n c a b =+-;②13n n nb c a -=.这两个条件中任选一个,补充在上面的横线中,并加以解答. 【答案】(Ⅰ)13n n a -=,2n b n =;(Ⅱ)见解析【过程详解】(Ⅰ)因为322b a =,341a b =+,所以142b q +=,217q b =+, 解得12b =,3q =,所以1113n n n a a q --==,2(1)22n b n n =+-⨯=. (Ⅱ)选择①3(1)3(21)n n n n c a b n =+-=+-,所以123123123(13)(121)13(32)(33)(35)[3(21)](3333)(13521)313222n n n n n n n S n n n +-+-=++++++⋯++-=+++⋯+++++⋯+-=+=⋅+--.选择②12133n n n n b n c a --==, 所以123135213333n nn S -=+++⋯+, 所以234111352321333333n n n n n S +--=+++⋯++,两式相减得,1123111111(1)21222211212229321333333333313n n n n n n n n n S -+++---+=+++⋯+-=+⨯-=--, 所以113n n n S +=-. 21.(2022•辽宁模拟)记n S 为数列{}n a 的前n 项和,已知22n n S a n =+. (1)证明:数列1{}n n a a ++为等差数列; (2)求{}n a 的通项公式.【答案】(1)见解析;(2)n a n =,*n N ∈ 【过程详解】(1)证明: 22n n S a n =+,∴2112(1)n n S a n ++=++,两式相减得11221n n n a a a n ++=-++, 121n n a a n +∴+=+,又1212()()[2(1)1](21)2n n n n n n a a a a a a n n +++++-+=-=++-+=,又123a a +=1{}n n a a +∴+是以首项为3,公差为2的等差数列;(2)由(1)知22n n a a +-=,又1121S a =+,11S a =,11a ∴=,由(1)中123a a +=,22a ∴=, ∴数列{}n a 奇数项构成一个以1为首项,2为公差的等差数列,偶数项构成一个以2为首项,2为公差的等差数列,211(1)221k a k k -∴=+-⋅=-,*k N ∈,n a n ∴=,n 为奇数,*n N ∈; 22(1)22k a k k ∴=+-⋅=,*k N ∈,n a n ∴=,n 为偶数,*n N ∈,综合得n a n =,*n N ∈.22.(2022•辽宁二模)已知数列{}n a 满足11a =,22a =,对于任意正整数n ,有2132n n n a a a ++=-.若12n n n b a a +=-.(1)判断数列{}n b 是等差数列还是等比数列,并求数列{}n a 的通项公式; (2)设21log n n n c a a +=⋅,求数列{}n c 的前n 项和n S . 【答案】(1)见解析;(2)(1)21n n S n =-⋅+【过程详解】(1)由2132n n n a a a ++=-,得21122n n n n a a a a +++-=-,又12n n n b a a +=-,所以1n n b b +=, 1212220b a a =-=-= ,且0不能是等比数列中的项, {}n b ∴是以0为首项,以0为公差的等差数列;12n n a a +∴=,即*12()n n a a n N +=∈,{}n a ∴是以11a =为首项,以2为公比的等比数列,1*2()n n a n N -∴=∈;(2)由(1)可知21log n a n +=,则12n n c n -=⋅,所以01112222n n S n -=⨯+⨯+⋅⋅⋅+⋅,故12212222n n S n =⨯+⨯+⋅⋅⋅+⋅, 两式相减得121121222222(1)112nn nn n n S n n n ---=+++'''+-⋅=-⋅=---,所以(1)21n n S n =-⋅+.23.(2022•辽宁模拟)已知等比数列{}n b 和递增的等差数列{}n a 满足112a =,11b =,225a b =,332a b =. (1)求数列{}n a 和数列{}n b 的通项公式;(2)数列{}n a 和数列{}n b 中的所有项分别构成集合A 和B ,将A B 的所有元素按从小到大依次排列构成一个新数列{}n c ,求数列{}n c 前63项和63S .【答案】(1)39n a n =+,13n n b -=;(2)6043【过程详解】(1)设等差数列{}n a 的公差为(0)d d >,等比数列{}n b 的公比为(0)q q ≠, 由112a =,11b =,225a b =,332a b =,得21251222d q d q +=⎧⎨+=⎩,消去d ,可得2560q q -+=, 解得2q =或3q =,当2q =时,5120d q =-<(舍去), 当3q =时,5123d q =-=,符合题意, 123(1)39n a n n ∴=+-=+,11133n n n b --=⨯=;(2)633639198a =⨯+=,45381198243b ==<<, ∴数列{}n b 的前5项分别为1,3,9,27,81,其中27与81与数列{}n a 中的项相同,由集合中元素的互异性,可知新数列{}n c 的前63项中,有数列{}n a 中的60项,有数列{}n b 的5项(两项重复). ∴数列{}n c 前63项和6360596012313960432S ⨯=⨯+⨯+++=. 24.(2022•鞍山模拟)在①231n n S n =--,②123n n a a +=+,12a =-,这两个条件中任选一个,补充在下面的问题中,并作答.设数列{}n a 的前n 项和为n S ,且____(只需填入序号). (1)求数列{}n a 的通项公式;(2)若(3)n n b n a =⋅+,求数列{}n b 的n 项和n T . 【答案】见解析 【过程详解】选①, (1)由231n n S n =--, 则1123(1)1n n S n --=---,两式相减可得:123n n a -=-,(2)n …, 又112a S ==-满足上式, 即123n n a -=-,()n N +∈;(2)由(1)可得1(3)2n n n b n a n -=⋅+=⋅,则0111222...2n n T n -=⨯+⨯++⨯,()i 则1221222...2n n T n =⨯+⨯++⨯,()ii 由()()i ii -得:21122...22n n n T n --=++++-⨯,故(1)21n n T n =-+. 选②,由123n n a a +=+, 则132(3)n n a a -+=+, 又12a =-, 则131a +=,即数列{3}n a +是以1为首项,2为公比的等比数列, 即132n n a -+=,即123n n a -=-,()n N +∈;(2)由(1)可得1(3)2n n n b n a n -=⋅+=⋅, 则0111222...2n n T n -=⨯+⨯++⨯,()i 则1221222...2n n T n =⨯+⨯++⨯,()ii 由()()i ii -得:21122...22n n n T n --=++++-⨯,故(1)21n n T n =-+.25.(2022•辽宁三模)已知数列{}n a 中,满足1a a =,2a b =,12()n n n a k a a ++=+对任意*n N ∈都成立,数列{}n a 的前n 项和为n S .(1)若{}n a 是等差数列,求k 的值;(2)若1a b ==,且1{}n n a a ++是等比数列,求k 的值,并求n S .【答案】(1)12k =;(2)当12k =时,n S n =;当12k =-时,即2,21,,2,n n n k k N S n n k k N ++⎧-=-∈=⎨=∈⎩【过程详解】(1)由{}n a 是等差数列, 则121n n n n a a a a +++-=-, 即122n n n a a a ++=+. 所以121()2n n n a a a ++=+,故12k =; (2)因为121a a == 且12()n n n a k a a ++=+,得3421111,1a a k k k=-=--, 又且1{}n n a a ++是等比数列,则2231234()()()a a a a a a +=++, 即22112(2)k k=-,即12k =±, 当12k =时,1n a =,数列1{}n n a a ++ 是以2为首项,公比为1的等比数列, 此时{}n a 的前n 项和n S n =; 当12k =- 时,121()2n n n a a a ++=-+,即122n n n a a a ++=--, 所以211()n n n n a a a a ++++=-+, 又1220a a +=≠,所以数列1{}n n a a ++ 以12a a + 为首项,公比为1-的等比数列, 又32211()n n n n n n a a a a a a ++++++=-+=+,所以当n 是偶数时,123411234112()()()()2n n n n n nS a a a a a a a a a a a a a a n --=++++++=++++++=+= ,当n 是奇数时,2312()2a a a a +=-+=-,1234112311...()...()1(2)22n n n n n n S a a a a a a a a a a a n ---=++++++=++++=+⨯-=-, 即2,21,,2,n n n k k N S n n k k N++⎧-=-∈=⎨=∈⎩, 综上可得:当12k =时,n S n =; 当12k =-时,即2,21,,2,n n n k k N S n n k k N ++⎧-=-∈=⎨=∈⎩. 26.(2022•沈阳模拟)已知公差大于1的等差数列{}n a 中,23a =,且11a +,31a -,63a -成等比数列.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设数列11{}n n a a +的前n 项和为n S ,求证:1132n S <….【答案】(Ⅰ)21n a n =-;(Ⅱ)见解析 【过程详解】(Ⅰ)设等差数列{}n a 的公差为1d >,23a = ,且11a +,31a -,63a -成等比数列, 13a d ∴+=,2316(1)(1)(3)a a a -=+-,即2111(21)(1)(53)a d a a d +-=++-,解得11a =,2d =. 12(1)21n a n n ∴=+-=-.(Ⅱ)证明:111111()(21)(21)22121n n a a n n n n +==--+-+, 11111111(1(123352121221n S n n n ∴=-+-+⋯+-=--++,1111()022123n n S S n n +-=->++ ,∴数列{}n S 单调递增,112n S S ∴<…, 即1132n S <…. 27.(2022•辽宁模拟)已知数列{}n a 中,132a =且*1241()n n a a n n N +=+-∈. (1)求证:数列2n n a ⎧⎫+⎨⎩⎭为等比数列;(2)求数列{}n a 的前n 项和n S . 【答案】(1)见解析;(2)n S 21224n n n++=--【过程详解】证明:(1)1241n n a a n +=+- , ∴11222n n n a a +=+-, ∴11112222222222n n n n n n n n n a a a n n n n a a a +++++-++===+++, 11312222a +=+=, ∴2n n a ⎧⎫+⎨⎬⎩⎭是首项为2,公比为2的等比数列;。
高考数学必考点专项第18练-等比数列(练习及答案)(全国通用)(新高考专用)

高考数学必考点专项第18练等比数列习题精选一、单选题1. 已知数列{}n a 的前 n 项和为n S ,11a =,12n n S a +=,则n S =( ) A. 12n -B.C.D.2. 记n S 为等比数列{}n a 的前n 项和.若5312a a -=,6424a a -=,则nnS a =( ) A. 21n -B. 122n --C. 122n --D. 121n --3. 已知等差数列的公差0d ≠,且1a ,3a ,9a 成等比数列,则1392410a a a a a a ++++的值为( )A.914B.1115C.1316D.15174. 一个等比数列{}n a 的前n 项和为48,前2n 项和为60,则前3n 项和为( ) A. 63B. 108C. 75D. 835. 记n S 为正项等比数列{}n a 的前n 项和,若21S =,45S =,则7S =( ) A. 710S =B. 723S =C. 7623S =D. 71273S =6. 已知等比数列中,234=1a a a ,678=64a a a ,则456=(a a a ) A. 8±B. 8-C. 8D. 167. 音乐与数学有着密切的联系,我国春秋时期有个著名的“三分损益法”:以“宫”为基本音,“宫”经过一次“损”,频率变为原来的32,得到“徵”;“徵”经过一{}n a {}n a次“益”,频率变为原来的34,得到“商”;…….依次损益交替变化,获得了“宫、徵、商、羽、角”五个音阶.据此可推得( )A. “宫、商、角”的频率成等比数列B. “宫、徵、商”的频率成等比数列C. “商、羽、角”的频率成等比数列D. “徵、商、羽”的频率成等比数列8. 数列{}n a 中,已知对任意*n N ∈,123a a a +++…31n n a +=-,则222123a a a +++ (2)n a +等于( )A. 2(31)n -B.1(91)2n- C. 91n -D.1(31)4n- 9. 记方程①:2110x a x ++=,方程②:2220x a x ++=,方程③:2340x a x ++=,其中1a ,2a ,3a 是正实数.当1a ,2a ,3a 成等比数列时,下列选项中,能推出方程③无实根的是( )A. 方程①有实根,且②有实根B. 方程①有实根,且②无实根C. 方程①无实根,且②有实根D. 方程①无实根,且②无实根10. 已知正项等比数列{}n a 的前n 项和为n S ,若22352628100a a a a ++=,4236S S -=,则2021S =( )A. 2021312020-B. 2020312-C. 2021312-D. 2021212020-11. 数列{}n a 中,12a =,.m n m n a a a +=若12k k a a ++++…1551022k a ++=-,则k =( )A. 2B. 3C. 4D. 5二、多选题12. 在“全面脱贫”行动中,贫困户小王2020年1月初向银行借了扶贫免息贷款10000元,用于自己开设的农产品土特产品加工厂的原材料进货,因产品质优价廉,上市后供不应求,据测算每月获得的利润是该月月初投入资金的20%,每月月底需缴纳房租600元和水电费400元,余款作为资金全部用于再进货,如此继续.设第n 月月底小王手中有现款为n a ,则下列论述正确的有( )(参考数据:111.27.5=,121.29)=A. 112000a =B. 1 1.21000n n a a +=-C. 2020年小王的年利润为40000元D. 两年后,小王手中现款达41万13. 已知n S 是数列{}n a 的前n 项和,且121a a ==,122(3)n n n a a a n --=+,则下列结论正确的是( )A. 数列1{}n n a a ++为等比数列B. 数列1{2}n n a a +-为等比数列C. 12(1)3n nn a ++-=D. 10202(41)3S =-三、填空题14. 等比数列{}n a 的各项均为实数,其前n 项和为n S ,已知374S =,6634S =,则8a =__________.15. 已知正项等比数列{}n a 的前n 项和为n S ,2122S a =+,534a a =,则数列{}n a 中不超过2021的所有项的和为__________.16. 已知数列{}n a 的前n 项和为n S ,且11a =,{lg }n S 是公差为lg 3的等筹数列,则24a a ++…2n a +=_______. 四、解答题17. 等比数列{}n a 的各项均为正数,52a ,4a ,64a 成等差数列,且满足243=4.a a (1)求数列{}n a 的通项公式; (2)设+1+1=(1)(1)n n n n a b a a --,*n N ∈,求数列{}n b 的前n 项和.n S18. 已知数列{}n a 满足12a =,且*1321().n n a a n n N +=+-∈(1)求证:数列{}n a n +为等比数列; (2)求数列{}n a 的通项公式;(3)求数列{}n a 的前n 项和.n S19. 已知数列{}n a 为正项等比数列,满足34a =,且5a ,43a ,6a 构成等差数列,数列{}n b 满足221log log .n n n b a a +=+()Ⅰ求数列{}n a ,{}n b 的通项公式;()Ⅱ若数列{}n b 的前n 项和为n S ,数列{}n c 满足141n n c S =-,求数列{}n c 的前n 项和.n T20. 已知数列的前n 项和为n S 满足:33.2n n S a n =+- {}n a(1)求证:数列是等比数列;(2)令,令1,nnd c =求数列的前n 项和.n T{1}n a -31323(1)(1)(1)nn c log a log a log a =-+-++-答案和解析1.【答案】B解:当1n =时,122S a =,又因111S a ==, 所以,.显然只有B 项符合.2.【答案】B解:设等比数列的公比为q ,5312a a -=, 6453()a a q a a ∴-=-, 2q ∴=,421112a q a q ∴-=,11212a ∴=,11a ∴=,122112nn n S -∴==--,12n n a -=,1121222n n n n n S a ---∴==-, 故选:.B3.【答案】C解:等差数列{}n a 中,312a a d =+,918a a d =+, 因为1a 、3a 、9a 恰好成等比数列,所以有2319a a a =,即,解得1d a =,所以该等差数列的通项为n a nd =, 则139********.241016a a a d d d a a a d d d ++++==++++故选:.C4.【答案】A解:由等比数列的性质可知等比数列中每k 项的和也成等比数列. 则等比数列的第一个n 项的和为48,第二个n 项的和为604812-=,∴第三个n 项的和为:212348=, ∴前3n 项的和为60363.+=故选.A5.【答案】D解:n S 为正项等比数列{}n a 的前n 项和,21S =,45S =,21410(1)11(1)51q a q qa q q ⎧⎪>⎪⎪-⎪∴=⎨-⎪⎪-=⎪-⎪⎩,解得113a =,2q =,771(12)1273.123S -∴==-故选:.D6.【答案】C解:依题意,323431a a a a ==,即31a =,同理3678764a a a a ==,即74a =,所以23754a a a ⋅==,又等比数列奇数项符号相同,所以52a =,所以345658.a a a a ==故选:.C7.【答案】A解:设“宫”的频率为a ,由题意经过一次“损”,可得“徵”的频率为32a ,“徵”经过一次“益”,可得“商”的频率为98a ,“商”经过一次“损”,可得“羽”频率为2716a ,最后“羽”经过一次“益”,可得“角”的频率是8164a , 由于a ,98a ,8164a 成等比数列,所以“宫、商、角”的频率成等比数列, 故选:.A8.【答案】B解:123a a a +++…31n n a +=-,①123a a a ∴+++…1131n n a +++=-,②②-①得:113323n n nn a ++=-=⨯,123(2).n n a n -∴=⨯当1n =时,11312a =-=,符合上式,123.n n a -∴=⨯2149n n a -∴=⨯,∴数列2{}na 是以4为首项,9为公比的等比数列, 2222123n a a a a ∴++++4(19)1(91).192n n⨯-==--故选.B9.【答案】B解:当方程①有实根,且②无实根时,21140a ∆=-,22280a ∆=-<,即214a ,228a <,1a ,2a ,3a 成等比数列,2213a a a ∴=,即2231a a a =,则242222232118()164a a a a a ==<=,则:方程③的判别式233160a ∆=-<,此时方程③无实根,同理可得其他三个选项不符合, 故选:.B10.【答案】C解:22352628100a a a a ++=,3526,a a a a =235()8100.a a ∴+=又0n a >,3590.a a ∴+= 设数列{}n a 的公比为(0)q q >,则解得,故2021202112021(1)31.12a q S q --==- 故选.C11.【答案】C解:由12a =,且m n m n a a a +=, 取1m =,得112n n n a a a a +==,12n na a +∴=, 则数列{}n a 是以2为首项,以2为公比的等比数列,则11222k k k a ++=⋅=,12k k a a ++∴++ (11011115510)2(12)222212k k k k a ++++-+==-=--,15k ∴+=,即 4.k =故选:.C12.【答案】BCD解:1(120%)10000100011000a =+⨯-=元,故A 错误; 由题意1 1.21000n n a a +=-,故B 正确;由1 1.21000n n a a +=-,得15000 1.2(5000)n n a a +-=-, 所以数列{5000}n a -是首项为6000,公比为1.2的等比数列, 111250006000 1.2a ∴-=⨯,即11126000 1.2500050000a =⨯+=, 2020年小王的年利润为500001000040000-=元,故C 正确;22324950006000 1.2500060004100001.2a =+⨯=+⨯=元,即41万,故D 正确. 故选.BCD13.【答案】ABD解:因为121a a ==,122(3)n n n a a a n --=+, 所以1112122()2n n n n n n n n a a a a a a a a ------++=+⇒=+, 因为121a a ==,所以31223a a a =+=,322142()a a a a +==+,所以是以2为首项,公比为2的等比数列,故A 正确;则112.n n n a a --+=,322321a a -=-=,212121a a -=-=-,所以是以1-为首项,公比为1-的等比数列,故B 正确;则112(1).n n n a a ---=-,故C 错误;201220S a a a =+++1234()()a a a a =++++…1920()a a ++ 135222=+++…192+19221102222222(41)1233-⋅-===--,故D 正确, 故选.ABD14.【答案】32解:设等比数列{}n a 的公比为q ,易得1q ≠, 374S =,6634S =, 31(1)714a q q -∴=-,61(1)6314a q q -=-, 解得114a =, 2.q = 则781232.4a =⨯= 故答案为:32.15.【答案】2046解:设{}n a 的公比为(0)q q >, 由已知得解得12a q ==,所以2n n a =,令2021n a <,则22021n <, 解得10n ,所以数列{}n a 中的前10项的和为10234102(12)222222046.12-+++++==- 故答案为2046.16.【答案】914n - 解:由111S a ==, 1lg 0S =,{lg }n S 是公差为lg 3的等筹数列, 所以所以13n n S -= 当2n ,213n n S --=,故12213323n n n n n n a S S ----=-=-=⨯,所以2a ,4a ,…2n a 是以22a =为首项,以9为公比的等比数列; 故24a a ++…故答案为914n - 17.【答案】解:(1)设等比数列的公比为0q >, 因为52a ,4a ,64a 成等差数列,0n a >,所以456224a a a =+,所以24422(2)a a q q =+,化为:2210q q +-=,0q >,解得1.2q =又满足2434a a = , 所以322114()a q a q =,化为:114a q =,解得112a =, {}n a所以1()2n n a =,*n N ∈; , 所以2231111111()()++()212121212121n n n S +=-+-------- 11121n +=--,*.n N ∈18.【答案】解:(1)证明:由1321n n a a n +=+-, 得, 113n n a n a n+++∴=+,又113a +=, 是首项为3,公比为3的等比数列.(2)由(1)得,1333n n n a n -+=⨯=, 3.n n a n ∴=-(3)由(2)得:133(1)132n n n +-+=-- 11233(1)33.222n n n n n n ++-+---=-=19.【答案】解:()Ⅰ设等比数列{}n a 的公比为(0)q q >,由题意,得256466a a a q q +=⇒+=,解得2q =或3(q =-舍),又3141a a =⇒=,所以 1112n n n a a q --==,221log log 121n n n b a a n n n +=+=-+=-; 21()[1(21)]()22n n n b b n n S n ++-===Ⅱ, 21111()4122121n c n n n ∴==---+, 111111[(1)()()].2335212121n n T n n n ∴=-+-++-=-++20.【答案】证明:(1)当1n =时, 111322S a a ==-,解得14a =, 当2n 时,由332n n S a n =+-得11342n n S a n --=+-, 两式相减,得1133122n n n n S S a a ---=-+,即132(2)n n a a n -=-, 则113(1)n n a a --=-,故数列{1}n a -是以113a -=为首项,公比为3的等比数列;(2)由(1)知13n n a -=,31323(1)(1)(1)n n c log a log a log a =-+-++- (1)122n n n +=+++=, 所以12112()(1)1n c n n n n ==-++, 则12111n nT c c c =+++ 111112[(1)()()]2231n n =-+-++-+ 122(1).11n n n =-=++。
2023年高考备考三年 数列(含答案)

an 1
2,
an
n 1
n
所以,数列 an 是以 2 为首项,以 2 为公比的等比数列,则 an 2 2 2 ,
ak 1 ak 2 ak 10
ak 1 1 210
1 2
2k 1 1 210
1 2
2k 1 210 1 25 210 1 ,
所以 S3n S2 n S2 n Sn 729 ,
即
3n(9 27n ) 2n(9 18n ) 2n(9 18n ) n(9 9n )
729
2
2
2
2
即 9n 2 729 ,解得 n 9 ,
所以 S3n S27
27(9 9 27)
3402 .
圆形石板(称为天心石),围绕天心石砌 9 块扇面形石板构成第—环,向外每环依次增加 9 块,下一层的第
—环比上一层的最后一环多 9 块,向外每环依次也增加 9 块,已知每层环数相同,且下层比中层多 729
块,则三层共有扇面形石板(不含天心石)〔 〕
高考材料
高考材料
A.3699 块
B.3474 块
C.3402 块
(详解)
设第 n 环天石心块数为 an ,第—层共有 n 环,
则 {an } 是以 9 为首项,9 为公差的等差数列, an 9 (n 1) 9 9n ,
设 S n 为 {an } 的前 n 项和,则第—层、第二层、第三层的块数分
别为 S n , S 2 n S n , S3n S 2 n ,因为下层比中层多 729 块,
∴ S2 4 , S4 S2 6 4 2
专题32 等比数列(解析版)
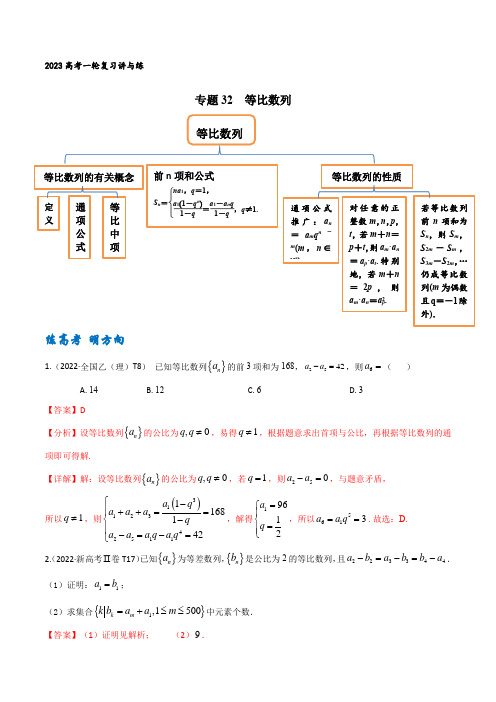
(2)等比中项:如果a,G,b成等比数列,那么G叫做a与b的等比中项.即:G是a与b的等比中项⇔a,G,b成等比数列⇒G2=ab.
【小问2详解】由(1)知, ,所以 ,即 ,亦即 ,解得 ,所以满足等式的解 ,故集合 中的元素个数为 .
3.(2022·浙江卷T20)已知等差数列 的首项 ,公差 .记 的前n项和为 .
(1)若 ,求 ;
(2)若对于每个 ,存在实数 ,使 成等比数列,求d的取值范围.
【答案】(1) (2)
【分析】(1)利用等差数列通项公式及前 项和公式化简条件,求出 ,再求 ;
2023高考一轮复习讲与练
专题32等比数列
练高考 明方向
1.(2022·全国乙(理)T8)已知等比数列 的前3项和为168, ,则 ()
A.14B.12C.6D.3
【答案】D
【分析】设等比数列 的公比为 ,易得 ,根据题意求出首项与公比,再根据等比数列的通项即可得解.
【详解】解:设等比数列 的公比为 ,若 ,则 ,与题意矛盾,
基本方法:
等比数列的三种常用判定方法:
定义法:若 =q(q为非零常数,n∈N*),则{an}是等比数列
等比中项法:若数列{an}中,an≠0,且a =an·an+2(n∈N*),则数列{an}是等比数列
通项公式法:若数列通项公式可写成an=c·qn(c,q均是不为0的常数,n∈N*),则{an}是等比数列
(Ⅰ)证明 是等比数列,并求其通项公式;
(Ⅱ)若 ,求 .
【答案】(Ⅰ) ;(Ⅱ) .
2023年高考数学一轮复习(新高考地区专用)4-2 等比数列(精讲)(含详解)
4.2 等比数列(精讲)(基础版)思维导图考点一 等比数列基本量的计算【例1】(1)(2022·北京丰台·一模)若数列{}n a 满足12n n a a +=,且41a =,则数列{}n a 的前4项和等于( )考点呈现例题剖析A .15B .14C .158 D .78(2)(2022·重庆·模拟预测)已知等比数列{}n a 的前n 项和为n S ,且2a ,53a ,89a 成等差数列,则63S S =( ) A .13B .43C .3D .4【一隅三反】1.(2022·江西·新余四中)已知n S 为等比数列{}n a 的前n 项和,若38a =,324S =,则公比q =( ) A .12-B .13-C .12-或1D .13-或12.(2022·河北廊坊·高三阶段练习)已知n S 为等比数列{}n a 的前n 项和,且公比1q >,则“51a a >”是“40S >”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.(2022·全国·高三专题练习)已知{}n a 为等比数列,n S 为其前n 项和,若213S a =,223a a =,则4S =( )A .7B .8C .15D .314.(2022·河北石家庄·高三期末)等比数列{}n a 的前n 项和为n S ,33S =,69S =,则公比q =( )A .3B .2C .33D .325(2022·四川·三模(理))已知n S 是各项均为正数的等比数列{}n a 的前n 项和,若2481a a ⋅=,313S =,则6a =( ).A .21B .81C .243D .729考点二 等比中项【例2-1】(2022·江西·上饶市第一中学二模)等比数列{}n a 中,若59a =,则3436log log a a +=( ) A .2B .3C .4D .91.等比数列中有五个量a 1,n ,q ,a n ,S n ,一般可以“知三求二”,通过列方程(组)便可迎刃而解.2.等比数列的前n 项和公式涉及对公比q 的分类讨论,当q =1时,{a n }的前n 项和S n =na 1;当q ≠1时,{a n }的前n 项和S n =a 1(1-q n )1-q =a 1-a n q1-q.温馨提示【例2-2】(2022·福建·模拟预测)已知数列{}n a 为等比数列,则“5a ,7a 是方程2202210x x ++=的两实根”是”61a =,或61a =-”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【一隅三反】1.(2022·安徽黄山·一模)在等比数列{}n a 中,1a ,13a 是方程21390x x -+=的两根,则2127a a a 的值为( ) AB .3 C.D .3±2.(2022·吉林吉林)已知各项均为正数的等比数列{}n a 中,23a =,93453a a a =,则3a =( ) A .6B .9C .27D .813.(2022·全国·高三专题练习)设a ,b ,c ,d 是非零实数,则“a ,b ,c ,d 成等比数列”是“ad bc =”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件4.(2022·广西柳州)在等比数列{}n a 中,已知22a =,8462a a =,则公比q =( ) A .2-BC .2D .2±考点三 等比数列前n 项和的性质【例3-1】(2022·全国·高三专题练习)已知等比数列{an }的前n 项和为Sn ,S 10=1,S 30=13,S 40=( ) A .﹣51B .﹣20C .27D .40【例3-2】(2022·全国·高三专题练习)等比数列{}n a 的前n 项和为n S ,若121n n S t -=⋅-,则t =( )A .2B .-2C .1D .-1【例3-3】(2022·全国·高三专题练习)已知数列}{n a 的前n 项和121n n S -=+,则数列}{n a 的前10项中所有奇数项之和与所有偶数项之和的比为( ) A .12B .2C .172341D .341172【例3-4】(2022·全国·高三专题练习)数列{}n a 中,12a =,对任意 ,,m n m n m n N a a a ++∈=,若155121022k k k a a a ++++++=-,则 k =( )A .2B .3C .4D .5【例3-5】(2022·全国·高三专题练习)各项均为正数的等比数列{}n a 的前n 项和n S ,若264a a =,31a =,则29()42n n S a +的最小值为( )A .4B .6C .8D .12【一隅三反】1.(2022·湖南·长沙一中)一个等比数列的前7项和为48,前14项和为60,则前21项和为( ) A .180 B .108 C .75D .632.(2022·全国·高三专题练习)已知一个等比数列首项为1,项数是偶数,其奇数项之和为85,偶数项之和为170,则这个数列的项数为( ) A .2B .4C .8D .163.(2022·全国·高三专题练习)等比数列{}n a 的前n 项和为213n n S r -=+,则r 的值为 A .13B .13-C .19D .19-4.(2021·全国·高三专题练习)已知等比数列{}n a 中,11a =,132185k a a a ++++=,24242k a a a +++=,则k =( ) A .2B .3C .4D .55.(2022·四川绵阳·一模)已知正项等比数列{}n a 的前n 项和为n S ,若5-,3S ,6S 成等差数列,则96S S -的最小值为( )A .25B .20C .15D .10考点四 等比数列定义及其运用【例4】(2022·全国·高三专题练习)已知数列{}n a 满足12a =,121nn n a a a +=+,则下列结论正确的是( )A .数列1n a ⎧⎫⎨⎬⎩⎭是公差为12的等差数列 B .数列1n a ⎧⎫⎨⎬⎩⎭是公差为2的等差数列C .数列11n a ⎧⎫-⎨⎬⎩⎭是公比为12的等比数列 D .数列11n a ⎧⎫-⎨⎬⎩⎭是公比为2的等比数列 【一隅三反】1.(2021·江苏盐城)(多选)设等比数列{}n a 的前n 项和为n S ,则下列数列一定是等比数列的有( )A .12a a +,23a a +,34a a +,…B .13a a ,35a a +,57a a +,…C .2S ,42S S -,64S S -,…D .3S ,63S S -,96S S -,…2.(2022·广东·佛山一中)已知数列{n a }满足:11232n n a a a +==+, (1)求证:数列{1n a +}是等比数列;(2)()3log 1n n b a =+,求数列{n a ·n b }的前n 项和n S .3.(2022·全国·高三专题练习)已知数列{}n a 的前n 项和为n S ,且112a =,11()*2n n n a a N n n ++=∈. (1)证明数列{}n an为等比数列,并求数列{}n a 的通项公式;(2)设(2)n n b n S =-,求数列32{}nn b -前n 项和n T . 考点五 等比数列的实际应用【例5-1】(2022·浙江省义乌中学模拟预测)我国古代的数学名著《九章算术》中有“衰分问题”:今有女子善织,日自倍,五日织五尺,问日织几何?其意为:一女子每天织布的尺数是前一天的2倍,5天共织布5尺,问第五天织布的尺数是多少你的答案是( ) A .531B .1C .52D .8031【例5-2】(2022·江苏·沭阳如东中学模拟预测)著名的“康托三分集”是数学理性思维的构造产物,具有典型的分形特征,其操作过程如下:将闭区间[0,1]均分为三段,去掉中间的区间段12,33⎛⎫⎪⎝⎭,记为第一次操作;再将剩下的两个区120,,,133⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦分别均分为三段,并各自去掉中间的区间段,记为第二次操作;…,如此这样,每次在上一次操作的基础上,将剩下的各个区间分别均分为三段,同样各自去掉中间的区间段.操作过程不断地进行下去,以至无穷,剩下的区间集合即是“康托三分集”.若使去掉的各区间长度之和不小于1415,则需要操作的次数n 的最小值为( ) 参考数据:lg2=0.3010,lg3=0.4771 A .6B .7C .8D .9【一隅三反】1.(2022·全国·模拟预测)在适宜的环境中,一种细菌的一部分不断分裂产生新的细菌,另一部分则死亡.为研究这种细菌的分裂情况,在培养皿中放入m 个细菌,在1小时内,有34的细菌分裂为原来的2倍,14的细菌死亡,此时记为第一小时的记录数据.若每隔一小时记录一次细菌个数,则细菌数超过原来的10倍的记录时间为第( )A .6小时末B .7小时末C .8小时末D .9小时末2.(2022·湖南湖南·二模)在流行病学中,基本传染数0R 是指在没有外力介入,同时所有人都没有免疫力的情况下,一个感染者平均传染的人数.0R 一般由疾病的感染周期、感染者与其他人的接触频率、每次接触过程中传染的概率决定,假设某种传染病的基本传染数02R =,平均感染周期为7天,那么感染人数由1(初始感染者)增加到999大约需要的天数为( )(初始感染者传染0R 个人为第一轮传染,这0R 个人每人再传染0R 个人为第二轮传染……参考数据:lg20.3010≈) A .42B .56C .63D .703.(2022·云南·高三阶段练习(理))为了更好地解决就业问题,国家在2020年提出了“地摊经济”为响应国家号召,有不少地区出台了相关政策去鼓励“地摊经济”.老王2020年6月1日向银行借了免息贷款10000元,用于进货.因质优价廉,供不应求,据测算:每月获得的利润是该月初投入资金的20%,每月底扣除生活费1000元,余款作为资金全部用于下月再进货,如此继续,预计到2021年5月底该摊主的年所得收入为( )(取()111.27.5=,()121.29=) A .32500元 B .40000元C .42500元D .50000元4.2 等比数列(精讲)(基础版)思维导图考点一 等比数列基本量的计算【例1】(1)(2022·北京丰台·一模)若数列{}n a 满足12n n a a +=,且41a =,则数列{}n a 的前4项和等于( )考点呈现例题剖析A .15B .14C .158 D .78(2)(2022·重庆·模拟预测)已知等比数列{}n a 的前n 项和为n S ,且2a ,53a ,89a 成等差数列,则63S S =( ) A .13B .43C .3D .4【答案】(1)C (2)B【解析】(1)因为12n n a a +=,且41a =,所以数列{}n a 是以2为公比的等比数列,又3411a a q ==,得118a =,所以44141(12)(1)1581128a q S q --===--.故选:C (2)设等比数列公比为q ,由2a ,53a ,89a 成等差数列可得,47111239a q a q a q ⨯⋅=⋅+⋅,化简得639610q q -+=,解得313q =,()()61363311411311a q S q q S a q q--==+=--.故选:B. 【一隅三反】1.(2022·江西·新余四中)已知n S 为等比数列{}n a 的前n 项和,若38a =,324S =,则公比q =( )A .12-B .13-C .12-或1D .13-或1【答案】C【解析】设等比数列{}n a 的公比为q .因为38a =,324S =,所以38a =,1216a a +=,即218a q =,()1116a q +=,所以212q q +=,解得12q =-或1q =.故选:C.2.(2022·河北廊坊·高三阶段练习)已知n S 为等比数列{}n a 的前n 项和,且公比1q >,则“51a a >”是“40S >”的( )1.等比数列中有五个量a 1,n ,q ,a n ,S n ,一般可以“知三求二”,通过列方程(组)便可迎刃而解.2.等比数列的前n 项和公式涉及对公比q 的分类讨论,当q =1时,{a n }的前n 项和S n =na 1;当q ≠1时,{a n }的前n 项和S n =a 1(1-q n )1-q =a 1-a n q1-q.温馨提示A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】C【解析】由40S >,得1514011a a a a q q q--=>--,因为1q >,所以510a a ->,即51a a >.故必要性满足; 1514411a a a a q S q q--==--.因为1q >,51a a >,所以40S >.故充分性满足.所以“51a a >”是“40S >”的充要条件.故选:C3.(2022·全国·高三专题练习)已知{}n a 为等比数列,n S 为其前n 项和,若213S a =,223a a =,则4S =( )A .7B .8C .15D .31【答案】C【解析】设等比数列{}n a 的公比为q ,则21213S a a a =+=,则212a a =,所以,212a q a ==, 因为223a a =,即()21124a a =,10a ≠,解得11a =,因此,()441411215112a q S q--===--.故选:C.4.(2022·河北石家庄·高三期末)等比数列{}n a 的前n 项和为n S ,33S =,69S =,则公比q =( ) ABCD【答案】D【解析】依题意,等比数列{}n a 满足,33S =,69S =,则1q ≠,()()3611113,911a q a q qq--==--,两式相除得()()3363331113,1311q q q q q q-+-==+=--,32,q q ==故选:D 5(2022·四川·三模(理))已知n S 是各项均为正数的等比数列{}n a 的前n 项和,若2481a a ⋅=,313S =,则6a =( ).A .21B .81C .243D .729【答案】C【解析】224381a a a ⋅==,因为0n a >,所以0q >,39a =,又313S =,故124a a +=,设公比是q ,则()121149a q a q ⎧+=⎨=⎩,两式相除得:2149q q +=,解得:3q =或34q =-(舍去),故336393243a a q ==⨯=.故选:C 考点二 等比中项【例2-1】(2022·江西·上饶市第一中学二模)等比数列{}n a 中,若59a =,则3436log log a a +=( )A .2B .3C .4D .9【答案】C【解析】根据等比中项得2546a a a =,所以()2434334353663log log log log log 81log 34a a a a a +=====.故选:C.【例2-2】(2022·福建·模拟预测)已知数列{}n a 为等比数列,则“5a ,7a 是方程2202210x x ++=的两实根”是”61a =,或61a =-”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A【解析】在等比数列中,若5a ,7a 是方程2202210x x ++=的两实根,571a a ∴=,5720220a a +=-<,则50a <,70a <,则57661a a a a ==,则61a =或61a =-,即充分性成立,当61a =,或61a =-时,能推出57661a a a a ==,但无法推出572022a a +=-,即必要性不成立, 即“5a ,7a 是方程2202210x x ++=的两实根”是“61a =,或61a =-”的充分不必要条件,故选:A . 【一隅三反】1.(2022·安徽黄山·一模)在等比数列{}n a 中,1a ,13a 是方程21390x x -+=的两根,则2127a a a 的值为( ) AB .3 C.D .3±【答案】B【解析】因为1a 、13a 是方程21390x x -+=的两根,所以3119=a a ,11313+=a a ,所以10a >,130a >,又{}n a 为等比数列,则6710=>a q a ,所以213212719===a a a a a ,所以73a =或73a =-(舍去),所以212773==a a a a .故选:B. 2.(2022·吉林吉林)已知各项均为正数的等比数列{}n a 中,23a =,93453a a a =,则3a =( )A .6B .9C .27D .81【答案】B【解析】()3239335444,,3327a a a a a =∴==∴=,39a ∴=.故选:B 3.(2022·全国·高三专题练习)设a ,b ,c ,d 是非零实数,则“a ,b ,c ,d 成等比数列”是“ad bc =”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件【答案】A【解析】由a b c d ,,,成等比数列可得ad bc =,但当14,1,1,4a b c d ====时,a b c d ,,,不是等比数列,所以“a ,b ,c ,d 成等比数列”是“ad=bc ”的充分而不必要条件,故选:A.4.(2022·广西柳州)在等比数列{}n a 中,已知22a =,8462a a =,则公比q =( ) A.2- B C .2 D .2±【答案】D【解析】由等比数列284652a a a ==,解得452a =±,所以33522a q a ==±,所以2q =±,故选:D. 考点三 等比数列前n 项和的性质【例3-1】(2022·全国·高三专题练习)已知等比数列{an }的前n 项和为Sn ,S 10=1,S 30=13,S 40=( ) A .﹣51 B .﹣20 C .27 D .40【答案】D【解析】由{an }是等比数列,且S 10=1>0,S 30=13>0,得S 20>0,S 40>0,且1<S 20<13,S 40>13 所以S 10,S 20﹣S 10,S 30﹣S 20,S 40﹣S 30成等比数列, 即1,S 20﹣1,13﹣S 20,S 40﹣13构成等比数列,∴(S 20﹣1)2=1×(13﹣S 20),解得S 20=4或S 20=﹣3(舍去),∴(13﹣S 20)2=(S 20﹣1)(S 40﹣13),即92=3×(S 40﹣13),解得S 40=40.故选:D .【例3-2】(2022·全国·高三专题练习)等比数列{}n a 的前n 项和为n S ,若121n n S t -=⋅-,则t =( )A .2B .-2C .1D .-1【答案】A【解析】设等比数列的公比为q ,当1q =时,1n S na =,不合题意; 当1q ≠时,等比数列前n 项和公式()1111111n n n a q a aS q qq q-==-⋅+---, 依题意()111212110,222n nn S t t t t -=⋅-=⋅-⇒+-==.故选:A【例3-3】(2022·全国·高三专题练习)已知数列}{n a 的前n 项和121n n S -=+,则数列}{n a 的前10项中所有奇数项之和与所有偶数项之和的比为( ) A .12 B .2 C .172341D .341172【答案】C【解析】当2n ≥时,212n n n n a S S --=-=,又112a S ==,即前10项分别为2,1,2,4,8,16,32,64,128,256,所以数列}{n a 的前10项中5141023341143S -===-偶,)(421451022172143S -=+=+=-奇,所以172341S S =奇偶, 故选:C .【例3-4】(2022·全国·高三专题练习)数列{}n a 中,12a =,对任意 ,,m n m n m n N a a a ++∈=,若155121022k k k a a a ++++++=-,则 k =( )A .2B .3C .4D .5【答案】C【解析】在等式m n m n a a a +=中,令1m =,可得112n n n a a a a +==,12n na a +∴=, 所以,数列{}n a 是以2为首项,以2为公比的等比数列,则1222n nn a -=⨯=,()()()()1011011105101210122122212211212k k k k k k a a a a ++++++⋅-⋅-∴+++===-=---,1522k +∴=,则15k +=,解得4k =.故选:C.【例3-5】(2022·全国·高三专题练习)各项均为正数的等比数列{}n a 的前n 项和n S ,若264a a =,31a =,则29()42n n S a +的最小值为( )A .4B .6C .8D .12【答案】C【解析】因为264a a =,且等比数列{}n a 各项均为正数,所以2444,2a a ==,公比432,a q a ==首项114a =, 所以1(1)2114n n n a q S q --==- ,通项11124n n n a a q --==,所以29()2164448242n nn n S a +=++≥=,当且仅当216,342n n n =∴=,所以当3n =时,29()42n nS a+的最小值为8.故选:C.【一隅三反】1.(2022·湖南·长沙一中)一个等比数列的前7项和为48,前14项和为60,则前21项和为( ) A .180 B .108 C .75D .63【答案】D【解析】由题意得S 7,S 14-S 7,S 21-S 14组成等比数列48,12,3,即S 21-S 14=3,∴S 21=63. 故选:D2.(2022·全国·高三专题练习)已知一个等比数列首项为1,项数是偶数,其奇数项之和为85,偶数项之和为170,则这个数列的项数为( ) A .2 B .4 C .8 D .16【答案】C【解析】设这个等比数列{}n a 共有()2k k N *∈项,公比为q ,则奇数项之和为132185k S a a a -=+++=奇,偶数项之和为()2421321170n n S a a a q a a a qS -=+++=+++==奇偶,170285S q S ∴===偶奇, 等比数列{}n a 的所有项之和为()212212211708525512kkk a S -==-=+=-,则22256k=,解得4k =,因此,这个等比数列的项数为8.故选:C.3.(2022·全国·高三专题练习)等比数列{}n a 的前n 项和为213n n S r -=+,则r 的值为A .13B .13-C .19D .19-【答案】B【解析】当1n =时,113a S r ==+,当2n ≥时,212323223221118333(31)8383393n n n n n n n n n a S S --------=-=-=-=⋅=⋅⋅=⋅ 所以81333r r +=∴=-,故选B. 4.(2021·全国·高三专题练习)已知等比数列{}n a 中,11a =,132185k a a a ++++=,24242k a a a +++=,则k =( ) A .2 B .3 C .4 D .5【答案】B【解析】设等比数列{}n a 的公比为q ,则132112285k k a a a a a a q q +++++++==,即()2285184k q a a ++=-=,因为24242k a a a +++=,所以2q,则()21123221112854212712k k k a a a a a ++⨯-+++++=+==-,即211282k +=,解得3k =,故选:B.5.(2022·四川绵阳·一模)已知正项等比数列{}n a 的前n 项和为n S ,若5-,3S ,6S 成等差数列,则96S S -的最小值为( ) A .25 B .20 C .15 D .10【答案】B【解析】因为{}n a 是正项等比数列,所以3S ,63S S -,96S S -仍然构成等比数列,所以263396()()S S S S S -=-.又5-,3S ,6S 成等差数列,所以6352S S -=,6335S S S -=+,所以()()2263396333352510S S S S S S S S S -+-===++. 又{}n a 是正项等比数列,所以30S >,3325101020S S ++≥=,当且仅当35S =时取等号.故选:B.考点四 等比数列定义及其运用【例4】(2022·全国·高三专题练习)已知数列{}n a 满足12a =,121nn n a a a +=+,则下列结论正确的是( )A .数列1n a ⎧⎫⎨⎬⎩⎭是公差为12的等差数列 B .数列1n a ⎧⎫⎨⎬⎩⎭是公差为2的等差数列C .数列11n a ⎧⎫-⎨⎬⎩⎭是公比为12的等比数列 D .数列11n a ⎧⎫-⎨⎬⎩⎭是公比为2的等比数列【答案】C 【解析】∴121n n n a a a +=+,∴111111222n n n n a a a a ++==⋅+,1n a ⎧⎫∴⎨⎬⎩⎭既不是等比数列也不是等差数列; ∴1111112n n a a +⎛⎫-=- ⎪⎝⎭,∴数列11n a ⎧⎫-⎨⎬⎩⎭是公比为12的等比数列.故选:C【一隅三反】1.(2021·江苏盐城)(多选)设等比数列{}n a 的前n 项和为n S ,则下列数列一定是等比数列的有( ) A .12a a +,23a a +,34a a +,… B .13a a ,35a a +,57a a +,… C .2S ,42S S -,64S S -,… D .3S ,63S S -,96S S -,…【答案】BD【解析】设数列{}n a 的公比为q ,0q ≠,对于A 和C ,都有首项121(1)a a a q +=+,当1q =-时,120a a +=,不满足等比数列,故AC 错误;对于B ,2131(1)0a a a q +=+≠,且2235131313()a a q a a q a a a a ++==++, 同理25735a a q a a +=+,故数列13a a ,35a a +,57a a +,…为等比数列,B 正确; 对于D ,231231(1)0S a a a a q q =++=++≠,且3633S S q S -=,39663S S q S S -=-, 故数列3S ,63S S -,96S S -,…为等比数列,D 正确;故选:BD 2.(2022·广东·佛山一中)已知数列{n a }满足:11232n n a a a +==+, (1)求证:数列{1n a +}是等比数列;(2)()3log 1n n b a =+,求数列{n a ·n b }的前n 项和n S . 【答案】(1)证明见解析(2)()()12133142n nn n n S +-⨯++=-【解析】(1)因为11232n n a a a +==+,,所以1131n n a a ++=+(). 而113a +=,所以数列{1n a +}是以113a +=为首项,以3为公比的等比数列,所以13nn a +=,即31n n a =-.(2)由(1)可得()3log 1n n b a n =+=∴()31nn n a b n ⋅=-记1213233n n T n =⨯+⨯++⨯……∴所以()23131323133n n n T n n +=⨯+⨯++-⨯+⨯……∴∴-∴得:12123333nn n T n +-=+++-⨯ ()1313313n n n +-=-⨯-∴()121334n nn T +-⨯+=∴()()()1213311242n nn n n n S T n +-⨯++=-+++=-. 3.(2022·全国·高三专题练习)已知数列{}n a 的前n 项和为n S ,且112a =,11()*2n n n a a N n n ++=∈. (1)证明数列{}n an为等比数列,并求数列{}n a 的通项公式;(2)设(2)n n b n S =-,求数列32{}n n b -前n 项和n T . 【答案】(1)证明见解析;2n n na =;(2) 1(34)24(1)(2)n n n T n n ++=-++.【解析】(1)因为112n n n a a n ++=,所以1112n n a n a n++=,又因为11112a a ==,所以数列{}n a n是以首项为12,公比为12的等比数列,从而1111()()222n n n a n -=⨯=,故2n n n a =. (2)由(1)中结论可知,2311111112()3()(1)()()22222n n n S n n -=⨯+⨯+⨯++-+ ∴,所以23411111111()2()3()(1)()()222222n n n S n n +=⨯+⨯+⨯++-+ ∴,由∴-∴得,231111111()()()()222222n n n S n +=++++- 111[1()]122()1212n n n +-=-- 化简整理得,222n nn S +=-,所以222n n nn n b n S ()(), 故2232(32)22222()(2)22n n n n n n n n b n n n n n n ++--==-=--+++, 所以324351122222222222[()()()()()]132435112n n n n n T n n n n -++=--+-+-++-+--++,故1(34)24(1)(2)n n n T n n ++=-++. 考点五 等比数列的实际应用【例5-1】(2022·浙江省义乌中学模拟预测)我国古代的数学名著《九章算术》中有“衰分问题”:今有女子善织,日自倍,五日织五尺,问日织几何其意为:一女子每天织布的尺数是前一天的2倍,5天共织布5尺,问第五天织布的尺数是多少你的答案是( ) A .531B .1C .52D .8031【答案】D【解析】根据题意可知该女子每天织布的尺数成等比数列,设该等比数列为{}n a ,公比q =2, 则第1天织布的尺数为1a ,第5天织布的尺数为5a ,前5天共织布为55S =, 则()51112551231a a-=⇒=-,∴445158023131a a q =⋅=⨯=.故选:D.【例5-2】(2022·江苏·沭阳如东中学模拟预测)著名的“康托三分集”是数学理性思维的构造产物,具有典型的分形特征,其操作过程如下:将闭区间[0,1]均分为三段,去掉中间的区间段12,33⎛⎫⎪⎝⎭,记为第一次操作;再将剩下的两个区120,,,133⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦分别均分为三段,并各自去掉中间的区间段,记为第二次操作;…,如此这样,每次在上一次操作的基础上,将剩下的各个区间分别均分为三段,同样各自去掉中间的区间段.操作过程不断地进行下去,以至无穷,剩下的区间集合即是“康托三分集”.若使去掉的各区间长度之和不小于1415,则需要操作的次数n 的最小值为( ) 参考数据:lg2=0.3010,lg3=0.4771 A .6 B .7 C .8 D .9【答案】B【解析】第一次操作去掉13,设为1a ;第二次操作去掉29,设为2a ;第三次操作去掉427,设为3a , 依次类推,11233n n a -⎛⎫=⋅ ⎪⎝⎭.故0111222[()()()]3333n n S -=⨯+++ 2113121412331513n n⎡⎤⎛⎫⨯-⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦=⨯=-≥ ⎪⎝⎭-, 整理,得12153n⎛⎫≥ ⎪⎝⎭,()21lg lg lg2lg3lg15315nn ⎛⎫∴≤∴-≤- ⎪⎝⎭,,()lg3lg5lg3lg5lg31lg211 6.7lg2lg3lg3lg2lg3lg2lg3lg2n -+++-∴≥===+≈----,故n 的最小值为7. 故选:B. 【一隅三反】1.(2022·全国·模拟预测)在适宜的环境中,一种细菌的一部分不断分裂产生新的细菌,另一部分则死亡.为研究这种细菌的分裂情况,在培养皿中放入m 个细菌,在1小时内,有34的细菌分裂为原来的2倍,14的细菌死亡,此时记为第一小时的记录数据.若每隔一小时记录一次细菌个数,则细菌数超过原来的10倍的记录时间为第( ) A .6小时末 B .7小时末C .8小时末D .9小时末【答案】A【解析】设n a 表示第n 小时末的细菌数,依题意有()11332242n n n a a a n --=⨯=≥,133242a m m =⨯=,则{}n a 是等比数列,首项为32m ,公比32q =,所以32nn a m ⎛⎫= ⎪⎝⎭.依题意,10n a m >,即3102n m m ⎛⎫> ⎪⎝⎭,所以3102n⎛⎫> ⎪⎝⎭, 由于563310,24372932102642⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝=⎭=<,又*N n ∈,所以6n ≥,所以第6小时末记录的细菌数超过原来的10倍, 故选:A.2.(2022·湖南湖南·二模)在流行病学中,基本传染数0R 是指在没有外力介入,同时所有人都没有免疫力的情况下,一个感染者平均传染的人数.0R 一般由疾病的感染周期、感染者与其他人的接触频率、每次接触过程中传染的概率决定,假设某种传染病的基本传染数02R =,平均感染周期为7天,那么感染人数由1(初始感染者)增加到999大约需要的天数为( )(初始感染者传染0R 个人为第一轮传染,这0R 个人每人再传染0R 个人为第二轮传染……参考数据:lg20.3010≈) A .42 B .56 C .63 D .70【答案】C【解析】设第n 轮感染的人数为n a ,则数列{}n a 是12a =,公比2q的等比数列,由()2121199912nn S ⨯-+=+=-,可得121000n +=,解得2500n =,两边取对数得lg 2lg500n =,则lg 23lg 2n =-,所以33118.979lg 20.3010n =-=-≈=, 故需要的天数约为9763⨯=. 故选:C3.(2022·云南·高三阶段练习(理))为了更好地解决就业问题,国家在2020年提出了“地摊经济”为响应国家号召,有不少地区出台了相关政策去鼓励“地摊经济”.老王2020年6月1日向银行借了免息贷款10000元,用于进货.因质优价廉,供不应求,据测算:每月获得的利润是该月初投入资金的20%,每月底扣除生活费1000元,余款作为资金全部用于下月再进货,如此继续,预计到2021年5月底该摊主的年所得收入为( )(取()111.27.5=,()121.29=)A .32500元B .40000元C .42500元D .50000元【答案】B 【解析】设010000a =,从6月份起每月底用于下月进货的资金依次记为1a ,2a ,…,12a ,()100120%1000 1.21000a a a =⨯+-=-,同理可得1 1.21000n n a a +=-, 所以()15000 1.25000n n a a +-=-, 而050005000a -=,所以数列{}5000n a -是等比数列,公比为1.2,所以50005000 1.2n n a -=⨯,12125000 1.2500050009500050000a =⨯+=⨯+=,∴总利润为500001000040000-=,故选:B .。
2023-2024学年高考数学数列专项练习题(含答案)

2023-2024学年高考数学数列小专题一、单选题1.已知等比数列的前项和为,且,则数列的前项和为( ){}n a n n S 11n n a S +=+{}2n a n A .B .413n -213n -C .D .41n-21n-2.已知函数在上的最小值为,最大值为,且在等差数列中,2log y x =[]16,256m M {}n a ,则( )24,a m a M ==10a =A .17B .18C .20D .243.数列满足,(),,若数列是递减数{}n a 18a =11nn n a a na +=+*n ∈N 112nn n b a λ⎛⎫⎛⎫=+⋅ ⎪ ⎪⎝⎭⎝⎭{}n b 列,则实数的取值范围是( )λA .B .C .D .8,7⎛⎫-+∞ ⎪⎝⎭7,8⎛⎫-+∞ ⎪⎝⎭8,7⎛⎫+∞ ⎪⎝⎭7,8⎛⎫+∞ ⎪⎝⎭4.等差数列中的,是函数的极值点,则{}n a 2a 2024a ()32642024=-+-f x x x x ( )81013log =a A .B .C .3D .133-13-5.已知数列的前项和为,且等比数列满足,若,则{}n c n n S {}n a 2log n n c a =2364a a =( )9S =A .3B .4C .5D .66.已知数列是公比为q ()的正项等比数列,且,若,则{}n b 1q ≠10122ln 0b =()241f x x =+( )()()()122023f b f b f b +++=A .4069B .2023C .2024D .40467.已知等比数列的前项和为,若,则( ){}n a n n S 132n n S λ+=⨯+λ=A .B .C .D .33-66-8.已知数列的前4项分别为,,,,则该数列的一个通项公式可以为132-354+578-7916+( )n a =A .2121(1)2nn n n -++-B .12121(1)2n n n n +-++-C .12121(1)2n n n n--++-D .2121(1)2nnn n -++-二、多选题9.已知是等比数列的前项和,且,则下列说法正确的是( )n S {}n a n 11(2)n n S a -=+-A .2a =-B .中任意奇数项的值始终大于任意偶数项的值{}n S C .的最大项为,最小项为{}n S 13S =232S =D .12231011201612a a a a a a ⎛⎫+++=- ⎪⎝⎭ 10.数列中,,则( ){}n a 1112,1,n na a n a ++=+=∈N A .202412a =B .12320221011a a a a +++⋅⋅⋅+=C .12320242a a a a ⋅⋅⋅=-D .122334202220231011a a a a a a a a +++⋅⋅⋅+=-11.已知数列满足,,为的前项和,则( ){}n a 126a =132n n a a +=-n S {}n a n A .为等比数列{}1n a +B .的通项公式为{}n a 4131n n a -=-C .为递减数列{}n aD .当或时,取得最大值4n =5n =n S 12.等差数列的前n 项和为,若,,则( ){}n a n S 79a =443S a =A .的公差为1B .的公差为2{}n a {}n a C .D .418S =20232025a =三、填空题13.在等比数列中,,则.{}n a 12563,6a a a a +=+=910a a +=14.某网店统计了商品近30天的日销售量,日销售量依次构成数列,已知,且A {}n a 120a=,则商品近30天的总销量为 .()()111nn n a a n ++-=+-∈N A 15.在数列与中,已知,则{}n a {}n b ()1111112,2,2n n n n n n n n a b a b a b a b a b ++++==+=+=.2023202311a b +=16.已知数列满足.且,若,则{}n a 1265n n a a n ++=+13a =()1nn n b a =-.1232024b b b b ++++=答案:1.A【分析】根据关系得出等比数列求出,最后再根据等比数列前项和计算求解,n n a S 12n n a -=n 即可.【详解】因为,所以当时,,两式相减,得,11n n a S +=+2n ≥11n n a S -=+12n n a a +=所以数列从第2项起是公比为2的等比数列.又数列是等比数列,所以.{}n a {}n a 212a a =由,解得,所以数列是首项为1,公比为2的等比数列,所以21111a S a =+=+11a ={}n a ,12n n a -=所以,所以数列是首项为1,公比为4的等比数列,()212124n n n a --=={}2na 所以数列的前项和为.{}2n a n 1441143n n --=-故选:A .2.C【分析】利用对数函数单调性先求出函数最小值为,最大值为,再由等差数列通项公式m M 求解.【详解】因为函数在上单调递增,2log y x =[]16,256所以,,2log 164m ==2log 2568M ==所以,所以等差数列的公差,244,8a a =={}n a 42842422a a d --===-所以.()10210248220a a d =+-=+⨯=故选:C .3.D【分析】将取倒数结合累加法求得,再利用数列单调递减列不等式11nn n a a na +=+()22118n n a -=并分离参数,求出新数列的最大值即可求得答案【详解】由题意,,两边取倒数可化为,所以,11nn n a a na +=+1111n n n n na n a a a ++==+21111a a -=,,由累加法可得,,因为32112a a -=1111--=-n n n a a ()()11111212n n n n a a --=++⋅⋅⋅+-=,所以,18a =()()212111288n n n n a --=+=所以,因为数列是递减数列,故,即()221111282nn n n n b a λλ⎡⎤-⎛⎫⎛⎫⎛⎫=+=+⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎝⎭⎣⎦{}n b 1n n b b -<,整理可得,()()2212123118282n n n n λλ-⎡⎤⎡⎤--⎛⎫⎛⎫+<+⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦,因为,,所以2254842017288n n n λ⎛⎫--+ ⎪-+-⎝⎭>=2n ≥*n ∈N ,故.22max 5548428722888n ⎛⎫⎛⎫⎛⎫--+-⨯-+ ⎪⎪ ⎪⎝⎭⎝⎭ ⎪==⎪ ⎪⎝⎭7,8λ⎛⎫∈+∞ ⎪⎝⎭故选:D.4.A【分析】利用导数求出函数的两个极值点,再利用等差数列性质求出即可计算得解.()f x 1013a 【详解】由求导得:,()32642024=-+-f x x x x 2()3124f x x x '=-+有,即有两个不等实根,2124340∆=-⨯⨯>()0f x '=12,x x 显然是的变号零点,即函数的两个极值点,12,x x ()f x '()f x 依题意,,在等差数列中,,24122024a x a x ++=={}n a 22024101322a a a +==所以.38101321log log 23a ==故选:A 5.D【分析】设等比数列的公比为,根据题意,求得,结合对数运算性质有{}n a q 354a =,即可求解.9925log S a =【详解】设等比数列的公比为,{}n a q因为,()2235365524a a a a q a q ===所以9128212228299log log log log S c c a c c a a a =++++++=++ .()9321289252log log log 46a a a a a ==== 故选:D.6.D【分析】由等比数列的性质可得,由,可得1202322022202311b b b b b b ⋅=⋅==⋅= ()241f x x =+,故有,即可计()14f x f x ⎛⎫+= ⎪⎝⎭()()()()()()1202322022202314f b f b f b f b f b f b +=+==+= 算.()()()122023f b f b f b +++ 【详解】由数列是公比为q ()的正项等比数列,故,{}n b 1q ≠0n b >,故,()210121012120232ln ln ln 0b b b b ==⋅=120231b b ⋅=即有,1202322022202311b b b b b b ⋅=⋅==⋅= 由,则当时,()241f x x =+0x >有,()2222214444411111x f x f x x x x x ⎛⎫+=+=+= ⎪+++⎝⎭⎛⎫+ ⎪⎝⎭故,()()()()()()1202322022202314f b f b f b f b f b f b +=+==+= 故()()()()()()()12202312023220222f b f b f b f b f b f b f b ⎡⎤⎡⎤⎡⎤+++=++++⎣⎦⎣⎦⎣⎦ ,()()()()202312023120238092f b f b f b f b ⎡⎤⎡⎤++=+=⎣⎦⎣⎦故.()()()1220234046f b f b f b +++= 故选:D.7.D【分析】根据题意,求得,结合等比数列的定义,得到,即可求解.12,2n na n a +=≥212a a =【详解】由,132n n S λ+=⨯+当时,,可得,2n ≥1132(32)32n n nn n n a S S λλ+--==⨯+-⨯+=⋅12,2n na n a +=≥当时,,1n =21132a S λ==⨯+因为数列为等比数列,可得,解得.{}n a 222132232a a λ⨯==⨯+6λ=-故选:D.8.D【分析】观察数列的项的特点,找到各项之间的规律,即可写出一个通项公式,结合选项,即得答案.【详解】观察可知,该数列的前面整数部分为奇数,后面分数部分正负相间,首项的分21n +数部分为负,分母为,分子为,2n 21n-故该数列的一个通项公式可以为,2121(1)2nn n n a n -=++-故选:D 9.BCD【分析】由等比数列的前项和公式可得,可判断选项A ;根据的解析式判断奇数项n 2a =n S 与偶数项的公式,从而判断BC ;由得到的通项公式,从而表示出的通项公式n S n a 1n n n b a a +=即可判断D.【详解】由题可知,此时等比数列的公比,所以设前项和公式应为:1q ≠n ,n n S A q A =-⋅+,A 错误;12,22nn S a a ⎛⎫=-⋅-+∴= ⎪⎝⎭因此,1112,1222122,2nn n n n S n --⎧+⎪⎪⎛⎫=-⋅-+=⎨⎪⎝⎭⎪-+⎪⎩为奇数为偶数可得中,奇数项递减,且始终大于2,最大值为,{}n S 13S =偶数项递增,且始终小于2,最小值为,因此BC 正确;232S =由可得,令,n S 23122n n a -⎛⎫=-- ⎪⎝⎭23121919422n n n n n b a a -+-⎛⎫==-=-⎪⎝⎭所以,故D 正确1012231011121020911124611214a a a a a a b b b ⎛⎫-- ⎪⎛⎫⎝⎭+++=+++==- ⎪⎝⎭- 故选:BCD 10.ABD【分析】根据递推公式可得数列是以3为周期的周期数列,再逐个选项判断即可.{}n a 【详解】由题意得:,234512341111111,11,12,1,22a a a a a a a a =-==-=-=-==-=⋅⋅⋅数列是以3为周期的周期数列.∴{}n a 对于A ,,A 正确;202467432212a a a ⨯+===对于B ,,B 正确;()1232022123367467410112a a a a a a a +++⋅⋅⋅+=++=⨯=对于C ,,C 错误;()6741232024123202320241a a a a a a a a a ⋅⋅⋅==对于D ,由递推关系式知:,11n n n a a a +=-()()()12233420222023122022111a a a a a a a a a a a ∴+++⋅⋅⋅+=-+-+⋅⋅⋅+-,D 正确.12320222022101120221011a a a a =+++⋅⋅⋅+-=-=-故选:ABD .11.AC【分析】利用构造法得,判断出为首项为,公比为的等比数列,()1311n n a a ++=+{}11n a ++2713判断A 选项;利用等比数列通项公式求出通项公式,判断B 选项;根据函数是减函数,1n a +判断C 选项;令,解得,判断D 选项.n a =4n =【详解】因为,所以,即,,132n n a a +=-1331n n a a ++=+()1311n n a a ++=+11113n na a ++=+又因为,所以,所以为首项为,公比为的等比数列,A 正确;126a =1127a +={}11n a ++2713B 错误;C 正确;D 错误.故选:AC 12.ACD【分析】列出方程组,求出等差数列的公差和首项,判断A ,B ;根据等差数列通项公式以及前n 项和公式即可判断C ,D.【详解】设的公差为d ,由,,得,{}n a 79a =443S a =111694639a d a d a d +=⎧⎨+=+⎩解得,故A 正确,B 错误;131a d =⎧⎨=⎩,,C ,D 正确.414618S a d =+=2023120222025a a d =+=故选:ACD 13.12【分析】根据等比数列的通项公式可得结果.【详解】设等比数列的公比为,,所以,{}n a q ()44561236a a q a a q +=+==42q =所以,()4910562612a a q a a +=+=⨯=故12.14.1020【分析】根据题目所给递推关系找到数列的规律,进而求和.【详解】当时,,当时,,21n k =-221k k a a -=2n k =2122k k a a +=+,∴21212k k a a +-=+中奇数项是公差为2,首项为20的等差数列,{}n a ∴∴1232930a a a a a +++++ ()135292a a a a =++++ .151421520210202⨯⎛⎫=⨯⨯+⨯= ⎪⎝⎭商品近30天的总销量为.∴A 1020故答案为.102015.1【分析】由已知计算可得为常数列,进而可得结果.1111n n a b +++11{}n n a b +【详解】由题意知,,()111111211112n n n n n n n n n n n n a b a b a b a b a b a b +++++++++===+所以为常数列,即,11{}n n a b +11111111122n n a b a b +=+=+=所以.20232023111a b +=故1.16.2024【分析】利用构造法与迭代法求得,从而利用并项求和法即可得解.21n a n =+【详解】因为,所以,1265n n a a n ++=+()12(1)1221n n a n a n +-+-=---又,则,13a =12113210a -⨯-=--=所以()[]12112(1)1(2)21(2)2(1)1n n n a n a n a n +--+-=---=----=,()1(2)2110n a =--⨯-=故,则,210n a n --=21n a n =+所以,()()11(21)nnn n b a n =-=-+则的各项分别为,{}n b 3,5,7,9,11,13,--- 所以()()()()12320243579111340474049b b b b ++++=-++-++-+++-+ .210122024=⨯=故2024关键点点睛:本题解决的关键在于将推递关系式化得,从而()12(1)1221n n a n a n +-+-=---求得,由此得解.n a。
2023年高考数学一轮复习第六章数列3等比数列练习含解析

等比数列考试要求 1.理解等比数列的概念.2.掌握等比数列的通项公式与前n 项和公式.3.了解等比数列与指数函数的关系.知识梳理1.等比数列的有关概念(1)定义:一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数(不为零),那么这个数列叫做等比数列.这个常数叫做等比数列的公比,通常用字母q 表示,定义的表达式为a n +1a n=q (n ∈N *,q 为非零常数). (2)等比中项:如果在a 与b 中间插入一个数G ,使a ,G ,b 成等比数列,那么G 叫做a 与b 的等比中项,此时,G 2=ab . 2.等比数列的有关公式 (1)通项公式:a n =a 1q n -1.(2)前n 项和公式:S n =⎩⎪⎨⎪⎧na 1,q =1,a 11-q n 1-q=a 1-a n q1-q ,q ≠1.3.等比数列的性质(1)通项公式的推广:a n =a m ·qn -m(m ,n ∈N *).(2)对任意的正整数m ,n ,p ,q ,若m +n =p +q =2k ,则a m ·a n =a p ·a q =a 2k .(3)若等比数列前n 项和为S n ,则S m ,S 2m -S m ,S 3m -S 2m 仍成等比数列(m 为偶数且q =-1除外). (4)在等比数列{a n }中,等距离取出若干项也构成一个等比数列,即a n ,a n +k ,a n +2k ,a n +3k ,…为等比数列,公比为q k. (5)若⎩⎪⎨⎪⎧a 1>0,q >1或⎩⎪⎨⎪⎧a 1<0,0<q <1,则等比数列{a n }递增.若⎩⎪⎨⎪⎧a 1>0,0<q <1或⎩⎪⎨⎪⎧a 1<0,q >1,则等比数列{a n }递减.常用结论1.若数列{a n },{b n }(项数相同)是等比数列,则数列{c ·a n }(c ≠0),{|a n |},{a 2n },⎩⎨⎧⎭⎬⎫1a n ,{a n ·b n },⎩⎨⎧⎭⎬⎫a nb n 也是等比数列. 2.等比数列{a n }的通项公式可以写成a n =cq n,这里c ≠0,q ≠0. 3.等比数列{a n }的前n 项和S n 可以写成S n =Aq n-A (A ≠0,q ≠1,0). 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)等比数列的公比q 是一个常数,它可以是任意实数.( × ) (2)三个数a ,b ,c 成等比数列的充要条件是b 2=ac .( × )(3)数列{a n }的通项公式是a n =a n,则其前n 项和为S n =a 1-a n1-a.( × )(4)数列{a n }为等比数列,则S 4,S 8-S 4,S 12-S 8成等比数列.( × ) 教材改编题1.已知{a n }是等比数列,a 2=2,a 4=12,则公比q 等于( )A .-12B .-2C .2D .±12答案 D解析 设等比数列的公比为q , ∵{a n }是等比数列,a 2=2,a 4=12,∴a 4=a 2q 2,∴q 2=a 4a 2=14,∴q =±12.2.在各项均为正数的等比数列{a n }中,a 1a 11+2a 6a 8+a 3a 13=25,则a 6+a 8=______. 答案 5解析 ∵{a n }是等比数列, 且a 1a 11+2a 6a 8+a 3a 13=25, ∴a 26+2a 6a 8+a 28=(a 6+a 8)2=25. 又∵a n >0,∴a 6+a 8=5.3.已知三个数成等比数列,若它们的和等于13,积等于27,则这三个数为________. 答案 1,3,9或9,3,1解析 设这三个数为a q,a ,aq ,则⎩⎪⎨⎪⎧a +aq +aq =13,a ·aq ·aq =27,解得⎩⎪⎨⎪⎧a =3,q =13或⎩⎪⎨⎪⎧a =3,q =3,∴这三个数为1,3,9或9,3,1.题型一 等比数列基本量的运算例1 (1)(2020·全国Ⅱ)记S n 为等比数列{a n }的前n 项和.若a 5-a 3=12,a 6-a 4=24,则S na n等于( ) A .2n-1 B .2-21-nC .2-2n -1D .21-n-1答案 B解析 方法一 设等比数列{a n }的公比为q , 则q =a 6-a 4a 5-a 3=2412=2. 由a 5-a 3=a 1q 4-a 1q 2=12a 1=12,得a 1=1. 所以a n =a 1qn -1=2n -1,S n =a 11-q n 1-q =2n-1,所以S n a n =2n -12n -1=2-21-n.方法二 设等比数列{a n }的公比为q ,则⎩⎪⎨⎪⎧a 3q 2-a 3=12,①a 4q 2-a 4=24,②②①得a 4a 3=q =2. 将q =2代入①,解得a 3=4. 所以a 1=a 3q2=1,下同方法一.(2)(2019·全国Ⅰ)记S n 为等比数列{a n }的前n 项和.若a 1=13,a 24=a 6,则S 5=________.答案1213解析 设等比数列{a n }的公比为q , 因为a 24=a 6,所以(a 1q 3)2=a 1q 5, 所以a 1q =1,又a 1=13,所以q =3,所以S 5=a 11-q 51-q=13×1-351-3=1213. 教师备选1.已知数列{a n }为等比数列,a 2=6,6a 1+a 3=30,则a 4=________. 答案 54或24解析 由⎩⎪⎨⎪⎧ a 1·q =6,6a 1+a 1·q 2=30,解得⎩⎪⎨⎪⎧q =3,a 1=2或⎩⎪⎨⎪⎧q =2,a 1=3,a 4=a 1·q 3=2×33=54或a 4=3×23=3×8=24.2.已知数列{a n }为等比数列,其前n 项和为S n ,若a 2a 6=-2a 7,S 3=-6,则a 6等于( ) A .-2或32 B .-2或64 C .2或-32 D .2或-64答案 B解析 ∵数列{a n }为等比数列,a 2a 6=-2a 7=a 1a 7,解得a 1=-2,设数列的公比为q ,S 3=-6=-2-2q -2q 2, 解得q =-2或q =1,当q =-2时,则a 6=(-2)6=64, 当q =1时,则a 6=-2.思维升华 (1)等比数列中有五个量a 1,n ,q ,a n ,S n ,一般可以“知三求二”,通过列方程(组)便可迎刃而解.(2)等比数列的前n 项和公式涉及对公比q 的分类讨论,当q =1时,{a n }的前n 项和S n =na 1;当q ≠1时,{a n }的前n 项和S n =a 11-q n 1-q =a 1-a n q 1-q.跟踪训练1 (1)(2020·全国Ⅱ)数列{a n }中,a 1=2,a m +n =a m a n ,若a k +1+a k +2+…+a k +10=215-25,则k 等于( )A .2B .3C .4D .5 答案 C解析 a 1=2,a m +n =a m a n , 令m =1,则a n +1=a 1a n =2a n ,∴{a n }是以a 1=2为首项,q =2为公比的等比数列, ∴a n =2×2n -1=2n.又∵a k +1+a k +2+…+a k +10=215-25, ∴2k +11-2101-2=215-25,即2k +1(210-1)=25(210-1),∴2k +1=25,∴k +1=5,∴k =4.(2)(2020·新高考全国Ⅱ)已知公比大于1的等比数列{a n }满足a 2+a 4=20,a 3=8. ①求{a n }的通项公式; ②求a 1a 2-a 2a 3+…+(-1)n -1a n a n +1.解 ①设{a n }的公比为q (q >1).由题设得⎩⎪⎨⎪⎧a 1q +a 1q 3=20,a 1q 2=8,解得⎩⎪⎨⎪⎧q =2,a 1=2或⎩⎪⎨⎪⎧q =12,a 1=32(舍去).所以{a n }的通项公式为a n =2n,n ∈N *. ②由于(-1)n -1a n a n +1=(-1)n -1×2n ×2n +1=(-1)n -122n +1,故a 1a 2-a 2a 3+…+(-1)n -1a n a n +1=23-25+27-29+…+(-1)n -1·22n +1=23[1--22n]1--22=85-(-1)n 22n +35. 题型二 等比数列的判定与证明例2 已知数列{a n }满足a 1=1,na n +1=2(n +1)a n ,设b n =a n n. (1)求b 1,b 2,b 3;(2)判断数列{b n }是否为等比数列,并说明理由; (3)求{a n }的通项公式. 解 (1)由条件可得a n +1=2n +1na n .将n =1代入得,a 2=4a 1,而a 1=1,所以a 2=4. 将n =2代入得,a 3=3a 2,所以a 3=12. 从而b 1=1,b 2=2,b 3=4.(2){b n }是首项为1,公比为2的等比数列, 由条件可得a n +1n +1=2a nn,即b n +1=2b n , 又b 1=1,所以{b n }是首项为1,公比为2的等比数列. (3)由(2)可得a nn=2n -1,所以a n =n ·2n -1.教师备选已知各项都为正数的数列{a n }满足a n +2=2a n +1+3a n . (1)证明:数列{a n +a n +1}为等比数列; (2)若a 1=12,a 2=32,求{a n }的通项公式.(1)证明 a n +2=2a n +1+3a n , 所以a n +2+a n +1=3(a n +1+a n ), 因为{a n }中各项均为正数, 所以a n +1+a n >0,所以a n +2+a n +1a n +1+a n=3,所以数列{a n +a n +1}是公比为3的等比数列. (2)解 由题意知a n +a n +1=(a 1+a 2)3n -1=2×3n -1,因为a n +2=2a n +1+3a n ,所以a n +2-3a n +1=-(a n +1-3a n ),a 2=3a 1, 所以a 2-3a 1=0,所以a n +1-3a n =0, 故a n +1=3a n , 所以4a n =2×3n -1,a n =12×3n -1.思维升华 等比数列的三种常用判定方法 (1)定义法:若a n +1a n =q (q 为非零常数,n ∈N *)或a n a n -1=q (q 为非零常数且n ≥2,n ∈N *),则{a n }是等比数列.(2)等比中项法:若数列{a n }中,a n ≠0且a 2n +1=a n ·a n +2(n ∈N *),则{a n }是等比数列. (3)前n 项和公式法:若数列{a n }的前n 项和S n =k ·q n-k (k 为常数且k ≠0,q ≠0,1),则{a n }是等比数列.跟踪训练2 S n 为等比数列{a n }的前n 项和,已知a 4=9a 2,S 3=13,且公比q >0.(1)求a n 及S n ;(2)是否存在常数λ,使得数列{S n +λ}是等比数列?若存在,求λ的值;若不存在,请说明理由.解 (1)易知q ≠1,由题意可得⎩⎪⎨⎪⎧a 1q 3=9a 1q ,a 11-q31-q=13,q >0,解得a 1=1,q =3, ∴a n =3n -1,S n =1-3n 1-3=3n-12.(2)假设存在常数λ,使得数列{S n +λ}是等比数列, ∵S 1+λ=λ+1,S 2+λ=λ+4,S 3+λ=λ+13, ∴(λ+4)2=(λ+1)(λ+13), 解得λ=12,此时S n +12=12×3n,则S n +1+12S n +12=12×3n +112×3n=3,故存在常数λ=12,使得数列⎩⎨⎧⎭⎬⎫S n +12是以32为首项,3为公比的等比数列.题型三 等比数列的性质例3 (1)若等比数列{a n }中的a 5,a 2019是方程x 2-4x +3=0的两个根,则log 3a 1+log 3a 2+log 3a 3+…+log 3a 2023等于( ) A.20243 B .1011 C.20232D .1012答案 C解析 由题意得a 5a 2019=3, 根据等比数列性质知,a 1a 2023=a 2a 2022=…=a 1011a 1013=a 1012a 1012=3,于是a 1012=123,则log 3a 1+log 3a 2+log 3a 3+…+log 3a 2023 =log 3(a 1a 2a 3…a 2023)11011232023=l 3·og 3.2⎛⎫= ⎪⎝⎭(2)已知数列{a n }是等比数列,S n 为其前n 项和,若a 1+a 2+a 3=4,a 4+a 5+a 6=8,则S 12等于( )A .40B .60C .32D .50 答案 B解析 数列S 3,S 6-S 3,S 9-S 6,S 12-S 9是等比数列, 即4,8,S 9-S 6,S 12-S 9是等比数列, ∴S 12=4+8+16+32=60. 教师备选1.设等比数列{a n }的前n 项和为S n ,若S 6S 3=3,则S 9S 6=__________. 答案 73解析 设等比数列{a n }的公比为q ,易知q ≠-1,由等比数列前n 项和的性质可知S 3,S 6-S 3,S 9-S 6仍成等比数列,∴S 6-S 3S 3=S 9-S 6S 6-S 3, 又由已知得S 6=3S 3, ∴S 9-S 6=4S 3, ∴S 9=7S 3,∴S 9S 6=73. 2.已知等比数列{a n }共有2n 项,其和为-240,且奇数项的和比偶数项的和大80,则公比q =________. 答案 2解析 由题意,得⎩⎪⎨⎪⎧S 奇+S 偶=-240,S 奇-S 偶=80,解得⎩⎪⎨⎪⎧S 奇=-80,S 偶=-160,所以q =S 偶S 奇=-160-80=2. 思维升华 (1)等比数列的性质可以分为三类:一是通项公式的变形,二是等比中项的变形,三是前n 项和公式的变形,根据题目条件,认真分析,发现具体的变化特征即可找出解决问题的突破口.(2)巧用性质,减少运算量,在解题中非常重要.跟踪训练3 (1)(2022·安康模拟)等比数列{a n }的前n 项和为S n ,若S 10=1,S 30=7,则S 40等于( )A .5B .10C .15D .-20 答案 C解析 易知等比数列{a n }的前n 项和S n 满足S 10,S 20-S 10,S 30-S 20,S 40-S 30,…成等比数列.设{a n }的公比为q ,则S 20-S 10S 10=q 10>0,故S 10,S 20-S 10,S 30-S 20,S 40-S 30,…均大于0. 故(S 20-S 10)2=S 10·(S 30-S 20),即(S 20-1)2=1·(7-S 20)⇒S 220-S 20-6=0. 因为S 20>0,所以S 20=3.又(S 30-S 20)2=(S 20-S 10)(S 40-S 30), 所以(7-3)2=(3-1)(S 40-7),故S 40=15.(2)在等比数列{a n }中,a n >0,a 1+a 2+a 3+…+a 8=4,a 1a 2·…·a 8=16,则1a 1+1a 2+…+1a 8的值为( ) A .2 B .4 C .8 D .16答案 A解析 ∵a 1a 2…a 8=16, ∴a 1a 8=a 2a 7=a 3a 6=a 4a 5=2,∴1a 1+1a 2+…+1a 8=⎝ ⎛⎭⎪⎫1a 1+1a 8+⎝ ⎛⎭⎪⎫1a 2+1a 7+⎝ ⎛⎭⎪⎫1a 3+1a 6+⎝ ⎛⎭⎪⎫1a 4+1a 5=12(a 1+a 8)+12(a 2+a 7)+12(a 3+a 6)+12(a 4+a 5) =12(a 1+a 2+…+a 8)=2. 课时精练1.(2022·合肥市第六中学模拟)若等比数列{a n }满足a 1+a 2=1,a 4+a 5=8,则a 7等于( ) A.643B .-643C.323 D .-323答案 A解析 设等比数列{a n }的公比为q , 则a 4+a 5a 1+a 2=q 3=8, 所以q =2,又a 1+a 2=a 1(1+q )=1, 所以a 1=13,所以a 7=a 1×q 6=13×26=643.2.已知等比数列{a n }满足a 1=1,a 3·a 5=4(a 4-1),则a 7的值为( ) A .2B .4C.92D .6答案 B解析 根据等比数列的性质得a 3a 5=a 24, ∴a 24=4(a 4-1),即(a 4-2)2=0,解得a 4=2. 又∵a 1=1,a 1a 7=a 24=4,∴a 7=4.3.(2022·开封模拟)等比数列{a n }的前n 项和为S n =32n -1+r ,则r 的值为( )A.13B .-13C.19D .-19 答案 B解析 由等比数列前n 项和的性质知,S n =32n -1+r =13×9n +r ,∴r =-13.4.(2022·天津北辰区模拟)我国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛,每天走的路程为前一天的一半,走了6天后到达目的地.”则该人第四天走的路程为( ) A .6里 B .12里 C .24里 D .48里答案 C解析 由题意可知,该人所走路程形成等比数列{a n },其中q =12,因为S 6=a 1⎝⎛⎭⎪⎫1-1261-12=378,解得a 1=192,所以a 4=a 1·q 3=192×18=24.5.(多选)设等比数列{a n }的公比为q ,则下列结论正确的是( ) A .数列{a n a n +1}是公比为q 2的等比数列 B .数列{a n +a n +1}是公比为q 的等比数列 C .数列{a n -a n +1}是公比为q 的等比数列D .数列⎩⎨⎧⎭⎬⎫1a n 是公比为1q的等比数列答案 AD 解析 对于A ,由a n a n +1a n -1a n=q 2(n ≥2)知数列{a n a n +1}是公比为q 2的等比数列; 对于B ,当q =-1时,数列{a n +a n +1}的项中有0,不是等比数列; 对于C ,当q =1时,数列{a n -a n +1}的项中有0,不是等比数列;对于D ,1a n +11a n=a n a n +1=1q, 所以数列⎩⎨⎧⎭⎬⎫1a n 是公比为1q 的等比数列.6.(多选)数列{a n }的前n 项和为S n ,若a 1=1,a n +1=2S n (n ∈N *),则有( ) A .S n =3n -1B .{S n }为等比数列C .a n =2·3n -1D .a n =⎩⎪⎨⎪⎧1,n =1,2·3n -2,n ≥2答案 ABD解析 由题意,数列{a n }的前n 项和满足a n +1=2S n (n ∈N *), 当n ≥2时,a n =2S n -1,两式相减,可得a n +1-a n =2(S n -S n -1)=2a n , 可得a n +1=3a n ,即a n +1a n=3(n ≥2), 又a 1=1,则a 2=2S 1=2a 1=2,所以a 2a 1=2, 所以数列{a n }的通项公式为a n =⎩⎪⎨⎪⎧1,n =1,2·3n -2,n ≥2.当n ≥2时,S n =a n +12=2·3n -12=3n -1,又S 1=a 1=1,适合上式, 所以数列{a n }的前n 项和为S n =3n -1,又S n +1S n =3n3n -1=3, 所以数列{S n }为首项为1,公比为3的等比数列,综上可得选项ABD 是正确的.7.(2022·嘉兴联考)已知等比数列{a n }的前n 项和为S n ,若S 3=7,S 6=63,则a 1=________. 答案 1解析 由于S 3=7,S 6=63知公比q ≠1, 又S 6=S 3+q 3S 3, 得63=7+7q 3. ∴q 3=8,q =2.由S 3=a 11-q 31-q =a 11-81-2=7,得a 1=1.8.已知{a n }是等比数列,且a 3a 5a 7a 9a 11=243,则a 7=________;若公比q =13,则a 4=________.答案 3 81解析 由{a n }是等比数列, 得a 3a 5a 7a 9a 11=a 57=243, 故a 7=3,a 4=a 7q3=81.9.(2022·徐州模拟)已知等差数列{a n }的公差为2,其前n 项和S n =pn 2+2n ,n ∈N *. (1)求实数p 的值及数列{a n }的通项公式;(2)在等比数列{b n }中,b 3=a 1,b 4=a 2+4,若{b n }的前n 项和为T n ,求证:数列⎩⎨⎧⎭⎬⎫T n +16为等比数列. (1)解 S n =na 1+n n -12d =na 1+n (n -1)=n 2+(a 1-1)n , 又S n =pn 2+2n ,n ∈N *, 所以p =1,a 1-1=2,即a 1=3, 所以a n =3+2(n -1)=2n +1.(2)证明 因为b 3=a 1=3,b 4=a 2+4=9, 所以q =3, 所以b n =b 3·q n -3=3n -2,所以b 1=13,所以T n =131-3n1-3=3n-16,所以T n +16=3n 6,又T 1+16=12,所以T n +16T n -1+16=3n 63n -16=3(n ≥2),所以数列⎩⎨⎧⎭⎬⎫T n +16是以12为首项,3为公比的等比数列.10.(2022·威海模拟)记数列{a n }的前n 项和为S n ,已知a 1=1,S n +1=4a n +1.设b n =a n +1-2a n .(1)求证:数列{b n }为等比数列;(2)设c n =|b n -100|,T n 为数列{c n }的前n 项和.求T 10. (1)证明 由S n +1=4a n +1, 得S n =4a n -1+1(n ≥2,n ∈N *), 两式相减得a n +1=4a n -4a n -1(n ≥2), 所以a n +1-2a n =2(a n -2a n -1), 所以b n b n -1=a n +1-2a na n -2a n -1=2a n -2a n -1a n -2a n -1=2(n ≥2),又a 1=1,S 2=4a 1+1, 故a 2=4,a 2-2a 1=2=b 1≠0,所以数列{b n }为首项与公比均为2的等比数列. (2)解 由(1)可得b n =2·2n -1=2n,所以c n =|2n-100|=⎩⎪⎨⎪⎧100-2n,n ≤6,2n-100,n >6,所以T 10=600-(21+22+…+26)+27+28+29+210-400 =200-21-261-2+27+28+29+210=200+2+28+29+210=1 994.11.(多选)(2022·滨州模拟)已知S n 是数列{a n }的前n 项和,且a 1=a 2=1,a n =a n -1+2a n -2(n ≥3),则下列结论正确的是( )A .数列{a n +1+a n }为等比数列B .数列{a n +1-2a n }为等比数列C .a n =2n +1+-1n3D .S 20=23(410-1)答案 ABD解析 因为a n =a n -1+2a n -2(n ≥3), 所以a n +a n -1=2a n -1+2a n -2=2(a n -1+a n -2), 又a 1+a 2=2≠0,所以{a n +a n +1}是等比数列,A 正确;同理a n -2a n -1=a n -1+2a n -2-2a n -1=-a n -1+2a n -2=-(a n -1-2a n -2),而a 2-2a 1=-1, 所以{a n +1-2a n }是等比数列,B 正确; 若a n =2n +1+-1n3,则a 2=23+-123=3,但a 2=1≠3,C 错误;由A 知{a n +a n -1}是等比数列,且公比为2,因此数列a 1+a 2,a 3+a 4,a 5+a 6,…仍然是等比数列,公比为4, 所以S 20=(a 1+a 2)+(a 3+a 4)+…+(a 19+a 20)=21-4101-4=23(410-1),D 正确. 12.(多选)(2022·黄冈模拟)设等比数列{a n }的公比为q ,其前n 项和为S n ,前n 项积为T n ,并且满足条件a 1>1,a 7·a 8>1,a 7-1a 8-1<0.则下列结论正确的是( ) A .0<q <1B .a 7·a 9>1C .S n 的最大值为S 9D .T n 的最大值为T 7答案 AD解析 ∵a 1>1,a 7·a 8>1,a 7-1a 8-1<0, ∴a 7>1,0<a 8<1, ∴0<q <1,故A 正确;a 7a 9=a 28<1,故B 错误;∵a 1>1,0<q <1,∴数列为各项为正的递减数列, ∴S n 无最大值,故C 错误; 又a 7>1,0<a 8<1,∴T 7是数列{T n }中的最大项,故D 正确.13.(2022·衡阳八中模拟)设T n 为正项等比数列{a n }(公比q ≠1)前n 项的积,若T 2015=T 2021,则log 3a 2019log 3a 2021=________.答案 15解析 由题意得,T 2015=T 2021=T 2015·a 2016a 2017a 2018a 2019a 2020a 2021, 所以a 2016a 2017a 2018a 2019a 2020a 2021=1, 根据等比数列的性质,可得a 2016a 2021=a 2017a 2020=a 2018a 2019=1, 设等比数列的公比为q ,所以a 2016a 2021=a 20212q 5=1⇒a 2021=52,qa 2018a 2019=a 20192q=1⇒a 2019=12,q所以log 3a 2019log 3a 2021=123523log 1.5log q q14.如图所示,正方形上连接着等腰直角三角形,等腰直角三角形腰上再连接正方形,……,如此继续下去得到一个树状图形,称为“勾股树”.若某勾股树含有1023个正方形,且其最大的正方形的边长为22,则其最小正方形的边长为________.答案132解析 由题意,得正方形的边长构成以22为首项,22为公比的等比数列,现已知共含有1023个正方形,则有1+2+…+2n -1=1023,所以n =10,所以最小正方形的边长为⎝⎛⎭⎪⎫2210=132.15.(多选)在数列{a n }中,n ∈N *,若a n +2-a n +1a n +1-a n=k (k 为常数),则称{a n }为“等差比数列”,下列关于“等差比数列”的判断正确的是( ) A .k 不可能为0B .等差数列一定是“等差比数列”C .等比数列一定是“等差比数列”D .“等差比数列”中可以有无数项为0 答案 AD解析 对于A ,k 不可能为0,正确;对于B ,当a n =1时,{a n }为等差数列,但不是“等差比数列”,错误;对于C ,当等比数列的公比q =1时,a n +1-a n =0,分式无意义,所以{a n }不是“等差比数列”,错误;对于D ,数列0,1,0,1,0,1,…,0,1是“等差比数列”,且有无数项为0,正确. 16.已知等比数列{a n }的公比q >1,a 1=2,且a 1,a 2,a 3-8成等差数列,数列{a n b n }的前n 项和为2n -1·3n+12.(1)分别求出数列{a n }和{b n }的通项公式;(2)设数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和为S n ,∀n ∈N *,S n ≤m 恒成立,求实数m 的最小值.解 (1)因为a 1=2,且a 1,a 2,a 3-8成等差数列, 所以2a 2=a 1+a 3-8,即2a 1q =a 1+a 1q 2-8,所以q 2-2q -3=0, 所以q =3或q =-1,又q >1,所以q =3, 所以a n =2·3n -1(n ∈N *).因为a 1b 1+a 2b 2+…+a n b n =2n -1·3n+12,所以a 1b 1+a 2b 2+…+a n -1b n -1=2n -3·3n -1+12(n ≥2),两式相减,得a n b n =2n ·3n -1(n ≥2),因为a n =2·3n -1,所以b n =n (n ≥2),当n =1时,由a 1b 1=2及a 1=2,得b 1=1(符合上式),所以b n =n (n ∈N *).(2)因为数列{a n }是首项为2,公比为3的等比数列,所以数列⎩⎨⎧⎭⎬⎫1a n 是首项为12,公比为13的等比数列,所以S n =12⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫13n 1-13=34⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫13n <34.因为∀n ∈N *,S n ≤m 恒成立, 所以m ≥34,即实数m 的最小值为34.。
【高考冲刺】2023年高考数学(理数) 等差数列与等比数列小题练(含答案解析)

【高考冲刺】2023年高考数学(理数) 等差数列与等比数列小题练(含答案解析)等差数列与等比数列是高中数学中非常重要的概念,也是考试中经常考察的内容。
掌握了等差数列和等比数列的性质和计算方法,可以帮助我们快速解决一些数学题目。
在高考冲刺阶段,我们要加强对等差数列与等比数列的掌握,让自己能够熟练灵活地应用这些知识,提高解题效率。
下面,我将结合一些常见的小题,通过题目的解答和思路分析,帮助大家更好地理解等差数列与等比数列的相关知识。
一、等差数列的基本概念及性质1. 基本概念:等差数列是指一个数列中任意两个相邻的数之差都相等的数列。
我们通常用字母a表示首项,字母d表示公差。
等差数列的通项公式为:an=a1+(n-1)d。
2. 性质:(1)公差d的求法:对于等差数列an,若已知前两项a1和a2,则公差可通过d=a2-a1求得。
(2)前n项和Sn的求法:等差数列的前n项和Sn可以通过以下公式求得:Sn=n/2(a1+an)。
二、等差数列的计算方法1. 求第n项:根据等差数列的通项公式an=a1+(n-1)d,我们可以直接求得等差数列的第n项。
【例题1】已知等差数列的首项a1=3,公差d=5,请求其第7项。
解:根据等差数列的通项公式,我们可以直接计算出第7项:a7=a1+(7-1)d=3+6*5=33因此,等差数列的第7项为33。
2. 求前n项和:根据等差数列的前n项和公式Sn=n/2(a1+an),我们可以求得等差数列的前n项和。
【例题2】已知等差数列的首项a1=2,公差d=3,请求其前5项和。
解:根据等差数列的前n项和公式,我们计算前5项和:S5=5/2(a1+a5)=5/2(2+2+4*3)=5/2(2+14)=5/2*16=40因此,等差数列的前5项和为40。
三、等差数列与等差数列的应用1. 题型1:已知等差数列的前n项和Sn和公差d,求首项a1和末项an。
【例题3】已知等差数列的前6项和S6=78,公差d=4,请求该等差数列的首项a1和末项a6。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2023高考数学复习专项训练《等比数列》一、单选题(本大题共12小题,共60分)1.(5分)等比数列{a n}满足a1+a2+a3=13,a2+a3+a4=133,则a5=()A. 1B. 13C. 427D. 192.(5分)给出以下命题:①存在两个不等实数α,β,使得等式sin(α+β)=sinα+sinβ成立;②若数列{a n}是等差数列,且a m+a n=a s+a t(m、n、s、t∈N∗),则m+n=s+t;③若S n是等比数列{a n}的前n项和,则S6,S12−S6,S18−S12成等比数列;④若S n是等比数列{a n}的前n项和,且S n=Aq n+B;(其中A、B是非零常数,n∈N∗),则A+B为零;⑤已知ΔABC的三个内角A,B,C所对的边分别为a,b,c,若a2+b2>c2,则ΔABC一定是锐角三角形.其中正确的命题的个数是()A. 1个B. 2个C. 3个D. 4个3.(5分)设T n为等比数列{a n}的前n项之积,且a1=−6,a4=−34,则当T n最大时,n的值为()A. 4B. 6C. 8D. 104.(5分)等比数列{a n},满足a1+a2+a3+a4+a5=3,a12+a22+a32+a42+a52= 15,则a1−a2+a3−a4+a5的值是()A. 3B. √5C. −√5D. 55.(5分)已知在等比数列{a n}中,公比q是整数,a1+a4=18,a2+a3=12,则此数列的前8项和为()A. 514B. 513C. 512D. 5106.(5分)已知正项数列{a n},{b n}分别为等差、等比数列,公差、公比分别为d,q(d,q∈N∗),且d=q,a1+b1=1,a3+b3=3.若a n+b n=2013(n>3),则n= ()A. 2013B. 2012C. 100D. 997.(5分)若a,b,c成等比数列,则关于x的方程a x2+bx+c=0( )A. 必有两个不等实根B. 必有两个相等实根C. 必无实根D. 以上三种情况均有可能8.(5分)公比为2的等比数列{a n}的各项都是正数,且a3a11=16,则log2a10=()9.(5分)记Sn为等比数列{a n}的前n项和,已知S2=2,S3=−6.则{a n}的通项公式为()A. a n=(−2)nB. a n=−2nC. a n=(−3)nD. a n=−3n10.(5分)正项等比数列{a n}中,a3=2,a4.a6=64,则a5+a6a1+a2的值是()A. 4B. 8C. 16D. 6411.(5分)在等比数列{a n}中,a7,a11是方程x2+5x+2=0的二根,则a3.a9.a15a5.a13的值为()A. −2+√22B. −√2C. √2D. −√2或√212.(5分)已知等比数列{a n}的前n项和为S n,9S3=S6=63,则S10=A. 255B. 511C.1023 D. 2047二、填空题(本大题共5小题,共25分)13.(5分)已知等差数列{a n}的公差d≠0,且a3+a9=a10−a8.若a n=0,则n=__________14.(5分)若等比数列{an}的前n项和Sn满足:an+1=a1Sn+1(n∈N*),则a1=____.15.(5分)在等比数列{an}中,已知前n项和Sn=5n+1+a,则a的值为____________.16.(5分)若等比数列{a n}的首项为23,且a4=∫41(1+2x)dx,则公比q等于______.17.(5分)如图所示,将正整数排成三角形数阵,每排的数称为一个群,从上到下顺次为第1群,第2群,……,第n群,……,第n群恰好有n个数,则第n群中n个数的和是____________.123465812107162420149324840281811…三、解答题(本大题共6小题,共72分)18.(12分)已知{x n}是各项均为正数的等比数列,且x1+x2=3,x3−x2=2.(1)求数列{x n}的通项公式;(2)如图,在平面直角坐标系xOy中,依次连接点P1(x1,1),P2(x2,2),…,P n+1(x n+1,n+1)得到折线P1P2…P n+1,求由该折线与直线y=0,x=x1,x=x n+1所围成的区域的面积T n.19.(12分)如果等比数列{a n}中公比q>1,那么{a n}一定是递增数列吗?为什么?20.(12分)数列{a n}满足a1=1,a n=2a n−1-3n+6(n≥2,n∈N+).(1)设b n=a n-3n,求证:数列{b n}是等比数列;(2)求数列{a n}的通项公式.21.(12分)设各项均为正数的数列{a n}的前n项和为S n,满足4S n=a n+12−4n−1,n∈N∗,且a2,a5,a14构成等比数列.(1)证明:a2=√4a1+5;(2)求数列{a n}的通项公式;(3)证明:对一切正整数n,有1a1a2+1a2a3+…+1a n a n+1<12.22.(12分)已知数列{a n}是等差数列,其首项为2,且公差为2,若b n=2a n(n∈N∗).(Ⅰ)求证:数列{b n}是等比数列;(Ⅱ)设c n=a n+b n,求数列{c n right}的前n项和A n.23.(12分)已知等差数列{a n}和等比数列{b n}满足a1=b1=1,a2+a4=10,b2b4=a5.(Ⅰ)求{a n}的通项公式;(Ⅱ)求和:b1+b3+b5+⋯+b2n−1.四、多选题(本大题共5小题,共25分)24.(5分)已知等差数列{a n}的公差和首项都不等于0,且a2,a4,a8成等比数列,则下列说法正确的是()A. a1+a5+a9a2+a3的值为3 B. a1+a5+a9a2+a3的值为2C. 数列{a n}的公差和首项相等D. 数列{a n}的公差和首项不相等25.(5分)设数列{a n},{b n}的前n项和分别为S n,T n,则下列命题正确的是()A. 若a n+1-a n=2(n∈N∗),则数列{a n}为等差数列B. 若b n+1=2b n(n∈N∗),则数列{b n}为等比数列C. 若数列{a n}是等差数列,则S n,S2n-S n,S3n-S2n⋯⋯(n∈N∗)成等差数列D. 若数列{b n}是等比数列,则T n,T2n-T n,T3n-T2n⋯⋯(n∈N∗)成等比数列26.(5分)在公比q为整数的等比数列{a n}中,S n是数列{a n}的前n项,若a1+a4= 18,a2+a3=12,则下列说法正确的是()A. q=2B. 数列{S n+2}是等比数列C. S8=510D. 数列\left{ lg a n}是公差为2的等差数列27.(5分)已知等差数列{a n}的首项为1,公差d=4,前n项和为S n,则下列结论成立的有()A. 数列{S nn}的前10项和为100B. 若a1,a3,a m成等比数列,则m=21C. 若∑n i=11a i a i+1>625,则n的最小值为6D. 若a m+a n=a2+a10,则1m +16n的最小值为251228.(5分)已知数列{a n}为等差数列,{b n}为等比数列,{a n}的前n项和为S n,若a1+ a6+a11=3π,b1b5b9=8,则()A. S11=11πB. sin a2+a10b4b6=12C. a3+a7+a8=3πD. b3+b7⩾4答案和解析1.【答案】D;【解析】解:设等比数列{a n }的公比为q ,由a 2+a 3+a 4=(a 1+a 2+a 3)q ,得133=13q ,解得q =13, 又a 1+a 2+a 3=a 1+13a 1+19a 1=139a 1=13,解得a 1=9,所以a 5=a 1q 4=9×(13)4=19, 故选:D.设等比数列{a n }的公比为q ,通过a 2+a 3+a 4=(a 1+a 2+a 3)q 可求出q 值,进一步根据a 1+a 2+a 3=a 1+a 1q +a 1q 2=13可求出a 1,最后利用a 5=a 1q 4进行求解即可. 此题主要考查等比数列的通项公式,考查学生逻辑推理和运算求解的能力,属于基础题.2.【答案】B; 【解析】该题考查命题真假的判断,考查学生灵活运用等差、等比数列的性质,三角函数以及三角形的判断,是一道综合题,属于中档题.利用特殊值判断①的正误;利用特殊数列即可推出命题②的正误;根据等比数列的性质,判断③的正误;根据等比数列的前n 项的和推出A ,B 判断④的正误.利用特殊三角形判断⑤的正误;解:对于①,实数α=0,β≠0,则sin (α+β)=sinβ,sinα+sinβ=sinβ,所以等式成立;故①正确;对于②,当公差d =0时,命题显然不正确,例如a 1+a 2=a 3+a 4,1+2≠3+4,故②不正确;对于③,设a n =(−1)n ,则S 6=0,S 12−S 6=0,S 18−S 12=0,∴此数列不是等比数列,故③不正确;对于④,S n 是等比数列{a n }的前n 项和,且S n =Aq n +B ;(其中A 、B 是非零常数,n ∈N ∗),所以此数列为首项是a 1,公比为q ≠1的等比数列, 则S n =a 1(1−q n )1−q ,所以A =−a11−q ,B =a11−q ,∴A +B =0,故④正确;对于⑤,如果三角形是直角三角形,a =5,b =3,c =4,满足a 2+b 2>c 2,故⑤不正确;故选:B .3.【答案】A;【解析】解:因为等比数列{a n }中,a 1=−6,a 4=−34,则由a 4=a 1q 3可得q =12. ∵T n 为等比数列{a n }的前n 项之积,∴T n =(−6)n .(12)n(n−1)2,因为求最大值,故只需考虑n 为偶数的情况, ∵T 2n +2T 2n =36×(12)4n +1,由T 2n +2T 2n⩾1可得n =1,∴T 2<T 4>T 6>T 8>⋯.则公比q =12,当T n 最大时,n 的值为4.故选:A .由已知可得q =12.只需考虑n 为偶数的情况,由T 2n +2T 2n⩾1可得n =1,即可求解.该题考查了等比数列的通项公式及其前n 项和公式,考查了推理能力与计算能力,属于中档题.4.【答案】D;【解析】解:设数列{a n }的公比为q ,且q ≠1,则 a 1+a 2+a 3+a 4+a 5=a 1(1−q 5)1−q =3①, a 12+a 22+a 32+a 42+a 52=a 12(1−q 10)1−q 2=15②∴②÷①得a 12(1−q 10)1−q 2÷a 1(1−q 5)1−q=a 1(1+q 5)1+q=5,∴a 1−a 2+a 3−a 4+a 5=a 1(1+q 5)1+q=5.故选:D.先设等比数列{a n }公比为q ,分别用a 1和q 表示出a 12+a 22+a 32+a 42+a 52,a 1+a 2+a 3+a 4+a 5和a 1−a 2+a 3−a 4+a 5,发现a 12+a 22+a 32+a 42+a 52除以a 1+a 2+a 3+a 4+a 5正好与a 1−a 2+a 3−a 4+a 5相等,进而得到答案.此题主要考查了等比数列的性质.属基础题.解题时要认真审题,注意等比数列的性质的灵活运用.5.【答案】D;【解析】由已知得{a 1+a 1q 3=18a 1q +a 1q 2=12,解得:q =2或q =12.∵q 为整数,∴q =2.∴a 1=2.∴S 8=2(1−28)1−2=29−2=510.6.【答案】A;【解析】此题主要考查等差数列和等比数列的通项公式和性质的应用.计算时要认真仔细.解:∵{_1+b1=1a3+b3=3,∴{_1+b1=1a1+2d+b1q2=3,∵d=q,所以{_1+b1=1a1+2q+b1q2=3,解得d=q=1,∴a n+b n=a1+(n−1)d+b1q n−1=a1+n−1+b1=2013,∴n=2013.故选A.7.【答案】C;【解析】若a,b,c成等比数列,则b²=ac由题意得△=b²-4ac=b²-4b²=-3b²等比数列中没有为0的项,∴-3b²<0∴△小于0,即方程a x2+bx+c=0必无实根故选C。
