信号分析与处理_习题答案

∫
t −∞
x(τ )dτ
（3） y (t ) = x 2 (2t ) （5） y (t ) = x(t ) ，其中 x(t ) 为实信号 解： （1） y (t ) = x(t − 2) + x(2 − t )
（4） y ( = t ) x (1 − t )ε (t ) （6） y (t ) = x(t ) cos(t )
t 有可能小于 1 − t ，非因果系统。
（5） y (t ) = x(t ) ，其中 x(t ) 为实信号。
T ax1 ( t ) + bx2 ( t ) = ax1 ( t ) + bx2 ( t ) ≠ ay1 ( t ) + by2 ( t ) ，非线性系统。 T x ( t − t0 ) = x ( t − t0 ) = y ( t − t0 ) ，时不变系统。
= W =
∞
e sin (ωt ) e ( t ) dt ∫ ∫=
-∞
∞
∞ 2 -at 2 at 0
e
1 - cos ( 2ωt ) dt 2
∞ 1 ∞ -e 2 at dt - ∫ e 2 at cos ( 2ωt ) dt ∫ 0 0 2
= e dt ∫
−2 at 0
−1 −2 at ∞ 1 = e 0 2a 2a
− at
sin(ωt ) ε (t )
（2） cos(10t ) + cos(30t )
（3） cos(2t ) + sin(π t )
（4） 5sin (8t )
2
（5） ε (t ) − ε (t − 10)
（6） x ( n ) = 2
1 n n≥0 ( ) n<0 0
解:（1）只在大于零的时间段内有信号，非周期信号；判断能量值 若 a > 0 则为指数衰减信号为能量信号。
t 有可能小于 2t ，非因果系统。 （4） y (t ) = x(1 − t )ε (t )
T ax1 ( t ) + bx2 ( t )= aT x1 ( t ) + bT x2 ( t ) ，线性系统。 T x ( t − t0 ) = x(1 − t − t0 )ε (t ) ≠ y (t − t0 ) ，时变系统。
（4） y[n] = e x[ n ]
n] T { x1[n] + x2 [n= ]} e x1 [ n ]+ x2 [= e x1 [ n ]e x2 [ n ] ≠ y1[n] + y2 [n] ，非线性系统。
p = lim
def
1 75 75 p1 = lim = T →∞ T T →∞ 8 8
<∞
功率信号
（5）能量信号，非周期信号；
1 n ( ) n ≥ 0 （6） x ( n ) = 2 n<0 0
指数衰减信号则为能量信号，非周期信号
∞ 1 4 1 1 W ∑ = = = ∑ = 1 3 2 n 0= n 0 4 = 1− 4 ∞ 2n n
1 ∞ −2 at 2 jωt 1 ∞ −2( a − jω )t −2( a + jω )t t e ( e + e −2 jω= dt e +e dt ) ∫ 0 2 0 2 ∫0 1 1 1 −2 a − jω t ∞ −2 a + jω t ∞ e ( ) 0 + e ( ) 0 a 2 −2 ( a − jω ) −2 ( a + jω ) −1 2a a = = −1) 2 2 ( 4 a +ω 2 ( a2 + ω 2 )
y (t ) 只与当前时刻的输入有关，故为因果系统。
（6） y (t ) = x(t ) cos(t )
T ay1 ( t ) + by2 ( t ) ，线性系统。 ax1 ( t ) + bx2 ( t ) = ax1 ( t ) + bx2 ( t ) cos ( t ) =
余弦信号在一个周期内积分为零。
T 2 T − 2
p = lim
def
T →∞
1 p1 = lim 1 = 1 T →∞ T
2
<∞
功率信号
5 4.5 4 3.5 3 2.5 2 1.5 1
（3）功率信号，非周期信号； （4） 5sin (8t )
5 π 周期信号 T = 5sin 2 (8 = t) 1 − cos (16t ) 2 8
T x ( t − t0 ) = x ( t − t0 ) cos ( t ) ≠ y ( t − t0 ) ，时变系统。
因果系统。 1.7 判定下列离散系统是否为线性的，时不变的？ （1） y ( n ) = x ( n ) + 2 x ( n − 1) （3） y ( = n ) n[ x ( n ) − x ( −n )] 解： （1） y[n] = x[n] + 2 x[n − 1] （2） = y (n)
x(t) 4 2 o
4 2 -1 o1 2 3 t
4 2 o1 2 3 4 t
4 2 -1 o 1 2 t
-2
2
t
题 .3 图
2
4 2 o 2 4 6 8 t
-2 -2 -4
o
1.4 给定序列
2 n + 1 −3 ≤ n ≤ −1 x(n) 1 0≤n≤3 = 0 其它n
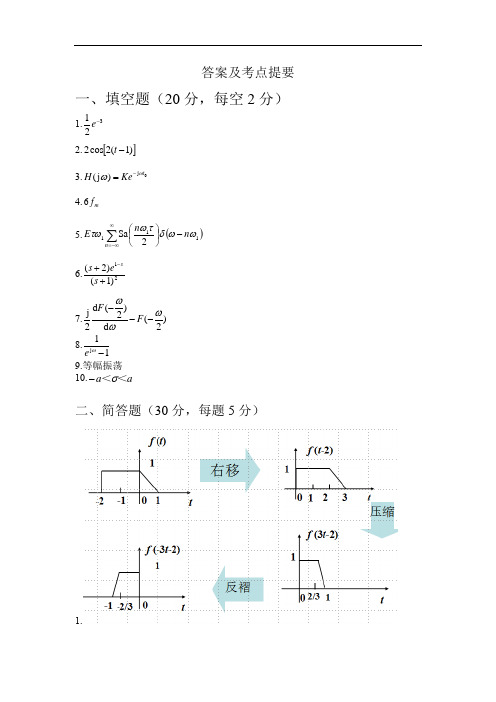
（2）画出 2 x (2 − n ) 的波形； （3）画出 2 x (2 − n ) x ( n ) 的波形。 （1）画出 x ( n ) 的波形； 解：
有限幅值的周期信号——功率信号
0.5 0
p1 = ∫ =
T 2 T − 2 T
25 x(t ) dt = 4 ∫
2
T 2 T − 2
[1 − 2 cos(16t ) + cos
0
2
(16t ) dt
]
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
25 3 75 cos(32t ) + 1 25 2 dt = T T= T 1 − 2 cos(16t ) + ∫ 2 4 2 8 4 −2
1.3 已知信号 x (t ) 的波形如题 1.3 所示，试画出下列各信号的波形。 （1） x (t − 1)ε (t ) ； （4） x ( t − 2) ； （2） x (2 − t ) ； （5） （3） x (1 − 2t ) ； （6）
1 2
dx (t ) ； dt
∫
t
−∞
x (x )d x
，线性系统。
T { x[n − n0 ]} = x[n − n0 ] + 2 x[n − n0 − 1]= y[n − n0 ] ，时不变系统。
因果系统。 （2） y[n] =
m =0
∑ x[n − m]
10
线性，时不变，因果系统。 （3） y[n] = n{x[n] − x[−n]}
T {ax1[n] + bx= n {ax1[n] + bx2 [n] − ax1[−n] − bx2 [−n]} 2 [ n]} = a { x1[n] − x1[−n]} + b { x2 [n] − x2 [−n]} = ay1[n] + by2 [n]
d
−∞
∫ 10
8 6 4
t
ξ (ξ)dξ
2
t
2
−2
o
2
t
2 n -2
O
1 O -1 -3 -5 n
题 1.4 图 1
2 n -2
O -2
题 1.4 图 3 1.5 信号 x(t ) 的波形如题 1.5 所示。
（1）画出 y (t ) =
dx(t ) 的波形； （2）画出 y (t ) = dt
∫
t
m =0
∑ x(n − m)
x(n)
10
（4） y ( n ) = e
T {ax1[n] + bx2 [n = ]} ax1[n] + bx2 [n] + 2 {ax1[n − 1] + bx2 [n − 1]} = a { x1[n] + 2 x1[n − 1]} + b { x2 [n] + 2 x2 [n − 1]} = ay1[n] + by2 [n]
，线性系统。
T x ( t − t0 ) = x(t − t0 − 2) + x(2 − t − t0 ) ≠ y (t − t0 ) ，时变系统。
t 有可能小于 2 − t ，故为非因果系统。
（2） y (t ) =
∫
t −∞
x(τ )dτ
T ax1 ( t ) + bx2 ( t )= aT x1 ( t ) + bT x2 ( t ) ，线性系统。
设 y (t ) = T x ( t )
T = ax1 (t − 2) + bx2 (t − 2) + ax1 (2 − t ) + bx2 (2 − t ) ax1 ( t ) + bx2 ( t ) = ay1 ( t ) + by2 ( t )
= a [ x1 (t − 2) + x1 (2 − t ) ] + b [ x2 (t − 2) + x2 (2 − t ) ]
−∞
x (x )dx 的波形。
1
x(t) 2 1 -1 1 t