重邮大学物理英文版PPT (5)
r r Φ e = ∫ E ⋅ dS
S
=
1
ε0
∑Q
i
=
1
ε0
∫ dQ
2012-3-31
16
Φe =
∫
S
r r E ⋅ dS
=
1
ε0
∑
Qi
=
1
ε0
∫ dQ
∫
S
S： The closed surface, i.e. gaussian surface. It is an imaginary surface and need not coincide with any real physical surface. r r E ⋅ dS The close surface integral is over all gaussian surface.
S2
+
2012-3-31
21
There are many charges inside the guassian surface.
q3
q1
+ +
S
+
q2
+
2012-3-31
22
A point charge located outside a closed surface. The number of lines entering the surface equals the number leaving the surface.
2. Electric Flux Φe Ring Amount
Flux Amount
∫
L
r r A • d lr
∆S i
r Ei
v v A ⋅ ds ∫∫
r dS
r E
S
S
8
2012-3-31
S
rr nE
1. Uniform electric field
r r E ↑↑ n
Φe = ES
S
r n r E
If the surfaces is closed,
r r E ⋅dA
If the surface is unclosed, the positive normal direction can be free chosen.
φ is a scalar. Its SI unit: N·m2/C.
Example
2012-3-31 11
n
n
⊕
Φ =0
Φ >0
Φ <0
2012-3-31
12
Attention
φ = ∫∫ S r According to the convention, dA > 0, outward the r closed surface; dA < 0,inward the closed surface.
§2. 3 ELECTRIC FLUX , GAUSS’S LAW
1. Electric Field Lines A convenient specialized pictorial representation for visualizing electric field patterns is created by drawing lines which are called electric field lines. The electric field lines are related to the electric field in any region of space in the following manner:
r E is the total electric field at any point on the surface due to all
charges.
v ds
Surface element. Its orientation is perpendicular to the surface and points outward from the inside region.
2012-3-31
2
+
+
∞
+
−
∞
−
For a positive point charge, the lines are directed radially outward. For a negative point charge, the lines are directed radially inward.
2012-3-31
1
(1) The tangent direction at every point on an electric field line is just the direction of the field intensity at that point or the direction of the force on the positive point charge at that point. (2) The electric field lines are denser in the place where the field intensity is stronger, and the electric field lines are sparser in the place where the field intensity is weaker. (3) The electric field lines start on positive charges and terminate on negative charges , and never intersected each other. It is never interrupted in region without charge; this is called the continuity of electric field line. (4) Keep in mind: electric field lines do not actually exist.
UNIT：Vm ：
r r Φ e = ∫∫ E ⋅ dS＝∫∫ E cos θds
Where
r v Eds = θ
〈 〈 〈 〈
2012-3-31
10
A closed surface is defined as one that completely divides space into an inside region and outside region, so that movement cannot take place from one region to the other without penetrating the surface. For a closed surface, usually define the normal line at every point on the surface points out of the closed surface A closed surface A open surface
The electric field lines for two positive point charges.
+
+
The electric field lines for a point charge +2q and a second point charge –q.
2q
+
q
++ ++ + + + + +
2012-3-31
3
The electric field lines for two charges of equal magnitude and opposite sign (an electric dipole)
+
NOTE: the number of lines leaving the positive charge equals the number terminating at the negative charge.
There is a cube surface of edge length a in the uniform r r r electric field E = E 0 ( i + j )（ E 0 is a constant）as shown ） in figure. Find the electric flux of every plane and the cube surface. Z
= 1
q
ε0
A system of charges
Φe =
∫
S
r r E ⋅ dS
ε0
∑
Qi
=
1
ε0
∫ dQ
Continuous distribution of charges
2012-3-31
18
(2) Proving A spherical gaussian surface of radius r surrounding a point charge q which is at the centre of the sphere. The electric field is normal to the surface and constant in magnitude everywhere on the surface.
2 .Uniform electric field
θ
rr En =θ r r Φe = ES cosθ = E ⋅ S
3. Nonuniform electric field, arbitrary r surface r 〈 〈 〈 〈
合集下载
大学物理课件英文版课件,现代物理An Aperitif of Modern Physics
3
§26.1 Some important discoveries at the end of the 20th century
2. The discovery of X-rays
§26.1 Some important discoveries at the end of the 20th century
J. J. Thomson’s original tube
2
§26.1 Some important discoveries at the end of the 20th century
a. Measured the charge of the cathode rays; b. Make a static electric deflection of the cathode rays; c. Measured the charge to mass ratio of the cathode rays; d. Prove the universal existence of the electron. The charge to mass ratio of electron
Radioactivity occur naturally and have with us on the earth from the very beginning. Henri Becquerel discovered Uranium, Marie Curie discovered Polonium and Radium Ernest Rutherford found that the substances emit several distinct types of radiations. One is a penetrating radiation, dubbed α, that propagates through several centimeters in air and can even penetrate very thin metal foils. Another less penetrating radiation, dubbed β, is easily stopped by even a sheet of paper. Another type, called γ, was discovered in 1900 and is much more penetrating than even the α radiation.
英文版大学物理 第五章
m r
2
i i
K 1 I 2 2
5-3. Calculating the Rotational Inertia If a rigid body consists of a few particles
If a rigid body consists of a great many of particles(it is continuous) Linear distribution: Surface distribution: Volume distribution:
The unit of angular acceleration is commonly the radian per second-squared (rad/s2) or the revolution per second-squared (rev/s2).
Are Angular Quantities Vectors?
(radian measure)
Equation of motion for a rotating body: = (t)
2. Angular Displacement When the body rotates about the rotation axis from 1 to 2, the body undergoes an angular displacement y 2 1 Reference At t2 line An angular displacement in the counterclockwise direction is positive, in the clockwise direction is negative. At t1 1 2 x 3. Angular Velocity O Rotation axis Average angular velocity The angular velocity is either 2 1 avg positive or negative, depending t2 t1 t on whether the body is rotating Angular velocity counterclockwise (positive) or d lim clockwise (negative). t 0 t dt
大学物理 Lecture5 W&KE&PE
aL
b aL
F1 dr
F2 dr
b aL
Fn dr W1 W2 Wn
a. Find the vector sum of the forces and integrate it over the displacement, or b. Find the work done by each individual force and add them.
Chapter 5 Work, Kinetic Energy , Potential Energy and Conservation of Energy
Main Points of Chapter 5
• Kinetic energy and the work-energy theorem • Conservative and nonconservative forces • Potential energy
(b), (a), (c), (d)
Work done by variable force in 3-D
• Work dWF of a force F acting
z
a M
F θ
r
through an infinitesimal displacementdr is:
dWF F dr
Scalar product
Work done by a constant force F
W F r • Only the component of F along the displacement is doing work. The force component perpendicular to the displacement does zero work
b aL
F1 dr
F2 dr
b aL
Fn dr W1 W2 Wn
a. Find the vector sum of the forces and integrate it over the displacement, or b. Find the work done by each individual force and add them.
Chapter 5 Work, Kinetic Energy , Potential Energy and Conservation of Energy
Main Points of Chapter 5
• Kinetic energy and the work-energy theorem • Conservative and nonconservative forces • Potential energy
(b), (a), (c), (d)
Work done by variable force in 3-D
• Work dWF of a force F acting
z
a M
F θ
r
through an infinitesimal displacementdr is:
dWF F dr
Scalar product
Work done by a constant force F
W F r • Only the component of F along the displacement is doing work. The force component perpendicular to the displacement does zero work
英文版大学物理 第五章
Example 5-2 Show that the rotational inertia of a uniform annular cylinder (or ring) of inner radius R1, outer radius R2, and mass M, is I 1 M( R12 R22 ) , 2 as stated in Table 5-1b, if the rotation axis is through the center along the axis of symmetry. Divide the cylinder into thin concentric Solution： cylindrical rings or hoops of thickness dr, each with mass R1 r dm dV dr is the mass density of the body. or
1 2 2 1 1 1 2 2 2 2
2 i i
o
ri
mi
vi
mi is the mass of the ith particle and vi is its speed.
K 1 mi vi2 1 ( mi ri2 ) 2 2 2
rotational inertia (or moment of inertia) I Kinetic Energy of Rotation
z
Rotation axis
y Body Reference line y
r s
O
Rotation axis
x
O
x
Zero angular position
1. Angular Position A reference line fixed in the body, perpendicular to the rotation axis, and rotating with the body. The angular position of reference line describes the angular position of the body:
L11_Chap5英文版原子物理课件
(2.55)
A single electron has s= 1/2 so, for each l, its total angular momentum quantum number j has two possible values:
j = l + 1/ 2
or
l 1/ 2
From eqn2.54 we find that the energy interval between these levels,
2 s +1
LJ for the LS-coupling scheme is often used even for systems in the
intermediate regime and also for one - electron systems e.g.is 1s 1S1/ 2 for the ground state of hydrogen.
Shanxi University Atomic Physics
5.3 Intermediate coupling: the transition between coupling schemes-7
The table gives the values of J and the energy, in units of m-1 measured from the ground state, for the levels of the ls2p configuration in helium. The 3P term has a fine-structure splitting of about 100 m-1 that is much smaller than the singlet-triplet separation of 10-6 m-1 from the electrostatic interaction (twice the exchange integral). Thus the LS - coupling scheme gives an excellent description of the helium atom and the selection rules in Table 5.1 are well obeyed. But the interval rule is not obeyed -the intervals between the J levels are 7 m-1 and 99 m-1 and the fine structure is inverted. This occurs in helium because spin-spin and spin-other-orbit interactions have energy comparable with that of the spin-orbit interaction. However, for atoms other than helium, the rapid increase in the strength of the spin-orbit interaction with Z ensures that H s o dominates over the others. Therefore the fine structure of atoms in the LS-coupling scheme usually leads to an interval rule.
PhysicsChpt5物理双语课件
5.2 Calculate force
A tennis ball contacts the racquet for much less than one second. High-speed photographs show that the speed of the ball changes from -30 to +30 m/sec in 0.006 seconds. If the mass of the ball is 0.2 kg, how much force is applied by the racquet?
A static problem usually means there is no motion.
5.2 Calculate force
A woman is holding two dogs on a leash. If each dog pulls with a force of 80 newtons, how much force does the woman have to exert to keep the dogs from moving?
Three people are each applying 250 newtons of force to try to move a heavy cart. The people are standing on a rug. Someone nearby notices that the rug is slipping. How much force must be applied to the rug to keep it from slipping?
dynamic equilibrium
重邮大学物理英文版-(4)PPT课件
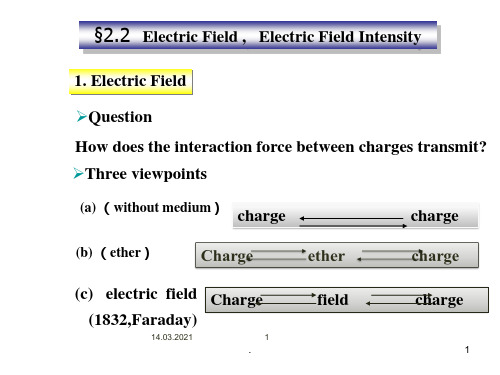
➢Coulomb’s force is really electrostatic field force.
.
3
14.03.2021
3
What force will a positive “test” charge feel if placed into the electric field?
+
.
4
10
4. Calculation
(1). EDue to the System of Point Charges (The
charges are countable ).
FF 1F 2F 3
Q2
E
F
Q0
F1
Q0
F2
Q0
F3
Q0
E1E2E3
QQ 1
rrF12
Q0
F1
Q3 F3
.
6
14.03.2021
6
2. Definition
➢At a point in the given electrostatic field the ratio of the electric field force F on the test point charge q 0 with its electric quantity
E
E
2 x
E
2 y
E
2 z
,
cos E x , cos E y , cos Ez .
E
E
E
.
9
14.03.2021
9
3. Superposition Principle of Electrostatic Field
F F1 F2 F3 Fn
.
3
14.03.2021
3
What force will a positive “test” charge feel if placed into the electric field?
+
.
4
10
4. Calculation
(1). EDue to the System of Point Charges (The
charges are countable ).
FF 1F 2F 3
Q2
E
F
Q0
F1
Q0
F2
Q0
F3
Q0
E1E2E3
QQ 1
rrF12
Q0
F1
Q3 F3
.
6
14.03.2021
6
2. Definition
➢At a point in the given electrostatic field the ratio of the electric field force F on the test point charge q 0 with its electric quantity
E
E
2 x
E
2 y
E
2 z
,
cos E x , cos E y , cos Ez .
E
E
E
.
9
14.03.2021
9
3. Superposition Principle of Electrostatic Field
F F1 F2 F3 Fn
重邮大学物理英文版 (5)ppt课件
➢(3) The electric field lines start on positive charges and terminate on negative charges , and never intersected each other. It is never interrupted in region without charge; this is called the continuity of electric field line. ➢(4) Keep in mind: electric field lines do not actually exist.
➢The electric field lines are related to the electric field in any region of space in the following manner:
08.04.2020
1
➢(1) The tangent direction at every point on an electric field line is just the direction of the field intensity at that point or the direction of the force on the positive point charge at that point.
If the surface is unclosed, the positive normal direction can be free chosen.
is a scalar. Its SI unit: N·m2/C.
Example
There is a cube surface of edge length a in the uniform
➢The electric field lines are related to the electric field in any region of space in the following manner:
08.04.2020
1
➢(1) The tangent direction at every point on an electric field line is just the direction of the field intensity at that point or the direction of the force on the positive point charge at that point.
If the surface is unclosed, the positive normal direction can be free chosen.
is a scalar. Its SI unit: N·m2/C.
Example
There is a cube surface of edge length a in the uniform
物理英文版
Beijing University of Posts and TelecommunicationsUniversity PhysicsDepartment of Physics School of Science2006Professor XiaoguangZhangReference BooksPhysics for Scientists and Engineers with Modern Physics: D. C. Giancoli. (高等教育出版社)Sears and Zemansky’s University Physics: 西尔斯物理学，Young & Freedman, (机械工业出版社)《大学物理学》(五本)，张三慧，(清华大学出版社)《大学物理学》(三本)，吴百诗主编，(高等教育出版社) 习题指导书——《吴百诗大学物理学习题分析与解答》，李存志等，(高等教育出版社)。
Chapter 1 Introduction and VectorsImportant contentsSignificant figures （有效数字）.¾How to denote the significant figures for a number?¾Scientific notation.¾How to treat the number of significant figures when multiplying or dividing, and adding or subtracting.SI unit system （单位制）.¾Base units & derived units; 7 base units for SI unit system.¾The standards of Length, Time, and Mass.¾Unit prefixes.Dimensions and Dimensional analysis （量纲与量纲分析）.¾Check an equation by dimensional consistency.Order-of-magnitude.§1 Measurements, Estimating (Self taught)The transmission speed for optical fiber telecommunicationsAmerican standard: SONET (synchronous optical network).International standard: SDH (synchronous digital hierarchy).bit rate for OC-768 (STM-256)=39.813 Gbit/s ≈40Gbit/s, the bit period T B ≈25 ps20.0 ps/div40 Gbit/s RZ code50.0 ps/div10 Gbit/s RZ codeThe screens of an oscilloscopeAn older unit of length used for atomic scale: angstrom (A)In Bohr theory of hydrogen, the orbits of the electron around the proton are quantized: r n =n 2a 0The smallest radius a 0is called the Bohr Radius .。
大学物理英文版PPT
4.Units 单位
International System of Units SI: Syst me International d’Unit s 法语 is used in China
mass
m
kg:千克 kilogram
length
L m:米 meter
Time
t s:秒 second
5. Scalar and vector 标量和矢量 : Two types of physical quantities 量 :
主要讲授内容：
经典力学 相对论
电磁学
振动与波动 日常生活
波动光学
热学
量子论简介
puter 计算机科学
Medicine 医学
Physics
Chemistry 化学
Mechanics 机械学
Biology 生物学
Physics: fundamentals and methods.
References 参考书
主要贡献： •发明了望远镜,维护、坚持和发展了哥白尼学说, 发现木星的四个卫星； •摆的等时性、惯性定律、落体运动定律； •运动的合成原理和独立性原理,相对性原理； •方法：实验科学。
§1-1 Frame of Reference Particle 质点
1. Frame of Reference 参照系
C=A+B B
A
B C
A
In Cartesi an coordinate system 直角坐标系 :
A A xiA yjA zk
i,jankd are unit vectors along OX,OY,OZ Y
O
X
Z