C A R T 分 类 与 回 归 树
8.2一元线性回归模型参数的最小二乘估计(第二课时)课件-人教A版选择性必修第三册

式,其图形称为经验回归直线. 这种求经验回归方程的方法叫做最小二乘法.
2. 什么是最小二乘估计?
经验回归方程中的参数计算公式为:
n
( xi x )( yi y )
bˆ i 1 n
2
(
x
x
)
i
i 1
aˆ y bx
n
x y
i 1
n
i
i
nx y
注意点:在含有一元线性回归模型中,决定系数R2=r2.在线性回归模型中有0≤R2≤1,
因此R2和r都能刻画用线性回归模型拟合数据的效果.
|r|越大,R2就越大,线性回归模型拟合数据的效果就越好.
编
号
1
2
3
4
5
6
7
8
t
1896
1912
1921
1930
1936
1956
1960
1968
0.591
-0.284
,
8.
两个经验回归方程的残差(精确到0.001)如下表所示.
编
号
1
2
3
4
5
6
7
8
t
1896
1912
1921
1930
1936
1956
1960
1968
0.591
-0.284
-0.301
-0.218
-0.196
0.111
0.092
0.205
-0.001
0.007
-0.012
0.015
-0.018
CDALEVELII建模分析师模拟题

22、答案(D)
第 6 页,共 31 页 版权所有,侵权必究
CDA LEVEL II 建模分析师模拟题
对于缺失值,以下说法正确的是? A.所有的有监督学习模型都不支持有缺失值的情况 B.遇到有缺失值的情况,优先考虑删除变量 C.对于分类数据,考虑使用均值填充 D.对于连续型数据,考虑使用均值填充
13、答案(A) 使用历史数据构造训练(Train)集、验证(Validation)集和检验(Test)集后,使用哪个数 据集来训练模型? A.训练(Train)集 B.验证(Validation)集 C.检验(Test)集 D.以上都不用 解析:用训练集来训练模型
14、答案(A) 数据清洗阶段,对于以下哪些处理方式可以用来处理缺失值? ① 用均值填充 ② 转换为哑变量(0,1) ,代表数据是否缺失 ③ 使用回归模型去预测缺失值 A.①②③ B.②③ C.①③ D.①② 解析:三种都可以用来处理缺失值
33、答案(A) 通过聚集多个分类器的预测来提高分类准确率的技术称为? A.组合(ensemble) B.聚集(aggregate) C.合并(combination) D.投票(voting)
第 9 页,共 31 页 版权所有,侵权必究
CDA LEVEL II 建模分析师模拟题
Nave Bayes 是一种特殊的 Bayes 分类器,特征变量是 X,类别标签是 C,它的一个假定是? A.各类别的先验概率 P(C)是相等的 B.以 0 为均值,sqr(2)/2 为标准差的正态分布 C.特征变量 X 的各个维度是类别条件独立随机变量 D.P(X|C)是高斯分布
CDA LEVEL II 建模分析师模拟题
C.电信用户离网预警 D.预测 GDP 与工业产值之间的关系
李航-统计学习方法-笔记-5:决策树
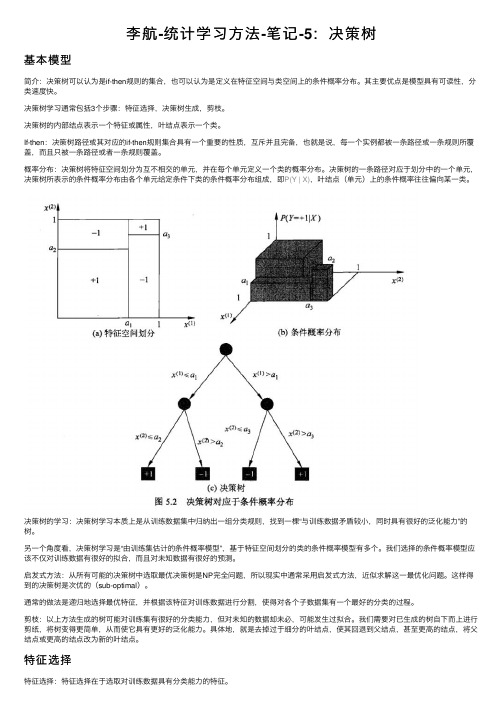
李航-统计学习⽅法-笔记-5:决策树基本模型简介:决策树可以认为是if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布。
其主要优点是模型具有可读性,分类速度快。
决策树学习通常包括3个步骤:特征选择,决策树⽣成,剪枝。
决策树的内部结点表⽰⼀个特征或属性,叶结点表⽰⼀个类。
If-then:决策树路径或其对应的if-then规则集合具有⼀个重要的性质,互斥并且完备,也就是说,每⼀个实例都被⼀条路径或⼀条规则所覆盖,⽽且只被⼀条路径或者⼀条规则覆盖。
概率分布:决策树将特征空间划分为互不相交的单元,并在每个单元定义⼀个类的概率分布。
决策树的⼀条路径对应于划分中的⼀个单元,决策树所表⽰的条件概率分布由各个单元给定条件下类的条件概率分布组成,即P(Y | X),叶结点(单元)上的条件概率往往偏向某⼀类。
决策树的学习:决策树学习本质上是从训练数据集中归纳出⼀组分类规则,找到⼀棵“与训练数据⽭盾较⼩,同时具有很好的泛化能⼒”的树。
另⼀个⾓度看,决策树学习是“由训练集估计的条件概率模型”,基于特征空间划分的类的条件概率模型有多个。
我们选择的条件概率模型应该不仅对训练数据有很好的拟合,⽽且对未知数据有很好的预测。
启发式⽅法:从所有可能的决策树中选取最优决策树是NP完全问题,所以现实中通常采⽤启发式⽅法,近似求解这⼀最优化问题。
这样得到的决策树是次优的(sub-optimal)。
通常的做法是递归地选择最优特征,并根据该特征对训练数据进⾏分割,使得对各个⼦数据集有⼀个最好的分类的过程。
剪枝:以上⽅法⽣成的树可能对训练集有很好的分类能⼒,但对未知的数据却未必,可能发⽣过拟合。
我们需要对已⽣成的树⾃下⽽上进⾏剪纸,将树变得更简单,从⽽使它具有更好的泛化能⼒。
具体地,就是去掉过于细分的叶结点,使其回退到⽗结点,甚⾄更⾼的结点,将⽗结点或更⾼的结点改为新的叶结点。
特征选择特征选择:特征选择在于选取对训练数据具有分类能⼒的特征。
集合论与图论第十章 树

间添加一边,恰得一条回路(称T为最大无回路图); (5) T是连通图,但删去任一边后,便不连通(称T为
最小连通图)。
(6) T的每一对不同的顶点之间有唯一的一条路。
(n1-1)+(n2-1)+ ……+(n -1) =(n1+n2+……+n )= n-
10.1 树及其性质
定理10.2 在任一棵非平凡树T中,至少有两片树
叶。
证明方法:分而治之/反证法。
证明:
若T中只有一片树叶,则 d(vi)≥2(n1)+1=2n-1。
若T中没有树叶,则d(vi)≥2n。 均与d(vi)=2e=2(n-1)矛盾,所以在任
路与生成树的补必有一公共边,所以在r中
必存在一条边fT’; 对于树T(边集至少为
{ e1 ,…..., ei , f }),若用ei+1 代换f,得一棵新 树T1(边集至少为{e1 ,…..., ei , ei+1 }) 。则T1 的权W(T1)=W(T1)+W(ei+1)-W(f) 。
因为T为最小生成树,所以W(T)≤W(T1), 则W(ei+1)≥W(f);又根据T’生成法,自
给出图和生成树,求基本割集组和基本 回路组。
10.2 生成树与割集
四、树的基本变换 图10.4 1 定义10.8(树的基本变换)
设连通图G的生成树T,通过上述加一 弦,再删去一枝得到另一棵生成树,这 种变换称为树的基本变换。
2 定义10.9(距离)
而 记不为设d出连(T现通i, 在T图j)T。Gj的的边生数成称树为Ti和Ti和Tj,Tj的出距现离在,Ti
统计学智慧树知到答案章节测试2023年河南大学

第一章测试1.在相同或近似相同的时间点搜集的数据成为()A:截面数据B:实验数据C:时间序列数据D:观测数据答案:A2.只能归于某一有序类别的非数字型数据成为()A:数值型变量B:数值型数据C:分类数据D:顺序数据答案:D3.最近发表的一份报告称,“由150部新车组成的一个样本表明,外国新车的价格明显高于本国生产的新车”。
这项结论属于()A:对总体的描述B:对总体的推断C:对样本的描述D:对样本的推断答案:B4.一项调查表明,在所抽取的1000个消费者中,他们每月在网上购物的平均花费是200元,他们选择在网上购物的主要原因是“价格便宜”。
这里的参数是()A:所有在网上购物的消费者的平均花费金额B:1000个消费者的平均花费C:所有在网上购物的消费者D:1000个消费者答案:A5.某年全国汽车总产量(万辆)是()A:随机变量B:离散变量C:连续变量D:任意变量答案:A6.统计数据的研究的基本方法()A:统计分组法B:综合指标法C:统计推断法D:大量观察法答案:ABCD7.以下信息是通过描述统计取得的有()A:调查某些班学生统计学考试分数而得到的全校学生的平均成绩B:调查某班统计学分数而得到的优秀比例C:一幅表示某班学生统计学考试分数的统计图D:调查某班学生统计学考试分数而得到的该班学生的平均成绩答案:BCD8.下面属于顺序数据的有()A:学生对考试成绩的满意度B:学生的智商等级C:学生到达教室的距离D:学生按出生地的分组答案:AB9.统计推断学研究的主要问题是()A:如何科学的从总体中抽取样本B:如何科学的确定总体C:怎么科学控制样本对总体的代表性误差D:如何由所抽样本去推断总体特征答案:ABD10.大数据按存在形态不同,大数据可以分为()A:非结构型数据B:流程型数据C:交易型数据D:结构型数据答案:AD11.统计量是不包含任何未知参数的样本的函数()A:错B:对答案:B12.变量按其所受影响因素不同,可以分为确定性变量和随机性变量()A:错B:对答案:B13.按指标的性质不同,可以分为数量指标和质量指标()A:错B:对答案:B14.统计指标和标志是同一个概念()A:对B:错答案:B15.按照统计数据的收集方法,可以将其分为观测数据和实验数据()A:对B:错答案:A第二章测试1.如果一个样本因人为故意操纵而出现偏差,这种误差属于()A:实验误差B:设计误差C:非抽样误差D:抽样误差答案:C2.对一批牛奶的质量进行调查,应该采用()A:典型调查B:普查C:重点调查D:抽样调查答案:D3.抽样误差产生的原因()A:测量误差造成的B:抽样框误差产生的C:抽样的随机性产生的D:人为因素产生的答案:C4.抽样误差的特点()A:不可以计算的B:不可以控制C:和样本多少无关D:不可避免答案:D5.为了掌握商品销售情况,对占该地区商品销售额70%的十家大型商场进行调查,这种调查方式属于()A:抽样调查B:重点调查C:非抽样调查D:统计报表答案:B6.不同的调查问卷在具体结构、题型、措词、版式设计上会有所不同,但在结构上一般都由( )A:问卷标题B:问卷说明C:主体内容成D:填写要求答案:ABCD7.重点调查的特点( )A:有意识地选取若干具有典型意义的单位进行的调查B:属于范围较小的全面调查,即对所有重点单位都要进行观测C:解剖麻雀式D:以客观原则来确定观测单位答案:ABCD8.简单随机抽样的特点()A:抽样方法保证了样本中包含有各种特征的抽样单位,样本的结构与总体的结构比较相近B:抽选的概率相同,用样本统计量对总体参数进行估计及计算估计量误差都比较方便C:每个单位的入样概率是相等的D:可以对各层的目标量进行估计答案:BC9.根据封闭性问题的回答方法可分为()A:两项选择法B:顺序选择法C:评定尺度法D:多项选择法答案:ABCD10.搜集数据的方式有()A:访问B:统计调查方式C:实验方式D:网络数据采集方式答案:ABCD11.普查是根特定研究目的而专门组的一次性的全面调查,以搜集研究对象的全面资料数据()A:对B:错答案:A12.统计报表是指按照国家统一规定的表格形式、指标内容、报送程序和报送时间,由填报单位自下而上逐级提供统计资料的一种统计调查方式。
MFC树形控件(CTreeCtrl)用法

MFC树形控件(CTreeCtrl)用法树形控件可以用于树形的结构,其中有一个根接点(Root)然后下面有许多子结点,而每个子结点上有允许有一个或多个或没有子结点。
MFC中使用CTreeCtrl类来封装树形控件的各种操作。
通过调用BOOL Create( DWORD dwStyle, const RECT& rect, CWnd* pParentWnd, UINT nID );创建一个窗口,dwStyle中可以使用以下一些树形控件的专用风格:TVS_HASLINES 在父/子结点之间绘制连线TVS_LINESATROOT 在根/子结点之间绘制连线TVS_HASBUTTONS 在每一个结点前添加一个按钮,用于表示当前结点是否已被展开TVS_EDITLABELS 结点的显示字符可以被编辑TVS_SHOWSELALWAYS 在失去焦点时也显示当前选中的结点TVS_DISABLEDRAGDROP 不允许Drag/DropTVS_NOTOOLTIPS 不使用ToolTip显示结点的显示字符在树形控件中每一个结点都有一个句柄(HTREEITEM),同时添加结点时必须提供的参数是该结点的父结点句柄,(其中根Root结点只有一个,既不可以添加也不可以删除)利用HTREEITEM InsertItem( LPCTSTR lpszItem, HTREEITEM hParent = TVI_ROOT, HTREEITEM hInsertAf ter = TVI_LAST );可以添加一个结点,pszItem为显示的字符,hParent代表父结点的句柄,当前添加的结点会排在hInsertAf ter表示的结点的后面,返回值为当前创建的结点的句柄。
下面的代码会建立一个如下形式的树形结构:+--- Parent1+--- Child1_1+--- Child1_2+--- Child1_3+--- Parent2+--- Parent3/*假设m_tree为一个CTreeCtrl对象,而且该窗口已经创建*/HTREEITEM hItem,hSubItem;hItem = m_tree.InsertItem("Parent1",TVI_ROOT);在根结点上添加Parent1hSubItem = m_tree.InsertItem("Child1_1",hItem);//在Parent1上添加一个子结点hSubItem = m_tree.InsertItem("Child1_2",hItem,hSubItem);//在Parent1上添加一个子结点,排在Child1_1后面hSubItem = m_tree.InsertItem("Child1_3",hItem,hSubItem);hItem = m_tree.InsertItem("Parent2",TVI_ROOT,hItem);hItem = m_tree.InsertItem("Parent3",TVI_ROOT,hItem);如果你希望在每个结点前添加一个小图标,就必需先调用CImageList* SetImageList( CImageList * pImageList, int nImageListType );指明当前所使用的ImageList,nImageListType为TVSIL_NORMAL。
决策树-上-ID3 C4.5 CART 及剪枝

Entropy(S ) pi log 2 ( pi )
i 1
C
9 9 5 5 log log 0.940286 14 14 14 14
2 2 3 3 Entropy ( Soutlook sunny ) log log 0.970951 5 5 5 5 3 3 2 2 Entropy ( Soutlook rain ) log log 0.970951 5 5 5 5
i 1 C C vVofF
p (v)Entropy ( Sv ) p (v){ pvj log 2 ( pvj )}
j 1 C
pi log 2 ( pi )
i 1 C
vVofF
pi log 2 ( pi )
i 1
vVofF
p(v) pvj log 2 ( pvj )
– 创建根节点R – 如果当前DataSet中的数据都属于同一类,则标记R的类别为该 类 – 如果当前featureList 集合为空,则标记R的类别为当前 DataSet 中样本最多的类别 – 递归情况:
• 从featureList中选择属性F(选择Gain(DataSet, F)最大的属性) • 根据F的每一个值v,将DataSet划分为不同的子集DS,对于每一个DS:
– 基于错误剪枝EBP(Error-Based Pruning)
C4.5-连续型属性
• 离散化处理:将连续型的属性变量进行离散化处 理,形成决策树的训练集
– 把需要处理的样本(对应根节点)或样本子集 (对应子树)按照连续变量的大小从小到大进 行排序 – 假设该属性对应的不同的属性值一共有N个, 那么总共有N-1个可能的候选分割阈值点,每个 候选的分割阈值点的值为上述排序后的属性值 中两两前后连续元素的中点 – 用信息增益率选择最佳划分
决策树系列(五)——CART

决策树系列(五)——CARTCART,⼜名分类回归树,是在ID3的基础上进⾏优化的决策树,学习CART记住以下⼏个关键点:(1)CART既能是分类树,⼜能是分类树;(2)当CART是分类树时,采⽤GINI值作为节点分裂的依据;当CART是回归树时,采⽤样本的最⼩⽅差作为节点分裂的依据;(3)CART是⼀棵⼆叉树。
接下来将以⼀个实际的例⼦对CART进⾏介绍: 表1 原始数据表看电视时间婚姻情况职业年龄3未婚学⽣124未婚学⽣182已婚⽼师265已婚上班族472.5已婚上班族363.5未婚⽼师294已婚学⽣21从以下的思路理解CART:分类树?回归树?分类树的作⽤是通过⼀个对象的特征来预测该对象所属的类别,⽽回归树的⽬的是根据⼀个对象的信息预测该对象的属性,并以数值表⽰。
CART既能是分类树,⼜能是决策树,如上表所⽰,如果我们想预测⼀个⼈是否已婚,那么构建的CART将是分类树;如果想预测⼀个⼈的年龄,那么构建的将是回归树。
分类树和回归树是怎么做决策的?假设我们构建了两棵决策树分别预测⽤户是否已婚和实际的年龄,如图1和图2所⽰: 图1 预测婚姻情况决策树图2 预测年龄的决策树图1表⽰⼀棵分类树,其叶⼦节点的输出结果为⼀个实际的类别,在这个例⼦⾥是婚姻的情况(已婚或者未婚),选择叶⼦节点中数量占⽐最⼤的类别作为输出的类别;图2是⼀棵回归树,预测⽤户的实际年龄,是⼀个具体的输出值。
怎样得到这个输出值?⼀般情况下选择使⽤中值、平均值或者众数进⾏表⽰,图2使⽤节点年龄数据的平均值作为输出值。
CART如何选择分裂的属性?分裂的⽬的是为了能够让数据变纯,使决策树输出的结果更接近真实值。
那么CART是如何评价节点的纯度呢?如果是分类树,CART采⽤GINI值衡量节点纯度;如果是回归树,采⽤样本⽅差衡量节点纯度。
节点越不纯,节点分类或者预测的效果就越差。
GINI值的计算公式:节点越不纯,GINI值越⼤。
以⼆分类为例,如果节点的所有数据只有⼀个类别,则,如果两类数量相同,则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
决策树(ID3 C4.5 CART)原理+推导+代码文章目录简介初识决策树特征选择信息增益信息增益比ID3C4.5决策树剪枝CART 分类与回归树简述:回归树的生成分类树的生成CART剪枝优缺点决策树ID3、C4.5算法CART分类与回归树适用场景代码决策树模型,自己总结了很久,也认为比较全面了。
现在分享一下自己总结的东西。
这里面我只捡精炼的说,基本上都是干货,然后能用人话说的,我也不会疯狂排列数学公式。
初识决策树决策树其实是用于分类的方法,尤其是二分类就是是非题,不过当然不限于二分,然后CART可以应用于分类和回归。
其中对于回归的处理让我很是佩服。
树形结构模型,可以理解为if-else集合。
三个步骤特征选择生成决策树节点和有向边组成。
结点包括内节点(一个特征和属性)叶子节点(一个类)先看一下模型图每个有向边都是一条规则,节点出度规则是完备的。
算法基本流程根据训练集生成决策树。
根据测试集剪枝。
特征选择特征选择我们有一个潜意识里的认识,就是希望选取对于分类有帮助的特征。
那么这里采用信息增益的指标来判断。
什么是信息增益?信息增益什么是熵用来度量随机变量的不确定性的,熵越大,不确定性越高。
所以我们得到了信息增益的算法:根据上述方法我们可以得到一个属性的排序。
信息增益比根据上面的公式其实是更有益于选择那些属性值多的属性,这是需要改进的,所以我们增加一个分母。
得到信息增益比的定义:知道了我们如何选择特征了,接下来就是生成决策树的算法了,一共有两种,先介绍一下ID3。
简单来说就是根据信息增益从大到小进行排序来选择结点。
算法简述:从根节点开始,选择信息增益最大的属性来划分children结点。
然后选择每个孩子结点来作为根节点,再根据信息增益选择下一个属性来划分。
当信息增益小于阈值,或者没有剩余属性的时候停止。
这里其实思想完全和ID3一样,唯一不同的就是使用的是信息增益比。
决策树剪枝当我们把所有的属性或者过多的属性来生成决策树的时候,很可能过拟合,也就是说对于训练集有很好的表现,但是在真正的预测阶段不尽如人意。
所以我们进行剪枝操作:极小化决策树整体损失函数。
首先来看一下损失函数的定义:抱歉这里我写的有点乱,解释一下。
Nt表示的是叶子节点t有多少个样本点。
Ht(T)表示叶子节点t上的熵,然后求解方法和上面说到的熵的求解是一样的。
然后第二项是一个正则项,也就是把对模型的复杂度的要求加入进来。
用|T|,叶子节点的个数来表示模型复杂度。
那么第一项就是整个模型的误差了,肯定是越小越好的。
然后α控制模型的复杂度,具体的在上述图片的下面。
剪枝的过程描述:计算每个节点的经验熵递归:从每个叶子结点回缩,也就是向上递归,如果去掉子树的随时函数小于不去掉之前的随时函数,就要剪枝。
CART 分类与回归树CART是二叉树,左是右否剪枝的时候使用测试集交叉验证,然后随时函数作为标准。
生成:回归树使用平方误差最小化,分裂树使用基尼指数。
回归树的生成遵循最小二乘生成法这里很难理解。
首先我们想要对于连续的数据使用树的结构来分解,最终就是得到的每个叶子节点一定是一个空间。
然后在这个空间里面对应着预测值y。
那么其中的关键就是如何将输入空间进行划分。
这里使用的是自启发的方法,来找到最优的分割点。
(也叫决策点)上面是统计学习一书中的解释,可能会有些晦涩,简单来说,大家可以联想最小二乘法,如果你对于最小二乘法的思想不理解的话,真的不可能看懂这个方法的精髓。
给大家推荐一个最小二乘法的blog,我认为写的非常好。
然后最终得到的x(j) = s,就是最优的决策点。
然后用这个点来划分空间。
一个决策点就划分了两个空间,然后在对这两个空间使用同样的方法。
将连续的数据使用离散的模型表示出来了。
由此决策树的生成就完成了。
分类树的生成分类树的生成使用的是基尼系数。
其实基尼系数和信息增益所表达的是一样的。
定义:基尼指数(基尼不纯度):表示在样本集合中一个随机选中的样本被分错的概率。
Gini指数越小表示集合中被选中的样本被分错的概率越小,也就是说集合的纯度越高,反之,集合越不纯。
基尼指数(基尼不纯度)= 样本被选中的概率 * 样本被分错的概率所以这里树的生成和ID3同样是一样的。
不在多赘述。
CART剪枝CART的剪枝有些复杂,目的是生成一个子树序列,然后通过交叉验证来选择最优子树。
决策树易于理解和解释,可以可视化分析,容易提取出规则;可以同时处理标称型和数值型数据;比较适合处理有缺失属性的样本;能够处理不相关的特征;测试数据集时,运行速度比较快;在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
容易发生过拟合(随机森林可以很大程度上减少过拟合);容易忽略数据集中属性的相互关联;对于那些各类别样本数量不一致的数据,在决策树中,进行属性划分时,不同的判定准则会带来不同的属性选择倾向;信息增益准则对可取数目较多的属性有所偏好(典型代表ID3算法),而增益率准则(CART)则对可取数目较少的属性有所偏好,但CART进行属性划分时候不再简单地直接利用增益率尽心划分,而是采用一种启发式规则)(只要是使用了信息增益,都有这个缺点,如RF)。
ID3算法计算信息增益时结果偏向数值比较多的特征。
改进措施对决策树进行剪枝。
可以采用交叉验证法和加入正则化的方法;使用基于决策树的combination算法,如bagging算法,randomforest 算法,可以解决过拟合的问题。
ID3、C4.5算法产生的分类规则易于理解,准确率较高。
在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,因而导致算法的低效;C4.5只适合于能够驻留于内存的数据集,当训练集大得无法在内存容纳时程序无法运行。
CART分类与回归树非常灵活,可以允许有部分错分成本,还可指定先验概率分布,可使用自动的成本复杂性剪枝来得到归纳性更强的树;在面对诸如存在缺失值、变量数多等问题时CART 显得非常稳健。
适用场景企业管理实践,企业投资决策,由于决策树很好的分析能力,在决策过程应用较多。
import numpy as npimport matplotlib.pyplot as pltimport matplotlib as mplfrom sklearn.tree import DecisionTreeClassifierdef iris_type(s):it = {b'Iris-setosa': 0, b'Iris-versicolor': 1, b'Iris-virginica': 2}return it[s]iris_feature = u'花萼长度', u'花萼宽度', u'花瓣长度', u'花瓣宽度'if __name__ == "__main__":mpl.rcParams['font.sans-serif'] = [u'SimHei']mpl.rcParams['axes.unicode_minus'] = Falsepath = '.-dataSet-iris.data' # 数据文件路径data = np.loadtxt(path, dtype=float, delimiter=',', converters={4: iris_type})x_prime, y = np.split(data, (4,), axis=1)feature_pairs = [[0, 1], [0, 2], [0, 3], [1, 2], [1, 3], [2, 3]]plt.figure(figsize=(10, 9), facecolor='#FFFFFF')for i, pair in enumerate(feature_pairs):# 准备数据x = x_prime[:, pair]# 决策树学习clf = DecisionTreeClassifier(criterion='entropy', min_samples_leaf=3)dt_clf = clf.fit(x, y)N, M = 500, 500x1_min, x1_max = x[:, 0].min(), x[:, 0].max()x2_min, x2_max = x[:, 1].min(), x[:, 1].max()t1 = np.linspace(x1_min, x1_max, N)t2 = np.linspace(x2_min, x2_max, M)x1, x2 = np.meshgrid(t1, t2)x_test = np.stack((x1.flat, x2.flat), axis=1)y_hat = dt_clf.predict(x)y = y.reshape(-1)c = np.count_nonzero(y_hat == y) # 统计预测正确的个数print('特征:', iris_feature[pair[0]], ' + ', iris_feature[pair[1]])print('t预测正确数目:', c)print('t准确率: %.2f%%' % (100 * float(c) - float(len(y)))) cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])y_hat = dt_clf.predict(x_test) # 预测值y_hat = y_hat.reshape(x1.shape)plt.subplot(2, 3, i+1)plt.pcolormesh(x1, x2, y_hat, cmap=cm_light)plt.scatter(x[:, 0], x[:, 1], c=y, edgecolors='k', cmap=cm_dark)plt.xlabel(iris_feature[pair[0]], fontsize=14)plt.ylabel(iris_feature[pair[1]], fontsize=14)plt.xlim(x1_min, x1_max)plt.ylim(x2_min, x2_max)plt.grid()plt.suptitle(u'决策树对鸢尾花数据的两特征组合的分类结果', fontsize=18)plt.tight_layout(2)plt.subplots_adjust(top=0.92)plt.show()大家共勉~欢迎指正Gini(p) = sum_{k=1}^{K}p_k (1 - p_k) = 1 - sum_{k=1}^{K} {p_k}^2 容易求得在R1R1,R2R2内部使得平方损失误差达到最小值的c1c1,c2c2为:bestIndex = featIndex# 对于每一个可能的二分结果计算gini增益list1.append(row){married} | {single,divorced}{single} | {married,divorced}{divorced} | {single,married}(2)两个特征取值之间的中点作为可能的分裂点,将数据集分成两部分,计算每个可能的分裂点的GiniGain。
