大学物理 热力学
大学物理热力学PPT课件
02
对应态原理
不同物质在相同的对应状态下具有相同 的热力学性质。对应态参数包括对比压 强、对比体积和对比温度。
03
范德华方程与对应态 原理的应用
预测真实气体的性质，如液化温度、临 界参数等。
真实气体行为描述
压缩因子
描述真实气体与理想气体偏差程度的物理量，定义为Z = pV/nRT。对于理想气体，Z = 1；对于真实气体，Z ≠ 1。
细管电泳等。
固体熔化与升华过程分析
固体熔化
升华过程
熔化与升华的应用
固体在加热过程中，当温度达到 熔点时开始熔化，由固态转变为 液态。熔化过程中吸收热量，温 度保持不变。
某些物质在固态时可以直接升华 为气态，而无需经过液态阶段。 升华过程中也吸收热量，但温度 同样保持不变。
熔化与升华是物质相变的重要过 程，对于理解物质的热力学性质 和相变规律具有重要意义。同时， 在实际应用中也具有广泛用途， 如金属冶炼、材料制备等领域。
阿马伽分体积定律
混合气体的总体积等于各组分气体分体积之和，即V_total = V_1 + V_2 + ... + V_n。
理想气体混合物的性质
各组分气体遵守理想气体状态方程，且相互之间无化学反应。
范德华方程与对应态原理
01
范德华方程
对真实气体行为的描述，考虑了分子体 积和分子间相互作用力，形式为(p + a/V^2)(V - b) = RT，其中a、b为与物 质特性相关的常数。
维里方程
描述真实气体行为的另一种方程形式，考虑了高阶分子间 相互作用项，形式为pV = nRT(1 + B/V + C/V^2 + ...)， 其中B、C等为维里系数。
大学物理第8章：热力学基础
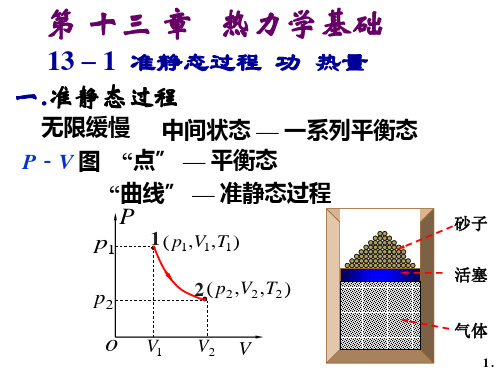
说明：A. 准静态过程为理想过程
弛豫时间 ( )：系统的平衡态被 破坏后再恢复到新的平衡态所需 要的时间。
气缸
B.一个热力学过程为准静态过程的必要条件为过程 所经历的时间大于驰豫时间 t 如：若气缸缸长 L 101 (m )，则 103 ~ 104 ( s ) 若活塞以每秒几十次的频率运动时， 每移动一次经 1 tt 时 t 10 ( s ) ，则满足 ， C.准静态过程可以用宏观参量图给予表示
讨论： (1) n=0, 等压过程，Cp=CV+R ,过程方程: T/V=C4; (2) n=1, 等温过程，CT = , 过程方程: pV=C5; (3) n= , 等体过程, CV =iR/2 , 过程方程: p/T=C6; (4) n= , 绝热过程，CQ=0, 过程方程:
pV C1 , TV
RdT
由 pV=RT 于是得
C CV
pdV
pdV+Vdp=RdT
R pdV (1 ) Vdp 0 C CV dp R dV (1 ) 0 p C CV V
令
R 1 n —多方指数 C C V
21
dp dV n 0 p V
完成积分就得多方过程的过程方程：
V1
V2
i ( p2V2 p1V1 ) 2
只与始末状态有关
M i RT 2
( if
c const )
Q cM (T2 T1 )
与过程有关
特点
与过程有关
对微小过程：dQ=dE + dA
M i dQ RdT pdV 2
14
例题 8-2 如图所示，一定量气体经过程abc吸热 700J,问：经历过程abcda吸热是多少？ 解 Q= E2-E1 + A i 过程abc : 700= Ec -Ea+ Aabc= ( pcVc paVa ) Aabc
大学物理热力学基础
大学物理热力学基础热力学是物理学的一个分支，它研究热现象中的物理规律，包括物质的热性质、热运动和热转化。
在大学物理课程中，热力学基础是物理学、化学、材料科学、工程学等学科的基础课程之一。
热力学基础主要涉及以下几个方面的内容：1、热力学第一定律热力学第一定律，也称为能量守恒定律，是指在一个封闭系统中，能量不能被创造或消除，只能从一种形式转化为另一种形式。
这个定律说明，能量在传递和转化过程中是守恒的，不会发生质的损失。
2、热力学第二定律热力学第二定律是指热量只能从高温物体传递到低温物体，而不能反过来。
这个定律说明，热量传递的方向是单向的，不可逆的。
这个定律对于理解能源转换和利用具有重要意义。
3、热力学第三定律热力学第三定律是指绝对零度下，物质的熵（表示物质混乱度的量）为零。
这个定律说明，在绝对零度下，所有物质的分子和原子都处于静止状态，没有热运动，因此熵为零。
这个定律对于理解物质在低温下的性质和行为具有重要意义。
4、理想气体状态方程理想气体状态方程是指一定质量的气体在恒温条件下，其压力、体积和密度之间的关系。
这个方程对于理解气体在平衡状态下的性质和行为具有重要意义。
5、热容和焓热容和焓是描述物质在加热和冷却过程中性质变化的物理量。
热容表示物质吸收或释放热量的能力，焓表示物质在恒温条件下加热或冷却时所吸收或释放的热量。
这两个物理量对于理解和分析热现象具有重要意义。
大学物理热力学基础是物理学的重要分支之一，它为我们提供了理解和分析热现象的基本理论工具。
通过学习热力学基础，我们可以更好地理解能源转换和利用的原理，为未来的学习和职业生涯打下坚实的基础。
在无机化学的领域中，化学热力学基础是理解物质性质、反应过程和能量转换的重要工具。
本篇文章将探讨化学热力学的基础概念、热力学第一定律、热力学第二定律以及热力学第三定律。
一、化学热力学的基础概念化学热力学是研究化学反应和相变过程中能量转换的科学。
它主要涉及物质的能量、压力、温度和体积等物理量之间的关系。
大学物理热学
ΔU=Q+W，其中ΔU表示系统内能的增量，Q表示外界对系统传递的热量，W表示外界对系统做的功。
热力学第二定律
内容
不可能把热从低温物体传到高温物体而不产生其他影响，或不可能从单一热源 取热使之完全转换为有用的功而不产生其他影响，或不可逆热力过程中熵的微 增量总是大于零。
表达式
对于可逆过程，有dS=(dQ/T)；对于不可逆过程，有dS>(dQ/T)，其中S表示熵， T表示热力学温度。
02
辐射传热特点
不需要介质，可在真空中传播；伴 随能量形式的转换；辐射强度与物
体温度的四次方成正比。
04
应用
太阳能利用、红外遥感测温、激光 器等。
复合传热过程分析
复合传热 分析方法 影响因素
应用
实际传热过程中往往同时存在热传导、对流和辐射三种传热方式。 根据具体传热条件，建立物理模型，综合运用热传导、对流和辐 射的传热规律进行分析计算。
02
理想气体性质及应用
理想气体状态方程
01
理想气体状态方程
pV = nRT，其中p为压强，V为 体积，n为物质的量，R为气体常 数，T为热力学温度。
02
理想气体状态方程 的适用条件
适用于稀薄气体，即气体分子间 距离较大，相互作用力可忽略不 计。
03
理想气体状态方程 的应用
可用于计算气体的压强、体积、 温度等物理量，以及进行气体状 态变化的分析。
热力学在其他领域应用
化学工业
制冷与空调
新能源领域
在化学工业中，热力学原理被广泛应用 于化学反应过程的分析和优化。通过热 力学计算和分析，可以确定化学反应的 条件、反应热、反应平衡常数等关键参 数，为化学工业的生产提供理论指导。
大学物理第九章热力学讲解
i C R
V2
单 i 3 双 i 5 多 i 6
i 气体分子的自由度
ν摩尔理想气体在等体过程中, 温度从T1升高到 T2(或降低) ,吸收的热量为
Q V
E - E
2
1
i RT - T
2
2
1
CV T2 - T1
2
1
2
2
1
V
Q E - E + pV V
p
2
1
2
1
C DT + RDT V
定压摩尔热容: 1mol 理想气体在等压过程中吸
收的热量dQp ，温度升高 dT，其定压摩尔热容为
dQ C p
dT p ,m
dQ C dT
p
p ,m
定压摩尔热容另一表述: 1mol 理想气体在等压
p
等 p2 体
升 压
p1
o
2 ( p2,V ,T2 )
1 ( p1,V ,T1)
V
V
T1 T2 Q 0 DE 0
QV
E1
E2
p
等 p1
体
降 压
p2
o
Q E - E i RT - T
V
2
1
2
2
1
1( p1,V ,T1)
2( p2,V ,T2 )
V
V
T1 T2 Q 0 DE 0
2 公式适用条件 气体压强不太大，温度不太低，密度不太高
例1 一容器内贮有氧气 0.10kg，压强为10atm， 温度为 470C。因容器漏气，过一段时间后，压强 减到原来的 5/8，温度降到 270C。问： （1）容器体积为多大？ （2）漏去了多少氧气？
大学物理热力学与统计物理
大学物理热力学与统计物理热力学与统计物理是大学物理中重要的分支，它研究了物质的热学性质以及微观粒子的统计规律。
本文将简要介绍热力学与统计物理的基本概念、原理和应用。
一、热力学基本概念热力学研究的是能量的转化与守恒，包括传热、传能和能量转换等方面的内容。
热力学基本定律包括能量守恒定律、熵增加原理等。
能量守恒定律指出能量在封闭系统中不会凭空产生或消失，只能通过各种形式的转化转移到其他物体或形式。
熵增加原理则是指随着时间的推移，封闭系统中的熵（系统无序程度）总是增加的。
二、热力学基本原理热力学基本原理包括热平衡、热力学第一定律和热力学第二定律。
热平衡是指系统内各部分之间的温度是相等的状态，这是热力学的基础概念。
热力学第一定律是能量守恒的表示，它表明系统的内能变化等于吸收的热量与对外做功的代数和。
热力学第二定律则是热力学的核心内容，它描述了自然界的不可逆性和熵增加的趋势。
三、统计物理基本原理统计物理是热力学的基础，它从微观角度研究了物质中微观粒子的统计规律。
统计物理主要利用统计学方法描述了大量微观粒子的行为，并推导出宏观热力学定律。
基于统计物理，我们可以计算系统的平均能量、熵以及其他宏观状态量。
四、热力学与统计物理的应用热力学和统计物理在各个领域具有广泛的应用，包括能源开发、材料科学、天体物理等。
在工程领域，热力学可以用来设计高效的能源转换系统，提高能源利用效率。
在材料科学领域，热力学对材料的相变、热膨胀等性质有着重要的解释和研究价值。
而在天体物理学中，热力学与统计物理的应用可以帮助我们理解星际物质的形成和演化过程。
总结：本文简要介绍了大学物理中的热力学与统计物理。
热力学是研究能量转化与守恒的学科，其基本定律包括能量守恒定律和熵增加原理。
统计物理是基于热力学的微观解释，通过统计学方法研究大量微观粒子的行为，推导出宏观热力学规律。
热力学与统计物理在能源、材料和天体等领域有着广泛的应用。
通过深入研究热力学与统计物理，我们能够更好地理解和解释自然界中的物质与能量转化过程。
大学物理《热力学基础》
热力学第二定律的实验验证
卡诺循环实验
通过比较可逆卡诺循环和不可逆卡诺循环的效率， 证明了热力学第二定律的正确性。
焦耳实验
通测量热量和功之间的转换关系，证明了热力 学第二定律的正确性。
热辐射实验
通过测量不同温度下物体的辐射能，证明了熵增 加原理的正确性。
05 热力学的应用
热机效率的提高
热机效率的概念
热力学第二定律定义
熵增原理
热力学第二定律的本质
不可能把热从低温物体传到高温物体而不产 生其他影响；不可能从单一热源取热使之完 全转换为有用的功而不产生其他影响；不可 逆热力过程中熵的微增量总是大于零。
在封闭系统中，自发过程总是向着熵 增加的方向进行，即熵增加原理。
揭示了热量传递和做功过程的不可逆 性，是能量耗散和转化过程的宏观规 律。
通过学习热力学基础，学生可以了解热现象的本质和规律，掌握热力学的 分析方法，为后续的物理学习和实际应用打下基础。
热力学的重要性
热力学在能源、化工、材料 、环保等领域有广泛应用， 是解决实际问题的重要工具
。
热力学的基本原理和方法对 于理解其他物理分支（如电 磁学、光学）以及交叉学科 （如生物物理、地球物理）
热力学第二定律的应用
空调制冷原理
利用制冷剂在蒸发器中吸热蒸发而降低温度，再通过冷凝器放出热 量，使室内温度降低。
汽车发动机效率
汽车发动机效率不可能达到100%，因为发动机工作时会产生热量 损失，这些热量无法完全转化为机械功。
热机效率
热机效率不可能达到100%，因为燃料燃烧产生的热量不可能完全转 化为机械功，其中一部分热量会以热量的形式散失到环境中。
THANKS FOR WATCHING
大学物理-热力学基础-课件
Wa
CV m (T2
T1)
p1V1 p2V2
1
本题用 Wa E 计算较方便
关键用绝热方程
T2
T1
( V1 V2
)
1
先求出 T2
p
p2
2 T2
T2' T1
Q0
p2'
2'
p1
TC
T1
1
o V2 V2' V1 10 V1 V
18.
*四. 多方过程 — 实际过程( 满足 PV n C)
绝热 n = ( CPm / CVm )
等温 n = 1 等压 n = 0
W p1V1 p2V2 n 1
满足 E CV (T2 T1)
Q Cn (T2 T1)
等体 n = ∞
p
可以证明
n= n=∞
n=1
Cn
(
n
n 1
)CV
n=0
o
V
19.
13 – 5 循环过程 卡诺循环
一. 循环过程
1. 特点 E 0 W = Q ( 热功转换 )
1
2
W
(2)热一定律 dQP dE PdV
o V1
V2 V
QP
E
V2 PdV
V1
v
i 2
R(T2
T1 )
P(V2
V1 )
7.
2.摩尔定压热容 CPm
1mol
:
CPm
dQp dT
理论值：
CPm
dE pdV dT
CVm
R
i2R 2
(近似)
实验值：查表 (精确)
QP
dQP
大学物理~热力学基础
气体的内能
E i RT
2
(内能是态函数！)
气体的内能的增量
E i RT
2
二. 功
热量
P
S
dl
（1）功
计算系统在准静态膨胀过程中所作的功： dW F dl P S dl PdV
当活塞移动一段有限距离时
压强作功
W V2 P dV V1
V2
W PdV
热机发展简介
1698年萨维利和1705年纽可门先后发 明了蒸气机 ，当时蒸气机的效率极低 . 1765年瓦特进行了重大改进 ，大大提高了 效率 . 人们一直在为提高热机的效率而努 力，从理论上研究热机效率问题， 一方面 指明了提高效率的方向， 另一方面也推动 了热学理论的发展 .
各种热机的效率
大型柴油机效率
通过外界对系统作功的方法，提高系统的温 度，当系统的温度高于外界时，系统将当初所 吸的热量及由外界作功所转变的内能全部交还 给外界，系统恢复了原状。
外界呢？总能量没减少，但原来付出的机械能 变成了热能，外界没有恢复原状。所以
结论
热量从高温物体传到低温物 体的过程是不可逆的！
（3）气体的自由膨胀过程
dQ dE CV ( dT )V (dT )V
∵
1mol理想气体dE=
i 2
RdT
∴
Cv
=
i 2
R
（i为分子自由度）
所以，理想气体内能表达式又可写成
E CvT
2.定压摩尔热容量（Cp）：
1mol气体在定压过程中吸收热量dQ与温度的变化dT之比
Cp
dQ ( dT )p
dE+PdV ( dT )p
大学物理热力学基础教案
大学物理热力学基础教案一、引言1.1 热力学的概念解释热力学是研究物质系统在温度、压力等条件变化时，其宏观性质如何变化的科学。
强调热力学在工程、物理等领域的应用重要性。
1.2 热力学的研究方法描述热力学通过实验和理论分析来研究物质系统的宏观性质。
介绍热力学的基本定律和理论模型。
二、热力学第一定律2.1 能量守恒定律解释能量守恒定律的内容，即在一个封闭系统中，能量不会凭空产生或消失，只能从一种形式转化为另一种形式。
通过示例或实验现象展示能量守恒定律的应用。
2.2 内能定义内能的概念，即系统内部所有分子和原子的动能和势能之和。
解释内能与系统温度、体积等参数的关系。
三、热力学第二定律3.1 熵的概念介绍熵的概念，即系统混乱程度的度量，熵值越大，系统越混乱。
解释熵与系统温度、分子运动等的关系。
3.2 热力学第二定律的表述表述热力学第二定律的不同形式，如熵增原理、卡诺定理等。
通过实际例子或图示展示熵增原理的应用。
四、热力学第三定律4.1 绝对零度的概念解释绝对零度是理论上最低可能的温度，即物质的熵为零的状态。
介绍开尔文温标与摄氏温标的关系。
4.2 熵与绝对零度解释熵与绝对零度之间的关系，即随着温度的降低，熵逐渐减小并趋近于零。
强调熵与绝对零度在热力学研究中的重要性。
五、热力学应用5.1 热机介绍热机的概念，即利用热能转换为机械能的装置。
解释热机的效率和热力学第二定律的关系。
5.2 热传递描述热传递的基本方式，包括导热、对流和辐射。
解释热传递的规律，如傅里叶定律、牛顿热传递定律等。
六、热力学状态方程6.1 理想气体状态方程推导理想气体状态方程PV=nRT，其中P 为压强，V 为体积，n 为物质的量，R 为理想气体常数，T 为温度。
解释理想气体状态方程在一定条件下的适用性。
6.2 物态方程介绍物态方程的概念，它是描述在不同温度和压力下，物质的状态（如固体、液体、气体）如何变化的方程。
举例说明物态方程在实际应用中的重要性。
大学热学物理知识点总结
大学热学物理知识点总结1.热力学基本定律热力学基本定律是热学物理的基础，它包括三个基本定律，分别是热力学第一定律、热力学第二定律和热力学第三定律。
（1）热力学第一定律热力学第一定律是能量守恒定律的热学表述，它规定了热力学系统能量的守恒性质。
简单地说，热力学第一定律表明了热力学系统能量的增减只与系统对外界做功和与外界热交换有关。
热力学第一定律的数学表达式为ΔU=Q-W，其中ΔU表示系统内能的增量，Q表示系统吸热的大小，W表示系统对外界所作的功。
由此可以看出，系统的内能变化量等于吸收热量减去做的功。
（2）热力学第二定律热力学第二定律是热力学系统不可逆性的表述，它规定了热力学系统内部的熵增原理，即系统的熵不会减小，而只会增加或保持不变。
简单地说，热力学第二定律表明了热力学系统内部的任何一种热力学过程都是不可逆的。
这意味着热力学系统永远无法使热量全部转化为功，总会有一部分热量被转化为无效热。
热力学第二定律还表明了热力学过程的方向性，即热量只能从高温物体传递到低温物体，而不能反向传递。
（3）热力学第三定律热力学第三定律规定了当温度趋于绝对零度时，任何物质的熵都将趋于一个有限值，这个有限值通常被定义为零。
简单地说，热力学第三定律表明了在绝对零度时，任何系统的熵都将趋于零。
热力学第三定律的提出对于热学物理的研究具有非常重要的意义，它为我们理解热学系统的性质提供了重要的基础。
2.热力学过程热力学过程是指热力学系统内部发生的一系列变化，包括各种状态参数的变化和热力学系统对外界的能量交换。
常见的热力学过程有等温过程、绝热过程、等容过程和等压过程等。
这些过程在日常生活以及工业生产中都有着广泛的应用。
（1）等温过程等温过程是指在恒定温度下进行的热力学过程。
在等温过程中，系统对外界做的功和吸收的热量之比是一个常数。
这意味着等温过程的压强和体积成反比，在P-V图上表现为一条双曲线。
常见的等温过程有等温膨胀和等温压缩等。
（2）绝热过程绝热过程是指在无热交换的情况下进行的热力学过程。
大学物理-热力学
存在温差而发生的能量传递 .
功与热量的异同 1）过程量：与过程有关；
T1 T2
T1 Q T2
2）等效性：改变系统热运动状态作用相同；
1卡 = 4.18 J ， 1 J = 0.24 卡
3）功与热量的物理本质不同 .
功
宏观运动
分子热运动
热量
分子热运动
分子热运动
五、 内 能 （状态量）
物体内分子做无规运动的动能和势能的总和叫做 物体的内能。内能由系统的状态唯一地决定。内能的 改变量只由初末状态决定，和变化的具体过程无关。
p
A*
1
p
A*
1
2 *B
o
V
2 *B
o
V
理想气体内能 : 表征系统状态的单值函数 ,
理想气体 的内能仅是温度的函数 U U (T )
永 动 机 的 设 想 图
第一类永动机试图在不获 取能源的前提下使体系持续 地向外界输出能量。历史上 最著名的第一类永动机是法 国人亨内考在十三世纪提出 的“魔轮”，十五世纪，著 名学者达芬奇也曾经设计了 一个相同原理的类似装置， 1667年曾有人将达芬奇的设 计付诸实践，制造了一部直 径5米的庞大机械，但是这些 装置经过试验均以失败告终。
Cp,m CV ,m R
CV ,m
CV ,m
CV ,m
R 1
R
1
W 1 (T1 T2 ) 1 ( p1V1 p2V2 )
绝热过程方程的推导
dQ 0, dW dU pdV vCV ,mdT
pV vRT
pdV Vdp R pdV CV ,m
整理得
dp dV 0
pV
p
p2
2 T2
大学物理热力学
02
数学表达式为：不可能通过有限个步骤将一个单一 热源的热量全部转化为机械功而不产生其他影响
04
此外，热力学第二定律还揭示了机械能与内能之间 的转化是不可逆的，即机械能可以完全转化为内能， 而内能不能完全转化为机械能而不产生其他影响
5
卡诺循环与卡 诺定理
卡诺循环与卡诺定理
01
02
卡诺循环是由法国物理学家 卡诺提出的一种理想化循环 过程，包括四个步骤：等温 膨胀、绝热膨胀、等温压缩 和绝热压缩
1
热力学的基本 概念
热力学的基本概念
热力学的基本概念包括系 统、状态、过程和循环等
系统是指研究对象的整体， 可以是气体、液体、固体
等
状态是指系统在某一时刻 的宏观物理量，如温度、
压力、体积等
过程是指系统状态的变化 历程，可以分为等温过程、
等压过程、绝热过程等
循环是指系统经过一系列 状态变化后又回到初始状
此外，热力学还在航天工 程、材料科学等领域得到
应用
11
热力学与其他 学科的联系
热力学与其他学科的联系
热力学与其他学科有着密切的 联系
例如，热力学与统计力学的关 系密切，统计力学从微观角度 研究物质的热力学性质，提供
了对热现象的微观描述
此外，热力学与电动力学也有 一定的联系，如电磁场的能量 和动量等物理量可以与热力学 中的熵和温度等概念相对应
12
未来展望
未来展望
随着科学技术的发展，热力学的研究和应用将 不断深入和扩展
例如，随着能源问题的日益严重，热力学在能 源利用和环境保护方面的应用将更加广泛；随 着纳米技术的发展，热力学在纳米材料和纳米 器件方面的应用将更加深入；随着气候变化和 环境问题的日益严重，热力学在地球科学和环 境科学方面的应用将更加重要
大学物理第三章热力学第一定律第四章热力学第二定律
A1 A绝热 Q1 0 A2 A绝热 Q2 0
放热 吸热
（B）对
38
补充作业（4692）如图所示，C是固定的绝热壁， D是可动活塞，C、D将容器分成A、B两部分。 开始时A、B两室中各装入同种类的理想气体， 它们的温度T、体积V、压强P均相同，并与大 气压强相平衡。现对A、B两部分气体缓慢地 加热，当对A和B给予相等的热量Q以后，A室 中气体的温度升高度数与B室中气体的温度升 高度数之比为7:5。求:
内能：态函数,系统每个状态都对应着一定内能的数值。 功、热量：只有在状态变化过程中才有意义，状态不
变，无功、热可言。
8
五、热力学第一定律
1. 数学表式
★ 积分形式 Q E A
★ 微分形式 dQ dE dA
9
2. 热力学第一定律的物理意义
（1）外界对系统所传递的热量 Q , 一部分用于 系统对外作功，一部分使系统内能增加。
（4）内能增量： dE 2i（R适dT用于任C何V d过T程!!）
E E2 E1 CV (T2 T1 )
等容过程
Q等容 E E2 E1 CV (T2 T1 )
A等容 0
CV
iR 2
14
2. 等压过程
（1）特征： P=恒量 ，dP=0， P
参量关系: V T 恒量 （2）热一律表式：
E EA EB
E A
3
2
RTA
3 2
RTA
5 EB 2 RTB
C是导热板，因此A、B两部分气体的温度
始终相同。即：TA TB T
T A 4R
5
5
EB 2 RT 8 A
36
例4（4313）一定量的理想气体，从P-V图 上初态a经历（1）或（2）过程到达末 态b，已知a、b两态处于同一条绝热线 上（图中虚线是绝热线），问两过程中 气体吸热还是放热？ （A）（1）过程吸热 （2）过程放热 （B）（1）过程放热 （2）过程吸热
大学物理(热学篇)
v1
v´1
x
A1 y °
z
1秒钟A1受到分子的总冲量
2mv x
vx 2x
mv
2 x
x
第三步 N个分子在1秒内对A1的碰撞
A1在1秒内受到的冲量——平均作用力F
F 2mv1x
v1 x 2x
2mv2x
v2x 2x
2mv Nx
vNx 2x
m x
(v12x
v22x
vN2 x )
m x
N
即在平衡态，一个自由度，代表一种独立的 运动和一份能量
如某种分子有t个平动自由度，r个转动自由度v振动 自由度，则分子具有：
平均平动动能 平均转动动能 平均振动动能
为什么均分到各自由度所对应的运动能量都 是二分之一KT呢？ 主要是分子不断碰撞以达到平衡态的结果。
注意
１、 一般温度下（T <10 3 K）振
（1)每个分子作用于气壁的冲量I
解（1）每个分子作用于气壁的冲量等于气体 分子动量增量的负值
I 2mv 1.21024kgm/ s
（2)每秒钟碰在器壁单位面积上的分子数n0
解（2）器壁ΔA面积上在Δt时间内碰撞的分子数
N A vt n
z
6
n0
N At
nv 6
n0
1 6
nv
0.31028
/
m3
物体运动形式：平动、转动、振动
自由度数目 i t r v
平转振 动动动
例1 自由运动的质点 (三维空间) 3 个 平动自由度 记作 t = 3
若受到限制，自由度降低 平面上 ： t=2 直线上 ：t=1
例2 自由运动刚体 (如手榴弹)自由度。
大学物理中的热力学实验结果分析
大学物理中的热力学实验结果分析热力学是研究能量转化和宏观物体间相互作用的一门学科。
在大学物理中，热力学实验是非常重要的一部分，通过实验可以验证和探索各种热力学定律和原理。
本文将对大学物理中常见的热力学实验结果进行分析和解读。
一、摩尔热容实验摩尔热容实验是研究气体热容的一种实验方法。
通过测量气体在等压条件下的温度变化，可以得到气体的摩尔热容。
实验中，通常使用恒压容器，并使气体与热源接触，然后测量气体的温度变化。
根据理想气体状态方程，PV=nRT，可以得到气体的摩尔热容公式：Cp = q / (nΔT)。
二、焓变实验焓变实验是热力学中研究化学反应焓变的一种实验方法。
通过测量反应前后系统的温度变化，以及实验过程中吸取或释放的热量，可以计算出反应的焓变。
在实验中，通常采用绝热容器，以确保热量不流入或流出系统。
三、热传导实验热传导实验是研究热传导现象的一种实验方法。
通过测量不同材料的导热性能，可以了解材料的热导率和热传导机制。
实验中，通常使用热敏电阻或热电偶来测量不同位置的温度变化，并根据温度变化与时间的关系，计算出导热系数。
四、卡诺循环实验卡诺循环实验是研究理想热机效率的一种实验方法。
通过在一个热机中进行四个不可逆过程（绝热膨胀、等温膨胀、绝热压缩、等温压缩），可以验证卡诺循环的效率最大。
实验中，通常使用气体或蒸汽作为工作物质，测量其压力、体积和温度的变化，并计算出热机的效率。
五、热辐射实验热辐射实验是研究物体辐射能力和辐射规律的一种实验方法。
通过测量不同温度下物体的辐射能量和波长分布，可以得到物体的辐射谱和辐射功率。
实验中，通常使用辐射计或热电偶来测量辐射能量，并分析其与温度的关系。
总结起来，大学物理中的热力学实验主要包括摩尔热容实验、焓变实验、热传导实验、卡诺循环实验和热辐射实验。
通过这些实验，可以深入了解热力学的基本概念和定律，并将理论知识与实际应用相结合。
热力学实验结果的分析和解读是物理学学习中的重要环节，通过深入分析实验数据，可以得出结论并验证理论模型的准确性，进一步提升学生对热力学的理解和应用能力。
大学专业课热学知识点总结
大学专业课热学知识点总结热学是研究热现象和热能转化规律的科学，是物理学的一个重要分支。
在大学物理专业课程中，热学作为一个重要的内容，涵盖了许多重要的知识点和理论。
本文将对大学专业课热学知识点进行总结，包括热力学定律、热力学过程、理想气体、热传导、辐射和相变等内容，并侧重于内容的清晰性和深度。
热力学定律热力学是研究热现象和热能转化规律的科学，热力学定律是热学研究的基础，包括热力学第一定律、热力学第二定律和热力学第三定律。
热力学第一定律是能量守恒定律的推广，它表明了系统的内能和对外界做功的能力之间的关系。
在热力学中，内能的变化等于系统对外界做功与热量的和，即ΔU=Q-W，其中ΔU 代表内能的变化，Q代表系统吸收的热量，W代表系统对外界做的功。
热力学第二定律是描述自然界热现象发展方向的规律，它表明了热量不能自发地从低温物体传递到高温物体，热力学第二定律还包括卡诺定理和卡诺循环等内容。
热力学第三定律是研究温度趋向绝对零度的规律，它指出了温度趋向绝对零度时，物体的熵趋于零的规律。
热力学过程热力学过程是指系统由一个平衡态转变到另一个平衡态的全过程。
在热力学中，主要研究了等体过程、等压过程、等温过程、绝热过程和多种不可逆过程等。
理想气体理想气体是热力学中常用的模型之一，它包括玻意尔定律、查理定律和瓦伦定律等内容。
在热力学中，主要研究了理想气体的状态方程、理想气体的内能、理想气体的焓和理想气体的熵等内容。
热传导热传导是研究物质内部热能传递的过程，它包括导热系数、傅里叶定律、导热方程和多种传热方式等内容。
在热力学中，主要研究了热传导的基本原理和热传导的应用。
辐射辐射是研究物体之间通过辐射方式传递热能的过程，它包括黑体辐射、辐射热力学和多种辐射计算方法等内容。
在热力学中，主要研究了辐射的基本原理和辐射的应用。
相变相变是研究物质的相变过程和相变规律的过程，它包括凝固、熔化、升华和凝华等多种物质的相变过程。
在热力学中，主要研究了相变的基本原理和相变的应用。
大学物理热力学知识点汇总
大学物理热力学知识点汇总热力学是大学物理中的一个重要部分，它研究的是热现象的规律以及与热相关的能量转化和传递。
以下将对大学物理热力学中的关键知识点进行汇总。
一、热力学系统和热力学平衡态热力学系统是指研究的对象，它可以是一个气体、液体或固体，也可以是由多个物体组成的系统。
而热力学平衡态则是指系统的宏观性质在长时间内不随时间变化的状态。
这包括热平衡（系统各部分温度相等）、力学平衡（系统各部分压力相等）、化学平衡（系统内各化学组分的浓度不再变化）。
二、热力学第零定律如果两个热力学系统中的每一个都与第三个热力学系统处于热平衡，那么这两个热力学系统也必定处于热平衡。
这个定律为我们定义了温度的概念，使我们能够通过比较不同系统之间的热平衡来测量温度。
三、热力学第一定律也被称为能量守恒定律，它表明一个热力学系统内能的增量等于外界向它传递的热量与外界对它所做的功之和。
用公式表示为：ΔU ＝ Q ＋ W。
其中，ΔU 是系统内能的变化，Q 是系统吸收的热量，W 是系统对外界所做的功。
在这个定律中，需要注意功的正负。
当系统对外做功时，W 为负；外界对系统做功时，W 为正。
同样，当系统吸收热量时，Q 为正；系统放出热量时，Q 为负。
四、等容过程等容过程是指系统的体积保持不变。
在等容过程中，系统不做功（W ＝ 0），内能的变化等于吸收或放出的热量，即ΔU ＝ Q。
五、等压过程等压过程中系统的压力保持不变。
此时，系统所做的功为 W ＝pΔV，内能的变化和吸收的热量的关系为ΔU ＝Q pΔV 。
六、等温过程等温过程中系统的温度保持不变。
在理想气体的等温过程中，内能不变（ΔU ＝0），系统吸收的热量等于对外界所做的功，即Q ＝W 。
七、绝热过程绝热过程是指系统与外界没有热量交换（Q ＝0）。
在绝热过程中，系统做功导致内能变化，即 W ＝ΔU 。
八、热力学第二定律它有多种表述方式，常见的有克劳修斯表述（热量不能自发地从低温物体传到高温物体）和开尔文表述（不可能从单一热源吸取热量，使之完全变为有用功而不产生其他影响）。
大学物理热力学公式(2024)
2024/1/30
1
目录
2024/1/30
• 热力学基本概念与公式 • 热力学第一定律 • 热力学第二定律 • 气体动理论基础与公式 • 相变与潜热公式 • 热力学循环与效率公式
2
01
热力学基本概念与公式
Chapter
2024/1/30
3
热力学系统与环境
01
热力学系统
所研究的对象，与周 围环境有物质和能量 的交换。
14
热力学第二定律表述及意义
克劳修斯表述
热量不能自发地从低温物体传到 高温物体。它说明在没有外界影 响的条件下，热传导过程是不可 逆的。
开尔文表述
不可能从单一热源吸收热量，使 之完全变成功，而不产生其他影 响。它说明功转变为热的实际宏 观过程是不可逆的。
热力学第二定律的意义
揭示了自然界中与热现象有关的 宏观过程的不可逆性，反映了宏 观自然过程的方向性。
自由膨胀过程
气体在真空中自由膨胀时，不受外界约束，体积自发增大。该过程中，系统的熵增加，表明自由膨胀是一个 不可逆过程。
17
04
气体动理论基础与公式
Chapter
2024/1/30
18
气体分子运动论概述
气体分子运动论是研究气体分子热运动的宏观规律和微观机制的理论基础。
气体分子运动论的基本假设包括：气体分子是由大量不断运动的质点组成，分子间的作用力可以忽略不 计，分子与器壁之间的碰撞是完全弹性的。
朗肯循环
朗肯循环是一种蒸汽动力循环，由锅 炉、汽轮机、凝汽器和给水泵等设备 组成。朗肯循环在火力发电厂、核电 站等领域得到广泛应用。其优点是可 以利用低品位的热能；缺点是需要消 耗大量的水资源，并且对环境有一定 影响。
大学物理热学知识点归纳总结
大学物理热学知识点归纳总结在大学物理中，热学是一个重要的分支学科，研究热与能量的传递、转化以及物体的热性质。
下面将对大学物理热学的知识点进行归纳总结，帮助读者更好地理解和掌握这一领域的知识。
一、热传递1. 热传递方式热传递主要有三种方式：传导、对流和辐射。
传导是通过物质内部的分子碰撞传递能量；对流是通过流体的运动传递能量；辐射是通过波的传播传递能量。
2. 热传导定律热传导可以用傅里叶定律来描述，该定律表示热流密度与温度梯度成正比。
热传导系数是描述物质导热性能的物理量。
3. 对流换热对流换热是通过流体对流传热的现象，常见的例子包括空气对流、水的对流等。
对流换热可以通过牛顿冷却定律进行计算。
4. 辐射换热辐射换热是通过电磁波的辐射传递能量，不需要介质参与。
斯特藩-玻尔兹曼定律描述了辐射换热的关系，还有黑体辐射以及斯特藩定律可用于描述辐射换热的各种特性。
二、热力学1. 温度和热量温度是物体内部分子热运动的强弱程度的度量，用热力学温标来表示；热量是物体之间传递的热能。
2. 理想气体状态方程理想气体状态方程描述了气体的状态参数之间的关系，一般形式为PV = nRT，其中P是气体的压强，V是体积，n是物质的物质量，R是理想气体常数，T是温度。
3. 热力学第一定律热力学第一定律是能量守恒定律在热学过程中的表现，表示了热量与功的转化关系。
ΔU = Q - W，其中ΔU是内能变化，Q是吸收的热量，W是对外界做的功。
4. 热力学第二定律热力学第二定律描述了自然界热现象发生的方向性，主要有熵增定律和开尔文定律。
熵增定律指出自发过程的总熵增不会小于零，开尔文定律则根据热机和热泵的运行原理提出了热力学温标的概念。
三、热量传递的应用1. 热膨胀热膨胀是物体随着温度变化而引起的体积、长度等物理量的变化。
线膨胀、面膨胀和体膨胀是常见的热膨胀现象，可以通过热膨胀系数进行定量描述。
2. 热传感器热传感器是利用物体温度变化引起的一些物性变化进行温度测量的装置，如热电偶、热电阻等。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0
Qad Aad Ead
（＋） （—）
Aad Aae
Aae Eae
Aad Eae Ead
Eae Ead
另解： a
同理：a
d
Qad 0
Pa
e V1
b c d e f V2 V
e
循环adea中： Qea=0 Qde<0
故： Qad>0
f
循环afea中： Qea=0 Qfe>0
故：Qaf<0
200
100
C
B
o
2
4
6 V (m3)
1mol双原子分子理想气体，经1231循环，
1 2直线，2 3绝热，3 1等温。且T2 2T1，V3 8V1
求：1）各个过程的 A、E、Q；
2）循环效率。
P
P2
解：1）1 2：PV 1 常数
（自测P30-4）
2
n 1
E12 CV (T2 T1 )
2）
＝ A
Q1
A12
A23 Q12
A31
0.31
或 1 Q2 1 Q31 0.31
Q1
Q12
P1 1
绝热
等温
3
o V1 V2
V V3
[例].一动力暖气装置由一台 卡诺热机和一台卡诺致冷机 组合而成。热机靠燃料燃烧 时释放的热量工作并向暖气 系统的放热，同时，热机带 动致冷机，致冷机从天然蓄 水池中吸热，也向暖气系统 放热，假定热机锅炉的温度 为T1=483K，天然蓄水池中 水的温度T2=288K， 暖气系统的温度为T3=333K ，热机从燃料燃烧时获得热量 2.1×107J。 计算暖气系统所得的热量。
锅炉 T1=483K Q1= 2.1×107J
热机 Q2
暖气系统T3=333K
Q1
A 致冷机
Q2
蓄水池 T2=288K
锅炉 T1=483K Q1= 2.1×107J
热机 Q2
暖气系统T3=333K
Q1
A 致冷机
Q2
蓄水池 T2=288K
解：Q Q2 Q1
Q2 Q1
T3 T1
Q2
T3 T1
Q1
b c
吸热的是，放热的是，
d e
热容正的是，热容负的是，
f
解：（1） pivi 恒量 Ti
V不变
pi 恒量 Ti
V1
V2
Tb TC Td Te Tf 又 Ta Tc
V
升温：ab, 降温：ad、ae、af .
(2) Qab Aab Eab
（＋） （＋）
0
Qac Aac
解：1）C A：等容
P (Pa)
400
A
PA PC TA TC
TC 75K
300 200
B C：等压
VB TB
VC TC
TB
100
225K o
C 2
4
B 6 V (m3)
2）B
C：QBC
m M
CPT
0.321
7 2
R(TC
TB )
1400J
CP i 2 1.4 i 5：双原子分子
A23
5RT1 2
P2V2 RT2 2RT1 2P1V1 P3V3 RT3 RT1 P1V1
E31 0
CP 7
CV 5
（等温）
A31
m M
Байду номын сангаас
RT1
ln
V1 V3
RT1 ln
1 8
2.08 RT1
Q31
A31
2.08 RT1 （放热）
P P2
已知：1mol双原子
2 T2 2T1，V3 8V1
指明热力学过程进行的方向和限度。
开尔文表述。 二种等价的表述
克劳修斯表述。
宏观意义：一切与热相联系的现象中，自发实现的过程都是 不可逆的。
微观意义：一切自然过程总是沿着无序性增大(熵增）的方向进 行
在P V图中的五个准静态过程中，a c为等温过程，
a e为绝热过程。在这些过程中： P a
升温的是，降温的是，
Q2 Qcd Qdb Eab Adb < Q1 Eab
理想气体做acba 循环，在此过程中气体净吸热为
A）Q
m M
C P (Tb
Ta )
B）Q
m M
C P (Tb
Ta )
C）Q
m M
C P (Tb
Ta )
D）不能确定
解： Q净 Q1 Q2 A净
P 2Pa Pa a
Va
c Q1
5 2
R(2T1
T1 )
5 2
RT1
1
P1
o V1 V2
3
V V3
A12
P1V1 P2V2 n1
RT1 RT2 RT1
2
2
PV RT
Q12 E12 A12 3RT1（吸热）
23:
(绝热）
3 1:
Q23 0
A23
P2V2
P3V3 1
2P1V1 P1V1 7 1
5RT1 2
5
E23
使活塞缓慢向右移动，至 V2 18l 。
求：（1）末态的 P1 ,T1 ；
自测P34-2
（2）外界传给气体1的热量
解：（1）2气体：绝热压缩
P0V0 P2V2
Q
1
P2
P1
2
V2
V0 2
P2 P0 2 2.63atm P1
CP 7 CV 5
气体1，始末态满足：P0V0 T0
P1V1 T1
A
b
A1 Q2
Vb V
m M
CP (Tb
Ta )
QPab
A1
m M
CV
(Tb
Ta )
A1 QP
而A净 A1
Q
QP
m M
CP (Tb
T2 )
自测P31-5
绝热容器左端导热，活塞绝热、无摩擦。已知：
1、2容积均为36l，初始1、2各有0ºc，1atm的双
原子分子理想气体。现从左端缓慢加热气体1，
对理想气体等值过程的分析.
a b : Q1
比较大小 P
b
c d b : Q2
解: ab : P kT 等容过程
a
d
cd : P kT
c
db:
等温过程
O
T1
T2
T
Ta Tc T1,Tb Td T2 Q1 Qab Eab Aab Eab 0
Qcd Ecd Acd Ecd Eab Qdb Edb Adb Adb 0
三、循环过程: E 0
1、正循环（热机）
Q净 A净 0
A净 1 Q放
Q吸
Q吸
Q净 Q吸 Q放 A净 2、负循环（制冷机）
Q净 A净 0
Q吸 Q吸
A Q放 Q吸
卡诺热机
卡诺制冷机
η 卡 =1
Q 2 1 T2
Q1
T1
卡
Q吸 Q放 Q吸
T2 T1 T2
四、热力学第二定律：
(3) C Q T
a b
Qab 0 Tab 0
Cab 0
a c : Cac
ad
Qad 0 Tad 0
Cad 0
a e : Cae 0
Qa f 0
a f : Taf 0
Caf 0
C
nr n 1
CV
1 n r时，C 0
n r或n 1时，C 0
Pa
V1
b c(n=1) d e(n=γ) f V2 V
Q1 Q2 A
A
Q1
Q2
(1 T3 Q2T1
)Q1
T2
A Q1 Q2 T3 T2
Q2
T2 T3 T2
A
Q1
T3 (T1 T1 (T3
T3) T2 )
Q1
则：
Q
Q2
Q1
(T1 (T3
T2 )T3 T2 )T1
Q1
6.27
107
(J
)
CV
i
且 m PAVA 0.321 M RTA
C
A：QCA
m M
CV T
0.321
5 2
R(TA
TC )
1500J
Q净 QCA QAB QBC A净
而A净
S ABC
1 2
(PA
PC ) (VB
VC )
600J
QAB A QCA QBC 500J
P (Pa)
A 400
300
热力学
一、热力学第一定律:
Q E A (dQ dE PdV )
其中：E m i RT — —与过程无关的状态量 M2
A = V 2 p dV ——过程量 V1
Q
m M
CmolT
—
—过程量
dQ Cmol dT
CV
i 2
R
CP CV R
CP i 2
CV i
——过程量
二、理想气体准静态过程: （教材P265 表7－2） 三个等值过程、绝热过程、多方过程
T1
1.08103 k
求:（2）外界传给气体1的热量
Q1 E1 A1 2.98104 J
E1
m M
CV
T1
T0
P0V0 T0
5 2
T1
T0
2.69104 J
A1
A2
P0V0 P2V2
1
2.92 103 J
Q
1
P2