(完整word版)大学物理学热力学基础练习题
热力学统计物理练习试题和答案
WORD 格式 整理 热力学·统计物理练习题一、填空题 . 本大题 70 个小题，把答案写在横线上。
1. 当热力学系统与外界无相互作用时 , 经过足够长时间 , 其宏观性质时 间改变，其所处的 为热力学平衡态。
2． 系统，经过足够长时间，其不随时间改变，其所处的状态为热力学平衡态。
3．均匀物质系统的热力学平衡态可由力学参量、电磁参量、几何参量、化 学参量等四类参量描述，但有 是独立的。
4．对于非孤立系统， 当其与外界作为一个整体处于热力学平衡态时，此时 的系统所处的状态是 。
5．欲描述非平衡系统的状态，需要将系统分成若干个小部分，使每小部分具有 小，但微观上又包含大量粒子，则每小部分都可视 为。
6．描述热力学系统平衡态的独立参量和 之间关系的方程式叫物态方程，其一般表达式为 。
7．均匀物质系统的独立参量有 个，而过程方程独立参量只有个。
8．定压膨胀系数的意义是在 不变的条件下系统体积随 的相对变化。
9．定容压力系数的意义是在 不变条件下系统的压强随的相 对变化。
10．等温压缩系数的意义是在 不变条件下系统的体积随的 相对变化。
11．循环关系的表达式为。
12．在无摩擦准静态过程中存在着几种不同形式的功，则系统对外界作的功 W Y i dy i ，其中 y i 是， Y i 是与 y i 相应的。
13． U B U A Q W ，其中 是作的功。
W14． dUQW0 ，-W 是作的功，且 -W 等于。
22（ 、 均为热力学平衡态1、L2 为15．Q W QW ,L 1L 1 1 2 1L 2准静态过程）。
16．第一类永动机是指的永动机。
17．内能是 函数，内能的改变决定于和。
18．焓是函数，在等压过程中，焓的变化等于的热量。
19．理想气体内能温度有关，而与体积。
学习参考资料分享WORD 格式整理20．理想气体的焓温度的函数与无关。
21．热力学第二定律指明了一切与热现象有关的实际过程进行的。
(完整word版)热力学与统计物理期末复习题
热力学统计物理1、请给出熵、焓、自由能和吉布斯函数的定义和物理意义解：熵的定义：S B−S A=∫dQT ⟹B A dS=dQT沿可逆过程的热温比的积分，只取决于始、末状态，而与过程无关，与保守力作功类似。
因而可认为存在一个态函数，定义为熵。
焓的定义：H=U+pV焓的变化是系统在等压可逆过程中所吸收的热量的度量。
自由能的定义：F=U−TS自由能的减小是在等温过程中从系统所获得的最大功。
吉布斯函数的定义：G =F+pV= U – TS + pV在等温等压过程中，系统的吉布斯函数永不增加。
也就是说，在等温等压条件下，系统中发生的不可逆过程总是朝着吉布斯函数减少的方向进行的。
2、请给出热力学第零、第一、第二、第三定律的完整表述解：热力学第零定律：如果两个热力学系统中的每一个都与第三个热力学系统处于热平衡(温度相同)，则它们彼此也必定处于热平衡。
热力学第一定律：自然界一切物体都具有能量，能量有各种不同形式，它能从一种形式转化为另一种形式，从一个物体传递给另一个物体，在转化和传递过程中能量的总和不变。
热力学第二定律：克氏表述：不可能把热量从低温物体传到高温物体而不引起其他变化；开氏表述：不可能从单一热源吸热使之完全变成有用的功而不引起其他变化。
热力学第三定律：能氏定理：凝聚系的熵在等温过程中的改变随热力学温度趋于零，即limT→0(∆S)T=0绝对零度不能达到原理：不肯能通过有限的步骤使一个物体冷却到热力学温度的零度。
通常认为，能氏定理和绝对零度不能达到原理是热力学第三定律的两种表述。
3、请给出定压热容与定容热容的定义，并推导出理想气体的定压热容与定容热容关系式：C p−C V=nR解：定容热容： C V=(ðUðT )V表示在体积不变的条件下内能随温度的变化率；定压热容：C p=(ðUðT )p−p(ðVðT)P=(ðHðT)P表示在压强不变的情况下的熵增；对于理想气体，定容热容C V的偏导数可以写为导数，即C V=dUdT（1）定压热容C p的偏导数可以写为导数，即C P=dHdT（2）理想气体的熵为 H=U+pV=U+nRT（3）由（1）（2）（3）式可得理想气体的定压热容与定容热容关系式：C p−C V=nR4、分别给出体涨系数α，压强系数β和等温压缩系数κT的定义，并证明三者之间的关系：α=κTβp解：体涨系数：α=1V (ðVðT)P，α 给出在压强不变的条件下，温度升高1 K所引起的物体的体积的相对变化；压强系数：β=1p (ðp ðT )v ，β 给出在体积不变的条件下，温度升高1 K 所引起的物体的体积的相对变化；等温压缩系数：κT =−1V (ðV ðp )T ，κT 给出在温度不变的条件下，增加单位压强所引起的物体的体积的相对变化；由于p 、V 、T 三个变量之间存在函数关系f （p ，T ，V ）=0，其偏导数存在以下关系：(ðV ðp )T (ðp ðT )v (ðT ðV )P =−1 因此α， β， κT 满足α=κT βp5、分别给出内能，焓，自由能，吉布斯函数四个热力学基本方程及其对应的麦克斯韦关系式解：内能的热力学基本方程：dU =TdS −pdV对应的麦克斯韦关系式：(ðT ðV )S =−(ðp ðS )V 焓的热力学基本方程：dH =TdS +Vdp对应的麦克斯韦关系式：(ðT ðp )s =(ðV ðS )p 自由能的热力学基本方程：dF =−SdT +Vdp对应的麦克斯韦关系式：(ðS ðV )T =(ðp ðT )V 吉布斯函数的热力学基本方程：dG =−SdT −pdV对应的麦克斯韦关系式： (ðS ðp )T =−(ðV ðT )p 6、选择T ，V 为独立变量，证明：C V =T (ðS ðT )V ，(ðU ðV )T = T (ðp ðT )V −p 证明：选择T ，V 为独立变量，内能U 的全微分为dU =(ðU ðT )V dT +(ðU ðV )T dV （1） 又已知内能的热力学基本方程 dU =TdS −pdV （2）以T ，V 为自变量时，熵S 的全微分为dS =(ðS ðT )V dT +(ðS ðV )T dV （3） 将（3）式代入（2）式可得dU =T (ðS ðT )V dT +[T (ðS ðV )T −P]dV （4） 将（4）式与（1）式比较可得C V =(ðU ðT )V =T (ðS ðT )V （5） (ðU ðV )T = T (ðp ðT )V −p （6） 7、简述节流过程制冷，气体绝热膨胀制冷，磁致冷却法的原理和优缺点解：节流过程制冷：原理：让被压缩的气体通过一绝热管，管子的中间放置一多孔塞或颈缩管。
热力学练习题全解
热力学练习题全解热力学是研究热能转化和热力学性质的科学，它是物理学和化学的重要分支之一。
在热力学中，我们通过解决一系列练习题来巩固和应用所学知识。
本文将为您解答一些热力学练习题，帮助您更好地理解和应用热力学的基本概念和计算方法。
1. 练习题一题目：一个理想气体在等体过程中，吸收了50 J 的热量，对外界做了30 J 的功，求该气体内能的变化量。
解析：根据热力学第一定律，内能变化量等于热量和功之和。
即ΔU = Q - W = 50 J - 30 J = 20 J。
2. 练习题二题目：一摩尔理想气体从A状态经过两个等温过程和一段绝热过程转变为B状态，A状态和B状态的压强和体积分别为P₁、P₂和V₁、V₂，已知 P₂ = 4P₁，V₁ = 2V₂，求这个过程中气体对外界做的总功。
解析：由两个等温过程可知，气体对外界做的总功等于两个等温过程的功之和。
即 W = W₁ + W₂。
根据绝热过程的特性，绝热过程中气体对外做功为零。
因此，只需要计算两个等温过程的功即可。
根据理想气体的状态方程 PV = nRT，结合已知条件可得：P₁V₁ = nRT₁①P₂V₂ = nRT₂②又已知 P₂ = 4P₁，V₁ = 2V₂，代入式①和式②可得：8P₁V₂ = nRT₁③4P₁V₂ = nRT₂④将式③和式④相减，可得：4P₁V₂ = nR(T₁ - T₂) ⑤由于这两个等温过程温度相等，即 T₁ = T₂，代入式⑤可得：4P₁V₂ = 0所以，这个过程中气体对外界做的总功 W = 0 J。
通过以上两个练习题的解答，我们可以看到在热力学中，我们通过应用热力学第一定律和理想气体的状态方程等基本原理，可以解答各种热力学问题。
熟练掌握这些计算方法，有助于我们更深入地理解热力学的基本概念，并应用于实际问题的解决中。
总结：本文对两道热力学练习题进行了详细解答，分别涉及了等体过程和等温过程。
通过这些例题的解析，读者可以理解和掌握热力学的基本计算方法，并将其应用于实际问题的求解中。
大学物理 第八章 热力学基础
CV
2019/5/21
P.12/42
§8.2 热力学第一定律
热力学基础
§8.2.1 热力学第一定律 本质：包括热现象在内的能量守恒和转换定律。
E2 E1 W Q (E2 E1) W E W
Q
dQ dE dW
Q
E E2 E1
W
+ 系统吸热 内能增加 系统对外界做功
系统放热 内能减少 外界对系统做功
2019/5/21
P.13/42
热力学基础
热力学第一定律适用于任何系统(气液固)的任何过 程(非准静态过程也适用),
Q E PdV
热力学第一定律的另一叙述：第一类永动机 是不可 能制成的。
第一类永动机：Q = 0， E = 0 ，A > 0的机器;
过一系列变化后又回一开始的状态，用W1表示外界对 气体做的功，W2表示气体对外界做的功，Q1表示气体 吸收的热量，Q2表示气体放出的热量，则在整个过程中 一定有（ A ）
A．Q1—Q2=W2—W1 ; B．Q1=Q2
C．W1=W2 ;
D．Q1>Q2
2019/5/21
P.16/42
【例8-4】如图,一个四周绝热的气缸热,力中学基间础 有 一固定的用导热材料制成的导热板C把气缸分 成 A.B 两部分,D是一绝热活塞, A中盛有 1mol He, B中盛有1mol N2, 今外界缓慢地
等压膨胀过程 V2>V1 , A>0 又T2>T1, 即E2-E1>0 ∴Q>0 。气体吸收的热量，一部分用于内能的增加，
一部分用于对外作功；
等压压缩过程 A<0 ， T2<T1, 即E2－E1<0 ∴Q<0 。
《大学物理学》热力学基础练习题
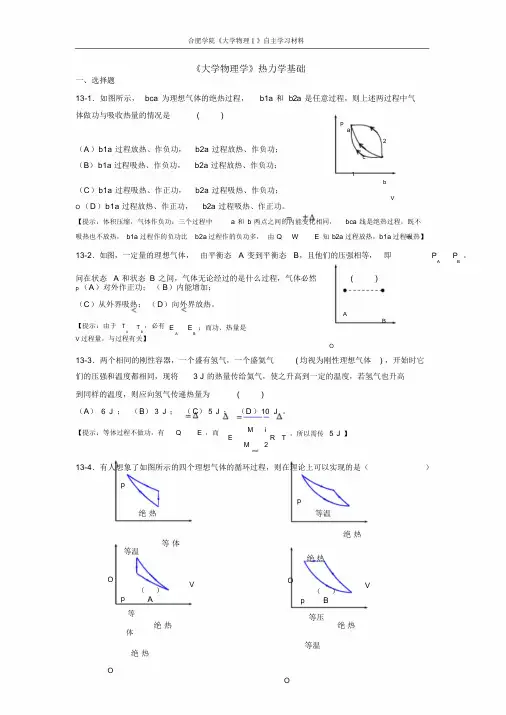
合肥学院《大学物理Ⅰ》自主学习材料《大学物理学》热力学基础一、选择题13-1．如图所示，bca 为理想气体的绝热过程，b1a 和b2a 是任意过程，则上述两过程中气体做功与吸收热量的情况是( )pa2（A）b1a 过程放热、作负功，b2a 过程放热、作负功；c（B）b1a 过程吸热、作负功，b2a 过程放热、作负功；1b（C）b1a 过程吸热、作正功，b2a 过程吸热、作负功；VO （D）b1a 过程放热、作正功，b2a 过程吸热、作正功。
【提示：体积压缩，气体作负功；三个过程中 a 和b 两点之间的内能变化相同，bca 线是绝热过程，既不吸热也不放热，b1a 过程作的负功比b2a 过程作的负功多，由Q W E 知b2a 过程放热，b1a 过程吸热】13-2．如图，一定量的理想气体，由平衡态 A 变到平衡态B，且他们的压强相等，即P P 。
A B问在状态 A 和状态 B 之间，气体无论经过的是什么过程，气体必然( )p （A）对外作正功；（B）内能增加；（C）从外界吸热；（D）向外界放热。
AB【提示：由于T T ，必有A B E E ；而功、热量是A BV 过程量，与过程有关】O13-3．两个相同的刚性容器，一个盛有氢气，一个盛氦气( 均视为刚性理想气体) ，开始时它们的压强和温度都相同，现将 3 J 的热量传给氦气，使之升高到一定的温度，若氢气也升高到同样的温度，则应向氢气传递热量为( )（A） 6 J ；（B）3 J ；（C）5 J ；（D）10 J 。
【提示：等体过程不做功，有Q E ，而M iE R TM 2mol，所以需传 5 J 】13-4．有人想象了如图所示的四个理想气体的循环过程，则在理论上可以实现的是（）pp绝热等温绝热等体等温绝热Op 等（）AV Op（）B等压V 绝热绝热体等温绝热OOVV （）C（）D【提示：(A) 绝热线应该比等温线陡，（B）和（C）两条绝热线不能相交】热力学基础-1合肥学院《大学物理Ⅰ》自主学习材料13-5．一台工作于温度分别为327℃和27℃的高温热源与低温热源之间的卡诺热机，每经历一个循环吸热2000J，则对外做功（）（A）2000 J ；（B）1000 J ；（C）4000 J ；（D）500 J 。
热力学第一定律练习题
第一章 热力学第一定律练习题一、判断题（说法对否）：1．道尔顿分压定律，对理想气体和实际混合气体来说关系式PB=Nb(RT/V)都成立。
2．在两个封闭的容器中，装有同一种理想气体，压力、体积相同，那么温度也相同。
3．物质的温度越高，则热量越多；天气预报：今天很热。
其热的概念与热力学相同。
4．恒压过程也就是恒外压过程，恒外压过程也就是恒过程。
5．实际气体在恒温膨胀时所做的功等于所吸收的热。
6．凡是温度升高的过程体系一定吸热；而恒温过程体系不吸热也不放热。
7．当系统的状态一定时，所有的状态函数都有一定的数值。
当系统的状态发生变化时， 所有的状态函数的数值也随之发生变化。
8．体积是广度性质的状态函数；在有过剩NaCl(s) 存在的饱和水溶液中，当温度、压力 一定时；系统的体积与系统中水和NaCl 的总量成正比。
9．在101.325kPa 、100℃下有lmol 的水和水蒸气共存的系统，该系统的状态完全确定。
10．一定量的理想气体，当热力学能与温度确定之后，则所有的状态函数也完全确定。
11．系统温度升高则一定从环境吸热，系统温度不变就不与环境换热。
12．从同一始态经不同的过程到达同一终态，则Q 和W 的值一般不同，Q + W 的值一般也不相同。
13．因Q P = ΔH ，Q V = ΔU ，所以Q P 与Q V 都是状态函数。
14．封闭系统在压力恒定的过程中吸收的热等于该系统的焓。
15．对于一定量的理想气体，当温度一定时热力学能与焓的值一定，其差值也一定。
16．在101.325kPa 下，1mol l00℃的水恒温蒸发为100℃的水蒸气。
若水蒸气可视为理想 气体，那么由于过程等温，所以该过程ΔU = 0。
17．1mol ，80.1℃、101.325kPa 的液态苯向真空蒸发为80.1℃、101.325kPa 的气态苯。
已 知该过程的焓变为30.87kJ ，所以此过程的Q = 30.87kJ 。
18．1mol 水在l01.325kPa 下由25℃升温至120℃，其ΔH = ∑C P ,m d T 。
大学物理《热力学基础》
热力学第二定律的实验验证
卡诺循环实验
通过比较可逆卡诺循环和不可逆卡诺循环的效率， 证明了热力学第二定律的正确性。
焦耳实验
通测量热量和功之间的转换关系，证明了热力 学第二定律的正确性。
热辐射实验
通过测量不同温度下物体的辐射能，证明了熵增 加原理的正确性。
05 热力学的应用
热机效率的提高
热机效率的概念
热力学第二定律定义
熵增原理
热力学第二定律的本质
不可能把热从低温物体传到高温物体而不产 生其他影响；不可能从单一热源取热使之完 全转换为有用的功而不产生其他影响；不可 逆热力过程中熵的微增量总是大于零。
在封闭系统中，自发过程总是向着熵 增加的方向进行，即熵增加原理。
揭示了热量传递和做功过程的不可逆 性，是能量耗散和转化过程的宏观规 律。
通过学习热力学基础，学生可以了解热现象的本质和规律，掌握热力学的 分析方法，为后续的物理学习和实际应用打下基础。
热力学的重要性
热力学在能源、化工、材料 、环保等领域有广泛应用， 是解决实际问题的重要工具
。
热力学的基本原理和方法对 于理解其他物理分支（如电 磁学、光学）以及交叉学科 （如生物物理、地球物理）
热力学第二定律的应用
空调制冷原理
利用制冷剂在蒸发器中吸热蒸发而降低温度，再通过冷凝器放出热 量，使室内温度降低。
汽车发动机效率
汽车发动机效率不可能达到100%，因为发动机工作时会产生热量 损失，这些热量无法完全转化为机械功。
热机效率
热机效率不可能达到100%，因为燃料燃烧产生的热量不可能完全转 化为机械功，其中一部分热量会以热量的形式散失到环境中。
THANKS FOR WATCHING
热力学基本定律练习题
热力学基本定律练习题1-1 0.1kg C6H6(l)在，沸点353.35K下蒸发，已知(C6H6) =30.80 kJ mol-1。
试计算此过程Q，W，ΔU和ΔH值。
解：等温等压相变。
n/mol =100/78 , ΔH = Q = n= 39.5 kJ ,W= - nRT = -3.77 kJ , ΔU =Q+W=35.7 kJ1-2 设一礼堂的体积是1000m3，室温是290K，气压为，今欲将温度升至300K，需吸收热量多少"(若将空气视为理想气体，并已知其C p,m为29.29 J K-1 ·mol-1。
)解：理想气体等压升温（n变）。
,=1.2×107 J1-3 2 mol单原子理想气体，由600K，1.0MPa对抗恒外压绝热膨胀到。
计算该过程的Q、W、ΔU和ΔH。
(C p ,m=2.5 R)解：理想气体绝热不可逆膨胀Q＝0 。
ΔU＝W，即nC V,m(T2-T1)= - p2 (V2-V1),因V2= nRT2/ p2 , V1= nRT1/ p1 ，求出T2=384K。
ΔU＝W＝nC V,m(T2-T1)＝-5.39kJ ，ΔH＝nC p,m(T2-T1)＝-8.98 kJ1-4 在298.15K，6×101.3kPa压力下，1 mol单原子理想气体进行绝热膨胀，最后压力为，若为；(1)可逆膨胀(2)对抗恒外压膨胀，求上述二绝热膨胀过程的气体的最终温度；气体对外界所作的功；气体的热力学能变化及焓变。
(已知C p ,m=2.5 R)。
解：(1)绝热可逆膨胀:γ=5/3 , 过程方程p11-γT1γ= p21-γT2γ, T2=145.6 K ,ΔU＝W＝nC V,m(T2-T1)＝-1.9 kJ , ΔH＝nC p,m(T2-T1)＝-3.17kJ(2)对抗恒外压膨胀,利用ΔU＝W，即nC V,m(T2-T1)= - p2 (V2-V1) ，求出T2=198.8K。
大学物理热学练习题及答案
大学物理热学练习题及答案第一题：一个物体的质量是1 kg，温度从20°C升高到30°C，如果物体的比热容是4200 J/(kg·°C)，求物体吸收的热量。
解答：根据热量公式Q = mcΔθ，其中 Q 表示吸收的热量，m 表示物体的质量，c 表示比热容，Δθ 表示温度变化。
代入数据得：Q = 1 kg × 4200 J/(kg·°C) × (30°C - 20°C)= 1 kg × 4200 J/(kg·°C) × 10°C= 42,000 J所以物体吸收的热量为42,000 J。
第二题：一块金属材料的质量是0.5 kg，它的比热容是400 J/(kg·°C)，经过加热后，材料的温度升高了60°C。
求该金属材料所吸收的热量。
解答：根据热量公式Q = mcΔθ，其中 Q 表示吸收的热量，m 表示物体的质量，c 表示比热容，Δθ 表示温度变化。
代入数据得：Q = 0.5 kg × 400 J/(kg·°C) × 60°C= 12,000 J所以金属材料吸收的热量为12,000 J。
第三题：一个热容为300 J/(kg·°C)的物体，吸收了500 J的热量后，温度升高了多少摄氏度？解答：根据热量公式Q = mcΔθ，其中 Q 表示吸收的热量，m 表示物体的质量，c 表示比热容，Δθ 表示温度变化。
将已知数据代入公式：500 J = m × 300 J/(kg·°C) × Δθ解方程得：Δθ = 500 J / (m × 300 J/(kg·°C))= 500 J / (m/(kg·°C)) × (kg·°C/300 J)= (500/300) °C≈ 1.67°C所以温度升高了约1.67°C。
物理化学第二章热力学第二定律练习题及答案
第二章 热力学第二定律练习题一、判断题（说法正确否）：1．自然界发生的过程一定是不可逆过程。
2．不可逆过程一定是自发过程。
3．熵增加的过程一定是自发过程。
4．绝热可逆过程的∆S = 0，绝热不可逆膨胀过程的∆S > 0，绝热不可逆压缩过程的∆S < 0。
5．为了计算绝热不可逆过程的熵变，可以在始末态之间设计一条绝热可逆途径来计算。
6．由于系统经循环过程后回到始态，∆S = 0，所以一定是一个可逆循环过程。
7．平衡态熵最大。
8．在任意一可逆过程中∆S = 0，不可逆过程中∆S > 0。
9．理想气体经等温膨胀后，由于∆U = 0，所以吸的热全部转化为功，这与热力学第二定律矛盾吗?10．自发过程的熵变∆S > 0。
11．相变过程的熵变可由T H S ∆=∆计算。
12．当系统向环境传热时(Q < 0)，系统的熵一定减少。
13．一切物质蒸发时，摩尔熵都增大。
14．冰在0℃，pT H S ∆=∆>0，所以该过程为自发过程。
15．自发过程的方向就是系统混乱度增加的方向。
16．吉布斯函数减小的过程一定是自发过程。
17．在等温、等压下，吉布斯函数变化大于零的化学变化都不能进行。
18．系统由V 1膨胀到V 2，其中经过可逆途径时做的功最多。
19．过冷水结冰的过程是在恒温、恒压、不做其他功的条件下进行的，由基本方程可得∆G = 0。
20．理想气体等温自由膨胀时，对环境没有做功，所以 -p d V = 0，此过程温度不变，∆U = 0，代入热力学基本方程d U = T d S - p d V ，因而可得d S = 0，为恒熵过程。
21．是非题：⑴“某体系处于不同的状态，可以具有相同的熵值”，此话对否？ ⑵“体系状态变化了，所有的状态函数都要变化”，此话对否？ ⑶ 绝热可逆线与绝热不可逆线能否有两个交点？⑷ 自然界可否存在温度降低，熵值增加的过程？举一例。
⑸ 1mol 理想气体进行绝热自由膨胀，体积由V 1变到V 2，能否用公式：⎪⎪⎭⎫⎝⎛=∆12ln VV R S计算该过程的熵变？22．在100℃、p 时，1mol 水与100℃的大热源接触，使其向真空容器中蒸发成 100℃、p 的水蒸气，试计算此过程的∆S 、∆S (环)。
热力学中的热量传递与功练习题及
热力学中的热量传递与功练习题及解答题目：热力学中的热量传递与功练习题及解答热力学是研究能量转化与传递的学科，其中热量传递和功是研究的重点内容。
本文将为读者提供一些热力学中有关热量传递与功的练习题，并给出详细解答，帮助读者巩固和加深对该知识点的理解。
题目1：一个物体从20℃升到80℃，在这个过程中吸收了500J的热量。
该物体的内能变化和对外界所做的功分别是多少？解答：根据热力学第一定律，物体的内能变化等于吸收的热量减去对外界做的功。
因此，物体的内能变化为：ΔU = Q - W其中，ΔU表示内能的变化，Q表示吸收的热量，W表示对外界做的功。
根据题目，吸收的热量Q等于500J，代入公式可得：ΔU = 500J - W题目并没有直接给出对外界做功W的数值，所以我们需要通过其他方式来求解。
根据热力学第二定律，物体的温度升高时，它对外界所做的功为正值，即W>0。
在这个过程中，物体的内能增加，所以ΔU>0。
根据物体升温的公式，可以得到：ΔU = mcΔT其中，m表示物体的质量，c表示物体的比热容，ΔT表示温度变化。
根据上述公式，可以得到：500J - W = mcΔT由题可知，初始温度T1为20℃，末温度T2为80℃，代入公式可得：500J - W = mc(T2 - T1)由此，我们可以求解出对外界所做的功W的数值。
解答完毕。
题目2：一个气缸中有一升的理想气体，初始温度为300K，末温度为600K。
在这个过程中，系统对外界做了40J的功，求该过程中的热量变化量。
解答：根据热力学第一定律，系统对外界所做的功等于系统吸收的热量减去内能的变化量。
由于题目给出了功W的数值，我们可以使用下面的公式来求解热量变化量Q：Q = ΔU + W其中，Q表示热量变化量，ΔU表示内能的变化，W表示对外界所做的功。
根据题目可知，系统对外界做的功W为40J，代入公式可得：Q = ΔU + 40J由题目可知，初始温度T1为300K，末温度T2为600K。
大学物理下册第十一章 热力学基础
1. 定义：系统经历一系列变化后又回到初始状态的整 个过程。
准静态循环过程 ~ p-V图中的闭合曲线
p 正
O 2. 共同特征
E0
顺时针：正循环 逆
逆时针：逆循环 V
热力学第一定律： Q净 W净
3. 正循环及其效率
p
b
T1
a 净正正功 c
负功d功
W
O V1
V2
V
特征：
T2
Q净Q吸Q放
W净W对外 W外对系
第十一章 热力学基础
§11—1 内能 功 热量 一.热力学系统（系统）
需研究的对象——气、液、固，也称为工作物质。 以理想气体为系统，与之相互作用的环境称为外界。
二、内能
１．内能：大量分子的平均动能与分子间相互作用 的势能的总和．
实际气体：E=E (T,V )
对于理想气体，由于分子间无相互作用力，所以，理想气体
a. EM mCVT0
V2
m V 2
dV
b .
W p pdV
V1
M V 1
RT
V
m RT ln V 2 m RT ln p1
M
V1 M
p2
T Q
恒温热源 T
p
p1
(p1,V1,T)
P1V 1
ln
V2 V1
P2V 2
ln
V2 V1
P1V 1 ln
P1 P2
P2V 2 ln
P1 P2
(p2,V2,T)
PdVP1V1P2V2
1
系统要对外做功，必须以牺牲自身的内 能为代价．
p
4．P-V 图: 一条曲线.
绝热线比等温线陡.
绝热线 A
高等工程热力学14题全
1、简述温度的定义、物理意义及温度测量的工程应用意义。
温度是表征物体冷热程度的物理量，是物质微粒热运动的宏观体现。
根据热力学第零定律说明，物质具备某种宏观性质，当各物体的这一性质不同时，它们若相互接触，其间将有净能流传递；当这一性质相同时，它们之间达到热平衡。
人们把这一宏观物理性质称为温度。
物理意义：从微观上看，温度标志物质分子热运动的剧烈程度。
温度和热平衡概念直接联系，两个物系只要温度相同，它们间就处于热平衡，而与其它状态参数如压力、体积等的数值是否相同无关，只有温度才是热平衡的判据。
温度测量的工程应用意义：温度是用以判别它与其它物系是否处于热平衡状态的参数。
被测物体与温度计处于热平衡，可以从温度计的读书确定被测物体的温度。
2简述热与功的联系与区别区别：功是系统与外界交换的一种有序能，有序能即有序运动的能量，如宏观物体（固体和流体）整体运动的动能，潜在宏观运动的位能，电子有序流动的电能，磁力能等。
在热力学中，我们这样定义功：“功是物系间相互作用而传递的能量。
当系统完成功时，其对外界的作用可用在外间举起重物的单一效果来代替。
”一般来说，各种形式的功通常都可以看成是由两个参数，即强度参数和广延参数组成，功带有方向性。
功的方向由系统与外界的强度量之差来决定，当系统对外界的作用力大于外界的抵抗力时，系统克服外界力而对外界做功。
功的大小则由系统与外界两方的较小强度量的标值与广延量的变化量的乘积决定，而功的正号或负号就随广延量的变化量增大或减小而自然决定。
热量是一种过程量，在温差作用下，系统以分子无规则运动的热力学能的形式与外界交换的能量，是一种无序热能，因此和功一样热量也可以看成是由两个参数，即强度参数和广延参数组成的量。
传递热量的强度参数是温度，因此有温差的存在热量传递才可以进行。
热量的大小也可以由系统的与外界两方的较小强度量的标量与广延量变化量的乘积决定。
热量也有方向性。
热量的方向由系统与外界的温度之差来决定，当外界的温度高于系统的温度时，外界对系统传热。
热工基础习题和答案（手动word版）.doc
第一章热力学基础知识一、填空题1．实现能和能相互转化的工作物质就叫做。
2．热能动力装置的工作过程，概括起来就是工质从吸取热能，将其中一部分转化为，并把余下的一部分传给的过程。
3．热力系统与外界间的相互作用一般说有三种，即系统与外界间的交换、交换和交换。
4．按系统与外界进行物质交换的情况，热力系统可分为和两类。
5．状态参数的变化量等于两状态下，该物理量的差值，而与无关。
6．决定简单可压缩系统状态的独立状态参数的数目只需个。
7．1mmHg= Pa；1mmH2O= Pa。
8．气压计读数为750mmHg，绝对压力为2.5×105Pa的表压力为MPa。
9．用U形管差压计测量凝汽器的压力，采用水银作测量液体，测得水银柱高为720.6mm。
已知当时当地大气压力Pb=750mmHg，则凝汽器内蒸汽的绝对压力为MPa。
10．一个可逆过程必须是过程，而且在过程中没有。
11．只有状态才能用参数坐标图上的点表示，只有过程才能用参数坐标图上的连续实线表示。
12．热量和功都是系统与外界的度量，它们不是而是量。
13．工质作膨胀功时w 0，工质受到压缩时w 0，功的大小决定于。
二、名词解释1．标准状态——2．平衡状态——3．准平衡过程——4．可逆过程——5．热机——6．热源——7．热力系统——8．体积变化功——9．热力学温标——10．孤立系——三、判断题1．物质的温度越高，则所具有的热量愈多。
2．气体的压力越大，则所具有的功量愈大。
3．比体积和密度不是两个相互独立的状态参数。
4．绝对压力、表压力和真空都可以作为状态参数。
6．孤立系内工质的状态不会发生变化。
7．可逆过程是不存在任何能量损耗的理想过程。
8．凝汽器的真空下降时，则其内蒸汽的绝对压力增大。
9．若容器中气体的压力没有改变，则压力表上的读数就一定不会改变。
四、选择题1．下列各量可作为工质状态参数的是：（1）表压力；（2）真空；（3）绝对压力。
2．水的三相点温度比冰点温度应：（1）相等；（2）略高些；（3）略低些。
(完整word版)热力学练习题2
热力学练习题2一 选择题1. 蒸汽压缩制冷循环过程中，制冷剂蒸发吸收的热量一定 C 制冷剂冷却和冷凝放出的热量A 大于B 等于C 小于2.卡诺制冷循环的制冷系数与 B 有关。
A 制冷剂的性质B 制冷剂的工作温度C 制冷剂的循环速率D 压缩机的功率3．汽液平衡关系li v i f f ˆˆ=的适用的条件 （A ）A 无限制条件B 低压条件下的非理想液相C 理想气体和理想溶液D 理想溶液和非理想气体4．汽液平衡关系i l i i v i x y ϕϕˆˆ=的适用的条件 （A ） A 无限制条件 B 低压条件下的非理想液相 C 理想气体和理想溶液 D 理想溶液和非理想气体5．汽液平衡关系i i si i x P Py γ=的适用的条件 （B ）A 无限制条件B 低压条件下的非理想液相C 理想气体和理想溶液D 理想溶液和非理想气体6．汽液平衡关系si i i Py P x =的适用的条件 （C ）A 无限制条件B 低压条件下的非理想液相C 理想气体和理想溶液D 理想溶液和非理想气体。
7. 关于化工热力学应用的下列说法中不正确的是 BA. 可以判断新工艺、新方法的可行性B. 预测反应的速率C. 通过热力学模型，用易测得数据推算难测数据；用少量实验数据推算大量有用数据D. 相平衡数据是分离技术及分离设备开发、设计的理论基础8. 超临界流体存在的条件是 AA. 高于T c 和高于p cB. 高于T c 和低于p cC. 低于T c 和高于p cD. 低于T c 和低于p c9. 对应态原理认为，在相同的对比态下，所有物质表现出相同的性质。
即 DA. 若V r ，p r 相同，则ω相同B. 若T r ，Z r 相同，则V r 相同C. 若p r ，ω相同，则V r 相同D. 若T r ，p r 相同，则V r 相同 10. 汽液平衡计算方程式S i i i i py x p γ=适用于 BA. 汽液相均为理想体系B. 汽相为理想体系且液相为非理想体系C. 汽液两相均为非理想体系D. 汽相非理想体系且液相为理想体系11. 以下4个偏导数中，表示偏摩尔性质的是 CA. ()j i i nS ,nV ,n nU n ≠⎡⎤∂⎢⎥∂⎣⎦B. ()j i i nS ,p,n nH n ≠⎡⎤∂⎢⎥∂⎣⎦ C. ()j i T ,p,n nG n ⎡⎤∂⎢⎥∂⎣⎦ D. ()j ii nV ,T ,n nA n ≠⎡⎤∂⎢⎥∂⎣⎦ 12. 绝热可逆膨胀过程线在T-S 图上是 BA. 平行于横坐标的直线B. 平行于纵坐标的直线C. 沿等焓线变化的D. 沿等干度线变化的13. 关于理想溶液的各种表达中错误的是 DA. 分子结构相似，大小一样；分子间的作用力相同；混合时没有热量和体积变化B. 在全浓度范围内，每个组分均遵守Lewis-Randall 定则C. ii id i x f f 0ˆ= D. V G H ∆∆∆,,均为零14. 对理想溶液具有负偏差的体系中，各组分活度系数i γ DA. >1B. = 0C. = 1D. < 115. 气体经过稳流绝热过程，对外作功，如忽略动能和位能变化，无摩擦损失，则此过程气体焓值 BA. 增加B. 减少C. 不变D. 不能确定16. 不可逆过程中孤立体系的DA. 总熵是增加的，也是增加的B. 总熵是减少的，也是减少的C. 总熵是减少的，但是增加的D. 总熵是增加的，但是减少的17. 关于做功和加热本领的描述，不正确的是 CA. 压力相同，过热蒸汽的做功本领比饱和蒸汽大B. 温度相同，高压蒸汽的作功本领比低压蒸汽强C. 温度相同，高压蒸汽的加热能力比低压蒸汽强D. 放出的热相同，高温高压蒸汽的作功本领比低温低压蒸汽的大18. 对同一朗肯循环装置，在绝热条件下如果提高汽轮机入口蒸汽压力，而温度等其余条件不变，则其热效率 AA. 有所提高，乏气干度下降B. 不变，乏气干度增加C. 有所提高，乏气干度增加D. 热效率和干度都不变 19. 关于制冷原理，以下说法不正确的是 DA. 任何气体，经等熵膨胀后，温度都会下降B. 只有当0J μ>，经节流膨胀后，气体温度才会降低C. 在相同初态下，等熵膨胀温度下降比节流膨胀温度下降的多D. 任何气体，经节流膨胀后，温度都会下降20. 吸收式制冷循环中解吸器，换热器，吸收器和泵这一系统的作用相当于蒸汽压缩制冷循环的 CA. 节流阀B. 膨胀机C. 压缩机D. 蒸发器 21. 关于化工热力学研究特点的下列说法中不正确的是 BA. 研究体系为实际状态B. 解释微观本质及其产生某种现象的内部原因C. 处理方法为以理想态为标准态加上校正D. 应用领域是解决工厂中的能量利用和平衡问题22. Pitzer 提出的由偏心因子ω计算第二维里系数的普遍化关系式是 CA. 01B B B ω=⋅B. 01B B B ω=+C.01c c Bp B B RT ω=+ D. 01ccBp B B RT ω=⋅ 23. 下列关于G E 关系式正确的是 CA. ()E i i G RT x ln x =∑B. ()E i i ˆG RT x lna =∑C. ()E i i G RT x ln γ=∑D. ()E i i G R x ln x =∑24. 下列偏摩尔自由焓表达式中，错误的是 DA. i i G μ=B. i i i dG V dp S dT =-C. ()j i i i T ,p,n nG G n ≠⎡⎤∂=⎢⎥∂⎣⎦ D. ()j ii i T ,nV ,n nG G n ≠⎡⎤∂=⎢⎥∂⎣⎦ 25. 体系从同一初态到同一终态，经历二个不同过程，一为可逆过程，一为不可逆过程，此二过程环境熵变关系为 AA. （ΔS 环）可逆< （ΔS 环）不可逆B. （ΔS 环）可逆 >（ΔS 环）不可逆C. （ΔS 环）可逆 = （ΔS 环）不可逆D. （ΔS 环）可逆= 026. 混合气体的第二维里系数是 CA. T 和p 的函数B. 仅为T 的函数C. T 和组成的函数D. p 和组成的函数27.衡算的依据是 D A. 热力学第一定律 B. 热力学第二定律 C. 热力学第三定律 D. 热力学第一、二定律28. 混合物的逸度与纯组分逸度之间的关系是 CA.i i ˆf x f =∑B. iˆf f =∑ C. i i iˆfln f x ln x =∑ D. 0i ln f x lnf =∑29. 在T-S 图上，绝热可逆过程工质的状态总是沿着下列哪条线进行的 BA. 等焓线B. 等熵线C. 等干度线D. 等压线30. 理想功实现的条件为 BA. 完全不可逆B. 完全可逆C. 部分可逆D. 部分不可逆31. 气体真空节流膨胀产生冷效应时的微分节流系数是 BA. 0J μ=B. 0J μ>C. 0J μ<D. 不确定32. 可逆绝热膨胀过程的特征是 BA. 等焓B. 等熵C. 等温D. 等压33. 熵产是由于下列哪种原因而引起的 CA. 体系与环境之间的热量交换B. 体系与外界功的交换C. 体系内部的不可逆性D. 体系与外界的物质交换二、填空题1. 状态函数的特点是：状态函数的变化与途径无关，仅决定于初、终态 。
基础物理学热力学部分试卷及答案详解
20XX-20XX第一学期基础物理学⑵试卷(热学部分)常数表R = 8.31 J mol-1 K-1.选择题(每题1分，共15分)1.三个容器A、B、C中装有同种理想气体，其分子数密度n相同，而方均根速率之比为(A) 1 ：2 ：4.(C) 1 ：4 ：16.(B) 1 ：4 ：8.(D) 4 ：2 ：1.2.金属导体中的电子，在金属内部作无规则运动，与容器中的气体分子很类似.设金属中共有N个自由电子其中电子的最大速率为v m，电子速率在v〜v + d v之间的概率为d N \A v2d v 0W v W v m——=< 一mN 0 v > v m式中A为常数.则该电子气电子的平均速率为A (A) -v3.3 m A (B) v4 .4 m(C) v m .A (D) -v2 .3 m[ ]3.按照麦克斯韦分子速率分布定律，具有最概然速率v的分子，P3一一3,一(A)万RT. (B)万kT.其动能为：(C) kT. (D) 2 RT . [ ]4.关于温度的意义，有下列几种说法：(1)气体的温度是分子平均平动动能的量度.(2)气体的温度是大量气体分子热运动的集体表现，具有统计意义.(3)温度的高低反映物质内部分子运动剧烈程度的不同.(4)从微观上看，气体的温度表示每个气体分子的冷热程度.这些说法中正确的是(A) (1)、(2) 、(4). (B) (1)、(2) 、(3).(C) (2)、(3)、(4). (D) (1)、(3)、(4). [ ]5.一定量的理想气体，开始时处于压强，体积，温度分别为p』匕，T1的平衡态，后来变到压强，体积，温度分别为p2, 丫2, T2的终态.若已知丫2 >匕，且T2 = T]，则以下各种说法中正确的是：(A)不论经历的是什么过程，气体对外净作的功一定为正值.(B)不论经历的是什么过程，气体从外界净吸的热一定为正值.(C)若气体从始态变到终态经历的是等温过程，则气体吸收的热量最少.(D)如果不给定气体所经历的是什么过程，则气体在过程中对外净作功和从外界净吸热的正负皆无法判断. [ ]6.一定量的理想气体，其状态变化遵从多方过程方程pV n =常量，已知其体积增大为原来的二倍1：2：4，则其压强之比七：P B：P C为：时，温度相应降低为原来的四分之一，则多方指数n为(A) 3. (B) 2.(D)7. 一定量的理想气体，从。
大学物理---热学部分和近代物理部分练习题及答案解析
大学物理---热学部分和近代物理部分练习题及答案解析一、选择题1. 已知氢气与氧气的温度相同，请判断下列说法哪个正确？(A) 氧分子的质量比氢分子大，所以氧气的压强一定大于氢气的压强．(B) 氧分子的质量比氢分子大，所以氧气的密度一定大于氢气的密度．(C) 氧分子的质量比氢分子大，所以氢分子的速率一定比氧分子的速率大.(D) 氧分子的质量比氢分子大，所以氢分子的方均根速率一定比氧分子的方均根速率大． ［ D ］2. 两种不同的理想气体，若它们的最概然速率相等，则它们的(A) 平均速率相等，方均根速率相等．(B) 平均速率相等，方均根速率不相等．(C) 平均速率不相等，方均根速率相等．(D) 平均速率不相等，方均根速率不相等． ［ A ］3. 若理想气体的体积为V ，压强为p ，温度为T ，一个分子的质量为m ，k 为玻尔兹曼常量，R 为普适气体常量，则该理想气体的分子数为：(A) pV / m (B) pV / (kT )(C) pV / (RT ) (D) pV / (mT ) ［ B ］4. 1 mol 刚性双原子分子理想气体，当温度为T 时，其内能为（式中R 为普适气体常量，k为玻尔兹曼常量）(A) ． (B)．(C)． (D)． [ C ]5. 一物质系统从外界吸收一定的热量，则(A) 系统的内能一定增加．(B) 系统的内能一定减少．(C) 系统的内能一定保持不变．(D) 系统的内能可能增加，也可能减少或保持不变． [ D ]6．如果在一固定容器内，理想气体分子速率都提高为原来的二倍，那么（A ）温度和压强都升高为原来的二倍；（B ）温度升高为原来的二倍，压强升高为原来的四倍；RT 23kT23RT 25kT25（C）温度升高为原来的四倍，压强升高为原来的二倍；（D）温度与压强都升高为原来的四倍。
[ D ]7.两容器内分别盛有氢气和氦气，若它们的温度和质量分别相等，则：(A) 两种气体分子的平均平动动能相等．(B) 两种气体分子的平均动能相等．(C) 两种气体分子的平均速率相等．(D) 两种气体的内能相等．［ A ］8.麦克斯韦速率分布曲线如图所示，图中A、B两部分面积相等，则该图表示v为最概然速率．(A)v为平均速率．(B)v为方均根速率．(C)v的分子数各占一半．［ D ](D) 速率大于和小于f(v)9. 速率分布函数f(v)的物理意义为：(A) 具有速率v的分子占总分子数的百分比．(B) 速率分布在v附近的单位速率间隔中的分子数占总分子数的百分比．(C) 具有速率v的分子数．(D) 速率分布在v附近的单位速率间隔中的分子数．［ B ］10. 根据热力学第二定律可知：(A) 功可以全部转换为热，但热不能全部转换为功．(B) 热可以从高温物体传到低温物体，但不能从低温物体传到高温物体(C) 不可逆过程就是不能向相反方向进行的过程．(D) 一切自发过程都是不可逆的．［ D ］11.根据热力学第二定律判断下列哪种说法是正确的．(A) 热量能从高温物体传到低温物体，但不能从低温物体传到高温物体．(B) 功可以全部变为热，但热不能全部变为功．(C) 气体能够自由膨胀，但不能自动收缩．(D) 有规则运动的能量能够变为无规则运动的能量，但无规则运动的能量不能变为有规则运动的能量 ［ C ］12.热力学第二定律表明：(A) 不可能从单一热源吸收热量使之全部变为有用的功．(B) 在一个可逆过程中，工作物质净吸热等于对外作的功.(C) 摩擦生热的过程是不可逆的.(D) 热量不可能从温度低的物体传到温度高的物体． ［ C ］一、填空题1. 质量为M ，摩尔质量为mol M ，分子数密度为n 的理想气体，处于平衡态时，系统压强P 与温度T 的关系为 P nkT =。
大学物理气体动理论热力学基础复习题及答案详解
第12章 气体动理论一、填空题：1、一打足气的自行车内胎，若在7℃时轮胎中空气压强为4.0×.则在温度变为37℃，轮胎内空气510pa 的压强是。
（设内胎容积不变）2、在湖面下50.0m 深处（温度为4.0℃），有一个体积为的空气泡升到水面上来，若湖面的531.010m -⨯温度为17.0℃，则气泡到达湖面的体积是 。
（取大气压强为）50 1.01310ppa =⨯3、一容器内储有氧气，其压强为，温度为27.0℃，则气体分子的数密度为50 1.0110p pa =⨯；氧气的密度为 ；分子的平均平动动能为 ；分子间的平均距离为。
（设分子均匀等距排列）4、星际空间温度可达2.7k ，则氢分子的平均速率为 ，方均根速率为，最概然速率为。
5、在压强为下，氮气分子的平均自由程为，当温度不变时，压强为51.0110pa ⨯66.010cm -⨯，则其平均自由程为1.0mm 。
6、若氖气分子的有效直径为，则在温度为600k ，压强为时，氖分子1s 内的82.5910cm -⨯21.3310pa ⨯平均碰撞次数为。
7、如图12-1所示两条曲线(1)和(2),分别定性的表示一定量的某种理想气体不同温度下的速率分布曲线,对应温度高的曲线是 .若图中两条曲线定性的表示相同温度下的氢气和氧气的速率分布曲线,则表示氧气速率分布曲线的是 .8、试说明下列各量的物理物理意义：（1）， （2），12kT 32kT （3）， （4），2ikT 2iRT （5），（6）。
32RT 2M iRT Mmol 参考答案：1、 2、54.4310pa ⨯536.1110m -⨯3、25332192.4410 1.30 6.2110 3.4510m kg m J m----⨯⋅⨯⨯4、2121121.69101.8310 1.5010m s m s m s ---⨯⋅⨯⋅⨯⋅图12-15、 6、 7、（2） ，（2）6.06pa 613.8110s -⨯8、略二、选择题：教材习题12-1，12-2，12-3，12-4. （见课本p207～208）参考答案：12-1～12-4 C, C, B, B.第十三章热力学基础一、选择题1、有两个相同的容器，容积不变，一个盛有氦气，另一个盛有氢气（均可看成刚性分子）它们的压强和温度都相等，现将 5 J 的热量传给氢气，使氢气温度升高，如果使氦气也升高同样的温度，则应向氦气传递的热量是（ ）（A ） 6 J（B ） 5 J（C ） 3 J（D ） 2 J2、一定量理想气体，经历某过程后，它的温度升高了，则根据热力学定理可以断定：（1）该理想气体系统在此过程中作了功；（2）在此过程中外界对该理想气体系统作了正功；（3）该理想气体系统的内能增加了；（4）在此过程中理想气体系统既从外界吸了热，又对外作了正功。
《大学物理学》热力学基础练习题
《大学物理学》热力学基础练习题《大学物理学》热力学基础一、选择题13-1．如图所示，bcab 1a 和b 2a 功与吸收热量的情况是( )（A ）b 1a 过程放热、作负功，b 2a 过程放热、作负功；（B ）b 1a 过程吸热、作负功，b 2a 过程放热、作负功；（C ）b 1a 过程吸热、作正功，b 2a 过程吸热、作负功；（D ）b 1a 过程放热、作正功，b 2a 过程吸热、作正功。
【提示：体积压缩，气体作负功；三个过程中a 和b 两点之间的内能变化相同，bca 线是绝热过程，既不吸热也不放热，b 1a 过程作的负功比b 2a 过程作的负功多，由Q W E =+∆知b 2a 过程放热，b 1a 过程吸热】13-2．如图，一定量的理想气体，由平衡态A 变到平衡态B 状态A 和状态B 过程，气体必然 ( )（A ）对外作正功；（B ）内能增加； （C ）从外界吸热；（D ）向外界放热。
【提示：由于A B T T <，必有A B E E <；而功、热量是 过程量，与过程有关】13-3．两个相同的刚性容器，一个盛有氢气，一个盛氦气(均视为刚性理想气体)，开始时它们的压强和温度都相同，现将3 J 的热量传给氦气，使之升高到一定的温度，若氢气也升高到同样的温度，则应向氢气传递热量为 ( ) （A ）6J ； （B ）3J ； （C ）5J ； （D ）10J 。
【提示：等体过程不做功，有Q E =∆，而2mol M iE R T M ∆=∆，所以需传5J 】13-4．有人想象了如图所示的四个理想气体的循）A （）B （）【提示：(A) 绝热线应该比等温线陡，（B ）和（C ）两条绝热线不能相交】13-5．一台工作于温度分别为327℃和27℃的高温热源与低温热源之间的卡诺热机，每经历一个循环吸热2000J ，则对外做功（ ） （A ）2000J ； （B ）1000J ； （C ）4000J ； （D ）500J。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《大学物理学》热力学基础一、选择题13-1．如图所示，bca 为理想气体的绝热过程，b 1a 和b 2a 是任意过程，则上述两过程中气体做功与吸收热量的情况是 ( )（A ）b 1a 过程放热、作负功，b 2a 过程放热、作负功； （B ）b 1a 过程吸热、作负功，b 2a 过程放热、作负功； （C ）b 1a 过程吸热、作正功，b 2a 过程吸热、作负功； （D ）b 1a 过程放热、作正功，b 2a 过程吸热、作正功。
【提示：体积压缩，气体作负功；三个过程中a 和b 两点之间的内能变化相同，bca 线是绝热过程，既不吸热也不放热，b 1a 过程作的负功比b 2a 过程作的负功多，由Q W E =+∆知b 2a 过程放热，b 1a 过程吸热】13-2．如图，一定量的理想气体，由平衡态A 变到平衡态B ，且他们的压强相等，即A B P P =。
问在状态A 和状态B 之间，气体无论经过的是什么过程，气体必然 ( ) （A ）对外作正功；（B ）内能增加； （C ）从外界吸热；（D ）向外界放热。
【提示：由于A B T T <，必有A B E E <；而功、热量是 过程量，与过程有关】13-3．两个相同的刚性容器，一个盛有氢气，一个盛氦气(均视为刚性理想气体)，开始时它们的压强和温度都相同，现将3 J 的热量传给氦气，使之升高到一定的温度，若氢气也升高到同样的温度，则应向氢气传递热量为 ( ) （A ）6J ； （B ）3J ； （C ）5J ； （D ）10J 。
【提示：等体过程不做功，有Q E =∆，而2mol M iE R T M ∆=∆，所以需传5J 】13-4．有人想象了如图所示的四个理想气体的循环过程，则在理论上可以实现的是（ ）A （）C （）B （）D （）【提示：(A) 绝热线应该比等温线陡，（B ）和（C ）两条绝热线不能相交】13-5．一台工作于温度分别为327℃和27℃的高温热源与低温热源之间的卡诺热机，每经历一个循环吸热2000J ，则对外做功（ ）（A ）2000J ； （B ）1000J ； （C ）4000J ； （D ）500J 。
【卡诺热机的效率为211T T η=-，W Qη=，可求得300150%600η=-=，则1000W Q J η==】 13-6．根据热力学第二定律（ ）（A ）自然界中的一切自发过程都是不可逆的； （B ）不可逆过程就是不能向相反方向进行的过程；（C ）热量可以从高温物体传到低温物体，但不能从低温物体传到高温物体； （D ）任何过程总是沿熵增加的方向进行。
【（A ）正确；（B ）少“不引起其他变化”；（C ）想想空调和冰箱热量；（D ）少“孤立系统”条件】7．如图所示为一定量的理想气体的p —V 图，由图可得出结论 ( )（A ）ABC 是等温过程；（B ）B A T T >； （C ）B A T T <； （D ）B A T T =。
【提示：等温线是一条有关原点对称的反比例函数曲线】13--2．对于室温下定体摩尔热容 2.5V C R =的理想气体，在等压膨胀的情况下，系统对外做功与从外界吸收的热量之比/W Q 等于 （ ） （A ）1/3； （B ）1/4； （C ）2/5； （D ）2/7。
【提示：等压膨胀吸热为()VmolM Q C R T M =+∆，内能变化为V molM E C T M ∆=∆，所以，功为mol MW R T M =∆，则13.5A Q =】 13-9．气缸内储有2.0mol 的空气，温度为27℃，若使空气的体积等压膨胀到原来的3倍，则因为空气而对外界所作的功为 （ ）（A ）897J ； （B ）4986J ； （C ）9972J ； （D ）14958J 。
【提示：等压膨胀对外功为W R T ν=∆，而等压变化满足盖•吕萨克方程1212V V T T =，可求出2900T K =，则28.316009972WJ =⨯⨯=】10．一定量的理想气体，处在某一初始状态，现在要使它的温度经过一系列状态变化后回到初始状态的温度，可能实现的过程为 （ ）（A ）先保持压强不变而使它的体积膨胀，接着保持体积不变而增大压强； （B ）先保持压强不变而使它的体积减小，接着保持体积不变而减小压强； （C ）先保持体积不变而使它的压强增大，接着保持压强不变而使它体积膨胀；)33m -533/(10)V m -2133（D ）先保持体积不变而使它的压强减小，接着保持压强不变而使它体积膨胀。
【提示：（A ）选项温度一直升高，（B ）选项温度一直降低，（C ）选项温度一直升高】11．气体的定压摩尔热容P C 大于定体摩尔热容V C ，其主要原因是 ( ) （A ）膨胀系数不同； （B ）温度不同； （C ）气体膨胀需作功； （D ）分子引力不同。
【提示：P V C C R =+的原因是定压时气体膨胀做功，但定体时气体体积不变不做功】12．压强、体积和温度都相同（常温条件）的氧气和氦气在等压过程中吸收了相等的热量，它们对外作的功之比为 ( )（A ）1:1； （B ）5:9； （C ）5:7； （D ）9:5。
【提示：双原子分子的氧气在等压过程中吸收热量为225()2OO mol M Q R R T M =+∆，单原子分子的氦气在等压过程中吸收热量为3()2HeHe mol M Q R R T M =+∆，当2O He Q Q =时，2O He T T ∆<∆，即257O He T T ∆=∆而2mol M iE R T M ∆=∆，所以22222275225322O O O O O O He He HeHe He He R T R T W Q E TW Q E T R T R T ∆-∆-∆∆===-∆∆∆-∆】13．一摩尔单原子理想气体，从初态温度1T 、压强1p 、体积1V ，准静态地等温压缩至体积2V ，外界需作多少功？ ( )（A ）121lnV V RT ； （B ）211ln V VRT ； （C ）)(121V V p -； （D ）1122V p V p -。
【提示：等温过程做功为21V V mol M RTW dV M V=⎰】14．对于理想气体系统来说，在下列过程中，那个过程系统所吸收的热量、内能的增量和对外做功三者均为负值 ( )（A ）等容降压过程；（B ）等温膨胀过程；（C ）等压压缩过程；（D ）绝热膨胀过程。
【提示：等容过程不做功，等温过程无内能的增量，绝热过程无热量传递，等压压缩过程系统对外作负功，温度降低，向外放热】13-15．如图所示，一定量的理想气体经历ACB 过程时吸热700 J ，则经历ACBDA 过程时吸热为 ( )（A ）700 J ； （B ）-700 J ； （C ）500 J ； （D ）-500 J 。
【提示：∵A A B B P V P V =，∴A B T T =，表明A 、B 两位置等温， 等温过程无内能的增量；B D →为等容过程，不做功，吸收热 量全部使得内能增加；D A →为等压过程，放出热量，对外做负功，同时内能减少，对外做的负功为()1200DA A A D W P V V J =-=-；∴理想气体经历BDA 过程内能不变，对外做的负功为1200J -，由Q E W =∆+知1200BDA Q J =-，则1200700500ACBDA Q J =-+=-】13--3．“理想气体和单一热源接触做等温膨胀时，吸收的热量全部用来对外做功”。
对此说法，有以下几种评论，哪个正确？ ( )（A ）不违反热力学第一定律，但违反热力学第二定律； （B ）不违反热力学第二定律，但违反热力学第一定律； （C ）不违反热力学第一定律，也不违反热力学第二定律； （D ）违反热力学第一定律，也违反热力学第二定律。
【提示：热力学第二定律强调的是“…循环工作的热机…”】17．在P V -图上有两条曲线abc 和a d c ，由此可以得出以下结论： ( ) （A ）其中一条是绝热线，另一条是等温线； （B ）两个过程吸收的热量相同； （C ）两个过程中系统对外作的功相等； （D ）两个过程中系统的内能变化相同。
【提示：只有内能是状态量】18．理想气体卡诺循环过程的两条绝热线下的面积大小（图中阴影部分）分别为1S 和2S ，则两者的大小关系为：( ) （A ）12S S >；（B ）12S S <；（C ）12S S =；（D ）无法确定。
【提示：由于理想气体卡诺循环过程的另两条是等温线，所以两者 内能变化相同；绝热过程无吸放热量，所以功为内能变化的负值，相等】13--4．关于可逆过程和不可逆过程有以下几种说法：（1）可逆过程一定是准静态过程；（2）准静态过程一定是可逆过程； （3）对不可逆过程，一定找不到另一过程使系统和外界同时复原； （4）非静态过程一定是不可逆过程。
以上几种说法，正确的是： ( )（A ）（1）（2）（3）； （B ）（2）（3）（4）； （C ）（1）（3）（4）； （D ）（1）（2）（3）（4）。
13--5．一绝热容器被隔板分为两半，一半是为真空，一半为理想气体，若抽去隔板，气体将自由膨胀，达到平衡后 ( ) （A ）温度不变，熵增加； （B ）温度升高，熵增加； （C ）温度降低，熵增加； （D ）温度不变，熵不变。
【见书P246页例4，气体自由膨胀不对外做功，气体的内能也没有改变，所以温度不变；但气体自由膨胀后，不可能自发的回到原始的一半是真空状态，所以熵增加】二、填空题1．有1mol 刚性双原子分子理想气体，在等压膨胀中对外做功W ，则其温度变化53)m T ∆= ；从外界吸收的热量P Q = 。
【双原子分子内能变化为52ER T ν∆=∆，等压膨胀中吸热为5()2Q R R T ν=+∆，则由热力学第一定律，W R T ν=∆，而1ν=，有T ∆=/W R ；P Q =7/2W 】 2．有1mol 单原子分子理想气体，从状态111( )A p V T ，，变化至状态 222( )B p V T ，，，如图所示，则此过程气体对外做功W = ； 吸收热量Q = 。
【气体对外做功可由p V-图的梯形面积求出，有W =12211()()2p p V V +-；单原子分子内能变化为213()2E R T T ν∆=-，再由热力学第一定律，Q W E =+∆=12212113()()()p p V V R T T +-+-】13--7循环过程中吸热和放热的情况是：1→2过程： ，2→3过程： ，3→1过程： 。
【提示，注意到给出的是VT -图，所以1→2过程是等压膨胀，系统吸热并对外做功，内能增加；2→3过程是等容降温，不做功，内能减少，系统放热；3→1过程是等温压缩，系统做负功，内能不变，系统放热】4．如图所示，一理想气体系统由状态a 沿acb 到达状态b ，系统吸收热量350J ，而系统做功为130J 。