理论力学期末试卷-模拟试卷04(带答案)
理论力学考试试的题目(的题目库-带答案)

理论力学期末考试试题1-1、自重为P=100kN的T字形钢架ABD,置于铅垂面内,载荷如图所示。
其中转矩M=20kN.m,拉力F=400kN,分布力q=20kN/m,长度l=1m。
试求固定端A的约束力。
解:取T型刚架为受力对象,画受力图.1-2 如图所示,飞机机翼上安装一台发动机,作用在机翼OA上的气动力按梯形分布:q=60kN/m,2q=40kN/m,机翼重1p=45kN,1发动机重p=20kN,发动机螺旋桨的反作用力偶矩M=18kN.m。
求2机翼处于平衡状态时,机翼根部固定端O所受的力。
解:1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,已知q=10kN/m,F=50kN,M=6kN.m,各尺寸如图。
求固定端A 处及支座C的约束力。
1-4 已知:如图所示结构,a, M=Fa, 12F F F ==, 求:A ,D 处约束力.解:1-5、平面桁架受力如图所示。
ABC为等边三角形,且AD=DB。
求杆CD的内力。
1-6、如图所示的平面桁架,A端采用铰链约束,B端采用滚动支座约束,各杆件长度为1m。
在节点E和G上分别作用载荷F=10kN,EF=7 kN。
试计算杆1、2和3的内力。
G解:2-1 图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面内,且与铅直线成45º角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=DM。
若F=10kN,求各杆的内力。
2-2 杆系由铰链连接,位于正方形的边和对角线上,如图所示。
在节点D沿对角线LD方向作用力F。
在节点C沿CH边铅直向下作用D力F。
如铰链B,L和H是固定的,杆重不计,求各杆的内力。
2-3 重为P=980 N,半径为r =100mm的滚子A与重为2P=4901N的板B由通过定滑轮C的柔绳相连。
已知板与斜面的静滑动摩擦因数f=0.1。
滚子A与板B间的滚阻系数为δ=0.5mm,斜面倾角αs=30º,柔绳与斜面平行,柔绳与滑轮自重不计,铰链C为光滑的。
理论力学期末模拟试卷8套
B
D
a
FgR
A mg FD
F Ax
F Ay
第 4页共 5页
B
h= 1m
a
l
D 30° A
解:以杆为研究对象 , 受力如图,虚加惯性力
M A (F ) 0
点系的mg达l c朗os3伯0 原FD理l FgR l sin 30 0
2
2
2
FgR= - ma, 则由质
FD m( g cos30 a sin30 )
( D )M1 点科氏加速度大小为 2 v1 sin ,方向垂直纸面向里
解:( 研究 AB,已知
的方向,因此可确定出 P 点为速度瞬心
v A l , AP l AB v A / AP l / l
vB BP AB
2l ( )
四.一根直杆和一个圆盘焊接组成的系统, 它们的质量均为 8 kg, 可绕 O 点转动,当 OA 处于水平位置时 , 系统具有角速度 =4rad/s 。求该瞬时轴承 O的反力。( 15 分)
( B)其它同( A ),但其中 LQ 1 ml 2
12
( C)仅为作用于杆质心的一个力: RQ 1 ml
2
( D )仅为作用于图面内的一个力偶:
LQ 1 ml 2 3
M 2 点科氏加速度为 0
A
C
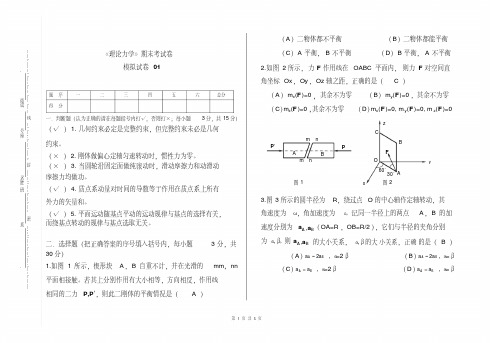
9. 两个相同的定滑轮如下图示,开始时都处于静止,问下面描述
正确的是( A ) ( A ) A B, A B ( C) A B , A B
外力的矢量和。
(√ ) 5. 平面运动随基点平动的运动规律与基点的选择有关, 而绕基点转动的规律与基点选取无关。
二.选择题(把正确答案的序号填入括号内,每小题 30 分) 1.如图 1 所示,楔形块 A , B 自重不计,并在光滑的
理论力学期末试卷-模拟试卷03(带答案)

《理论力学》期末考试模拟试卷03题 序 一 二 三 四 五 六 总分 得 分一. 填空题(每空3分, 共30分)1.已知力 沿直线AB 作用, 其中一个分力的作用线与AB 成30°角, 若欲使另一个分力的大小在所有分力中为最小, 则此二分力间的夹角..9. 度。
2.已知力 的大小为60(N ),则力 对x 轴的矩.160(N ·cm.;对z 轴的矩.100(N ·cm )。
3.设一质点的质量为m, 其速度 与x 轴的夹角为 , 则其动量在x 轴上的投影为mv.=mvcos 。
4.图示结构受矩为M=10KN.m 的力偶作用。
若a=1m, 各杆自重不计。
则固定铰支座D 的反力的大小为 10kN , 方向 水平向右 。
5.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
6.已知A 重100kN ,B 重25kN ,A 物与地面间摩擦系数为0.2。
端铰处摩擦不计。
则物体A 与地面间的摩擦力的大小.. 1.k.....。
二. 选择题(把正确答案的序号填入括号内, 每小题3分, 共15分)1. 作用在一个刚体上的两个力 A 、 B ,满足 A=- B 的条件,则该二力可能....... 。
(A )作用力和反作用力或一对平衡的力; (B )一对平衡的力或一个力偶; (V )一对平衡的力或一个力和一个力偶; (D )作用力和反作用力或一个力偶。
2. 某平面任意力系向O 点简化, 得到如图所示的一个力 (和一个力偶矩为Mo 的力偶, 则该力系的最后合成结果... ... 。
(A )作用在O 点的一个合力; (B )合力偶;(C )作用在O 点左边某点的一个合力;(D )作用在O 点右边某点的一个合力。
3.一动点在圆盘内运动, 同时圆盘又绕直径轴x 以角速度ω转动, 若AB ∥OX, CD ⊥OX, 则当动点....运动时, 可使科氏加速度恒等于零。
理论力学期末试卷-模拟试卷04(带答案)

理论⼒学期末试卷-模拟试卷04(带答案)《理论⼒学》期末考试模拟试卷04⼀.判断题(认为正确的请在每题括号内打√,否则打×;每⼩题3分,共30分)1. 在任意初始条件下,刚体不受⼒的作⽤、则应保持静⽌或作等速直线平移。
(错)2. 不论牵连运动的何种运动,点的速度合成定理a =e +r 皆成⽴。
(对)3. 在点的合成运动中,动点的绝对加速度总是等于牵连加速度与相对加速度的⽮量和。
(错)4. 某⼀⼒偶系,若其⼒偶矩⽮构成的多边形是封闭的,则该⼒偶系向⼀点简化时,主⽮⼀定等于零,主矩也⼀定等于零。
(对) 5. 某空间⼒系由两个⼒构成,此⼆⼒既不平⾏,⼜不相交,则该⼒系简化的最后结果必为⼒螺旋。
(对) 6. 某⼒系在任意轴上的投影都等于零,则该⼒系⼀定是平衡⼒系。
(错) 7. 已知直⾓坐标描述的点的运动⽅程为X=f 1(t ),y=f 2(t ),z=f 3(t ),则任⼀瞬时点的速度、加速度即可确定。
(对) 8. ⼀动点如果在某瞬时的法向加速度等于零,⽽其切向加速度不等于零,尚不能决定该点是作直线运动还是作曲线运动。
(对) 9. 刚体作平⾯运动时,平⾯图形内两点的速度在任意轴上的投影相等。
(错) 10. 某刚体作平⾯运动时,若A 和B 是其平⾯图形上的任意两点,则速度投影定理[][]A AB B AB v v =永远成⽴。
(对)⼆.填空题(把正确答案括号内,每空1分,共15分) 1. 已知点沿半径为R 的圆周运动,其规律为①S=20t ;②S=20t2(S 以⽶计,t 以秒计),若t=1秒,R=40⽶,则上述两种情况下点的速度为① 20m/s ,② 40m/s ;点的加速度为① 10m/s2 ,②2. 已知A 重100kN ,B 重25kN ,A 物与地⾯间摩擦系数为0.2。
端铰处摩擦不计。
则物体A 与地⾯间的摩擦⼒的⼤⼩为 15 kN 。
3. 定轴转动刚体上点的速度可以⽤⽮积表⽰为v =ω×4. 若将动坐标取在作定轴转动的刚体上,则刚体内沿平⾏于转动轴的直线运动的动点,其加速度⼀定等于牵连加速度和相对加速度的⽮量和5. 如右图所⽰的平⾯机构,由摇杆A O 1、B O 2,“T 字形”刚架ABCD ,连杆DE 和竖直滑块E 组成,21O O ⽔平,刚架的CD 段垂直AB 段,且AB=21O O ,已知l BO AO ==21,DE=l 4 ,A O 11DE 的质量均匀分布且⼤⼩为M 。
理论力学期末考试试题(卷)(试题(库)带答案解析)

理论力学 期末考试试题1-1、自重为P=100kN 的T 字形钢架ABD,置于铅垂面,载荷如图所示。
其中转矩M=20kN.m ,拉力F=400kN,分布力q=20kN/m,长度l=1m 。
试求固定端A 的约束力。
解:取T 型刚架为受力对象,画受力图.1-2 如图所示,飞机机翼上安装一台发动机,作用在机翼OA 上的气动力按梯形分布:1q =60kN/m ,2q =40kN/m ,机翼重1p =45kN ,发动机重2p =20kN ,发动机螺旋桨的反作用力偶矩M=18kN.m 。
求机翼处于平衡状态时,机翼根部固定端O 所受的力。
解:1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,已知q=10kN/m,F=50kN,M=6kN.m,各尺寸如图。
求固定端A处及支座C的约束力。
1-4 已知:如图所示结构,a, M=Fa, 12F F F ==, 求:A ,D 处约束力.解:1-5、平面桁架受力如图所示。
ABC 为等边三角形,且AD=DB 。
求杆CD 的力。
1-6、如图所示的平面桁架,A 端采用铰链约束,B 端采用滚动支座约束,各杆件长度为1m 。
在节点E 和G 上分别作用载荷E F =10kN ,G F =7 kN 。
试计算杆1、2和3的力。
解:2-1 图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面,且与铅直线成45º角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=DM。
若F=10kN,求各杆的力。
2-2 杆系由铰链连接,位于正方形的边和对角线上,如图所示。
在节点D沿对角线LD方向作用力F。
在节点C沿CH边铅直向下作用力F。
如铰链B,L和H是固定的,杆重不D计,求各杆的力。
2-3 重为1P =980 N ,半径为r =100mm 的滚子A 与重为2P =490 N 的板B 由通过定滑轮C 的柔绳相连。
已知板与斜面的静滑动摩擦因数s f =0.1。
《理论力学》模拟试题答案.docx
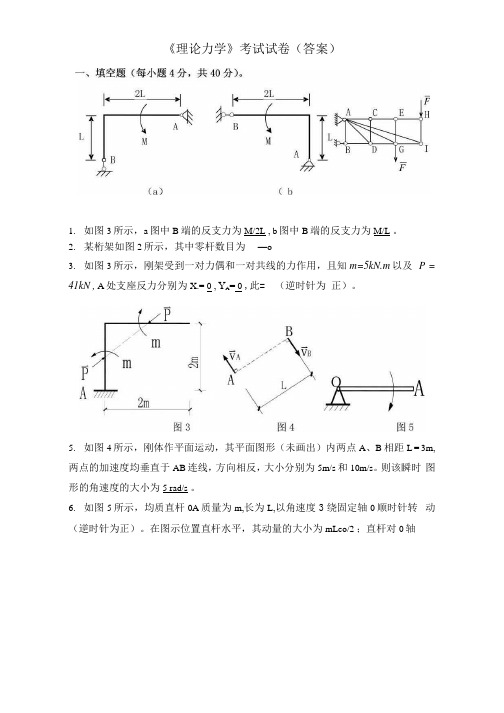
《理论力学》考试试卷(答案)1.如图3所示,a图中B端的反支力为M/2L , b图中B端的反支力为M/L 。
2.某桁架如图2所示,其中零杆数目为—o3.如图3所示,刚架受到一对力偶和一对共线的力作用,且知m=5kN.m以及P = 41kN , A处支座反力分别为X.= 0 ,Y A= 0 ,此= (逆时针为正)。
5.如图4所示,刚体作平面运动,其平面图形(未画出)内两点A、B相距L = 3m, 两点的加速度均垂直于AB连线,方向相反,大小分别为5m/s和10m/s。
则该瞬时图形的角速度的大小为5 rad/s 。
6.如图5所示,均质直杆0A质量为m,长为L,以角速度3绕固定轴0顺时针转动(逆时针为正)。
在图示位置直杆水平,其动量的大小为mLco/2 ;直杆对0轴动量矩的大小为ml? 3/3 ,杆动能大小为ml; 3 76。
二、计算题(共60分)。
1.如图所示,梁AC用三根链杆支承,梁受集中力P和均布荷载作用,已知P=40kN, q=5kN/m,试求各链杆的内力。
(本题15分)解:受力分析如图所示:2.桁架如图所示,试求杆件CD, CE和EF的内力。
(本题15分)解:由图分析可知CD杆为0杆。
……(1分)1)先取整体分析,如图所示分别对A点和B点取矩:Am尸)=o-2x10-4x10-6x10-8x5 + 8x7? = 0D2>*)=°2x10 + 4x10 + 6x10 + 8x5-8x7?^ =0解得:R A =20kN, R B =20kN如图取I - I截面左半部分对A点取矩,取II-11截面右部分对B点取矩£ 〃很了)= 0-2xl0-2x S CE sin(cif)-lx S CE cos(o) = 0£ 〃七(了)= o8X7?A +8X5+6X10+4X10+6X S CE sin(。
)-lx S CE cos(。
)+ 4x S FE = 0上式解得:S^=—11.18KN, S FF = 1QKNCc r Zi3,图示机构中,曲柄04长为r,绕。
完整版理论力学期末考试试题题库带答案

理论力学期末测试试题1-1、自重为P=100kN的T字形钢架ABD,置于铅垂面内,载荷如下列图.其中转矩M=20kN.m ,拉力F=400kN,分布力q=20kN/m,长度l=1m.试求固定端A的约束力.解:取T型刚架为受力对象,画受力图其中耳一;q •次-3(ikN工已二“产看十骂—F£m6<r = 0工弓=0 ^-?-Fcos600 = 0一.一^ A必-W-Fi/十外必60F + F疝g= 0i^ = 3164kN 为二SOQkNMi= - IlSSkNm1-2如下列图,飞机机翼上安装一台发动机,作用在机翼OA上的气动力按梯形分布:解:q i=60kN/m, q2 =40kN/m ,机翼重P i=45kN ,发动机重P2 =20kN ,发动机螺旋桨的反作用力偶矩M=18kN.m .求机翼处于平衡状态时,机翼根部固定端.所受的力.幅研究机翼.把梯形教荷分解为一三角形载荷与一轮修救荷,其合力分利为Fja = y(^)- q2) , 9 = 90 kN,F k2= 9 * = 36° kN分别作用在矩赛.点3m与4.5 m处,如下列图,由= 口,F山=01Y = 0, F% - K - P# 1 中k=0SM0(F1 = Q t Mo - 3.6P| — 4.2尸工一M + 3F RI + 4.$F R1 = 0解得For = 0T F Q,=- 3S5 k\, M0 二-1 626 kN * m1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,q=10kN/m , F=50kN , M=6kN.m ,各尺寸如图.求固定端A处及支座C的约束力.6 m 1 i m } I m !M 先研究构架EBD如图(b),由WX= 0, F小-F sin30' = 0E Y = 0.F HJ + F3 - F mfi30 = 02A什⑺=0T F2 T - M + 2F = 0 解得= 25 kN. = 87.3 kN. F/ =-44 kN 再研究AB梁如图(a).由解:XX = 04 -如* 6 sinJO* * F旭一Fn, = 0XV - 0,为-1 6 (xx3tf . F* 二UEM八F) - 0, - 2 * -j * & * fl coeJO -白产皿"0懈得F〞 = 40 kN. F A I= 113 3 kN. M A= 575,S kN - m it愿也可先研究EBD,求得F*之后.再研究整体,求a处反力।这样祈减少平街方程数■但计算鼠并未明髭减少,1-4:如下列图结构, a, M=Fa, F1 F2 F,求:A, D处约束力.以上修为明究时聚.受力如下列图.广%-0 加-:'=. T工… 4・%七.二工9口 : 0 A<P -I %'二昌1'二小l nF吗一:F /=F1-5、平面桁架受力如下列图. ABC为等边三角形,且AD=DB .求杆CD的内力.H 翌体受力如图Q).由工M A(F)=0,方,/\ *F\B"4B - F - 1■心・sinbU- - Q 6蹲得Fw 一§F⑸.反将桁架微升.研究右边局部,如图化)所 \ __________________示,由人汽J^*Wf)= g Fft* ■ DB * sinfiO f+ F.nc , flH - F , £)P - sinGO,= 0 %⑻解樗Ffp = -|F/再研究节点匚,如图(cl由尔工K =①(Ftr- F在加曲,=0 代〞的EV = 0, -(F CF +F C¥)m&S0,- F QJ = Q *3 57ffl解得Fm =一与F t) 866F(压)本剧晟筒单的解法是.菖先断定QE杆为零杆,再觎取&BDF来研兆,只由一个方覆LM a(f> =.,即可健出R* ,读者不妨一试.1-6、如下列图的平面桁架,A端采用钱链约束,B端采用滚动支座约束, 各杆件长度为1m.在节点E和G上分别作用载荷F E=10kN, F G=7 kN.试计算杆1、2和3的内力.解:取圣体.求支庄为束力.工…小口口小0%+品一3%A取= 9kN / = SLN用盘面法,取疗架上边局部,s城■ g一月1 y〔峪3.“ 一/.」二9▽5=.&+鸟/疝16.“ 一鸟二0 E氏=0 F{\H 十巴83600 —.^ = l04kN(aj ^=l.l?kN 但弓।牛iilkNlji】2-1图示空间力系由6根桁架构成.在节点A上作用力F,此力在矩形ABDC平面内,且与铅直线成45o角.A EAK= A FBM.等腰三角形EAK , FBM和NDB在顶点A, B和D处均为直角,又EC=CK=FD=DM .假设F=10kN ,求各杆的内力.解节点受力分别如图所开:,对节点八,由工X —0, F1 sin45 - % sin45 = 0+ F sin45' = 0£Y " F3= 0, —F] C3s45 —F± COH45-F cos45 - 0解得Fi = F:= -5kN〔压〕, F3=一7.07 kN〔压〕再对节点B,由SX ~ 0, F$ stn45* - F< sin45, ; 0EV = 0. Fi sin45 - F3 = 0三2 士0, 一居a>s45 - F? crt?45" - F6 co^45' = 0 解得F4 = 5 kN〔拉〕,R=5卜^1〔拉〕,5& =- 10 kN〔压〕2-2杆系由钱链连接, 位于正方形的边和对角线上,如下列图.在节点D沿对角线LD方向作用力F D.在节点C沿CH边铅直向下作用力F.如钱链B, L和H是固定的,杆重不计, 求各杆的内力.求解TY = 0,SZ = 0,求二 0,F| 4M5* + Fj + F. sn45 = 0 厕 4,30 图解得 Fi = F D (1C),F $ =F J =二 Ji F 虱电然后研究节点c ,由SX = 0, - Fj - F*W cut45' - 0v3 £Y = ar -Fj - Fi — sin45 = 0心SZ = 0h - F, - F - F4言=0得 Fj = 7年户口,匕=-/5匹口. Fs M- (F + \2F D )2-3 重为R=980 N,半径为r =100mm 的滚子A 与重为P 2 = 490 N 的板B 由通过定滑轮 C 的柔绳相连.板与斜面的静滑动摩擦因数f s =0.1 o 滚子A 与板B 间的滚阻系数为8C 为光滑的.求各杆的内力. 先研究节点D,由- F)cts?45 + F 口 au45 - 0=0.5mm,斜面倾角a =30o,柔绳与斜面平行,柔绳与滑轮自重不计,钱链 拉动板B 且平行于斜面的力 F 的大小.〔l i 设闻拄口有向下漆动慧等.取国校DFsu 话出—凡-H-3=0EFf =❶ /一 Fcosfl = 0一% /Vine 7- co*?i 算豉圄杜.有向匕浪动越势.虢S ]社“ 三H 』二UJ£ 一%】R l J 'O U _EF F - 0 及-Fai%一.又Mn>« =的&- /J(siii 口 \ — u.凶 81J JI ,13.jp."系怩平衍叶F4五河n 日一)co* 6}工A4 尸I 五m n 8一 3 cow R'\-3/c - 0 1氏-A& =0 工尸j 二.尸M -FCQ博.二.只浪不滑3t.应点 门“用=¥斗型8那么上之£ y K 同理一圆柱.有向上填动趋势时得二二三 K 间柱匀速蛇淳时. f一 R2-4两个均质杆AB 和BC 分别重P i 和P 2 ,其端点A 和C 用球较固定在水平面, 另一端B 由 球镀链相连接,靠在光滑的铅直墙上,墙面与 AC 平行,如下列图.如 AB 与水平线的交角 为45o, / BAC=90.,求A 和C 的支座约束力以及墙上点B 所受的压力.解先研究AB 杆,受力如图(b),由। n 投阅柱.有向下滚动越舜O题4.27-SMjF)三0, 一几,QA = 0 得1 0 再取AB、CD两杆为一体来研究,受力如图(月海茉:由EM AC(F)= 0t(P[ + Pj) <WG45_F N* AB 热in45 —0XX = 0,九十 % = 0工My(F)= 0, Fc - AC - pj • AC = 0 LNZ 〞开工+如一2】一丹=0(F) —0, -(F AT+ FQ • OA - Fc y *- AC= 0工M塞2 K = 0, % + % + Fn = 0解得Fx = y(Pi + Pj)»Fer =.产值=2^P:t町=Pi +yp2>F o= 0,%=-2(P[ + 尸口3-1:如下列图平面机构中,曲柄OA=r,以匀角速度°转动.套筒A沿BC杆滑动.BC=DE ,且BD=CE=l.求图示位置时,杆BD的角速度和角加速度.解:].动点:滑块T 动系:贰广杆绝对运动:国周运动〔.点〕相对运动:直线运动〔£「二)j|iij V V V&加速度4_ 3/十&*)疝13伊_ J5诏r(/+r)耳cos30Q ST?收属/(/ + r)cz w= 1—1=----- 不 ------w BD 3 户3-2 图示钱链四边形机构中, O i A = O2B =100mm ,又QO2 = AB,杆O〔A以等角速度=2rad/s绕轴01转动.杆AB上有一套筒C,此套筒与杆CD相较接.机构的各部件都在同一铅直面内.求当①二60o时杆CD的速度和加速度.〔15分〕解取CD杆上的点C为动点,AB杆为动系,时动点作速度分析和加速度分析,如图S〕、〔b〕所示,图中式中口月=〔八一4 •田二0一2 ir〕/s5 - 0iA • J = 0*4 m/s2 解出杆CD的速度.加速度为G =-UA coep = 0. I mA&3 = since;= 0,3464 m/s2«1aAM1Al1V!4-1:如下列图凸轮机构中,凸轮以匀角速度3绕水平.轴转动,带动直杆AB沿铅直线上、下运动,且O, A, B共线.凸轮上与点A接触的点为A',图示瞬时凸轮轮缘线上' '点A的曲率半径为 A ,点A的法线与OA夹角为e , OA=l.求该瞬时AB的速度及加速度.〔15 分〕绝对运动: 相对运动: 奉连道处:2.速度大小 方向 1, 二、Ja 】iH=「WkmH I丫3,加速度 比=凡."'+ %r 门 大小9炉『『、;"2 方向 / /4-2:如下列图,在外啮合行星齿轮机构中,系杆以匀角速度 定,行星轮半径为r,在大轮上只滚不滑.设 A 和B 是行星轮缘 上的两点,点 A 在O 1O 的延长线上,而点 B 在垂直于o 1o 的半径上.求:点 A 和B 的加速度.解:2.选基点为〔〕亓*二后.*疗;口 +疗;. 大小0 *忒0 1时 方向“ J JJi7A ~ a ? +^C?I .轮I 作平面运动,瞬心为「沿"轴投勉乙8々4 * ■献i 1+ .1绕O i 转动.大齿轮固S 二「" 直线运动 曲线运动 定购林动 功系:凸轮. C 凸轮外边瘴〕〔.轴〕大小,方向?% ="g =仃口+ "什=fuclaii——=闺.㈢11 -4-3: 动.摇杆OC铅直,〔科氏加速度〕如下列图平面机构, AB长为1,滑块A可沿摇杆OC的长槽滑OC以匀角速度3绕轴O转动,滑块B以匀速v 1沿水平导轨滑动.图示瞬时AB与水平线OB夹角为300.求:此瞬时AB杆的角速度及角加速度.〔20分〕* *沿】:方向投彩大小方句V4B COS30J LD F福:速度分析1-杆.〞作平面运动,族点为瓦V A = V S - y AP2.动点:滑块.心动系:〞抨沿£方向强彩以一=1■沿吃方向表恁% ; gin 30" -4?os 对15-1如下列图均质圆盘,质量为m 、半径为R,沿地面纯滚动,角加速为3.求圆盘对图中A,C 和P 三点的动量矩. 平行轴定理:4二=一十/嫉 一或点P 为睡心 3hL ? = ^^R-\ L e =mP 2it 〕\ 1相?\"= -15-2 〔动量矩定理〕:如下列图均质圆环半径为 r,质量为m,其上焊接刚杆 OA,杆加生度介册 0f Ai = = 3VJtv 2AB点「为眉心上匚二J屯+ 1师;-G长为r,质量也为m.用手扶住圆环使其在OA水平位置静止.设圆环与地面间为纯滚动.独汰庵一方「.斗管力加玛所示建丸平为走动微分方程2f -月—+Y2由朱加R先K熹法瑞拽彩到水平强错乱两个才向20 r3"悟105-3 11-23 〔动量矩定理〕均质圆柱体的质量为m,半径为r,放在倾角为60o的斜面上, 一细绳绕在圆柱体上,其一端固定在A点,此绳和A点相连局部与斜面平行,如下列图.如圆柱体与斜面间的东摩擦因数为f=1/3,求圆柱体的加速度.〔15〕(15)解:解IW柱受力与运动分析如图.平而运动徽分方程为nta〔;= mg sin60* 一尸一Fj,.=F\ —fiig CQt^ff』社- 〔F=—广〕『式中F = /Fv» ac - fQ解得口c=O.355q5-4 11-28 〔动量矩定理〕均质圆柱体A和B的质量均为m,半径均为r, 一细绳缠在绕固定轴.转动的圆柱A上,绳的另一端绕在圆柱B上,直线绳段铅垂,如下列图.不计摩擦.求:〔1〕圆柱体B下落时质心的加速度;〔2〕假设在圆柱体A上作用一逆时针转向力偶矩M,试问在什么条彳^下圆柱体B的质心加速度将向上.〔15分〕解:解“〕两轮的受力与运动分析分别如用w.1 2 ET™r=近]对E轮,有以轮与直樊和切点为基点,明轮心B的加速度〃工,M t s4解得5g〔2〕再分别对两卷作受力与运动分析如图〔b〕对内轮,有fflaa =ntg -Ppj~2 tfrr~afj —rFj2依然存运动学关系dj}二皿用+的日J但Q.i中也B〕令< 0,可解得31柱体B的质心加速度向上的条件:M〉217UJT6-1:轮O的半径为R1 ,质量为ml,质量分布在轮缘上;均质轮C的半径为R2 , 质量为m2 ,与斜面纯滚动,初始静止.斜面倾角为.,轮.受到常力偶M驱动. 求: 轮心C走过路程s时的速度和加速度.〔15分〕韩:轮C1月轮0扶同作为一个质点系九一a『w 一阁7j = o石—,血人"吊斗!岫甘&岫对网」言必二% =9 1V :3/聚TH得J弘口日=-^―〔+3JJL〕旭〕中二二¥ =:羡居迎日一式G〕是函数关系式.两端计『求导,得-〔Jffij + 访看网收=M -Kin H - 鸟2 例U 尸―- :〔加1+.%啊〕局6-2均质杆 OB=AB=l,质量均为 m,在铅垂面内运动,AB 杆上作用一不变的力偶矩M,系统初始静止,不计摩擦.求当端点 A 运动到与端点 .重合时的速度. 〔15分〕解:由于A 京不离并地面,那么,EAO= /BOA.牝=可=H嫌同:是否可以利用求寻求此蜓时的商和速段? 〔H 与行没 有必然联系,角度不是时间的函数.〕6-3:重物m,以v 匀速下降,钢索刚度系数为 k .求轮D 突然卡住时,钢索的最大张 力.〔15分〕1J 上口『9-"将『〔1-E 穹 2/ V itt由「二心〞;有6-4均质杆 AB 的质量m=4kg,长l=600mm,均匀圆盘B 的质量为6kg,半径为r=600mm, 作纯滚动.弹簧刚度为 k=2N/mm,不计套筒A 及弹簧的质量.连杆在与水平面成 30o 角时无 初速释放.求〔1〕当AB 杆达水平位置而接触弹簧时,圆盘与连杆的角速度;〔2〕弹簧的最大压缩量 max o 〔 15分〕彝:卡住前E 二些 s* kF - kS SJ - mg - 2.45kN卡隹后取点物平街位苜1为更力加弹性力的 搴势T ; 一"解U〕该系统初始静tL.动能为杆达水平位置时.B 点是33杆的速度瞬心,网盅的角速度3H = 0,设杆的角速度为那么业,山幼能近理,得\ * ;配%品-0 = mg * ~ 5in341,解得连杆的角速度号〞:4;殳巴丝⑵AB杆达水平位置接触赢亚,统的动能为“,弹簧达到最大压缩量bz.的瞬时,系魂再次鄢止.动能丁;:= 0.由72 - 7】二五得0 _ [■闻]品=-J 6ra«二+ mJ片0 W *■解得1AM= 87.1 mm。
理论力学期末试卷-模拟试卷03(带答案)

《理论力学》期末考试模拟试卷03题 序 一 二 三 四 五 六 总分 得 分一.填空题(每空3分,共30分)1. 已知力F 沿直线AB 作用,其中一个分力的作用线与AB 成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为 90 度。
2. 已知力F 的大小为60(N ),则力F 对x 轴的矩为 160(N·cm ) ;对z 轴的矩为 100(N·cm )。
3. 设一质点的质量为m ,其速度v 与x 轴的夹角为α,则其动量在x 轴上的投影为mvx =mvcos α。
4.图示结构受矩为M=10KN.m 的力偶作用。
若a=1m ,各杆自重不计。
则固定铰支座D 的反力的大小为 10kN ,方向水平向右 。
5. 作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
6. 已知A 重100kN ,B 重25kN ,A 物与地面间摩擦系数为0.2。
端铰处摩擦不计。
则物体A 与地面间的摩擦力的大小为 15 kN 。
二.选择题(把正确答案的序号填入括号内,每小题3分,共15分)1. 作用在一个刚体上的两个力F A 、F B ,满足F A=-F B 的条件,则该二力可能是B 。
(A )作用力和反作用力或一对平衡的力; (B )一对平衡的力或一个力偶; (V )一对平衡的力或一个力和一个力偶; (D )作用力和反作用力或一个力偶。
2. 某平面任意力系向O 点简化,得到如图所示的一个力R '和一个力偶矩为Mo 的力偶,则该力系的最后合成结果为 C 。
(A )作用在O 点的一个合力; (B )合力偶;(C )作用在O 点左边某点的一个合力; (D )作用在O 点右边某点的一个合力。
3. 一动点在圆盘内运动,同时圆盘又绕直径轴x 以角速度ω转动,若AB ∥OX ,CD ⊥OX ,则当动点沿 C 运动时,可使科氏加速度恒等于零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《理论力学》期末考试
模拟试卷04
一.判断题(认为正确的请在每题括号内打√,否则打×;每小题3分,共30分)
1. 在任意初始条件下,刚体不受力的作用、则应保持静止或作等速直线平移。
(错)
2. 不论牵连运动的何种运动,点的速度合成定理a =e +r 皆成立。
(对)
3. 在点的合成运动中,动点的绝对加速度总是等于牵连加速度与相对加速度的矢量
和。
(错)
4. 某一力偶系,若其力偶矩矢构成的多边形是封闭的,则该力偶系向一点简化时,主矢
一定等于零,主矩也一定等于零。
(对) 5. 某空间力系由两个力构成,此二力既不平行,又不相交,则该力系简化的最后结果必
为力螺旋。
(对) 6. 某力系在任意轴上的投影都等于零,则该力系一定是平衡力系。
(错) 7. 已知直角坐标描述的点的运动方程为X=f 1(t ),y=f 2(t ),z=f 3(t ),则任一瞬时点的
速度、加速度即可确定。
(对) 8. 一动点如果在某瞬时的法向加速度等于零,而其切向加速度不等于零,尚不能决定该点是作直线运动还是作曲线运动。
(对) 9. 刚体作平面运动时,平面图形内两点的速度在任意轴上的投影相等。
(错) 10. 某刚体作平面运动时,若A 和B 是其平面图形上的任意两点,则速度投影定理[][]A AB B AB v v =永远成立。
(对)
二.填空题(把正确答案括号内,每空1分,共15分) 1. 已知点沿半径为R 的圆周运动,其规律为①S=20t ;②S=20t2(S 以米计,t 以秒计),若t=1秒,R=40米,则上述两种情况下点的速度为① 20m/s ,② 40m/s ;点的加 速度为① 10m/s2 ,②
2. 已知A 重100kN ,B 重25kN ,A 物与地面间摩擦系数为0.2。
端铰处摩擦不计。
则物体
A 与地面间的摩擦力的大小为 15 kN 。
3. 定轴转动刚体上点的速度可以用矢积表示为v =ω×
4. 若将动坐标取在作定轴转动的刚体上,则刚体内沿平行于转动轴
的直线运动的动点,其加速度一定等于牵连加速度和相对加速度的矢量和
5. 如右图所示的平面机构,由摇杆
A O 1、
B O 2,“T 字形”刚架ABCD ,连杆
DE 和竖直滑块E 组成,21O O 水平,刚架的CD 段垂直AB 段,且AB=21O O ,已知
l BO AO ==21,DE=l 4 ,A O 11DE 的质量均匀分布且大小为M 。
在图示位置瞬时,若A O 1杆竖直,连杆DE 与刚架CD 段的夹
角为o CDE 60=∠,则在该瞬时:A 点的速度大小为 l ω ,A 点的加速度大小为 l 2ω ,D
点的速度大小为 l ω ,连杆DE 的速度瞬心到连杆DE 的质心即其中点的距离为 l 2 ,连
杆DE 的角速度大小为 2ω ,连杆DE 的动量大小为 l M ω ,连杆DE 的动能大小为
2
232l M ω。
三、机构如图所示,已知:
3t
πϕ=
(ϕ以rad 计,t 以
s 计),杆cm r AB OA 15===,
cm OO 201=,杆
cm C O 501=,试求当s t 7=时,机构中滑块B 的速度,
杆C O 1的角速度和点C 的速度。
(10分)
解:当7t s =时,πϕ3
7
=,此时杆OA 的角速度为
3
π
ωϕ==
A 点速度为
5(/)A v r cm s ωπ== (2分)
杆AB 作平面运动,根据速度投影定理,有
cos 60cos30a A v v =
解得B 点的绝对速度为
cos30
27.21(/)cos 60
A
a v v cm s =
= (5分)
以滑块B 为动点,杆1O C 为动系,由a e r =+v v v 作B 点的速度合成图。
由图可知(3分)
4
cos 27.2121.77/5
e a v v cm s θ==⨯=
故杆C O 1的角速度为
1
121.770.8708/25
e O C
v rad s O B ω=== 点C 的速度为
1143.54(/)C O C v O C cm s ω=⋅= (5分)
四.在图示平面结构中,C 处铰接,各杆自重不计。
已知:q C = 600N/m ,M = 3000N·m ,L 1 = 1 m ,L 2 = 3 m 。
试求:(1)支座A 及光滑面B 的反力;(2)绳EG 的拉力。
(15分)
解:以整体为研究对象,受力如图所示,由
0=ΣFx ,0=-T Ax F F ……①
0=ΣF y ,0221
2=⋅-+L q F F l NB Ay … …②
0)(=∑F M A ,0)22(23
2
22121222=-++⋅-⋅⋅⋅-M L L F L F L L q NB T t ③
再以BC 杆为研究对象受力如图所示,由
0)(=∑F M C ,0221=⋅-⋅L F L F T NB ……④
联立①②③④得
Ax F = 1133.3 N , Ay F = 100 N , NB F = 1700N T F = 1133.3N
五.如下图所示,滚子A 沿倾角为θ=030的固定斜面作纯滚动。
滚子A 通过一根跨过定滑轮B 的绳子与物块C 相连。
滚子A 与定滑轮B 都为均质圆盘,半径相等均为
r ,滚子A 、定滑轮B 和物块C 的质量相等均为m ,绳子的质量忽略不计。
系统由
静止开始运动,试求:(1)物块C 的加速度;(2)绳子对滚子A 的张力和固定斜面对滚子A 的摩擦力。
(15分)
解:(1)以系统为研究对象,设当物块C 下降h 时,其速度为v 。
采用动能定理:
∑-=-)(2112e W T T ,其中:2223mv T =,01=T ,)sin 1()
(2
1θ-=-mgh W e ,即:mgh mv 21232=。
对上式求一次导数,得g a 6
1
=。
(5分)
(2)以滚子A 为研究对象,设绳子对滚子A 的拉力为T ,固定台面对滚子A 的摩擦力为F ,方向平行斜面向下。
物块C 下降的加速度为a ,由运动学关系得滚子A
质心的a a C =和角加速度为r a
=α,由平面运动微分方程得:
ma ma mg F T C ==--θsin ;mra mr Fr 21
212==α
联立解得:mg T 4
3=;mg F 12
1= (10分)
六.在对称连杆的A 点上作用一铅垂方向的恒力F ,开始时系统静止,且知OA 与水
平线间的夹角为θ,求当连杆达到0
0=θ的位置时的角速度ω的值。
设OA=AB=L ,质
量均为m1,均质圆盘B 的质量为m2,半径为r ,在水平面上作纯滚动。
(15分)
解:(1) 取整体为研究对象(2分) (2) 分析受力(4分)
(3) 应用动能定理,可知
∑=-12
12W
T T (2分
其中:
01=T 122123
1
23121ωm L m T =⨯⨯=
2s i n 2
s i n 112⨯+=∑
θθL
g
m FL W θθsin sin 1gL m FL += (4分) 代入后,可得
θωsin )(3
1
1221L g m F L m += L
m g m F 11sin )(3θ
ω+=
(3分)。
