小学三年级奥数 第22讲最短路线
小学奥数知识讲解-最短路线问题

在日常生活、工作中,经常会遇到有关行程路线的问题。
比如:邮递员送信,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求能够走最近的路而达到目的地,等等。
这样的问题,就是我们所要研究学习的“最短路线问题”。
典型例题例[1] 假如直线AB 是一条公路,公路两旁有甲乙两个村子,如下图1。
现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短。
问:车站应该建在什么地方?分析 如果只考虑甲村的人距离公路AB 最近,只要由甲村向公路AB 画一条垂直线,交AB 于C 点,那么C 点是甲村到公路AB 最甲乙 AB 甲乙图1图2最短路线近的点,但是乙村到C点就较远了。
反过来,由乙村向公路AB画垂线,交AB于D点,那么D点是乙村到公路AB最近的点。
但是这时甲村到公路AB的D点又远了。
因为本题要求我们在公路AB上取的建站点,能够兼顾甲村和乙村的人到这个车站来不走冤枉路(既路程之和最短),根据我们的经验:两个地点之间走直线最近,所以,只要在甲村乙村间连一条直线,这条直线与公路AB交点P,就是所求的公共汽车站的建站点了(图2)。
解用直线把甲村、乙村连起来。
因为甲村乙村在公路的两侧,所以这条连线必与公路AB有一个交点,设这个交点为P,那么在P 点建立汽车站,就能使甲村乙村的人到汽车站所走的路程之和最短。
例[2] 一个邮递员投送信件的街道如图3所示,图上数字表示各段街道的千米数。
他从邮局出发,要走遍各街道,最后回到邮局。
问:走什么样的路线最合理?全程要走多少千米?3分析选择最短的路线最合理。
那么,什么路线最短呢?一笔画路线应该是最短的。
邮递员从邮局出发,还要回到邮局,按一笔画问题,就是从偶点出发,回到偶点。
因此,要能一笔把路线画出来,必须途径的各点全是偶点。
但是图中有8个奇点,显然邮递员要走遍所有街道而又不走重复的路是不可能的。
要使邮递员从邮局出发,仍回到邮局,必须使8个奇点都变成偶点,就是要考虑应在哪些街道上重复走,也就是相当于在图上添哪些线段,能使奇点变成偶点。
小学奥数习题版三年级三大原理最短路线学生版

知识要点快乐热身【例 1】 如下图所示,小虎家在A 地,姥姥家在B 地。
一天,他要去看望姥姥,但不知有几条路可走,走哪条路最短,热心的小朋友们快帮帮他吧?最短路线【例2】如下图所示,从甲地到乙地一共有两条路可走,请问哪条路长?哪条路短?【例3】观察下图,若黑猫与白猫奔跑速度相同,那么哪只猫先捉到老鼠?白猫黑猫鼠【例4】直线AB是一条公路,公路两侧有甲、乙两个村庄。
现在要在公路上建一个汽车站,让两个村子的人到汽车站的路线之和最短,问汽车站建在哪儿最好?乙甲BA走格子边【例5】一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路最近。
小朋友们你能给它找到几条这样的最短路线呢?BA【例6】如果A、B 两点变成下面两图这样的位置关系,那么从A到B的最短路线有几条呢?BA【例7】方格纸上取一点A作为起点,再在A的右上方任取一点B作为终点,画一条由A到B的最短路线,聪明的小朋友,你能画出来吗?总共能画出几条呢?【例8】小明和小强到少年宫参加2010上海世博会志愿者培训,少年宫和学校之间的地图如下。
如果他们从学校出发,共有多少种不同的最短路线?学校少年宫【例9】小虎和小羊是好朋友,它们居住的小区的平面图如下。
星期天,两人相约去博物馆看展览,现在小虎要先去小羊家和小羊会和,请问小虎去小羊家的最短路线有多少条?【例10】小聪明想从北村到南村上学,可是他不知道最短路线的走法共有几种?小朋友们,快帮帮忙呀!北村南村【例11】如图,从F点出发到G点,走最短的路程,有多少种不同的走法?GF【例12】“五一”长假就要到了,小新和爸爸决定去黄山玩。
聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?北京黄山【例13】下图是小明家和学校的示意图,亲爱的同学们,你们觉得小明从家到学校共有几条最短路线呢?学校小明家【例14】小海龟在小猪家玩,它们想去游乐场坐碰碰车,爱动脑筋的小朋友,请你想一想,从小猪家到游乐场共有几条最短路线呢?游乐场小猪家【例15】学校组织三年级的小朋友去帮助农民伯伯锄草,大家从学校乘车出发,去往的李家村(如图)。
三年级下册数学试题-竞赛思维能力训练:03最短路线(三年级竞赛)教师版
B C
B48 28 14 20 14 14 5 6 C9 52
65 4 32
1
A
1 1 1 11 A
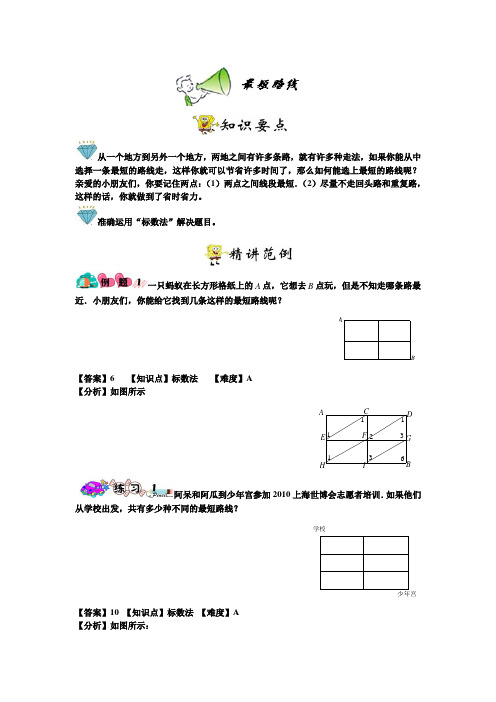
【答案】48,;1600 【知识点】标数法 【难度】C 【分析】用对角相加法,考虑到某些道路不能通行,在图形中用虚线标写出来,再在图中 依次标数,如上图所示:
所以,从 A 地到 B 地有 48 条最短路线。 从 A 地到 B 地最少要行使的距离:200×5+150×4=1600(米)
下面是一个街道的平面图,从街道的 A 地出发到 B 地,问有多少条最短路线?
【答案】18 【知识点】标数法 【难度】B 【分析】如图所示:
下图为某城市的街道示意图,C 处正在挖下水道,不能通车,从 A 到 B 处的最短路 线共有多少条?
B
【答案】431 【知识点】标数法 【难度】B 【分析】如图所示:
甲 C
A B D
乙
甲
1 11
1 2C 1
A 22 33 3
B 2 5 8 11
2D
8 19
2 2 10
2乙9
解:用虚线将不能通行的道路表示出来,再利用“对角线法”依次标数,如上图所示。 所以从甲地到乙地有 29 条最短路线。 从甲地到乙地至少要行驶的距离:5×180+320×5=2500(米)。
1
5
15
1
4
10
1
3
6
1
2
3
学校
1
1
市中心
养老院
25
40
66
10
15
26
5
11
4
5
6
1
1
1
是多少条?
如图,从 A 到 B 沿网格线不经过线段 CD 和 EF 的最短路径的条数
小学三年级奥数精品讲义1-34讲全

小学三年级奥数精品讲义目录第一讲加减法的巧算(一)第二讲加减法的巧算(二)第三讲乘法的巧算第四讲配对求和第五讲找简单的数列规律第六讲图形的排列规律第七讲数图形第八讲分类枚举第九讲填符号组算式第十讲填数游戏第十一讲算式谜(一)第十二讲算式谜(二)第十三讲火柴棒游戏(一)第十四讲火柴棒游戏(二)第十五讲从数量的变化中找规律第十六讲数阵中的规律第十七讲时间与日期第十八讲推理第十九讲循环第二十讲最大和最小第二十一讲最短路线第二十二讲图形的分与合第二十三讲格点与面积第二十四讲一笔画第二十五讲移多补少与求平均数第二十六讲上楼梯与植树第二十七讲简单的倍数问题第二十八讲年龄问题第二十九讲鸡兔同笼问题第三十讲盈亏问题第三十一讲还原问题第三十二讲周长的计算第三十三讲等量代换第三十四讲一题多解第三十五讲总复习第一讲加减法的巧算森林王国的歌舞比赛进行得既紧张又激烈。
选手们为争夺冠军,都在舞台上发挥着自己的最好水平。
台下的工作人员小熊和小白兔正在统计着最后的得分。
由于他们对每个选手分数的及时通报,台下的观众频频为选手取得的好成绩而热烈鼓掌,同时,观众也带着更浓厚的兴趣边看边猜测谁能拿到冠军。
观众的情绪也影响着两位分数统计者。
只见分数一到小白兔手中,就像变魔术般地得出了答案。
等小熊满头大汗地算出来时,小白兔已欣赏了一阵比赛,结果每次小熊算得结果和小白兔是一样的。
小熊不禁问:“白兔弟弟,你这么快就算出了答案,有什么决窍吗?”小白兔说:“比如2号选手是93、95、98、96、88、89、87、91、93、91,去掉最高分98,去掉最低分87,剩下的都接近90为基准数,超过90的表示成90+‘零头数’,不足90的表示成90-‘零头数’。
于是(93+95+96+88+89+91+93+91)÷8=90+(3+5+6―2―1+1+3+1)÷8=90+2=92。
你可以试一试。
”小熊照着小白兔说的去做,果然既快又对。
高斯小学奥数含答案三年级(上)第22讲 等差数列应用

6- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -这几个等差数列虽然都不一样,但它们的项数、和与中间数都是相同的:项数都是7,和都是112,中间数都是16.其实只要项数与和相同,中间数就自然相同了,因为我们学过公式:和=中间数×项数,那么中间数=和÷项数.也就是说,可以通过项数与和求出一个等差数列的中间数.这种通过公式反向求解的方法在等差数列的问题中非常常见.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题1一个等差数列的第1项是21,前7项的和为105,这个数列的第10项是多少?分析:前7项的和是105,根据公式可以求出第几项呢?练习1一个等差数列的第1项是3,前11项之和为198,这个数列的第20项是多少?第1项 第2项 第7项 21第10项 和105第二十二讲 等差数列应用9个连续自然数的和是126,其中最小的数是多少?分析:这9个数是等差数列吗?如果是的话,公差是几?练习27个连续奇数之和为91,其中最小的数是多少?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 当然,要使用公式:和=中间数×项数来解题的话,这个数列的项数必须是奇数.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3已知一个等差数列的前15项之和为450,前21项之和为819,请问:这个数列的公差是多少?首项是多少?第1项第2项第15第21和为450和为819分析:如果知道任何两项具体的数值,就能算出公差.能不能找到这样的两项呢?练习3已知一个等差数列的前13项之和为533,前15项之和为690.请问:这个等差数列的首项是多少?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 但并不是所有的等差数列的项数都是奇数.当项数是偶数时,只能根据公式:和=(首项+末项)×项数÷2,算出首项与末项的和.如果再能求出首项与末项的差,便能求出首项与末项的具体数值了.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -7把248表示成8个连续偶数的和,其中最大的偶数是多少?分析:首项与末项的和是多少?差是多少?练习4把115表示成10个连续自然数之和,其中最小的数是几?例题5已知一个等差数列的前15项之和为450,前20项之和为750.请问:这个数列的公差是多少?首项是多少?分析:通过“前15项之和为450”这个条件除了能知道“中间数”之外,还能知道其他一些信息吗?例题6在一次考试中,第一组同学的分数恰好构成了公差为3的等差数列,总分为609.小高发现自己的分数算少了,找老师更正后,加了21分,这时他们的成绩还是一个等差数列.请问小高正确的分数是多少?分析:思考下一共有几个人?改分前小高是第几个,改分后小高是第几个?89作业1. 已知一个等差数列的首项是17,前7项之和为161,这个数列的第11项是多少?2. 7个连续偶数之和为112,其中最小的那个数是多少?3. 8个连续奇数之和为112,其中最小的那个数是多少? 课 堂 内 外根据历史传说记载,国际象棋起源于古印度,至今见诸于文献最早的记录是在萨珊王朝时期用波斯文写的.据说,有位印度教宰相见国王自负虚浮,决定给他一个教训.他向国王推荐了一种在当时尚无人知晓的游戏.国王当时整天被一群溜须拍马的大臣们包围,百无聊赖,很需要通过游戏方式来排遣郁闷的心情.国王对这种新奇的游戏很快就产生了浓厚的兴趣,高兴之余,他便问那位宰相,作为对他忠心的奖赏,他需要得到什么赏赐.宰相开口说道:请您在棋盘上的第一个格子上放1粒麦子,第二个格子上放2粒,第三个格子上放4粒,第四个格子上放8粒,……即每一个次序在后的格子中放的麦粒都必须是前一个格子麦粒数目的倍数,直到最后一个格子第64格放满为止,这样我就十分满足了.“好吧!”国王哈哈大笑,慷慨地答应了宰相的这个谦卑的请求.这位聪明的宰相到底要求的是多少麦粒呢?稍微算一下就可以得出:234636412222221+++++⋅⋅⋅+=-,直接写出数字来就是18446744073709551615粒,这位宰相所要求的,竟是全世界在两千年内所产的小麦的总和!如果造一个宽四米,高四米的粮仓来储存这些粮食,那么这个粮仓就要长三亿千米,可以绕地球赤道7500圈,或在日地之间打个来回.国王哪有这么多的麦子呢?他的一句慷慨之言,成了他欠宰相西萨·班·达依尔的一笔永远也无法还清的债.正当国王一筹莫展之际,王太子的数学教师知道了这件事,他笑着对国王说:“陛下,这个问题很简单啊,就像1+1=2一样容易,您怎么会被它难倒?”国王大怒:“难道你要我把全世界两千年产的小麦都给他?”年轻的教师说:“没有必要啊,陛下.其实,您只要让宰相大人到粮仓去,自己数出那些麦子就可以了.假如宰相大人一秒钟数一粒,数完18446744073709551615粒麦子所需要的时间,大约是5800亿年(大家可以自己用计算器算一下!).就算宰相大人日夜不停地数,数到他自己魂归极乐,也只是数出了那些麦粒中极小的一部分.这样的话,就不是陛下无法支付赏赐,而是宰相大人自己没有能力取走赏赐.”国王恍然大悟,当下就召来宰相,将教师的方法告诉了他.西萨·班·达依尔沉思片刻后笑道:“陛下啊,您的智慧超过了我,那些赏赐……我也只好不要了!”当然,最后宰相还是获得了很多赏赐.等比数列小故事4.把325表示成10个连续自然数之和,其中最小的数是多少?5.已知一个等差数列的前11项之和为451,前19项之和为1235,这个数列的首项是多少?1011第二十二讲 等差数列应用1. 例题1答案:3详解:先求出第4项:105715÷=,所以公差为:()()2115412-÷-=,第10项为:()2121013-⨯-=. 2. 例题2答案:10详解:9个连续自然数是一个公差为1的等差数列,第5项为:126914÷=,所以最小的数为:14410-=.3. 例题3答案:3;9详解:先根据前15项之和,求出第8项为:4501530÷=.再根据21项之和,求出第11项为:8192139÷=.所以公差是:()()39301183-÷-=,首项为:()303819-⨯-=.4. 例题4答案:38详解:8个连续偶数构成的是公差为2的一个等差数列,最大数应该比最小数大2714⨯=,再算出最小数与最大数的和:2482862⨯÷=,所以最大数为:()6214238+÷=.5. 例题5答案:3;9详解:“前15项之和为450”,所以第1项与第15项之和为:45021560⨯÷=.同样地,算出第1项与第20项之和为75,都含有第1项,所以第20项比第15项大了756015-=,公差为:1553÷=,第15项比首项大31442⨯=,所以首项为:()604229-÷=.6. 例题6答案:99分详解:原来是最低的,加了21分之后应该变成最高的,公差是3,所以小组里共有7人.原来中间的数为609787÷=分,所以最后小高是99分.7. 练习1答案:60简答:第6项为:1981118÷=,公差为:()()183613-÷-=,第20项为:331960+⨯=. 8. 练习2答案:7简答:第4个是:91713÷=,最小数为7.9. 练习3答案:11简答:第7项为:5331341÷=,第8项为:6901546÷=,公差为5,则首项为:415611-⨯=.10. 练习4答案:7简答:最小数比最大数小9,且最小数与最大数之和为:11521023⨯÷=,则最小数为7. 11. 作业112 答案:37简答:第4项为161723÷=,而首项为17,那么公差为(2317)(41)2-÷-=,第11项为1721037+⨯=.12. 作业2答案:10简答:中间项即第4个数为112716÷=,则最小的是10.13. 作业3答案:7简答:()82112+⨯÷=首项末项,所以28+=首项末项,而对于8个连续奇数,末项比首项大2714⨯=,则首项为7.14. 作业4答案:28简答:这10个连续自然数构成一个公差为1的等差数列,()102325+⨯÷=首项末项,所以65+=首项末项,而首项又比末项小9,则首项为28.15. 作业5答案:11简答:第6项为4511141÷=,第10项为12351965÷=,则公差为(6541)(106)6-÷-=,首项为41(61)611--⨯=.。
三年级下册数学培优教案-3.2 最短路线 全国通用

2 最短路线学习目标:1.掌握最短路线的相关概念:①两点之间,线段最短;②最短路线并不止一条;③路线要最短必须不走重复路,不走反方向。
2.会熟练运用标注法求最短路线。
教学重点:1.掌握“两点之间线段最短”解最短路线问题;2.掌握“标注法”解最短路线问题。
教学难点:掌握“标注法”解最短路线问题。
教学过程:一、情景体验展示PPT上故事(教师讲述,请学生思考回答感受)师总结:一把剪刀,轻轻一剪,难题就解决了,生活中许多时候,只要我们多思考多观察,就能找到省时省力的方法。
现在就有一个问题需要同学们帮忙解决!看看你们能不能找到省时省力的方法!展示PPT情景体验图片师:到底走哪条路最近呢?这就是我们今天要学的内容是:最短路线。
(板书课题:最短路线)二、思维探索(建立模型)展示例1例1:如下图,A点表示公园入口处,B点表示儿童美术馆,朋朋与程程想从A 处到B处,走哪条路最近?师:从A处到B处,一共有几条路可走?生:4条师:走哪条最近呢?可以猜一猜生1:第②条最近生2:第③条最近师:看来同学们猜的答案各不一样,你能想个办法验证下到底走哪条路最近吗?生:可以量一量(学生动手操作,比较后得出结论)师:也就是说两点之间,线段最短。
师回顾引导总结:生活经验及事实告诉我们:两点之间,线段最短。
展示例2例2:下图中A表示灰太狼所在地,D表示喜羊羊所在地,横线和竖线表示灰太狼能走的路。
找一找,把你找到的从A走到D的最近路线用字母表示出来。
(例如:A—E—B—F—D)师:灰太狼怎样走才能使路线最短呢?生:不走回头路生:不走重复路线师:回答得很好!终点D在起点A的什么方向呢?从A点出发到D点,应该向什么方向走才能使路线最短?(可以组织学生分组讨论)生:只能够向下或向右走,路线才会最短!师:对,下面我们一起来研究。
课件演示师:遵循“最短路线只能向右和向下走”①看E点:只有从A到E的这一条路线。
同样道理:从A→B、从A→G、从A→C 也都只有一条路线。
精品三年级奥数b第二章 最短路线

【方法点拨 】
最短路线问题我们一般用画“树形 图”或“对角求和法”解决。对角求和 口诀:边上一条路,其余对角加。
(3b) 第二章 最短路线
【技巧感悟 】
例1: 小马要把麦子驼到磨坊去,有几种走法?
分析:我们可以这样表示路线图: 小马从A地到B地有2条路线,这2条路线从B地到C地又分别有3种走 法,所以一共有2 X 3 = 6种不同的路线。 解答:小马把麦子驼到磨坊去,共有2 X 3 = 6种走法。
金杯数学(3b)
(3b) 第二章 最短路线 天津科学技术出版社
同学们看了这幅图之 后有什么感觉?…是 不是觉得山路十八弯, 那你们在生活中还有 见过类似弯弯的东西?
(3b) 第二章 最短路线
河流也好弯吧? 那 大家有没有想过:如果 我们走路、开车、坐船 是沿着弯曲的道路走快 点还是沿着直线走快呢?
(3b) 第二章 最短路线
【热身演练 】
1、小兔邀松鼠一起去山羊家做客,小兔有几条路线可以走?
(3b) 第二章 最短路线
【技巧感悟 】
例2、 乔乔要去上课,有哪些最短线路?
分析:乔乔要去学校,只能向上走或 向右走,为了方便分析,我们在道路的交 叉点标上字母,可以把每一步的走法用右 面的树形图表示出来:
分析:在图中的各点标上字母,小牛要从A点回到B点,只能向右走或向上走。 解答:
(3b) 第二章 最短路线
【热身演练 】
3、根据对角求和的方法标出图1、图2中从A点到B点的路线一共 有多少条。
(3b) 第二章 最短路线
【技巧感悟 】
例4: 蚂蚁要把食物从A洞运往B洞处,最近 的路线有几条?
分析:怎样计数从A到B的最短路线的条数 呢?我们将介绍一种非常巧妙的方法--对角求和 法。
小学三年级奥数 第22讲最短路线

最短路线【课前铺垫】
标数法
标数法:一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路最近。
小朋友们,你能给它找到几条这样的最短路线呢?
寒假到了,艾伦和爸爸决定去黄山玩。
聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?阿强和牛牛结伴骑车去图书馆看书,第一天他们从学校直接去图书馆;第二天他们先去公园看大熊猫再去图书馆;第三天公园修路不能通行。
聪明的小朋友们,请你帮阿强和牛牛想想这三天从学校到图书馆的最短路线分别有多少种不同的走法?
图中的“我爱史老师”有多少种不同的读法。
一只密蜂从A处出发,A回到家里B处,每次只能从一个蜂房爬向右侧
邻近的蜂房而不准逆行,共有多少种回家的方法?
城市街道如下图所示,有几处街区有积水不能通行,那么从A到B的最
短路线有几条?
短路线有条。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最短路线
【例1】(☆☆)
【课前铺垫】
一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路最
近。
小朋友们,你能给它找到几条这样的最短路线呢?
标数法:用来解决最短路线问题的方法,在给出的图形中的每一个结点标出
到达该点的
,。
【例2】(☆☆☆)【例3】(☆☆☆)
寒假到了,艾伦和爸爸决定去黄山玩。
聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?阿强和牛牛结伴骑车去图书馆看书,第一天他们从学校直接去图书馆;第二天他们先去公园看大熊猫再去图书馆;第三天公园修路不能通行。
聪明的小朋友们,请你帮阿强和牛牛想想这三天从学校到图书馆的最短路线分别有多少种不同的走法?
1
【例4】(☆☆☆☆)【例5】(☆☆☆☆☆)
图中的“我爱史老师”有多少种不同的读法。
一只密蜂从A处出发,A回到家里B处,每次只能从一个蜂房爬向右侧
邻近的蜂房而不准逆行,共有多少种回家的方法?
【例6】(☆☆☆☆☆)
城市街道如下图所示,有几处街区有积水不能通行,那么从A到B的最
短路线有几条?
【本讲总结】
最短路线
宗旨:不走冤枉路,就要朝着目标走
方法:标数法
标数法四步:
1.找目标、定方向
2.从起点标数,起点标1
3.按顺序每个点都要标到
4.某点数字=指向该点箭头
尾巴上的数字相加
注意:
.坏点可以划去或看成
2.必须经过,分段标出
2。
