三年级奥数:最短路线问题详解2013
小学奥数知识讲解-最短路线问题

在日常生活、工作中,经常会遇到有关行程路线的问题。
比如:邮递员送信,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求能够走最近的路而达到目的地,等等。
这样的问题,就是我们所要研究学习的“最短路线问题”。
典型例题例[1] 假如直线AB 是一条公路,公路两旁有甲乙两个村子,如下图1。
现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短。
问:车站应该建在什么地方?分析 如果只考虑甲村的人距离公路AB 最近,只要由甲村向公路AB 画一条垂直线,交AB 于C 点,那么C 点是甲村到公路AB 最甲乙 AB 甲乙图1图2最短路线近的点,但是乙村到C点就较远了。
反过来,由乙村向公路AB画垂线,交AB于D点,那么D点是乙村到公路AB最近的点。
但是这时甲村到公路AB的D点又远了。
因为本题要求我们在公路AB上取的建站点,能够兼顾甲村和乙村的人到这个车站来不走冤枉路(既路程之和最短),根据我们的经验:两个地点之间走直线最近,所以,只要在甲村乙村间连一条直线,这条直线与公路AB交点P,就是所求的公共汽车站的建站点了(图2)。
解用直线把甲村、乙村连起来。
因为甲村乙村在公路的两侧,所以这条连线必与公路AB有一个交点,设这个交点为P,那么在P 点建立汽车站,就能使甲村乙村的人到汽车站所走的路程之和最短。
例[2] 一个邮递员投送信件的街道如图3所示,图上数字表示各段街道的千米数。
他从邮局出发,要走遍各街道,最后回到邮局。
问:走什么样的路线最合理?全程要走多少千米?3分析选择最短的路线最合理。
那么,什么路线最短呢?一笔画路线应该是最短的。
邮递员从邮局出发,还要回到邮局,按一笔画问题,就是从偶点出发,回到偶点。
因此,要能一笔把路线画出来,必须途径的各点全是偶点。
但是图中有8个奇点,显然邮递员要走遍所有街道而又不走重复的路是不可能的。
要使邮递员从邮局出发,仍回到邮局,必须使8个奇点都变成偶点,就是要考虑应在哪些街道上重复走,也就是相当于在图上添哪些线段,能使奇点变成偶点。
《三年级奥数》数学最短路线课件

以下赠品教育通用模板
前言
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。您的内容打在这 里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。 在此录入上述图表的综合描述说明。 您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。您的内容打在这 里,或者通过复制您的文本后。
例题【五】(★ ★ ★ ★ ★ )
城市街道如下图所示,有几处街区有积水不能通行,那么 从A到B的最短路线有几条?
从起点开始标数,注意积水处都是 坏点,那好把这些点划去或看成0。
例题【五】(★ ★ ★ ★ ★ )
城市街道如下图所示,有几处街区有积水不能通行,那么 从A到B的最短路线有几条?
111111
例题【一】(★ ★ )
一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路 最近。小朋友们,你能给它找到几条这样的最短路线呢?
例题【一】(★ ★ )
A→C→D→G→B、A→C→F→G→B、 A→E→F→G→B、A→C→F→I→B、 A→E→F→I→B、A→E→H→I→B、
例题【一】(★ ★ )
标数法
例题【三】(★ ★ ★ ★ )
图中的“我爱史老师”有多少种不同的读法。
1
1 1 11
起点是“我” 每个字看做“点”(车站) 共有1+4+6+4+1=16(种)
1 234 1 36 14 1
例题【四】(★ ★ ★ ★ ★ )
一只密蜂从A处出发,A回到家里B处,每次只能从一个蜂房 爬向右侧 邻近的蜂房而不准逆行,共有多少种回家的方法?
小学三年级奥数 第22讲最短路线
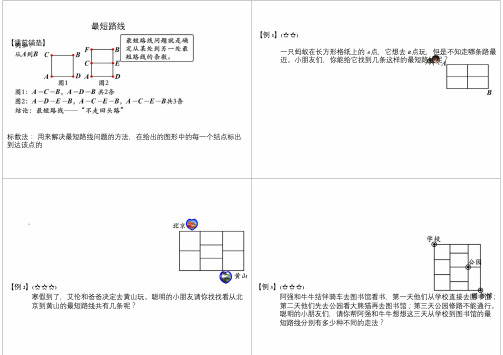
最短路线
【例1】(☆☆)
【课前铺垫】
一只蚂蚁在长方形格纸上的A点,它想去B点玩,但是不知走哪条路最
近。
小朋友们,你能给它找到几条这样的最短路线呢?
标数法:用来解决最短路线问题的方法,在给出的图形中的每一个结点标出
到达该点的
,。
【例2】(☆☆☆)【例3】(☆☆☆)
寒假到了,艾伦和爸爸决定去黄山玩。
聪明的小朋友请你找找看从北京到黄山的最短路线共有几条呢?阿强和牛牛结伴骑车去图书馆看书,第一天他们从学校直接去图书馆;第二天他们先去公园看大熊猫再去图书馆;第三天公园修路不能通行。
聪明的小朋友们,请你帮阿强和牛牛想想这三天从学校到图书馆的最短路线分别有多少种不同的走法?
1
【例4】(☆☆☆☆)【例5】(☆☆☆☆☆)
图中的“我爱史老师”有多少种不同的读法。
一只密蜂从A处出发,A回到家里B处,每次只能从一个蜂房爬向右侧
邻近的蜂房而不准逆行,共有多少种回家的方法?
【例6】(☆☆☆☆☆)
城市街道如下图所示,有几处街区有积水不能通行,那么从A到B的最
短路线有几条?
【本讲总结】
最短路线
宗旨:不走冤枉路,就要朝着目标走
方法:标数法
标数法四步:
1.找目标、定方向
2.从起点标数,起点标1
3.按顺序每个点都要标到
4.某点数字=指向该点箭头
尾巴上的数字相加
注意:
.坏点可以划去或看成
2.必须经过,分段标出
2。
三年级数学奥赛起跑线第23讲 最短路线

三年级数学奥赛起跑线第23讲最短路线1、如图,在一条河的两边有A、B两个小区。
为了便于两个小区的居民往来,准备在河上建一座桥,请问:这座桥建在何处,才能使两个小区的懵懂来往路程最短?A·河·B2、古希腊有一位著名的学者,名叫海伦。
有一天,一位将军不远千里专程前来向海伦求教一个百思不得其问题:从甲地出发到河边饮马(如图),然后再去乙地,走什么样的路线最短呢?这就是后来被人们称为“将军饮马”的问题。
小朋友,你来回答这位将军提出的问题好吗?·乙甲·小河3、右图是一个街区街道的平面图,邮递员从邮局出发,跑遍所有街道投送信件。
请你为他安排一条最短的路线,并按图中标出的千米数算出这条路线的长度。
(单位:千米)3邮局4、如图是一个街道平面图,王宏要从A处到B处。
在不走回头路,不走重复路的条件下,可以有多少种不同的路线?请你用在交叉点上标数的方法计算一下。
B 5、从学校到少年宫有4条东西向的马路和3条南北向的马路相通(如图)。
李楠从学校出发,步行到少年宫(只许向东或向南行进),最多有多少条不同的行走路线?北少年宫6、如图,从P到Q共有多少条不同的最短路线?7、如图所示是某城市的街道图,若从A走到B(只能由北向南、由西向东),共有多少种不同的走法?8、如图所示,从甲地到乙地,最近的道路有几条?9、右图为某城市的街道示意图,C处正在挖下水道不能通国。
那么从A到B处最短路线共有多少条?10、某城市的街道非常整齐,如右图所示。
从西南角A处到东北角B处要求走最近的路,并且不能通过十字路口C(正在修路),共有多少种不同的走法?。
三年级思维拓展- 最短路线

最短路线☜知识要点在日常生活中,我们经常会遇到关于行程的路线问题。
比如从一个地方到另一个地方,两地之间有许多条路,我们就需要选择哪一条路最近,也就是要选择一条最短路线,这样可以省时省力,这就是最短路线问题。
本讲我们就一起来学习怎样找最短路线。
☜精选例题【例1】:如图,甲、乙两个村庄分别在公路的两侧,现在要在公路旁建造一个汽车站,使甲、乙两个村庄到车站的距离之和最短,那么,车站应建在公路何处?☝思路点拨:根据两点之间线段最短,连接甲、乙两点,如图,这条线段与公路有一个交点O,在O点处建一个车站,就能使甲、乙两个村庄到车站的距离之和最短。
☝标准答案:活学巧用1.小明和小强分别住在河岸的两边,现在要修一条路,让小明和小强能去河岸旁取水,并要求这条路使小明和小强去取水的距离之和最短,这条路应该怎么修?小明河岸小强2.如下图,在一条河的两边有A、B两个小区,为了方便两个小区的居民出行,准备在河上建一座桥,请问,这座桥建在何处,使两个小区的居民来往的路程最短?河【例2】:小华、小明两家分别住在河岸边的A、B两地,如图,如果两家想在河边合修一个取水码头,请问,这个码头的点选在何处,才能使小华、小明两家取水时所走的路程之和最短?河☝思路点拨:如图,先在河对岸找到以河为对称轴的对称点A’,再连接A’B,线段A’B与河的交点在O点处,A’O=AO。
因为两个点之间线段最短,所以A’B是两点间最短的距离,而A’B=A’O+OB =AO+OB。
所以应把取水码头的点选在O点,这样小华和小明两家取水时所走的路程之和最短。
☝标准答案:河✌活学巧用1.古希腊有一位著名的学者,名叫海伦。
有一天,一位将军不远千里专程前来向海伦求教一个百思不得其解的问题:从甲地出发到河边饮马(如图),然后再去乙地,走什么样的路线最短呢?这就是后来被人们称为“将军饮马”的问题。
小朋友,你来回答这位将军提出的问题,好吗?2.在公路一边有A、B两个小区,为了方便两个小区居民出行,准备在公路边安放一个汽车站牌,问应该安放在何处才能使两个小区的居民所走的路程之和最短。
精品三年级奥数b第二章 最短路线

【方法点拨 】
最短路线问题我们一般用画“树形 图”或“对角求和法”解决。对角求和 口诀:边上一条路,其余对角加。
(3b) 第二章 最短路线
【技巧感悟 】
例1: 小马要把麦子驼到磨坊去,有几种走法?
分析:我们可以这样表示路线图: 小马从A地到B地有2条路线,这2条路线从B地到C地又分别有3种走 法,所以一共有2 X 3 = 6种不同的路线。 解答:小马把麦子驼到磨坊去,共有2 X 3 = 6种走法。
金杯数学(3b)
(3b) 第二章 最短路线 天津科学技术出版社
同学们看了这幅图之 后有什么感觉?…是 不是觉得山路十八弯, 那你们在生活中还有 见过类似弯弯的东西?
(3b) 第二章 最短路线
河流也好弯吧? 那 大家有没有想过:如果 我们走路、开车、坐船 是沿着弯曲的道路走快 点还是沿着直线走快呢?
(3b) 第二章 最短路线
【热身演练 】
1、小兔邀松鼠一起去山羊家做客,小兔有几条路线可以走?
(3b) 第二章 最短路线
【技巧感悟 】
例2、 乔乔要去上课,有哪些最短线路?
分析:乔乔要去学校,只能向上走或 向右走,为了方便分析,我们在道路的交 叉点标上字母,可以把每一步的走法用右 面的树形图表示出来:
分析:在图中的各点标上字母,小牛要从A点回到B点,只能向右走或向上走。 解答:
(3b) 第二章 最短路线
【热身演练 】
3、根据对角求和的方法标出图1、图2中从A点到B点的路线一共 有多少条。
(3b) 第二章 最短路线
【技巧感悟 】
例4: 蚂蚁要把食物从A洞运往B洞处,最近 的路线有几条?
分析:怎样计数从A到B的最短路线的条数 呢?我们将介绍一种非常巧妙的方法--对角求和 法。
小学三年级奥数最短路线问题【三篇】

【导语】海阔凭你跃,天⾼任你飞。
愿你信⼼满满,尽展聪明才智;妙笔⽣花,谱下锦绣第⼏篇。
学习的敌⼈是⾃⼰的知⾜,要使⾃⼰学⼀点东西,必需从不⾃满开始。
以下是为⼤家整理的《⼩学三年级奥数最短路线问题【三篇】》供您查阅。
【第⼀篇】
练习题:
图4-18是某城市的主要公路⽰意图,今在C、D、E、F、G、H路⼝修建⽴交桥,车辆不能通⾏,那么从A到B的最近路线共有⼏条?
答案解析:
【第⼆篇】
练习题:
如图4-17所⽰是⼀个街道的平⾯图,在不⾛回头路、不⾛重复路的条件下,可以有多少种不同的⾛法?
答案解析:
【第三篇】
练习题:
图4-16为某城市的街道⽰意图,C处正在挖下⽔道,不能通车,从A到B处的最短路线共有多少条?
答案解析:。
小学奥数全国推荐三年级奥数通用学案附带练习题解析答案23最短路线(一)

年级三年级学科奥数版本通用版课程标题最短路线(一)本讲中,我们将解决一个特殊的计数问题:最短路线问题。
怎样计数从A到B的最短路线的条数呢?我们将介绍一种非常巧妙的方法——对角线法(也叫标号法)。
一、例证:小冬和小悦到少年宫参加志愿者培训。
如果他们从学校出发,最多有多少种不同的行走路线?分析:要求从学校到少年宫的最短路线,只能向右或向下走。
我们可以先看A点:从学校到A点最短路线只有1种走法,我们在A点标上1。
B、E、F、G点同理。
再看J点:最短路线可以是A-J、E-J共2条,我们在J点标上2。
我们发现2=1+1正好是对角线A点和E点上的数字和。
是不是所有的最短路线都符合这个规律呢?再看I、C、H、D点,我们发现每一个小格右下角上标的数正好是这个小格右上角与左下角的数的和,这样,我们可以通过计算来确定从学校到少年宫共有10种走法。
二、总结:每个格左下角与右上角所标的数字和即为这格右下角应标的数字,我们称这种方法为对角线法,也叫标号法。
例1利用标号法确定从A点到B点所有最短路线有多少条。
分析与解:从A到B的最短路线,只能向上或向右走,先标最短路线只有一种走法的几个点(C、D、H、G),利用标号法得到一共有6条最短路线。
本题中每格右上角的数是右下角和左上角的两个数之和。
例2 小猫汤姆和老鼠杰克在博物馆看连环画,突然它们发现了一张千年藏宝图,于是它们决定去寻宝。
请你帮他们想想共有几条最短路线能到藏宝地呢?分析与解:先标出最短路线只有1种走法的几个点,用对角线法标出其他点上的数,共有20条最短路线。
例3亲爱的同学们,你们觉得小明从学校到家一共有几条最短路线呢?分析与解:我们采用对角线法(如图),但本题图形有变化,例如D点,从学校到C点有2种走法,再到D点最短路线的选择只能从C点走,所以从学校到D点的最短路线与从学校到C点的最短路线走法相同,有2 种走法,同理可以知道E点的最短路线也有2种走法,从而得到小明可以选择的最短路线共有12条。
