2018年浙江工业大学920信号与系统考研真题试题试卷
浙江省1月高等教育自学考试信号与系统试题及答案解析历年试卷及答案解析

浙江省2018年1月高等教育自学考试信号与系统试题课程代码:02354一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题3分,共30分)1.设:如图—1所示信号。
则:信号f(t)的数学表示式为( )。
(A)f(t)=t ε(t)-t ε(t-1)(B)f(t)=t ε(t)-(t-1)ε(t-1)(C)f(t)=(1-t)ε(t)-(t-1)ε(t-1)(D)f(t)=(1+t)ε(t)-(t+1)ε(t+1)2.设:两信号f 1(t)和f 2(t)如图—2。
则:f 1(t)与f 2(t)间变换关系为( )。
(A)f 2(t)=f 1(21t+3) (B)f 2(t)=f 1(3+2t)(C)f 2(t)=f 1(5+2t) (D)f 2(t)=f 1(5+21t)3.已知:f(t)=SgN(t)的傅里叶变换为F(j ω)=ωj 2, 则:F 1(j ω)=j πSgN(ω)的傅里叶反变换f 1(t)为( )。
(A)f 1(t)=t1 (B)f 1(t)=-t2 (C)f 1(t)=-t1 (D)f 1(t)=t2 4.周期性非正弦连续时间信号的频谱,其特点为( )。
(A)频谱是连续的,收敛的(B)频谱是离散的,谐波的,周期的(C)频谱是离散的,谐波的,收敛的(D)频谱是连续的,周期的5.设:二端口网络N 可用A 参数矩阵{a ij }表示,其出端与入端特性阻抗为Z c2、Z c1,后接负载Z L ,电源•U s 的频率为ωs ,内阻抗为Z s 。
则:特性阻抗Z c1、Z c2仅与( )有关。
(A){a ij },Z L(B){a ij },Z L ,Z s(C){a ij },ωs , *U s(D){a ij }6.设:f(t)↔F(j ω) 则:f 1(t)=f(at+b) ↔F 1(j ω)为( )(A)F 1(j ω)=aF(j a ω)e -jb ω (B)F 1(j ω)=a 1F(j a ω)e -jb ω (C)F 1(j ω)= a 1F(j a ω)ω-a bj e (D)F 1(j ω)=aF(j aω)ω-a b j e 7.已知某一线性时不变系统对信号X(t)的零状态响应为4dt)2t (dX -,则该系统函数H(S)=( )。
(NEW)浙江大学《842信号系统与数字电路》历年考研真题汇编(含部分答案)

表三 74LS161功能表 CP
EP ET
工作状态 × 0 × × × 置零 ↑ 1 0 × × 预置数 × 1 1 0 1 保持 ×
2.设计代码转换电路,输入为3为格雷码,输出3位二进制码,要 求用一个8线-3线高优先级编码器74148和一个3线-8线译码器74138,不 能外加其他器件。3位格雷码表如表一所示。
十、(15分)有一个外输入A及一个外输出Z的时钟电路其状态表 如表而所示,试用JK触发器及二选一数据选择器设计此时序电路,要求 电路尽量简单,写出设计电路,画出电路图。
2.分别画出无失真传输系统和理想低通滤波器的频率响应曲线。 (5分)
三、计算题(每题5分,共计15分)
1.求出
的傅氏变换。(5分)
2.已知
收敛域为 ,求h[n]。(5分)
3.一个LTI系统的输入x(t)和输出y(t)如下图所示,求该系统的单位 冲激响应h(t)。
四、(10分)已知某因果离散LTI系统的系统函数的差分方程为:
表二 状态表 A=0 A=1 A=0 A=1 000 000/0 001/0 100 000/1 001/0 001 000/0
010/0 101 000/1 010/0 010 000/0 011/0 110 000/1 011/0 011 100/0 011/0 111 000/1 011/0 十一、(共12分,每小题6分)图1为两片16进制同步计数器 74LS161构成的计数器。74LS161的功能表如表三所示。
一、选择题(四选一,每题2分,共计20分) 1.一个因果、稳定的离散时间系统函数H(z)的极点必定在: ( ) A.单位圆以外; B.实轴上; C.z平面左半平面; D.单位圆以内
浙江7月高等教育自学考试信号与系统试题及答案解析

浙江省2018年7月高等教育自学考试信号与系统试题课程代码:02354一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。
每小题3分,共30分)1. 设:如图—1所示信号。
则:信号f(t)的数学表示式为( )。
(A)f(t)=t ε(t)-(t-1)ε(t-1)(B)f(t)=(1-t)ε(t)-(t-1)ε(t-1)(C)f(t)=t ε(t)-t ε(t-1)(D)f(t)=(t-1)ε(t)-(t-1)ε(t-1)2. 设:信号f 1(t)和f 2(t)如图—2。
则:f 1(t)与f 2(t)间关系为( )。
(A)f 2(t)=f 1(t+1)ε(t)(B)f 2(t)=f 1(t+1)ε(t+1)(C)f 2(t)=f 1(t)ε(t-1)(D)f 2(t)=f 1(t-1)ε(t-1)3. 设:g τ(t)↔G τ(j ω)则:g τ(t)t j 0e ω ↔G ω0τ(j ω)为( )(A)G ω0τ(j ω)=0ωτSa [2)(0τω-ω] (B)G ω0τ(j ω)=τSa [2)(0τω+ω] (C)G ω0τ(j ω)=τSa [2)(0τω-ω] (D)G ω0τ(j ω)= 0ωτSa [2)(0τω+ω] 4. 设:一非正弦周期电源为:u s (t)=u S0+u S1+u S2+…+u S N 其中:U S0为直流电压(V), u sn =U snm cosn ω0t n=1,2,…N ,U snm 为幅值(V)则:电源的平均功率P T 为( )。
(A)P T =∑=N 0n 21 U snm (B)P T =21U 2S0+∑=N 1n U snm(C)P T =U 2S0+∑=N 1n 21U snm (D)P T =U 2S0+∑=N 1n U 2snm 5. 设:一并联RLC 谐振回路,电感存在电阻R ,负载电阻R L ,信号源U&s 与内阻R s 串接,分别与回路并联连接。
(完整版)浙工大数字信号处理题库

(完整版)浙⼯⼤数字信号处理题库信号采样、奈奎斯特定律选择题1. 在对连续信号均匀采样时,若采样⾓频率为Ωs ,信号最⾼截⽌频率为Ωc ,则折叠频率为( D )。
采样频率之半。
A. ΩsB. ΩcC. Ωc /2D. Ωs /22. 要从抽样信号不失真恢复原连续信号,应满⾜下列条件的哪⼏条( D )。
(Ⅰ) 原信号为带限(Ⅱ) 抽样频率⼤于两倍信号谱的最⾼频率 (Ⅲ) 抽样信号通过理想低通滤波器A.Ⅰ、ⅡB.Ⅱ、ⅢC.Ⅰ、ⅢD.Ⅰ、Ⅱ、Ⅲ3. 在对连续信号均匀采样时,要从离散采样值不失真恢复原信号,则采样周期Ts 与信号最⾼截⽌频率f h 应满⾜关系( D )。
A. Ts>2/f h B. Ts>1/f h C. Ts<1/f h D. Ts<1/(2f h )4. 若⼀模拟信号为带限,且对其抽样满⾜奈奎斯特条件,则只要将抽样信号通过( A )即可完全不失真恢复原信号。
A. 理想低通滤波器B. 理想⾼通滤波器C. 理想带通滤波器D. 理想带阻滤波器5. 若序列的长度为M ,要能够由频域抽样信号X(k)恢复原序列,⽽不发⽣时域混叠现象,则频域抽样点数N 需满⾜的条件是( A ) A. N ≥M B. N ≤M C. N ≥M/2 D. N ≤M/2信号、序列选择题1. 数字信号的特征是( B )A. 时间离散、幅值连续B. 时间离散、幅值量化C. 时间连续、幅值量化D. 时间连续、幅值连续 2. 下列哪⼀个单位抽样响应所表⽰的系统不是因果系统?( D )A. h(n)=δ(n)B. h(n)=u(n)C. h(n)=u(n)-u(n-1)D. h(n)=u(n)-u(n+1) 与未来有关,⾮因果 3.下列关系正确的为( C )A .u(n)=k 0δ (n)B .u(n)=∑∞=0k δ (n) C .u(n)=∑-∞=n k δ (n) D .u(n)=∑∞-∞=k δ (n)4.下列序列中属周期序列的为( D )。
信号与系统标准试题库附答案

B。2 Sa[2 (t 3)] D。2 Sa (2t )
B。稳定的物理不可实现系统 D。不稳定的物理不可实现系统
e ( s 3) 的原函数 f (t ) ( C ) s3
B。 e 3(t 3) (t 3) D。 e 3t (t 3)
50.当输入信号的复频率等于系统函数的零点时,系统的强迫响应分量为( C ) A.无穷大 B。不为零的常数 C。0 D。随输入信号而定
《信号与系统》总复习参考练习题 一、单项选择题:
B
D
C
B
A
1
C
A
B
C
2
A
D
B
B
14、已知连续时间信号 f (t )
sin 50(t 2) C , 则信号 f (t )·cos10 4 t 所占有的频带宽度为() 100(t 2)
A.400rad/s
B。200 rad/s
C。100 rad/s
5
5
(t 3) (t 2)dt 等于( A )
B。1 C。0 D。-0。5
A.-1
67.已知某连续时间系统的系统函数 H ( s ) A.高通滤波器 B。低通滤波器
1 ,该系统属于什么类型 ( B ) s 1
C。带通滤波器 D。带阻滤波器
68.以下为 4 个信号的拉普拉斯变换,其中不存在傅里叶变换的信号是 ( D ) A.
1 > 2 , 则信号 f (t ) f 1 (t 1) f 2 (t 2) 的奈奎斯特取样频率为( C )
A. 1 B。 2 C。 1 + 2 D。 1 2
58.某信号的频谱是周期的离散谱,则对应的时域信号为( D ) A.连续的周期信号 C.离散的非周期信号 B。连续的非周期信号 D。离散的周期信号
浙江工业大学浙江工业大学2018- 2019学年电路试卷
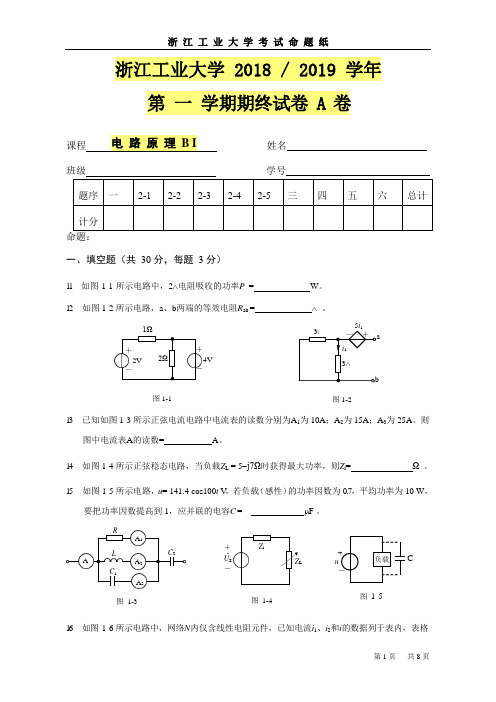
+ -载负浙江工业大学 2018 / 2019 学年第 一 学期期终试卷 A 卷课程电 路 原 理 B I姓名班级学号题序一2-12-22-32-42-5三四五六总计计分命题:一、填空题(共 30 分,每题 3 分)1-1 如图 1-1 所示电路中,2∧电阻吸收的功率P =W 。
1-2 如图 1-2 所示电路,a 、b 两端的等效电阻R ab =∧ 。
1Ω 3∧5i 1— + a i 1 3∧b图 1-1图 1-21-3 已知如图 1-3 所示正弦电流电路中电流表的读数分别为A 1为 10A ;A 2为 15A ;A 3为 25A 。
则图中电流表A 的读数=A 。
1-4 如图 1-4 所示正弦稳态电路,当负载Z L = 5-j7Ω时获得最大功率,则Z i =Ω 。
1-5 如图 1-5 所示电路,u = 141.4 cos100t V ,若负载(感性)的功率因数为 0.7,平均功率为 10 W ,要把功率因数提高到 1,应并联的电容C =μF 。
u C图 1-3图 1-4图 1-51-6 如图 1-6 所示电路中,网络N 内仅含线性电阻元件,已知电流i 1、i 2和i 的数据列于表内,表格+2V -2Ω+ 4V -+.U S -Z iZ LR A 1ALC 2A 2C 1A 3Si L (t ) +R 1R 2L-Ri S中的未知数据 ? 应为 =A 。
1-7 如图 1-7(a)所示电路中,u S = 6V ,R 1 = 1∧,R 2 = 2∧,它的戴维宁等效电路如图 1-7(b )所示,u OC =V 。
R 1R 2A AR i+u (a)图 1-6(b)S(a)B图 1-7u OC — B (b)1-8 电压u (t )的波形如图 1-8 所示,用阶跃函数表示为u (t )=V 。
u /V 2 1 L 11t /su SR 3o 11-8图 1-91'图 1-101-9 图 1-9 所示电路换路前处于稳态,u S = 20V ,L = 1H ,R 1= R 2= R 3= 10 ∧,i L (0+) = A 。
信号与系统标准试题库附答案
C. Sa(2t) 48.理想低通滤波器一定是( B )
A.稳定的物理可实现系统 C.不稳定的物理可实现系统
D。2 Sa(2t)
B。稳定的物理不可实现系统 D。不稳定的物理不可实现系统
49.单边拉氏变换 F (s) e(s3) 的原函数 f (t) ( C ) s3
A. e3(t1) (t 1)
s 1
A.
s2
s2
B。
s 1
80.信号 e j2t (t) 的傅氏变换是( A )
D。系统是稳定的
A.1 Hz
B。2 Hz
C。4 Hz
D。8 Hz
38.理想低通滤波器是( C )
A.因果系统
B。物理可实现系统
C。非因果系统
39. 1 j 具有( B )
D。响应不超前于激励发生的系统
A.微分特性
B。积分特性
C。延时特性
D。因果特性
40. sin (t 2) (t 1) 等于( D )
C。1
D。0
46.连续周期信号的频谱有( D )
A.连续性、周期性
B。连续性、收敛性
C。离散性、周期性
D。离散性、收敛性
47.某信号的频谱密度函数为 F ( j) [ ( 2 ) ( 2 )]e j3 , 则 f (t) ( B )
A. Sa[2 (t 3)]
B。2 Sa[2 (t 3)]
1
A.
s
B。1
1
C。
s2
1
D。
s2
69.已知一连续系统在输入 f (t) 的作用下的零状态响应为 yzs (t) f (4t) ,则该系统为(B)
A.线性时不变系统
B。线性时变系统
宁波大学2018年《912信号与系统》考研专业课真题试卷
n
1 2
n
(4)当输入 x(n) = 2 + cos n u(n) 时,求系统的稳态响应。
π 4
第 3 页 共 3 页
x(t) 1 -2 O -1 2 4 6 8 t
h(t) 2 -1 O 1 2 3 t
题 3.1 图 (2)试计算卷积和 y[n]= x[n]* h[n],其中 x[n]={1, 2, 0, 3, 2}(n=-3, -2,-1,0, 1),h[n]={1, 4, 3}(n=-1, 0, 1)。 4.(12 分)试画出信号 f (t ) = sgn{sin[ 叶级数表示式。 5.(14 分)求信号 f (t ) =
2
(t − 1)]} 的波形,并求出该信号的指数函数形式傅里
sin(2t ) cos(5t ) 的傅里叶变换 F ( j) ,并画出其频谱图。 t
6. (18 分)某系统如题 6 图所示,输入 f1(t)为带限信号,H(jω)为带通滤波器。 (1)当 2 = 21 , a = 1 , b = 2 , T =
总分值:
150
科目名称:
信号与系统
f1(t) p(t)
fs(t)
H(j)
f2(t) -2 -1
F1(j) 1 O A
1
H(j)
2
p(t) (1) ... -2T -T O ... T 2T 3T 4T 5T t -b -a O
a
b
题6图 7.(14 分)已知系统函数 H (s) 的极点位于 s = −3 处,零点在 s = −a 且 H () = 1 。此系统的阶 跃响应中包含一项 K1e
−3t
。若 a 从 0 变到 5,确定相应的 K1 值如何随之改变。
