§83 第一类边界条件下(tw=c)半无限大平板一维非稳态导热20110420155222
合集下载
非稳态导热--讲义
非稳态导热
一、
二、 三、
非稳态导热基本概念
一维非稳态导热的解析解 半无限大物体的非稳态导热
一、
非稳态导热基本概念
1 2
非稳态导热的定义 . t f ( x, y, z, )
物体温度随时间变化的导热过程。
非稳态导热的分类
周期性非稳态导热 (定义及特点)
瞬态非稳态导热 (定义及特点)
物体的温度随时间的推移逐渐趋近于恒定的值。 物体的温度随时间而作周期性的变化。
erf ( x) 2
x v 2 e dv 0
x erf ( x) 1 x有限大小时， erf ( x) 1
令
x 4a
erf 0
( )
令 y x 4 a 若 y 2 erf ( 2 ) 0.9953 即 0 0.9953 可认为该处温度没有变化
Φ1－－板左侧导入的热流量 Φ2－－板右侧导出的热流量
6 非稳态导热求解：
(1) 温度分布和热流量分布随时间和空间的变化规律
t f ( x, y, z, ) ;
Φ f(x, y, z, )
(2) 非稳态导热的导热微分方程式：
t t t t c ( ) ( ) ( ) qv x x y y z z
0 x , 0
0
x0 x
用分离变量法可得其分析解为：
( x , ) 2 sin( n ) cos( n x ) e 0 n 1 n sin( n ) cos( n )
若令 n n 则上式可改写为：
2 1 0
三个变量，因此，需要分开来画 (2) 先画
一、
二、 三、
非稳态导热基本概念
一维非稳态导热的解析解 半无限大物体的非稳态导热
一、
非稳态导热基本概念
1 2
非稳态导热的定义 . t f ( x, y, z, )
物体温度随时间变化的导热过程。
非稳态导热的分类
周期性非稳态导热 (定义及特点)
瞬态非稳态导热 (定义及特点)
物体的温度随时间的推移逐渐趋近于恒定的值。 物体的温度随时间而作周期性的变化。
erf ( x) 2
x v 2 e dv 0
x erf ( x) 1 x有限大小时， erf ( x) 1
令
x 4a
erf 0
( )
令 y x 4 a 若 y 2 erf ( 2 ) 0.9953 即 0 0.9953 可认为该处温度没有变化
Φ1－－板左侧导入的热流量 Φ2－－板右侧导出的热流量
6 非稳态导热求解：
(1) 温度分布和热流量分布随时间和空间的变化规律
t f ( x, y, z, ) ;
Φ f(x, y, z, )
(2) 非稳态导热的导热微分方程式：
t t t t c ( ) ( ) ( ) qv x x y y z z
0 x , 0
0
x0 x
用分离变量法可得其分析解为：
( x , ) 2 sin( n ) cos( n x ) e 0 n 1 n sin( n ) cos( n )
若令 n n 则上式可改写为：
2 1 0
三个变量，因此，需要分开来画 (2) 先画
传热学 第3章
2
1) 数学模型
2 τ = 0, Θ = Θ 0 = 1 δ Fo是无量纲特征数 Fo是无量纲特征数， 是无量纲特征数， Θ X = 0, =0 称为傅里叶数 称为傅里叶数 x hδ Θ hδ 称为毕渥数 称为毕渥数 4 X = 1, = Θ Bi = λ X λ
2Θ = ( Fo) X 2 τ = 0, Θ = Θ 0 = 1 Θ X = 0, =0 X Θ X = 1, = Bi Θ X
2 1
上面两式之比
x f Bi , δ 可见， 非稳态导热进入正规状况阶段以后， 可见，当Fo ≥ 0.2，非稳态导热进入正规状况阶段以后， 都随时间变化，但它们的比值与时间无关， 虽然θ与θm都随时间变化，但它们的比值与时间无关， 只取决于毕渥数Bi与几何位置 与几何位置x/ 只取决于毕渥数Bi与几何位置x/δ 。 认识正规状况阶段的温度变化规律具有重要的实 际意义， 际意义，因为工程技术中的非稳态导热过程绝大部分 时间都处于正规状况阶段 。 10
第三章
主要内容： 主要内容：
非稳态导热
非稳态导热过程中温度场的变化规律及换热量的分 析求解方法。包括： 析求解方法。包括： 1. 一维非稳态导热的分析解法； 一维非稳态导热的分析解法； 2. 非稳态导热的集总参数分析法； 非稳态导热的集总参数分析法； 3. 半无限大固体的非稳态导热 ；
3－1 非稳态导热的基本概念
14
（ 2）
θ θ0 θ x = = cos 1 = θm θm θ0 δ
x f Bi , δ
15
2 Q 2sin 1 1 Fo （ 3） = 1 2 e = f ( Bi , Fo ) 1 + 1 sin 1 cos 1 Q0
2
16
几点说明：
1) 数学模型
2 τ = 0, Θ = Θ 0 = 1 δ Fo是无量纲特征数 Fo是无量纲特征数， 是无量纲特征数， Θ X = 0, =0 称为傅里叶数 称为傅里叶数 x hδ Θ hδ 称为毕渥数 称为毕渥数 4 X = 1, = Θ Bi = λ X λ
2Θ = ( Fo) X 2 τ = 0, Θ = Θ 0 = 1 Θ X = 0, =0 X Θ X = 1, = Bi Θ X
2 1
上面两式之比
x f Bi , δ 可见， 非稳态导热进入正规状况阶段以后， 可见，当Fo ≥ 0.2，非稳态导热进入正规状况阶段以后， 都随时间变化，但它们的比值与时间无关， 虽然θ与θm都随时间变化，但它们的比值与时间无关， 只取决于毕渥数Bi与几何位置 与几何位置x/ 只取决于毕渥数Bi与几何位置x/δ 。 认识正规状况阶段的温度变化规律具有重要的实 际意义， 际意义，因为工程技术中的非稳态导热过程绝大部分 时间都处于正规状况阶段 。 10
第三章
主要内容： 主要内容：
非稳态导热
非稳态导热过程中温度场的变化规律及换热量的分 析求解方法。包括： 析求解方法。包括： 1. 一维非稳态导热的分析解法； 一维非稳态导热的分析解法； 2. 非稳态导热的集总参数分析法； 非稳态导热的集总参数分析法； 3. 半无限大固体的非稳态导热 ；
3－1 非稳态导热的基本概念
14
（ 2）
θ θ0 θ x = = cos 1 = θm θm θ0 δ
x f Bi , δ
15
2 Q 2sin 1 1 Fo （ 3） = 1 2 e = f ( Bi , Fo ) 1 + 1 sin 1 cos 1 Q0
2
16
几点说明：
大平板第一类边界条件下非稳态传热近似解析解
K K
-
G ; $ * ! % & B ( *+ ? L G *
?
K G ; $ * ! % & B ( *+ K L G *
, -
’$ % &
G ; $ * ! % & ( *$ B F & G %
此 阶 段 的温度分 布取决 于 " 和" 的 确 定! $ & $ & % % / # 于是 ! 根据积分方程有
& F ’
图 F 大平板非稳态传热坐标系示意图
令 & U I V ’W Q& U I V ’] Q$ Z\ W Q ] Q Y\ $ [\ RW Q R] Q $
E 收稿日期 H ! $ $ ! $ F ! # 李格升 男I 副教授 I 主要研究领域为热能工程 H G %岁 I 万方数据
D 国家自然科学基金
K
-
G ; $ * ! % & B ( *+ ? A" $ % & L G * #
K
-
G ; $ * ! % & ( * A" $ % & G % # $ N &
; $ * ! % &+ ; /A
-A " $ % &@ *@ # 将式 $ 分别代入式 可求得 J & $ M & ! $ N & " $ % &+ OB ? L % / " $ % &+ OB ? L % # 由" $ 9" $ +-可求得 % % / -& # -&
ZQ Z ) 增大 ! 减小 ! 它们的相遇点 ’$ 此处 ( & $ $ & + % " % # ( * 即无热流界面不断向右推进 ! 直到 ’$ 到达 ,& ! & % 右边 界 ! 即 % 此 时! +% & +, ! $ & + " % " % ’-为 止 . #$ / 即 热 流 由 左 边 界 传 递 至 右 边 界! 渗透整个平 ! 再 此 后! 热 渗 透 层 无 任 何 物 理 意 义! 平板已整 板0 体渗透 ! 热量由高温侧向低温侧传递 ! 直至传热过 根据上述分析 ! 整个求 解 过 程分 为 1 程稳定为止 . 个阶段进行 . 即7 2 . 3 4 54 ! $ & 97 $ & 56阶段 4 4 6 8 : 假设此阶段平板内温度分布为 ; $ * ! % &+ % &9 = $ % & *9 D<$ ? > $ % & * C, <B$ % &9 = $ % & *9 B ? E > $ % & * B 此时边界条件有 $ , ! & +; ! $ ! & +; ! $ ! & +, ! $ A" ! & ; % ; % ; " % ; % / # / # G ; $ * ! % & G ; $ * ! % & H +, ! H +, +,! * +" * +A" / # G * G * 将边界条件代入式 $ 中可确定相应的待定系数 ! F & 于是可得到如下结果 I ; $ * ! % &+ D; $ BA / C, * ? $ BA & # E; " $ % & # * ? & " $ % & / ,@ *@ " $ % & / " $ % &@ *@ -A " $ % & $ J & / # -A " $ % &@ *@ # ,@ *@ " $ % & / $ % &@ *@ -A " $ % & " / # -A " $ % &@ *@ # $ F & ; $ * ! % &+ D ; $ BA / C, * ? ; $ BA & # OB E ? L % * ? & OB ? L % ,@ *@ OB ? L % OB ? L % @ *@ -A OB ? L % -A OB ? L % @ *@ -
传热学11 一维稳态和非稳态导热
• 两个边界条件中：一个为r=R时，T=Tw，由于内热源均 匀分布，圆柱体表面温度均为Tw，圆柱体内温度分布对 称于中心线，另一个边界条件可表示为 r=0时，dT/dr=0。 将微分方程分离变量后两次积分，结果为：
11.2 通过圆筒壁的一维稳态导热
qv 2 qv 2 dT T r C1 ln r C2 r r C1 4 dr 2 • 根据边界条件，在r=0时， dT/dr=0。可得C1=0；利用 另一个边界条件，在r=R时，T=Tw，可得
• 可见，该条件下平壁内温度是按抛物线规律分布。令 温度分布关系式中的x=0，则得平壁中心温度为：
qv 2 T Tw s 2
11.1 通过平壁的一维稳态导热
• 例题2：炉墙内层为粘土砖，外层为硅藻土砖， 它们的厚度分别为s1=460 mm；s2=230 mm，导 热系数分别为：λ1=0.7+0.64× 10-3T W/m℃； λ2=0.14+0.12× 10-3T W/m℃。炉墙两侧表面温度 各为T1=1400℃；T3=100℃，求稳态时通过炉墙 的导热通量和两层砖交界处的温度。
1
2
Tf1 Tf2 dT q C1 1 s 1 dx
q K (Tf1 Tf2 )
1 s
1
2
1
综合传热系数或传热系数 多层平壁
K
Tf1 Tf2 q n si 1 1
1
2
1
1
i 1
i
2
平壁面积A
Tf1 Tf2 Q n si 1 1 1 A i 1 i A 2 A
11.1 通过平壁的一维稳态导热
对T求导，得： dT C1
第4章 非稳态导热
2
材料
铸铁 砂型 金属型 46.5 0.314 61.64 753.6 963.0 544.3 7000 1350 7100
例题4-1 一大型平壁状铸铁件在砂型中凝固冷却。设砂 型内侧表面温度维持1200℃不变，砂型初始温度为 20℃，热扩散率������ = 2.41 × 10−7 m2 s，试求浇注后 1.5h砂型中离内侧表面50mm处的温度
4.3 伴有相变边界的一维非稳态导热
ⅆ������ ′ ������������ = −������������ ⅆ������ ������ ⟵ ������ + ������ ������������ − ������������
′ ������������
������ 砂 型 ������0 ⅆ������ ⅆ������
������
∞
1.温度场求解 常物性一维非稳态无内热源导热微分方程： ������������ ������ ������ 2 ������ ������ 2 ������ ������ 2 ������ ������ = + 2+ 2 + 2 ������������ ������������ ������������ ������������ ������������ ������������
������������ =0 边界条件： ������ = 0, ������������ ������������ ������ = ������, −������ = ℎ������ ������������
采用分离变量法求解：
������������ ������������
2 n
2sin n ( x, ) e 0 sin cos n 1 n n n
大平板第一类边界条件下非稳态传热近似解析解
收 稿 日期 ｚ０ ２—０ ２ ２０ １— ４
热渗 透层 概念 ， 侧 的热渗 透层 厚 度分 别 为 （ ） 两 ｒ （） ２
和 瓯 （） 随 着 时 间 的 延 长 ， 至 （ ） ｒ， 直 ｒ ＋ ｂ ｒ 一 （）
，
即Ｉ ／ ／ ＂ ＂ Ｌ时为 止． ＝Ｉ 此后 ， 着 时 间的 延 长 ， （ ） 随 ｒ
第 ４期
李 格 升 等 ： 平 板 第 一 类 边 界 条 件 下 非 稳 态传 热 近 似 解 析 解 大
Ｏ ｘ， ）一 （ ｒ
・４ ３。 ３
增大 ， （ ） ｒ 减小 ， 们 的相 遇点 Ⅳ（ ） 此 处 它 ｒ（
一
０） 即无 热流 界 面不 断 向右推 进 ， 到 Ⅳ （） ， 直 ｒ 到达 右 边 界 ， ｒ ｒＬ 止 ． 时 ， （ ） ０ （ ） 即 — Ⅳ为 此 ｒ 一 ， ｒ 一
个 阶 段进 行 ． ２ １ Ｔ Ｔ， ． ＜ Ｌ 即 （ ） ｂＴ ＜ Ｌ 阶 段 Ｔ ＋６ （ ）
＿ ｛ ０
≤ Ｘ Ｌ一 ≤
￣１ ａ ／ ２ ｔ
１（一圭 １ ０ ｂ
【
） 。
Ｌ一 瓜
≤ｚ ≤Ｌ
（ １ １ ）
２ ２ １ ＜Ｔ Ｔ 即 尚未 整体 渗 透 阶段 ． － ＜ ， Ｌ 假 设此 阶段 平 板 内温度 分 布为
ｌ（一圭 １
Ｉ
￣１ａ ／２ ｔ
） ｚ
０ ≤瓜 ≤ｚ
Ｌ， 热 流 由 左 边 界 传 递 至 右 边 界 ， 透 整 个 平 即 渗 板 ； 此 后 ， 渗 透层 无 任 何 物 理 意 义 ， 板 已整 再 热 平 体渗透， 热量 由高温 侧 向低 温侧 传递 ， 至传 热过 直 程 稳 定 为止 ． 据 上 述分 析 ， 个 求解 过 程 分 为 ３ 根 整
热渗 透层 概念 ， 侧 的热渗 透层 厚 度分 别 为 （ ） 两 ｒ （） ２
和 瓯 （） 随 着 时 间 的 延 长 ， 至 （ ） ｒ， 直 ｒ ＋ ｂ ｒ 一 （）
，
即Ｉ ／ ／ ＂ ＂ Ｌ时为 止． ＝Ｉ 此后 ， 着 时 间的 延 长 ， （ ） 随 ｒ
第 ４期
李 格 升 等 ： 平 板 第 一 类 边 界 条 件 下 非 稳 态传 热 近 似 解 析 解 大
Ｏ ｘ， ）一 （ ｒ
・４ ３。 ３
增大 ， （ ） ｒ 减小 ， 们 的相 遇点 Ⅳ（ ） 此 处 它 ｒ（
一
０） 即无 热流 界 面不 断 向右推 进 ， 到 Ⅳ （） ， 直 ｒ 到达 右 边 界 ， ｒ ｒＬ 止 ． 时 ， （ ） ０ （ ） 即 — Ⅳ为 此 ｒ 一 ， ｒ 一
个 阶 段进 行 ． ２ １ Ｔ Ｔ， ． ＜ Ｌ 即 （ ） ｂＴ ＜ Ｌ 阶 段 Ｔ ＋６ （ ）
＿ ｛ ０
≤ Ｘ Ｌ一 ≤
￣１ ａ ／ ２ ｔ
１（一圭 １ ０ ｂ
【
） 。
Ｌ一 瓜
≤ｚ ≤Ｌ
（ １ １ ）
２ ２ １ ＜Ｔ Ｔ 即 尚未 整体 渗 透 阶段 ． － ＜ ， Ｌ 假 设此 阶段 平 板 内温度 分 布为
ｌ（一圭 １
Ｉ
￣１ａ ／２ ｔ
） ｚ
０ ≤瓜 ≤ｚ
Ｌ， 热 流 由 左 边 界 传 递 至 右 边 界 ， 透 整 个 平 即 渗 板 ； 此 后 ， 渗 透层 无 任 何 物 理 意 义 ， 板 已整 再 热 平 体渗透， 热量 由高温 侧 向低 温侧 传递 ， 至传 热过 直 程 稳 定 为止 ． 据 上 述分 析 ， 个 求解 过 程 分 为 ３ 根 整
第三章第三节 一维非稳态导热的分析解
θ
( x,τ θ0
)
=
μ1
+
2 sin μ1 sin μ1 cos
μ1
cos(
μ1
e x ) − μ12F0 δ
θ
(0,τ θ0
)
=
θ m (τ θ0
)
=
μ1
+
2 sin μ 1 sin μ1 cos
μ1
e − μ12 F0
第三节一维非稳态导热的分析解
θ
( x,τ θ0
)
=
μ1
+
2 sin μ1 sin μ1 cos
式中常数a ,b ,c ,d 见P75表3-3 a`,b`,c`,d`见P75表3-4
第三节一维非稳态导热的分析解
3 正规热状况的实用计算方法－线算图法
诺谟图
以无限大平板为例，F0>0.2 时，取其级数首项即可
θ (x,τ ) =θ0
μ1
+
2sin μ1 sin μ1 cos
μ1
e−μ12
F0
cos(μ1
第三节一维非稳态导热的分析解
上式化为：
∂θ = a ∂ 2θ
∂τ
∂x 2
θ =θ0
∂θ = 0 ∂x
0 < x < δ ,τ > 0 τ =0 x=0
− λ ∂θ = hθ x = δ ∂x
第三节一维非稳态导热的分析解
用分离变量法可得其分析解为：
θ
( x,τ θ0
)
=
∞
∑
n =1
2 sin( β nδ ) cos( β n x) β nδ + sin( β nδ ) cos( β nδ
传热学讲义——第三章
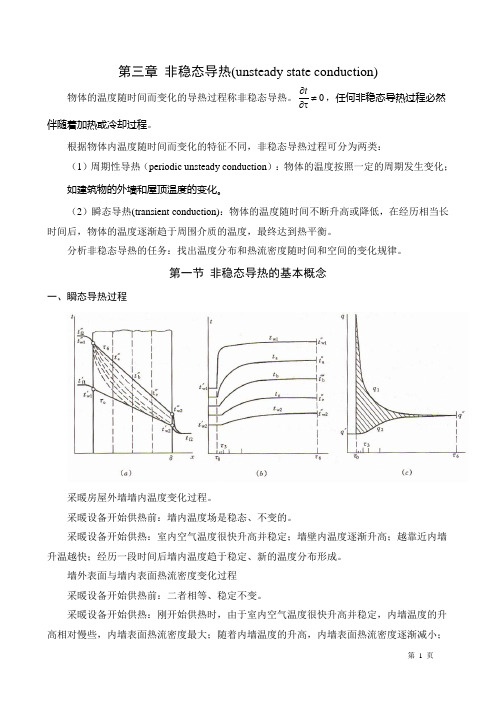
第三章 非稳态导热(unsteady state conduction)物体的温度随时间而变化的导热过程称非稳态导热。
0≠τ∂∂t，任何非稳态导热过程必然伴随着加热或冷却过程。
根据物体内温度随时间而变化的特征不同，非稳态导热过程可分为两类：（1）周期性导热（periodic unsteady conduction ）：物体的温度按照一定的周期发生变化； 如建筑物的外墙和屋顶温度的变化。
（2）瞬态导热(transient conduction)：物体的温度随时间不断升高或降低，在经历相当长时间后，物体的温度逐渐趋于周围介质的温度，最终达到热平衡。
分析非稳态导热的任务：找出温度分布和热流密度随时间和空间的变化规律。
第一节 非稳态导热的基本概念一、瞬态导热过程采暖房屋外墙墙内温度变化过程。
采暖设备开始供热前：墙内温度场是稳态、不变的。
采暖设备开始供热：室内空气温度很快升高并稳定；墙壁内温度逐渐升高；越靠近内墙升温越快；经历一段时间后墙内温度趋于稳定、新的温度分布形成。
墙外表面与墙内表面热流密度变化过程 采暖设备开始供热前：二者相等、稳定不变。
采暖设备开始供热：刚开始供热时，由于室内空气温度很快升高并稳定，内墙温度的升高相对慢些，内墙表面热流密度最大；随着内墙温度的升高，内墙表面热流密度逐渐减小；随着外墙表面的缓慢升高，外墙表面热流密度逐渐增大；最终二者相等。
上述非稳态导热过程，存在着右侧面参与换热与不参与换热的两个不同阶段。
（1）第一阶段（右侧面不参与换热）是过程开始的一段时间，特点是：物体中的一部分温度已经发生变化，而另一部分仍维持初始状态时的温度分布（未受到界面温度变化的影响），温度分布显现出部分为非稳态导热规律控制区和部分为初始温度区的混合分布，物体内各处温度随时间的变化率是不一样的，即：在此阶段物体温度分布受t分布的影响较大，此阶段称非正规状况阶段或初始阶段（initialregime）。
（2）第二阶段（右侧面参与换热）当右侧面参与换热以后，物体中的温度分布不受t影响，主要取决于边界条件及物性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§8.3 第一类边界条件下(tw=C)半无限 大平板一维非稳态导热
tw t tw t0
erf 2
x a
erf
2
1 Fo
式中：
erf
x
2
x
2 a ed
2 a
0
为高斯误差函数，其值可由附录中查得。
当
x 2 时， tw t 1
在0~时间内的总传热量为：
Q0~
0 Q d
0 h(t f
t0 ) e Bi Fo d
VCP (t f to )(1 e Bi Fo )
J
或： Q0~
Q0~
1 e Bi Fo
Qmax VCP (t f to )
注意使用中首先要判定是不是薄材，不然不能使用。
§8.5 第三类边界条件下有限厚物体的 加热或冷却
设有一厚度为2的无限大平
板，初始温度为t0， 将其放置于 温度为tf的流体介质中，设tf >t0 ，
hf ,t f
t
hf ,t f
流体与板面间的对流换热系数为h
4
且为常数。试确定在非稳态传热
3
过程中板内的温度分布。
Hale Waihona Puke 21由于是双面对称加热，板内的
的值均在0.95以上，即物体中各点的温差均小于0.5%， 工程上可视为薄材。
根据给出的是m／0 和x／m 的计算图，可用下
式确定x／0 ：
x／0 = x／m ×m／0
P104 图9.14~9.16给出了圆柱体的非稳态加热线算图。要 求熟练掌握其应用
例1（P103）
厚度为200mm的钢坯，在温度为1200℃的加热炉内双 面对称加热，假定铸坯初始温度为30℃，在加热过 程中炉内平均给热系数为h=174W/（m2·℃），钢的 热物性参数为λ=34.8W/m·℃，a=0.555×10-5 m2/s， 求(1)钢坯在炉内加热36min时钢坯的表面温度和断面 温差；(2)钢坯表面温度达到800℃所需要的时间及在 此时间内钢坯每平方米获得的热量。
x
f (F0 , Bi , )
x=0处即为物体的中心温度，
x= 处为物体的表面温度 Q0=2F·ρCp(tf –t0 ) J
解的结果都是无穷级数的形式，为便于计算, 绘 成线算图以供使用。 （P102 图9.11; 图9.12）
图9.12为一定加热时间下（相同Fo），板内温度
的分布情况： 在同一Fo下 ，当Bi ＜0. 1时, x／ m
F
式变为： t f t eBi Fo 或：t f t0 eBi Fo
t f t0
tf t
物体的瞬时热流量：
Q h(t f t)F h(t f t0 )F eBi Fo
将介质温度tf 与物体温度t间的差值(tf - t)或 (t - tf) 称为过余温度，记为θ
0 x , x0
x
t t0
t （ 0 对称性） x x0
t x
xx＝δ0
h(t
f
t ) xx＝δ0
(x, ) t(x, ) t f
0
t0 t f
x
f (F0, Bi , )
(x, ) t(x, ) t f
0
t0 t f
2 a
tw t0
经 时间后壁内温度开始变化的距离为：
x 4 a
在 时刻，通过壁面的热通量为：
q t tw t0
x x0
a
w Wm/m22
F CP
§h8.4薄CP材（ (在FV第恒)三2 温类介h边l 质界al中2条的件F加O）热Bi或冷却
t0
＝0
温度分布也是对称的，取坐标如
x
-
图所示：
大平板加热过程中的温度分布
该加热过程的微分方 程从导热微分方程的一 般形式简化为：
t 2t
a x2
hf ,t f t0
t
4 3 2 1
-
hf ,t f
＝0
x
定解条件：
0, 0,
0,
解的结果：
tw t tw t0
erf 2
x a
erf
2
1 Fo
式中：
erf
x
2
x
2 a ed
2 a
0
为高斯误差函数，其值可由附录中查得。
当
x 2 时， tw t 1
在0~时间内的总传热量为：
Q0~
0 Q d
0 h(t f
t0 ) e Bi Fo d
VCP (t f to )(1 e Bi Fo )
J
或： Q0~
Q0~
1 e Bi Fo
Qmax VCP (t f to )
注意使用中首先要判定是不是薄材，不然不能使用。
§8.5 第三类边界条件下有限厚物体的 加热或冷却
设有一厚度为2的无限大平
板，初始温度为t0， 将其放置于 温度为tf的流体介质中，设tf >t0 ，
hf ,t f
t
hf ,t f
流体与板面间的对流换热系数为h
4
且为常数。试确定在非稳态传热
3
过程中板内的温度分布。
Hale Waihona Puke 21由于是双面对称加热，板内的
的值均在0.95以上，即物体中各点的温差均小于0.5%， 工程上可视为薄材。
根据给出的是m／0 和x／m 的计算图，可用下
式确定x／0 ：
x／0 = x／m ×m／0
P104 图9.14~9.16给出了圆柱体的非稳态加热线算图。要 求熟练掌握其应用
例1（P103）
厚度为200mm的钢坯，在温度为1200℃的加热炉内双 面对称加热，假定铸坯初始温度为30℃，在加热过 程中炉内平均给热系数为h=174W/（m2·℃），钢的 热物性参数为λ=34.8W/m·℃，a=0.555×10-5 m2/s， 求(1)钢坯在炉内加热36min时钢坯的表面温度和断面 温差；(2)钢坯表面温度达到800℃所需要的时间及在 此时间内钢坯每平方米获得的热量。
x
f (F0 , Bi , )
x=0处即为物体的中心温度，
x= 处为物体的表面温度 Q0=2F·ρCp(tf –t0 ) J
解的结果都是无穷级数的形式，为便于计算, 绘 成线算图以供使用。 （P102 图9.11; 图9.12）
图9.12为一定加热时间下（相同Fo），板内温度
的分布情况： 在同一Fo下 ，当Bi ＜0. 1时, x／ m
F
式变为： t f t eBi Fo 或：t f t0 eBi Fo
t f t0
tf t
物体的瞬时热流量：
Q h(t f t)F h(t f t0 )F eBi Fo
将介质温度tf 与物体温度t间的差值(tf - t)或 (t - tf) 称为过余温度，记为θ
0 x , x0
x
t t0
t （ 0 对称性） x x0
t x
xx＝δ0
h(t
f
t ) xx＝δ0
(x, ) t(x, ) t f
0
t0 t f
x
f (F0, Bi , )
(x, ) t(x, ) t f
0
t0 t f
2 a
tw t0
经 时间后壁内温度开始变化的距离为：
x 4 a
在 时刻，通过壁面的热通量为：
q t tw t0
x x0
a
w Wm/m22
F CP
§h8.4薄CP材（ (在FV第恒)三2 温类介h边l 质界al中2条的件F加O）热Bi或冷却
t0
＝0
温度分布也是对称的，取坐标如
x
-
图所示：
大平板加热过程中的温度分布
该加热过程的微分方 程从导热微分方程的一 般形式简化为：
t 2t
a x2
hf ,t f t0
t
4 3 2 1
-
hf ,t f
＝0
x
定解条件：
0, 0,
0,
解的结果：