周建方版材料力学习题解答[第十章]
材料力学习题解答周建方

� � � � � AB �
MM 0 dx � EI
FN FN 0 dx � 2
l
(
2 F)x �
2 xdx �
2
l 2 F � 2 dx
EA
EI 0 2
2
EA 0 2
2
Fl 3 =
�
Fl
(移开)
3EI EA
当不考虑轴力的影响时� � AB �
Fl 3 3 EI
(移开)
1
9-10 题 9-10 图所示简单桁架�两杆截面积为 A�材料应力~应变关系为�� � C� 2 。试求 结点 B 的垂直位移△V。 解�由节点 B 的平衡条件求出 BD 杆的轴力和应力�再由应力-应变关系求出应变。结果为�
l 2GI p
l1 2GI p1
M x 2 ( x)dx
�
M
2 x
�
l
(
1
�
1)
l2 2GI p 2
2G 2 I p1 I p2
�
M
2 x
l
4G
32 (�d14
�
512
81� d
4 1
)
�
776
M
2 x
l
81�
d
4 1
G
9-4 试用互等定理求题 9-4 图所示结构跨度中点 C 的挠度�设 EI=常数。 题 9-4a 解�设力 F 为第一组力�设想在 C 处作用一单位
EI
x1 )
dx 1
�
l l 2
F (x2
� l)� 2
EI
1 4
x2
dx 2
�
5l 4 l
�
Fl
(x3 � 2 EI
材料力学第2版 课后习题答案 第10章 强度理论

解: t ≥
pD =
2[σ ]
3×106 ×1 2 × 300×106
= 0.01m = 1.0cm
2
9-8 铸铁圆柱形容器外直径D = 20 cm,壁厚t=2cm,受内压强p=4MPa,并在容器两端
受轴向压力P=200 kN作用,设 µ = 0.25 ,
许用拉应力[σ +]=25 MPa,(1)用第二强
论作强度校核。 解:
σ
4 xd
=
σ 2 + 3τ 2
σ
= 1202 + 3× 402 = 138MPa < [σ ]
τ
σ τ
题 9-3 图
所以安全。
9-4 某梁在平面弯曲下,已知危险截面上作用有弯矩M=50.9 kN ⋅ m ,剪力FS=134.6 kN,截面为No. 22b工字钢,[σ ]=160 MPa,试根据第三强度理对梁作主应力校核。
σ
m xd
=
σ
1
−
σ σ
+ b − b
σ3
= 1.027 −
256 × (−101.027)
625
=
42.4MPa
9-12 内径为d,壁厚为t的圆筒容器,内部盛有比重为γ ,高度为H的液体,竖直吊装如
图示。试按第三强度理论沿容器器壁的母线绘制圆筒的相当应力σ
3 xd
图(不计端部影响)。
解:
σ
y
=
πd2 4
应力校核。
70
(+)
(−) 30
( Q −图)
(−) 20
(−) 30
24.44 (+)
(M −图)
(−) 20
Wz
材料力学答案第十章
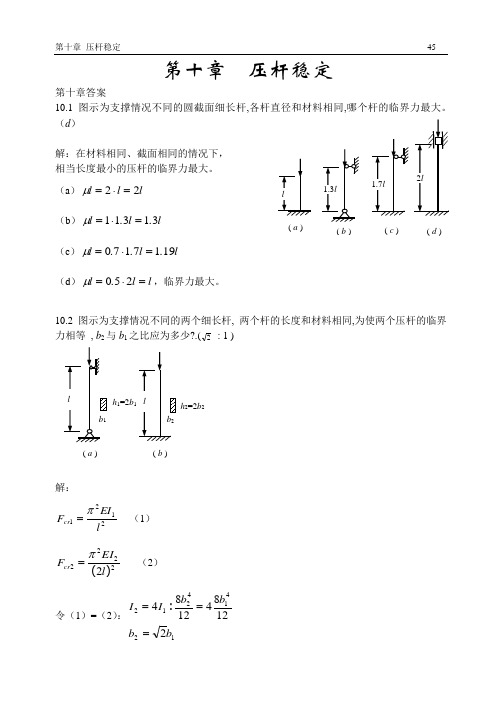
第十章 压杆稳定第十章答案10.1图示为支撑情况不同的圆截面细长杆,各杆直径和材料相同,哪个杆的临界力最大。
(d )解:在材料相同、截面相同的情况下, 相当长度最小的压杆的临界力最大。
(a )l l l 22=⋅=μ (b )l .l .l 31311=⋅=μ (c )l .l ..l 1917170=⋅=μ(d )l l .l =⋅=250μ,临界力最大。
10.2图示为支撑情况不同的两个细长杆, 两个杆的长度和材料相同,为使两个压杆的临界力相等 , b 2与b 1之比应为多少?.(2 : 1 )解:2121l EI F cr π=(1)22222)(l EI F cr π=(2)令(1)=(2):12414212212841284b b b b I I ===:( a)( b) ( c) ( d )( a ) ( b ) h 1=2b h 2=2b 210.3 铰接结构ABC 由截面和材料相同的细长杆组成,若由于杆件在ABC 平面内失稳而引起破坏,试确定荷载F 为最大时(两个杆同时失稳时)的θ (0<θ<π/2)角。
(θ=arctan (1/3)=18.44°) 解:θπcos F l EIF cr ==21212)( (1)θπsin F l EIF cr ==22222)( (2)(1/3))(:(2)(1)arctan cos l sin l l l tan ====θθ3130302222110.4图示压杆,型号为20a 工字钢,在xoz 平面内为两端固定,在xoy 平面内为一端固定,一端自由,材料的弹性模量E = 200GPa ,比例极限σp = 200MPa ,试求此压杆的临界力。
(F c r = 402.2kN )解:(1)柔度计算 查表知:6010012158122=-=========bE a ,E.AI i .A I i s p y y zz σλλσπλs 0p 23558mm A mm,mm,(2)xoz 平面内失稳:7894121200050..i l .y ===y λ 为中柔度杆,kN MPa,7048197===-=A F .b a cr cr y cr σλσ (2) (2)xoy 平面内失稳:169858180002..i l Z ===Z λ 为中柔度杆,kN MPa,6901194===-=A F .b a cr cr z cr σλσx10.5 结构如图,二杆的直径均为d =20mm ,材料相同,材料的弹性模量E = 210GPa , 比例极限σP = 200MPa ,屈服极限 σs = 240MPa ,强度安全系数n =2 ,规定的稳定安全系数n st =2.5 ,试校核结构是否安全。
《材料力学》第十章课后习题答案

在解题前要认真审题,明确题目要求和解题方向 ,避免出现理解偏差或误解题意的情况。同时, 在解题过程中要细心计算,注意检查计算过程和 结果是否正确。
05 知识点拓展与延伸
相关概念深入理解
材料的力学性能
材料在受到外力作用时,其变形、 破坏以及抵抗变形的能力,包括
弹性、塑性、强度、韧性等。
应力与应变
错误原因剖析
学习态度不认真
部分学生平时学习态度不认真,对课 堂知识掌握不扎实,导致在解题时无 法正确运用所学知识。
缺乏练习
部分学生平时缺乏练习,对解题方法 和技巧不熟悉,导致在考试时无法熟 练应对各种问题。
思维能力不足
部分学生思维能力较弱,无法灵活运 用所学知识解决实际问题。
粗心大意
部分学生在解题过程中粗心大意,忽 略了一些关键信息或步骤,导致解题 错误。
《材料力学》第十章课后习题答案
contents
目录
• 第十章课后习题概览 • 习题解答方法与技巧 • 典型习题详解 • 易错习题剖析及避免方法 • 知识点拓展与延伸 • 自我检测与提高建议
01 第十章课后习题概览
习题类型与数量
选择题
共10道,涵盖基本概念和理论 应用。
填空题
共5道,考查对知识点的理解和 记忆。
典型选择题解析
题目:下列关于剪切应力的说法中, 错误的是?
B. 剪切应力与材料的剪切模量成正比。
A. 剪切应力是相邻两部分材料发生相 对错动时的阻力。
典型选择题解析
C. 剪切应力只存在于受扭转的 杆件中。
D. 剪切应力的方向与材料错动 的方向垂直。
解析:正确答案是C。剪切应力 不仅存在于受扭转的杆件中,还 存在于受剪切的梁、板等构件中。
材料力学课后习题答案

2 2 Fl 2 4 Fl E (d1 d 2 ) d 2 d1 Ed 1 d 2
[习题 2-10] 受轴向拉力 F 作用的箱形薄壁杆如图所示。已知该材料的弹性常数为 E , ,试 求 C 与 D 两点间的距离改变量 CD 。
解:
'
(2)由变形能原理求 A 点的铅垂方向的位移
2 N12 l1 N 2 l2 1 F A 2 2 EA1 2 EA2 2 l2 1 N12 l1 N 2 ( ) F EA1 EA2
A
式中, l1 1000 / sin 45o 1414(mm) ; l 2 800 / sin 30 o 1600(mm)
解:墩身底面的轴力为:
N ( F G) F Alg
2-3 图
1000 (3 2 3.14 12 ) 10 2.35 9.8 3104.942(kN)
墩身底面积: A (3 2 3.14 12 ) 9.14(m 2 ) 因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
FN 2l 40 107 0.15 l2 4.76 EA2 210 109 12 106 从而得,Ax l2 4.76, Ay l2 2 l1 3 20.23 ( )
( 2)
V F Ay F1 l1 +F2 l2 0 Ay 20.33 ()
F 35kN 。已知杆 AB 和 AC 的直径分别为 d1 12mm 和 d 2 15mm ,钢的弹性模量
E 210GPa 。试求 A 点在铅垂方向的位移。 解: (1)求 AB、AC 杆的轴力 以节点 A 为研究对象,其受力图如图所示。 由平衡条件得出:
材料力学:ch10 组合变形

第十章 组合变形10-2 图a 所示板件,b =20mm ,δ=5mm ,载荷F = 12 kN ,许用应力[σ] = 100 MPa ,试求板边切口的允许深度x 。
题10-2图解:在切口处切取左半段为研究对象(图b ),该处横截面上的轴力与弯矩分别为F F =N(a) )(a b F M −=显然,222xb x b a −=−=(b) 将式(b)代入式(a),得2FxM =切口段处于弯拉组合受力状态,该处横截面上的最大拉应力为22N max 432(2a)6 22a Fx a F Fx a F W M A F δδδδσ+=+=+=根据强度要求,在极限情况下,][4322σδδ=+a Fx a F 将式(b)与相关数据代入上式,得01039.61277.042=×+−−x x 由此得切口的允许深度为mm 20.5=x10-3 图示矩形截面钢杆,用应变片测得上、下表面的纵向正应变分别为=1.0×10aε-3与=0.4×10b ε-3,材料的弹性模量E =210GPa 。
试绘横截面上的正应力分布图,并求拉力F 及其偏心距e 的数值。
题10-3图解:1.求和a σb σ截面的上、下边缘处均处于单向受力状态,故有MPa84Pa 104.010210 MPa 210Pa 100.1102103939=×××===×××==−−b b a a E εσE εσ偏心拉伸问题,正应力沿截面高度线性变化,据此即可绘出横截面上的正应力分布图,如图10-3所示。
图10-32.求和F e 将F 平移至杆轴线,得Fe M F F ==,N 于是有 a za E εW Fe A F σ=+=E εW Fe AF σzb =−=代入相关数据后,上述方程分别成为26250240=+Fe F 10500240=−Fe F 经联立求解,于是得mm 786.1m 10786.1kN 38.18N 183753=×=≈=−e F ,10-6 图示直径为d 的圆截面铸铁杆,承受偏心距为e 的载荷F 作用。
材料力学课后题答案7-10

作业参考答案(7-10章)7-1 (a )已知:045201030=-===ατσσMPa MPaMPaxy y xMPa MPa xy yx xy yx yx 1045220452210302224045220452210302103022224545=︒⨯-︒⨯-=+-==︒⨯+︒⨯-++=--++=cos sin cos sin sin cos sin cos ατασστατασσσσσ (b )已知:05.67203010-=-=-==ατσσMPaMPa MPaxy y x567220567223010222343856722056722(-30)102(-30)102222=︒⨯--+︒⨯-+=+-=-=︒⨯-+︒⨯--++=--++=).cos()().sin(cos sin .).sin().cos(sin cos ατασστατασσσσσααxy y x xy yx y x MPa(d )已知:012003050-====ατσσxy y x MPaMPaMPa MPa xy yx xy yx yx 668240230502223524023050230502222..)sin(cos sin )cos(sin cos -=︒--=+-==︒--++=--++=ατασστατασσσσσαα7-2 (a )已知:MPa MPaMPaxy y x 202040===τσσ︒-=︒︒-=-=-⨯-=--====⎩⎨⎧=+⎪⎭⎫ ⎝⎛-±+=+⎪⎪⎭⎫ ⎝⎛-±+=⎩⎨⎧3587316116463222040202220647365264736522022040220402200003212222....tan ....min max αασστασσστσσσσσσyx xyxy y x y x xMPa MPa MPa MPa(a )7-3(a )解:MPaMPa MPaMPaMPa 6527060260703060311321=+=-===-===σστσσσσσmax max(b )解:给定应力状态中有一个主应力是已知的,即σz =30MPa 。
【工程力学 课后习题及答案全解】第10章应力状态分析习题解
10-13 关于弹性体受力后某一方向的应力与应变关系, 有如下论述,试选择哪一种是正确的。
cos(2× (−15°)) + 0
=
−3.84
MPa
(b)切应力
τ x′y′ = −1.25 cos(2× (−15°)) = −1.08 MPa 正应力
σ x′ = −(−1.25) sin(2× (−15°)) = −0.625 MPa
10-2 结构中某点处的应力状态为两种应力状态的叠加结果。试求叠加后所得应力状
1 2
=
200 + 2
40
±
1 2
⎪⎩σ 3 = −90MPa
(200 − 40)2
+ 4 × (−150)2
=
⎧290MPa ⎩⎨− 50MPa
τ max
= σ1
−σ3 2
=
290 − (−90) 2
= 190 MPa
10-5 图示外径为 300mm 的钢管由厚度为 8mm 的钢带沿 20°角的螺旋线卷曲焊接而
解:(1)图
a: σ x
=
FP πDδ
=
250 ×10 3 π× (300 − 8)
×
8
= 34.07 MPa(压)
— 47 —
σ x′
=
−34.07 2
+
−34.07 2
cos(2× 20°)
=
−30.09
MPa
τ
x′y′
=
−34.07 2
sin(2
×
20°)
=
−10.95
MPa
(2)图
b: σ x
3 + cos 2θ 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10-1 题10-1图所示木制短柱的四角用四个40mm ⨯40mm ⨯4mm 的等边角钢加固。
已知角钢的许用应力G P a E M P a 200,160][==钢钢σ;木材的许用应力GPa E MPa 10,12][==木木σ。
试求许可载荷。
解:由静力平衡条件:F F F =+钢木 (1)变形协调条件:钢钢钢木木木l E l F l E l F l ==∆ (2)20625.025.025.0m A =⨯=木[]241016.12036.004.0004.04m A -⨯=+⨯⨯=钢代入(2)式可得钢钢木F F F 57.21016.2102000625.01010499=⨯⨯⨯⨯⨯=- (3) 题10-1图由于:[][]kN A F 7500625.010126=⨯⨯==木木木σ[][]kN A F 4.4911016.121016046=⨯⨯⨯==-钢钢钢σ 从(3)是可知,当角钢达到一定的许用载荷时(194.4kN ),而木材未达到2.57⨯194.4kN=499.6kN 的许用载荷[][][]kN F F F 6944.19457.24.194=⨯+=+=∴木钢10-2 受予拉力10kN 拉紧的缆索如题10-2图所示。
若在C 点再作用向下的载荷15kN ,并设缆索不能承受压力,试求在5l h =和54l h =两种情况下,AC 和BC 两段内的内力。
解:已知预拉力kN F y 10=,图a 所示,再在C 处加F=15kN 载荷,缆索中所产生的轴力如图所示,然后叠加起来。
平衡条件: F F F NB NA =+ (1) 变形协调条件: 0=∆+∆BC AC l l (2)即()0=--EAhF EA h l F NA NB (3)由1)、3)式得 F l h l F F lhF NA NB ⎪⎭⎫ ⎝⎛-==,于是缆索AC,BC 所受轴力分别为 题10-2图F l hF F F F y NB y NBC +=+= (4) F lhl F F F F y NA y NAC --=-= (5)当l h 51=时02<-=--=⋅kN F lh l F F Y AC N由于缆索不能承受压力,所以 0=NAC F 即kN F NA 10= 代入(1) 式kN F NB 5= 则kN F F F NB y NBC 15=+= 当 l h 54=时 kN F l h l F F y NAC 7155110=⨯-=--= kN F l h F F y NBC 22155410=⨯+=+=10-3 在题10-3图所示结构中,设横梁AB 的变形可以忽略,杆1、2的横截面面积相等,材料相同。
试求杆1、2的内力。
题10-3图解:由静力平衡条件0=∑AMa F aF a F N N 3cos 221⋅=⋅+⋅α (1)变形协调条件a al l 2cos 21=∆∆α(2) 物理方程EAlF l EAlF l N N αcos ,2211⋅=∆=∆ (3) 联立(1)、(2)和(3)式解得 :1cos 4cos 6,1cos 4332231+=+=αααF F F F N N 10-1 题10-1图所示木制短柱的四角用四个40mm ⨯40mm ⨯4mm 的等边角钢加固。
已知角钢的许用应力G P a E M P a 200,160][==钢钢σ;木材的许用应力GPa E MPa 10,12][==木木σ。
试求许可载荷。
解:由静力平衡条件:F F F =+钢木 (1)变形协调条件:钢钢钢木木木l E l F l E l F l ==∆ (2)20625.025.025.0m A =⨯=木[]241016.12036.004.0004.04m A -⨯=+⨯⨯=钢代入(2)式可得钢钢木F F F 57.21016.2102000625.01010499=⨯⨯⨯⨯⨯=- (3) 题10-1图 由于:[][]kN A F 7500625.010126=⨯⨯==木木木σ[][]kN A F 4.4911016.121016046=⨯⨯⨯==-钢钢钢σ从(3)是可知,当角钢达到一定的许用载荷时(194.4kN ),而木材未达到2.57⨯194.4kN=499.6kN 的许用载荷[][][]kN F F F 6944.19457.24.194=⨯+=+=∴木钢10-3 在题10-3图所示结构中,设横梁AB 的变形可以忽略,杆1、2的横截面面积相等,材料相同。
试求杆1、2的内力。
题10-3图解:由静力平衡条件0=∑AMa F aF a F N N 3cos 221⋅=⋅+⋅α (1)变形协调条件a al l 2cos 21=∆∆α(2) 物理方程EAlF l EAlF l N N αcos ,2211⋅=∆=∆ (3) 联立(1)、(2)和(3)式解得 :1cos 4cos 6,1cos 4332231+=+=αααF F F F N N 10-4题10-4图所示刚杆AB 悬挂于1、2两杆上,杆1的横截面面积为60mm 2,杆2为120 mm 2,且两杆材料相同。
若F=6 kN ,试求两杆的轴力及支座A 的反力。
题10-4图解:静力平衡条件0=∑AM: 3221⋅=+F F F N N (1)变形协调条件:212211=∆+∆+l l l l (2)物理方程:EAl F l EAl F l N N 222111,⋅=∆⋅=∆ (3) 而 m tg l m tg l 342,32121===⨯=αα 联立(1)、(2)和(3)解得 kN F KN F N N 2.7,6.321==A 支座反力:kN F F F F N N AY 8.421=-+= (向下)10-5 在题10-5图所示杆系中,沿对角线AC 的杆6比名义长度略短,误差为δ。
诸杆的抗拉(压)刚度都是EA 。
试求诸杆的内力。
题10-5图解: 解除6号杆,用轴力6N F 代替,并分别作用于A,C 两点。
如图b 所示。
则在6N F 作用下。
A 、C 两点间的位移计算如下:由莫尔定理,在A 、C 两点沿AC 方向加以单位力F 0=1。
由静力平衡条件分别计算出在F N6和F 单独作用下各杆的内力如下表:则有:()l F EA EA l F F N i i N Ni C A 6510221+==∆+∆∑= (1) 由于杆6略短δ,则变形协调条件:δ=∆+∆+∆6l C A (2)EAlF EA l F l N N 26666⋅==∆ (3) 将(1)、(3)式代入(2)式得:l EA l EA F N δδ208.022216=⋅+=所以:l EA l EA F F F F N N N N δδ146.022414321-=⋅+-==== lEA F F N N δ208.065== 10-6 题10-6图所示刚架梁由三根钢杆支承,钢杆的横截面面积均为2cm 2,材料的弹性模量E=210GPa ,其中一杆的长度短了100005l=δ。
在按下述两种情况装配后,试求各杆横截面上的应力。
(1)短杆在中间(题10-6图a );(2)短杆在一侧(题10-6图b )。
题10-6图a题10-6a 解:当装配后,杆1、3受压,杆2受拉,则由图知,其变形协调条件:δ=∆+∆21l l (1)物理方程:EAlF l l EAlF l N N 22311,=∆∆==∆ (2) 将(2)式代入(1)式得,δ=+EA l F EA l F N N 21,即:lEA F F N N δ=+21 (3) 由静力平衡条件:321N N N F F F +=, 即122N N F F = (4) 解得 : lEAF lEAF N N 32,321δδ==则:压)(3531021010000539113MPa ll l E A F N =⨯⨯====δσσ 拉)(703222MPa lEA F N ===δσ题10-6图b题10-6b 解: 设装配后,各杆及横梁的位置如图变形协调条件:()δ-∆+∆=∆3122l l l 即:δ=∆-∆+∆2312l l l (1) 根据横梁的静力平衡条件:0321=++N N N F F F 、031=⋅-⋅a F a F N N (2) 变形物理方程:EAl F l EAl F l EAl F l N N N ⋅=∆⋅=∆⋅=∆332211,, (3)将(3)代入(1)式 ,得:l EA F F F N N N δ=-+2312 (4) 联立(2)、(4)式,得:lEAF l EA F lEAF N N N 6,33,6321δδδ=-== 各杆的装配应力MPa lE7.16613===δσσMPa lE3.3332-=-=δσ10-7题10-7图所示结构的两杆同为钢杆,横截面面积同为A=10cm 2,E =200GPa ,线膨涨系数6105.12-⨯=α/C 0。
若杆BC 的温度降低20C 0,而杆BD 的温度不变,试求两杆的应力。
题10-7图解:BC 杆内力为F N1,BD 杆内力为F N2,变形后B 点到B’ 则 EAl F tl l N 1111-∆=∆α (1) 而 EAl F l N 222=∆ (2) 变形协调条件:30cos 21l l ∆=∆ (3) 将(1)、(2)代入(3)得: 30cos 22111EAl F EA l F tl N N =-∆α (4) 几何条件 l l =2,30cos 1ll =(5) 静力平衡条件30cos 12N N F F = (6) 将(5)、(6)代入(4)式解得: kN F kN F N N 2.26,3.3021==则BC 杆应力:)(3.301压MPa AF N BC ==σ BD 杆应力:MPa AF N BD 2.262==σ 10-8 阶梯形钢杆的两端在5C 0时被固定,如题10-8图所示,杆件上、下两段的横截面面积分别是A 上=5cm 2,A 下=10cm 2。
钢材的6105.12-⨯=α/C 0,E =200GPa 。
当温度升高至25C时,试求杆内各部分的温度应力。
解: 当阶梯杆处于自由状态时,其温度变化引起的伸长为()αααt l l t l t ∆=-∆=∆2下上 设杆内的内力(压力)为N F则由于 N F 使杆缩短为:下下上上EA l F EA l F l N N 11+=∆协调条件: 0=∆-∆l l t 即 0211=--∆下下上上EA l F EA l F ta N N α KNA A A A E t F N 3.332=+⋅⋅⋅∆=下上下上α(压)上上MPa A F N 7.6610500103.3363=⨯⨯==-σ (压)下下MPa A F N 3.33101000103.3363=⨯⨯==-σ 题10-8图 10-9 组合柱由钢和铸铁制成(题10-9图),其横截面是边长为2b 的正方形,钢和铸铁各占一半)2(b b ⨯。
