实数复习课件公开课
合集下载
实数复习公开课课件

实数按定义分类
有限小数及无限循环小数
整数
有理数
实 数 无理数
无限不循环小数
分数
正整数 0 负整数 正分数 负分数
正无理数 负无理数
按正负分类
正有理数
正实数
正无理数
实数
0 负实数
负有理数 负无理数
针对练习二——实数分类
22 、 1、在下列各数 0、 0 .2 3、 、 7 6.1010010001 、6 中无理数的个 数是(B )个
弧,交数轴正半轴于点A,则点A表示的数是(C ) A.1.5 C. 2 B.1.4 D. 3
针对练习三——实数相关概念、运算
4.
3
0 - 1 (- 1) _________ ;
3 2
2 2 3 __。 2 ( 3 2 ) __________
5.计算 6.求
3
27 (1 )
【学习目标】
1.知道平方根、立方根的概念,会进 行开平方和开立方运算,会求一个非负数 的平方根、算术平方根; 2.知道实数的分类;会对实数准确分 类; 3.知道实数的有关概念,会进行实数 大小比较; 4.能够运用实数的有关知识解决问题。
平方根、算术平方根、立方根的定义
一般地,如果一个数的平方等于 a ,这个数叫做 a 的平方根。 (也叫二次方根)
3 2. 已知3 5.25= 1.738, 52 .5=3.744,
17.38 则3 5250= _________ 。 3. 5 的整数部分是 2 ,则它的小数
部分是 5 2 。
4.
2 (1) 2 2 3
2 3
3 3 ( 2) 3 3 8 8 4 4 (3) 4 4 15 15 5 根据规律请写出 5 24 再写出两个等式? ;
第六章实数复习(公开课)ppt课件

金融
在金融领域,实数被用来表示各种数据,例如,股票价格、 汇率等。
统计
在统计学中,实数被用来表示各种数据,例如,平均值、中 位数、众数等。
05
实数的扩展知识
实数的连续性
实数的连续性定义
实数连续性的性质
实数具有连续性,即任意两个实数之 间都存在无数个其他实数。
实数的连续性是实数的基本性质之一 ,它在数学分析中有着广泛的应用, 如极限的定义、函数的连续性等。
实数连续性的几何意义
在数轴上,任意两个不同的实数之间 都存在一个线段,这个线段上包含无 数个点,这些点都是实数。
无理数的性质和证明
无理数的定义
无理数是不能表示为两个整数的 比的数,如π和√2。
无理数的性质
无理数具有无限不循环小数表示的 特性,它们既不是整数也不是分数 。
无理数的证明
无理数的存在可以通过反证法或构 造法等方式进行证明,例如通过反 证法证明√2是无理数。
体积
实数可以用来表示三维物 体的体积,例如,圆柱体 的体积可以用实数表示。
科学计算和工程计算
科学计算
实数在科学计算中有着广泛的应用, 例如,物理、化学、生物等学科中的 计算都需要用到实数。
工程计算
在工程领域,实数被广泛应用于各种 计算中,例如,建筑设计、机械制造 、航空航天等。
金融和统计中的数据表示
第六章实数复习( 公开课)ppt课件
汇报人:可编辑 2023-12-22
目录
• 实数的定义与性质 • 实数的运算 • 实数的分类 • 实数的应用 • 实数的扩展知识
01
实数的定义与性质
实数的定义
实数是有理数和无理数的总称,即既包括有理数又包括无理数的数。实 数可以用来表示长度、重量、时间等实际量,也可以表示数学中的概念 和运算结果。
在金融领域,实数被用来表示各种数据,例如,股票价格、 汇率等。
统计
在统计学中,实数被用来表示各种数据,例如,平均值、中 位数、众数等。
05
实数的扩展知识
实数的连续性
实数的连续性定义
实数连续性的性质
实数具有连续性,即任意两个实数之 间都存在无数个其他实数。
实数的连续性是实数的基本性质之一 ,它在数学分析中有着广泛的应用, 如极限的定义、函数的连续性等。
实数连续性的几何意义
在数轴上,任意两个不同的实数之间 都存在一个线段,这个线段上包含无 数个点,这些点都是实数。
无理数的性质和证明
无理数的定义
无理数是不能表示为两个整数的 比的数,如π和√2。
无理数的性质
无理数具有无限不循环小数表示的 特性,它们既不是整数也不是分数 。
无理数的证明
无理数的存在可以通过反证法或构 造法等方式进行证明,例如通过反 证法证明√2是无理数。
体积
实数可以用来表示三维物 体的体积,例如,圆柱体 的体积可以用实数表示。
科学计算和工程计算
科学计算
实数在科学计算中有着广泛的应用, 例如,物理、化学、生物等学科中的 计算都需要用到实数。
工程计算
在工程领域,实数被广泛应用于各种 计算中,例如,建筑设计、机械制造 、航空航天等。
金融和统计中的数据表示
第六章实数复习( 公开课)ppt课件
汇报人:可编辑 2023-12-22
目录
• 实数的定义与性质 • 实数的运算 • 实数的分类 • 实数的应用 • 实数的扩展知识
01
实数的定义与性质
实数的定义
实数是有理数和无理数的总称,即既包括有理数又包括无理数的数。实 数可以用来表示长度、重量、时间等实际量,也可以表示数学中的概念 和运算结果。
实数复习课课件人教版ppt
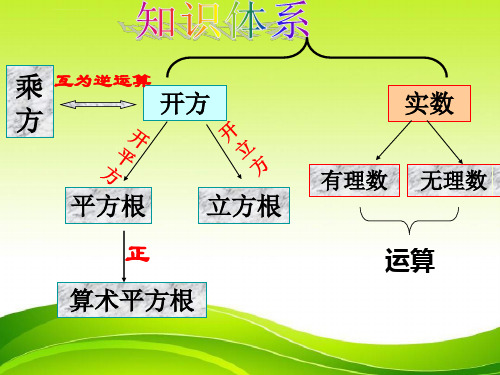
实数的分类
有理数和无理数统称实数.
无理数的特征:
1.圆周率及一些含有的数
2.开不尽方的数 3.无限不循环小数
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
把下列各数分别填入相应的集合内:
3 4 , 7 , 8 , 2 1, 1 , 0,
说明:立方根的性质可以概括为立方根 的唯一性,即一个数的立方根是唯一的.
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
6、开平方:
求一个数的平方根的运算,叫做开平方 .
开平方与平方互为逆运算。
我们可以运用平方运算来求一个数的平方根。
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
已知 1.72011.31, 11.72014.14,7
那0么 .0017的 20平 1 方根 0.0是 4147
已知 2.361.53,623.64.85,8
掌
若x0.485,则 8x是 0.236
不 要 遗 漏
解下列方程:
1. 9(3y)2
解: (3 y)2
3 y
2
4
4
9
49Biblioteka 2. 2( 7x2) 31250
解: 27(3x2)3 125
3
(x2)3 125
3
27
x 2 3 125
y 3
3
y21或y32
3
3
3
27
x 25
有理数和无理数统称实数.
无理数的特征:
1.圆周率及一些含有的数
2.开不尽方的数 3.无限不循环小数
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
把下列各数分别填入相应的集合内:
3 4 , 7 , 8 , 2 1, 1 , 0,
说明:立方根的性质可以概括为立方根 的唯一性,即一个数的立方根是唯一的.
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
6、开平方:
求一个数的平方根的运算,叫做开平方 .
开平方与平方互为逆运算。
我们可以运用平方运算来求一个数的平方根。
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
已知 1.72011.31, 11.72014.14,7
那0么 .0017的 20平 1 方根 0.0是 4147
已知 2.361.53,623.64.85,8
掌
若x0.485,则 8x是 0.236
不 要 遗 漏
解下列方程:
1. 9(3y)2
解: (3 y)2
3 y
2
4
4
9
49Biblioteka 2. 2( 7x2) 31250
解: 27(3x2)3 125
3
(x2)3 125
3
27
x 2 3 125
y 3
3
y21或y32
3
3
3
27
x 25
第六章实数复习(公开课)ppt课件

在几何图形中,我们也需要使用在绘制函数图像时,我们需要使用实 数。例如,绘制一次函数、二次函数 、三角函数等图像时都需要用到实数 。
科学问题中的实数应用
物理测量
在物理学中,许多物理量都是用 实数来表示的。例如,物体的速 度、加速度、力等都需要用到实
总结词
实数减法的运算律
详细描述
实数减法具有一些重要的运算律,如差不变性质、减法结 合律和减法交换律等。这些运算律可以帮助我们简化复杂 的减法计算,提高计算的准确性和效率。
实数的乘法
总结词
实数乘法的定义与性质
详细描述
实数乘法是数学中的基本运算之一,它具有结合律、交换 律和分配律等性质。实数乘法可以用来解决许多实际问题 ,如计算面积、解决概率问题等。
根式的化简
化简根式是指将根式化简为一个最简 形式的过程。例如,√8=2√2,因为8 可以分解为4×2,而4的平方根是2, 所以√8=2√2。
Part
05
实数的应用
生活中的实数应用
长度测量
在日常生活中,我们经常需要测 量物体的长度、宽度和高度等, 这些都需要用到实数。例如,测 量房间的尺寸、家具的大小等。
总结词
实数乘法的几何意义
详细描述
实数乘法的几何意义可以理解为将数轴上的点进行拉伸或 压缩。在数轴上,一个数乘以另一个数的结果等于一个数 覆盖另一个数的长度。
总结词
实数乘法的运算律
详细描述
实数乘法具有结合律、交换律和分配律。结合律是指 (ab)c=a(bc);交换律是指ab=ba;分配律是指 a(b+c)=ab+ac。这些运算律可以帮助我们简化复杂的乘 法计算,提高计算的准确性和效率。
在数轴上进行乘法运算时,将数 轴上的每个点乘以一个正数或负 数,长度会相应地扩大或缩小。
(中考复习)第1讲 实数的有关概念 公开课获奖课件

对接点一:有理数与无理数
常考角度:1.实数的分类,无理数的定义; 2.算术平方根、零指数、负整数指数的直接计算; 3.特殊角的三角函数值.
【例题 1】 (2013·湖州)实数π ,15,0,-1 中,无理数
是
()
A.π
1 B.5
Hale Waihona Puke C.0D.-1解析 根据常见的无理数的三种形式判断,只有π
是无理数.
-1,∴a2 013=(-1)2 013=-1.
答案 B
对接点三:科学记数法、近似数与有效数字
常考角度:1.用科学记数法表示一个数及单位换算;
2.根据要求取近似数和保留有效数字;
3.近似数精确到的位数.
【例题3】 (2013·嘉兴)据统计,1959年南湖革命纪念馆成
立以来,约有2 500万人次参观了南湖红船(中共一大会
-1 在 3 和 4 之间.
答案 C
【名师课堂】
1.两边逼近法:用能开的尽方的两个正数的算术平方根逼 近:如(1) 9< 13< 16,即 3< 13<4;(2) 2.42< 6<
2.52,2.4< 6<2.5. 2.要特别注意算术平方根和平方根的区别和联系.
【预测4】 实数-27的立方根是____________. 解析 ∵(-3)3=-27,∴-27的立方根是-3. 答案 -3
第一板块 基础知识梳理
第一部分 数与式 第一讲 实数的有关概念
考纲要求
1.理解有理数的意义,能用数轴上的点表示有理数; b 2.理解相反数和绝对值的意义,会求有理数的相反数、 b
倒数和绝对值(绝对值符号内不含字母); 3.了解无理数和实数的概念,知道实数与数轴上的点的 a
一一对应关系; 4.了解平方根、算术平方根、立方根的概念;知道开方 a
第六章实数复习(公开课)ppt课件

19世纪
数学家逐步完善实数理论 ,形成了完备的实数体系 ,为数学分析、连续函数 等研究奠定了基础。
减法运算
总结词
减法运算的基本性质
详细描述
实数的减法运算可以转化为加法运算,即a-b=a+(-b)。
总结词
减法运算的运算律
详细描述
减法运算同样满足交换律和结合律,即a-b=b-a和(ab)-c=a-(b+c)。
总结词
减法运算的运算性质
详细描述
减法的可逆性也是减法的一个重要性质,每一个数都有 唯一的相反数;另外,0是减法的单位元,任何数与0 相减都等于它本身。
总结词
加法运算的运算律
详细描述
加法运算还有一些特殊的运算律,例如,任何数与0相加 都等于它本身,即a+0=a;相反数相加等于0,即a+(a)=0。
总结词
加法运算的运算性质
详细描述
加法运算还有一些重要的运算性质,例如,加法的可逆性 ,即每一个数都有加法逆元,与它相加等于0;加法的单 位元,即有一个特殊的数0,任何数与它相加都等于它本 身。
实数在几何学中有着广泛的应用,例如在计算长度 、面积和体积时,需要使用实数表示测量值。
函数定义域与值域
实数可以用来定义各种数学函数,包括代数函数、 三角函数、指数函数和对数函数等,同时函数的值 域也由实数构成。
数学分析基础
实数对于数学分析来说是必不可少的基础,极限、 连续性和可微性的定义都离不开实数。
在物理中的应用
80%
测量与计算
在物理学中,实数常被用于表示 和计算各种物理量,如长度、时 间、质量、电荷等。
100%
物理定律的数学表达
许多物理定律可以用实数表示的 数学公式来描述,例如牛顿第二 定律 F=ma。
第六章实数复习(公开课)ppt课件

$a times (b + c) = a times b + a times c$
。
特别注意
乘法中负负得正,即负 数乘以负数结果为正。
除法运算规则
除数为0的情况
任何数除以0都是无意义的,结果不确定。
被除数为0的情况
0除以任何非零数都等于0。
特别注意
在除法中,负负得正,即负数除以负数结果为正 。
03
3完备性Βιβλιοθήκη 实数集具有完备性,即任何实数域上的柯西序列 都收敛于一个实数,这保证了数学分析的严密性 。
无理数和有理数在解决实际问题中应用
几何应用
物理应用
在几何学中,无理数常常出现,如√2代表 对角线长度与边长之比为√2的等腰直角三 角形的边长。
在物理学中,许多常数都是无理数,如圆 周率π和自然对数的底e等,这些常数在描 述自然现象时具有重要作用。
开方运算应用
开方运算在数学、物理、工程等领域有广泛应用,如求解方程、计算面积和体积等。
05
无理数和有理数在实数范 围内地位和作用
无理数和有理数定义及分类
有理数定义
01
可以表示为两个整数之比的数,包括整数、有限小数和无限循
环小数。
无理数定义
02
无法表示为两个整数之比的数,即无限不循环小数。
分类
03
数值大小与结果
正数减去正数结果可能为 正也可能为负,负数减去 负数结果为正,正数减去 负数结果为正。
特别注意
减法没有交换律,即$ab$和$b-a$的结果不同。
乘法运算规则
乘法交换律
$a times b = b times a$。
乘法结合律
乘法分配律
$(a times b) times c = a times (b times c)$。
《实数》课件精品 (公开课)2022年数学PPT

情境引入2
两位同学背靠背,规定向前为正,
一人向前走3步,记作
,
一人向后走3步 ,记作
.
对照数轴,说出-3与+3两数的相同点和不同点. 你还能说出具备这些特征的成对的数吗?
一 相反数
探究一 相反数的概念
活动1:观察下列一组数+1和-1,+2.5和-2.5, +4和-4,并把它们在数轴上表示出来.
思考: 1)上述各对数之间有什么特点? 2)请写出一组具有上述特点的数 3)你能得出相反数的概念吗? 4)表示各对数的点在数轴上有什么位置关系?
9 35
64
π
•
0.6
3 4
3 9
0.13
(1)有理数: {
9
64
•
0.6
3
4
3 0.13
π (2)无理数: { 3 5
3 9
(3)整数: { 9
(4)负数: { 3
4
(5)分数: {
•
0.6
(6)实数: {
64 3
3 9
3 0.13
4
3
}
}
} } }
}
5. 比较 3 7 与6的大小.
解: ∵37 >36 ∴ 3 7 > 6.
二 多重符号的化简 问题1:a的相反数是什么?
a 的相反数是-a , a可表示任意有理数. 问题2:如何求一个数的相反数?
在这个数前加一个“-”号.
问题3:若把 a分别换成+5,-7,0时,这些数的相 反数怎样表示?
a = +5, a = -7, a = 0,
- a = -(+5) - a = -(-7) -a = 0
思考 由此你可以得到什么结论? 有理数都可以化成有限小数或无限循环
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实 数复习
第一单元《数与式》
实数的有关概念和运算
复习目标
1、掌握实数的分类,能根据实数的相关概念 及性质解决实际问题;
2、会用科学计数法表示较大的数或较小的数, 理解精确度与近似数的概念;
3、能熟练准确的进行实Байду номын сангаас的运算。
知识网络
一、实数的概念及其分类
二、数轴、相反数、绝对值、倒数、算 术平方根、平方根、立方根的意义。
1、节约是一种美德,节约是一种智慧.据不完
全统计,全国每年浪费食物总量折合粮食可养活约
3亿5千万人350000000用科学记数法表示为(B )
A.3.5×107
B.3.5×108
C.3.5×109
D.3.5×1010
考点5:实数运算
1、实数运算顺序: 先乘方开方,再乘除,最后加减 2、常见的运算类型及法则; (1)0次幂 (2)负整数指数幂 (3)乘方 (4)开方
达标测试
1.选择题
(1)实数 3 27、0、- 、16、1、0.1010010001 (相相邻两个1之间
3
依次多一个0),其中无理数是( B )个。
A.1 B.2 C.3 D.4
(2)实数a在数轴上的位置如图4所示,则 a 2.5 ( B )
A.a 2.5
B.2.5 a
a
C.a 2.5
D. a 2.5
(3) 11 估计的值在( B )之间。
A.1与2之间 B.2与3之间
C.3与4之间 D.4与5之间
2.填空题 (1) 5、、- 4、0 这四个数中,最大的是 。
(2) 的平方根是 ±3 。
a2
(3)若实数 a 、b满足| a 2 | b 4 0 则 b = 1 。
(4)5 的整数部分是 2 ,则它的小数 部分是 5 - 2 。
正无理数 负无理数
正有理数 正实数 正无理数
0 正有理数
负实数 负无理数
典型例题
例1、判断下列各数哪些是有理数哪些是无理数
31;
8;
3 27 ; ;
22 ; 7
3.14;
••
0.321;
0.1010010001;
B
sin 600;
tan 450 3;
3.2
方法归纳
1.一个数是不是无理数,应先计算或者化简再判断 2.无理数常见的类型:
1、数轴:规定了原点、正方向、单位长 度的直线。数轴上的点与实数一 一对应
2、相反数:只有符号不同的两个数 3、倒数:乘积为1的两数互为倒数,特别
的0没有倒数 4、绝对值:在数轴上,一个数到原点的
距离叫做该数的绝对值. 5、算术平方根、平方根、立方根、
典型例题
例1: -(-2)的相反数是 - 1 的倒数是 3
典型例题
例1 (1)据有关部门统计,截止到2014年5月1日,
重庆市私家小轿车已到达563000辆,将 563000这 个数用科学计数法表示为
(2)某种计算机完成一次基本运算的时间约为 0.000 000 001秒,把0.000 000 001用科学计数法 表示为
(3) 506亿用科学计数法表示为
所以4< 10+1<5.所以[ 10+1]=4. 答案:4
方法归纳
科学计数法表示的法:
(1)当原数大于等于10时,n等于原数的整位 数减1.
(2)当原数大于0小等于1时,n是负整数,它 的绝对值等于原数中左起第一位非零数字前所 有0的个数(包括小数点前的0).
(3)有数字单位的科学计数法,可以用1亿= 1×108 ,一万= 1×104,一千= 1×103来表示 这样能提高解题效率。
3 - 2 的绝对值是
;3 - 2 的相反数是
; - 3 的倒数是
的平方根是
。
典型例题
例2、已知实数a、b在数轴上对应点的位置如图; 化简:a b (a b)2
ba
0
方法归纳
1、取绝对值符号一定要先对该数正负进行
a 判断
a a≥0 a a<0
2、初中所涉及的三个非负数 a2, | a︱ ,
3.计算:
5 2 3 0 6(1 1) 12 . 32
新定义运算
【典例】(中考)规定用符号[m]表示一个实数m的整数部分,
例如:[ 2 ]=0,[3.14]=3.按此规定[ 10 +1]的值为
.
3
突 (1)估算 1的0 值 破 (2)计算 10+1的取值范围 【口自主(解3)答根】据因符为号9[<m10]<的16规,所定以计3算<10出<[410, +1]的值
(1)(根号型)开不尽方的数,如
2; 3 9;
;
(2)具有特定意义的数,如
; 7
(3)具有特定结构的数,如 0.1010010001;
(4)三角函数中的一些数,如 sin 10 0 ;
; 1、在实数0,
22 ; 7
中,无理数的个数有( )
2; - 9;
A 1个 B 2个
C、3个 D、4个
考点2:实数的有关概念
(5)特殊三角函数值
例1:计算
(1)1 12 2 0 3 2 .
2
【解析】原式 2 2 3 1 2 3 3 3.
1、2 2 • sin 45 (2012)0 1 2 ( 1 )2 2
2、-12 27 6 tan 30 3 2
3、(2)2 8 2 sin 45o | 1 2 |
a, a
若几个非负数的和为0,则这几个非负数应同 时为0.
(a+1)2+|b-2︱=0,则(a-b)2012=
考点3:实数大小比较
例1、若m= 40 - 4 则估计m的值取值范围是
例2、比较大小: 2 5 与 2 3
例3、已知实数m、n在数轴上的对应点的位置如图所示,则下 列判断正确的是
A.m>0 B.n<0
C.mn<0 D.m-n>0
方法归纳
比较实数大小长用方法: 1、数轴比较法; 2、绝对值比较法; 3、差值比较法; 4、根式比较法;
1.已知、为两个连续的整数,则
A ab0
C ba
B ab 0
D ba
2.已知、为两个连续的整且
ab
a< 1,1<b则
考点4:科学计数法
1、科学计数法:
是一种记数的方法,即把一个绝对值小于1(或 者大于等于10)的实数记为a×10n的形式(其 中1≤︳a ︳<10)。
三、科学计数法及近似数的概念
四、实数的运算
考点一:实数的概念及其分类
1、实数概念
有理数和无理数统称为实数
(1)有理数
整数和分数统称为有理数 有理数是有限小数或无限循环小数
(2)无理数
无限不循环小数
考点一:实数的概念及其分类
2、实数的分类
整数
有理数 分数
正整数 0 负整数
正分数
实数
负分数 实数
无理数
第一单元《数与式》
实数的有关概念和运算
复习目标
1、掌握实数的分类,能根据实数的相关概念 及性质解决实际问题;
2、会用科学计数法表示较大的数或较小的数, 理解精确度与近似数的概念;
3、能熟练准确的进行实Байду номын сангаас的运算。
知识网络
一、实数的概念及其分类
二、数轴、相反数、绝对值、倒数、算 术平方根、平方根、立方根的意义。
1、节约是一种美德,节约是一种智慧.据不完
全统计,全国每年浪费食物总量折合粮食可养活约
3亿5千万人350000000用科学记数法表示为(B )
A.3.5×107
B.3.5×108
C.3.5×109
D.3.5×1010
考点5:实数运算
1、实数运算顺序: 先乘方开方,再乘除,最后加减 2、常见的运算类型及法则; (1)0次幂 (2)负整数指数幂 (3)乘方 (4)开方
达标测试
1.选择题
(1)实数 3 27、0、- 、16、1、0.1010010001 (相相邻两个1之间
3
依次多一个0),其中无理数是( B )个。
A.1 B.2 C.3 D.4
(2)实数a在数轴上的位置如图4所示,则 a 2.5 ( B )
A.a 2.5
B.2.5 a
a
C.a 2.5
D. a 2.5
(3) 11 估计的值在( B )之间。
A.1与2之间 B.2与3之间
C.3与4之间 D.4与5之间
2.填空题 (1) 5、、- 4、0 这四个数中,最大的是 。
(2) 的平方根是 ±3 。
a2
(3)若实数 a 、b满足| a 2 | b 4 0 则 b = 1 。
(4)5 的整数部分是 2 ,则它的小数 部分是 5 - 2 。
正无理数 负无理数
正有理数 正实数 正无理数
0 正有理数
负实数 负无理数
典型例题
例1、判断下列各数哪些是有理数哪些是无理数
31;
8;
3 27 ; ;
22 ; 7
3.14;
••
0.321;
0.1010010001;
B
sin 600;
tan 450 3;
3.2
方法归纳
1.一个数是不是无理数,应先计算或者化简再判断 2.无理数常见的类型:
1、数轴:规定了原点、正方向、单位长 度的直线。数轴上的点与实数一 一对应
2、相反数:只有符号不同的两个数 3、倒数:乘积为1的两数互为倒数,特别
的0没有倒数 4、绝对值:在数轴上,一个数到原点的
距离叫做该数的绝对值. 5、算术平方根、平方根、立方根、
典型例题
例1: -(-2)的相反数是 - 1 的倒数是 3
典型例题
例1 (1)据有关部门统计,截止到2014年5月1日,
重庆市私家小轿车已到达563000辆,将 563000这 个数用科学计数法表示为
(2)某种计算机完成一次基本运算的时间约为 0.000 000 001秒,把0.000 000 001用科学计数法 表示为
(3) 506亿用科学计数法表示为
所以4< 10+1<5.所以[ 10+1]=4. 答案:4
方法归纳
科学计数法表示的法:
(1)当原数大于等于10时,n等于原数的整位 数减1.
(2)当原数大于0小等于1时,n是负整数,它 的绝对值等于原数中左起第一位非零数字前所 有0的个数(包括小数点前的0).
(3)有数字单位的科学计数法,可以用1亿= 1×108 ,一万= 1×104,一千= 1×103来表示 这样能提高解题效率。
3 - 2 的绝对值是
;3 - 2 的相反数是
; - 3 的倒数是
的平方根是
。
典型例题
例2、已知实数a、b在数轴上对应点的位置如图; 化简:a b (a b)2
ba
0
方法归纳
1、取绝对值符号一定要先对该数正负进行
a 判断
a a≥0 a a<0
2、初中所涉及的三个非负数 a2, | a︱ ,
3.计算:
5 2 3 0 6(1 1) 12 . 32
新定义运算
【典例】(中考)规定用符号[m]表示一个实数m的整数部分,
例如:[ 2 ]=0,[3.14]=3.按此规定[ 10 +1]的值为
.
3
突 (1)估算 1的0 值 破 (2)计算 10+1的取值范围 【口自主(解3)答根】据因符为号9[<m10]<的16规,所定以计3算<10出<[410, +1]的值
(1)(根号型)开不尽方的数,如
2; 3 9;
;
(2)具有特定意义的数,如
; 7
(3)具有特定结构的数,如 0.1010010001;
(4)三角函数中的一些数,如 sin 10 0 ;
; 1、在实数0,
22 ; 7
中,无理数的个数有( )
2; - 9;
A 1个 B 2个
C、3个 D、4个
考点2:实数的有关概念
(5)特殊三角函数值
例1:计算
(1)1 12 2 0 3 2 .
2
【解析】原式 2 2 3 1 2 3 3 3.
1、2 2 • sin 45 (2012)0 1 2 ( 1 )2 2
2、-12 27 6 tan 30 3 2
3、(2)2 8 2 sin 45o | 1 2 |
a, a
若几个非负数的和为0,则这几个非负数应同 时为0.
(a+1)2+|b-2︱=0,则(a-b)2012=
考点3:实数大小比较
例1、若m= 40 - 4 则估计m的值取值范围是
例2、比较大小: 2 5 与 2 3
例3、已知实数m、n在数轴上的对应点的位置如图所示,则下 列判断正确的是
A.m>0 B.n<0
C.mn<0 D.m-n>0
方法归纳
比较实数大小长用方法: 1、数轴比较法; 2、绝对值比较法; 3、差值比较法; 4、根式比较法;
1.已知、为两个连续的整数,则
A ab0
C ba
B ab 0
D ba
2.已知、为两个连续的整且
ab
a< 1,1<b则
考点4:科学计数法
1、科学计数法:
是一种记数的方法,即把一个绝对值小于1(或 者大于等于10)的实数记为a×10n的形式(其 中1≤︳a ︳<10)。
三、科学计数法及近似数的概念
四、实数的运算
考点一:实数的概念及其分类
1、实数概念
有理数和无理数统称为实数
(1)有理数
整数和分数统称为有理数 有理数是有限小数或无限循环小数
(2)无理数
无限不循环小数
考点一:实数的概念及其分类
2、实数的分类
整数
有理数 分数
正整数 0 负整数
正分数
实数
负分数 实数
无理数
