定期寿险的趸交纯保费-保险精算习题
寿险精算习题及答案
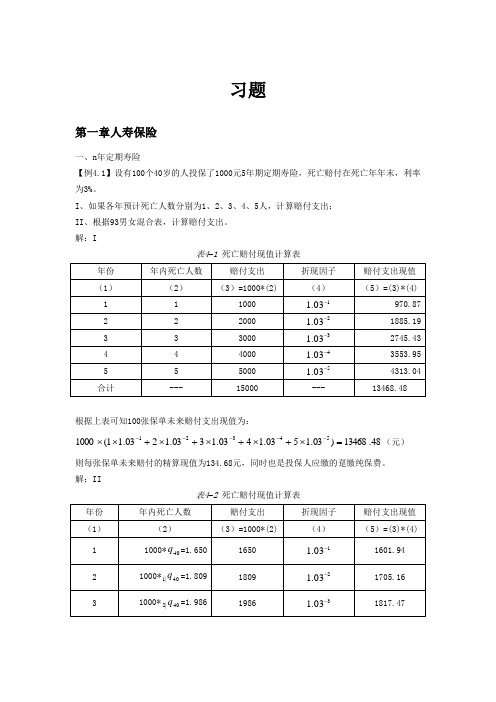
习题第一章人寿保险一、n 年定期寿险【例4.1】设有100个40岁的人投保了1000元5年期定期寿险,死亡赔付在死亡年年末,利率为3%。
I 、如果各年预计死亡人数分别为1、2、3、4、5人,计算赔付支出; II 、根据93男女混合表,计算赔付支出。
解:I表4–1 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:48.13468)03.1503.1403.1303.1203.11(100054321=⨯+⨯+⨯+⨯+⨯⨯-----(元)则每张保单未来赔付的精算现值为134.68元,同时也是投保人应缴的趸缴纯保费。
解:II表4–2 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:86.9124)03.103.103.103.103.1(1000540|4440|3340|2240|11402=⨯+⨯+⨯+⨯+⨯⨯-----q q q q q (元)则每张保单未来赔付的精算现值为91.25元,同时也是投保人应缴的趸缴纯保费。
【例4.2】某人在40岁时投保了10000元3年期定期寿险,死亡赔付在死亡年年末,利率为5%。
根据93男女混合表计算:I 、单位趸缴纯保费;II 、单位赔付现值期望的方差;III 、(总)趸缴纯保费; 解:I 、单位趸缴纯保费为,)()(424023414024040|2340|1240240|11|3:40q p v q p v vq q v q v vq q v Ak k k ++=++=⨯=∑=+]05.1001993.0)001812.01()00165.01(05.1001812.0)00165.01(05.100165.0[32⨯-⨯-+⨯-+=00492793.0=(元)。
II 、单位赔付现值期望的方差为,00444265.0)()()()(21|3:4040|2640|1440221|3:40240|)1(221|3:401|3:402=-++=-⨯=-∑=+A q v q v q v A q v AAk k k III 、趸缴纯保费为,28.49100001|3:40=⨯A (元) 【例4.3】某人在50岁时投保了100000元30年期定期寿险,利率为8%。
保险精算学-趸缴纯保费(2)

计算
(1)A 30:10
, 0 x 100
(2)Var(zt )
例4.3.4答案
由例3.1已知:
A1 0.092 30:10
Var(zt )1 0.055
(1)
1
A30:10
v10 10 p30
1.110 60 0.33 70
A 30:10
A1 30:10
1
A30:10
计算
1
fT
(t)
60
, 0 t 60
0 , 其它
(1)Ax (2)Var(zt )
(3) Pr(z 0.9 ) 0.9的0.9.
例4.3.2答案
(1) Ax
0
e t
fT
(t)dt
e 60 t
1
1 e60 dt
0
60
60
(2)Var(zt ) 2 Ax ( Ax )2
e 60 2 t
基本符号
(x) —— 投保年龄x 的人。
——人的极限年龄 bt ——保险金给付函数。
vt ——贴现函数。
zt ——保险给付金在保单生效时的现
时值
zt bt vt
1、n年定期寿险
定义
保险人只对被保险人在投保后的n年内发生的保险 责任范围内的死亡给付保险金的险种,又称为n年 死亡保险。
zt btvt 0 , t m
死亡即付定期寿险趸缴纯保费的厘定
符号:m Ax
厘定:
m Ax E(zt ) m zt fT (t)dt
m
0 zt fT (t)dt 0 zt fT (t)dt
1
Ax Ax:m
现值随机变量的方差
方差公式
保险精算第二版习题及答案

保险精算(第二版)第一章:利息的基本概念练 习 题1.已知()2a t at b =+,如果在0时投资100元,能在时刻5积累到180元,试确定在时刻5投资300元,在时刻8的积累值。
(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+= 2.(1)假设A(t)=100+10t, 试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======(2)假设()()100 1.1nA n =⨯,试确定 135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3.已知投资500元,3年后得到120元的利息,试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。
11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4.已知某笔投资在3年后的积累值为1000元,第1年的利率为 110%i =,第2年的利率为28%i =,第3年的利率为 36%i =,求该笔投资的原始金额。
123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5.确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。
(2)名义贴现率为每4年计息一次的年名义贴现率6%。
(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎫ ⎪=+= ⎪ ⎪⎝⎭6.设m >1,按从大到小的次序排列()()m m d di i δ<<<<。
保险精算课程三(寿险精算)
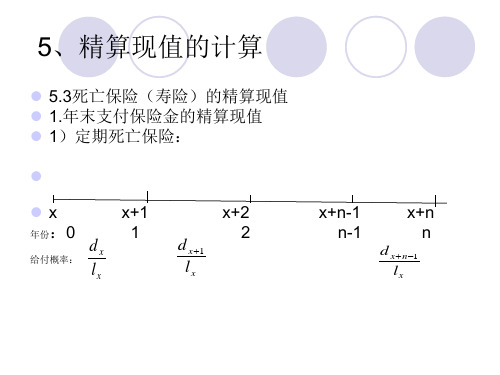
x
xn
x
xh
2.终身寿险的年缴纯保费
h Px
Ax ax:h|
Mx Nx Nxh
3.两全保险的年缴纯保费
P h x:n|
Ax:n| ax:h |
Mx
M xn Dxn Nx Nxh
课堂练习:
1.某人30岁投保20年期,延期10年,5年限期缴费的定期 人寿险,保险金额为100000元,求年缴纯保险费?
N x N x1 Dx
S x N x N x1
(Ia) x
Sx Dx
( Ia) x
S x 1 Dx
( Ia) x:n |
S x 1
S x n1 Dx
nN x n1
作业:
1.某人30岁(女)时投保寿险,约定45岁前死亡给付保险金 150000元,40岁至60岁之间死亡给付保险金为100000 元,60岁以后给付保险金50000元,求趸缴纯保险费?
(In| A)x (IA)1x:n| n|Ax
Rx Rxn nM xn N M xn
Dx
Dx
标准递减也可以看作:
A1 x:n |
A1 x:n 1|
A1 x:n 2|
A1 x:1|
nM x [Rx1 Rxn1 ] Dx
课堂练习
(x)=30,定期寿险保单。第一年死亡给付1000元, 第二年死亡给付1200元,第三年1400元,这样依次按 200元比例递增,n=20,求保险金的精算现值:
x:n |
Dx
Ax:n|
Mx
M xn Dx
Dxn
Ax
Mx Dx
m| Ax
M xm Dx
A1 x :n|
Mx
M Dx
保险精算习题及答案

第一章:利息的基本概念练 习 题1.已知()2a t at b =+,如果在0时投资100元,能在时刻5积累到180元,试确定在时刻5投资300元,在时刻8的积累值。
(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+= 2.(1)假设A(t)=100+10t, 试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======(2)假设()()100 1.1nA n =⨯,试确定 135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3.已知投资500元,3年后得到120元的利息,试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。
11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4.已知某笔投资在3年后的积累值为1000元,第1年的利率为 110%i =,第2年的利率为28%i =,第3年的利率为 36%i =,求该笔投资的原始金额。
123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5.确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。
(2)名义贴现率为每4年计息一次的年名义贴现率6%。
(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎫ ⎪=+= ⎪ ⎪⎝⎭6.设m >1,按从大到小的次序排列()()m m d di i δ<<<<。
保险精算专业天大15秋季[保险精算导论]在线作业一答案
![保险精算专业天大15秋季[保险精算导论]在线作业一答案](https://img.taocdn.com/s3/m/5f8ce35550e2524de4187e24.png)
保险精算专业天大15秋季[保险精算导论]在线作业一答案《保险精算导论》在线作业一一、单选题(共 15 道,共 75 分。
)1. 现年30岁的人,付趸缴纯保费5 000元,购买一张20年定期寿险保单,保险金于被保险人死亡时所处保单年度末支付,试求该保单的保险金额( ). 283285.07元. 283280元. 280280元. 282283.05元正确答案:2. 题目见图片....正确答案:3. 某人现年23岁,约定于36年内每年年初缴付2 000元给某人寿保险公司,如中途死亡,即行停止,所缴付款额也不退还。
而当此人活到60岁时,人寿保险公司便开始给付第一次年金,直至死亡为止。
试求此人每次所获得的年金额。
. 25 692.23元. 25695.53元. 25697.73元. 26784.87元正确答案:4. 题目见图片 ....正确答案:5. 题目见图片 ...正确答案:6. 题目见图片....正确答案:7. 某人将期末延期终身生存年金1万元遗留给其子,约定延期10年,其子现年30岁,求此年金的精算现值。
. 83 629.47元. 83658.87元. 85000.56元. 86754.83元正确答案:8. 某人从50岁时起,每年年初在银行存入5000元,共存10年,自60岁起,每年年初从银行提出一笔款作为生活费用,拟提取10年。
年利率为10%,计算其每年生活费用。
. 12 986.71元. 12 698.71元. 12 968.71元. 12 689.71元正确答案:9. 题目见图片....正确答案:10. 某人现年55岁,在人寿保险公司购有终身生存年金,每月末给付年金额250元,试在U假设和利率6%下,计算其精算现值。
. 36227.89元. 36772.98元. 35773.78元. 38979.63元正确答案:11. 题面见图片....正确答案:12. 某人现年50岁,以10000元购买于51岁开始给付的终身生存年金,试求其每年所得年金额。
第4章 人寿保险的精算现值

第4章 人寿保险的精算现值人寿保险的精算现值也称为趸交纯保费。
4.2 死亡年末给付的人寿保险死亡年末给付的人寿保险是指保险金的支付是在死亡发生的(保险期)年末进行的人寿保险。
4.2.1 定期寿险的趸交纯保费设)(x 投保n 年期定期寿险,保险金额为1元,保险金在死亡年度末给付。
设K = ][T ,即取整余命随机变量,给付函数用b K 1+表示,则有 b K 1+ = 1,当K = 0,1,2,…,n-10, 其它相应的贴现因子用v K 1+表示,保险金给付额折换成购买保险合同签单时的现值用随机变量Z 表示。
Z 的可能取值为z K 1+(K = 0,1,2,…,n-1)z K 1+ = v b K K 11++⋅ = vK 1+定期寿险的趸交纯保费用统一的精算符号1x n A 表示,那么1x nA= )(Z E =∑-=++⋅⋅11n k kx xk qp vk)(Z Var = )]([22)(ZE Z E -=2211()x nx nAA-其中 21x nA= )(2Z E = ∑-=++⋅⋅1)1(2n k kx xk qp vk4.2.2 生存保险n 年期生存保险是当被保险人生存至n 年期满时,保险人在第n 年年末支付保险金的保险。
设)(x 投保n 年期生存寿险,保险金额为1元,保险金在第n 年年末给付。
精算中用1x nA表示该生存保险的趸交纯保费。
可以推出1x nA=pvnxn⋅相应的方差为)(Z Var = )]([22)(Z E Z E - = 2112()x nx n A A-= q pvn nxxn⋅⋅24.2.3 终身寿险的趸交纯保费Ax=1lim x nn A→∞=∑∞=++⋅⋅1k kx xk qp vk相应的方差为)(Z Var = )]([22)(ZE Z E -= )(22A Ax x-4.2.4 两全保险的趸交纯保费设)(x 投保n 年期两全保险,保险金额为1元,若)(x 在n 年内死亡,则在死亡年末给付保险金,若)(x 生存满n 年,则在第n 年年末支付满期保险金。
保险精算第二版习题及答案

保险精算(第二版)第一章:利息的基本概念练 习 题1.已知()2a t at b =+,如果在0时投资100元,能在时刻5积累到180元,试确定在时刻5投资300元,在时刻8的积累值。
(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+= 2.(1)假设A(t)=100+10t, 试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======(2)假设()()100 1.1nA n =⨯,试确定 135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3.已知投资500元,3年后得到120元的利息,试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。
11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4.已知某笔投资在3年后的积累值为1000元,第1年的利率为 110%i =,第2年的利率为28%i =,第3年的利率为 36%i =,求该笔投资的原始金额。
123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5.确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。
(2)名义贴现率为每4年计息一次的年名义贴现率6%。
(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎫ ⎪=+= ⎪ ⎪⎝⎭6.设m >1,按从大到小的次序排列()()m m d di i δ<<<<。
