建筑力学 自由度
建筑力学第八章 结构体系的几何组成分析

第一节 几何组成分析的基本概念 第二节 平面体系的自由度 第三节 几何不变体系的组成规则 第四节 几何组成的分析方法 第五节 体系的几何组成与静定性的关系
第一节 几何组成分析的基本概念
几何组成分析,是以几何不变体系的组成规则为根据,确定体系的几何形状和空 间位置是否稳定的一种分析方法
分析时可针对体系的具体情况,从以下几个方面入手: ①、依次撤除体系上的一元片及二元片,使体系的组成简化,再根据基本组成 规则进行分析 ②尽可能地将体系中几何不变的局部归结为两个或三个刚片,然后考察刚片间 的连接方式是否满足几何不变体系的组成规则; ③体系仅用不共点的三根链杆与地基相连时,可先拆除这三根链杆,再由体系 的内部可变性确定整个体系的几何性质。
解:将图8-13a中的AEC、DFB与基础分别视为刚片I、II、III,刚片I和III以 铰A相联,A铰用(1,3)表示,B铰联系刚片II、III以(2,3)表示,刚片I和 刚片II是用CD、EF两链杆相联,相当于一个虚铰O用(1,2)表示,如图813b所示。则连接三刚片的三个铰(1,3)、(2,3)、(1,2)不在一直线上, 符合规则二,故为不变体系,且无多余约束。
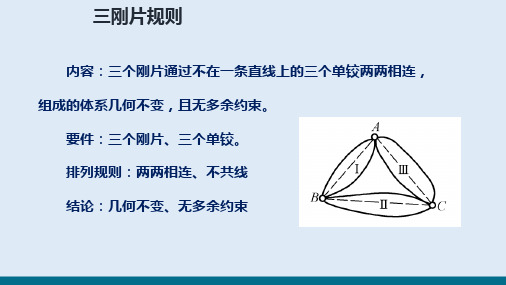
二 、 三刚片规则
三刚片规则:三个刚片用不共线的三个铰两两相连,组成几何不变体系, 且无ቤተ መጻሕፍቲ ባይዱ余约束。
第三节 几何不变体系的组成规则
常变体系 瞬变体系
瞬变体系是不可以用于工程结构的
第四节 几何组成的分析方法
一、计算体系的自由度W,判别体系是否满足几何不变的必要条件。 若自由度W>0,体系是几何可变的 若自由度W≤0,在此基础上进一步对体系进行几何组成分析。 二、对体系进行几何组成分析,判别其是否满足几何不变的充分条件。 (1)一元片撤除 (2)二元片撤除 (3)刚片的合成
结构力学自由度的概念

结构力学自由度的概念结构力学是研究物体在外力作用下的变形和破坏规律的学科。
在结构力学中,自由度是一个非常重要的概念。
本文将从定义、分类和应用三个方面来介绍结构力学自由度的概念。
一、定义自由度是指一个物体在空间中能够自由运动的方向数。
在结构力学中,自由度是指一个结构体系中能够自由变形的方向数。
例如,一个悬臂梁在平面内只能够沿着梁轴方向和垂直于梁轴方向进行变形,因此它的自由度为2。
而一个三维空间中的刚性立方体可以沿着三个方向进行自由变形,因此它的自由度为3。
二、分类结构力学中的自由度可以分为平动自由度和转动自由度两种。
平动自由度是指结构体系中能够沿着直线方向自由变形的方向数,例如悬臂梁的平动自由度为1。
转动自由度是指结构体系中能够绕某个轴线自由旋转的方向数,例如悬臂梁的转动自由度为1。
在实际工程中,结构体系的自由度往往是非常复杂的,需要通过数学方法进行求解。
例如,对于一个由n个节点和m个杆件组成的平面桁架,其总自由度为3n-6-m。
这个公式的推导过程比较复杂,需要运用到刚度矩阵和位移向量等概念。
三、应用结构力学中的自由度概念在实际工程中有着广泛的应用。
例如,在建筑设计中,需要对结构体系的自由度进行分析,以确定结构体系的稳定性和安全性。
在机械设计中,需要对机械结构的自由度进行分析,以确定机械结构的刚度和稳定性。
在航空航天领域中,需要对飞行器的自由度进行分析,以确定飞行器的稳定性和控制性能。
总之,结构力学自由度是一个非常重要的概念,它在实际工程中有着广泛的应用。
通过对自由度的分析,可以确定结构体系的稳定性和安全性,为工程设计提供重要的理论依据。
建筑力学(第二版)第1章至第13章知识点节选

绪论部分荷载:直接施加在结构上的力,在工程上统称荷载。
结构:在建筑物中承受和传递荷载而起骨架作用的部分。
构件:组成结构的每一个部分。
平衡状态:建筑的结构及组成结构的各构件,都相对于地面保持着静止状态,这种状态在工程上称为平衡状态。
要保证构件的正常工作,必须同时满足三个要求:1)在荷载作用下构件不发生破坏,即应具有足够的强度2)在荷载作用下构件所产生的变形在工程的允许范围内,即应具有足够的刚度3)承受荷载作用时,构件在其原有形状下应保持稳定,即应具有足够的稳定性※构件的强度、刚度和稳定性统称为构件的承载能力建筑力学的任务是:研究和分析作用在结构(或构件)上力与平衡的关系,结构(或构件)的内力、应力、变形的计算方法以及构件的强度、刚度与稳定条件,为保证结构(或构件)既安全可靠又经济合理提供计算理论依据。
杆系结构:由杆件组成的结构。
建筑力学:是由研究建筑结构的力学计算理论和方法的一门科学。
第一章静力学的基本概念力的定义:力是物体间的相互机械运动。
用一个带有箭头的有向线段来表示一个力(注意作用点的位置)物体在受到力的作用后,产生的效应可以分成两种:外效应,也称为运动效应,使物体的运动状态发生改变。
内效应,也称为变形效应,使物体的形状发生变化。
力的三要素:大小、方向、作用点力的大小反应物体之间的相互机械作用的强弱程度力的方向包含力的作用线在空间的方位和指向力的作用点是指力在物体的作用位置当接触面面积很小时,则可以将微小面积抽象为一个点,这个点称为力的作用点。
该作用力称为集中力;反之,如果接触面积较大而不能忽略时,则力在整个接触面上分布作用,此时的作用力称为分布力。
分布力的大小用单位面积上的力的大小来度量,称为荷载集度。
力是矢量,记作F刚体:在外力的作用下,不发生形变的物体。
平衡:在外力作用下,物体相对于地球保持静止或匀速直线运动状态,我们就称物体在外力作用下保持平衡。
力系分类汇交力系:力系中各力作用线汇交于一点力偶系:力系中各力可以组成若干力偶或力系由若干力偶组成平行力系:力系中各力作用线相互平行一般力系:力系中各力作用线既不完全交于一点,也不完全相互平行等效力系:若某一力系对物体产生的效应,可以用另一个力系来代替,则这两个力系称为等效力系。
几何组成分析—刚片、自由度、约束的概念(建筑力学)

m2
(2)g
m5
m3 (3)r
(1)h (1)g m6
(2)g (1)h m8
m7
(3)r
m=9,g=6,r=9
(1)h
m9 (3)r
W = 3m-(3g+2h+r) = 3×9-(3×6+2×4+9) = -8
式中: m为刚片数,g为结点数; h为体系内部链杆数; r为支承链杆数 。
图3.8 链杆的约束简图 (a)梁AB有一个约束;(b)梁AB有两个约束; (c)梁AB有三个约束
I B
1根链杆(支杆)相当于1个约束
A II
铰的约束作用
(1) 单铰(连接两个刚片的铰)
1个单铰相当于2个约束,减少2个自由度。
(2) 复铰(连接两个刚片以上的铰)
连接n个刚片的复铰可折算成(n-1)个 单束的概念
刚片、自由度、约束的概念 一、刚片
体系的几何组成分析不考虑材料的应变,任一杆件(或体系中一 几何不变部分)均可看为一个刚体,一个平面刚体称为一个刚片。
注意:链杆和几何不变体系都可看成钢片。
刚片、自由度、约束的概念
二. 自由度:
体系的自由度是指体系运动时, 可以独立改变的几何参数的数目; 即确定体系位置所需要的独立坐标 的数目。
r 为与地基之间加入的支杆数。
刚片、自由度、约束的概念
三、约束
减少自由度的装置称为约束(或联系)。可以减少1个自由度的装 置是1个约束。
杆件与地基之间常用的约束是支杆、固定铰支座和固定支座,称 为外部约束;
杆件之间常用的约束是链杆、铰结和刚结,称为内部约束。
刚片、自由度、约束的概念
链杆(支杆)的约束作用
刚结的约束作用
建筑力学与结构第4章

【学习目标】通过本章的学习,了解几何不变体系和 几何可变体系的概念,理解几何组成分析的目的;掌握平 面体系的几何组成规则并能熟练应用;了解静定结构和超 静定结构的联系和区别。 【学习重点】平面体系的几何组成分析规则,运用规 则判定体系是否为几何不变体系。
4.1 概述
若干个杆件按一定规律相互连接,并与基础连接成一 整体,构成杆件体系。如果体系的所有杆件和约束及外部 作用均在同一平面内,则称为平面体系。 1.几何不变体系和几何可变体系 在不考虑材料变形的条件下,体系受力后,能保持 其几何形状和位置的不变,且不发生刚体形式的运动,这 类体系称为几何不变体系。
图4-16 例4-4图
例4-5 对如图4-17所示结构进行几何组成分析。已 知体系中杆DE、FG、AB互相平行。 解 拆除二元 体D-C-E,剩下部 分中三角形ADF 和BEG是两刚片, 这两刚片用互相 平行的三根链杆 连接,故构成瞬 变体系。
图4-17 例4-5图
例4-6
对如图4-18所示结构进行几何组成分析。
一个单铰相当于两 个约束,也就是相当于 两根链杆的作用。
连接n个刚片的复铰, 其作用相当于(n-1)个单 铰,也即相当于2(n-1) 个约束。
相当于3个单铰
相当于2个单铰
单铰数为1
图4-5 复铰和单铰示例
刚片Ⅰ和刚片Ⅱ间为刚性联结。
图4-6 刚性联结
一个刚性连接相对于三个约束。
必要约束: 凡使体系的自由度减少为零所需要的最少约束。 多余约束: 如果在一个体系中增加一个约束,而体系的自由度并不 因此而减少。
2.几何组成分析的目的
对体系进行几何组成分析,目的在于: 1)判断体系是否为几何不变体系,从而决定他能 否作为结构。 2)研究几何不变体系的组成规则,以保证所设计 的结构是几何不变的。 3)正确区分静定结构和超静定结构,为进行结构 的内力计算打下必要的基础。
第五讲:杆件的组成分析

3、切断一根梁式杆或去掉一个固定支座,相当去 掉三个约束;
4、在连续杆(梁式杆)上加一个单铰,相当去掉 一个约束。
第二章 杆件的几何性质 例2-3-5 对图示各体系作几何组成分析。
第二章 杆件的几何性质—小结
一、本章要求 1、了解几何不变体系、几何可变体系、瞬变体系、刚片、体系的自由度、 虚铰、约束及多余约束的概念; 2、重点理解并掌握平面几何不变体系的简单组成规则,并能灵活应用到对 体系的分析中; 二、简单规则应用要点 简单规则中的四个要素:刚片个数、约束个数、约束方式、结论。 应用简单规则对体系进行几何组成分析的要点是:紧扣规则。即,将体系简 化或分步取为两个或三个刚片,由相应的规则进行分析;分析过程中,规则中的 四个要素均要明确表达,缺一不可。 三、对体系作几何组成分析的一般途径 1、恰当灵活地确定体系中的刚片和约束 体系中的单个杆件、折杆、曲杆或已确定的几何不变体系,一般视为刚片。 但当它们中若有用两个铰与体系的其它部分连接时,则可用一根过两铰心的链杆 代替,视其为一根链杆的作用。 2、如果上部体系与大地的连接符合两个刚片的规则,则可去掉与大地的约 束,只分析上部体系。 3、通过依次从外部拆除二元体或从内部(基础、基本三角形)加二元体的 方法,简化体系后再作分析。
3、多余约束
在体系上加上或撤除某一约束并不改变原体系的自由度数,则该 约束就是多余约束。
第二章 杆件的几何性质
三、平面体系的几何组成分析
几
何 规则一 (两刚片规则):
不
两个刚片用不全交于一点也不全平行的三根链杆相连,组
变 成无多余约束的几何不变体系。
体
或:两个刚片用一个单铰和杆轴不过该铰铰心的一根链杆
平面体系几何组成分析的方法(静定的概念)(建筑力学)
例题分析
例1.分析图示体系的几何构造性。 解析:(1)计算自由度
W 4244 0
自由度为0,说明体系具有成为几何不变体系的最少约束数目。 进一步判断,依次去掉二元体DFE、BDC、BEC、BCA后,整个体系只剩下 地基了,为几何不变体系。由于去掉二元体并不改变原体系的几何构造性,因此 原体系也是几何不变体系。
二元体规则是非常好用的规则,特别是去二元体,可以大大简化体系 构件数目,使判断简化,其主要有以下几个技巧:
(1)根据需要进行链杆与刚片之间的转化,巧妙使用二元体; (2)当体系比较复杂时,可以先考虑其中的一个它部分之间的连接关系, 判定整个体系的几何构造性。
例题分析
例2.分析图示体系的几何构造性。 解析:(1)计算自由度
W 72 113 0
自由度为0,说明体系具有成为几何不变体系的最少约束数目。 体系没有二元体,但体系本身是有二元体的,去掉所有二元体,只剩下一个 杆件,所以体系本身几何不变,再考虑其与地基的连接方式,判定体系几何不变。
总结与技巧
示例
例1.分析图示体系的几何构造性。
解析:(1)计算自由度
W 7277 0
体系具有成为几何不变体系的最少约束数目,需进一步判断。 (2)依次去掉二元体FAB、IED、FBJ、IDC如图所示。 (3)三角形GCH看作刚片Ⅰ,地基看作特殊刚片Ⅱ。 (4)刚片Ⅰ、Ⅱ之间通过三根链杆相连,三链杆汇交
建筑力学 第四章

O
I A 1 B C 2 D
在体系运动的过程中,瞬铰的位臵随之变 化。 用瞬铰替换对应的两个链杆约束,这种约 束的等效变换只适用于瞬时微小运动。
八、无穷远处的瞬铰
∞
如果用两根平行的链杆把刚片I和基础相连,则其 瞬铰在无穷远处—瞬时平动。 在几何构造分析中应用无穷远瞬铰的概念时,采 用影射几何中关于∞点和∞线的四点结论:
B 1
I II A
2
C
3、对于A点增加两根共线的链杆后,仍然具有1个自由度。 可见在链杆1和2这两个约束中有一个是多余约束。
一般来说,在任一瞬变体系中必然存在多余约束。
七、瞬铰 点O: 瞬时转动中心 此时刚片I 的瞬时运动情况与刚片I在O点 用铰和基础相连的运动情况完全相同。 从瞬时微小运动来看,两根链杆所起的约 束作用相当于在链杆交点处的一个铰所起 的约束作用,这个铰称为 瞬铰(虚铰)
I II A
1 2
I
C
A
II
B
1 B
2 C
两根链杆彼此共线 1、从微小运动的角度看,这是一个可变体系。 左图两圆弧相切,A点可作微小运动; 右图两圆弧相交,A点被完全固定。
B 1
I II A
2
C
2、当A点沿公切线发生微小位移后,两根链杆不再共线, 因而体系就不再是可变体系。 本来是几何可变,经微小位移后又成为几何不变的体系 称为瞬变体系。 可变体系分为瞬变体系和常变体系,如果一个几何可变 体系可以发生大位移,则称为常变体系。
一点在平面内有两个自由度
一个刚片在平面内有三个自 由度
三、自由度
一般来说,如果一个体系有 n 个独立的运动方式,则这 个体系有 n 个自由度。
一个体系的自由度,等于这个体系运动时可以独立改变 的坐标的数目。 普通机械中使用的机构有一个自由度,即只有一种运动 方式; 一般工程结构都是几何不变体系,其自由度为零。 凡是自由度大于零的体系就是几何可变体系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.4 平面杆件体系的自由度计算
教学要求
掌握实际自由度分析方法,了解计算自由度的计算方法。
2.4.1 平面杆件体系自由度
(1)实际自由度S(即前面讲的“运动自由度”):体系运动时,可以独立变化的几何参数数目,也就是确定该体系运动所需要的独立参数数目。
之所以称之为实际自由度,是为了与下面讲的计算自由度相区别。
S = (各部件自由度总和a)-(必要约束数总和c)(2-1)(2)计算自由度W
W = (各部件自由度总和a)-(全部约束数总和d)(2-2)
由上式可见,计算自由度是由体系部件的自由度和全部约束计算而得,但没有区别非多余约束和多余约束。
因此,一般地说,计算自由度不一定就是实际自由度。
多余约束数n:等于实际自由度与计算自由度之差,即:
n = S -W (2-3)
图2-25
分析:
自由度S=a-c=2-2=0;计算自由度W=a-d=2-4=-2
[讨论]:
W > 0 则S > 0 几何可变
W = 0 则S = n 若n = 0 几何不变
W = 0 则S = n 若n > 0 几何可变
W < 0 则n > 0 体系有多余约束,但不一定几何不变。
结论:
W ≤0只是几何不变的必要条件,不是充分条件。
各部件自由度总和a=2(1个自由点);约束总数d=4;其中:非多余约束c=2;
2.4.2 约束的计算
(1)刚片内部多余约束。
n=0 n=1 n=2 n=3
图2-8 刚片内部多余约束
[注释]自由端n=0;一根链杆n=1;一个铰n=2;一个刚结n=3;
(2)单约束和复约束
a.铰结点
图2-9a 单铰图2-9b 复铰
1单铰=2个约束复铰=(n-1)单铰=2(n-1)个约束
b.刚结点
图2-11a 单链图2-11b 复链
1单链杆=1个约束1复链杆= (2×n-3)单链=(2×n-3)个约束杆
2.4.3 平面体系的计算自由度W 的求法
(1)刚片法:体系看作由刚片组成,铰结、刚结、链杆为约束。
刚片数m ;
约束数:单铰数h ,简单刚结数g ,单链杆数b 。
W = 3m - 2h - 3g - b (2-4)
(2)节点法:体系由结点组成,链杆为约束。
结点数j ;
约束数:链杆(含支杆)数b 。
W = 2j – b (2-5)
(3)组合算法
约束对象:刚片数m ,结点数j
约束条件:单铰数h ,简单刚结数g ,单链杆(含支杆)数b
W = (3m + 2j)-(3g + 2h + b)(2-6)
例:求如下图示刚片系的计算自由度。
题1:图2-12
解:
方法1 方法2 方法3
方法1:(刚片法)
m = 7,h = 4,g = 2,b = 6
W = 3×7 - 2×4 - 3×2 - 6 = 1
方法2:(刚片法)
m = 5,h = 4,g = 0,b = 6
W = 3×5 - 2×4 - 6 = 1
方法3:(节点法)――最好
j=6,b=11
W=2j-b=2*6-11=1
题2:图2-13
解:
方法1 方法2
方法1:(节点法)――最好
j=7,b=14
W=2j-b=2*7-14=0
方法2:(刚片法)
m = 7,h = 9,g = 0,b = 3
W = 3×7 - 2×9 - 3 = 0
题3:图2-14
此题要了解什么是结点;固定端相当于3个单链
解:
方法1:(刚片法)
m = 1,h = 0,g = 3,b = 4
W = 3×1- 3×3- 4 = -10
方法2:(节点法)――最好j=0,b=10
W=2j-b=0-10=0。
