薄膜厚度及折射率的计算方法
光学厚度计算公式

光学厚度计算公式
光学厚度计算公式是计算物体薄膜厚度的必备工具,它能够精确
地对物体表面的厚度进行测量,并且可以应用于学术研究、工业生产
等众多领域,是一项非常重要的技术手段。
光学厚度计算公式的原理是基于菲涅尔反射原理和光程差原理。
菲涅尔反射原理认为,在光线从空气垂直射向透明介质时,会发生反射,反射波和入射波之间存在相位差,这个相位差随着入射角度的变
化而变化。
光程差原理指的是,在空气和介质交界处,由于两种介质
的光速不同,光线通过介质时会产生相位差,这个相位差与介质厚度
相关。
综合菲涅尔反射原理和光程差原理,光学厚度计算公式主要有以
下两种形式:
公式一:d = λ/4n,其中,d为物体的光学厚度,λ为入射波长,n为物体所处介质的折射率。
公式二:d = (λ/2π)·arctan[(2π·m)/N],其中,d为物体的光学厚度,λ为入射波长,m为反射光强的相对强度差,N为物体的折射指数。
这两种公式都是通过测量反射波的相位差来计算物体厚度的。
在
实际使用中,我们首先需要确定入射波的波长,并且需要了解物体所
处的介质折射率和折射指数等参数,以便计算出物体的光学厚度。
如
果测量结果不准确,我们还可以通过调整入射角度、改变光源位置等
方式来提高测量精度。
总的来说,光学厚度计算公式是一项非常实用的技术,在物体表
面的薄膜厚度测量、材料分析、工业生产等领域都起到了重要的作用。
在使用时需要注意,我们要充分理解它的原理和计算公式,并结合实
际情况选择适合的方法来进行测量,以确保数据的真实可靠。
折射率与厚度的估算方法
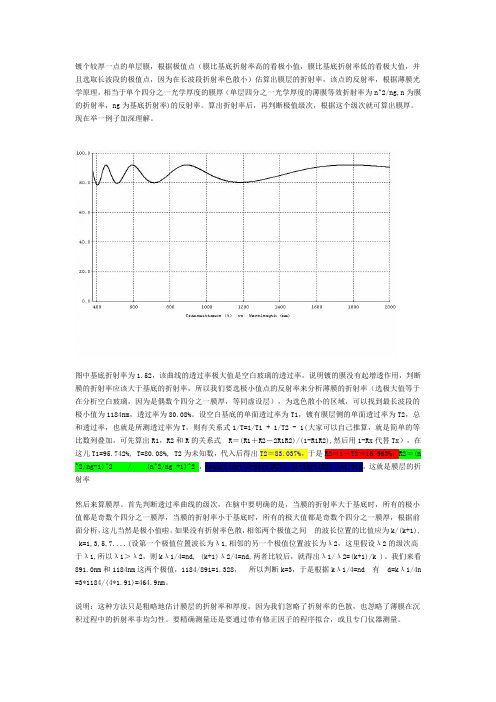
镀个较厚一点的单层膜,根据极值点(膜比基底折射率高的看极小值,膜比基底折射率低的看极大值,并且选取长波段的极值点,因为在长波段折射率色散小)估算出膜层的折射率,该点的反射率,根据薄膜光学原理,相当于单个四分之一光学厚度的膜厚(单层四分之一光学厚度的薄膜等效折射率为n^2/ng,n为膜的折射率,ng为基底折射率)的反射率。
算出折射率后,再判断极值级次,根据这个级次就可算出膜厚。
现在举一例子加深理解。
图中基底折射率为1.52,该曲线的透过率极大值是空白玻璃的透过率,说明镀的膜没有起增透作用,判断膜的折射率应该大于基底的折射率,所以我们要选极小值点的反射率来分析薄膜的折射率(选极大值等于在分析空白玻璃,因为是偶数个四分之一膜厚,等同虚设层),为选色散小的区域,可以找到最长波段的极小值为1184nm,透过率为80.08%。
设空白基底的单面透过率为T1,镀有膜层侧的单面透过率为T2,总和透过率,也就是所测透过率为T,则有关系式1/T=1/T1 + 1/T2 - 1(大家可以自己推算,就是简单的等比数列叠加,可先算出R1,R2和R的关系式R=(R1+R2-2R1R2)/(1-R1R2),然后用1-Rx代替Tx),在这儿T1=95.742%, T=80.08%, T2为未知数,代入后得出T2=83.037%,于是R2=1-T2=16.963%,R2=(n ^2/ng-1)^2 / (n^2/ng +1)^2 ,n=sqrt(ng*(1+sqrt(R2))/(1-sqrt(R2) )=1.910,这就是膜层的折射率然后来算膜厚。
首先判断透过率曲线的级次,在脑中要明确的是,当膜的折射率大于基底时,所有的极小值都是奇数个四分之一膜厚,当膜的折射率小于基底时,所有的极大值都是奇数个四分之一膜厚,根据前面分析,这儿当然是极小值啦。
如果没有折射率色散,相邻两个极值之间的波长位置的比值应为k/(k+1), k=1,3,5,7....(设第一个极值位置波长为λ1,相邻的另一个极值位置波长为λ2,这里假设λ2的级次高于λ1,所以λ1>λ2,则kλ1/4=nd, (k+1)λ2/4=nd,两者比较后,就得出λ1/λ2=(k+1)/k )。
光学薄膜折射率和厚度测试技术及研究

e l l i p s o m e t r y i s u s e d t o s e t t h e p r i m a r y s t a n d a r d o f o p t i c a l f i l m r e f r a c t i v e i n d e x a n d t h i c k n e s s
硕{ 一 论文
光学薄膜折射率和厚度测试技术及研究
毋响着各种新型薄膜器件和技术在新型武器装备上的应) I I . 而在国外,美国和英国已建立了光学薄膜折射率及厚度标准装置,美国的 . J . A . W o o la m公司和法国的 J Y公司生产的测量薄膜折射率及厚度的椭偏仪更是处于世
各向异性材料的测量等,并对这些测试结果进行了详尽的数据分析。
1 . 4 技术关键
光学薄膜折射率及厚度测试的难点及技术关键有以下几点: 1 ) 由于椭偏仪系统测试的直接值是甲和△, 而要获得光学薄膜折射率及厚度 值,必须先建立一个模型,由这个模型的预设值和实际测量值进行拟合, 通过计算机解超越方程从而得到折射率和厚度值。因此, 模型的建立是至
c o m m o n l y u s e d i n t h e w o r l d , a me t h o d w h i c h d e r i v e d f r o m v a r i a b l e a n g l e s p e c t r o s c o p i c
在以上参数中,薄膜的反射比、透射比标准我们已在 “ 八五”期间完成。而其他参数 目
前还没有标准, 例如折射率和厚度, 这些参数对薄膜的设计和工艺制造都是不可缺少的。 薄膜技术和器件的广泛应用, 推动着薄膜测试技术的发展, 同时面对武器装备的不 断更新和发展, 对提高薄膜的性能、评价膜系的优劣, 并对己有的测试仪器进行量值统 一提出了更高的要求。 在这方面国外研究起步较早,发展很快,加之先进的加工手段和
薄膜干涉研究实验报告(3篇)

第1篇一、实验目的1. 理解薄膜干涉的基本原理和现象。
2. 通过实验观察薄膜干涉条纹,分析薄膜的厚度和折射率。
3. 掌握使用薄膜干涉现象测量薄膜厚度和折射率的方法。
4. 了解薄膜干涉在光学器件中的应用。
二、实验原理薄膜干涉是指当光波照射到透明薄膜上时,从薄膜的前后表面分别反射的光波发生干涉,形成明暗相间的干涉条纹。
这种现象与薄膜的厚度、折射率和入射光的波长有关。
根据薄膜干涉的原理,当光波从光疏介质(如空气)进入光密介质(如薄膜)时,会发生部分反射和部分折射。
从薄膜的前表面反射的光波与从薄膜的后表面反射的光波之间会产生光程差,这个光程差与薄膜的厚度和折射率有关。
当光程差为波长的整数倍时,两束反射光波发生相长干涉,形成明条纹;当光程差为半波长的奇数倍时,两束反射光波发生相消干涉,形成暗条纹。
因此,通过观察干涉条纹的分布,可以计算出薄膜的厚度和折射率。
三、实验仪器与材料1. 薄膜干涉实验装置(包括光源、薄膜样品、显微镜等)。
2. 精密测量工具(如游标卡尺、读数显微镜等)。
3. 记录本和笔。
四、实验步骤1. 将薄膜样品放置在实验装置中,确保光源垂直照射到薄膜上。
2. 观察显微镜下的干涉条纹,调整薄膜样品的位置,使干涉条纹清晰可见。
3. 使用游标卡尺测量薄膜样品的厚度。
4. 通过显微镜观察干涉条纹,记录明暗条纹的位置。
5. 根据干涉条纹的位置和薄膜的厚度,计算薄膜的折射率。
五、实验结果与分析1. 通过实验观察,成功观察到了明暗相间的干涉条纹。
2. 使用游标卡尺测量薄膜样品的厚度,得到厚度为d。
3. 通过显微镜记录明暗条纹的位置,计算光程差ΔL。
4. 根据公式ΔL = 2nd,计算出薄膜的折射率n。
六、讨论与结论1. 实验结果表明,薄膜干涉现象确实存在,且与薄膜的厚度和折射率有关。
2. 通过实验,成功测量了薄膜的厚度和折射率,验证了薄膜干涉原理的正确性。
3. 薄膜干涉在光学器件中具有广泛的应用,如增透膜、滤光膜、偏振膜等。
介质薄膜不同方向折射率的计算

介质薄膜不同方向折射率的计算1 什么是介质薄膜?介质薄膜是由一层物质构成的薄膜,通常是几个纳米厚度。
在光学中,介质薄膜可以分为单层薄膜和多层薄膜。
它可以改变光通过的波长和幅度,还可以用于制造各种光学器件,例如反射镜、偏振器和全息图等。
2 什么是折射率?折射率描述了光在不同介质中的传播速度和路径的变化。
介质中的折射率越高,光传播速度越慢。
当光通过介质界面的时候,会发生折射现象。
在不同介质中,折射率通常不同,可以通过斯涅尔定律进行计算。
3 介质薄膜不同方向的折射率计算在介质薄膜中,折射率也可以有不同的方向。
在一般情况下,有两个主要方向,平行于薄膜表面和垂直于薄膜表面。
对于平行于薄膜表面的情况,折射率的计算如下:$$n_{\parallel}=n_1\frac{sin\theta_1}{sin\theta_2}$$其中,$n_{\parallel}$是平行于薄膜表面的折射率,$n_1$是薄膜的折射率,$\theta_1$是入射光与法线的夹角,$\theta_2$是折射光与法线的夹角。
对于垂直于薄膜表面的情况,折射率的计算如下:$$n_{\perp}=\frac{n_1n_2}{\sqrt{n_1^2cos^2\theta_1+n_2^2sin^2\theta_2}}$$其中,$n_{\perp}$是垂直于薄膜表面的折射率,$n_1$是薄膜的折射率,$n_2$是外部介质的折射率,$\theta_1$是入射光与法线的夹角,$\theta_2$是折射光与法线的夹角。
4 总结介质薄膜有不同方向的折射率,可以通过斯涅尔定律进行计算。
在平行于薄膜表面的情况下,折射率由入射角和薄膜折射率计算得出;在垂直于薄膜表面的情况下,折射率需要考虑外部介质的折射率。
这些计算对于光学器件的设计和制造非常重要。
椭偏光法测薄膜的折射率和厚度

实验五 椭偏光法测薄膜的折射率和厚度一、引言椭圆偏振测量术简称椭偏术。
它是利用光的偏振性质,将一椭圆偏振光射到被测样品表面,观测反射光偏振状态的变化来推知样品的光学常数。
就其理论范畴来讲,它与十涉法一样,都是利用光的波动性,以经典物理学为基础。
这种测量方法的原理早在上个世纪就提出来了,距今已有近百年的历史。
由于光波通过偏振器件及样品反射时,光波偏振状态变化得异常灵敏,使得椭偏术的理论精度之高是干涉法不能比拟的,又由于这种测理是非破坏性的,因此它的优越性是显而易见的。
长期以来,人们一直力图将这种测量方法付诸应用。
早在40年代就有人提出实验装置,但由于计算上的困难一直得不到发展。
电子计算机及激光技术的广泛应用,为椭偏术的实际应用及迅猛发展创造了条件。
今天椭偏术已成为测量技术的一个重要的分支。
椭偏术有很多优点,主要是测量灵敏、精度高,测量范围从1oA 到几个微米而且是非接触测量。
国外生产的高精度自动椭偏仪能测量正在生长的薄膜小于l o A 的厚度变化,可检测百分之儿的单分子层厚度,深入到原子数量级。
因此既可将其应用于精密分析测量,也可以用于表面研究,用于自动监控及分析液、固分界面的变化。
目前椭偏术已应用到电子工业,光学工业,金属材料工业,化学工业,表面科学和生物医学等领域。
在我们的实验中,使用消光椭偏仪测量薄膜的折射率和厚度。
除了能学习到其测量方法外,其巧妙的设计思想也将给我们极人的启发和收益。
二、椭偏术原理1.椭偏术基本方程椭圆偏振光入射到透明介质薄膜时,光在两个分界面(空气与薄膜,薄膜与衬底)来同反射和折射,如图5.1所示。
总反射光由多光束干涉而成,光在两个分界面的P 波和S 波的反射系数分别为1122p s p s r r r r 、、、图 5—1由菲涅尔公式有:121122112112211122322323223223322233cos cos cos cos cos cos cos cos cos cos cos cos cos cos cos cos p s p s n n r n n n n r n n n n r n n n n r n n ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ-⎧=⎪+⎪-⎪=⎪+⎪⎨-⎪=⎪+⎪-⎪=⎪+⎩以上各式中1n 为空气折射率,2n 为膜层的折射率,3n 为衬底折射率。
用椭偏仪测薄膜厚度与折射率解析

103实验十二 用椭偏仪测薄膜厚度与折射率随着半导体和大规模集成电路工艺的飞速发展,薄膜技术的应用也越加广泛。
因此,精确地测量薄膜厚度与其光学常数就是一种重要的物理测量技术。
目前测量薄膜厚度的方法很多。
如称重法、比色法、干涉法、椭圆偏振法等。
其中,椭圆偏振法成为主要的测试手段,广泛地应用在光学、材料、生物、医学等各个领域。
而测量薄膜材料的厚度、折射率和消光系数是椭圆偏振法最基本,也是非常重要的应用之一。
实验原理由于薄膜的光学参量强烈地依赖于制备方法的工艺条件,并表现出明显的离散性,因此,如何准确、快速测量给定样品的光学参量一直是薄膜研究中一个重要的问题。
椭圆偏振法由于无须测定光强的绝对值,因而具有较高的精度和灵敏度,而且测试方便,对样品无损伤,所以在光学薄膜和薄膜材料研究中受到极大的关注。
椭圆偏振法是利用椭圆偏振光入射到样品表面,观察反射光的偏振状态(振幅和位相)的变化,进而得出样品表面膜的厚度及折射率。
氦氖激光器发出激光束波长为632.8nm 的单色自然光,经平行光管变成单色平行光束,再经起偏器P 变成线偏振光,其振动方向由起偏器方位角决定,转动起偏器,可以改变线偏振光的振动方向,线偏振光经1/4波片后,由于双折射现象,寻常光和非寻常光产生π/2的位相差,两者的振动方向相互垂直,变为椭圆偏振光,其长、短轴沿着1/4波片的快、慢轴。
椭圆的形状由起偏器的方位角来决定。
椭圆偏振光以一定的角度入射到样品的表面,反射后偏振状态发生改变,一般仍为椭圆偏振光,但椭圆的方位和形状改变了。
从物理光学原理可以知道,这种改变与样品表面膜层厚度及其光学常数有关。
因而可以根据反射光的特性来确定膜层的厚度和折射率。
图1为基本原理光路。
图2为入射光由环境媒质入射到单层薄膜上,并在环境媒质——薄膜——衬底的两个界面上发生多次折射和反射。
此时,折射角满足菲涅尔折射定律332211sin sin sin ϕϕϕN N N ==(1)104 其中N 1,N 2和N 3分别是环境媒质、= n – i k );ϕ1为入射角、 ϕ2 和ϕ3分别为薄膜和衬底的折射角。
薄膜干涉的光程差公式

薄膜干涉的光程差公式薄膜干涉是一种光学干涉现象,是指当光线在两个介质之间传播时,由于不同介质的折射率不同,光线在介质中的传播路径不同,导致光程差的变化,从而产生干涉现象。
光程差是指光线传播过程中两条光线路径所走过的路程之差。
在薄膜干涉中,光线由真空中入射到一个介质中,然后再出射到另一个介质中。
设入射光线角度为θ,入射介质的折射率为n1,薄膜的厚度为d,薄膜的折射率为n2、在薄膜中,光线的路径可以分为两部分:一部分是入射光线在第一个介质中传播的路径,另一部分是入射光线在薄膜中传播的路径。
首先考虑入射光线在第一个介质中的传播路径。
入射光线在第一个介质中传播的路程为L1,由于第一个介质的折射率为n1,光线在此介质中的传播速度为c/n1,所以可以得到L1=c*t1,其中t1为光线在第一个介质中的传播时间。
根据物理学中的定义,光线在真空中的传播时间t为光线传播的路程L与光速c的比值,即t=L/c。
因此,L1=ct1=nc*t。
由此可见,入射光线在第一个介质中的传播路径与时间与真空中的传播路径和时间成正比。
接下来考虑入射光线在薄膜中的传播路径。
假设入射光线与薄膜表面的夹角为θ,入射光线在薄膜中传播的路程为L2、由于薄膜的厚度为d,光线传播的速度为c/n2,所以可以得到L2=d/cosθ*n2、其中cosθ为入射角的余弦值,n2为薄膜的折射率。
因此,入射光线在薄膜中的传播路径与薄膜的厚度和入射角的余弦值成正比。
最后考虑出射光线在第二个介质中的传播路径。
出射光线在第二个介质中的传播路径为L3、由于第二个介质的折射率为n1,光线在此介质中传播的速度为c/n1,所以可以得到L3=c*t3、根据上面的定义,可知L3=ct3=nc*t。
因此,出射光线在第二个介质中的传播路径与时间与真空中的传播路径和时间成正比。
根据光程差的定义,可以得到光程差为Δ=L1+L2+L3=(nc*t)+(d/cosθ*n2)+(nc*t)。
化简得到Δ=2nct+(d/cosθ*n2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
441
(PLD). The method is based on the determination of the upper and lower envelopes of the interference fringes in the measured transmission spectrum [5–7].
‘‘Refractor’’ has several advantages: (1) it gives accurate results in a short time and reduces the number of arithmetic operations needed to compute n, k and d as compared to other computer techniques [1–4]; (2) it takes into account possible inhomogeneities in the film thickness; (3) it is not based on minimisation techniques as other commercial software; (4) using the obtained n, k and d values, the simulated spectrum as well as the experimental one can be graphically compared.
PACS: 07.05.Tp; 78.66.Bz; 78.20.Àc
Keywords: Transmittance; Refractive index; Extinction coefficient; Pulsed laser deposition
1. Introduction
The performance of planar optical devices depends on the wavelength dependence of the optical constants, i.e., the refractive index n(l) and the extinction coefficient k(l) of thin films, and their geometrical thickness, d. n(l), k(lsee front matter # 2005 Elsevier B.V. All rights reserved. doi:10.1016/j.apsusc.2005.03.069
A.P. Caricato et al. / Applied Surface Science 248 (2005) 440–445
(1)
If the substrate refractive index is known, it is convenient to write this equation in terms of n(l) and x(l) = exp(Àad), the absorbance, where a = 4pk/l is the optical absorption coefficient of the thin film:
Applied Surface Science 248 (2005) 440–445
/locate/apsusc
A computer program for determination of thin films thickness and optical constants
Since À1 cos w 1, T(l) values can vary
between
Tm
¼
Ax BþCxþDx2
and
TM
¼
Ax BÀCxþDx2
.
A typical transmission spectrum at normal inci-
* Corresponding author. Tel.: +39 0832 297479; fax: +39 0832 297505.
E-mail address: leggieri@le.infn.it (G. Leggieri).
calculated from the interference fringes present in the transmission, T(l), and reflection, R(l), spectra by using various techniques. Current methods for determining the optical constants of thin films are usually based on sophisticated computer iteration techniques [1–4]. A relatively simple method for the computation of the optical constants of dielectric films deposited on visible transparent substrates such as glass has been implemented by a computer program developed by us named ‘‘Refractor’’ and tested on optical films deposited by pulsed laser deposition
T ¼ Tðn; xÞ:
For k2 ( n2, the expression for the transmittance can be written [7]:
Ax
TðlÞ ¼ B À Cx cos ’ þ Dx2
(2)
where A = 16n2s; B = (n + 1)3(n + s2); C = 2(n2 À 1) (n2 À s2); D = (n À 1)3(n À s2); w = 4pnd/l.
2. Preliminary theoretical considerations
The considered optical system is a thin homogeneous film deposited on a weakly absorbing substrate (extinction coefficient ks % 0) with a thickness several orders of magnitude greater than that of the film and with a refractive index s. The substrate surfaces are considered smooth but not perfectly parallel so that interference effects due to the substrate are negligible. When a monochromatic light beam impinges perpendicularly on the surface covered with a thin film, multiple reflections occur at the interfaces of the system. Assuming that these reflections are coherent in the film and incoherent in the substrate, both the reflected and transmitted beams are subject to interference phenomena. The interference fringes can be used to determine the optical constants and thickness of the film. The procedure is as follows.
Taking into account all the multiple reflections at the three interfaces, the transmission T is a complex function of the variables l, n, k, s and d:
T ¼ Tðl; n; k; s; dÞ:
A.P. Caricato, A. Fazzi, G. Leggieri *
INFM, Dipartimento di Fisica, Universita` di Lecce, 73100 Lecce, Italy
Available online 30 March 2005
Abstract
A computer simulation program for processing transmission spectra of amorphous optical thin films deposited on weakly absorbing substrates and evaluation of the refractive index n, extinction coefficient k and thickness d was developed. The computer code is the implementation of an optical characterisation algorithm based on the determination of the upper and lower envelopes of the transmission spectrum interference fringes. Inhomogeneities in the thickness of the analysed films, which are responsible of a shrinking in the fringes amplitude, can be considered in the program. Relative errors in the calculated values of n, k and d have been determined using simulated transmission spectra in both cases of homogeneous and inhomogeneous films. The thickness and the refractive index of uniform films are calculated with an accuracy 0.5%, while the accuracy in the case including inhomogeneities is 2%. Simulation results for chalcogenide thin films deposited by pulsed laser deposition (PLD) on microscope slabs and glass slides are reported. # 2005 Elsevier B.V. All rights reserved.
