应用FLUENT进行射流流场的数值模拟
基于Fluent的径向水平井旋转射流钻头内外流场数值模拟
６ ０ ｍｉ ， １ Ｉ ｎ 钻杆 内径 为 ｄ ／ 一 ２ ｍｍ。 ５ 计算 人 口速度 为 ：
Ｑ
“ 一
—
≈ ２ ｍ／ ０ ｓ
训一 。
一ｏ
［ 收稿日期］２ １ 一Ｏ ０ １ ８—１ ２ ［ 基金项目］湖北省高等学校优秀中青年科技创新团队项 目 （ ０ ９ ６ 。 ： Ｔ２ ０ ） ［ 作者简介］杨雄 （ ９ ０ ） １ ６ 一 ，勇 ，１ ８ 年 大学毕业 ，硕士 ，教授 ，现主要从事材料工程、现代 加工技术和工程测试技术及控制工程等 ９２ 方面的教学和研究工作 。
第 ３ 卷 第 １ 期 ３ １
杨 雄 等 ：基 于 Ｆｕ ｎ 的 径 向 水 平 井 旋 转 射 流 钻 头 内外 流场 数 值 模 拟 ｌｅｔ
●●■■ ■
图 １ 旋 转 射 流 流 场 模 型
图 ２ 钻 头 内流 场 网格 划 分
２ ）出 口条件
Ｐ 。一 ０ 。
３ ）固壁边 界条 件 采用 无 滑移 边界 条件 。
１ ２ 网 格 划 分 ．
将 图 １ 示 流场模 型分 为 ３段进行 网格划分 ，由于旋转 射 流钻头 的内流场 结构 复杂 ，因此 采用 非结 所
构 网格 划分 ，节 点 间隔尺 寸 （ ｔｒａ ｓ ｅ 为 １ ｉ ｅｖ ｌ ｉ ） ｎ ｚ ，如 图 ２所示 。
１３ 控 制 方 程 ．
基 于 Ｆ ｕ ｎ 的 径 向水 平 井 旋 转 射 流 ｌｅ ｔ 钻 头 内外 流 场数 值 模 拟
杨 雄 ，冉 小丰 ，阳 婷 （ 长江大学机械工程学院，胡Ｅ Ｊｌ３０３ 、］ ￣０ ４ ２ ＊ ４ ）
［ 要 ］ 运 用 Ｆｕｎ 软 件 对 径 向水 平 井 旋 转 射 流 钻 头 的 内外 部 流 场 进 行 数 值 模 拟 ，提 出 了利 用 数 值 模 拟 手 摘 ｌｅｔ
基于cfd方法的小孔自由射流数值模拟
第35卷第2期化学反应工程与工艺V ol 35, No 2 2019年4月Chemical Reaction Engineering and Technology Apr 2019 文章编号：1001—7631 ( 2019 ) 02—0129—09 DOI: 10.11730/j.issn.1001-7631.2019.02.0129.09基于CFD方法的小孔自由射流数值模拟王权，李小江，陈勇，陈英浙江海洋大学石化与能源工程学院，浙江舟山316022摘要：针对流体的小孔喷射问题，采用了计算流体力学（CFD）方法对流体在流过小孔时的自由射流场进行了数值模拟研究。
模拟结果表明：在射流场中，主流区中心流体速度高且保持稳定，主流区边壁流体由于与气体摩擦而导致速度急剧下降；在气雾区，流体速度降低而形成气液分散状态；小孔内发生流体加速现象，且随着孔径和流体初速度的增加，小孔内流体的加速度相应增大；流体加速度的变化量随流体初速度的增加逐渐变大，随孔径增加而逐渐减小并趋近于零。
本研究得到了低速下小孔喷射状态的模拟模型，以及在不同孔径及初速度下喷射流的演化过程。
关键词：小孔射流特性数值模拟中图分类号：O358 文献标识码：A目前，在化工、冶金、能源、机械、水利水电工程、航空航天工程、给水排水工程以及环境工程等诸多领域，都存在大量的射流问题[1]。
20世纪20年代以来，前人利用理论、实验等手段，对射流现象进行了广泛且深入的研究，积累了大量的研究成果。
在层流射流理论方面，Schlichting[2]和Bickley[3]分别推导出平面层流射流的速度分布和流量分布，并经过Bickley等[3]的实验所证实。
董志勇[4]对圆形层流射流做了理论分析，推导出圆形层射流的速度分布和体积流量。
Hongo对层流射流作了详细地论述[5]。
对于湍流射流，有时间平均法和直接法[6]两种理论研究方法，前人应用雷诺平均法建立了湍流运动的基本方程，但由于雷诺应力的出现导致描述湍流运动的基本方程组不封闭，无法应用雷诺方程求解湍流问题。
基于FLUENT的非淹没式纯水射流喷嘴内部流场仿真
提高水射流效率及降低能耗的目的 。
然而， 有关水喷嘴内部流场， 尤其是混合室和混合 管内部流场特性的仿真研究少有报道。 本文用 Flunet 仿真了水喷嘴内部流场， 混合室与混合管内部流场， 以 及收敛角对流场的影响， 并进行了相关的实验验证。 假设高压水中不含空气， 在水射流的喷射过程中， 根据水喷嘴的结构特点， 可以假设它的内部一直充满 水； 而混合室与混合管的直径相比射流直径要大得多 ， 并且在初始状态充满空气， 所以在整个射流过程中， 它 们内部既有水也存在空气。 根据以上分析， 把喷嘴分 为两个部分进行仿真： 水喷嘴单相流稳态仿真和混合 室与混合管的多相流瞬态仿真。
［6 ］
vj ' =
W 2 πr0 t
（ 2）
r0 = 4 × 10 － 5 m， W 为水的体积， m3 。 式中， 将仿真值与实验值进行比较， 如表 1 所示， 可以看 出， 仿真值与实验值之间存在差异， 可能的原因： 一方 面是实际的水喷嘴内壁不够光滑， 导致了射流能量的 损失； 另一方面是仿真模型的网格数量较少 ， 网格尺寸 较大。尽管如此， 实验测得的射流速度与仿真模型预 测值的平均误差是 7. 9% ， 最大误差为 16% ， 而且预测 该仿真过程能 的射流速度的变化规律和实测值相似， 较好地预测射流速度。
1
水喷嘴内部流场仿真及实验验证
喷嘴是影响磨料水射流切割性能的关键的部分之 一， 其中水喷嘴对射流速度影响很大 ， 因此仿真分析水 喷嘴内部流场状态十分必要。 1 ． 1 仿真模型的建立与计算 Fluent 是目前 比 较 流 行 的 一 种 流 体 力 学 分 析 软 ， 本文用该软件分析了 14 种入口压力水平下的流 场状态。以入口压力为 10 MPa 为例， 进行水喷嘴内部 件 的纯水三维稳态仿真。模型几何尺寸均为水喷嘴的实 际尺寸， 其中锥段处上表面和下表面的直径分 别 为 3. 5 mm 和 3. 1 mm， 高度为 2. 1 mm； 下端圆柱半径 r0 为 0. 04 mm， 高度为 0. 4 mm； 水为不可压缩液体， 密度 ρ w 为 10 kg / m ； 由于水喷嘴内部的流场呈轴对称分 布， 在划分网格和求解计算时， 把整个模型沿着对称面 进行切割， 只对其 1 /4 进行仿真， 如图 2 所示。共划分 28 200 个六边形网格， 中心部分加密。
FLUENT软件在矩形喷嘴射流流场中的可视化研究与应用
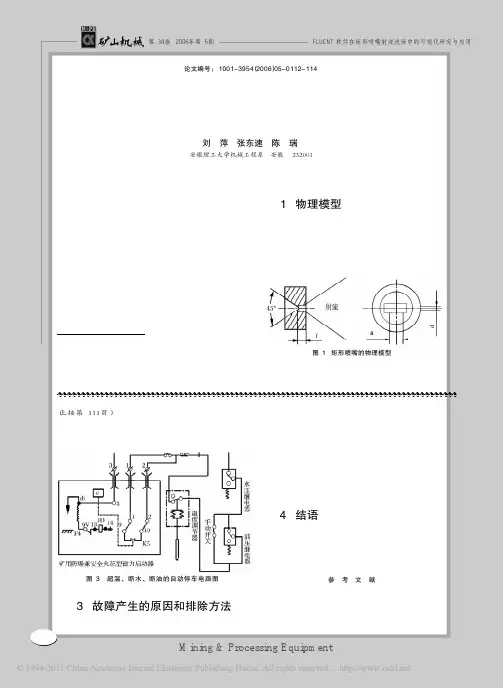
根据矩形射流的结构特点，在初步进行的实验研 究基础上作出下述假设：理想流体、不考虑能量方
安徽理工大学，硕士，讲师，研究方向为高压水射流。
88888888888888888888888888888888888888888888888888888888888888888888888888888888888888
程、定常流动、不可压；控制方程的离散采用有限体 积法；流场计算方法采用基于非结构网格的 ＳＩＭＰＬＥ 算法；多项流模型：ｍｉｘｔｕｒｅ。
ud H 176 ×1.3 ×10−3 = = 0.229 × 106 > 2 320 ， 因为 ReDH = ν 1.0 × 10−6 所以流体为湍流。由于前混合磨料射流是砂水在混合 腔内充分混合后，再从喷嘴喷出，所以我们可以将磨 料水射流视为均质流。本实验取笛卡尔坐标系下坐标 轴 （x，y，z），把速度矢量分解为轴向速度 vx 、径向速 度 vy 和切向速度 vz，选用笛卡尔坐标系下 x 轴为喷嘴 轴心线、稳定流动、不可压缩流体的 ＮａｖｉｅｒＳｔｏｋｅｓ 时 均方程作为控制方程，引入 Ｒｅｙｎｏｌｄｓ 平均法，采用 ＲＮＧ 三维湍流模型［２］建立封闭控制方程组。
η = ( 2 Eij Eij ) 2
η0 = 4.377
k ε
Eij =
４ 矩形射流流场的初值条件和边 界条件
设置 ｆａｃｅ１４ 的边界条件为速度进口条件 （ｖｅｌｏｃｉｔｙ ｉｎｌｅｔ），取名为 Ｉｎｌｅｔ１４。Ｖｅｌｏｃｉｔｙ Ｍａｇｎｉｔｕｄｅ：１７６；设 置 ｆａｃｅ１ 边界条件为压力出口条件 （Ｐｒｅｓｓｕｒｅ Ｏｕｔｌｅｔ）， 操作压力为 １０１ ３２５ Ｐａ ，测量压力为 ０ Ｐａ ；设置 ｆａｃｅ４、ｆａｃｅ１２ 边界条件为对称条件 （Ｓｙｍｍｅｔｒｙ）；设置 ｆ ａ ｃ ｅ ２ 、ｆ ａ ｃ ｅ ６ 、ｆ ａ ｃ ｅ １ １ 边界条件为压力远场条件 （Ｐｒｅｓｓｕｒｅ Ｆａｒ－ｆｉｅｌｄ）。
基于FLUENT的渗流场数值模拟分析
基于FLUENT的渗流场数值模拟分析李国栋;哈岸英;钟小彦;陈刚【摘要】Traditionally, the simulation of seepage flow is to seek for the solution of Laplace equation to the permeation head. In order to make use of the powerful calculating and pre-processing and post-processing functions of CFD software, by adding the penetration resistance terms, served as a source terms of moment, to the general fluid dynamic equations, we achieved seepage field simulation based on FLUENT software. The wetted surface of seepage is simulated with VOF ( Volume of fluid) method. Two examples of underground channel and square - shape dam shows that calculated seepage current, free surface and overflow location agreed very well with analysis and experimental results. The method provides a new vista for the seepage flow research.%传统上渗流问题的模拟都是求解渗透水头的拉普拉斯方程,为了利用CFD软件强大的计算及前后处理功能,通过在一般流体力学控制方程基础上增加渗透阻力的办法,以源项的形式导入FLUENT软件的求解器中实现了对渗流的数值模拟,并采用求解自由面的VOF 法进行浸润面的计算.地下河槽及矩形土坝两个算例表明,无论对于渗流量、浸润面还是溢出点,计算结果与解析分析及实验数据高度吻合,表明本研究方法精确可靠,为研究渗流问题提供了新的途径.【期刊名称】《西安理工大学学报》【年(卷),期】2011(027)003【总页数】4页(P317-320)【关键词】渗流;FLUENT;浸润面;VOF法【作者】李国栋;哈岸英;钟小彦;陈刚【作者单位】西安理工大学水利水电学院,陕西西安 710048;西安理工大学水利水电学院,陕西西安 710048;宁夏水利水电勘测设计研究院有限公司,宁夏银川750004;西安理工大学水利水电学院,陕西西安 710048;西安理工大学水利水电学院,陕西西安 710048;安康学院,陕西安康 725000【正文语种】中文【中图分类】TU43渗流控制是保证水利工程安全稳定的关键，而渗流分析是实现渗流控制的基础［1］。
fluent流体仿真实例
fluent流体仿真实例Fluent是一种流体仿真软件，它广泛用于研究和优化各种流体系统。
本文将介绍Fluent的基本工作原理，并以一个实例为例说明如何使用Fluent进行流体仿真。
首先，Fluent采用有限体积法来解决流体问题。
这种方法将流体域划分为许多小的控制体积，并在每个体积中计算流体的平均速度、压力和温度。
然后，通过在体积之间应用质量和动量守恒方程以及其他物理方程来求解流体行为。
最后，Fluent通过计算流场中的速度、压力和温度分布来描绘流体的行为。
为了演示Fluent的用途，我们将以水的流动为例说明如何使用它进行流体仿真。
我们考虑一个具有弯曲管道的水流系统。
假设管道入口处是一个稳定的水流，出口处是一个自由表面，即水流向大气中自由流动。
我们想研究如何通过改变管道形状和入口速度来优化整个系统。
首先，我们需要使用CAD软件绘制出整个系统的几何形状，并将其导入到Fluent中。
然后，我们需要定义出入口处的水流速度和出口处自由表面的边界条件。
这些边界条件将告诉Fluent在哪里应该施加水流速度和处理自由表面的行为。
接下来，我们需要在Fluent中定义数值方法和物理模型。
对于数值方法，我们可以选择不同的离散化方法和求解器，以达到速度和精度的平衡。
对于物理模型，我们需要考虑水的流动特性，包括湍流、速度分布、压力分布等。
这将有助于我们更准确地预测水流的行为，并优化我们的设计。
最后，我们可以开始运行Fluent并分析结果。
Fluent将生成一个包括速度、压力和温度分布的二维或三维图像。
我们可以通过这些图像来研究水流的行为，并探索如何通过改变管道形状和入口速度来优化整个系统。
例如，我们可以通过改变管道半径和斜率来优化水流速度和压力分布。
总之，Fluent是一种广泛使用的流体仿真软件，它可以帮助我们更好地理解和优化各种流体系统。
通过使用Fluent，我们可以确定管道的最佳形状和入口速度，以确保流体系统的最佳性能。
基于Fluent自进式旋转射流喷头的数值模拟
（ ）螺距 的影 响 ２
置 为 ０ ３ 密度设 置为 １ 体 积力 设 置 为 １ 动量 设置 ．， ， ，
为 ０ ７， 动 动 能 设 置 为 ０８ 湍 流 耗 散 率 设 置 为 ． 湍 ．， ０ ８湍 流粘度设 置 为 １ ．， 。
由速度矢量 图 ６７ ８看出， 、、 流体经过直段管进 入 加旋 元件 时 ， 随着 螺距 的增大 ， 在靠 近边界层 的流 体 速度 逐渐增 大 ； 在螺 旋管 道 中速度 逐渐减 小 ； 流体 经 喷嘴 喷 出的速 度也 增 大 ， 出 的发 散 角减 小 。所 喷 以， 随着螺距的增大 ， 进式喷头可以提高钻进速度 自 和钻进 效率 。
收缩段的简化几何模型。简化的直段管直径为 １ ８
ｍｍ， 长度 为 １ ０ｍｍ； 螺旋流道 长度 为 １ ５ｍｍ， 径 为 外 １ ｍ； 缩 段 的长 度 为 １ ｍ； 喷 嘴 直 径 为 ２ ８ｍ 收 ０ｍ 前 ｍ 双 头螺距 为 ８ｍ ｍ， ｍ。喷 嘴 内部 流场 模 型 如 图 １
Ａｂ ｔ ｃ ： Ｕｓ ｇ Ｐ ｏ Ｅ ｓ ｆ ｒ ｓｒ ｔ ａ ｉ ｒ ／ ｏｔ ｅ，ｔ ｅ ｇ ｏ ｔ ｃ ｍｏ ｅ ｆｓ ｉ ｅ ’ ｎ ｅ ｏ ｉｌ ｎ ｔ ｍｅ ｈ ｎ ｒ ａ ｒ ｄ ｎ ｗａ ｈ ｅ ｍｅｒ ｄ ｌｏ ｗ ｒ ｒ ｓ ｉ ｎ ｒ ｆ ｗ ｆ ｄ ａ ｄ ｉ ｓ ｉｇ ａ ｅ ｃ ｒｉ ｉ ｌ ｌ ｅ ｓ ｅ
ｍｍ， Ｃ； ｍｍ， 距 分 别 为 ８ｍ １ ｍ 及 ２ 中 ，Ｌ１ ｆ 螺 ｍ、６ｍ ４
ｍｍ。残 差迭 代 图 分 别 如 图 ３ ４ ５ 、 、 。模 型 进 口压 力
２１ 年第 ５ ００ 期
Ｅ ＼ ｄ 删鼷
煤
矿
机 电
fluent在喷管中的应用
Yves Marenghi AlliedSignal Engines Phoenix, Arizona
Copyright AlliedSignal Inc. 1999 All Rights Reserved
A Thrust Reverser Assists in Braking of the Aircraft by Reversing the Jet Engine Exhaust
Nacelle
Fan Ramp
Mixer Nozzle Bypass Hub
Rear Fuselage of the Airplane
Isometric View
CFD Analysis Can Help to Predict the Best Configuration for a Reverser Installation on a Specific Engine
(Photo courtesy NASA Marshall Center)
Benefits and CFD challenges
Nozzle flow adaptation. High efficiency.
Highly compressible flow. Complex flow structures. Low speed base regionhighly recirculating flow.
FLUENT
在喷管流动中的应用
喷管流场模拟的技术难点
¾复杂的几何外形（尤其需要考虑到喷管内流场时） ¾复杂的物理现象 气流掺混、卷吸、膨胀波系与压缩波系的相互干扰 ¾飞行器的工况往往有较大的变化（亚声速、跨声速与超声速） ¾计算量大（尤其在非定常计算时）
基于Fluent的油气两相射流仿真分析
基于Fluent的油气两相射流仿真分析牛鹏;孙启国;吕洪波【摘要】Based on the theories of two-phase flow, cylindrical nozzle models of three different outlets are established. Simulation a-nalysis of annular two-phase jet flow of the nozzle Is calculated by Fluent and two-phase velocity graphs of the nozzle are got from simulation results. Considering the oil-gas lubrication's requirements of rolling bearing, the results show that outlet diameter's optimal value is about 2mm in this model, because the continuous oil jet droplets and the moderate velocity can fulfil the better lubricate condition in this case. This conclusion provides the basis for choosing and optimizing the nozzle in oil-gas lubrication system.%基于两相流基本理论,建立了三种不同出口直径的圆柱形喷嘴模型,通过Fluent流体分析软件对喷嘴环状两相射流进行了仿真计算.分析仿真结果得出了喷嘴油气两相速度分布,并结合油气润滑条件下滚动轴承对油气两项速度的要求,比较仿真结果得出文中模型条件下,喷嘴出口直径在2mm附近时,射流油滴连续,速度适中,能够较好的满足润滑条件,为油气润滑系统中喷嘴的选择和优化提供了依据.【期刊名称】《机械制造与自动化》【年(卷),期】2013(042)002【总页数】3页(P91-93)【关键词】喷嘴;油气两相射流;出口速度【作者】牛鹏;孙启国;吕洪波【作者单位】北方工业大学机电工程学院,北京100144【正文语种】中文【中图分类】TP391.9油气润滑是一种新型的润滑技术，它具有单相流体润滑无可比拟的优越性，现今已经广泛应用于高温、重载、高速、极低速以及有冷却水和脏物侵入润滑点的恶劣工况条件的场合［1］。
基于FLUENT的淹没环境高压水射流数值模拟
基于FLUENT的淹没环境高压水射流数值模拟刘霄亮;高辉;焦向东;田路【摘要】海底管道配重混凝土的去除工作是大多数水下管道维抢修的前提,高压水射流应用于海底管道配重混凝土的去除工作相比于机械方法优势明显.将高压水射流应用于海底需要探究淹没环境对射流效果的影响,通过FLUENT数值分析,分别研究了喷嘴直径、环境压力、射流压力对淹没射流动压的影响,得到了一些对工程有重要指导意义的结论,结论指出:淹没环境对高压水射流的效果削弱很大;环境压力对射流影响相对较小;喷嘴直径和射流压力对射流效果影响明显.最后通过淹没环境高压水射流破碎混凝土实验应用和验证了仿真所得结论.【期刊名称】《机械设计与制造》【年(卷),期】2016(000)011【总页数】4页(P117-120)【关键词】高压水射流;淹没环境;FLUENT数值模拟;混凝土清除【作者】刘霄亮;高辉;焦向东;田路【作者单位】北京化工大学机电工程学院,北京100029;北京石油化工学院机械工程学院,北京102617;北京石油化工学院机械工程学院,北京102617;北京化工大学机电工程学院,北京100029【正文语种】中文【中图分类】TH16;TH137海底管道配重混凝土的去除是大多数水下管道维抢修的前提，高压水射流应用于海底管道配重混凝土的去除工作较机械去除的方法有很大的优势，工程应用广泛，但是目前国内还没有掌握这项技术。
高压水射流技术具有传递能量集中、无磨损、减尘和适应性强等优点[1-2]，广泛应用于清洗，切割、矿山开采、石油钻探以及建筑混凝土的破碎、清洗、打毛等项目[3-4]。
将高压水射流应用于海底混凝土的破碎有很大的优势，由于水下环境复杂，要求连续作业时间长，如果用机械去除的方法对刀具要求极高，容易磨损，维护成本很高，而且机械刀具也容易对海底管道造成额外损伤。
在海底应用高压水射流要注意淹没环境和海底高压环境对射流速度和动压较大的衰减作用，所以对淹没环境的高压水射流的相关研究很有必要。
基于Fluent的射流式增氧装置的数值模拟与试验研究
优点是 兼 有 推 流 和 增 氧 的双 重 作 用 … ，并 能 够 对 最 缺 氧的池底 水体 进行 直接增 氧 ，对提 高养殖 池底
ｔｓ ｗ ｃ 等分 别采 用几种 不 同的湍 流 方程 来 分 析空 ｏｉ ｉ ｅ ｚ 气 在射 流 器 内 的 流 动 情 况 Ｊ 为 了 提 高 射 流 器 的 。
性 能 ，近 年 来 研究 人 员 对 射 流器 进 行 了 深 入 的研 究 ，但 由于射 流器混 合 管 内 的流 动状 态较 为 复 一 杂 ， 目前 的生 产 设 计 中 不 得 不 采 用 经 验 公 式 。 为 优选射 流器 的设计 尺 寸并找 出各 尺寸对 性能 的影
摘要 ： 利用 — 双方程湍流模型对 自 行设计的射流式增氧机内部流场进行了模拟 ， 得到了流场内部各个参
数 的分布 图，揭示 了混合管 内部的流动状态 ，为射流式增 氧机 的参数优 化和性 能预测 提供 了可靠 的手段 。
通过对射流器仿真数据 的分析 ，得出混合管与喷嘴截面积 比的最佳值为 ２ ３ ，并通过增 氧试验验 证 ，证明 ．３
两 相或 多相混 合设 备 。国外学 者很早 就对 射流 器 的 工 作原 理 进 行 理 论 分 析 ，１４ ９ ２年 Ｋ ｅａ ｅｎ ｎ和 Ｎ ｕ ｅ－ ｍａｎ建立 了一 维 的能 量 、质 量 和 动 量守 恒 方 程 来 ｎ 预 测射 流 器 的性 能 ；Ｓ ｅｉ建 立 了 两相 流 模 型 ， ｈｒ ｆ 通 过引 入 含气 率 来 考 虑 两 相 的 相 互 作 用 ；Ｂ ｒ ａ－
基于FLUENT的后混合磨料水射流喷嘴内流场的数值模拟
ｎ ｍｉ ｅｆｒ ｎ ｅｉｓ ｅｐ ｓ－ ｘｄ ａ ｒｓｖ ａｅ ｔｎ ｚｌ ａ ａｒ ｄ ｏ ｔ ｙＦ Ｕ Ｎ Ａ ｓｒ ｓｏ ｉ ｌ ｉｎ ｒｓｌ ａ ｃｐ ｒ ｍａ ｃ ｎ ｉ ｏｔ ｅ ｂａｉｅｗ ｔｒ ｅ ｏｚ ｗ ｓｃ ｒ ｅ ｕ Ｌ Ｅ Ｔ． ｅ ｅ ｆｓ ａ ｏ ｅｕｔ ｏ ｄ ｍｉ ｊ ｅ ｉ ｂ ｉ ｍｕ ｔ ｓ
Ｊ ｔＮｏ ｚｅ Ｂａ ｅ ｎ Ｆ ｅ ｚ ｌ ｓ ｄ ｏ ＬＵＥＮＴ
Ｃｈ ｉ Ｌ ｙ ｎ Ｇｕ ｏｎ ｈ ａ Ｗ ａ ｇ Ｙｏ ｇ ｅｎ Ｌ ｎ ｅｉ Ｙｕ ｏ ｇ ｏＺ ｇ ｕ ｎ ｎ ｎ ｗｅｉ
（ ｃｏｌ ｆ ｅｈｎｃｌ ｎｉ ｅ ｎ ＆ Ａ ｔ ａ ｏ ，ｉｕ ｎｖｒ ｔ， ｈｎｄ ｉ ｕｎ６０ ３ ，ｈｎ ） Ｓｈｏ ｏ Ｍ ｃａｉ ｇ ｅｒ ｇ ａＥ ｎ ｉ ｕｏ ｔ ｎ Ｘｈ ａＵ ｉ ｓｙ Ｃ ｅｇｕＳｃ ａ １０ ９ Ｃ ｉａ ｍ ｉ ｅｉ ｈ
ｔ ａ ｈ ｘｔｖ ｌｃｔ ｎ ｉｅｉ ｎ ｒ ｓ ｓｇ ｉ ｃ ｎｌ ｅ ｕ ｅ ｅ ａ ｓ ｆｔ ｅｖ ｒｅ ｏ ａｉｎ ｍａ ｉ ｇ ｐ ｒ ｏ ｈ ｎ ｒ ｈ ｔｔ ｅ ｅ ｉ ｅｏ ｉｙａ ｄ ｋ ｎ ｔ ｅ ｅ ｇ ｉ ｉｎ ｆ ａ ｔｙ ｒｄ ｃ ｄ ｂ ｃ ｕ ｅ ｏ ｈ ｏｔｘ ｆｒ ｔｏ ｋ ｎ ａ ｆｔｅ ｅ ｅ ｇ ｃ ｙ ｉ ｍ ｔ ｙ ｌｓ ． ｄ ｔ ｅｅｉ ｐ ｉ ｚ ｄ ｎ ｚｌ ｅ ｇｈ ｔ ｅ ｘｍｕ ｖ ｌｃｔ ｆａ ｒ ｓｖ ａ ｔ ｌ ｓｉ ｓｄ ｏ ｚｅ Ｔ ｅｍａ ｉ ｍ ｘｔｖ － ｏ ｓ Ａｎ ｈ ｒ ｓｏ ｔ ｍｉｅ ｏ ｚｅｌｎ ｔ ｏｇ ｔｍａ ｉ ｍ ｅｏ ｉｙｏ ｂ ａ ｉｅｐ ｒｉ ｅ ｎ ｉ ｅｎ ｚ ｌ． ｈ ｘ ｍｕ ｅ ｉ ｅ ｃ ｌｃｔ ｆａ ｒｓｖ ａｔｃｅ ｓｏ ｔｉ ｅ ｅ ｈ ｙｉｄ ｒｐ ｒ ｉ ３～３ ｉ ｓｏ ｅ ｉｓｄ ｉｍｅｅ ． ｅｔｒ ｕ ｅ ｃ ｉｔｉ ｏ ｉｙ ｏ ｂ ａ ｉｅ ｐ ｒｉｌｓｉ ｂ ａｎ ｄ ｗｈ ｎ ｔｅ ｃ ｌ ｅ ａ ｓ２ ｎ ｔ ７ ｔｍｅ ｆｔ ｎ ｉ ｅｄａ ｔｒ Ｔｈ ｕ ｂ ｌｎ ｅ ｄ ｓｒ— ｈ ｂ ｔ ｎ ｉ ｓｄ ｈ ｏ ｚｅ ｃ ｎ ｂ ｏ ｕ ｅ ｎ ｔｅ ｎ ａ ｌ ｒｇｏ ｎ ｈ ｒ ａｗｈ ｃ ｅ ｍｅｒ ａ ａ ｇ ｒｃ ａ ｇ ｓ ｕ ｉ ｎ ｉ ｅ ｔｅ ｎ ｚ ｌ ａ ｅ ｆｃ ｓ ｄ ｏ ｈ ｅ ｒｗａｌ ｅ ｉｎ ａ ｄ ｔ ｅ ａｅ ｉｈ ｇ ｏ ｔｙ ｈ ｓｌｒ ｅ ｈ ｎ ｅ ． ｏ
应用FLUENT进行射流流场的数值模拟
应用FLUENT进行射流流场的数值模拟谢峻石何枫清华大学工程力学系一．引言射流是流体运动的一种重要类型，射流的研究涉及到许多领域，如热力学、航空航天学、气象学、环境学、燃烧学、航空声学等。
在机械制造与加工的过程中，就经常利用压缩空气喷枪喷射出高速射流进行除尘、除水、冷却、雾化、剥离、引射等。
在工业生产中，改善气枪喷嘴的设计，提高气枪的工作效率对于节约能源具有重大的意义。
FLUENT是目前国际上比较流行的商用CFD软件包，它具有丰富的物理模型、先进的数值方法以及强大的前后处理功能，在航空航天、汽车设计、石油天然气、涡轮机设计等方面都有着广泛的应用。
本文的工作就是将FLUENT应用于喷嘴射流流场的数值模拟，使我们更加深刻地理解问题产生的机理、为实验研究提供指导，节省实验所需的人力、物力和时间，并对实验结果的整理和规律的得出起到很好的指导作用.。
二．控制方程与湍流模式非定常可压缩的射流满足如下的N-S方程：（1）上式中，量，H是源项。
是控制体，是控制体边界面，W是求解变量，F是无粘通量，G 是粘性通采用二阶精度的有限体积法对控制方程进行空间离散，时间离散采用Gauss-Seidel隐式迭代。
FLUENT软件包中提供了S-A(Spalart-Allmaras)，K-Realizable K-选择RNG K-（包括标准K-、RNG K-和），Reynolds Stress等多种湍流模式，本文在大量数值实验的基础上，亚音速射流湍流模式，超音速射流选择S-A湍流模式。
三．算例分析（一）二维轴对称亚声速自由射流计算了一个出口直径为3mm的轴对称收缩喷嘴的亚声速射流流场，压比为1.45。
外流场的计算域为20D×5D（见图1）。
图1 计算域及网格示意图图2显示的是速度分布，图3、图4分别显示了轴线上的速度分布以及截面上的速度分布计算值与实验值的比较。
从图中可以看出，亚声速自由射流轴线上的速度核心区的长度约为5～6D，计算值与实验值吻合的比较一致，证明RNG k-模拟。
基于 FLUENT 的人工淹没射流喷嘴流场仿真
Ｊ ｏ ｕ ｒ ｎ ａ ｌ ｏ ｆ Ｃ ｈ ｅ ｎ ｇ ｄ ｕ Ｔ ｅ ｘ ｔ ｉ ｌ ｅ Ｃ ｏ ｌ ｌ ｅ ｇ ｅ
第 ３ １ 卷 第 ３期 （总 第 １ １ ３期 ） ２０ １ ４年 ７月
文章编号 ： １ ０ ０ ８— ５ ５ ８ ０ （ ２ ０ １ ４ ） ０ ３— ０ ２ ５— ０ ３
Ｖ ｏ １ ． ３ １， Ｎ ｏ ．３（Ｓ ｕ ｍ ｌ １ ３）
基于 Ｆ Ｌ Ｕ Ｅ Ｎ Ｔ的 人 工 淹 没 射 流 喷 嘴 流 场 仿 真
杨 涵 ， 雷 玉 勇
（ 西华大学机械制造与 自动化学院， 四川成都 ６ １ ０ ０ ３ ９ ）
摘要 根据 Ｆ ｌ ｕ ｅ ｎ ｔ 流体仿 真软 件和 人 工淹没射 流喷 嘴 内流 场的 特点 ， 基 于流体 力 学基 本理 论 ， 对人
２ 人 工 淹 没射 流 的数 学 模 型
人 工淹 没射 流喷 嘴 内 的流 场状态 属于 气液 两 相流， 在模 拟计 算 中通 常选 用 Ｆ ｌ ｕ ｅ ｎ ｔ 中 的混 合 模 型（ Ｍｉ ｘ ｔ ｕ ｒ ｅ Ｍｏ ｄ ｅ １ ） 和气穴模 型 （ Ｃ ａ ｖ ｉ ｔ ａ ｔ ｉ ｏ ｎ Ｍｏ ｄ －
关键词 人 工 淹没 数 值模 拟 剪切 作 用 负压 区
中图分类 号 ： Ｔ Ｇ ６ ６ ４ 文 献标识 码 ： Ａ
０ 引言
空化 射流 技术 是 在 高 速水 射 流 技 术 中 ， 认 为 地沿 物体 某处 的局部 压力 低于 该处 的饱 和蒸 汽压 力， 使得水 流束 中充 满 了空泡 ， 空泡 会在 目标 物体 表 面破灭并 且 产生 局 部 高 压 ， 这 种 高 压加 强 了冲 蚀与破碎能力 ， 大 大 提 高 了清 洗 的 效果 与 效 率 。 有实 验研究 表 明 ， 当水 泵 的压力 一定 的时候 ， 即喷 嘴 内射 流的速 度 一定 ， 空 化 射 流 的冲 击 压力 与 在 同等 条件 下 的 连 续 射 流 相 比， 是其 的 ８ ． ６～１ ２ ４ 倍， 所以， 使用 空化射 流 喷嘴对 设备 的使 用要 求较 连续 射 流低得 多 。文 中通 过 Ｆ Ｌ Ｕ Ｅ Ｎ Ｔ流体仿 真软
基于fluent水射流仿真分析
本文还简要介绍了旋转锥形射流的基本理论和实现方法，以及实验采集数据的实践工作，据此，对旋转锥形射流的喷射过程和机理作出合理性分析；系统地介绍fluent软件的主要功能，以及旋转锥形射流得建模方法，并介绍以此模拟旋转锥形射流的计算机方法，最终，通过模拟所得到的能量云图，结合试验数据，对加旋体的结构如何影响旋转锥形射流的喷射性能作出合理的说明；使得旋转锥形射流钻孔技术现场应用进一步参数化。
KeyWords：whirling cone jetting; whirling chamber; jetting capability ; computer simulation; software fluent
目 录
Contents
Abstract……………………………………………………………………….……I
5.1.5 The sense and localization of numeric simulation……………………42
5.1.6 The constitute of CFD………………………………………………..44
5.1.6 The function of CFD…………………………………………………45
Simulation And Analysis Of Whirling Water Jet
Candidate:
Supervisor:
Department Of Mechanical Engineering
Fluent介绍及数值模型
Fluent文件类型
FLUENT软件文件类型： .jou文件：日志文档，可以编辑运行。 .dbs文件：Gambit工作文件，若想修改网格， 可以
打开进行再编辑, 可以打开进行再编辑。 .msh文件：Gambit输出的网格文件，不可编辑。 .cas文件：Fluent算例文件，包括网格及各项设置。 .dat文件： FLUENT计算数据结果的数据文件。 .pdf文件：prePDF生成文件，仅用于燃烧反应。
FLUENT应用培训—张光学
6
3
Fluent软件构成
FLUENT应该包括以下几个部分： FLUENT解法器 GAMBIT，网格生成 ICEM，网格生成 prePDF，用于模拟PDF燃烧过程
2013/11/17
FLUENT应用培训—张光学
7
Fluent软件构成
GAMBIT 设置几何形状 生成2D或3D网格
耗散率和 k 以及湍流长度尺度相关:
结合 k 方程, 涡粘系数可以表示为:
FLUENT应用培训—张光学
18
9
2013/11/17
标准 k–ε 模型
模型中的相关系数，主要根据一些特定条件下的试验结 果而确定的。
SKE 是工业应用中最广泛使用的模型 – 模型参数通过试验数据校验过，如管流、平板流等 – 对大多数应用有很好的稳定性和合理的精度 – 包括适用于压缩性、浮力、燃烧等子模型
FLUENT应用培训—张光学
4
2
2013/11/17
Fluent基本功能
多运动坐标系下的流动问题； 化学组分混合与反应； 可以处理热量、质量、动量和化学组分的源项； 用Lagrangian 轨道模型模拟稀疏相（颗粒，水滴，气
基于Fluent的高压喷嘴射流的数值模拟
作者简介:周章根(1984— ),男,西南科技大学硕士研究生,研究方向为高压水射流。
基于Fluent 的高压喷嘴射流的数值模拟周章根,马德毅(西南科技大学制造科学与工程学院,四川绵阳621010)摘 要:研究收缩型喷嘴在初始压力为100M Pa,出口直径为1mm 的情况下喷嘴流场的速度、压力、湍动能等物理量的分布规律。
选择不可压Reynolds 方程作为动量方程,利用Fluent 的SI M P LEC 算法进行求解,对收缩型喷嘴射流进行数值模拟。
结果表明:流体速度在喷嘴收缩段迅速增加,在离开喷嘴后出现等速流核区;流体动压在喷嘴收缩段增长快速,在等速流核区保持不变;仿真结果与理论推导相符合。
关键词:Fluent;喷嘴射流;Reynolds 方程;数值模拟中图分类号:TH12;TP6 文献标志码:A 文章编号:167125276(2010)0120061202Num er i ca l S i m ul a ti on of H i gh 2pressure Jet Nozzle Ba sed on Fluen tZHOU Zhang 2gen,MA De 2yi(Co ll ege ofManufacturi ng and Engi nee ri ng,Southwe st Uni ve rsity of Sci ence and Techno l o gy,M i anyang 621010,Chi na )Abstract:This p ap e r num e ri ca ll y s tud i e s the d is tri bu ti o n re gul a riti e s o f the p hys i ca l qua n tity o f ve l o c ity,p re ssu re ,rap i d ki ne ti c e ne rgya nd so on,i n the fl o w 2fi e l d o f the co n tra c ti ve no zz l e ,w hen the i niti a l p re s sure is p =100M P a and the o utl e t ou ts i de d i am e te r is 1mm.The i ncom p re s sib l e R e yno l ds e qua ti o n is t o se l ec ted a s the m om e ntum equa ti o n a nd the a l go rithm of S I M PLEC of F l uen t is u sed t o s i m ul a te the i n j e c ti o n s tream.The re sults show tha t the j e t ve l o c ity i nc re a se s qui ckl y i n the co n tra c ti ve se c ti o n o f no zz l e and a co re se c ti o n o f e qua l ve l o c ity is f o r m e d afte r the j e t depa rts fr om the no zz l e and the dynam i c p re s sure of j e t goe s up rap i dl y i n the con trac 2ti ve sec ti o n of nozz l e ,w h il e is s ta bl e i n the co re sec ti o n.The s i m ul a ti o n confo r m s t o theo re ti ca l a na l ys is.Key words:fl ue nt;i n j e c ti o n s tream ;re yno l d s 2a ve ra ge d na vi e r 2s t o ke s e qua ti o n;num e ri ca s i m ul a ti o n0 引言F LUE NT 是用于模拟和分析在复杂几何区域内的流体流动与热交换问题的专用CF D 软件,它提供了κ-ε紊流模型等多种紊流模型,可根据具体的情况进行选择。
基于FLUENT的小流量射流流场中的可视化研究_刘萍
算的影响, 将计算范围向左边扩展了5 d。网格类型 为三角形非结构性网格, 最后得到完整的面网格 图, 产生 31 796 个网格 (见图 1)。
图 1 完整的面网格图
根据水射流的结构特点, 在初步进行的实验研 究基础上作出下述假设: 射流为不可压缩黏性流体 的对称定常流动, 将其介质视为均质流。 采用离散 相模型, 湍流模型采用 RN GK - Ε形式 (采用标准 壁面函数)。
27
安徽理工大学学报 (自然科学版) 第 26 卷
性能最优, 但是核心段长度最短, 基本段的速率衰减 最快; 1. 84 mm 喷嘴的核心段速度值最小, 其核 心段长度最大, 基本段的速率衰减最慢。在切割过程 中, 通常是利用射流的核心段进行切割, 射流核心段
的速度值越大, 对射流切割物料越有利。 利用 F luen t 软件对上述六种喷嘴进行后处
(3) 随着喷嘴直径的减小, 射流的散射角也越 来越小, 射流的集束性越来越好。
综 上所述, 利用 FLU EN T 软件对小流量圆射 流的外部流场进行可视化研究是完全可行的, 数值 模拟与实验研究相结合的方法大大促进了水射流 技术的推广和应用。
参考文献:
[ 1 ] 刘萍, 张东速, 李峥. 小流量磨料射流切割性能的试样 研究[J ]. 安徽理工大学学报 (自然科学版) , 2004, 24
5(Θk ) 5t
+
d iv (ΘkU ) =
d iv [ Αk Λef f g radk ] +
2ΛtE ij E ij - ΘΕ
(4)
(4) Ε- 动量方程[2 ]124
5(ΘΕ) 5t
+
d iv (ΘΕU ) =
d iv [ ΑΕΛef f g radΕ] +
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
应用FLUENT进行射流流场的数值模拟
谢峻石何枫
清华大学工程力学系
一．引言
射流是流体运动的一种重要类型，射流的研究涉及到许多领域，如热力学、航空航天学、气象学、环境学、燃烧学、航空声学等。
在机械制造与加工的过程中，就经常利用压缩空气喷枪喷射出高速射流进行除尘、除水、冷却、雾化、剥离、引射等。
在工业生产中，改善气枪喷嘴的设计，提高气枪的工作效率对于节约能源具有重大的意义。
FLUENT是目前国际上比较流行的商用CFD软件包，它具有丰富的物理模型、先进的数值方法以及强大的前后处理功能，在航空航天、汽车设计、石油天然气、涡轮机设计等方面都有着广泛的应用。
本文的工作就是将FLUENT应用于喷嘴射流流场的数值模拟，使我们更加深刻地理解问题产生的机理、为实验研究提供指导，节省实验所需的人力、物力和时间，并对实验结果的整理和规律的得出起到很好的指导作用.。
二．控制方程与湍流模式
非定常可压缩的射流满足如下的N-S方程：
（1）
上式中，是控制体，是控制体边界面，W是求解变量，F是无粘通量，G是粘性通量，H是源项。
采用二阶精度的有限体积法对控制方程进行空间离散，时间离散采用Gauss-Seidel隐式迭代。
FLUENT软件包中提供了S-A(Spalart-Allmaras)，K-（包括标准K-、RNG K-和Realizable K-），Reynolds Stress等多种湍流模式，本文在大量数值实验的基础上，亚音速射流选择RNG K-湍流模式，超音速射流选择S-A湍流模式。
三．算例分析
（一）二维轴对称亚声速自由射流
计算了一个出口直径为3mm的轴对称收缩喷嘴的亚声速射流流场，压比为1.45。
外流场的计算域为20D×5D（见图1）。
图1 计算域及网格示意图
图2显示的是速度分布，图3、图4分别显示了轴线上的速度分布以及截面上的速度分布计算值与实验值的比较。
从图中可以看出，亚声速自由射流轴线上的速度核心区的长度约为5～6D，计算值与实验值吻合的比较一致，证明RNG k-湍流模式适合于轴对称亚音速自由射流的数值模拟。
图2 速度分布
图3 轴线上的速度分布图4 截面上的速度分布
（二）二维轴对称超声速自由射流
计算域与网格划分与算例一相同，压比分别为4和6。
图5、6显示了在不同压力下的马赫数分布。
图中可以清晰的看到喷嘴出口附近膨胀波与压缩波的相交与反射现象。
当压比为6时，喷嘴出口附近出现了马赫盘和滑移线。
图5 压比为4时的马赫数分布
图6 压比为6时的马赫数分布
图7压比为4时喷嘴出口附近的马赫数等值线分布以及出口截面上的马赫数分布。
从图中我们可以看出，声速线和出口截面不在一个平面内，在喷嘴出口截面上，轴线附近是亚声速流动，靠近壁面处为超声速流动。
这个结果与前人的研究结论是相符合的。
图7 压比为4时出口截面马赫数分布
图8 压比为6时出口截面马赫数分布
图9显示的是喷嘴出口附近马赫数等值线分布与阴影仪实验的比较。
从图中可以看出，马赫盘的位置与实验结果比较吻合。
图9 马赫数等值线分布
四．结论
通过上述两个算例证明采用Fluent对喷嘴高速射流进行数值模拟是可行的，计算结果与实验吻合的较好。
通过数值模拟，可以更好的了解喷嘴的内外流场的流动状况，对实验结果的整理和规律的得出起到很好的指导作用。