人教版高中数学高二-数学学案 余弦定理(一) (人教A版必修5)
人教A版高中数学高二必修5课件余弦定理(一)

第三边所对的角是直角.
1.1.2 余弦定理(一)
32
1.1.2 余弦定理(一)
5
[预习导引]
1.余弦定理 三角形中任何一边的 平方等于其他两边的 平方 的和 减去这两边与它们的 夹角 的余弦的积的 两倍 . 即a2=b2+c2-2bccos A ,b2= c2+a2-2cacos B , c2= a2+b2-2abcos C .
1.1.2 余弦定理(一)
1.1.2 余弦定理(一)
9
(2)在△ABC中,已知 a= 3,b= 2,B=45°,解此三角 形.
解 由余弦定理知 b2=a2+c2-2accos B.
∴2=3+c2-2 3·22c.
即 c2-
6c+1=0,解得 c=
6+ 2
2 或 c=
6- 2
2 ,
1.1.2 余弦定理(一)
10
当c=
6+ 2
1.1.2 余弦定理(一)
8
当 a=6 时,由正弦定理得 sin A=asibn B=6×3 21=1. ∴A=90°,∴C=60°. 法二 由正弦定理得 sin C=csibn B=3 33×21= 23, 由b<c,∴C=60°或120°, 当C=60°时,A=90°,
由勾股定理得 a= b2+c2= 32+3 32=6, 当C=120°时,A=30°,△ABC为等腰三角形. ∴a=3.
解 ∵c>a,c>b,∴角C最大. 由余弦定理,得c2=a2+b2-2abcos C, 即37=9+16-24cos C,∴cos C=-12, ∵0°<C<180°,∴C=120°. ∴△ABC的最大内角为120°.
1.1.2 余弦定理(一)
17
规律方法 (1)已知三角形三边求角时,可先利用余弦定理 求角,再用正弦定理求解,在用正弦定理求解时,要根据 边的大小确定角的大小,防止产生增解或漏解. (2)若已知三角形三边的比例关系,常根据比例的性质引入k, 从而转化为已知三边解三角形.
余弦定理的教案

余弦定理的教案余弦定理的教案作为一位杰出的老师,时常要开展教案准备工作,编写教案有利于我们准确把握教材的重点与难点,进而选择恰当的教学方法。
如何把教案做到重点突出呢?以下是小编收集整理的余弦定理的教案,欢迎阅读与收藏。
余弦定理的教案1一、教材分析《余弦定理》选自人教A版高中数学必修五第一章第一节第一课时。
本节课的主要教学内容是余弦定理的内容及证明,以及运用余弦定理解决“两边一夹角”“三边”的解三角形问题。
余弦定理的学习有充分的基础,初中的勾股定理、必修一中的向量知识、上一课时的正弦定理都是本节课内容学习的知识基础,同时又对本节课的学习提供了一定的方法指导。
其次,余弦定理在高中解三角形问题中有着重要的地位,是解决各种解三角形问题的常用方法,余弦定理也经常运用于空间几何中,所以余弦定理是高中数学学习的一个十分重要的内容。
二、教学目标知识与技能:1、理解并掌握余弦定理和余弦定理的推论。
2、掌握余弦定理的推导、证明过程。
3、能运用余弦定理及其推论解决“两边一夹角”“三边”问题。
过程与方法:1、通过从实际问题中抽象出数学问题,培养学生知识的迁移能力。
2、通过直角三角形到一般三角形的过渡,培养学生归纳总结能力。
3、通过余弦定理推导证明的过程,培养学生运用所学知识解决实际问题的能力。
情感态度与价值观:1、在交流合作的过程中增强合作探究、团结协作精神,体验解决问题的成功喜悦。
2、感受数学一般规律的美感,培养数学学习的兴趣。
三、教学重难点重点:余弦定理及其推论和余弦定理的运用。
难点:余弦定理的发现和推导过程以及多解情况的判断。
四、教学用具普通教学工具、多媒体工具(以上均为命题教学的准备)余弦定理的教案2一、教学内容分析人教版《普通高中课程标准实验教科书·必修(五)》(第2版)第一章《解三角形》第一单元第二课《余弦定理》。
通过利用向量的数量积方法推导余弦定理,正确理解其结构特征和表现形式,解决“边、角、边”和“边、边、边”问题,初步体会余弦定理解决“边、边、角”,体会方程思想,激发学生探究数学,应用数学的潜能。
高中数学余弦定理 教案(新人教A版必修5)

数学:1.1《正弦定理与余弦定理》教案(新人教版必修5)(原创)余弦定理一、教材依据:人民教育出版社(A版)数学必修5第一章第二节二、设计思想:1、教材分析:余弦定理是初中“勾股定理”内容的直接延拓,是解三角形这一章知识的一个重要定理,揭示了任意三角形边角之间的关系,是解三角形的重要工具,余弦定理与平面几何知识、向量、三角形有着密切的联系。
因此,做好“余弦定理”的教学,不仅能复习巩固旧知识,使学生掌握新的有用的知识,体会联系、发展等辩证观点,而且能培养学生的应用意识和实践操作能力,以及提出问题、解决问题等研究性学习的能力。
2、学情分析:这节课是在学生已经学习了正弦定理及有关知识的基础上,转入对余弦定理的学习,此时学生已经熟悉了探索新知识的数学教学过程,具备了一定的分析能力。
3、设计理念:由于余弦定理有较强的实践性,所以在设计本节课时,创设了一些数学情景,让学生从已有的几何知识出发,自己去分析、探索和证明。
激发学生浓厚的学习兴趣,提高学生的创新思维能力。
4、教学指导思想:根据当前学生的学习实际和本节课的内容特点,我采用的是“问题教学法”,精心设计教学内容,提出探究性问题,经过启发、引导,从不同的途径让学生自己去分析、探索,从而找到解决问题的方法。
三、教学目标:1、知识与技能:理解并掌握余弦定理的内容,会用向量法证明余弦定理,能用余弦定理解决一些简单的三角度量问题2.过程与方法:通过实例,体会余弦定理的内容,经历并体验使用余弦定理求解三角形的过程与方法,发展用数学工具解答现实生活问题的能力。
3.情感、态度与价值观:探索利用直观图形理解抽象概念,体会“数形结合”的思想。
通过余弦定理的应用,感受余弦定理在解决现实生活问题中的意义。
四、教学重点:通过对三角形边角关系的探索,证明余弦定理及其推论,并能应用它们解三角形及求解有关问题。
五、教学难点:余弦定理的灵活应用六、教学流程:(一)创设情境,课题导入:1、复习:已知A=045,b=16解三角形。
高中数学人教A版必修5 1.1.2余弦定理学案

高中数学人教A版必修5第一章解三角形1.1正弦定理和余弦定理1.1.2余弦定理学案【课前自主学习】预习课本P5~6,思考并完成以下问题(1)余弦定理的内容是什么?(2)已知三角形的两边及其夹角,如何解三角形?(3)已知三角形的三边,如何解三角形?【新知探究•夯实知识基础】余弦定理[点睛]余弦定理的特点(1)适用范围:余弦定理对任意的三角形都成立.(2)揭示的规律:余弦定理指的是三角形中三条边与其中一个角的余弦之间的关系,它含有四个不同的量,知道其中的三个量,就可求得第四个量.【学练结合】(1)余弦定理揭示了任意三角形边角之间的关系,因此,它适应于任何三角形()(2)在△ABC中,若a2>b2+c2,则△ABC一定为钝角三角形()(3)在△ABC中,已知两边和其夹角时,△ABC不唯一()解析:(1)正确.余弦定理反映了任意三角形的边角关系,它适合于任何三角形.(2)正确.当a2>b2+c2时,cos A=b2+c2-a22bc<0.因为0<A<π,故A一定为钝角,△ABC为钝角三角形.(3)错误.当△ABC已知两边及其夹角时可利用余弦定理求得第三边长且唯一,因此△ABC唯一确定.答案:(1)√(2)√(3)×2.在△ABC中,已知a=9,b=23,C=150°,则c等于()A.39B.8 3C.10 2 D.7 3解析:选D由余弦定理得:c=92+(23)2-2×9×23×cos 150°=147=7 3.3.在△ABC中,已知a2=b2+c2+bc,则角A等于()A.60°B.45°C.120°D.30°解析:选C由cos A=b2+c2-a22bc=-12,∴A=120°.4.在△ABC中,已知b2=ac且c=2a,则cos B等于()A.14 B.34C.24 D.23解析:选B由b2=ac且c=2a得cos B=a2+c2-b22ac=a2+4a2-2a22a·2a=34.故选B.【学以致用•探究解题方法】题型一已知两边与一角解三角形[典例](1)在△ABC中,已知b=60 cm,c=60 3 cm,A=π6,则a=________cm;(2)在△ABC中,若AB=5,AC=5,且cos C=910,则BC=________.[解析](1)由余弦定理得:a=602+(603)2-2×60×603×cos π6=4×602-3×602=60(cm).(2)由余弦定理得:(5)2=52+BC2-2×5×BC×910,所以BC2-9BC+20=0,解得BC=4或BC=5.[答案](1)60(2)4或5[解题规律总结][活学活用]在△ABC中,a=23,c=6+2,B=45°,解这个三角形.解:根据余弦定理得,b2=a2+c2-2ac cos B=(23)2+(6+2)2-2×23×(6+2)×cos 45°=8,∴b=2 2.又∵cos A=b2+c2-a22bc=8+(6+2)2-(23)22×22×(6+2)=12,∴A=60°,C=180°-(A+B)=75°.题型二已知三角形的三边解三角形[典例]在△ABC中,已知a=23,b=6,c=3+3,解此三角形.[解]法一:由余弦定理的推论得cos A=b2+c2-a22bc=(6)2+(3+3)2-(23)22×6×(3+3)=22,∴A=45°.同理可求B=30°,故C=180°-A-B=180°-45°-30°=105°.法二:由余弦定理的推论得cos A=b2+c2-a22bc=(6)2+(3+3)2-(23)22×6×(3+3)=22,∴A=45°.由正弦定理asin A=bsin B知23sin 45°=6sin B,得sin B=6·sin 45°23=12.由a>b知A>B,∴B=30°.故C=180°-A-B=180°-45°-30°=105°. [解题规律总结][活学活用]已知a ,b ,c 是△ABC 三边之长,若满足等式(a +b -c )·(a +b +c )=ab ,则C 的大小为( )A .60°B .90°C .120°D .150°解析:选C ∵(a +b -c )(a +b +c )=ab , ∴c 2=a 2+b 2+ab ,由余弦定理可得,cos C =a 2+b 2-c 22ab =a 2+b 2-(a 2+b 2+ab )2ab =-ab 2ab =-12, ∵0°<C <180°,∴C =120°,故选C.题型三 利用余弦定理判断三角形形状[典例] 在△ABC 中,若b 2sin 2C +c 2sin 2B =2bc cos B cos C ,试判断△ABC 的形状.解:[法一 化角为边] 将已知等式变形为b 2(1-cos 2C )+c 2(1-cos 2B )=2bc cos B cos C . 由余弦定理并整理,得b 2+c 2-b 2⎝⎛⎭⎪⎫a 2+b 2-c 22ab 2-c 2⎝⎛⎭⎪⎫a 2+c 2-b 22ac 2=2bc ×a 2+c 2-b 22ac ×a 2+b 2-c 22ab ,∴b 2+c 2=[(a 2+b 2-c 2)+(a 2+c 2-b 2)]24a 2=4a 44a 2=a 2.∴A =90°.∴△ABC 是直角三角形. [法二 化边为角]由正弦定理,已知条件可化为sin 2C sin 2B +sin 2C sin 2B =2sin B sin C cos B cos C . 又sin B sin C ≠0,∴sin B sin C =cos B cos C ,即cos(B +C )=0. 又∵0°<B +C <180°,∴B +C =90°,∴A =90°. ∴△ABC 是直角三角形.[解题规律总结][活学活用]在△ABC 中,已知a cos A =b cos B ,试判断△ABC 的形状.解:由正弦定理,a sin A =b sin B =csin C =2R ,所以a cos A =b cos B 可化为sin Acos A =sin B cos B ,sin 2A =sin 2B ,又△ABC 中,A ,B ,C ∈(0,π),所以2A =2B 或2A +2B =π,即A =B 或A +B =π2,所以△ABC 的形状为等腰或直角三角形.[活学活用]在△ABC 中,a cos A +b cos B =c cos C ,试判断△ABC 的形状.解:由余弦定理知cos A =b 2+c 2-a 22bc ,cos B =c 2+a 2-b 22ca ,cos C =a 2+b 2-c 22ab ,代入已知条件得a ·b 2+c 2-a 22bc +b ·c 2+a 2-b 22ca +c ·c 2-a 2-b 22ab =0,通分得a 2(b 2+c 2-a 2)+b 2(a 2+c 2-b 2)+c 2(c 2-a 2-b 2)=0, 展开整理得(a 2-b 2)2=c 4.∴a 2-b 2=±c 2,即a 2=b 2+c 2或b 2=a 2+c 2. 根据勾股定理知△ABC 是直角三角形.题型四 正、余弦定理的综合应用命题点一:利用正、余弦定理解三角形1.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,a sin A +c sin C -2a sin C =b sinB.(1)求角B 的大小;(2)若A =75°,b =2,求a ,c . 解:(1)由正弦定理得a 2+c 2-2ac =b 2. 由余弦定理得b 2=a 2+c 2-2ac cos B. 故cos B =22,因此B =45°. (2)sin A =sin (30°+45°)=sin 30°cos 45°+cos 30°sin 45°=2+64. 故由正弦定理得a =b ·sin Asin B =1+ 3. 由已知得,C =180°-45°-75°=60°, c =b ·sin Csin B =2×sin 60°sin 45°= 6.命题点二:利用正、余弦定理证明三角形中的恒等式 2.在△ABC 中,求证a 2sin 2B +b 2sin 2A =2ab sin C . 证明:法一:(化为角的关系式)a 2sin 2B +b 2sin 2A =(2R ·sin A )2·2sin B ·cos B +(2R ·sin B )2·2sin A ·cos A =8R 2sin A ·sin B (sin A ·cos B +cos A sin B )=8R 2sin A sin B sin C =2·2R sin A ·2R sin B ·sin C =2ab sin C .∴原式得证.法二:(化为边的关系式)左边=a 2·2sin B cos B +b 2·2sin A cos A =a 2·2b 2R ·a 2+c 2-b 22ac +b 2·2a2R ·b 2+c 2-a 22bc=ab 2Rc (a 2+c 2-b 2+b 2+c 2-a 2)=ab 2Rc ·2c 2=2ab ·c2R =2ab sin C =右边,∴原式得证.命题点三:正、余弦定理与三角函数、平面向量的交汇应用3.已知△ABC 的周长为4(2+1),角A ,B ,C 所对的边分别为a ,b ,c ,且有sin B +sin C =2sin A .(1)求边长a的值;(2)若△ABC的面积为S=3sin A,求AB·AC的值.解:(1)由正弦定理,得b+c=2a.①又a+b+c=4(2+1),②联立①②,解得a=4.(2)∵S△ABC=3sin A,∴12bc sin A=3sin A,即bc=6.又∵b+c=2a=42,∴由余弦定理得cos A=b2+c2-a22bc=(b+c)2-2bc-a22bc=13.∴AB·AC=bc cos A=2.[解题规律总结]高中数学人教A版必修5第一章解三角形1.1正弦定理和余弦定理1.1.2余弦定理同步检测基础达标题1.在△ABC中,已知(a+b+c)(b+c-a)=3bc,则角A等于() A.30°B.60°C.120°D.150°2.在△ABC中,若a=8,b=7,cos C=1314,则最大角的余弦值是()A.-15B.-16C.-17D.-183.在△ABC中,角A,B,C的对边分别为a,b,c,若c2-a2-b22ab>0,则△ABC()A.一定是锐角三角形B.一定是直角三角形C.一定是钝角三角形D.是锐角或直角三角形4.若△ABC的内角A,B,C所对的边a,b,c满足(a+b)2-c2=4,且C=60°,则ab的值为()A.43B.8-4 3C.1 D.2 35.在△ABC中,角A,B,C的对边分别为a,b,c,若(a2+c2-b2)tan B=3ac,则角B的值为()A.π6 B.π3或2π3C.π3 D.π6或5π66.已知a,b,c为△ABC的三边,B=120°,则a2+c2+ac-b2=________.7.在△ABC中,若b=1,c=3,C=2π3,则a=________.8.在△ABC中,若a=2,b+c=7,cos B=-14,则b=________.9.在△ABC中,A+C=2B,a+c=8,ac=15,求b.10.在△ABC中,已知a=7,b=3,c=5,求最大角和sin C.能力达标题1.在△ABC中,有下列关系式:①a sin B=b sin A;②a=b cos C+c cos B;③a2+b2-c2=2ab cos C;④b=c sin A+a sin C.一定成立的有()A.1个B.2个C.3个D.4个2.在△ABC中,角A,B,C所对的边分别为a,b,c,若C=120°,c=2a,则a,b的大小关系为()A.a>b B.a<bC.a=b D.不能确定3.在△ABC中,cos2B2=a+c2c,则△ABC是()A.正三角形B.直角三角形C.等腰三角形或直角三角形D.等腰直角三角形4.在△ABC中,内角A,B,C的对边分别为a,b,c.若b2+c2+bc-a2=0,则a sin (30°-C)b-c=()A.12 B.32 C.-12D.-325.在△ABC中,AB=2,AC=6,BC=1+3,AD为边BC上的高,则AD的长是________.6.在△ABC中,A=120°,AB=5,BC=7,则sin Bsin C的值为________.7.在△ABC中,内角A,B,C的对边分别为a,b,c.已知cos A-2cos Ccos B=2c-ab.(1)求sin Csin A的值;(2)若cos B=14,△ABC的周长为5,求b的长.8.如图,D是直角三角形△ABC斜边BC上一点,AC=3DC.(1)若∠DAC=30°,求B;(2)若BD=2DC,且AD=22,求DC.高中数学人教A版必修5第一章解三角形1.1正弦定理和余弦定理1.1.2余弦定理同步检测解析基础达标题1.在△ABC 中,已知(a +b +c )(b +c -a )=3bc ,则角A 等于( )A .30°B .60°C .120°D .150°解析:选B ∵(b +c )2-a 2=b 2+c 2+2bc -a 2=3bc , ∴b 2+c 2-a 2=bc ,∴cos A =b 2+c 2-a 22bc =12,∴A =60°.2.在△ABC 中,若a =8,b =7,cos C =1314,则最大角的余弦值是( )A .-15B .-16C .-17D .-18 解析:选C 由余弦定理,得c 2=a 2+b 2-2ab cos C =82+72-2×8×7×1314=9, 所以c =3,故a 最大, 所以最大角的余弦值为cos A =b 2+c 2-a 22bc =72+32-822×7×3=-17.3.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若c 2-a 2-b 22ab >0,则△ABC ( )A .一定是锐角三角形B .一定是直角三角形C .一定是钝角三角形D .是锐角或直角三角形 解析:选C 由c 2-a 2-b 22ab >0得-cos C >0,所以cos C <0,从而C 为钝角,因此△ABC 一定是钝角三角形.4.若△ABC 的内角A ,B ,C 所对的边a ,b ,c 满足(a +b )2-c 2=4,且C =60°,则ab 的值为( ) A.43 B .8-4 3 C .1D.23解析:选A 由(a +b )2-c 2=4,得a 2+b 2-c 2+2ab =4,由余弦定理得a 2+b 2-c 2=2ab cos C =2ab cos 60°=ab ,则ab +2ab =4,∴ab =43.5.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若(a 2+c 2-b 2)tan B =3ac ,则角B 的值为( ) A.π6 B.π3或2π3 C.π3D.π6或5π6解析:选B 因为(a 2+c 2-b 2)tan B =3ac , 所以2ac cos B tan B =3ac ,即sin B =32, 所以B =π3或B =2π3,故选 B.6.已知a ,b ,c 为△ABC 的三边,B =120°,则a 2+c 2+ac -b 2=________.解析:∵b 2=a 2+c 2-2ac cos B =a 2+c 2-2ac cos 120° =a 2+c 2+ac , ∴a 2+c 2+ac -b 2=0. 答案:07.在△ABC 中,若b =1,c =3,C =2π3,则a =________.解析:∵c 2=a 2+b 2-2ab cos C , ∴(3)2=a 2+12-2a ×1×cos 2π3, ∴a 2+a -2=0,即(a +2)(a -1)=0, ∴a =1,或a =-2(舍去).∴a =1. 答案:18.在△ABC 中,若a =2,b +c =7,cos B =-14,则b =________.解析:因为b +c =7,所以c =7-b . 由余弦定理得:b 2=a 2+c 2-2ac cos B , 即b 2=4+(7-b )2-2×2×(7-b )×⎝ ⎛⎭⎪⎫-14,解得b =4. 答案:49.在△ABC 中,A +C =2B ,a +c =8,ac =15,求b .解:在△ABC 中,∵A +C =2B ,A +B +C =180°, ∴B =60°. 由余弦定理,得b 2=a 2+c 2-2ac cos B =(a +c )2-2ac -2ac cos B =82-2×15-2×15×12=19. ∴b =19.10.在△ABC 中,已知a =7,b =3,c =5,求最大角和sin C .解:∵a >c >b ,∴A 为最大角. 由余弦定理的推论,得cos A =b 2+c 2-a 22bc =32+52-722×3×5=-12.又∵0°<A <180°, ∴A =120°,∴sin A =sin 120°=32.由正弦定理,得sin C =c sin A a =5×327=5314. ∴最大角A 为120°,sin C =5314.能力达标题1.在△ABC 中,有下列关系式:①a sin B =b sin A ;②a =b cos C +c cos B ;③a 2+b 2-c 2=2ab cos C ;④b =c sin A +a sin C .一定成立的有( ) A .1个 B .2个 C .3个D .4个解析:选C对于①③,由正弦、余弦定理,知一定成立.对于②,由正弦定理及sin A=sin(B+C)=sin B cos C+sin C cos B,知显然成立.对于④,利用正弦定理,变形得sin B=sin C sin A+sin A sin C=2sin A sin C,又sin B=sin(A+C)=cos C sin A+cos A sin C,与上式不一定相等,所以④不一定成立.故选C. 2.在△ABC中,角A,B,C所对的边分别为a,b,c,若C=120°,c=2a,则a,b的大小关系为()A.a>b B.a<bC.a=b D.不能确定解析:选A在△ABC中,c2=a2+b2-2ab cos 120°=a2+b2+ab.∵c=2 a,∴2a2=a2+b2+ab,∴a2-b2=ab>0,∴a2>b2,∴a>b.3.在△ABC中,cos2B2=a+c2c,则△ABC是()A.正三角形B.直角三角形C.等腰三角形或直角三角形D.等腰直角三角形解析:选B∵cos2B2=a+c2c,∴cos B+12=a+c2c,∴cos B=ac,∴a2+c2-b22ac=ac,∴a2+c2-b2=2a2,即a2+b2=c2,∴△ABC为直角三角形.4.在△ABC中,内角A,B,C的对边分别为a,b,c.若b2+c2+bc-a2=0,则a sin (30°-C)b-c=()A.12 B.32C.-12D.-32解析:选A由余弦定理得cos A=b2+c2-a22bc,又b2+c2+bc-a2=0,则cos A=-12,又0°<A<180°,则A=120°,有B=60°-C,所以a sin (30°-C)b-c=sin A sin (30°-C )sin (60°-C )-sin C =34cos C -34 sin C 32cos C -32sin C=12.故选A. 5.在△ABC 中,AB =2,AC =6,BC =1+3,AD 为边BC 上的高,则AD 的长是________.解析:∵cos C =BC 2+AC 2-AB 22BC ·AC =22,∴sin C =22, ∴AD =AC sin C = 3. 答案: 36.在△ABC 中,A =120°,AB =5,BC =7,则sin Bsin C 的值为________.解析:由余弦定理可得49=AC 2+25-2×5×AC ×cos 120°,整理得: AC 2+5·AC -24=0,解得AC =3或AC =-8(舍去), 再由正弦定理可得sin B sin C =AC AB =35. 答案:357.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A -2cos C cos B=2c -ab .(1)求sin Csin A 的值;(2)若cos B =14,△ABC 的周长为5,求b 的长. 解:(1)由正弦定理可设a sin A =b sin B =csin C =k , 则2c -a b =2k sin C -k sin A k sin B =2sin C -sin A sin B ,所以cos A -2cos C cos B =2sin C -sin A sin B,即(cos A -2cos C )sin B =(2sin C -sin A )cos B , 化简可得sin(A +B )=2sin(B +C ). 又A +B +C =π,所以sin C =2sin A ,因此sin C sin A =2.(2)由sin Csin A =2,得c =2a . 由余弦定理及cos B =14,得b 2=a 2+c 2-2ac cos B =a 2+4a 2-4a 2×14=4a 2, 所以b =2a .又a +b +c =5,所以a =1,因此b =2.8.如图,D 是直角三角形△ABC 斜边BC 上一点,AC =3DC .(1)若∠DAC =30°,求B ;(2)若BD =2DC ,且AD =22,求DC . 解:(1)在△ADC 中,根据正弦定理, 有AC sin ∠ADC =DC sin ∠DAC, ∵AC =3DC ,所以sin ∠ADC =3sin ∠DAC =32, 又∠ADC =∠B +∠BAD =∠B +60°>60°, ∴∠ADC =120°,∴∠C =180°-120°-30°=30°,∴∠B =60°. (2)设DC =x ,则BD =2x ,BC =3x ,AC =3x , ∴sin B =AC BC =33,cos B =63,AB =6x , 在△ABD 中,AD 2=AB 2+BD 2-2AB ·BD ·cos B , 即(22)2=6x 2+4x 2-2×6x ×2x ×63=2x 2, 得x =2.故DC =2.。
1.1.余弦定理-人教A版必修五教案

1.1.余弦定理-人教A版必修五教案一、教学目标1.知道余弦定理的表述和含义;2.掌握余弦定理的使用方法,能够解决与三角形边长和角度有关的问题;3.运用余弦定理解决实际问题。
二、教学重点1.了解余弦定理的含义和意义;2.掌握余弦定理的使用方法。
三、教学难点1.运用余弦定理解决实际问题。
四、课前准备1.根据教材内容,精心准备三角形问题的练习题;2.准备黑板笔、板书、三角板等教具。
五、教学步骤与内容1. 余弦定理的引入(5分钟)余弦定理是解决三角形问题的重要定理,那么在引入该定理的时候,我们可以从以下几个角度来讲解:1.引入三角形的“cos定理”;2.以实例讲解余弦公式的基本内涵;3.通过简单的问题分析帮助学生理解该定理的重要性。
2. 余弦定理的推导(10分钟)在学习定理的时候,很多时候我们需要通过推导,来观察其内涵和基本原理。
而在推导该定理的时候,我们可以运用以下几个步骤:1.通过向量的基本公式了解cos值的含义;2.通过向量的点积公式导出cos值的计算公式;3.运用将向量分解的方法,得到余弦定理的推导过程;4.总结上述步骤,为学生进行详细讲解。
3. 余弦定理的应用(25分钟)学生在学会余弦定理的推导过程后,我们需要让他们通过一些实际问题来进行余弦定理的应用练习。
为了使学生对余弦定理的应用有更多的了解,我们可以运用以下几个练习题:1.让学生描述自己在余弦定理的学习中的收获;2.通过代入余弦定理,让学生求解三角形边长问题;3.通过代入余弦定理,让学生求解三角形内角余弦值问题;4.设计更多实用的练习题,让学生在运用余弦定理中不断巩固知识。
4. 教学总结与思考(10分钟)在教学结束后,我们需要对本次教学进行总结和思考,可以从以下几个方面来进行:1.总结本次课堂主要内容和重点难点;2.整理一下学生在课堂上提出的问题,并对其进行解答;3.尝试引导学生思考本节课所包含的数学思想和意义;4.根据本次课程,给学生布置一组自主思考和解决的练习。
人教A版数学必修5第一章第2节《余弦定理》 教学设计

“体现高中数学相关分支教育价值的教学设计”余弦定理(人教A必修5第一章第2节)一、教学设计⏹内容和内容解析余弦定理是《普通高中课程标准实验教科书•数学》(人教版)必修5第1章“解三角形”的主要内容,是反映三角形边角之间等量关系的重要定理,是三角函数和平面向量知识在三角形中的具体运用,是解决可转化为三角形计算问题的其他数学问题以及生产、生活实际中的测量、设计、计算等问题的重要工具,具有广泛的应用价值.此前学生已经学习了“三角函数”、“平面向量”、“三角恒等变换”,并且学习了正弦定理的发现、证明和应用,具有初步的归纳、猜想和证明意识,因此在余弦定理教学中,应以学生的已有知识为固着点,突出问题引导,着眼多元联系,诱导学生展开有质量的联想,有效地激发学生的思维,让学生全程参与到定理的探究、发现和证明之中,体验数学发现和创造的历程.为此,本节课教学重点:余弦定理的探究、发现与证明.教学难点:余弦定理的证明思路的引导与发现.⏹目标和目标解析1经历发现、猜想、推导余弦定理的过程,享受数学发现的快乐,激发学习兴趣.2通过与三角、向量、平面几何等知识的联系,能多个角度证明余弦定理,体会向量方法的作用,比较不同证法的区别与联系,体验余弦定理的不同结构、表现形式和含义.3感悟“类比”、“函数与方程”、“特殊到一般”、“化归与转化”、“数形结合”、不变量”等思想方法. 4能用余弦定理解决一些简单的解三角形问题.⏹教学问题诊断分析在已有勾股定理和正弦定理学习的基础上,让学生独立地“再发现”余弦定理是有困难的,学生难以想到“由两边夹角求第三边“时还要先建立平方关系;让学生比较”自然地”想到向量方法来证明也是困难的,定理证明所包含的数学思想学生也不容易体会到.因此需要教师真正洞察余弦定理的知识结构,把握余弦定理的认知基础,在生成和证明余弦定理时,教师启发的着力点要放在如何发现余弦定理,怎样运用向量法去证明.⏹教学支持条件分析定理的教学绝对不应该是定理的直接灌输、简单记忆、表面应用,重要的是发现问题、提出问题、探索结论、猜想归纳、模拟实验、演绎证明。
人教A版数学必修5-1.1.2 余弦定理(第一课时) 教学设计
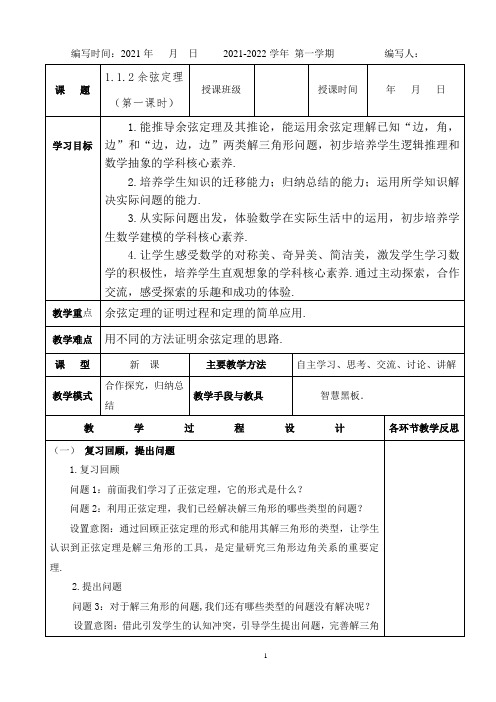
编写时间:2021年月日2021-2022学年第一学期编写人:形体系,确定边角边和边边边是两类可解的解三角形问题,使学生产生进一步探索解决问题的动机. (二) 分析问题,确定方案探究一:已知两边及其夹角解三角形问题:怎样确定解决问题的方案?设置意图:通过学生的独立思考,畅所欲言,确定思路,让更多的学生有的放矢,明确解决问题的方向.学生活动:小组合作,相互讨论,展示结果.过程说明:通过确定方案,放手让学生自己探究发现证明余弦定理.必要时加以引导如:第三边可以放在直角三角形中求解吗?涉及边长和夹角,三角形是三条线段首尾相接所组成的封闭图形,可以用向量的等式来表示吗?两点之间的距离,能用坐标法求解吗?设置意图:将原有的知识与现有的推理相联系,从多个角度联想去发现和解决问题,自主探究获得定理的证明.使其在探究中对问题本质的思考逐步深入,思维水平不断提高. (三) 发现定理,分析内涵不同方法探索并证明余弦定理之后,通过观察余弦定理结构特征,层层深入,去分析余弦定理的内涵.思考:观察C ab b a c cos 2222-+=的结构特征,谈一谈你对等式的理解.设置意图:分析等式的外延和内涵,自然的得到余弦定理及其推论. (四) 解决问题,理解定理得到了余弦定理,继续完成已知边角边求解角的过程,和已知三边解三角形的过程.探究二:已知三边解三角形设置意图:通过解三角形的过程,不但发现余弦定理,还能在求解中进一步理解和应用余弦定理. (五) 例题展示,巩固定理例:在ABC ∆中,已知,30,3,32︒===A b c 解三角形.设置意图:巩固熟悉余弦定理,从例题的思考,展示,交流,点评中使学生对正余弦定理解三角形有进一步的体验. (六) 课堂小结,提炼过程思考:余弦定理及其推论发现和证明的过程是怎样的?在这个过程中你有 什么体会?设置意图:小结环节设置了两个问题:谈过程,谈体会.目的是不但让学生经历整个探究学习过程,还能在此基础上对本节课有整体的认识,说出整个过程的环节,感受以及发现证明定理运用的方法等. (七) 布置作业,课后探究(1) 课本10P A 组3,4题(2) 拓展思考:相等和不等是一对辩证的关系,请根据角的范围讨论余弦定理中所蕴含的相等和不等关系.设置意图:作业一是巩固熟悉利用余弦定理解三角形,作业二的目的是进一步挖掘余弦定理的内涵.。
高中数学余弦定理教案(优秀5篇)

高中数学余弦定理教案(优秀5篇)高中数学余弦定理教案篇一一、说教材(一)教材地位与作用《余弦定理》是必修5第一章《解三角形》的第一节内容,前面已经学习了正弦定理以及必修4中的任意角、诱导公式以及恒等变换,为后面学习三角函数奠定了基础,因此本节课有承上启下的作用。
本节课是解决有关斜三角形问题以及应用问题的一个重要定理,它将三角形的边和角有机地联系起来,实现了边与角的互化,从而使三角与几何产生联系,为求与三角形有关的量提供了理论依据,同时也为判断三角形形状,证明三角形中的有关等式提供了重要依据。
(二)教学目标根据上述教材内容分析以及新课程标准,考虑到学生已有的认知结构,心理特征及原有知识水平,我将本课的教学目标定为:⒈知识与技能:掌握余弦定理的内容及公式;能初步运用余弦定理解决一些斜三角形⒈过程与方法:在探究学习的过程中,认识到余弦定理可以解决某些与测量和几何计算有关的实际问题,帮助学生提高运用有关知识解决实际问题的能力。
⒈情感、态度与价值观:培养学生的探索精神和创新意识;在运用余弦定理的过程中,让学生逐步养成实事求是,扎实严谨的科学态度,学习用数学的思维方式解决问题,认识世界;通过本节的运用实践,体会数学的科学价值,应用价值;(三)本节课的重难点教学重点是:运用余弦定理探求任意三角形的边角关系,解决与之有关的计算问题,运用余弦定理解决一些与测量以及几何计算有关的实际问题。
教学难点是:灵活运用余弦定理解决相关的实际问题。
教学关键是:熟练掌握并灵活应用余弦定理解决相关的实际问题。
下面为了讲清重点、难点,使学生能达到本节设定的教学目标,我再从教法和学法上谈谈:二、说学情从知识层面上看,高中学生通过前一节课的学习已经掌握了余弦定理及其推导过程;从能力层面上看,学生初步掌握运用余弦定理解决一些简单的斜三角形问题的技能;从情感层面上看,学生对教学新内容的学习有相当的兴趣和积极性,但在探究问题的能力以及合作交流等方面的发展不够均衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1.2 余弦定理(一)
课时目标 1.熟记余弦定理及其推论.2.能够初步运用余弦定理解斜三角形.
1.余弦定理
三角形中任何一边的______等于其他两边的______的和减去这两边与它们的____的余弦的积的______.即a 2=______________,b 2=__________________,c 2=_______. 2.余弦定理的推论
cos A =______________________;cos B =______________________;cos C =______. 3.在△ABC 中:
(1)若a 2+b 2-c 2=0,则C =______; (2)若c 2=a 2+b 2-ab ,则C =______; (3)若c 2=a 2+b 2+2ab ,则C =______.
一、选择题
1.在△ABC 中,已知a =1,b =2,C =60°,则c 等于( ) A. 3 B .3 C. 5 D .5
2.在△ABC 中,a =7,b =43,c =13,则△ABC 的最小角为( ) A.π3 B.π6 C.π4 D.π12
3.在△ABC 中,已知a =2,则b cos C +c cos B 等于( )
A .1 B. 2 C .2 D .4 4.在△ABC 中,已知b 2=ac 且c =2a ,则cos
B 等于( ) A.14 B.34 C.24 D.23
5.在△ABC 中,sin 2A 2=c -b
2c
(a ,b ,c 分别为角A ,B ,C 的对应边),则△ABC 的形
状为( )
A .正三角形
B .直角三角形
C .等腰直角三角形
D .等腰三角形
6.在△ABC 中,已知面积S =1
4
(a 2+b 2-c 2),则角C 的度数为( )
A .135°
B .45°
C .60°
D .120° 题 号 1 2 3 4 5 6 答 案
二、填空题
7.在△ABC 中,若a 2-b 2-c 2=bc ,则A =________. 8.△ABC 中,已知a =2,b =4,C =60°,则A =________.
9.三角形三边长为a ,b ,a 2+ab +b 2 (a >0,b >0),则最大角为________.
10.在△ABC 中,BC =1,B =π
3
,当△ABC 的面积等于3时,tan C =________.
三、解答题
11.在△ABC中,已知CB=7,AC=8,AB=9,试求AC边上的中线长.
12.在△ABC中,BC=a,AC=b,且a,b是方程x2-23x+2=0的两根,2cos(A+
B)=1.
(1)求角C的度数;
(2)求AB的长;
(3)求△ABC的面积.
能力提升
13.在△ABC中,AB=2,AC=6,BC=1+3,AD为边BC上的高,则AD的长是________.
14.在△ABC中,a cos A+b cos B=c cos C,试判断三角形的形状.
1.利用余弦定理可以解决两类有关三角形的问题: (1)已知两边和夹角,解三角形. (2)已知三边求三角形的任意一角. 2.余弦定理与勾股定理
余弦定理可以看作是勾股定理的推广,勾股定理可以看作是余弦定理的特例.
1.1.2 余弦定理(一)
知识梳理
1.平方 平方 夹角 两倍 b 2+c 2-2bc cos A a 2+c 2-2ac cos B a 2+b 2-2ab cos C 2.b 2+c 2-a 22bc c 2+a 2-b 22ca a 2+b 2-c 22ab
3.(1)90° (2)60° (3)135° 作业设计 1.A
2.B [∵a >b >c ,∴C 为最小角,由余弦定理cos C =a 2+b 2-c 2
2ab =
72+
432-13
2
2×7×43
=
3
2
. ∴C =π6
.]
3.C [b cos C +c cos B =b ·a 2+b 2-c 22ab +c ·c 2+a 2-b 22ac =2a 2
2a
=a =2.] 4.B
[∵b 2=ac ,c =2a ,∴b 2=2a 2,b =
2a ,∴cos B =a 2+c 2-b 22ac =a 2+4a 2-2a 22a ·2a =3
4
.]
5.B [∵sin 2
A 2=1-cos A 2=c -b 2c ,∴cos A =b c =
b 2+
c 2-a 2
2bc
a 2+
b 2=
c 2,
符合勾股定理.故△ABC 为直角三角形.] 6.B [∵S =14(a 2+b 2-c 2)=1
2ab sin C ,∴a 2+b 2-c 2=2ab sin C ,∴c 2=a 2+b 2-2ab sin C .
由余弦定理得:c 2=a 2+b 2-2ab cos C ,∴sin C =cos C ,∴C =45° .]
7.120° 8.30°
解析 ∵c 2=a 2+b 2-2ab cos C =22+42-2×2×4×cos 60°=12, ∴c =2 3.
由正弦定理a sin A =c sin C 得,sin A =1
2.
∵a <c ,∴A <60°,A =30°.
9.120°
解析 易知:a 2+ab +b 2>a ,a 2+ab +b 2>b ,设最大角为θ,则cos θ=a 2+b 2-
a 2+a
b +b 22
2ab
=-1
2
,∴θ=120°.
10.-2 3
解析 S △ABC =1
2
ac sin B =3,
∴c =4.
由余弦定理得,b 2=a 2+c 2-2ac cos B =13,
∴cos C =a 2+b 2-c 22ab =-113,sin C =12
13,
∴tan C =-12=-2 3.
11.解 由条件知:cos A =AB 2+AC 2-BC 22·AB ·AC =92+82-722×9×8=2
3,设中线长为x ,由余弦定
理知:x 2=⎝⎛⎭⎫AC 22+AB 2-2·AC 2·AB cos A =42+92-2×4×9×23=49, ∴x =7.
所以所求中线长为7.
12.解 (1)cos C =cos[π-(A +B )]=-cos(A +B )=-1
2,
又∵C ∈(0°,180°), ∴C =120°.
(2)∵a ,b 是方程x 2-23x +2=0的两根,
∴⎩⎨⎧
a +
b =23,ab =2.
∴AB 2=b 2+a 2-2ab cos 120°=(a +b )2-ab =10, ∴AB =10.
(3)S △ABC =12ab sin C =3
2.
13. 3
解析 ∵cos C =BC 2+AC 2-AB 22×BC ×AC =2
2,
∴sin C =
2
2
. ∴AD =AC ·sin C = 3. 14.解 由余弦定理知
cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 2
2ab ,
代入已知条件得
a ·
b 2+
c 2-a 22bc +b ·a 2+c 2-b 22ac +c ·c 2-a 2-b 22ab
=0,
通分得a 2(b 2+c 2-a 2)+b 2(a 2+c 2-b 2)+c 2(c 2-a 2-b 2)=0, 展开整理得(a 2-b 2)2=c 4. ∴a 2-b 2=±c 2,即a 2=b 2+c 2或b 2=a 2+c 2. 根据勾股定理知△ABC 是直角三角形.。
