晶体的定向和晶面符号(1)PPT
合集下载
晶体的定向和晶面符号

• 结晶轴的选择应当符合晶体固有的对称性
–首先选择对称轴和对称面的法线方向 –不存在对称轴和对称面,则平行晶棱方向选取
• 尽量使得晶轴之间夹角为90
晶轴选择遵循的(优选性)原则:
1、优选对称轴 2、其次选对称面的法线,如L22P 3、最后选择平行于发育晶棱的方向 4、使三个坐标轴尽可能互相垂直
每个晶系的对称特点不同,因此每个晶系的选择晶轴的具体方法 也 不 同 , 见 教 材 表 5-1( 此 表 非 常 重 要 , 要 熟 记 ).
三方和六方晶系的四轴定向:
– 选择唯一的高次轴作为直立结晶轴z轴,在垂直 z 轴 的平面内选择三个相同的、即互成60°交角的L2或 P的法线,或适当的显著晶棱方向作为水平结晶轴, 即x 轴、 y 轴以及 u 轴
– 晶体几何常数: a = b = 90°, g =120°, a = b < > c
– z 轴直立, y 轴左右水平, x 轴前后水平偏左30°
a、b、c和α、β、γ称之为晶体几何常数
•晶体的三轴定向:
–选择三个不共面的坐标轴 x, y, z安置晶体。
摆法:
X轴:前后,前为 +,后为 - Y轴:左右,右为+ Z轴:上下,上为+
晶体常数:轴率、轴角
Z
c
a
bY
X
•晶体的四轴定向:
–适用于六方和三方晶系 –一个直立轴,三个水平轴
二、晶体定向原则
晶体的定向和晶面符号
• 晶体定向的概念 • 晶体定向的原则 • 晶系的定向法则(重点) • 对称型的国际符号 • 晶面符号 • 晶棱符号 • 晶带符号
一、晶体定向的概念
晶体定向:就是在晶体上选定坐标系统,从而确 定晶面、晶棱的空间方位。
首选建立坐标系统
–首先选择对称轴和对称面的法线方向 –不存在对称轴和对称面,则平行晶棱方向选取
• 尽量使得晶轴之间夹角为90
晶轴选择遵循的(优选性)原则:
1、优选对称轴 2、其次选对称面的法线,如L22P 3、最后选择平行于发育晶棱的方向 4、使三个坐标轴尽可能互相垂直
每个晶系的对称特点不同,因此每个晶系的选择晶轴的具体方法 也 不 同 , 见 教 材 表 5-1( 此 表 非 常 重 要 , 要 熟 记 ).
三方和六方晶系的四轴定向:
– 选择唯一的高次轴作为直立结晶轴z轴,在垂直 z 轴 的平面内选择三个相同的、即互成60°交角的L2或 P的法线,或适当的显著晶棱方向作为水平结晶轴, 即x 轴、 y 轴以及 u 轴
– 晶体几何常数: a = b = 90°, g =120°, a = b < > c
– z 轴直立, y 轴左右水平, x 轴前后水平偏左30°
a、b、c和α、β、γ称之为晶体几何常数
•晶体的三轴定向:
–选择三个不共面的坐标轴 x, y, z安置晶体。
摆法:
X轴:前后,前为 +,后为 - Y轴:左右,右为+ Z轴:上下,上为+
晶体常数:轴率、轴角
Z
c
a
bY
X
•晶体的四轴定向:
–适用于六方和三方晶系 –一个直立轴,三个水平轴
二、晶体定向原则
晶体的定向和晶面符号
• 晶体定向的概念 • 晶体定向的原则 • 晶系的定向法则(重点) • 对称型的国际符号 • 晶面符号 • 晶棱符号 • 晶带符号
一、晶体定向的概念
晶体定向:就是在晶体上选定坐标系统,从而确 定晶面、晶棱的空间方位。
首选建立坐标系统
结晶学与矿物学课件-晶体定向、晶面符号和晶带定律

根據這一規律,我們可以由若干已知面或晶帶推導 出晶體上一切可能的晶面的位置。
在晶體定向、投影和運算中,晶帶和晶帶定律得到 了廣泛的應用。
晶帶定律和整數定律分別以不同的形式闡述了晶面 (面網)與晶核(行列)相互依存的幾何關係。
(2)軸角 系指晶軸正端之間的夾角,它 們分別以α (Y∧Z)、β (Z∧X)和γ(X∧Y)表 示。等軸、四方和斜方晶系晶軸為直角
坐標α=β=γ=90。;在三方和六方晶系 中α=β=90,γ=120。(X軸和Y軸正端 夾角),單斜晶系中一軸傾斜從而使α=γ =90,β>90。三斜晶系中三晶軸彼此斜 交,α≠β≠γ≠90。
確定晶棱符號的方法如下:
將晶Байду номын сангаас平移,使之通過晶軸的交點、然後在 其上任一點,取座標(x、y、z),並以軸長 來度量,即求得晶棱符號: (x/a):(y/b):(z/c)=r:s:t,晶棱符號採用[ ]表 示,即[ rst]。
2.晶帶
由布拉維法則可知,晶面是網面密度較大的 面網,所以晶體上所出現的實際晶面為數是 有限的;相應地,晶面的交棱也應當是結點 分佈較密的行列,這種行列的方向也是為數 量不多的,所以晶體上的許多晶棱常具有共 向的方向而相互平行。
交棱相互平行的一組晶面的組合,稱為一個 晶帶。
通過晶體中心的直線cc,晶棱與之平行,稱 該晶帶的晶帶軸;該組晶棱的符號也就是該 晶帶軸的符號。
3、晶帶定律
晶體是一個封閉的幾何多面體,每一晶面與其它晶 面相交,必有兩個以上的互不平行的晶棱。因此, 晶體上任一晶面至少屬於兩個晶帶。這一規律稱為 晶帶定律。它也可以這樣來表述,即:任意二晶棱 (晶帶)相交必可決定一個可能晶面.而任意二晶面 相交必可決定一可能晶棱(晶帶)。
(3)軸長與軸率 晶軸系格子構造中的行列, 該行列上的結點間距稱為軸長。X、Y、Z軸 上的軸長分別以a、b、c表示。由於結點間 距極小(以nm計),需藉X射線分析方能測定。 根據晶體外形的宏觀研究不能定出軸長, 但應用幾何結晶學的方法可以求出它們的 比率a:b:c,這一比率稱為軸率。
在晶體定向、投影和運算中,晶帶和晶帶定律得到 了廣泛的應用。
晶帶定律和整數定律分別以不同的形式闡述了晶面 (面網)與晶核(行列)相互依存的幾何關係。
(2)軸角 系指晶軸正端之間的夾角,它 們分別以α (Y∧Z)、β (Z∧X)和γ(X∧Y)表 示。等軸、四方和斜方晶系晶軸為直角
坐標α=β=γ=90。;在三方和六方晶系 中α=β=90,γ=120。(X軸和Y軸正端 夾角),單斜晶系中一軸傾斜從而使α=γ =90,β>90。三斜晶系中三晶軸彼此斜 交,α≠β≠γ≠90。
確定晶棱符號的方法如下:
將晶Байду номын сангаас平移,使之通過晶軸的交點、然後在 其上任一點,取座標(x、y、z),並以軸長 來度量,即求得晶棱符號: (x/a):(y/b):(z/c)=r:s:t,晶棱符號採用[ ]表 示,即[ rst]。
2.晶帶
由布拉維法則可知,晶面是網面密度較大的 面網,所以晶體上所出現的實際晶面為數是 有限的;相應地,晶面的交棱也應當是結點 分佈較密的行列,這種行列的方向也是為數 量不多的,所以晶體上的許多晶棱常具有共 向的方向而相互平行。
交棱相互平行的一組晶面的組合,稱為一個 晶帶。
通過晶體中心的直線cc,晶棱與之平行,稱 該晶帶的晶帶軸;該組晶棱的符號也就是該 晶帶軸的符號。
3、晶帶定律
晶體是一個封閉的幾何多面體,每一晶面與其它晶 面相交,必有兩個以上的互不平行的晶棱。因此, 晶體上任一晶面至少屬於兩個晶帶。這一規律稱為 晶帶定律。它也可以這樣來表述,即:任意二晶棱 (晶帶)相交必可決定一個可能晶面.而任意二晶面 相交必可決定一可能晶棱(晶帶)。
(3)軸長與軸率 晶軸系格子構造中的行列, 該行列上的結點間距稱為軸長。X、Y、Z軸 上的軸長分別以a、b、c表示。由於結點間 距極小(以nm計),需藉X射線分析方能測定。 根據晶體外形的宏觀研究不能定出軸長, 但應用幾何結晶學的方法可以求出它們的 比率a:b:c,這一比率稱為軸率。
第四章 晶体定向和晶面符号
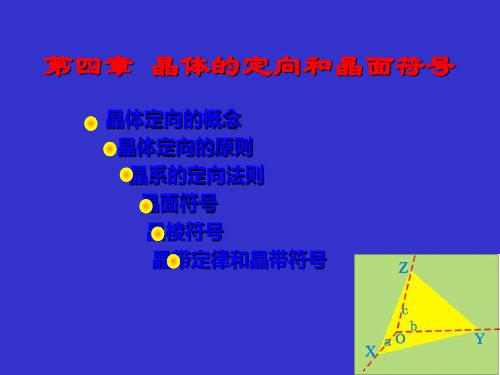
r = 0×0-1×0 =0,s = 0×0-1×0 =0,t = 1×1-0×0 =1,即此晶带
的符号为(001)。
35
⒉ 求位于晶带[rst]和晶带[uvw]交点的晶面(hkl)。 因为: hr +ks +lt =0 hu +kv +lw =0 则与例(1)类比,可用下列行列式计算:
27
整数定律
晶面在晶轴上的截距 系数之比为简单的整数比
b0
b1
b2
(010)
晶面指数为简单整数.
ao
为什么?
因为指数越简单的 晶面对应到内部结构是
a1
面网密度大的面网,而面
网密度大的面网容易形
成晶面,所以实际晶体上
的晶面就是晶面指数简
单的晶面。
b3
y
28
五、晶棱符号、晶带与晶带定律
1、晶棱符号:表征晶棱方向的 符号,所有平行的晶棱具有 同一个晶棱符号。
• 晶棱符号只涉及方向, 不涉及 具体位置。
• 截距系数比:表达为[rst]
r:s:t = MR/a : MK/b : MF/c
• [r s t] = [r s t]
此例:[rst] = [123]
29
四轴定向时的晶棱符号 • 以[u v m w]的形式表达 • 也有三指数形式: [u v w] • 四指数和三指数
c 直立,b 左右, a 前后
a=bc ===90
11
斜方晶系
3L2 a b c 轴 1L2 c轴 2P法线 a b 轴
c 直立,b 左右, a 前后
abc == =90
12
单斜晶系
1L2/1P法线 b轴, 2晶棱 a c轴
c 直立,b 左右 a 前后但向前下方倾斜 使>90
3.晶体定向及晶面符号

晶体的规则连生
第一节、 晶体定向及晶面符号
一、晶体定向
(一)、概念
晶体定向 —— 在晶体中确定一个坐标系统; 1、晶轴 ------ 晶体中的坐标轴; 2、轴单位---- 各晶轴上的量度单位:a、b、c
(二)晶轴的安置
晶轴----晶体中的坐标轴;是交晶体中心一点的 三条或四条直线。(内部构造的三条或四条行 列的方向)
复三方单锥
三方双锥
复六方单锥
复四方单锥
六方双锥
四方双锥
复三方双锥
复六方双锥
复四方双锥
三方柱
六方柱
四方柱
复三方柱
复六方柱
复四方柱
四方四面体
复四方偏三角面体
菱面体
复三方偏三角面体
斜三三方方方四偏偏面方方面体面体体
六六方方偏偏方方面面体体
四方偏方面体
高级晶族的单形
四面体 八面体
立方体 四六面体
偏方复十 二面体
(a1b2:x=1a ,y= 2b :即1: 2) (a2b4:x=2a ,y= 4b :即2: 4)
第二节、单形和聚形
1、单形
(1)概念
由对称要素联系起来的一组晶面的总合。
八面体
菱形十二面体
(2)特点
①. 在理想情况下, 同一单形各晶面 同形等大; ②. 在实际晶体上, 同一单形各晶面 性质相同;
1、三轴系统:X 、Y、Z:适用以下5个晶系:
(1)三斜晶系
(2)单斜晶系
(3)斜方晶系
(4)四方晶系
r
(5)等轴晶系
2、四轴系统:适用以下2个晶系:
(1)三方晶系: X 、Y、U、Z (2)六方晶系: X 、Y、U、Z
一
晶 轴: 轴单位:
第一节、 晶体定向及晶面符号
一、晶体定向
(一)、概念
晶体定向 —— 在晶体中确定一个坐标系统; 1、晶轴 ------ 晶体中的坐标轴; 2、轴单位---- 各晶轴上的量度单位:a、b、c
(二)晶轴的安置
晶轴----晶体中的坐标轴;是交晶体中心一点的 三条或四条直线。(内部构造的三条或四条行 列的方向)
复三方单锥
三方双锥
复六方单锥
复四方单锥
六方双锥
四方双锥
复三方双锥
复六方双锥
复四方双锥
三方柱
六方柱
四方柱
复三方柱
复六方柱
复四方柱
四方四面体
复四方偏三角面体
菱面体
复三方偏三角面体
斜三三方方方四偏偏面方方面体面体体
六六方方偏偏方方面面体体
四方偏方面体
高级晶族的单形
四面体 八面体
立方体 四六面体
偏方复十 二面体
(a1b2:x=1a ,y= 2b :即1: 2) (a2b4:x=2a ,y= 4b :即2: 4)
第二节、单形和聚形
1、单形
(1)概念
由对称要素联系起来的一组晶面的总合。
八面体
菱形十二面体
(2)特点
①. 在理想情况下, 同一单形各晶面 同形等大; ②. 在实际晶体上, 同一单形各晶面 性质相同;
1、三轴系统:X 、Y、Z:适用以下5个晶系:
(1)三斜晶系
(2)单斜晶系
(3)斜方晶系
(4)四方晶系
r
(5)等轴晶系
2、四轴系统:适用以下2个晶系:
(1)三方晶系: X 、Y、U、Z (2)六方晶系: X 、Y、U、Z
一
晶 轴: 轴单位:
第三章 晶体的定向和晶面符号
A
rc
qb
O
pa
BY
.
X
12
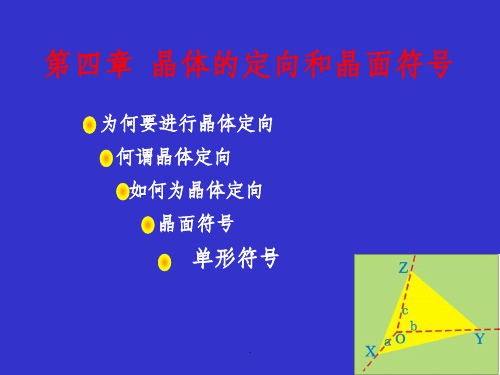
如图:所示晶面在三个结晶轴 上的截距分别为2a、3b、6c,
Z
截距系数分别为2,3,6。
C
那么
截距系数的倒数比为
1 h:k:l=2
:1 3
:1 6
=3:2:1
cb
aO
A
BY
该晶面的米氏符号为(321) X
晶面指数-米氏符号中小括号内的三个数字称晶面指数。
.
13
整数定律
晶面在晶轴上的截距 系数之比为简单的整数比
面网密度越大 越简单
晶面截晶轴于结点
简单的
整数比
.
14
在确定晶体上晶面的米氏符号时,并不需要知道a, b,c的大小。可以首先选择一个晶面作单位面。单位面 应该是晶体上发育很好、与三个晶轴都相截,而且截距 尽可能相等或相近的晶面。将单位面的符号定为(111 ),即认为该晶面的截距系数p=q=r,截距之比为a:b :c。确定了单位面之后,其它晶面的符号可通过与单 位面的比较而求得。
确定轴单位
Z+ _ _ +Y
+
X_
B4
晶轴 行列,轴单位 结点间距
B3
B2
晶体常数 轴率a:b:c和轴角, ,
.
B1 b
O a A 1 A 2 A 3 3A 4
三、如何为晶体定向
1、选择晶轴的原则
(1)晶轴平行行列方向。
优先
晶轴平行 对称轴
其次
对称面的法线
Z +_
_ +Y
+
X_ 再次
平行晶棱
构成双晶的两个个体之间其结晶
rc
qb
O
pa
BY
.
X
12
如图:所示晶面在三个结晶轴 上的截距分别为2a、3b、6c,
Z
截距系数分别为2,3,6。
C
那么
截距系数的倒数比为
1 h:k:l=2
:1 3
:1 6
=3:2:1
cb
aO
A
BY
该晶面的米氏符号为(321) X
晶面指数-米氏符号中小括号内的三个数字称晶面指数。
.
13
整数定律
晶面在晶轴上的截距 系数之比为简单的整数比
面网密度越大 越简单
晶面截晶轴于结点
简单的
整数比
.
14
在确定晶体上晶面的米氏符号时,并不需要知道a, b,c的大小。可以首先选择一个晶面作单位面。单位面 应该是晶体上发育很好、与三个晶轴都相截,而且截距 尽可能相等或相近的晶面。将单位面的符号定为(111 ),即认为该晶面的截距系数p=q=r,截距之比为a:b :c。确定了单位面之后,其它晶面的符号可通过与单 位面的比较而求得。
确定轴单位
Z+ _ _ +Y
+
X_
B4
晶轴 行列,轴单位 结点间距
B3
B2
晶体常数 轴率a:b:c和轴角, ,
.
B1 b
O a A 1 A 2 A 3 3A 4
三、如何为晶体定向
1、选择晶轴的原则
(1)晶轴平行行列方向。
优先
晶轴平行 对称轴
其次
对称面的法线
Z +_
_ +Y
+
X_ 再次
平行晶棱
构成双晶的两个个体之间其结晶
第五章晶体定向和晶面符号

聚形的概念
❖ 两个以上的单形的聚合称为聚形。下图分别 表示了四方柱和四方双锥、立方体和菱形十 二面体的 聚合,用粗线勾划出了它们的聚形 的形态。显然,有多少种单形相聚,其聚形 上就会出现多少种不同的晶面,它们的性质 各异;对于理想形态而言,同一单形的晶面 同形等大。
第五章 晶体的定向和晶面符号
晶体定向:设置坐标系 晶面符号:用数学符号表示方位 1 晶体定向 选择坐标轴和确定各轴上轴单位的比值。 1.1 晶轴和晶体几何常数 晶轴:于晶体上所设置的坐标轴。 轴角:每两个晶轴正端之间的夹角。 =Y∧Z =Z∧X =X∧Y
晶体定向的作用:
❖ 晶体定向后就可以对晶体上所有的面、线等 进行标定,给出这些面、线的晶体学方向性 符号;
关系式 :
θx、θy、θz
h:k:l=a Cosθx :b Cosθy : c Cosθz 可直接求出晶面指数
❖ 零表示与晶轴的 ❖ 平行关系,负数 ❖ 表示与晶轴负端 ❖ 相交。
四轴:形式(hkil)且h+k+i=0
h+
(三)单形符号
4 几个概念:
❖ 4.1 晶带
❖
晶面彼此相交的晶棱相互平行的一组晶面的组合。形
式 为〔rst〕
❖ 4.2 晶带定律
❖
晶体上任一晶面至少同时属于两个晶带;而一个晶带
❖ 有对称中心; ❖ 但没有对称面
斜方四面体
❖ 注意:三条边不等长, 所以没有对称面,只有 3个L2,单斜晶系,低级 晶族。
❖ L33L23P ❖ 晶系: ❖ 晶族:
复三方柱
❖ L66L27PC ❖ 晶族: ❖ 晶系:
六方柱
❖ L33P ❖ 晶族: ❖ 晶系:
复三方单锥
三方双锥
晶体定向和晶面符号

二、晶体定向原则
• 结晶轴的选择应当符合晶体固有的对称性
–首先选择对称轴和对称面的法线方向 –不存在对称轴和对称面,则平行晶棱方向选取
• 尽量使得晶轴之间夹角为90
每个晶系的对称特点不同,因此每个晶系的选择晶轴 的具体方法也不同,见表5-1(此表非常重要,要熟记).
等轴晶系的定向:
晶体几何常数为: a = b = g = 90°, a = b = c – 三个互相垂直的L4, Li4或L2为 x, y, z 轴 – z 轴直立,y 轴左右水平,x 轴前后水平
只写出对称型中的三类对称要素 只写出对称轴,对称面,旋转反伸轴,其它对称要素 可根据组合定理推导出来 国际符号中对称要素的表示法 对称面:m 对称轴:以轴次的数字表示,如1、2、3,4和6; 旋转反伸轴:轴次数字上面加“-”号,如1、2、3、 4和6。 由于1=Li1=C,2=Li2=P=m,习惯用1代表对称中心.m代 表2。
r:s:t = MR/a : MK/b : MF/c
• [r s t] = [r s t]
此例:[r v w] = [1 2 3]
2、晶带: (zone) 彼此间的交棱均相互平行的一组晶面之组合。 晶带轴(zone axis) 通过晶体中心的一根直线,它平行于该晶带中的所有晶 面,也就是平行于该晶带中各个晶面的公共交棱,用以 表示晶带方向。
卤钠石(sulphohalite )的平行连生体
赤铜矿的连生晶体
明矾八面体的平行连生
萤石立方体的平行连生
自然铜立方体的树枝状平行连生
内 部 的 晶 体 格 子 是 连 续 的
2、双晶(孪晶) twin
定义:互不平行的同种单体,彼此间按一定的 对称关系相互取向而组成的规则连生晶体。
第四章 晶体定向和晶面符号
晶
体
的
定
向
方
法
10
四方晶系
1L4 c轴 2L2 /2P法线/2晶棱 a b轴
c 直立,b 左右, a 前后
a=bc ===90
11
斜方晶系
3L2 a b c 轴 1L2 c轴 2P法线 a b 轴
c 直立,b 左右, a 前后
abc == =90
12
单斜晶系
1L2/1P法线 b轴, 2晶棱 a c轴
交可决定一可能晶带(晶棱).
33
3、晶带方程应用
即:任一属于[u v w]晶带的晶面(h k l),必定有: h u + k v + l w = 0 晶带方程
简单的证明: 三维空间的一般平面方程为 Ax + By + Cz + D = 0 系数A、B、C决定该平面的方向,常数项D决定距原点 的距离。 那么过坐标原点且平行于(h k l)的平面方程则可以表达 为
23
考察晶体模型晶面的晶面符号:
Cube
(001) (100) (010)
Octahedron
(111) (111)
Dodecahedron
(111)
(111)
101
011
_
110
110
_
_
101
011
24
All three combined:
001
_
101
111
011 111
_ 110
100
010 110
c 直立,b 左右 a 前后但向前下方倾斜 使>90
abc ==90 >90
13
三斜晶系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7
斜方晶系 (对称型:3L23PC、3L2、L22P)
3L2 X Y Z 轴 1L2 Z轴 2P法线 X Y 轴
Z 直立,Y 左右,X 前后
晶体常数特点:abc == =90
单斜晶系 (对称型:L2PC、L2、P)
1L2或1P法线 Y轴, 以垂直于Y轴的2晶
棱 X Z轴
Z 直立,Y 左右 X 前后但向前下方倾斜 使>90
:
1 r
=h:k:l
把hkl用小括号括起来,( hkl )就是 该晶面的米氏符号。
A
rc
qb
O
pa
BY
X
12
如图:所示晶面在三个结晶轴 上的截距分别为2a、3b、6c,
Z
截距系数分别为2,3,6。
C
那么
截距系数的倒数比为
1 h:k:l=2
:1 3
:1 6
=3:2:1
cb
aO
A
BY
该晶面的米氏符号为(321) X
Z +_
_
+Y
+
X
_
Z+
YX+
X-
Y+
Z-
5
三、如何为晶体定向
(4)三方、六方晶系选四个晶轴 (X、Y、U、Z),其中 Z轴-直立方向,上正、下负; X轴、Y轴、U轴均在一个水平面 上,其正端的夹角为1200,其正负 如右图所示,它们都与Z轴垂直。
U+_120Fra bibliotek + X
_
1200
+Y
1200
_
Z
U
-
(1011)
U+
Z+
-
(1121)
E
U
P2
O
P2
P1 P3
D A X
--
Y+
(1010)
X+
根据四轴定向时3个水平结晶轴的正 P 2 端互成120交角的关系,应当有:
Y h+k+i=0
B
即:3个水平结晶轴相应的晶面指数,
它们的代数和永远为0
17
五、单形符号
同一单形的各个晶面与晶 轴都有着基本相同的相对 位置
确定轴单位
Z+ _ _ +Y
+
X_
B4
晶轴 行列,轴单位 结点间距
B3
B2
晶体常数 轴率a:b:c和轴角, ,
B1 b
O a A 1 A 2 A 3 3A 4
三、如何为晶体定向
1、选择晶轴的原则
(1)晶轴平行行列方向。
优先
其次
晶轴平行 对称轴
对称面的法线
Z +_
_ +Y
+
X_ 再次
平行晶棱
(2)晶轴要尽可能的互相垂直或近于
垂直,即尽可能使 ===90,
具a体=步b=骤c
高次轴 L2 P 法线 显著晶棱 4
三、如何为晶体定向
(3)等轴、四方、斜方、单斜及 三斜等五个晶系选三个晶轴(X、 Y、Z),其中
Z轴-直立方向,上正、下负;
X轴-对着观察者,前正、后负;
Y轴-置于左右方向,右正、左负
举例:
15
晶面的米氏符号 (hkl) 晶面指数 h:k:l 取最简单的整数比
即:h, k, l 成为3个没有公约数的整数
注意:
晶面符号中不能同时出现数字和符号(除0外)
晶面指数有正负之分 (h- k l)
晶面与结晶轴平行时,相应的晶面指数为
1 ∞
=0
16
三方和六方晶系的晶面符号(hki-l)
h,k,i,l分别代表X,Y,U,Z轴 上的指数。其中h+k+i=0
11
例如:某晶面与三个晶轴X、Y、Z分别交于A、B、C三点,
那么该晶面在三个晶轴上截距是OA、OB、OC。如果用轴
单位a、b、c度量,得到:
OA=pa,OB=qb,OC=rc
或者说,晶面在晶轴上的截距分别为pa、qb、rc。
其中p,q,r就是该晶面的截距系数。
Z
C
截距系数的倒数比为:
1 p
:
1 q
为了准确描述晶体的形态,确定晶体的空间分布特点,
就必须……
2
二、何谓晶体定向
晶体定向:就是在晶体上建立坐标系统 选定结晶轴
晶体定向的任务:选择坐标系统,包括
结晶轴 交于晶体中心的三条直线 分别表示为X Y Z
轴单位 a、b、c(行列上结点的间距) 轴角 各晶轴正端之间的夹角
=YZ;=XZ;=XY
轴率 各晶轴上的轴单位之比 a:b:c?
晶面指数-米氏符号中小括号内的三个数字称晶面指数。
13
整数定律
晶面在晶轴上的截距 系数之比为简单的整数比
面网密度越大 越简单 简单的
晶面截晶轴于结点
整数比
14
在确定晶体上晶面的米氏符号时,并不需要知道a, b,c的大小。可以首先选择一个晶面作单位面。单位面 应该是晶体上发育很好、与三个晶轴都相截,而且截距 尽可能相等或相近的晶面。将单位面的符号定为(111 ),即认为该晶面的截距系数p=q=r,截距之比为a:b :c。确定了单位面之后,其它晶面的符号可通过与单 位面的比较而求得。
晶体常数特点:abc ==90 >90 8
三斜晶系
(对称型:L1、C)
选择3个显著的、而且相互间较接 近于90的晶棱方向作为X Y Z轴
Z 直立, Y 左右并朝右下方倾斜 X 大致前后方向并使之朝前下方倾斜
使>90,>90, 则可为钝角,亦可为锐角
晶体常数特点:abc 90
9
六方晶系和三方晶系
同一单形的各个晶面的指 数的绝对值不变,而只有 正负号的区别
知道了单形的一个晶面 的符号,则该单形的其 它晶面的符号即可导出
晶U30体轴 常左数后特—右点前:水a=平b,c正=前朝=9后0偏=左10120
四、晶面符号
晶面符号—代表晶面在空间的方位的符号 晶体定向后,晶面的空间方位可以借晶面与晶 轴的截交关系来确定。 晶面符号的表达方式—米氏符号 由英国人Miller(1839)创立 米氏符号用晶面在结晶轴上的截距系数的倒数比来表 示。
第四章 晶体的定向和晶面符号
为何要进行晶体定向 何谓晶体定向 如何为晶体定向 晶面符号
单形符号
1
一、为何要进行晶体定向
由四方柱和四方双锥 组成的两种聚形 (L44L25PC)
3L44L36L29PC
3L44L36L29PC 3L44L36L29PC
要了解晶体的具体形态,只知道对称型是不够的
晶体的具体形态取决于晶体的晶面与对称要素之 间的关系
U
对称特点:晶体中唯一的高次轴为L3
或L6
Y
选择1个直立结晶轴和3个水平结晶轴
X L3/L6 Z轴,
3个彼此相交1200的L2 / P 法线/晶棱(无L2或P时) X Y U轴
X Y U 轴正向之间的夹角为120
Z
Z 轴上下直立
Y 轴左右水平,右正左负
U
X
Y
X 轴左前—右后水平,正端朝前偏左 30
Y X
6
2、各晶系晶轴选择的具体方法
等轴晶系
3L4或3个互相垂直的Li4或L2 X Y Z轴
Z 直立,Y 左右,X 前后
晶体常数特点:a=b=c
=四方=晶=系90
1L4 Z轴 以两个相互垂直的L2 X Y轴
无L2时以相互垂直的2个对称面的法线方
向或晶棱方向为X Y轴
Z 直立,Y 左右,X 前后
晶体常数特点:a=bc
