平行线的判定与性质习题公开课一等奖ppt课件
合集下载
平行线的基本性质市公开课一等奖省赛课微课金奖PPT课件

第5页
你能利用刚才方法画出AB平行线吗?
A
B
E
F 利用垂线
画平行线
第6页
当直角三角尺这么放时,直尺该怎样放?
A
B
第7页
你当能直归角纳三出角这尺种这方么法放画时平,行直线尺方该法怎步样骤放吗??
A
B
推平行线法
一贴:把三角板一边贴在已知直线上; 二靠:紧靠三角板另一边放直尺. 三推:把三角板沿直角边推到不一样于原来任意位置. 四画:沿三角板这一边画直线.
A
B
a
bA
B
D'
A'
1、图1中两条直线平行吗?
C' B'
2、图2中两条线段有交点吗?它们平行吗?
3、图3中,AB所在直线与CC'所在直线有 交点吗?它们平行吗?
第3页
如图,在长方体中,和AA'平行棱有多 少条?请用符号把它们表示出来.
D A
D' A'
C B
C' B'
第4页
请用三角板及直尺,做一个长方形,说 说你作图方法,并观察所画长方形对边 所在直线有什么位置关系。
(P5课内练习3) A
P
B
C
第10页
2.如图,AB,BC是一个平行四边形相邻 两边。请把这个平行四边形补画完整 (P5作业题3)
C
A
B
第11页
3、如图,E是梯形ABCD下底BC上一点,小 芳说:“图中只有一组平行线,即AD∥BC”. 而小明说:“图中应该还有BE∥AD和EC∥AD, 共三组平行线.”你同意谁说法?为何?
A
D
BE
C
平行线是指两条直线位置关系.
第12页
4、找出图中各对相互平行直线
A
D
F
你能利用刚才方法画出AB平行线吗?
A
B
E
F 利用垂线
画平行线
第6页
当直角三角尺这么放时,直尺该怎样放?
A
B
第7页
你当能直归角纳三出角这尺种这方么法放画时平,行直线尺方该法怎步样骤放吗??
A
B
推平行线法
一贴:把三角板一边贴在已知直线上; 二靠:紧靠三角板另一边放直尺. 三推:把三角板沿直角边推到不一样于原来任意位置. 四画:沿三角板这一边画直线.
A
B
a
bA
B
D'
A'
1、图1中两条直线平行吗?
C' B'
2、图2中两条线段有交点吗?它们平行吗?
3、图3中,AB所在直线与CC'所在直线有 交点吗?它们平行吗?
第3页
如图,在长方体中,和AA'平行棱有多 少条?请用符号把它们表示出来.
D A
D' A'
C B
C' B'
第4页
请用三角板及直尺,做一个长方形,说 说你作图方法,并观察所画长方形对边 所在直线有什么位置关系。
(P5课内练习3) A
P
B
C
第10页
2.如图,AB,BC是一个平行四边形相邻 两边。请把这个平行四边形补画完整 (P5作业题3)
C
A
B
第11页
3、如图,E是梯形ABCD下底BC上一点,小 芳说:“图中只有一组平行线,即AD∥BC”. 而小明说:“图中应该还有BE∥AD和EC∥AD, 共三组平行线.”你同意谁说法?为何?
A
D
BE
C
平行线是指两条直线位置关系.
第12页
4、找出图中各对相互平行直线
A
D
F
平行线的判定PPT比赛课市公开课一等奖省优质课获奖课件

几何语言表述:
∵∠1=∠2 (已知) ∴AB∥CD(同位角相等, 两直线平行)
第6页
纸条,
第7页
1.如图,哪两个角相 等能判定直线 AB∥CD?
2.已知∠1=54°,
当
时,
AB∥CD?
第8页
3.假如∠∠123==∠∠2,54 能判定哪两条直线平行?
第9页
E
如图,直线AB、CD被EF A
所截,假如∠1=∠2,
1
3
A
∴ ∠2=∠3 (等量代换) ∴ DC∥AB (内错角相等,两直线平行)
C
2
B
第18页纸条,ຫໍສະໝຸດ 第19页本节课你有收获吗
教材p16 2、4题
第20页
文字叙述
图形表示
①________那么这两 条直线也相互平行。
② 同位角相等 两直线 平行。
③___________两直线 平行 ,
④___________两直线 平行。
系是_____b_∥. c
A
D
E
F
B
第2题
C
第15页
4.如图1所表示,以下条件中,能判断AB∥CD是( )
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
A
D
1
4
A
D
E
F
B
3
2
(1) C
B
C
(2)
5.如图2所表示,假如∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC
D.AD∥EF
第16页
6.如图3所表示,能判断AB∥CE条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA
∵∠1=∠2 (已知) ∴AB∥CD(同位角相等, 两直线平行)
第6页
纸条,
第7页
1.如图,哪两个角相 等能判定直线 AB∥CD?
2.已知∠1=54°,
当
时,
AB∥CD?
第8页
3.假如∠∠123==∠∠2,54 能判定哪两条直线平行?
第9页
E
如图,直线AB、CD被EF A
所截,假如∠1=∠2,
1
3
A
∴ ∠2=∠3 (等量代换) ∴ DC∥AB (内错角相等,两直线平行)
C
2
B
第18页纸条,ຫໍສະໝຸດ 第19页本节课你有收获吗
教材p16 2、4题
第20页
文字叙述
图形表示
①________那么这两 条直线也相互平行。
② 同位角相等 两直线 平行。
③___________两直线 平行 ,
④___________两直线 平行。
系是_____b_∥. c
A
D
E
F
B
第2题
C
第15页
4.如图1所表示,以下条件中,能判断AB∥CD是( )
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
A
D
1
4
A
D
E
F
B
3
2
(1) C
B
C
(2)
5.如图2所表示,假如∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC
D.AD∥EF
第16页
6.如图3所表示,能判断AB∥CE条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA
《平行线的性质》课件 (一等奖)2022年最新PPT(1)

和 EGF的度数。
D G E
FC
A
B
博达助教通
解:因为ABC≌ADE,
G E
所以ACB与AED,B与D是对应角, F
D C
所以ACBAED105,BD 25。
由三角形的内角和定理可得
A
B
CAB180ACBB1801052550, 又
CAD10 所以
DFBCADFCACADCABB 1050 25
出土了各种文物:金器、玉器、石器、 陶器、青铜器...等数千件。其中有享誉 中外的金杖、金面罩、青铜人像、头像、 人立像、画具等精品文物1000多件。
如图,是举世闻名的三星堆考古中开掘出 的一个梯形残缺玉片,工作人员从玉片上已经 量得∠A=115°,∠D=100°。梯形的两底 AD//BC,请你求出另外两个角的度数
我们遇到过形状、大小都相同的图形吗?
观察下面的图形,有没有形状不仅相同,而且大小也一样的 图形,如果有,试着找出来
1
2
3
5
6
7
9
10
11
博达助教通
4 8 12
博达助教通
如何判断两个图形的大小和形状是否完全相同呢?
可以把两个图形叠合在一起,看看是否完全重合 我们把能够完全重合的两个图形叫做全等图形
85 又D25,所以DGBDFBD852560,
• (至少找出两 种方法)
博达助教通
博达助教通
博达助教通
沿着图中的虚线,分别把下面的图形划分为两个全等的图形
博达助教通
博达助教通
全等多边形 两个全等的多边形,经过运动而重合,相互重合的 顶点叫做对应顶点,相互重合的边叫做对应边,相 互重合的角叫做对应角。
记作“ 〞 ,读作“全等于〞 全等多边形的特征与识别 特征:全等多边形的对应边、对应角分别相等。 识别:1.能够完全重合 2.对应边、对应角分别相等的两个多边形全等
D G E
FC
A
B
博达助教通
解:因为ABC≌ADE,
G E
所以ACB与AED,B与D是对应角, F
D C
所以ACBAED105,BD 25。
由三角形的内角和定理可得
A
B
CAB180ACBB1801052550, 又
CAD10 所以
DFBCADFCACADCABB 1050 25
出土了各种文物:金器、玉器、石器、 陶器、青铜器...等数千件。其中有享誉 中外的金杖、金面罩、青铜人像、头像、 人立像、画具等精品文物1000多件。
如图,是举世闻名的三星堆考古中开掘出 的一个梯形残缺玉片,工作人员从玉片上已经 量得∠A=115°,∠D=100°。梯形的两底 AD//BC,请你求出另外两个角的度数
我们遇到过形状、大小都相同的图形吗?
观察下面的图形,有没有形状不仅相同,而且大小也一样的 图形,如果有,试着找出来
1
2
3
5
6
7
9
10
11
博达助教通
4 8 12
博达助教通
如何判断两个图形的大小和形状是否完全相同呢?
可以把两个图形叠合在一起,看看是否完全重合 我们把能够完全重合的两个图形叫做全等图形
85 又D25,所以DGBDFBD852560,
• (至少找出两 种方法)
博达助教通
博达助教通
博达助教通
沿着图中的虚线,分别把下面的图形划分为两个全等的图形
博达助教通
博达助教通
全等多边形 两个全等的多边形,经过运动而重合,相互重合的 顶点叫做对应顶点,相互重合的边叫做对应边,相 互重合的角叫做对应角。
记作“ 〞 ,读作“全等于〞 全等多边形的特征与识别 特征:全等多边形的对应边、对应角分别相等。 识别:1.能够完全重合 2.对应边、对应角分别相等的两个多边形全等
《平行线的性质》PPT优质课件(第1课时)

b
a ∠1=∠5
65° c
65°
12
a
34
56
bb
78
∠1=∠5
c
∠1=∠5
12
a
3
41
56
b
78
结论:_两__条__平__行__线__被__第__三__条__直__线__所__截__,__同__位__角__相__等___.
问题2 由∠1=∠5,能推出∠1=∠7吗?∠2与∠8 也相等吗?为什么? ∠1=∠7. 理由:∵∠1=∠5(两直线平行,同位角相等),
A 3
1 D
2 4
C
B 理由分:析∵:∠∠11=和∠∠22(是已A知B,),CD被BD ∴AB所∥截C的D内(内错角错,角由相∠等1=,∠2两可直得线平行). ∴∠AA3BC=∥所∠C截4D(的.两∠内3直和错线∠角平4,是由行AAB,B,∥内CCD错D被,角相等).
可得∠3=∠4.
例2 已知:如图,EF∥AD,∠1=∠2,∠BAC=70 °,求
命题2 如图,AB∥CD,直线AB,CD被直线EF所截,则
∠1+∠2=180°. E
理由:
∵ AB∥CD ( 已知 ),
A
∴ ∠1=∠3
( 两直线平行,同位角相等 ) . C
3 42
B
1
D
∵∠3+∠2=180 °(补角定义 ),
∴ ∠1+∠2=180° 等量代换
F
(
).
结论:_两__直__线__平__行__,_同__旁__内__角__互__补___.
解析:①若AB∥CD,则∠3=∠4,正确; ②若∠1=∠BEG,则AB∥CD,错误; ③若∠FGH+∠3=180°,则EF∥GH,正确;
平行线的判定PPT经典教学课件市公开课一等奖省优质课获奖课件

请同学们想一想:
日常生活中有哪些例子给 你以不相交形象?
第2页
第3页
第4页
第5页
第6页
第7页
\
第8页
第9页
在这个画法中,我们能够看到: 经过直线外一点,有且只有一条直线 与这条直线平行.这叫平行线基本性质.
第10页
观察∠1和∠5两角:
8 7
5 6
43 12
第11页
观察∠1和∠5两角: 各有一边在同一直线上,
第24页
本节课你收获是什么? (1)什么是平行线; (2)平行线性质。 (3)同位角、内错角、同旁内角
第25页
8 7
5 6
43 12
第22页
角名称同位角
位置特征
图形结构特征
在两条被截直线同旁, 形如字母“F”
在截线同侧
(或倒置)
内错角 在两条被截直线之内, 形如字母“Z”
在截线两侧(交织)
(或反置)
同旁内角
在两条被截直线同旁, 在截线同侧
形如字母“U”
第23页
试一试:
请同学们分别用双手大拇指 ,食指各组成一个角,两食指相 对成一条线,保持在同一平面内 ,分别进行尝试,看能够组成哪 些角.
第15页
观察∠3和∠5两角: 各有一边在同一直线上 另一边在截线两侧, 方向相反
8 7
5 6
43 12
5 3
第16页
观察∠3和∠5两角:
一边都在截线上而且反 向,另一边在截线两侧 两个角
内错角
夹在两被截直线内, 分别在截线两侧(交织)
5 3
第17页
图中内错角除∠3和∠5外,还有……
8 7
5 6
43 12
日常生活中有哪些例子给 你以不相交形象?
第2页
第3页
第4页
第5页
第6页
第7页
\
第8页
第9页
在这个画法中,我们能够看到: 经过直线外一点,有且只有一条直线 与这条直线平行.这叫平行线基本性质.
第10页
观察∠1和∠5两角:
8 7
5 6
43 12
第11页
观察∠1和∠5两角: 各有一边在同一直线上,
第24页
本节课你收获是什么? (1)什么是平行线; (2)平行线性质。 (3)同位角、内错角、同旁内角
第25页
8 7
5 6
43 12
第22页
角名称同位角
位置特征
图形结构特征
在两条被截直线同旁, 形如字母“F”
在截线同侧
(或倒置)
内错角 在两条被截直线之内, 形如字母“Z”
在截线两侧(交织)
(或反置)
同旁内角
在两条被截直线同旁, 在截线同侧
形如字母“U”
第23页
试一试:
请同学们分别用双手大拇指 ,食指各组成一个角,两食指相 对成一条线,保持在同一平面内 ,分别进行尝试,看能够组成哪 些角.
第15页
观察∠3和∠5两角: 各有一边在同一直线上 另一边在截线两侧, 方向相反
8 7
5 6
43 12
5 3
第16页
观察∠3和∠5两角:
一边都在截线上而且反 向,另一边在截线两侧 两个角
内错角
夹在两被截直线内, 分别在截线两侧(交织)
5 3
第17页
图中内错角除∠3和∠5外,还有……
8 7
5 6
43 12
平行线的性质PPT市公开课一等奖省优质课获奖课件
c
d
a
1
2
3
b
第14页
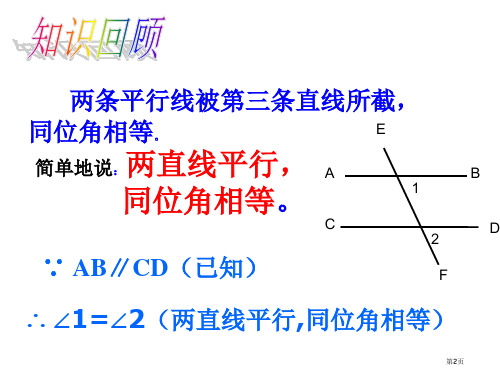
3.已知: ∠ 1=130 °, ∠4=45 °, ∠3=50 °,求:∠2等于多少度?
ab 12 c
3
4d
第15页
平行线判定
平行线性质
同位角相等,两直线平行. 两直线平行,同位角相等. 内错角相等,两直线平行. 两直线平行,内错角相等. 同旁内角互补,两直线平行.两直线平行,同旁内角互补.
如图(2):
ADE= B (已知),
DE BC (同位角相等,两直线平行),
CED+C=180º( 两直线平行,同旁内角互补 ).
A
A
B
D
E
C
D
(1)
B
C
(2)
第18页
2.如图所表示, 已知AB//CD ,AD//BC, BF平分 ∠ABC ,DE平分∠ADC,
则 DE//FB,请说明理由.
D
F
C
A
E
B
第19页
3、如图1,已知AD∥BC,∠BAD=∠BCD。判断AB与CD 是否平行,并说明理由
4 、 如 图 2 , 已 知 AB∥CD , AE∥DF 。 请 说 明 ∠BAE=∠CDF
D
C
A 图1
B
A
B
F
C
图2
E D
第20页
两条平行线被第三条直线所截,
同位角相等。
E
简单地说:两直线平行, A 同位角相等。
B 1
C
D
2
∵ AB∥CD(已知)
F
∴ ∠1=∠2(两直线平行,同位角相等)
第2页
如图,已知AG//CF,AB//CD,
平行线的判定华师大版七年级数学公开课一等奖优质课大赛微课获奖课件

2
C5
D
F
解:∵ ∠4+∠2=180 °(已知) ∠4+∠3=180°(补角定义) ∴ ∠2=∠3(同角补角相等)
∴ AB∥CD(同位角相等, 两直线平行)
你尚有其它说理办法吗?
第9页
思考
E
如图,假如
3
∠4+∠2=180°, A 1 4 B
能得出AB∥CD
2
C5
D
F
解∵ ∠4+∠2=180 °(已知) ∠4+∠1=180°(补角定义) ∴ ∠2=∠1(同角补角相等)
A F
1
B
D
2 C
G E
第20页
1 A
1.如图,AB⊥BC于B, 2
∠1=125°,∠2=35°, B
请阐明l1∥l2理由。
B
D
2.如图,∠B=40°, ∠DFC=140 ° ,
试判断AB与DE是否平行,
并阐明理由。
l1 C l2
A F
E C
第21页
你学到了什么? 你认为尚有什么不懂? 你有什么经验与收的
1.经历“平行线鉴定办法”发觉过 程。
2.掌握平行线鉴定办法。 3. 会用它进行简朴推理和表述。
第2页
试一试 猜一猜
如图,三根木条相交成 ∠1, ∠2,固定木条b、c, 转动木条a , 观测∠1, ∠2满 足什么条件时直线a与b平行.
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
①直线a和b不平行 ②直线a∥b ③直线a和b不平第3页行
C
第12页
已知直线l1 ,l2被l3所截,如图,
∠1=45°,∠2=135°,试 判断l1与l2是否平行.并阐明理由.
平行线的判定PPT市公开课一等奖省优质课获奖课件

1.2平行线判定(一)
这是一个平行四边形挂物架,工人师傅在钉木 条时该怎样确保AB平行CD呢?
A
B
D
C
第2页
合作学习 我们已经学习用三角尺和直尺画平行线方法,请
按如图所表示方法画两条平行线,然后讨论下面
问题: (1)上面画法能够看作 是怎样图形变换?
(2)把图中直线a , b看成被尺边
AB 所截,那么在画图过程中,什
相等,两直线平行)
1
a
2 b
C
第6页
想一想:
“在同一平面内,垂直于同一条直线两条直线 相互平行”是否能够看作平行线判定特殊情形
解:∵ ∵b⊥a , c, ⊥a
(已知)
∴ ∠1 =∠2=90° , (垂直定义)∴b来自c (同位角相等,两直线平行)
第7页
平行线判定方法2:
在同一平面内,垂直于同一条直线 两条直线相互平行
2、课内练习1、 3、课内练习3
4.如图6,木工师傅用角尺画出工件边缘两条垂线, 这两条垂线平行吗?为何?
5、作业题1、2、3、4
第17页
想一想
某人骑自行车从A地出发,沿正东方向前进
至B处后,右转15°,沿直线向前行驶到C处。 (如图)这时他想仍按正东方向行驶,那么他应 怎样调整行驶方向?请画出他应继续行驶路线, 并说明理由。
A
B
C
15°
15°
第15页
小结: 平行判定方法 1、平行定义 2、平行线判定公理 3、平行线判定公理推论
第16页
90
90
1
G R E A T 。PROTRACTOR
2
G R E A T 。PROTRACTOR
0 0
48.5° a
这是一个平行四边形挂物架,工人师傅在钉木 条时该怎样确保AB平行CD呢?
A
B
D
C
第2页
合作学习 我们已经学习用三角尺和直尺画平行线方法,请
按如图所表示方法画两条平行线,然后讨论下面
问题: (1)上面画法能够看作 是怎样图形变换?
(2)把图中直线a , b看成被尺边
AB 所截,那么在画图过程中,什
相等,两直线平行)
1
a
2 b
C
第6页
想一想:
“在同一平面内,垂直于同一条直线两条直线 相互平行”是否能够看作平行线判定特殊情形
解:∵ ∵b⊥a , c, ⊥a
(已知)
∴ ∠1 =∠2=90° , (垂直定义)∴b来自c (同位角相等,两直线平行)
第7页
平行线判定方法2:
在同一平面内,垂直于同一条直线 两条直线相互平行
2、课内练习1、 3、课内练习3
4.如图6,木工师傅用角尺画出工件边缘两条垂线, 这两条垂线平行吗?为何?
5、作业题1、2、3、4
第17页
想一想
某人骑自行车从A地出发,沿正东方向前进
至B处后,右转15°,沿直线向前行驶到C处。 (如图)这时他想仍按正东方向行驶,那么他应 怎样调整行驶方向?请画出他应继续行驶路线, 并说明理由。
A
B
C
15°
15°
第15页
小结: 平行判定方法 1、平行定义 2、平行线判定公理 3、平行线判定公理推论
第16页
90
90
1
G R E A T 。PROTRACTOR
2
G R E A T 。PROTRACTOR
0 0
48.5° a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
性质
内错角相等
理 同旁内角互补
两直线平行
同位角相等 内错角相等 同旁内角互补
4
课前热身
如图所示,下列推理正确的是( C)
A.∵∠1=∠4,∴BC∥AD
B.∵∠2=∠3,∴AB∥CD
C.∵AD∥BC,∴∠BCD+∠ADC=180°
D.∵∠ABC+∠C=180°,∴BC∥AD
B
A
1
2
43
C
D
5
中考链接
∴ BD∥CE(同位角相等,两直线平行)
1
∴ ∠C=∠ABD (两直线平行,同位角相等)
又∵∠C=∠D (已知)
A
∴ ∠D=∠ABD (等量代换)
BC
∴ DF∥AC (内错角相等,两直线平行)
∴ ∠A=∠F (两直线平行,内错角相等)
8
变式:如图,已知∠A=∠F,∠C=∠D, 求证:BD//CE.
区 角的数量关系 判定 别 角的数量关系 性质
两直线平行 两直线平行
ห้องสมุดไป่ตู้
7
1、 如图,点B、E分别在AC、DF上,BD、CE均
与AF相交,∠1=∠2,∠C=∠D,试问:∠A与∠F相等
吗?请说出你的理由。
解: ∠A=∠F 理由如下:
∵∠1=∠2 (已知)
D EF 2
∠1=∠3 (对顶角相等)
3
∴ ∠2=∠3 (等量代换)
内错角相等,两直线平行
)
∴∠3=__∠_4__( 两直线平行,同位角相等
)
∠3+___∠__5_=1800(两直线平行,同旁内角互补 )
cd
a
1
3
A
B
2 图1
5b
4
D
图2 C
(2)如图2∵∠A+ ∠D= 1800(已知) ∴__A__B__∥__C__D__( 同旁内角互补,两直线平行 ) ∴∠B+∠C=___1_8_0(0 两直线平行,同旁内角互补 )
(2)、 ∵AB ∥__D__F__, (已知)
B
D
∴ ∠2= ∠4,(____两_直__线__平_行__,_内__错_角__相__等_。_) 性质
F 5
C
(3)、∵ _A__B∥_D__F, (已知)
∴ ∠B= ∠3. (_两__直__线_平__行__, _ _同__位_角__相__等_.__) 性质
D EF 2
证明:∵∠A=∠F(已知)
3
∴ DF∥AC(内错角相等,两直线平行)
1
∴ ∠D=∠ABD
(两直线平行,内错角相等)
A
BC
又∵∠C=∠D (已知)
∴ ∠C=∠ABD(等量代换) ∴ BD∥CE(同位角相等,两直线平行)
9
体验成功——达标检测
1、填空
(1)如图1∵∠1= ∠2
a
b
∴______∥______(
掌1 声
巧辨孪生兄弟 —平行线的判定和性质
习题课
2
1. 了解平行线的判定与性质的区别。 2.掌握平行线的判定与性质,并能灵活的选择 运用它们进行推理证明。 3.在例题变式的过程中,体会转化的数学思想, 学会有条理表达自己,从而进一步增强分析、 概括、表达能力。
3
知
识
平行线的判定与性质的关系图
梳 判定 同位角相等
10
体验成功——达标检测
16 a
2、直线a、b与直线c相交,给出下列 5 4
条件: ①∠1= ∠2 ②∠3= ∠6
27 b
83
③∠4+∠7=1800
④∠3+ ∠5=1800,其中能判断a//b的
是
( B) A ①②③④ B ①③④ C ①③ D ④
11
体验成功——达标检测
3、如图,已知AB∥CD, ∠1=∠2,求证∠E=∠F. 证明 ∵AB∥CD(已知)
A
1 EG
3
B
C2 F
4D H
如图,∠1= ∠2=45 °,∠3=70 °,
则∠4等于
(B)
(A)70 °
(B)110 °
(C)45 °
(D)35°
6
抢答
A
(1)、∵ ∠A=_∠__4_, (已知) ∴ AC∥ED ,(_同_位__角__相_等__,__两_直__线__平_行__。__)判定E
42 13
∴ ∠BAD=∠ADC
(两直线平行,内错角相等) 又∵∠1=∠2 (已知)
∴ ∠BAD - ∠1 = ∠ADC - ∠2
(等式的性质)
即 ∠3=∠4 (等量代换)
A 1 3 E
C
B
F
4
2D
∴ AF∥DE (内错角相等,两直线平行)
∴ ∠E=∠F (两直线平行,内错角相等)
12
13
14
