函数图像问题综合
高考数学中的函数图像问题解析

高考数学中的函数图像问题解析高考数学是所有高中毕业生的噩梦之一,尤其是数学中的函数图像问题。
在高考数学中,函数图像问题是一个必须掌握的部分,因为它涉及到很多实际问题的解决方法。
在本文中,我们将详细讨论高考数学中的函数图像问题,帮助读者更好地理解这个难点。
一、简单的函数图像问题在高考数学中,最简单的函数图像问题是给定一个函数f(x),要求求出其图像。
这个问题看似简单,但实际上需要掌握一些技巧。
首先,我们需要了解一些常见的函数的图像,例如二次函数,指数函数,对数函数等。
这些函数的图像是高考数学中重点考察的,因此需要记住其基本形态。
其次,我们需要使用一些基本的图像变换技巧,例如平移,压缩等,来对函数的图像进行分析和绘制。
最后,我们需要了解如何使用数值表来绘制函数的图像。
数值表是一种非常有用的工具,可以帮助我们更好地理解函数的性质。
例如,我们可以使用数值表来确定函数的极值点,拐点,以及其他关键点。
此外,数值表还可以帮助我们确定函数的单调性,从而更好地理解函数的最大值和最小值,以及函数的攀升或下降趋势。
二、复杂的函数图像问题除了简单的函数图像问题外,高考数学中还存在一些更为复杂的函数图像问题。
例如,有时候我们需要对一个函数进行分段定义,这样函数的图像会变得更加复杂。
此时,我们需要了解分段函数的基本性质和图像变换规律,来更好地分析和绘制分段函数的图像。
另外,有时候函数的定义域和值域也受到限制,这会对函数的图像造成一些影响。
例如,如果定义域为负数,那么函数的图像可能会受到对称性的影响,这就需要我们使用对称性来分析和绘制函数的图像。
应用题中也会出现函数图像的问题,例如在求解物理问题时,需要根据函数的图像来解决问题。
因此,在应用题中需要有针对性地分析函数的图像,来解决具体的问题。
三、总结在高考数学中,函数图像问题是一个非常重要的考点,需要从多个方面进行思考和分析。
对于这个问题,我们需要掌握基本的图像变换和数值表技巧,以及对各种函数的基本形态和特殊性质有所了解。
专项训练:函数的图像
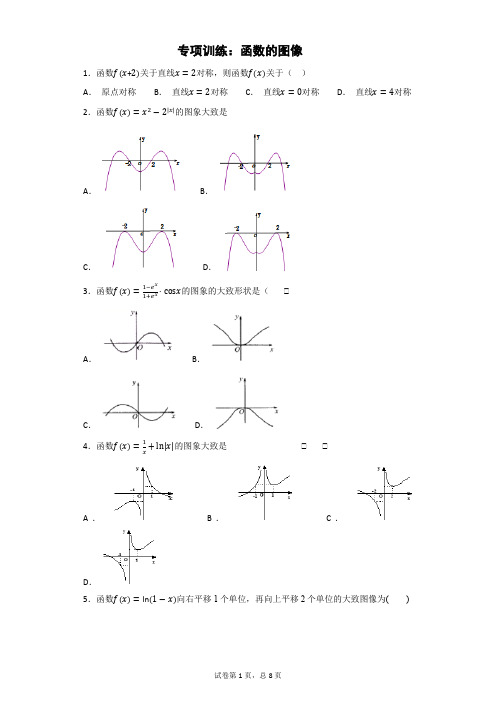
专项训练:函数的图像1.函数关于直线对称,则函数关于()A.原点对称B.直线对称C.直线对称D.直线对称2.函数的图象大致是A.B.C.D.3.函数的图象的大致形状是()A.B.C.D.4.函数的图象大致是()A.B.C.D.5.函数向右平移1个单位,再向上平移2个单位的大致图像为( )A.B.C.D.6.已知某函数图象如图所示,则图象所对应的函数可能是()A.B.C.D.﹣7.函数的图象大致为A.B.C.D.8.为了得到函数y=lg x的图象,只需将函数y=lg(10x)图象上A.所有点沿y轴向上平移10个单位长度B.所有点沿y轴向下平移10个单位长度C.所有点沿y轴向上平移1个单位长度D.所有点沿y轴向下平移1个单位长度9.函数y=的单调减区间和图象的对称中心分别为A.(–∞,0),(0,+∞);(1,1)B.(–∞,–1),(–1,+∞);(1,0)C.(–∞,1),(1,+∞);(1,0)D.(–∞,1),(1,+∞);(1,1)10.设函数在上可导,其导函数为,且函数在处取得极大值,则函数的图象可能是A.B.C.D.11.函数的图象是()A.B.C.D.12.函数的图象大致为()A.B.C.D.13.函数的图象大致是A.B.C.D.14.函数y=的大致图象只能是A.B.C.D.15.若f(x)的图象向左平移一个单位后与y=e x的图象关于y轴对称,则f(x)解析式是A.e x+1B.e x–1C.e–x+1D.e–x–116.函数的图象大致是()A.B.C.D.17.已知某函数图象如图所示,则图象所对应的函数可能是()A.B.C.D.﹣18.函数向右平移1个单位,再向上平移2个单位的大致图像为( )A.B.C.D.19.函数的图象大致为()A.B.C.D.20.若a>1,则函数y=a x与y=(1–a)x2的图象可能是下列四个选项中的A.B.C.D.21.函数与函数的图象如下图,则函数的图象可能是A.B.C.D.22.函数的图象的大致形状是()A.B.C.D.23.某学生离家去学校,一开始跑步前进,跑累了再走余下的路程.下列图中纵轴表示离校的距离,横轴表示出发后的时间,则较符合该学生走法的是( )A.B.C.D.24.直线与在同一直角坐标系中的图象可能是A.B.C.D.25.已知函数f(x)=ax2+bx+c,不等式f(x)<0的解集为,则函数y =f(-x)的图象可以为A.B.C.D.26.函数f(x)=ln(x2+1)的图象大致是( )A.B.C.D.27.设,,函数的定义域为,值域为,则的图象可以是()A.B.C.D.28.函数的图象是().A.B.C.D.29.函数f(x)=1-e|x|的图象大致是( )参考答案1.D【解析】【分析】由题意结合函数图象的变换规律确定函数的对称性即可.【详解】将函数的图象向左平移个单位长度即可得到函数的图象,结合函数关于直线对称,可知函数关于直线对称.本题选择D选项.【点睛】本题主要考查函数的对称性,函数的平移变换等知识,意在考查学生的转化能力和计算求解能力.2.B【解析】【分析】利用特殊值排排除即可【详解】∵函数,()>,故排除C,D,(),()<,故排除A,故选:B.【点睛】本题考了函数的图象的识别,充分利用排除法是解题的关键,属于基础题3.C【解析】【分析】分析函数的奇偶性,代入特殊值计算结果,排除错误答案,可得结论【详解】,函数为奇函数,排除,令,令,则故选:【点睛】本题考查的知识点是函数的图象,由于函数非基本初等函数,故用排除法,是解答的最佳选择,需要判定函数的奇偶性和单调性或者取值,属于基础题4.D【解析】【分析】当x<0时,函数f(x)=,由函数的单调性,排除A、B;当x>0时,函数f(x)=,此时,代入特殊值验证,排除C,只有D正确.【详解】当x<0时,函数f(x)=,由函数y=、y=ln(﹣x)递减知函数f(x)=递减,排除A、B;当x>0时,函数f(x)=,此时,f(1)==1,而选项A的最小值为2,故可排除C,只有D正确,故选:D.【点睛】函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的特征点,排除不合要求的图象.5.C【解析】【分析】根据函数图象的平移规律:在上的变化符合“左加右减”,在上的变化符合“上加下减”.再根据复合函数的单调性即可得出结论.【详解】将函数向右平移1个单位,得到函数为,再向上平移2个单位可得函数为.根据复合函数的单调性可知在上为单调减函数,且恒过点,故C正确.故选:C.【点睛】本题主要考查函数的“平移变换”.解答本题的关键是掌握函数的平移规律“左加右减,上加下减”,属于基础题.6.D【解析】【分析】对给出的四个选项分别进行分析、讨论后可得结果.【详解】对于A,函数,当时,;当时,,所以不满足题意.对于B,当时,单调递增,不满足题意.对于C,当时,,不满足题意.对于D,函数﹣为偶函数,且当时,函数有两个零点,满足题意.故选:D.【点睛】函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的周期性,判断图象的循环往复;(5)从函数的特征点,排除不合要求的图象.7.B【解析】【分析】确定函数是奇函数,利用(),()()>,即可得出结论.【详解】由题意,()()()(),函数是奇函数,(),()()>,故选:B.【点睛】本题考查函数的奇偶性,考查函数的图象,比较基础.8.D【解析】【分析】由于函数y=lg(10x)═lgx+1,把函数y=lg(10x)的图象上所有的点向下平移1个单位长度,可得函数函数y=lgx的图象,由此得出结论.【详解】由于函数y=lg(10x)═lgx+1,把函数y=lg(10x)的图象上所有的点向下平移1个单位长度,可得函数y=lgx的图象.故选:D.【点睛】本题主要考查函数的图象平移变换方法,依据x加减左右平移(左加右减),函数值加减上下平移(加向上、减向下),属于基础题.9.D【解析】【分析】先化简函数y==1+,通过图像的变换求出函数的对称中心和单调减区间.【详解】∵y==1+,x≠1,画出函数的图象如图所示,由图象可知函数的单调减区间是(–∞,1),(1,+∞).∵y=的对称中心为(0,0),∴y==1+的图象时由y=的图象先向右平移一个单位,再向上平移1个单位得到的,故对称中心为(1,1),故选D.【点睛】本题主要考查函数图像的变换,考查函数的图像和性质(单调性和对称中心),意在考查学生对这些知识的掌握水平和分析推理能力.10.D【解析】因为-1为即值点且为极小值点,故在-1的左侧<0,-1的右侧>0,所以当x>0时,排除AD,当x<-1时,故综合得选C11.C【解析】【分析】分和两种情况,将函数化为和两段考虑。
高考专题 《函数图像问题》考题归纳及详解
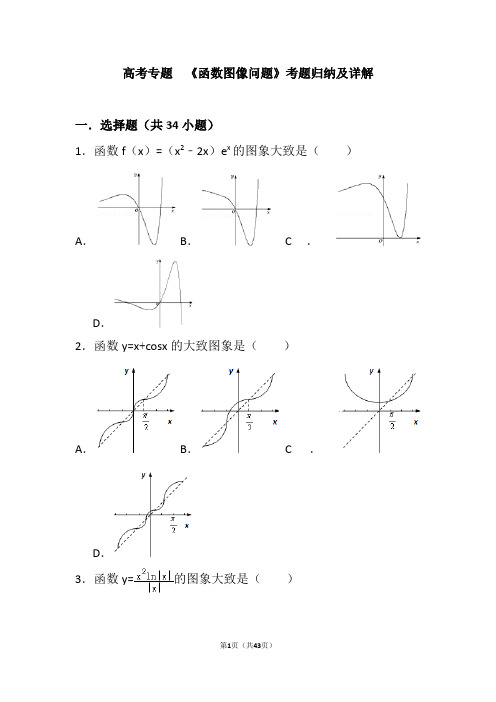
高考专题《函数图像问题》考题归纳及详解一.选择题(共34小题)1.函数f(x)=(x2﹣2x)e x的图象大致是()A. B.C.D.2.函数y=x+cosx的大致图象是()A.B.C.D.3.函数y=的图象大致是()A. B.C.D.4.函数y=xln|x|的大致图象是()A.B.C.D.5.函数f(x)=x2﹣2|x|的图象大致是()A. B.C.D.6.函数f(x)=+ln|x|的图象大致为()A.B.C.D.7.在下列图象中,二次函数y=ax2+bx及指数函数y=()x的图象只可能是()A.B. C.D.8.函数y=xln|x|的图象大致是()A.B.C.D.9.f(x)=的部分图象大致是()A.B.C. D.10.函数的图象大致为()A. B. C. D.11.函数f(x)=(其中e为自然对数的底数)的图象大致为()A. B.C.D.12.函数f(x)=(2x﹣2﹣x)cosx在区间[﹣5,5]上的图象大致为()A. B.C.D.13.函数的部分图象大致为()A.B.C.D.14.函数f(x)=的部分图象大致为()A.B.C.D.15.函数的部分图象大致为()A.B.C.D.16.函数y=x(x2﹣1)的大致图象是()A.B. C. D.17.函数y=x﹣2sinx,x∈[﹣,]的大致图象是()A.B.C.D.18.函数f(x)=的部分图象大致是()A.. B..C..D..19.函数y=﹣2x2+2|x|在[﹣2,2]的图象大致为()A.B.C.D.20.函数的图象大致是()A.B.C.D.21.函数f(x)=(x∈[﹣2,2])的大致图象是()A.B.C.D.22.函数的图象大致是()A.B.C.D.23.函数y=的大致图象是()A.B.C.D.24.函数y=sinx(1+cos2x)在区间[﹣2,2]上的图象大致为()A.B.C.D.25.函数f(x)=(x2﹣3)•ln|x|的大致图象为()A. B. C. D.26.函数f(x)=﹣e﹣ln|x|+x的大致图象为()A.B.C.D.27.函数y=1+x+的部分图象大致为()A.B.C.D.28.函数y=的部分图象大致为()A.B.C.D.29.函数f(x)=x•ln|x|的图象可能是()A.B.C.D.30.函数f(x)=e ln|x|+的大致图象为()A.B.C.D.31.函数y=的一段大致图象是()A. B.C.D.32.函数的图象大致是()A.B.C.D.33.函数的大致图象是()A.B.C.D.34.函数的图象大致为()A.B.C.D.二.解答题(共6小题)35.在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|•|OP|=16,求点P的轨迹C2的直角坐标方程;(2)设点A的极坐标为(2,),点B在曲线C2上,求△OAB 面积的最大值.36.在直角坐标系xOy中,曲线C1的参数方程为(t 为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cosθ.(Ⅰ)说明C1是哪种曲线,并将C1的方程化为极坐标方程;(Ⅱ)直线C3的极坐标方程为θ=α0,其中α0满足tanα0=2,若曲线C1与C2的公共点都在C3上,求a.37.在直角坐标系xOy中,曲线C1的参数方程为(α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+)=2.(1)写出C1的普通方程和C2的直角坐标方程;(2)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P 的直角坐标.38.在直角坐标系xOy中,曲线C的参数方程为,(θ为参数),直线l的参数方程为,(t为参数).(1)若a=﹣1,求C与l的交点坐标;(2)若C上的点到l距离的最大值为,求a.39.在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),曲线C的参数方程为(s为参数).设P为曲线C上的动点,求点P到直线l的距离的最小值.40.在直角坐标系xOy中,直线l1的参数方程为,(t为参数),直线l2的参数方程为,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣=0,M为l3与C的交点,求M的极径.函数图像问题高考试题精选参考答案与试题解析一.选择题(共34小题)1.函数f(x)=(x2﹣2x)e x的图象大致是()A. B.C.D.【解答】解:因为f(0)=(02﹣2×0)e0=0,排除C;因为f'(x)=(x2﹣2)e x,解f'(x)>0,所以或时f(x)单调递增,排除B,D.故选A.2.函数y=x+cosx的大致图象是()A.B.C.D.【解答】解:由于f(x)=x+cosx,∴f(﹣x)=﹣x+cosx,∴f(﹣x)≠f(x),且f(﹣x)≠﹣f(x),故此函数是非奇非偶函数,排除A、C;又当x=时,x+cosx=x,即f(x)的图象与直线y=x的交点中有一个点的横坐标为,排除D.故选:B.3.函数y=的图象大致是()A. B.C.D.【解答】解:当x>0时,y=xlnx,y′=1+lnx,即0<x<时,函数y单调递减,当x>,函数y单调递增,因为函数y为偶函数,故选:D4.函数y=xln|x|的大致图象是()A.B.C.D.【解答】解:令f(x)=xln|x|,易知f(﹣x)=﹣xln|﹣x|=﹣xln|x|=﹣f(x),所以该函数是奇函数,排除选项B;又x>0时,f(x)=xlnx,容易判断,当x→+∞时,xlnx→+∞,排除D选项;令f(x)=0,得xlnx=0,所以x=1,即x>0时,函数图象与x轴只有一个交点,所以C选项满足题意.故选:C.5.函数f(x)=x2﹣2|x|的图象大致是()A. B.C.D.【解答】解:∵函数f(x)=x2﹣2|x|,∴f(3)=9﹣8=1>0,故排除C,D,∵f(0)=﹣1,f()=﹣2=0.25﹣<﹣1,故排除A,故选:B当x>0时,f(x)=x2﹣2x,∴f′(x)=2x﹣2x ln2,故选:B6.函数f(x)=+ln|x|的图象大致为()A.B.C.D.【解答】解:当x<0时,函数f(x)=,由函数y=、y=ln(﹣x)递减知函数f(x)=递减,排除CD;当x>0时,函数f(x)=,此时,f(1)==1,而选项A的最小值为2,故可排除A,只有B正确,故选:B.7.在下列图象中,二次函数y=ax2+bx及指数函数y=()x的图象只可能是()A.B. C.D.【解答】解:根据指数函数y=()x可知a,b同号且不相等则二次函数y=ax2+bx的对称轴<0可排除B与D选项C,a﹣b>0,a<0,∴>1,则指数函数单调递增,故C 不正确故选:A8.函数y=xln|x|的图象大致是()A.B.C.D.【解答】解:∵函数f(x)=xln|x|,可得f(﹣x)=﹣f(x),f(x)是奇函数,其图象关于原点对称,排除A,D,当x→0时,f(x)→0,故排除B又f′(x)=lnx+1,令f′(x)>0得:x>,得出函数f(x)在(,+∞)上是增函数,故选:C.9.f(x)=的部分图象大致是()A.B.C. D.【解答】解:∵f(﹣x)=f(x)∴函数f(x)为奇函数,排除A,∵x∈(0,1)时,x>sinx,x2+x﹣2<0,故f(x)<0,故排除B;当x→+∞时,f(x)→0,故排除C;故选:D10.函数的图象大致为()A. B. C. D.【解答】解:函数是非奇非偶函数,排除A、B,函数的零点是x=e﹣1,当x=e时,f(e)=,排除选项D.故选:C.11.函数f(x)=(其中e为自然对数的底数)的图象大致为()A. B.C.D.【解答】解:f(﹣x)====f(x),∴f(x)是偶函数,故f(x)图形关于y轴对称,排除B,D;又x→0时,e x+1→2,x(e x﹣1)→0,∴→+∞,排除C,故选A.12.函数f(x)=(2x﹣2﹣x)cosx在区间[﹣5,5]上的图象大致为()A. B.C.D.【解答】解:当x∈[0,5]时,f(x)=(2x﹣2﹣x)cosx=0,可得函数的零点为:0,,,排除A,B,当x=π时,f(π)=﹣2π+2﹣π,<0,对应点在x轴下方,排除选项C,故选:D.13.函数的部分图象大致为()A.B.C.D.【解答】解:∵f(﹣x)=﹣f(x),可得f(x)为奇函数,排除B,∵<1,排除A.当x>0时,,,∴在区间(1,+∞)上f (x)单调递增,排除D,故选C.14.函数f(x)=的部分图象大致为()A.B.C.D.【解答】解:函数f(x)==﹣,当x=0时,可得f(0)=0,f(x)图象过原点,排除A.当﹣<x<0时;sin2x<0,而|x+1|>0,f(x)图象在上方,排除C.当x<﹣1,x→﹣1时,sin(﹣2)<0,|x+1|→0,那么f(x)→∞,当x=﹣时,sin2x=﹣,y=﹣=,对应点在第二象限,排除D,B满足题意.故选:B.15.函数的部分图象大致为()A.B.C.D.【解答】解:∵f(﹣x)=﹣f(x),可得f(x)为奇函数,排除B,∵<1,排除A.当x>0时,,,∴在区间(1,+∞)上f (x)单调递增,排除D,故选C.16.函数y=x(x2﹣1)的大致图象是()A.B. C. D.【解答】解:∵函数y=x(x2﹣1),令f(x)=x(x2﹣1),则f(﹣x)=﹣x(x2﹣1)=﹣f(x),故函数f(x)为奇函数,又当0<x<1时,f(x)<0,综上所述,函数y=x(x2﹣1)的大致图象是选项A.故选:A.17.函数y=x﹣2sinx,x∈[﹣,]的大致图象是()A.B.C.D.【解答】解:f(﹣x)=﹣x+2sinx=﹣(x﹣2sinx)=﹣f(x),所以函数为奇函数,故函数的图象关于原点对称,只有CD适合,y′=1﹣2cosx,由y′=0解得x=,∴当x=时,函数取极值,故D适合,故选:D.18.函数f(x)=的部分图象大致是()A.. B..C..D..【解答】解:由x2+|x|﹣2=0,解得x=﹣1或x=1,∴函数的定义域为(﹣∞,﹣1)∪(﹣1,1)∪(1,+∞),∵f(﹣x)==﹣f(x),∴f(x)为奇函数,∴f(x)的图象关于原点对称,故排除A,令f(x)=0,解得x=0,故排除C,当x=时,f()=<0,故排除B,故选:D19.函数y=﹣2x2+2|x|在[﹣2,2]的图象大致为()A.B.C.D.【解答】解:由y=﹣2x2+2|x|知函数为偶函数,即其图象关于y 轴对称,故可排除B,D.又当x=2时,y=﹣2•(﹣2)2+22=﹣4.所以,C是错误的,故选:A.20.函数的图象大致是()A.B.C.D.【解答】解:解:定义域为(﹣∞,0)∪(0,+∞),f(x)=)=﹣,∴f(﹣x)=f(x),f(x)为偶函数,.∴其图象关于y轴对称,可排除A、C,;又当x→0时,cos(πx)→1,x2→0,∴f(x)→﹣∞.故可排除B;而D均满足以上分析.故选:D.21.函数f(x)=(x∈[﹣2,2])的大致图象是()A.B.C.D.【解答】解:函数f(x)=(x∈[﹣2,2])满足f(﹣x)=﹣f(x)是奇函数,排除D,x=1时,f(1)=>0,对应点在第一象限,x=2时,f(2)=<0,对应点在第四象限;所以排除B,C;故选:A.22.函数的图象大致是()A.B.C.D.【解答】解:函数满足f(﹣x)=﹣f(x),故函数图象关于原点对称,排除A、B,当x∈(0,)时,,故排除D,故选:C23.函数y=的大致图象是()A.B.C.D.【解答】解:函数y=的导数为,令y′=0,得x=,时,y′<0,时,y′>0,时,y′<0.∴函数在(﹣),()递减,在()递增.且x=0时,y=0,故选:C24.函数y=sinx(1+cos2x)在区间[﹣2,2]上的图象大致为()A.B.C.D.【解答】解:函数y=sinx(1+cos2x),定义域为[﹣2,2]关于原点对称,且f(﹣x)=sin(﹣x)(1+cosx)=﹣sinx(1+cosx)=﹣f(x),则f(x)为奇函数,图象关于原点对称,排除D;由0<x<1时,y=sinx(1+cos2x)=2sinxcos2x>0,排除C;又2sinxcos2x=0,可得x=±(0<x≤2),则排除A,B正确.故选B.25.函数f(x)=(x2﹣3)•ln|x|的大致图象为()A. B. C. D.【解答】解:函数f(x)=(x2﹣3)•ln|x|是偶函数;排除选项A,D;当x→0时,f(x)→+∞,排除选项B,故选:C.26.函数f(x)=﹣e﹣ln|x|+x的大致图象为()A.B.C.D.【解答】解:函数f(x)=﹣e﹣ln|x|+x是非奇非偶函数,排除A,D;当x>0时,f(x)=﹣e﹣lnx+x=x﹣,函数是增函数,排除C;故选:B.27.函数y=1+x+的部分图象大致为()A.B.C.D.【解答】解:函数y=1+x+,可知:f(x)=x+是奇函数,所以函数的图象关于原点对称,则函数y=1+x+的图象关于(0,1)对称,当x→0+,f(x)>0,排除A、C,点x=π时,y=1+π,排除B.故选:D.28.函数y=的部分图象大致为()A.B.C.D.【解答】解:函数y=,可知函数是奇函数,排除选项B,当x=时,f()==,排除A,x=π时,f(π)=0,排除D.故选:C.29.函数f(x)=x•ln|x|的图象可能是()A.B.C.D.【解答】解:函数f(x)=x•ln|x|是奇函数,排除选项A,C;当x=时,y=,对应点在x轴下方,排除B;故选:D.30.函数f(x)=e ln|x|+的大致图象为()A.B.C.D.【解答】解:∵f(x)=e ln|x|+∴f(﹣x)=e ln|x|﹣f(﹣x)与f(x)即不恒等,也不恒反,故函数f(x)为非奇非偶函数,其图象不关于原点对称,也不关于y轴对称,可排除A,D,当x→0+时,y→+∞,故排除B故选:C.31.函数y=的一段大致图象是()A. B.C.D.【解答】解:f(﹣x)=﹣=﹣f(x),∴y=f(x)为奇函数,∴图象关于原点对称,∴当x=π时,y=﹣<0,故选:A.32.函数的图象大致是()A.B.C.D.【解答】解:由题意,函数在(﹣1,1)上单调递减,在(﹣∞,﹣1),(1,+∞)上单调递减,故选A.33.函数的大致图象是()A.B.C.D.【解答】解:f(﹣x)===﹣f(x),∴f(x)是奇函数,图象关于原点对称,故A,C错误;又当x>1时,ln|x|=lnx>0,∴f(x)>0,故D错误,故选B.34.函数的图象大致为()A.B.C.D.【解答】解:f(﹣x)==﹣=﹣f(x),∴函数f(x)为奇函数,则图象关于原点对称,故排A,B,当x=时,f()==故选:D二.解答题(共6小题)35.在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|•|OP|=16,求点P的轨迹C2的直角坐标方程;(2)设点A的极坐标为(2,),点B在曲线C2上,求△OAB 面积的最大值.【解答】解:(1)曲线C1的直角坐标方程为:x=4,设P(x,y),M(4,y0),则,∴y0=,∵|OM||OP|=16,∴=16,即(x2+y2)(1+)=16,∴x4+2x2y2+y4=16x2,即(x2+y2)2=16x2,两边开方得:x2+y2=4x,整理得:(x﹣2)2+y2=4(x≠0),∴点P的轨迹C2的直角坐标方程:(x﹣2)2+y2=4(x≠0).(2)点A的直角坐标为A(1,),显然点A在曲线C2上,|OA|=2,∴曲线C2的圆心(2,0)到弦OA的距离d==,∴△AOB的最大面积S=|OA|•(2+)=2+.36.在直角坐标系xOy中,曲线C1的参数方程为(t 为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cosθ.(Ⅰ)说明C1是哪种曲线,并将C1的方程化为极坐标方程;(Ⅱ)直线C3的极坐标方程为θ=α0,其中α0满足tanα0=2,若曲线C1与C2的公共点都在C3上,求a.【解答】解:(Ⅰ)由,得,两式平方相加得,x2+(y﹣1)2=a2.∴C1为以(0,1)为圆心,以a为半径的圆.化为一般式:x2+y2﹣2y+1﹣a2=0.①由x2+y2=ρ2,y=ρsinθ,得ρ2﹣2ρsinθ+1﹣a2=0;(Ⅱ)C2:ρ=4cosθ,两边同时乘ρ得ρ2=4ρcosθ,∴x2+y2=4x,②即(x﹣2)2+y2=4.由C3:θ=α0,其中α0满足tanα0=2,得y=2x,∵曲线C1与C2的公共点都在C3上,∴y=2x为圆C1与C2的公共弦所在直线方程,①﹣②得:4x﹣2y+1﹣a2=0,即为C3 ,∴1﹣a2=0,∴a=1(a>0).37.在直角坐标系xOy中,曲线C1的参数方程为(α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+)=2.(1)写出C1的普通方程和C2的直角坐标方程;(2)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P 的直角坐标.【解答】解:(1)曲线C1的参数方程为(α为参数),移项后两边平方可得+y2=cos2α+sin2α=1,即有椭圆C1:+y2=1;曲线C2的极坐标方程为ρsin(θ+)=2,即有ρ(sinθ+cosθ)=2,由x=ρcosθ,y=ρsinθ,可得x+y﹣4=0,即有C2的直角坐标方程为直线x+y﹣4=0;(2)由题意可得当直线x+y﹣4=0的平行线与椭圆相切时,|PQ|取得最值.设与直线x+y﹣4=0平行的直线方程为x+y+t=0,联立可得4x2+6tx+3t2﹣3=0,由直线与椭圆相切,可得△=36t2﹣16(3t2﹣3)=0,解得t=±2,显然t=﹣2时,|PQ|取得最小值,即有|PQ|==,此时4x2﹣12x+9=0,解得x=,即为P(,).另解:设P(cosα,sinα),由P到直线的距离为d==,当sin(α+)=1时,|PQ|的最小值为,此时可取α=,即有P(,).38.在直角坐标系xOy中,曲线C的参数方程为,(θ为参数),直线l的参数方程为,(t为参数).(1)若a=﹣1,求C与l的交点坐标;(2)若C上的点到l距离的最大值为,求a.【解答】解:(1)曲线C的参数方程为(θ为参数),化为标准方程是:+y2=1;a=﹣1时,直线l的参数方程化为一般方程是:x+4y﹣3=0;联立方程,解得或,所以椭圆C和直线l的交点为(3,0)和(﹣,).(2)l的参数方程(t为参数)化为一般方程是:x+4y﹣a ﹣4=0,椭圆C上的任一点P可以表示成P(3cosθ,sinθ),θ∈[0,2π),所以点P到直线l的距离d为:d==,φ满足tanφ=,且的d 的最大值为.①当﹣a﹣4≤0时,即a≥﹣4时,|5sin(θ+4)﹣a﹣4|≤|﹣5﹣a﹣4|=5+a+4=17解得a=8≥﹣4,符合题意.②当﹣a﹣4>0时,即a<﹣4时|5sin(θ+4)﹣a﹣4|≤|5﹣a﹣4|=5﹣a﹣4=1﹣a=17解得a=﹣16<﹣4,符合题意.39.在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),曲线C的参数方程为(s为参数).设P为曲线C上的动点,求点P到直线l的距离的最小值.【解答】解:直线l的直角坐标方程为x﹣2y+8=0,∴P到直线l的距离d==,∴当s=时,d取得最小值=.40.在直角坐标系xOy中,直线l1的参数方程为,(t为参数),直线l2的参数方程为,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣=0,M为l3与C的交点,求M的极径.【解答】解:(1)∵直线l1的参数方程为,(t为参数),∴消掉参数t得:直线l1的普通方程为:y=k(x﹣2)①;又直线l2的参数方程为,(m为参数),同理可得,直线l2的普通方程为:x=﹣2+ky②;联立①②,消去k得:x2﹣y2=4,即C的普通方程为x2﹣y2=4;(2)∵l3的极坐标方程为ρ(cosθ+sinθ)﹣=0,∴其普通方程为:x+y﹣=0,联立得:,∴ρ2=x2+y2=+=5.∴l3与C的交点M的极径为ρ=.。
函数的求导及函数图像的综合应用(含答案)

1.已知函数x x a x f ln )21()(2+-=.(R a ∈)(Ⅰ)当1=a 时,求)(x f 在区间[1,e ]上的最大值和最小值;(Ⅱ)若在区间(1,+∞)上,函数)(x f 的图象恒在直线ax y 2=下方,求a 的取值范围.解析:(Ⅰ)当1=a 时,x x x f ln 21)(2+=,xx xx x f 11)(2+=+=';………………2分对于∈x [1,e ],有0)(>'x f ,∴)(x f 在区间[1,e ]上为增函数,…………3分∴21)()(2max ee f x f +==,21)1()(min ==f x f .……………………………4分(Ⅱ)令x ax x a ax x f x g ln 2)21(2)()(2+--=-=,则)(x g 的定义域为(0,+∞).……………………………………………5分在区间(1,+∞)上,函数)(x f 的图象恒在直线ax y 2=下方等价于0)(<x g 在区间(1,+∞)上恒成立.∵xx a x xax x a xa x a x g ]1)12)[(1(12)12(12)12()(2---=+--=+--='① 若21>a ,令0)(='x g ,得极值点11=x ,1212-=a x ,………………6分当112=>x x ,即121<<a 时,在(2x ,+∞)上有0)(>'x g ,此时)(x g 在区间(2x ,+∞)上是增函数,并且在该区间上有)(x g ∈()(2x g ,+∞),不合题意;………………………………………7分当112=<x x ,即1≥a 时,同理可知,)(x g 在区间(1,+∞)上,有)(x g ∈()1(g ,+∞),也不合题意;………………………………………9分② 若21≤a ,则有012≤-a ,此时在区间(1,+∞)上恒有0)(<'x g ,从而)(x g 在区间(1,+∞)上是减函数;……………………………………11分 要使0)(<x g 在此区间上恒成立,只须满足021)1(≤--=a g 21-≥⇒a ,由此求得a 的范围是[21-,21].综合①②可知,当a ∈[21-,21]时,函数)(x f 的图象恒在直线ax y 2=下方.……12分2.已知函数()∈--=b a bx ax x x f ,(ln 2R ,且)0≠a .(1)当2=b 时,若函数()x f 存在单调递减区间,求a 的取值范围; (2)当0>a 且12=+b a 时,讨论函数()x f 的零点个数.解:(1)当2=b 时,函数()x f x ax x 2ln 2--=,其定义域是()∞+,0,∴()xx axax xx f1222212'-+-=--=.函数()x f 存在单调递减区间,∴()xx axx f1222'-+-=0≤在()∞+∈,0x 上有无穷多个解.∴关于x 的不等式01222≥-+x ax 在()∞+∈,0x 上有无穷多个解. ① 当0>a 时,函数1222-+=x ax y 的图象为开口向上的抛物线, 关于x 的不等式01222≥-+x ax 在()∞+∈,0x 上总有无穷多个解. ② 当0<a 时,函数1222-+=x ax y 的图象为开口向下的抛物线,其对称轴为01>-=a x .要使关于x 的不等式01222≥-+x ax 在()∞+∈,0x 上有无穷多个解. 必须480a ∆=+>,解得12a >-,此时102a -<<.综上所述,a 的取值范围为()1(,0)0,2-+∞ .另解:分离系数:不等式01222≥-+x ax 在()∞+∈,0x 上有无穷多个解, 则关于x 的不等式221212(1)1x a xx-≥=--在()∞+∈,0x 上有无穷多个解,∴21a >-,即12a >-,而0a ≠.∴a 的取值范围为()1(,0)0,2-+∞ .(2)当12b a =-时,函数()x f ()2ln 12x ax a x =---,其定义域是()∞+,0,∴()()2'12(12)1212ax a x fx ax a xx+--=---=-.令()0'=x f,得22(12)10ax a x x+--=,即22(12)10ax a x +--=,(1)(21)0x ax -+=, 0x > ,0a >,则210ax +>,∴1x = 当<<x 01时,()0'>x f;当>x 1时,()0'<x f.∴函数()x f 在区间()0,1上单调递增,在区间()1,+∞上单调递减. ∴当1x =时,函数()x f 取得最大值,其值为()1ln 1121f a b a a a =--=--+=-. ① 当1a =时,()10f =,若1≠x , 则()()1f x f <, 即()0<x f .此时,函数()x f 与x 轴只有一个交点,故函数()x f 只有一个零点; ② 当1a >时,()10f >,又()011112111ln 122<-⎪⎭⎫⎝⎛--=⨯--⎪⎭⎫ ⎝⎛⋅-=⎪⎭⎫ ⎝⎛a a a a a a e e a e a e a e e f ,()()()02121ln 2<---=---=e e ae e a aee ef ,函数()x f 与x 轴有两个交点,故函数()x f 有两个零点;③ 当01a <<时,()10f <,函数()x f 与x 轴没有交点,故函数()x f 没有零点. 3.已知函数.)(,ln )(x x g x x f ==(Ⅰ)若1>x ,求证:)11(2)(+->x x g x f ;(Ⅱ)是否存在实数k ,使方程k x f x g =+-)1()(2122有四个不同的实根?若存在,求出k 的取值范围;若不存在,说明理由.解:(I )令,1)1(2ln )11(2)()(+--=+--=x x x x x g x f x F则222)1()1()1()1(2)1(21)(+-=+--+-='x x x x x x xx F , ------4分因.0)(,1>'∴>x F x 故函数),1()(+∞在x F 上是增函数.又1)(=x x F 在处连续,所以,函数),1[)(+∞在x F 上是增函数.1>∴x 时,).11(2)(.0)1()(+->=>x x g x f F x F 即 ------7分(Ⅱ)令=+-=+-='=+-=+-=2322222112)(,).1ln(21)1()(21)(xx x xx x x h k y x x x f x g x h 由.1,1,0,0)(,1)1)(1(2-=='+-+x x h xx x x 则令 ------9分当x 变化时,)(x h '、)(x h 的变化关系如下表:据此可画出)(x h 的简图如下, ------12分 故存在)0,2ln 21(-∈k ,使原方程有4个不同实根. ------14分4.已知函数()()()⎪⎩⎪⎨⎧>-≤+=.01,03123x e x mx x x f x(1)当0≤x 时,函数()x f 在()()1,1--f 处的切线方程为013=+-y x ,求m 的值;(2)当0>x 时,设()1+x f 的反函数为()x g 1-(()x g 1-的定义域即是()1+x f 的值域).证明:函数()()x gx x h 131--=在区间()3,e 内无零点,在区间()2,3e 内有且只有一个零点;(3)求函数()x f 的极值.(本小题主要考察分段函数、函数与方程、函数导数、函数的极值、函数图象的切线等知识,考查化归与转化、分类与整合、函数与方程的数学思方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识) 解:(1)当0≤x 时,()2331mx x x f +=,()311-=-m f , ……1分()mx x x f 22+=',()m f 211-=-',……2分函数()x f 在()()1,1--f 处的切线方程为:()()12131+-=⎪⎭⎫⎝⎛--x m m y , ……3分 整理得:()032363=-+--m y x m ,所以有⎩⎨⎧=-=-132163m m ,解得.31=m ……4分(2) 当0>x 时,()x e x f =+1, 所以()()1ln 1>=-x x x g ,……5分()()x g x x h 131--==()1ln 31>-x x x ,()xx xx h 33131-=-=',令0)(>'x h 得3>x ;令0)(<'x h 得31<<x ,令0)(='x h 得3=x ,故知函数)(x h 在区间)3,1(上为减函数,在区间),3(+∞为增函数,在3=x 处取得极小值, 进而可知()x h 在()3,e 上为减函数,在()2,3e 上为增函数,在3=x 处取得极小值.……6分 又 ()023)(,03ln 13,013)(22>-=<-=<-=ee h h e e h .……7分所以,函数()()x gx x h 131--=在区间()3,e 内无零点,在区间()2,3e 有且只有一个零点.……8分(3)当0>x 时,()1-=x e x f 在()+∞,0上单调递增,且()1-=x e x f >0. ……9分 当0≤x 时,()()m x x mx x x f 222+=+='. ①若(),0,02≥='=x x f m 则()331x x f =在(]0,∞-上单调递增,且()0313<=x x f .又()00=f ,()x f ∴在R 上是增函数,无极值. ……10分 ②若0<m ,()()0222>+=+='m x x mx x x f ,则()2331mx x x f +=在(]0,∞-上单调递增.同理,()x f 在R 上是增函数,无极值. ……11分③若0>m ,()(),222m x x mx x x f +=+='令()0='x f ,得0,221=-=x m x .当m x 2-<时, ()0>'x f 当02<<-x m 时, ()0<'x f 所以,()2331mx x x f +=在(]m 2,-∞-上单调递增,在(]0,2m -上单调递减.又()x f 在()+∞,0上单调递增,故()[](),00==f x f 极小()[]()3342m m f x f =-=极大.……13分综上, 当0>m 时,()[](),00==f x f 极小()[]234m x f =极大.当0≤m 时, ()x f 无极值. ……14分5. 如图是函数y =f (x )的导函数y =f ′(x )的图象,则下面判断正确的是A.在区间(-2,1)内f (x )是增函数B.在(1,3)内f (x )是减函数C.在(4,5)内f (x )是增函数D.在x =2时,f (x )取到极小值 分析:本题主要考查函数的单调性、极值、最值与导函数的关系.解:在(-2,1)上,导函数的符号有正有负,所以函数f (x )在这个区间上不是单调函数;同理,函数在(1,3)上也不是单调函数.在x =2的左侧,函数在(-23,2)上是增函数,在x =2的右侧,函数在(2,4)上是减函数,所以在x =2时,f (x )取到极大值;在(4,5)上导数的符号为正,所以函数在这个区间上为增函数.答案:C6.函数a ax x y +-=23在)1,0(内有极小值,则实数a 的取值范围为( ) A.(0,3) B. )3,(-∞ C. ),0(+∞ D. )23,0(解析: 32,023)('2a x a x x f ±==-=,由题意知只要230,1320<<<<a a 即选D7.(1992全国卷)等差数列{}n a 中,312a =,12130,0S S ><。
1 代数小题之函数的图像与性质综合答案详解
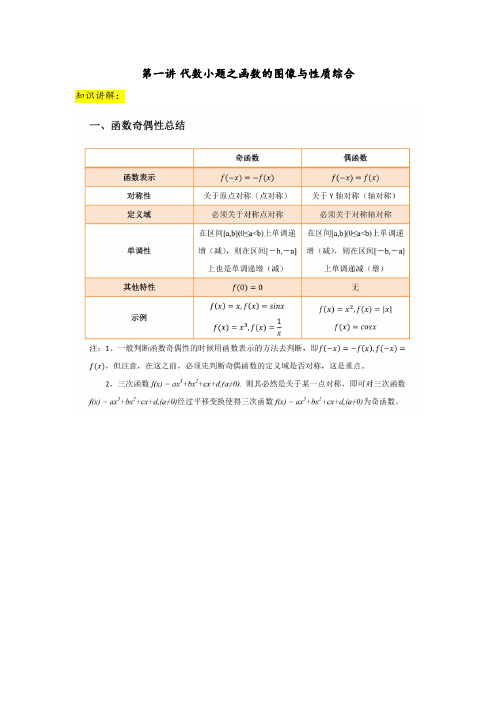
第一讲代数小题之函数的图像与性质综合知识讲解:【例题1】答案:D思路:根据奇函数,画出函数图像,结合图像分析不等式大于等于0的条件解析:f(x)是奇函数,所以f(x)在(-∞,0)上单调减,在(0,+∞)上单调递减,且f(2)=f(-2)=0,由xf(x-1)>=0可得,x>0时,f(x-1)>=0,因为f(2)=0,由单调性可得0<=x-1<=2,所以1<=x<=3,当x<=0时,f(x-1)<=0,由f(-2)=0结合单调性,可得-2<=x-1<=0,所以-1<=x<=0,综上,答案为D总结:利用奇函数分析对称区域得单调性,再通过对变量的分类讨论去解不等式【例题2】思路:由偶函数判断f(x)的对称性,由图像平移、f(x+1)的单调性、f(x)的对称性判断出f(x)的单调性,结合条件画出f(x)的图像,根据图像求出不等式的解集解析:因为f(x+1)是偶函数,所以f(x+1)=f(-x+1),所以f(x)的图像关于直线x=1对称,f(x+1)在(-∞,0)上减,所以f(x)在(-∞,1)上减,在(1,+∞)上增,且f(2)=f(0)=0,画出函数图像,当x>1时,f(x)<=0,1<x<=2,当x<1时,f(x)>=0,x<=0,但是由于f(x+1)的定义域为(-∞,0)U(0,+∞),所以x不能取1,综上,解集为(-∞,0)U(1,2] 总结:利用偶函数结合平移的特性分析原来函数的图像,再根据原函数的图像去解不等式【例题3】答案:A思路:首先分析函数的对称性,再求出函数的就行,将不等式转换为自变量的不等式进行求解解析:f(x)的定义域为(-1,1),f(-x)+f(x)=0,所以f(x)是奇函数,又因为f(x)=ln(-1-2/(x-1))+sinx在(-1,1)是单调增的,所以f(a-2)+f(a^2-4)<0可以转换为-1<a-2<1,-1<a^2-4<1,a^2-4<2-a,解得√3<a<2,选A总结:本题主要考察函数的概念与性质,对数与对数函数,三角函数以及解不等式。
函数的图像和性质及综合问题的解题技巧

函数的图像和性质及综合问题的解题技巧一、函数的图象与性质函数的图象与性质是高考考查的重点内容之一,函数的图像是研究和记忆函数性质的直观工具,利用它的直观性解题,可以起到化繁为简、化难为易的作用.因此,大家要掌握绘制函数图象的一般方法,掌握函数图象变化的一般规律,能利用函数的图象研究函数的性质.此类题目还很好的考查了数形结合的解题思想.1.作出下列函数的图象(1)y=|x-2|(x +1);(2)y=10|lgx|. 2.函数y=1+a x (0<a<1)的反函数的图象大致是 ( )(A ) (B ) (C ) (D ) 3.函数)1a ,0a ( 1ay 2-x ≠>+= 的图象必经过点( )A 、(0,1)B 、(1,1)C 、(2,0)D 、(2,2) 4.已知0<a<1,b<-1,函数f(x)=a x+b 的图象不经过( )A.第一象限;B.第二象限;C.第三象限;D.第四象限5.设函数y=f(x)的定义域为R,则函数y=f(x-1)与y=(1-x)的图象关系为( ) A、直线y=0对称B、直线x=0对称C、直线y=1对称D、直线x=1对称6.知直线1=x 是函数)2(x f y =的图象的一条对称轴,那么)23(x f y -=的图象关于 ( ) A 、直线21=x 对称 B 、直线21-=x 对称 C 、直线23=x 对称 D 、直线23-=x 对称 7.在下列给出的四个命题中:①y=f(x+2)与y=f(2-x)的图象关于直线x=2对称 ②若f(x+2)=f(2-x),则f(x)的图象关于直线x=2对称 ③y=f(x -2)与y=f(2-x)的图象关于y 轴对称 ④若f(x -2)=f(2-x),则f(x)的图象关于y 轴对称 其中正确命题的个数有( )A 、1个B 、2个C 、3个D 、4个 8.方程f (x ,y)=0的曲线如图所示,那么方程f (2-x ,y)=0的曲线是 ( )9.已知f(x)是奇函数,当x∈(0,1)时,f(x)=lg11x+,那么当x∈(-1,0)时,f(x)的表达式是_____.10.已知f(x+199)=4x2+4x+3(x∈R),那么函数f(x)的最小值为__ __.11.方程2x=2-x的解的个数为_____二、函数综合问题函数综合问题是历年高考的热点和重点内容之一,一般难度较大,考查内容和形式灵活多样. 这里主要帮助大家在掌握有关函数知识的基础上进一步深化综合运用知识的能力,掌握基本解题技巧和方法,并培养大家的思维和创新能力.1.设函数,x,1x,1)x(f⎩⎨⎧<>-=则)ba(2)ba(f)ba()ba(≠-⋅--+的值为 ( )A. aB. bC. a, b中较小的数D. a, b中较大的数2.定义运算a⊗b=⎩⎨⎧>≤b)(abb)(aa,则函数f(x)=1⊗2x的图象是()3.已知函数f(x),x∈F,那么集合{(x,y)|y=f(x),x∈F}∩{(x,y)|x=1}中所含元素的个数是.()A.0 B.1 C.0或1 D.1或24.方程lgx+x=3的解所在区间为()A.(0,1) B.(1,2)C.(2,3) D.(3,+∞)5.实数,x y满足xx yy=-,则x的取值范围是__________.6.已知方程22320x ax a-++=的两根都大于5,则实数a的取值范围7.关于x的方程9x+(a+4)·3x+4=0有解,则实数a的取值范围是()A.(-∞,-8]∪[0,+∞)B、(-∞,-4)[-8,4)D、(-∞,-8]8.方程2lg2lg20x a x a-+-=的两根均大于1,则实数a的取值范围9.已知函数()()()2212f x x a x a=+-+-的零点一个比1大,另一个零点比1小,则实数a取值范围10.若函数()23f x x mx m=+++至多有一个零点,则实数m的取值范围()2f x ≥11.(1)一次函数f(x)=kx+h(k ≠0),若m <n 有f(m)>0,f(n)>0,则对于任意x ∈(m ,n)都有f(x)>0,试证明之;(2)试用上面结论证明下面的命题:若a ,b ,c ∈R 且|a|<1,|b|<1,|c|<1,则ab+bc+ca >-1. (3)试用上面结论解决下面的问题:若()2140a x ax -++>在[]0,2a ∈上恒成立,求x 的取值范围.12.定义在R 上的单调函数f(x)满足f(3)=log 23且对任意x ,y ∈R 都有f(x+y)=f(x)+f(y).(1)求证f(x)为奇函数;(2)若f(k ·3x)+f(3x-9x-2)<0对任意x ∈R 恒成立,求实数k 的取值范围. 13. 已知函数2()3f x x ax a =++-,(1)在R 上()0f x ≥恒成立,求a 的取值范围;(2)若[]2,2x ∈-时,()0f x ≥恒成立,求a 的取值范围; (3)若[]2,2x ∈-时,恒成立,求a 的取值范围;(4) 若[]2,2x ∈-时,()0f x ≤恒成立,求a 的取值范围.14.设不等式2x -1>m(x 2-1)对满足|m|≤2的一切实数m 的取值都成立,求x 的取值范围.15. 设f(x)=lg 1243++x x a,如果当x ∈(-∞,1]时f(x)有意义,求实数a 的取值范围.16.设函数f (x )=x 2+|x -2|-1,x ∈R . (1)判断函数f (x )的奇偶性; (2)求函数f (x )的最小值.17.已知二次函数)(x f 的二次项系数为a ,且不等式x x f 2)(->的解集为(1,3) (1)若方程06)(=+a x f 有两个相等的根,求)(x f 的解析式; (2)若)(x f 的最大值为正数,求a 的取值范围.18.定义在R 上的函数f (X )满足:如果则任意X 1,X 2∈R ,都有f (221x x +)≤21[f (X )()21x f +),则称函数f (X )是R 上的凹函数.已知二次函数f (X )= a X 2+X (a ∈R, a ≠0). (1)求证:当a >0时,函数f (X )是凹函数.(2)如果X ∈[0,1]时,|f (X )|≤1,试求实数a 的范围.19.若定义在区间D 上的函数f (x )对于D 上的任意n 个值x 1,x 2,…,x n 总满足,n x f x f x f n )()()(21+++ ≤f (nx x x x n ++++ 321)则称f (x )为D 上的凸函数,(1)f (x )=cosx 在(0,2π)上是凸函数,则在锐角△ABC 中,cosA+cosB+cosC 的最大值是 . (2)函数y =sinx 在区间(0,π)上是凸函数,则在△ABC 中,sinA +sin B+sin C的最大值为 _.。
一次函数图像与面积综合题

中考专题复习:一次函数综合题(与面积有关)1.如图所示,在平面直角坐标系中,过点A(﹣,0)的两条直线分别交y轴于B,C两点,∠ABO=30°,OB=3OC.(1)证明:AC⊥AB;(2)将△ABC沿直线AB翻折得到△ABD,求直线BD的函数解析式;(3)在(2)的条件下,设直线BD交x轴于点E,嘉淇认为△ADE的面积与△AOB的面积相同,请判断嘉淇的观点是否正确.2.如图,直线l与x轴、y轴分别交于点A(3,0)、点B(0,2),以线段AB为直角边在第一象限内作等腰直角三角形ABC,∠BAC=90°,点P(1,a)为坐标系中的一个动点.(1)请直接写出直线l的表达式;(2)求出△ABC的面积;(3)当△ABC与△ABP面积相等时,求实数a的值.3.如图,四边形OABC是矩形,点A、C在坐标轴上,△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC、OC 的长是方程x2﹣6x+8=0的两个根,且OC>BC.(1)求直线BD的解析式;(2)求△OFH的面积;(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.4.一次函数y=kx+b的图象与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且sin∠ABO=.△OAB的外接圆的圆心M的横坐标为﹣3.(1)求一次函数的解析式;(2)求图中阴影部分的面积.5.如图1,在平面直角坐标系中,点O是坐标原点,直线y=2x+6交x轴于点B,交y轴于点A,且AO=BC.(1)求直线AC的解析式;(2)如图2,点P在线段AC上,连接PB交OA于点D,设点P的横坐标为t,△ABP 的面积为S,求S与t之间的函数解析式;(3)如图3,在(2)的条件下,过点A作∠CAO的平分线交DP于点E,点L在BP的延长线上,连接CE、CL,若∠ABP=2∠ACE,CL=AC,求DL的长.6.如图1,在平面直角坐标系中,点O为坐标原点,直线y=kx+4交x轴、y轴分别于点A、点B,且△ABO的面积为8.(1)如图2,求k的值;(2)如图3,点P是第一象限直线AB上的一个动点,连接PO,将线段OP绕点O顺时针旋转90°至线段OC,设点P的横坐标为t,点C的横坐标为m,求m与t之间的函数关系式(不要求写出自变量t的取值范围);(3)在(2)的条件下,过点B作直线BM⊥OP,交x轴于点M,垂足为点N,点K在线段MB的延长线上,连接PK,且PK+KB=OP,∠PMB=2∠KPB,连接MC,求四边形BOCM的面积.7.如图,直线y=kx+b与x轴,y轴分别交于点A,点B,点A的坐标为(﹣2,0),且2OA =OB.(1)求直线AB解析式;(2)如图,将△AOB向右平移6个单位长度,得到△A1O1B1,求线段OB1的长;(3)求(2)中△AOB扫过的面积.8.如图:一次函数y=﹣x+3的图象与坐标轴交于A、B两点,点P是函数y=﹣x+3(0<x<4)图象上任意一点,过点P作PM⊥y轴于点M,连接OP.(1)当AP为何值时,△OPM的面积最大?并求出最大值;(2)当△BOP为等腰三角形时,试确定点P的坐标.9.如图,直角坐标系xOy中,A(0,5),直线x=﹣5与x轴交于点D,直线y=﹣x﹣与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.(1)求点C,E的坐标及直线AB的解析式;(2)设面积的和S=S△CDE+S四边形ABDO,求S的值;(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积不更快捷吗?”但大家经反复演算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.10.如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x﹣15|+=0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=(1)求点B的坐标;(2)求直线BN的解析式;(3)将直线BN以每秒1个单位长度的速度沿y轴向下平移,求直线BN扫过矩形AOCB 的面积S关于运动的时间t(0<t≤13)的函数关系式.11.直线y=x﹣6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF ∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.(1)画出当t=2时,四边形ABEF沿直线EF折叠后的四边形CDEF(不写画法);(2)在点E运动过程中,CD交x轴于点G,交y轴于点H,试探究t为何值时,△CGF 的面积为;(3)设四边形CDEF落在第一象限内的图形面积为S,求S关于t的函数解析式,并求出S的最大值.12.如图,直线与x轴,y轴分别交于点A(6,0),B.点C(0,t)是线段OB 上一点,作直线AC.(1)若BC=2,求直线AC的函数解析式;(2)当1≤t≤4时,求△ABC面积的取值范围;(3)若AC平分∠OAB,记△ABC的周长为m,△AOC的周长为n,求m﹣n的值.13.如图,在平面直角坐标系中,Rt△AOC的直角边OA在y轴正半轴上,且顶点O与坐标原点重合,点C的坐标为(1,2),直线y=﹣x+b过点C,与x轴交于点B,与y轴交于点D.(1)B点的坐标为,D点的坐标为;(2)动点P从点O出发,以每秒1个单位长度的速度,沿O→A→C的路线向点C运动,同时动点Q从点B出发,以相同速度沿BO的方向向点O运动,过点Q作QH⊥x 轴,交线段BC或线段CO于点H.当点P到达点C时,点P和点Q都停止运动,在运动过程中,设动点P运动的时间为t秒:①设△CPH的面积为S,求S关于t的函数关系式;②是否存在以Q、P、H为顶点的三角形的面积与S相等?若存在,直接写出t的值;若不存在,请说明理由.14.阅读下列两则材料,回答问题:材料一:定义直线y=kx+b(kb≠0)与直线y=bx+k(kb≠0)互为“对称直线”.例如,直线y=x+2与直线y=2x+1互为“对称直线”;直线y=kx+b中,k称为斜率,若A(x1,y1),B(x2,y2)为直线y=kx+b上任意两点(x1≠x2),则斜率k=材料二:对于平面直角坐标系中的任意两点(x1,y1),B(x2,y2),定义一种新的运算:L(A,B)=x1x2+y1y2,例如:A(﹣3,1)、B(2,4),(A,B)=﹣3×2+1×4=﹣2(1)若点A(﹣3,1)、B(2,4)在直线y=kx+b上,则k=;直线y=2x+3上的一点P(x,y)又是它的“对称直线”上的点,求点P的坐标.(2)对于直线y=kx+b上的任意一点M(m,n),都有点N(2m,6n﹣34)在y=kx+b 的“对称直线”上:横坐标互不相同的三个点C,D,E满足L(C,D)=L(D,E),且D点的坐标为(2,2),过点D作DF∥y轴,交直线CE于点F,若DF=6,请求出直线CE、直线y=kx+b与x轴围成的三角形的面积.15.问题探究(1)如图①,在Rt△ABC中,∠B=90°,请你过点A作一条直线AD,其中点D为BC 上一点,使直线AD平分△ABC的面积;(2)如图②,点P为▱ABCD外一点,AB=6,BC=12,∠B=45°,请过点P作一条直线l,使其平分▱ABCD的面积,并求出▱ABCD的面积;问题解决(3)如图③,在平面直角坐标系中,四边形OABC是李爷爷家一块土地的示意图,其中OA∥BC,点P处有一个休息站点(占地面积忽略不计),李爷爷打算过点P修一条笔直的小路l(路的宽度不计),使直线l将四边形OABC分成面积相等的两部分,分别用来种植不同的农作物.已知点A(8,8)、B(6,12)、P(3,6).你认为直线1是否存在?若存在,求出直线l的表达式;若不存在,请说明理由.16.在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且OB =OA,直线l2:y=k2x+b经过点C(,1),与x轴、y轴、直线AB分别交于点E、F、D三点.(1)求直线l1的解析式;(2)如图1,连接CB,当CD⊥AB时,求点D的坐标和△BCD的面积;(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD 为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.17.如图,在平面直角坐标系中,一次函数y=﹣x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒.(1)当t=秒时,点Q的坐标是;(2)在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;(3)若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.18.如图,已知△ABC的顶点坐标分别为A(3,0),B(0,4),C(﹣3,0).动点M,N 同时从A点出发,M沿A→C,N沿折线A→B→C,均以每秒1个单位长度的速度移动,当一个动点到达终点C时,另一个动点也随之停止移动,移动的时间记为t秒.连接MN.(1)求直线BC的解析式;(2)移动过程中,将△AMN沿直线MN翻折,点A恰好落在BC边上点D处,求此时t 值及点D的坐标;(3)当点M,N移动时,记△ABC在直线MN右侧部分的面积为S,求S关于时间t的函数关系式.19.如图直线y=kx+k交x轴负半轴于点A,交y轴正半轴于点B,且AB=2(1)求k的值;(2)点P从A出发,以每秒1个单位的速度沿射线AB运动,过点P作直线AB的垂线交x轴于点Q,连接OP,设△PQO的面积为S,点P运动时间为t,求S与t的函数关系式,并直接写出t的取值范围;(3)在(2)的条件下,当P在AB的延长线上,若OQ+AB=(BQ﹣OP),求此时直线PQ的解析式.20.如图,等腰梯形OBCD中,DC∥OB,OD=CB,∠DOB=∠CBO,BD⊥OD,在平面直角坐标系中,等腰梯形OBCD的下底OB在x轴正半轴上,O为坐标原点,点B的坐标为(a,0),C、D两点落在第一象限,且BD=2a.点P以每秒1个单位长度的速度在对角线BD上由点B向点D运动(点P不与点B、点D重合),过点P作PE⊥BD,交下底OB于点E,交腰BC(或上底CD)于点F.(1)线段BC的长是(用含a的代数式表示);(2)已知直线PE经过点C时,直线PE的解析式为y=2x﹣,求a的值,并直接写出点B、C、D的坐标;(3)在(2)的条件下,设动点P运动时间为t(秒),在点P运动过程中,请直接写出△BEF为等腰三角形时t的值(或取值范围),并直接写出等腰△BEF面积的最大值.参考答案1.解:(1)证明:∵A(﹣,0),则OA=,∵∠ABO=30°,∴OB==3,∵OB=3OC,∴OC=1,∴点B的坐标为(0,3),点C的坐标为(0,﹣1),∴tan∠ACB==,∴∠ACB=60°,∴∠ACB+∠ABC=90°,∴∠BAC=90°,即AC⊥AB.(2)∵△ABD是由△ABC折叠得到的,∴∠ADB=∠ACB=60°,∠ABD=∠ABC=30°,∴∠DBC=60°,∴△BCD是等边三角形,∴BD=BC=4,如图1,过点D作DF⊥BC于F,则BF=2,DF=2,∴点D的坐标为(﹣2,1),设直线BD的函数解析式为y=kx+b(k≠0),将点B,D的坐标代入得:,解得:,∴直线BD的函数解析式为y=x+3.(3)如图2,∵点E是直线BD与x轴的交点,∴令y=x+3=0,解得x=﹣3,故OE=3,而AO=,∴AE=EO﹣AO=3﹣=2,∴S△AED=AE•y D=×2×1=,∵S△AOB=AO•OB=××3=,∴S△AED≠S△AOB,∴嘉淇的观点错误.2.解:(1)将点A、B的坐标代入一次函数表达式:y=kx+b得:,解得:,故直线l的表达式为:;(2)在Rt△ABC中,由勾股定理得:AB2=OA2+OB2=32+22=13∵△ABC为等腰直角三角形,∴S△ABC=AB2=;(3)连接BP,PO,P A,则:①若点P在第一象限时,如图1:∵S△ABO=3,S△APO=a,S△BOP=1,∴S△ABP=S△BOP+S△APO﹣S△ABO=,即,解得;②若点P在第四象限时,如图2:∵S△ABO=3,S△APO=﹣a,S△BOP=1,∴S△ABP=S△AOB+S△APO﹣S△BOP=,即,解得a=﹣3;故:当△ABC与△ABP面积相等时,实数a的值为或﹣3.3.解:(1)解方程x2﹣6x+8=0可得x=2或x=4,∵BC、OC的长是方程x2﹣6x+8=0的两个根,且OC>BC,∴BC=2,OC=4,∴B(﹣2,4),∵△ODE是△OCB绕点O顺时针旋转90°得到的,∴OD=OC=4,DE=BC=2,∴D(4,0),设直线BD解析式为y=kx+b,把B、D坐标代入可得,解得,∴直线BD的解析式为y=﹣x+;(2)由(1)可知E(4,2),设直线OE解析式为y=mx,把E点坐标代入可求得m=,∴直线OE解析式为y=x,令﹣x+=x,解得x=,∴H点到y轴的距离为,又由(1)可得F(0,),∴OF=,∴S△OFH=××=;(3)∵以点D、F、M、N为顶点的四边形是矩形,∴△DFM为直角三角形,①当∠MFD=90°时,则M只能在x轴上,连接FN交MD于点G,如图1,由(2)可知OF=,OD=4,则有△MOF∽△FOD,∴=,即=,解得OM=,∴M(﹣,0),且D(4,0),∴G(,0),设N点坐标为(x,y),则=,=0,解得x=,y=﹣,此时N点坐标为(,﹣);②当∠MDF=90°时,则M只能在y轴上,连接DN交MF于点G,如图2,则有△FOD∽△DOM,∴=,即=,解得OM=6,∴M(0,﹣6),且F(0,),∴MG=MF=,则OG=OM﹣MG=6﹣=,∴G(0,﹣),设N点坐标为(x,y),则=0,=﹣,解得x=﹣4,y=﹣,此时N(﹣4,﹣);③当∠FMD=90°时,则可知M点为O点,如图3,∵四边形MFND为矩形,∴NF=OD=4,ND=OF=,可求得N(4,);综上可知存在满足条件的N点,其坐标为(,﹣)或(﹣4,﹣)或(4,).4.解:(1)作MN⊥BO,由垂径定理得:点N为OB的中点,∴MN=OA,∵MN=3,∴OA=6,即A(﹣6,0),∵sin∠ABO=,OA=6,∴OB=,即B(0,),设y=kx+b,将A、B代入得:,(2)NB=OB=,MN=3,tan∠BMN==,则∠BMN=30°,∴∠ABO=60°,∴∠AMO=120°∴阴影部分面积为.5.解:(1)由题可求A(0,6),B(﹣3,0),∴AO=6,BO=3,∵AO=BC,∴BC=6,∴CO=BC﹣BO=3,∴C(3,0),设直线AC的解析式为y=kx+b,将点C与A代入,可得,∴,∴y=﹣2x+6;(2)过点P作PM⊥x轴交于点M,∵点P的横坐标为t,∴P(t,﹣2t+6),∴PM=﹣2t+6,∴S△PBC=BC•PM=×6×(﹣2t+6)=﹣6t+18,S△ABC=BC•AO=18,∴S=S△ABC﹣S△PBC=6t;(3)过点B作BF平分∠ABD,且BF=CE,连接AF ∵∠ABD=2∠ACE,∴∠ABF=∠ACE∵BO=CO,AO⊥BC,∴AB=AC,∴△ABF≌△ACE(SAS),∴AF=AE,∠BAF=∠CAE,∵AE平分∠OAC,∴∠OAE=∠CAE,∵∠BAO=∠CAO,∴∠BAF=∠F AO,过点F作FG⊥AB于点G,FK⊥AD于点K,FH⊥BD于点H,∵AF平分∠BAD,∴FG=FK,∵BF平分∠ABD,∴FG=FH,∴FH=FK,∴DF平分∠ADB,∴∠BDF=∠ADF,∵AF=AE,∠F AD=∠EAD,AD=AD,∴△AFD≌△AED(SAS),∴∠ADF=∠ADE,∴∠ADF=∠ADE=∠BDF=60°,∴∠CDP=∠CDO=60°,过点C作CN⊥BP于点N,∵CO⊥AO,∴CN=CO=3,∵CA=CL,∴△AOC≌△LNC(HL),∴NL=AO=6,∵tan∠NDC=,∴=,∴DN=,∴DL=6+.6.解:(1)把x=0代入y=kx+4,y=4,∴OB=4,∵△ABO的面积为8,∴=8,∴AO=4,∴A(﹣4,0),把x=﹣4,y=0代入y=kx+4,∴k=1;(2)把x=t代入y=x+4,∴P(t,t+4),如图1,过点P作PD⊥x轴,垂直为D过点C作CE⊥x轴,垂直为E;∴∠PDO=∠CEO=90°,∴∠POD=∠OPD=90°,∵线段OP绕点O顺时针旋转90°至线段OC,∴∠POC=90°,OP=OC,∴∠POD+∠EOC=90°,∴∠OPD=∠EOC,∴△OPD≌△OCE,∴OE=PD,m=t+4;(3)如图2,过点O作直线TO⊥AB,交直线BM于点Q,垂足为点T,连接QP,由(1)知,AO=BO=4,∴∠BOA=90°,∴△ABO为直角三角形,∴∠ABO=∠BAO=45°,∠BOT=90°﹣∠ABO=45°=∠ABO,∴BT=TO,∵∠BTO=90°,∴∠TPO+∠TOP=90°,∵OP⊥BM,∴∠BNO=90°,∴∠BQT=∠TPO,∴△QTB≌△PTO,∴QT=TP,PO=BQ,∴∠PQT=∠QPT,∵OP=PK+KB,∴QB=KP+KB,QK=KP,∴∠KQP=∠KPQ,∴∠PQT﹣∠KQP=∠QPT﹣∠KPQ,∠TQB=∠TPK,∴∠KPB=∠BPN,设∠KPB=x°,∴∠BPN=x°,∵∠PMB=2∠KPB,∴∠PMB=2x°,∠POM=∠P AO+∠APO=45°+x°,∠NMO=90°﹣∠POM=45°﹣x°,∴∠PMO=∠PMB+∠NMO=45°+x°=∠POM,∴PO=PM,过点P作PD⊥x轴,垂直为点D,∴OM=2OD=2t,∴∠OPD=90°﹣∠POD=45°﹣x°=∠BMO,∴tan∠OPD=tan∠BMO,∴,,∴t=4或t=﹣2(舍),∴OM=8,由(2)知:m=t+4=8=OM,∴CM∥y轴,∵∠PNM=∠POC=90°,∴BM∥OC,∴四边形BOCM是平行四边形,∴四边形BOCM的面BO×OM=4×8=32;7.解:(1)∵点A的坐标为(﹣2,0),∴OA=2,∵OB=2OA=4,∴B(0,4),把A(﹣2,0)和B(0,4)代入y=kx+b中得:,解得:,∴直线AB解析式为:y=2x+4;(2)∵∠AOB=90°,∴∠AO1B1=90°,由平移得:OO1=6,O1B1=OB=4,由勾股定理得:OB1==2,即线段OB1的长是2;(3)△AOB扫过的面积=+4×6=28.8.解:(1)令点P的坐标为P(x0,y0)∵PM⊥y轴∴S△OPM=OM•PM=将代入得S△OPM==﹣(x﹣2)2+∴当x0=2时,△OPM的面积,有最大值S max=,即:PM=2,∴PM∥OB,∴即∵直线AB分别交两坐标轴于点A、B,∴A(0,3),B(4,0),∴OA=3,OB=4,∴AB=5,∴AP=;(2)①在△BOP中,当BO=BP时BP=BO=4,AP=1∵PM∥OB,∴∴,将代入代入中,得∴P(,);②在△BOP中,当OP=BP时,如图,过点P作PN⊥OB于点N∵OP=BP,∴ON=将ON=2代入中得,NP=∴点P的坐标为P(2,),即:点P的坐标为(,)或(2,).9.解:(1)在直线y=﹣x﹣中,令y=0,则有0=﹣x﹣,∴x=﹣13,∴C(﹣13,0),令x=﹣5,则有y=﹣×(﹣5)﹣=﹣3,∴E(﹣5,﹣3),∵点B,E关于x轴对称,∴B(﹣5,3),∵A(0,5),∴设直线AB的解析式为y=kx+5,∴﹣5k+5=3,∴k=,∴直线AB的解析式为y=x+5;(2)由(1)知,E(﹣5,﹣3),∴DE=3,∵C(﹣13,0),∴CD=﹣5﹣(﹣13)=8,∴S△CDE=CD×DE=12,由题意知,OA=5,OD=5,BD=3,∴S四边形ABDO=(BD+OA)×OD=20,∴S=S△CDE+S四边形ABDO=12+20=32,(3)由(2)知,S=32,在△AOC中,OA=5,OC=13,∴S△AOC=OA×OC==32.5,∴S≠S△AOC,理由:由(1)知,直线AB的解析式为y=x+5,令y=0,则0=x+5,∴x=﹣≠﹣13,∴点C不在直线AB上,即:点A,B,C不在同一条直线上,∴S△AOC≠S.10.解:(1)∵|x﹣15|+=0,∴x=15,y=13,∴OA=BC=15,AB=OC=13,∴B(15,13);(2)如图1,过D作EF⊥OA于点E,交CB于点F,由折叠的性质可知BD=BC=15,∠BDN=∠BCN=90°,∵tan∠CBD=,∴=,且BF2+DF2=BD2=152,解得BF=12,DF=9,∴CF=OE=15﹣12=3,DE=EF﹣DF=13﹣9=4,∵∠CND+∠CBD=360°﹣90°﹣90°=180°,且∠ONM+∠CND=180°,∴∠ONM=∠CBD,∴=,∵DE∥ON,∴==,且OE=3,∴=,解得OM=6,∴ON=8,即N(0,8),把N、B的坐标代入y=kx+b可得,解得,∴直线BN的解析式为y=x+8;(3)设直线BN平移后交y轴于点N′,交AB于点B′,当点N′在x轴上方,即0<t≤8时,如图2,由题意可知四边形BNN′B′为平行四边形,且NN′=t,∴S=NN′•OA=15t;当点N′在y轴负半轴上,即8<t≤13时,设直线B′N′交x轴于点G,如图3,∵NN′=t,∴可设直线B′N′解析式为y=x+8﹣t,令y=0,可得x=3t﹣24,∴OG=3t﹣24,∵ON=8,NN′=t,∴ON′=t﹣8,∴S=S四边形BNN′B′﹣S△OGN′=15t﹣(t﹣8)(3t﹣24)=﹣t2+39t﹣96;综上可知S与t的函数关系式为S=.11.解:(1)如图1:(2)如图2:,由折叠的性质,得∠C=∠A=∠COA=45°,AF=BE=CF=t,S△CFG=CF•FG=t2=,解得t=,t=﹣(不符合题意,舍);(3)分两种情况讨论:①当0<t≤3时,如图2:四边形DCFE落在第一象限内的图形是△DFG,∴S=t2,∵S=t2,在t>0时,S随t增大而增大,∴t=3时,S最大=;②当3<t<6时,如图3:,四边形DCFE落在第一象限内的图形是四边形CHOF,∴S四边形CHOF=S△CGF﹣S△HGO,∴S=t2﹣2(2t﹣6)2=﹣t2+12t﹣18=﹣(t﹣4)2+6,∵a=﹣<0,∴S有最大值,∴当t=4时,S最大=6,综上所述,当t=4时,S最大值为6.12.解:(1)将A(6,0)代入y=﹣x+b,得:0=﹣×6+b,解得:b=8,∴点B的坐标为(0,8).∵BC=2,点C在线段OB上,∴点C的坐标为(0,6).设直线AC的函数解析式为y=mx+n(m≠0),将点A(6,0),C(0,6)代入y=mx+n,得:,解得:,∴直线AC的函数解析式为y=﹣x+6;(2)∵点C的坐标为(0,t),∴OC=t,BC=OB﹣OC=8﹣t,∴S△ABC=OA•BC=×6×(8﹣t)=﹣3t+24.∵1≤t≤4,∴12≤﹣3t+24≤21,∴△ABC面积的取值范围是12≤S△ABC≤21;(3)在Rt△AOB中,OA=6,OB=8,∴AB==10.过点C作CD⊥AB于点D,如图所示.∵AC平分∠OAB,∴CD=CO=t.∵∠CBD=∠ABO,∠CDB=∠AOB=90°,∴△BCD~△BAO,∴=,即=,解得:t=3,∴BC=5,∴m=AB+BC+AC=15+AC,n=AC+OC+OA=AC+9,∴m﹣n=(15+AC)﹣(AC+9)=6.13.解:(1)∵直线y=﹣x+b过点C(1,2)∴﹣1+b=2∴b=3,即直线为y=﹣x+3当y=0时,﹣x+3=0,得x=3;当x=0时,y=3∴B(3,0),D(0,3)故答案为:(3,0);(0,3).(2)①∵Rt△AOC中,∠OAC=90°,C(1,2)∴A(0,2),OA=2,AC=1∵OB=OD=3,∠BOD=90°∴OA+AC=OB=3,∠OBD=45°∴0≤t<3,且t≠2i)当0≤t<2时,点P在线段OA上,点H在线段BC上,如图1∴OP=BQ=t∴AP=OA﹣OP=2﹣t,OQ=OB﹣BQ=3﹣t∵HQ⊥x轴于点Q∴∠BQH=90°∴△BQH是等腰直角三角形∴HQ=BQ=t∴HQ∥OP且HQ=OP∴四边形OPHQ是平行四边形∴PH∥x轴,PH=OQ=3﹣t∴S=S△CPH=PH•AP=(3﹣t)(2﹣t)=t2﹣t+3ii)当2<t<3时,点P在线段AC上,点H在线段OC上,如图2∴CP=OA+AC﹣t=3﹣t,x H=OQ=3﹣t∵直线OC解析式为:y=2x∴QH=y H=2(3﹣t)=6﹣2t∴点H到CP的距离h=2﹣(6﹣2t)=2t﹣4∴S=S△CPH=CP•h=(3﹣t)(2t﹣4)=﹣t2+5t﹣6综上所述,S关于t的函数关系式为S=②存在以Q、P、H为顶点的三角形的面积与S相等.i)当0≤t<2时,如图3∵S△CPH=S△QPH,两三角形有公共底边为PH∴点C和点Q到PH距离相等,即AP=OP∴t=2﹣t∴t=1ii)当2<t≤2.5时,如图4,延长QH交AC于点E∴AE=OQ=3﹣t,AP=t﹣2,QH=6﹣2t∴PE=AE﹣AP=(3﹣t)﹣(t﹣2)=5﹣2t∴S△QPH=QH•PE=(6﹣2t)(5﹣2t)=2t2﹣11t+15∵S△CPH=S△QPH∴﹣t2+5t﹣6=2t2﹣11t+15解得:t1=3(舍去),t2=iii)当2.5<t<3时,如图5,延长QH交AC于点E∴PE=AP﹣AE=(t﹣2)﹣(3﹣t)=2t﹣5∴S△QPH=QH•PE=(6﹣2t)(2t﹣5)=﹣2t2+11t﹣15∴﹣t2+5t﹣6=﹣2t2+11t﹣15解得:t1=t2=3(舍去)综上所述,t=1或时,以Q、P、H为顶点的三角形的面积与S相等.14.解:(1)把A(﹣3,1)、B(2,4)分别代入y=kx+b,得.解得.∵直线y=2x+3上的一点P(x,y)又是它的“对称直线”上的点,∴点P(x,y)是直线y=2x+3与直线y=3x+2的交点.∴.解得.∴P(1,5)故答案是:;(2)∵点M(m,n)是直线y=kx+b上的任意一点,∴km+b=n①,∵点N(2m,6n﹣34)在y=kx+b的“对称直线”上,即N(2m,6n﹣34)在直线y=bx+k上∴2bm+k=6n﹣34②,将①代入②得,2bm+k=6km+6b﹣34,整理得:(2b﹣6k)m=6b﹣k﹣34,∵对于任意一点M(m,n)等式均成立,∴,解得,∴y=2x+6.∴B(﹣3,0).设点C,E的坐标分别为(x1,y1),(x2,y2)(x1≠x2),∵L(C,D)=L(D,E),且D点的坐标为(2,2),∴2x1+2y1=2x2+2y2,即x1+y1=x2+y2,由材料一可知:直线CE的斜率为k CE=﹣1,故设直线CE的解析式为:y=﹣x+d(c≠0)∵DF=6,DF∥y轴,∴F(2,﹣4).∴﹣2+d=﹣4.则d=﹣2.故直线CE的解析式是:y=﹣x﹣2.易得A(﹣2,0).由得到:,即G(﹣,).∴S△ABG=AB•|y G|=×1×=;同理,当直线C′E′的解析式为:y=﹣x+10时,B′(12,0),G′(,),此时S△AB′F=AB′•|y G|=×13×=;综上所述,直线CE、直线y=kx+b与x轴围成的三角形的面积是或.15.解:(1)如图1,点D为BC的中点,作直线AD,直线AD则平分△ABC的面积;(2)如图2,连接AC、BD,AC与BD交于点O,则点O为平行四边形ABCD的对称中心,作直线OP,直线OP即为所求;如图3,过A作AE⊥BC于E,∵∠ABC=45°,∴△ABE是等腰直角三角形,∴AE===3,∵BC=12,∴▱ABCD的面积=BC•AE=12×3=36;(3)∵A(8,8),∴直线OA的解析式为:y=x,过点B作BD⊥x轴于点D,交AO于E,连接OB,则E(6,6),∵B(6,12),点P(3,6),∴点P为线段OB的中点.∵OA∥BC,BE∥OC,∴四边形OEBC是平行四边形.∴点P是平行四边形OEBC的对称中心,∴过点P的直线平分平行四边形OEBC.∴过点P的直线PF只要平分△BEA的面积即可.设直线PF的表达式为y=kx+b,且过点P(3,6),∴3k+b=6,即b=6﹣3k,∴y=kx+6﹣3k.设直线AB的表达式为y=mx+n,且过点B(6,12),A(8,8),则,解得:,∴直线AB的函数表达式为y=﹣2x+24.∴,解得:x=,∴F的横坐标为,把x=6代入y=kx+6﹣3k得y=3k+6,∴G(6,3k+6)同理得直线AP的解析式为y=x+,当x=6时,y=,∴<3k+6<12,解得<k<2,∵S△BFG=B B G•(F x﹣6)=(12﹣3k﹣6)(﹣6)=(8﹣6)(12﹣6),解得k=或k=4(舍去),∴直线l的表达式为y=x+4.16.解:(1)y=k1x+6,当x=0时,y=6,∴OB=6,∵OB=OA,∴OA=2,∴A(﹣2,0),把A(﹣2,0)代入:y=k1x+6中得:﹣2k1+6=0,k1=,∴直线l1的解析式为:y=x+6;(2)如图1,过C作CH⊥x轴于H,∵C(,1),∴OH=,CH=1,Rt△ABO中,AB==4,∴AB=2OA,∴∠OBA=30°,∠OAB=60°,∵CD⊥AB,∴∠ADE=90°,∴∠AED=30°,∴EH=,∴OE=OH+EH=2,∴E(2,0),把E(2,0)和C(,1)代入y=k2x+b中得:,解得:,∴直线l2:y=﹣x+2,∴F(0,2)即BF=6﹣2=4,则,解得,∴D(﹣,3),∴S△BCD=BF(x C﹣x D)==4;(3)分四种情况:①当Q在y轴的正半轴上时,如图2,过D作DM⊥y轴于M,过C作CN⊥y轴于N,∵△QCD是以CD为底边的等腰直角三角形,∴∠CQD=90°,CQ=DQ,∴∠DMQ=∠CNQ=90°,∴∠MDQ=∠CQN,∴△DMQ≌△QNC(AAS),∴DM=QN,QM=CN=,设D(m,m+6)(m<0),则Q(0,﹣m+1),∴OQ=QN+ON=OM+QM,即﹣m+1=m+6+,m==1﹣2,∴Q(0,2);②当Q在x轴的负半轴上时,如图3,过D作DM⊥x轴于M,过C作CN⊥x轴于N,同理得:△DMQ≌△QNC(AAS),∴DM=QN,QM=CN=1,设D(m,m+6)(m<0),则Q(m+1,0),∴OQ=QN﹣ON=OM﹣QM,即m+6﹣=﹣m﹣1,m=5﹣4,∴Q(6﹣4,0);③当Q在x轴的负半轴上时,如图4,过D作DM⊥x轴于M,过C作CN⊥x轴于N,同理得:△DMQ≌△QNC(AAS),∴DM=QN,QM=CN=1,设D(m,m+6)(m<0),则Q(m﹣1,0),∴OQ=QN﹣ON=OM+QM,即﹣m﹣6﹣=﹣m+1,m=﹣4﹣5,④当Q在y轴的负半轴上时,如图5,过D作DM⊥y轴于M,过C作CN⊥y轴于N,同理得:△DMQ≌△QNC(AAS),∴DM=QN,QM=CN=,设D(m,m+6)(m<0),则Q(0,m+1),∴OQ=QN﹣ON=OM+QM,即﹣m﹣6+=﹣m﹣1,m=﹣2﹣1,∴Q(0,﹣2);综上,存在点Q,使△QCD是以CD为底边的等腰直角三角形,点Q的坐标是(0,±2)或(6﹣4,0)或(﹣4﹣6,0).17.解:(1)令y=0,∴﹣x+4=0,∴x=6,∴A(6,0),当t=秒时,AP=3×=1,∴OP=OA﹣AP=5,∴P(5,0),故答案为(4,0);(2)当点Q在原点O时,OA=6,∴AP=OA=3,∴t=3÷3=1,①当0<t≤1时,如图1,令x=0,∴y=4,∴B(0,4),∴OB=4,∵A(6,0),∴OA=6,在Rt△AOB中,tan∠OAB==,由运动知,AP=3t,∴P(6﹣3t,0),∴Q(6﹣6t,0),∴PQ=AP=3t,∵四边形PQMN是正方形,∴MN∥OA,PN=PQ=3t,在Rt△APD中,tan∠OAB===,∴PD=2t,∴DN=t,∵MN∥OA∴∠DCN=∠OAB,∴tan∠DCN===,∴CN=t,∴S=S正方形PQMN﹣S△CDN=(3t)2﹣t×t=t2;②当1<t≤时,如图2,同①的方法得,DN=t,CN=t,∴S=S矩形OENP﹣S△CDN=3t×(6﹣3t)﹣t×t=﹣t2+18t;③当<t≤2时,如图3,S=S梯形OBDP=(2t+4)(6﹣3t)=﹣3t2+12;(3)如图4,由运动知,P(6﹣3t,0),Q(6﹣6t,0),∴M(6﹣6t,3t),∵T是正方形PQMN的对角线交点,∴T(6﹣t,t),∴点T是直线y=﹣B x+2上的一段线段,(﹣3≤x<6),∵A(6,0)∴点N是直线AG:y=﹣x+6上的一段线段,(0≤x≤6),∴G(0,6),∴OG=6,∵A(6,0),∴AG=6,在Rt△AOG中,OA=6=OG,∴∠OAG=45°,∵PN⊥x轴,∴∠APN=90°,∴∠ANP=45°,∴∠TNA=90°,即:TN⊥AG,∵T正方形PQMN的对角线的交点,∴TN=TP,∴OT+TP=OT+TN,∴点O,T,N在同一条直线上(点Q与点O重合时),且ON⊥AG时,OT+TN最小,即:OT+TN最小,∵S△OAG=OA×OG=AG×ON,∴ON==3.即:OT+PT的最小值为3.18.解:(1)设直线BC的解析式为y=kx+b,则,解得,∴直线BC的解析式为y=x+4.(2)如图,连接AD交MN于点O′.由题意:四边形AMDN是菱形,M(3﹣t,0),N(3﹣t,t),∴O′(3﹣t,t),D(3﹣t,t),∵点D在BC上,∴t=×(3﹣t)+4,解得t=.∴t=s时,点A恰好落在BC边上点D处,此时D(﹣,).(3)如图2中,当0<t≤5时,△ABC在直线MN右侧部分是△AMN,S=•t•t=t2.如图3中,当5<t≤6时,△ABC在直线MN右侧部分是四边形ABNM.S=×6×4﹣×(6﹣t)•[4﹣(t﹣5)]=﹣t2+t﹣12.19.解:(1)对于直线y=kx+k,令y=0,可得x=﹣1,∴A(﹣1,0),∴OA=1,∵AB=2,∴OB==,∴k=.(2)如图,∵tan∠BAO==,∴∠BAO=60°,∵PQ⊥AB,∴∠APQ=90°,∴∠AQP=30°,∴AQ=2AP=2t,当0<t<时,S=•OQ•P y=(1﹣2t)•t=﹣t2+t.当t>时,S=OQ•P y=(2t﹣1)•t=t2﹣t.(3)∵OQ+AB=(BQ﹣OP),∴2t﹣1+2=(﹣),∴2t+1=•,∴4t2+4t+1=7t2﹣7t+7,∴3t2﹣11t+6=0,解得t=3或(舍弃),∴P(,),Q(5,0),设直线PQ的解析式为y=kx+b,则有,解得,∴直线PQ的解析式为y=﹣x+.20.解:(1)如图1中,∵BD⊥OD,∴∠BDO=90°,∵BD=2a,AB=a,∴OD==a,∵四边形ODCB是等腰梯形,∴BD=OD=a.故答案为a.(2)如图2中,作DM⊥OB于M,CN⊥OB于N.∵∠DOB=∠CBO,BC=a,∴sin∠CBO=sin∠DOB==a=,∴CN=a,BN==a,∴ON=OB﹣BN=a,∴C(a,a),∵直线y=2x﹣经过点C,∴a=a﹣,∴a=1.∴B(,0),C(,),D(,).(3)如图3﹣1中,当点F在线段BC上时,∵EF⊥BD,OD⊥BD,∴EF∥OD,∴∠FEB=∠DOB,∵∠DOB=∠CBO,∴FEB=∠FBE,∴FE=FB,∴△FEB是等腰三角形,如图2中,当直线EF经过点C时,E(,0),此时EB=,∴PB=EB•cos∠EBP=•=,共线图形可知当0<t≤时,△BFE是等腰三角形.如图3﹣2中,当点F在线段CD上,EF=BE时,1=t,∴t=.如图3﹣3中,当点F在线段CD上,BF=BE时,易证:PE=PF,∴t=,∴t=1,综上所述,t的值为0<t≤或或1时,△BEF是等腰三角形.当t=1时,△BEF的面积最大,最大值=××=.。
高中物理图像问题综合分析

图像问题一、函数图像重要信息①坐标:纵坐标,横坐标,纵坐标之差,横坐标之差。
涉及函数图像相关的问题,首先需要搞清楚纵横坐标分别表示什么物理量;而纵坐标之差,横坐标之差则分别表示纵坐标与横坐标表示的物理量的变化量。
函数图像的纵横坐标一般都表示状态量;如果为过程量,则表示从初始时刻到对应时刻的过程中的总量。
例如,W-t图像中,功W为过程量,于是W表示0~t时间内的总功;而t1~t2时间内,纵坐标的变化量则表示这段时间内的功。
另外,物理上,有时为了方便,纵坐标和横坐标都不一定是从零开始的,需格外注意。
②点:转折点,拐点,端点,断点,交点,截距。
将一个物理过程的各个阶段与图像中的每一段对应起来是有效提取信息前提条件;而将各个阶段与图像对应起来的关键在于将物理过程中的关键时刻,关键状态与图中的特殊点对应起来,这些点包括转折点,拐点,端点,断点,交点,截距(与坐标轴的交点)。
根据物理过程做物理量的函数图像时,也常常先描出关键时刻,关键状态在图像中对应的点。
另外,这些特殊点可能还对应一些临界情形;例如在同一直线上运动的两个物体的v-t图像,交点(彼此穿过对方图像)表示相对运动反向,从而也表示相距极远或极近。
③斜率:切线斜率,割线斜率,与原点连线斜率。
与原点连线斜率表示纵横坐标的比值;例如纯电阻元件U-I图像的点与原点的连线的斜率,表示该点对应的状态下,元件的电阻;理想气体的p-T图(或V-T图)上的点与原点连线的斜率,与该点对应的状态下,其体积(或压强)成反比。
割线斜率表示纵横坐标变化量的比值,如果有意义,通常是某物理量的平均值。
需要指出的是,物理量的平均值存在一个对什么的平均的问题;设A=ΔYΔX,若X表示时刻t,则是对时间的平均;若X表示位置x,则是对距离的平均。
例如:F̅=IΔt 表示力对时间的平均值;而F′̅=WΔx则表示力对距离的平均值;两者不能混淆!切线斜率表示纵横坐标变化量的比值在横坐标之差趋于零时的极限,数学上就是纵坐标作为横坐标的函数的导数,如果有意义,则表示某物理量的瞬时值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、指数函数图像应用练习一1.函数f(x)=a x-b的图象如图,其中a,b为常数,则下列结论正确的是( )A.a>1,b<0 B.a>1,b>0 C.0<a<1,b>0 D.0<a<1,b<02.已知a>0,且a≠1,若函数y=|a x-2|与y=3a的图象有两个交点,则实数a的取值范围是________.3.函数f(x)=1-e|x|的图象大致是( )4、若函数y=|3x-1|在(-∞,k]上单调递减,求k的取值范围.练习二1.函数y =a x -a (a >0,且a ≠1)的图象可能是( )2.函数y =2x 与y =2-x 的图象关系是( )A .关于x 轴对称B .关于y 轴对称C .关于原点对称D .关于直线y =x 对称3.已知函数y =kx +a 的图象如图所示,则函数y =a x +k 的图象可能是( )4.(2016·唐山二模)当x ∈[1,2]时,函数y =12x 2与y =a x (a >0)的图象有交点,则a 的取值范围是( )A.⎣⎢⎡⎦⎥⎤12,2B.⎣⎢⎡⎦⎥⎤12,2C.⎣⎢⎡⎦⎥⎤14,2D.⎣⎢⎡⎦⎥⎤14,2二、对数函数图像应用1.函数f(x)=ln|x-1|的图象大致是( )2、(2017·成都一诊)设f(x)=|ln(x+1)|,已知f(a)=f(b)(a<b),则( )A.a+b>0 B.a+b>1 C.2a+b>0 D.2a+b>13已知函数f(x)=log a(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )A.0<a-1<b<1 B.0<b<a-1<1 C.0<b-1<a<1 D.0<a-1<b-1<14.(2017·武汉调研)若函数y=a|x|(a>0,且a≠1)的值域为{y|y≥1},则函数y=log|x|的图象大致是( )a5.已知函数f (x )=⎩⎨⎧log 2x ,x >0,3x,x ≤0,关于x 的方程f (x )+x -a =0有且只有一个实根,则实数a 的取值范围是______.6.若f (x )=lg x ,g (x )=f (|x |),则g (lg x )>g (1)时,x 的取值范围是__________.7.设函数f (x )=⎩⎨⎧log 2x ,x >0,log12-x ,x <0,若f (a )>f (-a ),则实数a 的取值范围__.8.已知函数f (x )是定义在R 上的偶函数,f (0)=0,当x >0时,f (x )=log 12x .(1)求函数f (x )的解析式; (2)解不等式f (x 2-1)>-2.三、单调性、奇偶性与周期性结合1、设f (x )是定义在R 上的奇函数,且对任意实数x ,恒有f (x +2)=-f (x ),当x ∈[0,2]时,f (x )=2x -x 2.(1)求证:f (x )是周期函数;(2)计算f (0)+f (1)+f (2)+…+f (2 018).2.(2016·天津高考)已知f (x )是定义在R 上的偶函数,且在区间(-∞,0)上单调递增.若实数a 满足f (2|a -1|)>f (-2),则a 的取值范围是( )A.⎝ ⎛⎭⎪⎫-∞,12B.⎝ ⎛⎭⎪⎫-∞,12∪⎝ ⎛⎭⎪⎫32,+∞C.⎝ ⎛⎭⎪⎫12,32D.⎝ ⎛⎭⎪⎫32,+∞3.(2017·绵阳诊断)已知偶函数f (x )在区间[0,+∞)上单调递增,则满足f (2x -1)<f ⎝ ⎛⎭⎪⎫13的x 的取值范围是( )A.⎝ ⎛⎭⎪⎫13,23B.⎣⎢⎡⎭⎪⎫13,23C.⎝ ⎛⎭⎪⎫12,23D.⎣⎢⎡⎭⎪⎫12,234.已知函数f (x )是奇函数,在(0,+∞)上是减函数,且在区间[a ,b ](a <b <0)上的值域为[-3,4],则在区间[-b ,-a ]上( )A .有最大值4B .有最小值-4C .有最大值-3D .有最小值-35.设f (x )是定义在R 上周期为4的奇函数,若在区间[-2,0)∪(0,2]上,f (x )=⎩⎨⎧ax +b ,-2≤x <0,ax -1,0<x ≤2,则f (2018)=________.6.已知定义在R 上的奇函数f (x )满足f (x -4)=-f (x ),且在区间[0,2]上是增函数,则( )A .f (-25)<f (11)<f (80)B .f (80)<f (11)<f (-25)C .f (11)<f (80)<f (-25)D .f (-25)<f (80)<f (11)7.已知偶函数f (x )对于任意x ∈R 都有f (x +1)=-f (x ),且f (x )在区间[0,1]上是递增的,则f (-6.5),f (-1),f (0)的大小关系是( )A .f (0)<f (-6.5)<f (-1)B .f (-6.5)<f (0)<f (-1)C .f (-1)<f (-6.5)<f (0)D .f (-1)<f (0)<f (-6.5)8.设f (x )是定义在实数集上的函数,且f (2-x )=f (x ),若当x ≥1时,f (x )=ln x ,则有( )A .f ⎝ ⎛⎭⎪⎫13<f (2)<f ⎝ ⎛⎭⎪⎫12B .f ⎝ ⎛⎭⎪⎫12<f (2)<f ⎝ ⎛⎭⎪⎫13C .f ⎝ ⎛⎭⎪⎫12<f ⎝ ⎛⎭⎪⎫13<f (2)D .f (2)<f ⎝ ⎛⎭⎪⎫12<f ⎝ ⎛⎭⎪⎫13四、零点问题1、判断零点所在的区间1.函数f (x )=ln x +2x -6的零点所在的大致区间是( )A .(0,1)B .(1,2)C .(2,3)D .(3,4)2.已知实数a >1,0<b <1,则函数f (x )=a x+x -b 的零点所在的区间是( )A .(-2,-1)B .(-1,0)C .(0,1)D .(1,2)2、判断零点的个数问题1.已知函数f (x )=⎩⎨⎧x +1,x ≤0,log 2x ,x >0,则函数y =f (f (x ))+1的零点的个数是( ) A .4 B .3 C .2 D .12.(2017·郑州质检)已知函数f (x )=⎝ ⎛⎭⎪⎫12x -cos x ,则f (x )在[0,2π]上的零点个数为( ) A .1 B .2 C .3 D .43.已知函数f (x )=⎩⎪⎨⎪⎧3x,x ≤1,log 13x ,x >1,则函数y =f (x )+x -4的零点个数为( ) A .1 B .2 C .3 D .43、含参问题 定义法1.函数f (x )=kx +1在[1,2]上有零点,则k 的取值范围是________.2.函数f (x )=2x-2x-a 的一个零点在区间(1,2)内,则实数a 的取值范围是( )A .(1,3)B .(1,2)C .(0,3)D .(0,2)3.方程2x +3x =k 的解在[1,2)内,则k 的取值范围为______.分离系数法1、(2017·安庆摸底考试)若函数f (x )=4x -2x -a ,x ∈[-1,1]有零点,则实数a 的取值范围是________.2.(2016·宁夏育才中学第四次月考)已知函数f (x )=⎩⎨⎧e x+a ,x ≤0,3x -1,x >0(a ∈R),若函数f (x )在R 上有两个零点,则a 的取值范围是( )A .(-∞,-1)B .(-∞,0)C .(-1,0)D .[-1,0)数形结合法1.已知函数f (x )=⎩⎨⎧0,x ≤0,2x,x >0,则使函数g (x )=f (x )+x -m 有零点的实数m的取值范围是( )A .[0,1)B .(-∞,1)C .(-∞,0]∪(1,+∞)D .(-∞,1]∪(2,+∞)2.已知函数f (x )=⎩⎨⎧log 2x +1,x >0,-x 2-2x ,x ≤0,若函数g (x )=f (x )-m 有3个零点,则实数m 的取值范围是______.3.函数f (x )=⎩⎨⎧2x-1,x ≥0,f x +1,x <0,若方程f (x )=-x +a 有且只有两个不相等的实数根,则实数a 的取值范围为( )A .(-∞,0)B .[0,1)C .(-∞,1)D .[0,+∞)4、方程根的分布问题1.已知关于x 的方程x 2+mx -6=0的一个根比2大,另一个根比2小,则实数m 的取值范围是______.2.已知a 是正实数,函数f (x )=2ax 2+2x -3-a .如果函数y =f (x )在区间[-1,1]上有零点,求a 的取值范围.。
