推荐-棠湖中学高2018级高三月考试题(一)(文科)[原创] 精品
四川省棠湖中学2018届高三高考模拟考试数学文试题 含

四川省棠湖中学2018年高考适应性考试数学试卷(文史类)第Ⅰ卷(选择题 共60分)一.选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知i 为虚数单位,实数x ,y 满足(3)x i i y i +=-,则x yi -=( ) A .4 B .3 C2.已知集合2{|40}A x N x x =∈-≤,集合2{|20}B x x x a =++=,若{0,1,2,3,4,3}A B =-,则A B =( )A .{1,3}-B .{1}C .{3}-D .φ 3.函数()sin(2)f x x ϕ=+的图象向右平移6π个单位后所得的图象关于原点对称,则ϕ可以是( ) A .6π B .3π C .4π D .23π4.若tan 24πα⎛⎫-=-⎪⎝⎭,则tan 2α=( ) A .3- B .3 C .34- D .345.已知132a -=, 21log 3b =, 131log 4c =,则( ) A. a b c >> B. a c b >> C. c b a >> D. c a b >> 6.函数()3ln 8f x x x =+-的零点所在的区间为( )A. ()0,1B. ()1,2C. ()2,3D. ()3,4 7.如图所示的三视图表示的几何体的体积为323,则该几何体的外接球的表面积为( ) A .12π B .24π C .36π D .48π8.已知直线:l y m =+与圆22:(3)6C x y +-=相交于A ,B 两点,若120ACB ∠=︒,则实数m 的值为( )A.3或3.3+或3- C.9或3- D .8或2- 9.已知等差数列{}n a 的前n 项和为n S ,19a =,95495S S -=-,则n S 取最大值时的n 为( )A .4B .5C .6D .4或510.四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是边长为2的正方形,PA =E 为PC 的中点,则异面直线BE 与PD 所成角的余弦值为( )ABC11.已知函数()sin f x x x =+,若[2,1]x ∃∈-,使得2()()0f x x f x k ++-=成立,则实数k 的取值范围是( )A .[1,3]-B .[0,3]C .(,3]-∞D .[0,)+∞12.已知F 是椭圆2222:1(0)x y E a b a b +=>>的左焦点,经过原点的直线l 与椭圆E 交于P ,Q 两点,若||2||PF QF =,且120PFQ ∠=︒,则椭圆E 的离心率为( )A .13 B .12 C.二.填空题(每题5分,满分20分,将答案填在答题纸上)13.已知实数x ,y 满足条件2300x y x y x y -≥⎧⎪+≤⎪⎨≥⎪⎪≥⎩,则23x y +的最大值为 .14.已知{}n a 是等比数列,若)2,(2a a =,)3,(3a =,且a ∥b ,则2435+a a a a =+ .15.已知3sin()35πα-=,(,)42ππα∈,则tan α= . 16.已知点1(,0)F c -,2(,0)(0)F c c >是椭圆22221(0)x y a b a b+=>>的左、右焦点,点P 是这个椭圆上位于x 轴上方的点,点G 是12PF F ∆的外心,若存在实数λ,使得120GF GF GP λ++=,则当12PF F ∆的面积为8时,a 的最小值为 .三、解答题:本大题共6小题,第22(或23)小题10分,其余每题均为12分,共70分.解答应写出文字说明、证明过程、计算步骤. 17.(本大题满分12分)已知数列{}n a 满足11a =,121n n a a +=+.(Ⅰ)求证:数列{1}n a +为等比数列; (Ⅱ)求数列12n n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n T .18.(本大题满分12分)某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如表所示:(Ⅰ)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?(Ⅱ)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取2名学生参加某项活动,问2名学生中有1名男生的概率是多少?(III )学生的学习积极性与对待班级工作的态度是否有关系?请说明理由. 附:22()()()()()n ad bc K a b c d a c b d -=++++ 19.(本大题满分12分)如图,四棱锥ABCD P -中,⊥PA 平面ABCD ,M BC PA AC AD AB BC AD ,4,3,//=====为线段AD 上一点,MD AM 2=,N 为PC 的中点.(Ⅰ)证明:;//PAB MN 平面 (Ⅱ)求四面体BCM N -的体积.20.(本大题满分12分)已知椭圆()01:2222>>=+b a by a x C 的左右顶点分别为1A ,2A ,左右焦点为分别为1F ,2F ,焦距为2,离心率为21.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)若P 为椭圆上一动点,直线1l 过点1A 且与x 轴垂直,M 为直线P A 2与1l 的交点,N 为直线P A 1与直线2MF 的交点,求证:点N 在一个定圆上. 21.(本大题满分12分)已知函数2()2ln f x x x ax =-+()a R ∈.(Ⅰ)当2a =时,求()f x 的图象在1x =处的切线方程;(Ⅱ)若函数()f x 有两个不同零点1x ,2x ,且120x x <<,求证:12'()02x x f +<,其中'()f x 是()f x 的导函数.选考题,考生从22、23两题中任选一题作答,将选择的题号对应的方程用2B 铅笔涂黑,多做按所做的第一题记分.22.[选修4-4:坐标系与参数方程] (本大题满分10分)在平面直角坐标系xOy 中,曲线1C 的参数方程为为参数)ααα(sin 2cos 22⎩⎨⎧=+=y x .以平面直角坐标系的原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,直线2C 的极坐标方程为3sin =θρ.(Ⅰ)求曲线1C 的极坐标方程;(Ⅱ)设1C 和2C 交点的交点为A ,B ,求AOB ∆的面积.23.(本大题满分10分)已知函数2()2f x x =-,()g x x a =-. (Ⅰ)若1a =,解不等式()()3f x g x +≥;(Ⅱ)若不等式()()f x g x >至少有一个负数解,求实数a 的取值范围.四川省棠湖中学2018年高考适应性考试数学试卷(文史类)参考答案一.选择题二.填空题 13.213 14.32 15.1132548+- 16.4 17.解:(1)∵121n n a a +=+,∴112(1)n n a a ++=+. 又11a =,∴1120a +=≠,10n a +≠. ∴{1}n a +是以2为首项,2为公比的等比数列. (2)由(1)知21n n a =-,∴1122(21)(21)n nnn n n a a ++=--1112121n n +=---, ∴22111212121n T =-+---31111212121n n +-+⋅⋅⋅+---- 11121n +=--.18.解:(1)由题知,不积极参加班级工作且学习积极性不高的学生有19人,总人数为50人,所以1950P =. (2)设这7名学生分别为a ,b ,c ,d ,e ,A ,B (大写为男生),则从中抽取两名学生的情况有:(,)a b ,(,)a c ,(,)a d ,(,)a e ,(,)a A ,(,)a B ,(,)b c ,(,)b d ,(,)b e ,(,)b A ,(,)b B ,(,)c d ,(,)c e ,(,)c A ,(,)c B ,(,)d e ,(,)d A ,(,)d B ,(,)e A ,(,)e B ,(,)A B 共21种情况,其中有1名男生的有10种情况,∴1021P =.(3)由题意得,2250(181967)11.53810.82824262525K ⨯⨯-⨯=≈>⨯⨯⨯, 故有99.9%的把握认为“学生的学习积极性与对待班级工作的态度”有关系.19.解(1)由已知得232==AD AM ,取RP 的中点T ,连接TN AT ,,由N 为PC 中点知,221,//==BC TN BC TN ,即,AM TN =又BC AD //,即,//AM TN 故四边形AMNT 为平行四边形,于是,//AT MN 因为,,PAB MN PAB AT 平面平面⊄⊂所以,//PAB MN 平面(2)因为⊥PA 平面ABCD ,N 为PC 的中点,所以N 到平面ABCD 的距离为,21PA 取BC 得中点E ,连接AE ,由3==AC AB 得,5,22=-=⊥BE AB AE BC AE 由BC AM //得M 到BC 的距离为5,故5421⨯⨯=∆BCM S ,所以四面体BCM N -的体积为.354231=⨯⨯=∆-PA S V BCM BCM N 20.解: (I ) 21,22==e c 3,2==∴b aC ∴的方程13422=+∴y x(II )设点),(y x N()11,y x P ()221<<-x ,则1342121=+y x ,即3442121-=-x y,2:1-=x l 直线P A 2的方程:()2211--=x x y y ⎪⎪⎭⎫ ⎝⎛--∴24-,211x y M ,又2111+=x y k P A , ∴直线P A 1的方程为)1()2(211++=x x y y ∴)2(34112-=x y k MF∴直线2MF 的方程为)2()1()2(3411--=x x y y由(1),(2)得:)1)(2()4(3421212-+-=x x x y y ∴)1)(2(2-+-=x x y 即 0222=-++x y x 所以,点N 在定圆上。
四川省棠湖中学2018届高三下学期第二次月考数学(文)试题(解析版)

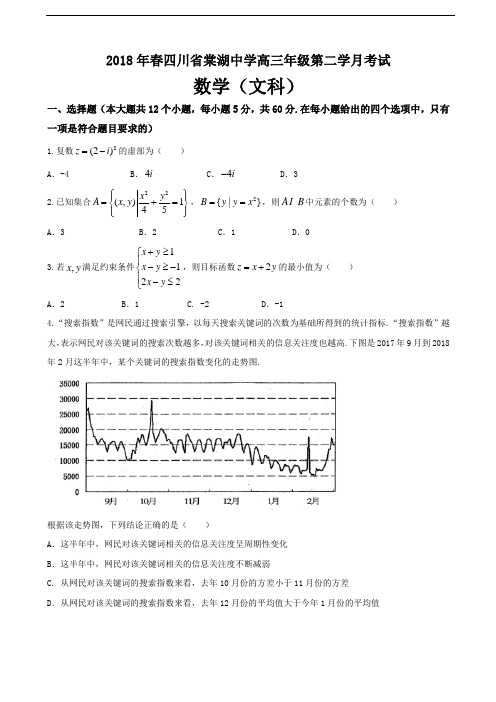
2018年春四川省棠湖中学高三年级第二学月考试数学(文科)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.复数的虚部为()A. -4B.C.D. 3【答案】A【解析】由题意,复数,所以复数的虚部为,故选A.2.已知集合,,则中元素的个数为()A. 3B. 2C. 1D. 0【答案】B【解析】集合的元素表示的是椭圆上的点,集合的元素表示的是抛物线上的点,由数形结合可知,两图象有两个交点,则中的元素个数为2,故选B.3.若满足约束条件,则目标函数的最小值为()A. 2B. 1C. -2D. -1【答案】B【解析】可行域如图,则直线过点A(1,0)时取最小值1,选B.4.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.根据该走势图,下列结论正确的是()A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化B. 这半年中,网民对该关键词相关的信息关注度不断减弱C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值【答案】D【解析】选项A错,并无周期变化,选项B错,并不是不断减弱,中间有增强。
C选项错,10月的波动大小11月分,所以方差要大。
D选项对,由图可知,12月起到1月份有下降的趋势,所以会比1月份。
选D.5.一个简单几何体的三视图如图所示,其中正视图是等腰直角三角形,侧视图是边长为2的等边三角形,则该几何体的体积等于()A. B. C. D. 2【答案】D【解析】由三视图可知,该几何体是一个四棱锥,由侧视图为边长为的正三角形,结合三视图的性质可知四棱锥底面是边长为和的矩形,四棱锥的高为,故四棱锥体积为,故选D.【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力,属于难题.三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响,对简单组合体三视图问题,先看俯视图确定底面的形状,根据正视图和侧视图,确定组合体的形状.6.我国古代数学名著《增删算法统宗》中有如下问题:“有个金球里面空,球高尺二厚三分,一寸自方十六两,试问金球几许金?”意思是:有一个空心金球,它的直径12寸,球壁厚0.3寸,1立方寸金重1斤,试问金球重是多少斤?(注)()A. 125.77B. 864C. 123.23D. 369.69【答案】C【解析】由题意知,大球半径,空心金球的半径,则其体积(立方寸).因1立方寸金重1斤,则金球重斤,故选C.7.执行下面的程序框图,如果输入,,则输出的()A. 7B. 20C. 22D. 54【答案】B【解析】初始值a=1,b=1,s=0,k=0s=2,a=2,b=3,k=2,s=7,a=5,b=8,k=4s=20,a=13,b=21,k=6输出s=20,选B.8.在中,“”是“”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】C【解析】由题意等价于,根据正弦定理可得,即,则中,“” 是“”的充要条件,故选C.9.若,则=()A. B. C. D.【答案】B【解析】由,解得,又,故选B.10.椭圆:的左、右顶点分别为、,点在上,且直线的斜率的取值范围是,那么直线斜率的取值范围是()A. B. C. D.【答案】A【解析】由椭圆,可知其左右顶点为,设,则,可得,因为,所以,因为,所以,解得,故选A.11.已知是函数的零点,是函数的零点,且满足,则实数的最小值是()A. B. C. D.【答案】A【解析】因为,所以函数在上单调递减,在单调递增,故,故为方程的根,故,故解得,所以在上有解,即在上有解,令,可求得,所以,解得,故选A.点睛:解题的关键是得到后,得到,然后将问题转化成方程在上有解的问题处理.在解题的过程中分离参数的方法,转化为求函数在闭区间的最值问题处理,求最值时可用导数或基本不等式处理,具体求解中要注意合理的变形.12.已知当时,函数的图象与的图象有且只有一个交点,则正实数m的取值范围是A. B.C. D.【答案】B【解析】当时,,单调递减,且,单调递增,且,此时有且仅有一个交点;当时,,在上单调递增,所以要有且仅有一个交点,需选B.【名师点睛】已知函数有零点求参数取值范围常用的方法和思路(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围;(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量,满足,|,,则|__________.【答案】【解析】由向量满足,所以,所以,解得.14.已知偶函数在上单调递减,且,若,则的取值范围是__________.【答案】【解析】根据题意为偶函数,则,又由在上单调递减,且,则,即,所以,解得或,即的取值范围是.15.设抛物线的焦点为是抛物线上一点,的延长线与轴相交于点,若,则__________.【答案】10【解析】抛物线的焦点为又则为的三等分点,故横坐标为,代入求得则故点睛:本题考查了直线与抛物线之间的位置关系,结合向量的综合运用题目,依据条件中,运用线性关系可得三点的位置关系,代入坐标计算,从而可以求出各点坐标,继而解得结果16.设函数与有公共点,且在公共点处的切线方程相同,则实数的最大值为__________.【答案】.【解析】由题意得,设与在公共点处的切线相同,由题意得,即,由可得或(舍去),∴,设,则,∴当时,单调递增,当时,单调递减.∴,∴实数的最大值为.答案:点睛:本题以导数的几何意义为载体,考查函数最值的求法.具体来讲就是根据两函数在交点处的切线相同得到关于切点坐标的方程组,根据得到的相等关系将问题转化为求函数的最大值的问题处理,最后根据导数求解即可.三、解答题(解答应写出文字说明、证明过程或演算步骤;17~21每题12分,选做题10分,共70分)17.已知数列的前项和为,向量,满足条件⊥(Ⅰ)求数列的通项公式;(Ⅱ)设,求数列的前项和.【答案】(1) (2)【解析】试题分析:(1)由⊥可得,然后根据与的关系可得.(2)由(1)可得,根据数列项的特征选择用错位相减法求和.试题解析:(1)∵⊥,,,∴,当时,,当时,满足上式,∴.(2)由(1)可得,∴,①∴,②①②,得,.点睛:(1)数列的通项a n与前n项和S n的关系是,当n=1时,a1若适合,则n=1的情况可并入n≥2时的通项a n;当n=1时,a1若不适合,则用分段函数的形式表示.(2)错位相减是数列求和的一种重要方法,但值得注意的是,这种方法运算过程复杂,运算量大,应加强对解题过程的训练,重视运算能力的培养.18.某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以(单位:盒,)表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.(1)根据直方图估计这个开学季内市场需求量的平均数;(2)将表示为的函数;(3)根据直方图估计利润不少于4000元的概率.【答案】(1)153;(2) ;(3)0.7.【解析】试题分析:(1)根据分布图先算出各频率,然后再计算求出平均数(2)分类讨论当时及当时两种情况,分别写出解析式(3)代入求解结果即可解析:(1)需求量为的频率,需求量为的频率,需求量为的频率,需求量为的频率,需求量为的频率.则平均数.(2)因为每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元,所以当时,,当时,,所以(3)因为利润不少于4000元,解得,解得.所以由(1)知利润不少于4000元的概率.19.如图,在四棱锥中,平面,底面是菱形,为与的交点,为棱上一点.(1)证明:平面平面;(2)若平面,求三棱锥的体积.【答案】(1)证明见解析;(2).【解析】试题分析:(1)由已知得由此能证明平面平面(2)由已知得,取中点,连结,由此利用可求得三棱锥的体积.试题解析:(1)∵平面平面,∴.∵四边形是菱形,∴.又∵,∴平面.而平面,∴平面平面;(2)连接,∵平面,平面平面,∴.∵是的中点,∴是的中点.取的中点,连接,∵四边形是菱形,,∴,又,∴平面,且,故.点睛:本题考查平面与平面垂直的证明,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的灵活应用.20.设椭圆的离心率,左焦点为,右顶点为,过点的直线交椭圆于两点,若直线垂直于轴时,有(1)求椭圆的方程;(2)设直线:上两点,关于轴对称,直线与椭圆相交于点(异于点),直线与轴相交于点.若的面积为,求直线的方程.【答案】(1);(2)或.【解析】试题分析:(1)由离心率可得的关系,再由,结合隐含条件,求得的值,即可得到椭圆的方程;(2)设直线的方程为,与直线的方程联立,可得点的坐标,进一步得到的坐标,联立直线与椭圆的方程,求得的坐标,则所在的直线方程可求,取,求得的坐标,得到,结合的面积为,即可求解实数的值,得到直线方程.试题解析:(1)设,因为所以有,又由得,且,得,因此椭圆的方程为:.(2)设直线的方程为,与直线的方程联立,可得点,故.将与联立,消去,整理,解得,或.由点异于点,可得点.由,可得直线的方程为,令,解得,故. 所以.又因为的面积为,故,整理得,解得,所以.所以,直线的方程为或.点睛:本题主要考查椭圆的方程与几何性质性质、直线与圆锥曲线的位置关系及直线方程的求解,解答此类题目,通常利用的关系,确定椭圆(圆锥曲线)方程是基础,通过联立直线方程与椭圆(圆锥曲线)方程的方程组,应用一元二次方程根与系数的关系,得到“目标函数”的解析式,确定函数的性质进行求解,本题能较好的考查考生的逻辑思维能力、运算求解能力、分析问题解决问题的能力等.21.函数.(I)求的单调区间;(II)若,求证:.【答案】(1)a≤0时,的单调递减区间是;时,的单调递减区间是,的单调递增区间是.(2) 证明见解析.【解析】试题分析:(1)求出导数,根据对的分类讨论,找到导数正负区间,即可求出;(2)求出函数的最小值,转化为证≥,构造,求其最小值,即可解决问题.试题解析:(Ⅰ).当a≤0时,,则在上单调递减;当时,由解得,由解得.即在上单调递减;在上单调递增;综上,a≤0时,的单调递减区间是;时,的单调递减区间是,的单调递增区间是.(Ⅱ)由(Ⅰ)知在上单调递减;在上单调递增,则.要证≥,即证≥,即+≥0,即证≥.构造函数,则,由解得,由解得,即在上单调递减;在上单调递增;∴,即≥0成立.从而≥成立.点睛:本题考查函数的单调性极值及恒成立问题,涉及函数不等式的证明,综合性强,难度大,属于难题.处理导数大题时,注意分层得分的原则,力争第一二问答对,第三问争取能写点,一般涉及求函数单调性及极值时,比较容易入手,求导后注意分类讨论,对于恒成立问题一般要分离参数,然后利用函数导数求函数的最大值或最小值,对于含有不等式的函数问题,一般要构造函数,利用函数的单调性来解决,但涉及技巧比较多,需要多加体会.请考生在22、23两题中任选一题作答,并用2B铅笔在答题卡上把所选题目的题号涂黑.注意所做题目的题号必须与所涂题目的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.选修4-4:坐标系与参数方程22.在平面直角坐标系中,直线的参数方程为(为参数),在以直角坐标系的原点为极点,轴的正半轴为极轴的极坐标系中,曲线的极坐标方程为.(1)求曲线的直角坐标方程和直线的普通方程;(2)若直线与曲线相交于,两点,求的面积.【答案】(Ⅰ)(Ⅱ)【解析】试题分析:(1)根据极坐标与直角坐标的互化公式,即得到曲线的直角坐标方程;由直线的参数方程,消去参数,即可得到直线的普通方程;(2)把直线的参数方程代入曲线的方程,得到,,利用弦长公式,得到的长,再利用点到直线的距离公式求的原点到直线的距离,即可求解三角形的面积.试题解析:(1)由曲线的极坐标方程为,得,所以曲线的直角坐标方程是.由直线的参数方程为(为参数),得直线的普通方程.·······6分(2)由直线的参数方程为(为参数),得(为参数),代入,得,设,两点对应的参数分别为,,则,,所以,因为原点到直线的距离,所以.选修4-5:不等式选讲23.选修4-5:不等式选讲已知定义在上的函数的最小值为.(Ⅰ)求的值;(Ⅱ)若,,为正实数,且,求证:.【答案】(1) (2)见解析【解析】试题分析:(1)利用绝对值不等式的几何意义可得,从而得的值;(2)利用柯西不等式,即可证明.试题解析:(1)因为,当且仅当时,等号成立,所以的最小值等于,即.(2)证明:由(1) 知,又因为是正实数,所以,即.考点:绝对值的几何意义;不等式的证明.。
四川省棠湖中学2019届高三数学上学期第三次月考试题文

2018年秋四川省棠湖中学高三第三学月考试数学(文)试卷第Ⅰ卷(选择题 共60分)一.选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.在复平面内,复数z 满足(1)2z i -=,则z 的共轭复数对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限 2.已知集合{12}M x x =-<,集合{(1)(3)0}N x Z x x =∈+-≤,则MN =A .{0,1,2}B .{1,0,1,2}-C .{1,0,2,3}-D .{0,1,2,3} 3.角θ的终边经过点(4,)P y ,且sin θ=35-,则n ta θ= A. 43- B.43 C. 34- D. 344.已知数列{}n a 的通项公式为n aa n n=+,则“12a a >”是“数列{}n a 单调递增”的 A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 5.若当x θ=时,函数()3sin 4cos f x x x =+取得最大值,则cos θ= A .35 B .45 C .35- D .45- 6.《周碑算经》中有这样一个问题:从冬至日起,依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气其日影长依次成等差数列,冬至、立春、春分日影长之和为31.5尺,前九个节气日影长之和为85.5尺,则小满日影长为 A.1.5尺 B.2.5尺 C.3.5尺 D.4.5尺 7.函数||()e 2||1x f x x =--的图象大致为8.已知向量,a b 满足0⋅=a b ,||m +=|a b |a ,若+a b 与-a b 的夹角为32π,则m 的值为A .2B .1 D .129.已知函数())ln31f x x =+,则()()3lg(lg3)lg(log 10)f f +=A .-1B .0C .1D .210.若1a >,设函数()4x f x a x =+-的零点为m ,()log 4a g x x x =+-的零点为n ,则11m n +的取值范围是A .(3.5,+∞)B .(1,+∞)C .(4,+∞)D .(4.5,+∞) 11.定义在R 上的奇函数)(x f 满足)83()83(x f x f -=+,并且当830≤≤x 时,116)(-=x x f ,则=)100(fA. 21-B. 1-C. 23- D. 2-12.己知直线0l y m ++=与双曲线()2222:10,0x y C a b a b-=>>右支交于M ,N 两点,点M 在第一象限,若点Q 满足0OM OQ +=(其中O 为坐标原点),且30MNQ ∠=,则双曲线C 的渐近线方程为A .12y x =±B .y x =±C .2y x =±D .y = 第Ⅱ卷(共90分)二.填空题:本大题共4小题,每小题5分,共20分。
四川省棠湖中学2018届高三3月月考语文

2018年春期四川省棠湖中学高三年级第一学月考试语文试题语文试题卷共8页,满分150分,考试时间150分钟。
一、现代文阅读(35分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1--3题。
具有五千多年历史的中华民族积淀了丰富多彩、辉煌灿烂的民族文化。
如何让这些优秀的传统文化得以传承和发展,在当代社会越来越成为一个值得思考的深刻问题。
中国传统文化的核心内容就是以儒、道、禅为一体的思想系统,这也体现了中国传统文化的丰富性、开放性和包容性。
要想把握中国传统文化的精神内核,就需要对它的思想体系进行学习和理解,因此教育在这里起着至关重要的作用。
从这个角度来看,立青少年去学习四书五经、古典诗词等国学经典是非常有意义的一个举措。
但是不能让学习中国传统经典成为一种形式主义一一为了考试而学习、为了背诗而背诗,这与让中国传统经典走进教育的真正目的-一学习理解中国传统文化的精神内核是本末倒置的。
只有通过教育让中国传统文化的思想观念内化于心,才能在传承中国传统文化的过程中把握住其精神内核。
中国传统文化其有丰富多彩的表现形式,而中国传统艺术可以说是其最集中的表现形式。
中国戏曲种类繁多,不论是昆曲、京剧,还是黄梅戏、河北梆子,其化妆、服裴、语调、唱词、步法无不体现着中国特色,这与以欧洲歌剧为代表的外国戏曲艺术明显不同。
中国的水墨画使用宣纸、毛笔、墨汁,讲究“逸笔草草,不求形似”,追求在一幅有限的画境里觅得无限的天地,这与西方油画的画布、笔刷、颜料等工具以及将绘画当做科学从而追求客观、逼真的传统绘画态度也大相径庭。
中国书法更是发展出篆书、隶书、楷书、”行书、草书等多种字体,成为世界艺术中的一朵奇葩。
中国传统艺术是中国传统文化的关的精华。
传统文化的传承不能缺少传统艺术。
传承中国传统文化不能仅仅停留在思想上,还应身体力行,落实到人们的生活实践中,构成具有中国特色的“思想行为范式”。
炎黄子孙在华夏文地躬耕多年,已形成许多对自然和生活的认识。
四川省棠湖中学高三上学期第一次月考数学(文)试题

2018年秋期四川省棠湖中学高三第一学月考试文科数学第I 卷 选择题(共60分)一.选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}是菱形或矩形x x A |=,{}是矩形x x B |=,则=B C A ( )A.{}是菱形x x |B.{}形是内角都不是直角的菱x x |C.{}是正方形x x |D.{}是邻边都不相等的矩形x x |2.已知向量(1,1),2(4,2)=+=a a b ,则向量,a b 的夹角的余弦值为( ) AB. C.2 D.2- 3.为了在一条河上建一座桥,施工前在河两岸打上两个桥位桩,A B (如图),要测算,A B 两点的距离,测量人员在岸边定出基线BC ,测得50BC m =,105,45ABC BCA ∠=∠=,就可以计算出,A B 两点的距离为A.m B.m C.mD. 2m 4.为了得到函数的图象,可以将函数的图象A .向左平移个单位长度B .向右平移个单位长度C .向左平移个单位长度 D .向右平移个单位长度5.设m ,n 是两条不同的直线, α,β,γ是三个不同的平面.有下列四个命题: ①若//αβ,m α⊂,n β⊂,则//m n ; ②若m α⊥,//m β,则αβ⊥;③ 若n α⊥,n β⊥,m α⊥,则m β⊥;④ 若αγ⊥,βγ⊥,m α⊥,则m β⊥. 其中错误..命题的序号是 A .①③ B .①④ C .②③④ D .②③ 6. 函数21()log f x x x=-的零点所在区间为 BACA.1(0,)2B.1(,1)2C.(1,2)D.(2,3) 7.如图所示,在边长为1的正方形OABC 中任取一点P ,则点P恰好取自阴影部分的概率为A .41 B .51 C .61 D .71 8.53)sin(=+πα,则=+)4(2sin παA.259B.259-C.错误!未找到引用源。
2018届四川省棠湖中学高三下学期第二次月考数学(文)试题含答案
2018年春四川省棠湖中学高三年级第二学月考试数学(文科)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.复数2(2)z i =-的虚部为( )A .-4B .4iC .4i -D .32.已知集合22(,)145x y A x y ⎧⎫⎪⎪=+=⎨⎬⎪⎪⎩⎭,2{|}B y y x ==,则A B 中元素的个数为( )A .3B .2C .1D .03.若,x y 满足约束条件1122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩,则目标函数2z x y =+的最小值为( )A .2B .1 C. -2 D .-14.“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.根据该走势图,下列结论正确的是( )A .这半年中,网民对该关键词相关的信息关注度呈周期性变化B .这半年中,网民对该关键词相关的信息关注度不断减弱C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差 D .从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值5.一个简单几何体的三视图如图所示,其中正视图是等腰直角三角形, 侧视图是边长为2的等边三角形,则该几何体的体积等于( )A .3.3C. .26.我国古代数学名著《增删算法统宗》中有如下问题:“有个金球里面空,球高尺二厚三分,一寸自方十六两,试问金球几许金?”意思是:有一个空心金球,它的直径12寸,球壁厚0.3寸,1立方寸金重1斤,试问金球重是多少斤?(注3π≈)( )A .125.77B .864C .123.23D .369.697.执行下面的程序框图,如果输入1a =,1b =,则输出的S =( )A .7B .20 C.22 D .54 8.在ABC ∆中,,""B A >是B A sin sin >的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件 9.若3)4tan(=-πα,则=-αα2cos 32sin =( )A .57 B .57- C .4- D .58- 10.椭圆C :22143x y +=的左、右顶点分别为1A 、2A ,点P 在C 上,且直线2PA 的斜率的取值范围是[]2,1--,那么直线1PA 斜率的取值范围是( )A .33,84⎡⎤⎢⎥⎣⎦ B .3,14⎡⎤⎢⎥⎣⎦ C .1,12⎡⎤⎢⎥⎣⎦ D .13,24⎡⎤⎢⎥⎣⎦11.已知1x 是函数()()1ln 2f x x x =+-+的零点,2x 是函数()2244g x x ax a =-++的零点,且满足121x x -≤,则实数a 的最小值是( )A .1-B .2-C .2-.1-12.已知当[]1.0∈x 时,函数2)1(m x y -=的图象与mx my 112+=的图象有且只有一个交点,则正实数m 的取值范围是( )A .(0,1]∪[3,+∞)B .(][)+∞,321,0C .(][)+∞,322,0D .(][)+∞,32,0第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量a ,b 满足a b ⊥,||2a =,|2|23a b +=,则||b = .14.已知偶函数()f x 在[)0,+∞上单调递减,且()45f =,若()215f x +<,则x 的取值范围是 .15.设抛物线28y x =的焦点为,F M 是抛物线上一点,FM 的延长线与y 轴相交于点N ,若2N M M F=,则FN = . 16.设函数()232(0)2f x x ax a =->与()2g x a lnx b =+有公共点,且在公共点处的切线方程相同,则实数b 的最大值为 .三、解答题(解答应写出文字说明、证明过程或演算步骤;17~21每题12分,选做题10分,共70分)17.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,向量)2,(n S =,(1,12)nb =-满足条件a ⊥b(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设n nnc a =,求数列{}n c 的前n 项和n T .18.某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以x (单位:盒,100200x ≤≤)表示这个开学季内的市场需求量,y (单位:元)表示这个开学季内经销该产品的利润.(Ⅰ)根据直方图估计这个开学季内市场需求量x 的平均数;(Ⅱ)将y 表示为x 的函数;(III )根据直方图估计利润y 不少于4000元的概率.19.如图,在四棱锥P ABCD -中,PD ⊥平面ABCD ,底面ABCD 是菱形,60BAD ∠=︒,2AB =,PD O 为AC 与BD 的交点,E 为棱PB 上一点.(Ⅰ)证明:平面EAC ⊥平面PBD ;(Ⅱ)若//PD 平面EAC ,求三棱锥P EAD -的体积.20.(本小题满分12分)设椭圆22221(0)x y a b a b+=>>的离心率12e =,左焦点为F ,右顶点为A ,过点F 的直线交椭圆于HE ,两点,若直线EH 垂直于x 轴时,有23=EH (Ⅰ)求椭圆的方程;(Ⅱ)设直线l :1x =-上两点P ,Q 关于x 轴对称,直线AP 与椭圆相交于点B (B 异于点A ),直线BQ与x 轴相交于点D .若APD △AP 的方程.21.函数()()()21ln 122f x x ax a x a =-++--∈R . (Ⅰ)求()f x 的单调区间; (Ⅱ)若0a >,求证:()32f x a≥-.请考生在22、23两题中任选一题作答,并用2B 铅笔在答题卡上把所选题目的题号涂黑.注意所做题目的题号必须与所涂题目的题号一致,在答题卡选答区域指定位置答题.如果多做,则按所做的第一题计分.22.[选修4-4:坐标系与参数方程]在平面直角坐标系xOy 中,直线l 的参数方程为21x ty t =-⎧⎨=-+⎩(t 为参数),在以直角坐标系的原点O 为极点,x 轴的正半轴为极轴的极坐标系中,曲线C 的极坐标方程为22sin cos θρθ=. (Ⅰ)求曲线C 的直角坐标方程和直线l 的普通方程;(Ⅱ)若直线l 与曲线C 相交于A ,B 两点,求AOB ∆的面积.23.选修4-5:不等式选讲已知定义在R 上的函数()|1||2|f x x x =++-的最小值为a . (Ⅰ)求a 的值;(Ⅱ)若p ,q ,r 为正实数,且p q r a ++=,求证:2223p q r ++≥.2018年春四川省棠湖中学高三年级第二学月考试数学(文科)答案一.选择题二.填空题13.2 14.),23()25,(+∞--∞ 15.10 16.221e 17.解:(1)∵⊥,∴221-=+n n S ,当2≥n 时,n n n n S S a 21=-=-, 当1=n 时,211==S a 满足上式,∴nn a 2=(2)2n nn c =1211212222n n n n nT --=++++L 两边同乘12,得231112122222n n n n nT +-=++++L ,两式相减得: 211111*********n n n n n n T +++=++-=-L , ()222n n n T n N ++∴=-∈.18.解:(1)需求量为[)100,120的频率0.005200.1=⨯=, 需求量为[)120,140的频率0.01200.2=⨯=, 需求量为[)140,160的频率0.015200.3=⨯=, 需求量为[)160,180的频率0.0125200.25=⨯=, 需求量为[)180,200的频率0.0075200.15=⨯=.则平均数1100.11300.21500.31700.251900.15153x =⨯+⨯+⨯+⨯+⨯=. (2)因为每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元,所以当100160x ≤≤时,()3010160401600y x x x =-⨯-=-, 当160200x <≤时,160304800y =⨯=,所以401600,1001604800,160200x x y x -≤≤⎧=⎨<≤⎩(3)因为利润不少于4000元,解得4016004000x -≥,解得140x ≥. 所以由(1)知利润不少于4000元的概率10.30.7p =-=. 19.(1)证明:∵PD ⊥平面ABCD ,AC ⊂平面ABCD , ∴AC PD ⊥.∵四边形ABCD 是菱形,∴AC BD ⊥. 又∵PDBD D =,∴AC ⊥平面PBD ,而AC ⊂平面EAC , ∴平面EAC ⊥平面PBD . (2)连接OE ,∵//PD 平面EAC ,平面EAC平面PBD OE =,∴//PD OE .∵O 是BD 的中点,∴E 是PB 的中点, 取AD 的中点H ,连接BH ,∵四边形ABCD 是菱形,60BAD ∠=︒,∴BH AD ⊥,又BH PD ⊥,AD PD D =,∴BH ⊥平面PAD ,且2BH AB ==故111112223622P EAD E PAD B PAD PAD V V V S BH ---∆===⨯⨯⨯=⨯⨯=. 20.解:(1)设(,0)(0)F c c ->,因为12e =所以有2a c =,又由23=EH 得2322=a b , 且222c b a +=,得43,12==b a ,因此椭圆的方程为:13422=+y x …4分 (2)设直线AP 的方程为1(0)x my m =+≠,与直线l 的方程1x =-联立,可得点2(1,)P m--,故2(1,)Q m -.将1x my =+与22413y x +=联立,消去x ,整理得22(34)60m y my ++=,解得0y =,或2634my m -=+.由点B 异于点A , 可得点222346(,)3434m m B m m -+-++.由2(1,)Q m -,可得直线BQ 的方程为22262342()(1)(1)()03434m m x y m m m m--+-+-+-=++,令0y =, 解得222332m x m -=+,故2223(,0)32m D m -+. 所以2222236||13232m m AD m m -=-=++.又因为APD △的面积为222162232||2m m m ⨯⨯=+,整理得23|20m m -+=,解得||m =,所以m =.所以,直线AP 的方程为330x -=,或330x -=.21.解:(Ⅰ)xx ax x x a ax a ax x x f )1)(1(1)1()1(1)(2+-=--+=-++-='. ① 当a ≤0时,0)(<'x f ,则)(x f 在)0(∞+,上单调递减; ② 当0>a 时,由0)(>'x f 解得a x 1>,由0)(<'x f 解得ax 10<<. 即)(x f 在)10(a ,上单调递减;)(x f 在)1(∞+,a上单调递增; 综上,a ≤0时,)(x f 的单调递减区间是)0(∞+,;0>a 时,)(x f 的单调递减区间是)10(a ,,)(x f 的单调递增区间是)1(∞+,a. (Ⅱ) 由(Ⅰ)知)(x f 在)10(a ,上单调递减;)(x f 在)1(∞+,a上单调递增, 则121ln )1()(min --==aa a f x f . 要证)(x f ≥a 23-,即证121ln --a a ≥a 23-,即a ln +11-a ≥0,即证a ln ≥a11-构造函数11ln )(-+=aa a μ,则22111)(a a a a a -=-='μ,由0)(>'a μ解得1>a ,由0)(<'a μ解得10<<a ,即)(a μ在)10(,上单调递减;)(a μ在)1(∞+,上单调递增; ∴ 01111ln )1()(min =-+==μμa ,即11ln -+aa ≥0成立.从而)(x f ≥a23-成立. 22.【选修4−4:坐标系与参数方程】 解:(Ⅰ)由曲线C 的极坐标方程为22sin cos θρθ=,得22cos 2sin ρθρθ=,所以曲线C 的直角坐标方程是22x y =.由直线l 的参数方程为21x t y t =-⎧⎨=-+⎩,,(t 为参数),得直线l 的普通方程10x y +-=.(Ⅱ)由直线l 的参数方程为21x t y t =-⎧⎨=-+⎩,,(t 为参数),得21x y ⎧=⎪⎪⎨⎪=-⎪⎩,,(t 为参数),代入22x y =,得2120t -+=,设A B ,两点对应的参数分别为12t t ,,则121212t t t t +==,所以12||||AB t t =-=,因为原点到直线10x y +-=的距离d ,所以11||22AOB S AB d ==⨯=△.23.解:(1)因为|1||2||(1)(2)|3x x x x ++-≥+--=,当且仅当12x -≤≤时,等号成立, 所以()f x 的最小值等于3,即3a =.(2)由(1)知3p q r ++=,又因为p ,q ,r 是正数,∴22222222()(111)(111)()9p q r p q r p q r ++++≥⨯+⨯+⨯=++=, 即2223p q r ++≥.。
精品解析:【全国百强校】四川省棠湖中学2018届高三3月月考英语试题(原卷版)
汇聚名校名师,奉献精品资源,打造不一样的教育!1 学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...学&科&网...2018年春期四川省棠湖中学高三年级第一学月考试英语试卷考试时间:120 分钟 满分:150 分第一部分 听力(共两节,满分30 分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案 转涂到答题卡上。
第一节 (共5 小题;每小题l.5 分,满分7.5 分)听下面5 段对话。
每段对话后有一个小题,从题中所给的A 、B 、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10 秒钟的时间来回答有关小题和阅 读下一小题。
每段对话仅读一遍。
1. What does the man suggest the woman do?A. Quit her job.B. Find another restaurant to work in.C. Work three nights a week.2. What are the speakers doing?A. Cooking.B. Having a meal at home.C. Eating in a restaurant.3. What car does the man have?A. An Audi.B. A Ford.C. A Ferrari.4. Who will begin the lecture now?A. Dr. White.B. Prof. Brookings.C. Dr. Mildens.5. What are the speakers discussing?A. Animal fur.B. Some coats.C. A free diamond.第二节 (共15 小题; 每小题1.5 分,满分22.5 分)听下面5 段对话。
四川省棠湖中学高三文综上学期第一次月考试题
2018年秋期四川省棠湖中学高三第一学月考试文科综合能力测试第I卷(选择题 140分)本卷共35个小题,每小题4分,共140分,在每小题给出的四个选项中,只有一项是符合题目要求的。
在南太平洋一处海拔约562米的波尔斯金字塔岛上,存活着被人们认为已灭绝多年的神秘昆虫“树龙虾”。
树龙虾曾生活在距离波尔斯金字塔约21千米的豪勋爵岛,是澳大利亚的特产。
1918年,一艘运输船在豪勋爵岛搁浅。
1920年,科学家遗憾地对外宣布树龙虾正式灭绝。
下图为波尔斯金字塔岛景观图,据此完成下面小题。
1.波尔斯金字塔岛是一座孤岛,陡峭的峰顶好似恐龙的背脊。
推测该岛由 ( )A.流水沉积而成 B.海底火山喷发产生C.地壳陷落或海平面上升与大陆分离而成 D.珊瑚虫遗体堆积而成2.分析“树龙虾曾灭绝”的原因,最可能是 ( )A.气候变化 B.天敌捕杀 C.食物短缺 D.物种入侵剑川县地处云南省西部的横断山区东部,这里水系发育,土壤肥沃。
该县稻麦复种系统这一特有的耕作方式已有3000多年的历史,是我国地方农业文化、生物多样性、人与自然和谐发展的典型代表。
下图示意云南省剑川县稻麦复种系统。
据此完成下面小题。
3.该县稻麦复种耕作方式的主要优点是( )A.促进劳动力就业 B.提高土地利用率 C.防止土地石漠化 D.减少水分蒸发量4.与稻田期相比,麦田期有利于小麦生长的优势条件是( )A.气温较高 B.降水丰富 C.光照充足 D.土壤肥沃近年来我国开始实施油气进口多元化战略,原油进口“四面八方”格局初现,且进口量持续攀升。
图是我国石油进口通道示意图。
读下图,完成下列各题。
5.下列说法正确的是( )A.东北通道沿线沼泽面积大,利于施工 B.西南油气通道沿线地势平坦,利于施工C.海上通道必须经过马六甲海峡,安全性差 D.西北通道跨温带大陆性气候和温带季风气候区6.我国目前原油进口“四面八方”格局的出现有利于( )①缓解能源供需矛盾②增强能源供应安全③改变我国以煤炭发电为主的现状④提高大气环境质量A.①② B.②③ C.③④ D.①④下图为俄罗斯西伯利亚地区,这里是俄罗斯的一个重要开发区,针叶林分布……读图,完成下列各题。
四川省棠湖中学2018届高三数学3月月考试题 文
四川省棠湖中学2018届高三数学3月月考试题 文第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合1,0,12A ⎧⎫=⎨⎬⎩⎭,{}|cos ,B y y x x A π==∈,则AB =( )A .{}0,1B .{}1-C .{}1D .∅2.已知复数21a ii--为纯虚数(其中i 是虚数单位),则a 的值为( ) A .2 B .-2 C .12 D .12-3.为了得到函数sin(2)4y x π=-的图象,可以将函数sin 2y x =的图象( )A .向左平移4π个单位长度B .向右平移4π个单位长度C .向左平移8π个单位长度 D .向右平移8π个单位长度 4.如表是降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对应数据,根据表中提供的数据,求出y 关于x 的线性回归方程为0.70.35y x =+,则表中m 的值为( )A .3B .3.5C .4.5D .2.5 5.“11()()33ab<”是“22log log a b >”的A. 充分不必要条件B. 充要条件C. 必要不充分条件D. 既不充分也不必要条件6.已知等差数列}{n a 的前n 项和为,n S ,4,6212129=+=a a a 则数列}1{n S 的前10项和为( ) A .1211 B .1110 C. 109 D .987.用一个平面去截正方体,则截面不可能是( )A .直角三角形B .等边三角形 C. 正方形 D .正六边形8.若1sin()34πα-+=,则cos(2)3πα+=( )A .58B .78-C .58-D .789.如图所示的程序框图,若输入,3,8==n m 则输出的S 值为( )A .56B .336 C.360 D .1440 10.在四面体ABC S -中,,2,2,====⊥SC SA BC AB BC AB 平面⊥SAC 平面BAC ,则该四面体外接球的表面积为() A .π316B .π8 C. π38 D .π411.设O 为坐标原点,P 是以F 为焦点的抛物线22y px =(0p >)上任意一点,M 是线段PF 上的点,且2PM MF =,则直线OM 的斜率的最大值为( )AB .23.112.定义在R 上的函数()f x 满足()()f x f x -=,且对任意的不相等的实数1x ,2[0,)x ∈+∞有1212()()0f x f x x x -<-成立,若关于x 的不等式(2ln 3)2(3)(2ln 3)f mx x f f mx x --≥--++在[1,3]x ∈上恒成立,则实数m 的取值范围( )A .1ln 6[,1]26e + B .1ln 6[,2]3e + C .1ln 3[,2]3e +D .1ln 3[,1]26e + 第Ⅱ卷(非选择题,满分90分)注意事项:1.请用蓝黑钢笔或圆珠笔在第Ⅱ卷答题卡上作答,不能答在此试卷上。
2018最新试题资料-四川棠湖中学2019届高三语文上学期第一次月考试卷(含答案)
四川棠湖中学2019届高三语文上学期第一次月考试卷(含
答案)
5 c -畲族歌舞及闽剧进校园活动在台湾华夏科技大学举行,将传统戏曲以朝歌夜弦的形式展示于台湾学子眼前。
③“冰花男孩”事所激荡起的涟漪,绝不应止于对迅速行动的欣慰,事后的反应再迅疾,也比不上未雨绸缪得精准。
④纪录片《一本书一座城》发掘“找寻”的内在动力,使和广大读者如胶似漆,让城市印象更加丰满突出,给人影像及字双重感动。
⑤作为中国表演艺术的殿堂,国家大剧院坚定化自信,荟萃中外化精品,吸引世界知名院团、艺术家纷至沓,成为中外化交流的巨大平台。
⑥在60年的岁月里,乌兰牧骑涌现出了德德玛、拉苏荣等一批优秀队员,他们让草原歌舞陈陈相因,奉献出《顶碗舞》等艺术精品。
A①③⑤ B②④⑥ c①③⑥ D②④⑤
18、下列各句中,没有语病的一句是( ) (3分)
A随着大工业时代的到,导致我国许多传统手工技艺大量流失,而匠人身上那种似乎是与生俱的“匠人精神”,也渐被世人甚至是工匠遗忘。
B不论从专业程度、品质规模还是关注范围看,视频网站自己制作的视频内容在短期之内都不可与卫视播出的影视剧、综艺节目相提并论。
c为防止扬尘污染,环保局要求工地对建筑垃圾采取严格的防尘措施,并要求所有未采取湿法作业的拆迁工地全部停止施工处罚。
D朝鲜2月7日宣布利用运载火箭成功发射卫星,美国、日本和韩国纷纷指责朝鲜发射卫星是没有道理的,将造成东亚及太平洋地区的“不稳定”。
19、下列各句中,表达得体的一句是()(3分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
棠湖中学高2018级高三月考试题(一)(文科)一、选择题:(本大题共12小题,每小题5分,共60分)1、已知集合{}21(),1,log ,1,2x A y y x B y y x x ⎧⎫==>==>⎨⎬⎩⎭则B A ⋂等于( )A .∅B . {}01y y << C .112yy ⎧⎫<<⎨⎬⎩⎭D . 102y y ⎧⎫<<⎨⎬⎩⎭2.a 、b 为实数,集合},{1abM =,},{0a N =,x x f →:表示把集合M 中的元素x 映射到集合N 中仍为x ,则a+b ( ) A . 1- B . 0 C . 1,或2 D . 1±3、已知⎩⎨⎧<--≥+-=)0()0()(22x xx x x x x f ,则不等式02)(>+x f 解集是( )A .)2,2(-B .),2()2,(∞+⋃--∞C .)1,1(- D .),1()1,(∞+⋃--∞4、将一张画了直角坐标系且两轴的长度单位相同的纸折叠一次,使点(2,0)与点(-2, 4)重合,若点(5,8)与点(m ,n )重合,则m+n 的值为( )A .4B .-4C .13D .-135、若a,b R ∈则|a| <1,|b|<1,是|a+b|+|a-b|<2成立的 ( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件6、若函数b x a x a ax x f +-+-+=)2(27)1()(23的图象关于原点中心对称,则)(x fA .在[-3,3]上为增函数B .),3[+∞上为增函数,在]3,(--∞上为减函数C .在]3,3[-上为减函数D .在]3,(--∞ ),3[+∞上为增函数7、设x x x f sin )(=,若1x 、⎥⎦⎤⎢⎣⎡-∈2,22ππx 且)()(21x f x f >,则下列不等式必定成立的是( )A .21x x >B .21x x <C .2221x x > D .021>+x x8、)x (f 是定义在R 上的偶函数,)x (g 是定义在R 上的奇函数,已知)x (g =)1x (f -,若)1(g -=2001,则)2004(f 的值是 ( )A.2001B.-2001C.-2018D.20189、二次函数()x f 满足)2()2(+-=+x f x f , 又3)0(=f ,1)2(=f .若在[]m ,0有最大值3, 最小值1, 则m 的取值范围是( )A .()+∞,0 B .⎪⎭⎫⎢⎣⎡∞+,2 C .⎥⎦⎤ ⎝⎛2,0 D .⎥⎦⎤⎢⎣⎡4,210.设函数f(x)的定义域是[-4,4],其图象如图,那么不等式0sin )(≤xx f 的解集( ) A .[-2,1] B .[-4,2]∪[1,4] C .[)π--,4∪[)02,-∪[)π,1 D .不同于(A )、(B )、(C )11.若方程021411=+⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-a x x 有正数解,则实数a 的取值范围是 ( )A .()1,∞-B .)2,(--∞C .()2,3--D .()0,3-12.一水池有2个进水口,1 个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则一定能确定正确的论断是 ( ) A .① B .①② C .①③ D .①②③棠湖中学2018级高三复习月考试题(一)(文)二、填空题:(本题每小题4分,共16分)13、函数)(x f y =在定义域)0,(-∞内存在反函数,且=-=--)3(,2)1(12fx x x f 则14.若f (x )在定义域(-1,1)上的导数存在且满足f '(x) <0;又当a,b )1,1(-∈,且a+b=0 时,f(a)+f(b)=0,则不等式f(1-m)+f(1-m 2)>0的解集为 ; 15.已知函数)(x f 是奇函数,当0<x 时,2s i n 3)(2xa x x f π-=,且63=)(f ,则a 等于 .16.某航空公司规定,乘机所携带行李的重量(kg )与其运费(元)由如图的一次函数图像确定,那么乘客免费可携带行李的最大重量为 ___________。
三、解答题:(本题17—20小题每题12分,21、22小题13分,共74分) 17. 已知)21121()(+-=xx x f ,求证:对任意.0)()0(>≠∈x f x R x ,总有18.(本题满分12分) 记函数f(x)=132++-x x 的定义域为A, g(x)=lg[(x -a -1)(2a -x)](a<1) 的定义域为B. (1) 求A ;(2) 若B ⊆A, 求实数a 的取值范围.19.(本小题满分12分)已知命题p :方程0222=-+ax x a 在[]1,1-上有解;命题q :只有一个实数x 满足不等式2220,x ax a ++≤若命题""p q 或是假命题,求实数a 的取值范围。
20.(本题满分12分)函数13))1(,1()(,)(23+==+++=x y f P x f y c bx ax x x f 的切线方程为上的点过曲线(1)若)(,2)(x f x x f y 求时有极值在-==的表达式;(2)在(1)的条件下,求]1,3[)(-=在x f y 上最大值; 21.(本小题满分12分)有一组数据:)(,,,2121n n x x x x x x <<< ,它们的算术平均值为10,若去掉其中最大的一个,余下数据的算术平均值为9;若去掉其中最小的一个,余下数据的算术平均值为11。
(Ⅰ)求出第一个数1x 关于n 的表达式及第n 个数n x 关于n 的表达式。
(Ⅱ)若n x x x ,,,21 都是正整数,试求第n 个数n x 的最大值,并举出满足题目要求且n x 取到最大值的一组数据。
22.(本小题满分14分)已知),,(42)(2R c b a c bx ax x f ∈++=(Ⅰ)当0≠a 时,若函数f (x )的图象与直线x y ±=均无公共点,求证;4142>-b ac (Ⅱ)时43,4==c b 对于给定的负数8-≤a ,有一个最大的正数M (a ),使得5|)(|)](,0[≤∈x f a M x 时都有,问a 为何值时,M(a )最大,并求出这个最大值M(a ),证明你的结论.棠湖中学高三复习同步测试(一)(文)(答案)13.-2; 14.()2,1; 15,1; 16.140. 三、解答题:(本题共74分)17. )(x f 的定义域是),0(≠∈x R x)21122()21212)(()21121)(()(1--=+--=+--=--x x x x x x x x f).()21121()2112112(x f x x x x x =+-=--+-=∴)(x f 是偶函数.∵对任意x >0时,总有)(,0)(x f x f 又>是偶函数,那么当0)(),0(.0)()(,0>≠∈∴>-=<x f x R x x f x f x 总有对任意时。
18. 解:(1)2-13++x x ≥0, 得11+-x x ≥0, x<-1或x≥1即A=(-∞,-1)∪[1,+ ∞)(2) 由(x -a -1)(2a -x)>0, 得(x -a -1)(x -2a)<0.∵a<1,∴a+1>2a, ∴B=(2a,a+1).∵B ⊆A, ∴2a≥1或a+1≤-1, 即a≥21或a≤-2, 而a<1, ∴21≤a<1或a≤-2, 故当B ⊆A 时, 实数a 的取值范围是 (-∞,-2)∪[21,1]19.]22222:20(2)(1)02104211,1,||1||1,||16220.22480.02,10a x ax ax ax a x x a a x a a ax ax a y x ax a x a a a +-=+-=≠∴=-=⎡∈-≤≤∴≥⎣++≤=++∴∆=-=∴=∴ 解由,得,显然或分故或分“只有一个实数满足”即抛物线与轴只有一个交点,或分命}{""||10"""|100112p q a a P Q a a a a ≥=∴-<<<< 题或为真命题"时或命题或为假命题的取值范围为或分20.(本题满分12分)542)(5,4,2)3)(2)(1()3(1240)2(,2)()2(3)1(021232313:))1(,1()()1)(23()1()1)(1()1(:))1(,1()(23)()(123223+-+==-==-=+-∴=-'-==⎩⎨⎧=++=+⎩⎨⎧=-++=+++==-++=+++--'=-=++='+++=x x x x f c b a b a f x x f y c b a b a c b a b a x y f P x f y x b a c b a y x f f y f P x f y bax x x f c bx ax x x f 相联立解得由故时有极值在即故的切线方程为过点而即的切线方程为上点过求导数得)由解:((2)22'极大4514121)1(3=+⨯-⨯+=f ]1,3[)(-∴在x f 上最大值为1321.(本题满分12分)解:依条件:⎪⎩⎪⎨⎧-=+++-=+++=+++-(3))1(11(2) )1(9)1(103212121n x x x n x x x n x x x n n n ……………………3分 (Ⅰ)由(1)-(2)得:9+=n x n再(1)-(3)得:n x -=111……………………6分(Ⅱ)∵1x 是正整数,∴1111≥-=n x ,101≤≤⇒n ,∴199≤+=n x n ……………………10分当n=10时,11=x ,1910=x80932=+++x x x此时,取62=x ,73=x ,84=x ,95=x ,116=x ,127=x ,138=x ,149=x 即可。
∴当n=10时,n x 的最大值是19。
……………………12分22.(Ⅰ))(x f 的图象与y =x 无公共点.)5.(414,041164,)(,)3.(04116416)12(.04)12(,42222222分得二式相加得无公共点的图象与由同理分从而无实根即>-<++--=<-+-=--=∆=+-+=++∴b ac b ac b x y x f b ac b ac b c x b ax x c bx ax (Ⅱ))14(.215)(,8.,8)12(21522042244232648)()8.(538)(,.4)(,5163,8163)(,0.163)4()(2max 2分取最大值时因此当等号成立时当且仅当分分的较大根是方程所以此时时所以+-=-=+=-≤--=---=-=++->≤--≤-=<-++⋅=a M a a a aaa M x ax a M aa M a a ax f a aa x a x f。
