分析化学-数据处理
分析化学 数据处理

解:
x = 10.43%
∑ d = di = 0.18% = 0.036%
n
5
d ×100% = 0.036% ×100% = 0.35%
x
10.43%
注意有效数字!
∑ s =
d
2 i
=
8.6 ×10−7 = 4.6 ×10−4 = 0.046%
n −1
4
s ×100% = 0.046% ×100% = 0.44%
Ea = x − T
Er
=
Ea T
× 100%
6
例: 滴定的体积误差 滴定剂体积应为20~30mL
V 20.00 mL 2.00 mL
Ea ± 0.02 mL ± 0.02 mL
Er ± 0.1% ± 1%
称量误差 称样质量应大于0.2g
m 0.2000 g 0.0200 g
Ea ± 0.2 mg ± 0.2 mg
值,可以舍弃
(-2.58,+2.58)
(μ-2.58σ, μ+2.58σ)
(-3,+3)
(μ-3σ, μ+3σ)
概 率p
68.3% 95.0% 95.5% 99.0% 99.7%
27
2.3 有限数据的统计处理
总体
抽样
样本
观测
数据
统计处理
样本容量n: 样本所含的个体数.
28
2.3.1 数据的集中趋势
标准偏差:
σx =
n
∑ (xi − μ)2
i =1
n
n
∑ (xi − x)2
Sx =
i =1
n −1
μ已知(测量次数无限多)
分析化学中的数据处理

分析化学中的数据处理分析化学中的数据处理是指针对实验数据进行整理、统计、分析和解释的一系列过程。
对数据进行适当的处理能够提取出更有意义的信息,从而为后续的研究和实验提供有效的支持。
下面将从数据处理的步骤、常用方法和应用领域等方面进行详细展开。
数据处理的步骤通常包括数据整理、数据检查、数据统计和数据分析等过程。
首先,数据整理是将实验数据进行归类、清理和排序的过程,以便后续的操作和分析。
其次,数据检查是指对数据进行质量控制,包括检查数据的完整性、准确性和可靠性等方面。
第三,数据统计是指对数据进行一定分组、计数和总结等统计分析的过程,从而得到特定指标和特征的统计结果。
最后,数据分析是指对统计结果进行解释和推理,从而得出一定的结论和判断。
在实际的数据处理中,常用的方法包括描述统计方法、回归分析方法、因子分析方法和聚类分析方法等。
描述统计方法主要用于对数据的中心趋势、离散程度和分布特征等进行描述和总结,常用的统计指标包括均值、中位数、标准差等。
回归分析方法主要用于研究两个或多个变量之间的关系,可通过拟合线性或非线性模型进行分析。
因子分析方法则用于确定一组变量之间的潜在关系,并提取出影响变量的主成分。
而聚类分析方法则用于对一组数据进行分类和归类,以找出相似性较高的样本或因素。
分析化学中的数据处理广泛应用于样品分析、光谱分析、色谱分析和电化学分析等领域。
在样品分析中,数据处理可以帮助提取出目标物质的浓度或含量信息,并估计分析结果的可靠性和准确性。
在光谱分析中,数据处理可以对光谱数据进行寻峰、峰面积计算和谱图解析等,以获得有关物质结构和组成的信息。
在色谱分析中,数据处理可以用于峰识别、峰分离和峰面积计算等,从而确定样品中的目标物质和杂质。
在电化学分析中,数据处理可以用于电流-电位曲线的拟合和分析,以确定反应的机理和动力学参数。
分析化学中的数据处理

第7章Management of Experimental Data in AnalyticalChemistry分析化学中的数据处理7.1 统计学(statistics)中常用术语1、总体:所考察的对象的全体。
2、样本(子样):自总体中随机抽出的一组测量值。
3、样本大小(或容量):样本中所含测量值的数目。
3、值表:f t ,α体现t , f , P 之间的关系已知f , P 时,可从表中查出相应的t 值。
表中置信度就是概率P ,它表示t 值一定时,测定值落在范围内的概率。
) (s t ⋅±μ显著性水准P −=1 α自由度n n f , 1−=为测定次数双边:表示P 是从-t 到+t 积分而得的面积。
检验时的标准置信度=P%95检验步骤a. 根据题意计算t计b. 计算出α , f, 查t表c. 比较t计与t表,然后作出结论计算α , f ,05.095.011 =−=−=P α3141=−=−=n f 查表7-3,得18.33,05.0=t 因为t 计= 8>t 0.05,3所以,平均值与标准值存在显著性差异。
分析结果存在系统误差。
•由F 的定义式可计算得F值若F→1,则s1与s2 相差不大;若F 较大,则s1与s2存在显著性差异。
检验步骤a. 计算F值,b. 计算f大,f小,查F值表得F表c. 比较:若F计>F表,存在显著性差异;反之,不存在显著性差异。
(3) 查F 值表:计算自由度516=−==小大f f 由表7-4 查得F 表= 5.05(4) 由于F 计= 2.22 , 故F 计<F 表所以,该两组数据的精密度无显著性差异。
作出此判断的置信度为90%。
检验步骤:①用F检验法:检验s1与s2 之间是否存在显著性差异。
如s1与s2 之间存在显著性差异,则两组分析数据存在显著性差异。
如s1与s2 之间不存在显著性差异,则可认为s1≈s2 ,可计算合并标准偏差继续进行下述检验。
查t 值表,得t表值。
分析化学中的数据处理

分析化学中的数据处理
1.正态分布(高斯GAUSS分布)
它在概率统计中占有特别重要的地位,因为 许多随机变量都服从或近似服从正态分布, 分析测定中的随机误差也是这样的,P55图 3-3即为正态分布曲线,它的数学表达式为:
分析化学中的数据处理
若对某试样作若干批测定,每批又作n个 平行测定
则
S
=
X
S n
由此可见:
(2-4)
①平均值的精密度比单次测定的精密度
更次好数,的S X平方S根;成平反均比值.的②标增准加偏测差定与次测数定,
可使平均值的标准偏差减小。
作
s x
n 关系图如P59图3-5所示。
s
分析化学中的数据处理
分析化学中的数据处理
§2.1 几个概念(P52)
研究对象的某种特性值的全体叫总体; 从总体中随机取出的一组数据叫样本; 样本所含测量值的数目叫样本容量。例 如,对某矿石中Fe的含量作了无限次测 定,所得无限多个数据的集合就是总体, 其中每个数据就是个体,从中随机取出 一组数据(例如8个数据)就是样本,样 本容量为8。
3)大多数测定值集中在µ的附 近,所以µ为最可信赖值或 最佳值
分析化学中的数据处理
正态分布曲线随µ、σ值不同而不同,应
用起来不方便,为此,采用变量转换的
方法,将其化为同一分布-标准正态分
布
即
u= x-
令 代入(2-5)式得
y=f(x)=
1
- u2
e2
2
又 dx= du
第三章 分析化学中的数据处理

m
◇分析天平(称至0.1mg):12.8228g(6) , 0.2348g(4) , 0.0600g(3) ◇千分之一天平(称至0.001g): 0.235g(3) ◇1%天平(称至0.01g): 4.03g(3), 0.23g(2) ◇台秤(称至0.1g): 4.0g(2), 0.2g(1)
V
☆滴定管(量至0.01mL):26.32mL(4), 3.97mL(3) ☆容量瓶:100.0mL(4),250.0mL (4) ☆移液管:25.00mL(4); ☆量筒(量至1mL或0.1mL):25mL(2), 4.0mL(2)
如果测量数据 不断增多,组分 得越来越细,直 方图则逐渐趋于 一条平滑的曲 线—正态分布曲 线。 离散特性:各数据是分散的,波动的
s: 总体标准偏差
s
x
i 1
n
i
2
n
29
集中趋势:有向某个值集中的趋势
: 总体平均值
1 n lim x n n i 1
i
d: 总体平均偏差
3、随机误差: 由一些随机的偶然的不可避免的原因所造成的误 差。 特点:①波动性,可变性,无法避免; 例如:已知某矿石中Fe2O3 真实含量为50.36%, 测量值具波动性如下所示:50.40%, 50.30%, 50.25%, 50.37%; ②符合统计规律:正态分布规律。
4、减小随机误差
在消除系统误差的前提下,平行测定次数愈多, 平均值愈接近真实值。因此,增加测定次数,可 以提高平均值精密度而减小随机误差。在一般化 学分析中,对于同一试样,通常要求平行测定 2 ~ 4次即可。
3.2.2 有效数字修约规则 舍去多余数字的过程,称为数字修约。数字修 约遵循的规则:四舍六入五成双。例:将下列 测量值修约为三位有效数字
第3章-2 分析化学中的数据处理
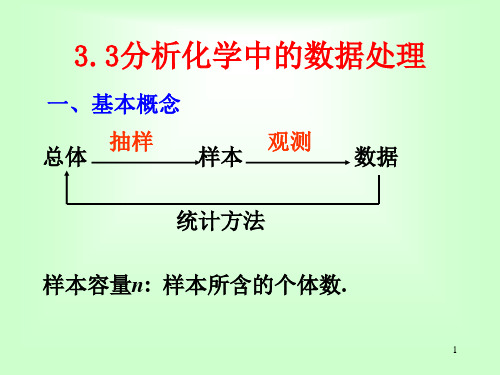
表3.2 正态分布概率积分表
随机误差出现的区间
测量值出现的区间
概率
(以σ为单位) u=±1 u=±1.96 u=±2 u=±2.58 u=±3
x=μ±1σ x=μ±1.96σ x=μ±2σ x=μ±2.58σ x=μ±3σ
68.3% 95.0% 95.5% 99.0% 99.7%
12
例1 已知某试样中质量分数的标准值为1.75%, σ=0.10%,又已知测量时没有系统误差,求分析 结果落在(1.75±0.15)%范围内的概率。 解: x x 1.75% 0.15%
(47.60 0.13)%
(47.60 0.23)%
置信度越高,置信区间就越大,所 估计的区间包括真值的可能性也就 越大,置信度定在 95%或 90%。
23
3.4 显著性检验
1. 平均值与标准值的比较-t检验法
步骤:a.将 x ,μ 和 n代入 t x n ,求t计
x 10.79%, s 0.042%
9 1.43
t
x s
n
10.79% 10.77% 0.042%
查表 ,P=0.95,f=8 时, t0.05 , 8=2.31 。 t<t0.05 , 8 ,故 x 与 μ 之间不存在显著性差异,即采用新方法后,没有 引起明显的系统误差。 25
涉及到的是测量值较少时的平均偏差;但在用统
计学处理数据时,广泛采用标准偏差来衡量数据
的分散程度。
2
总体标准偏差:
(测量次数为无限多次时)
σ
x
n
2
样本标准偏差:
(测量值不多时)
s
x x
n 1
2
分析化学数据处理及结果计算汇总

分析化学数据处理及结果计算汇总数据收集是进行化学实验和研究的基础,数据的准确性和全面性对于后续的数据处理和结果计算至关重要。
在进行实验时,我们需要记录实验条件、实验过程中的观察和测量结果,并将这些数据整理成清晰、统一的格式。
在进行数据收集时,应注意以下几点:1.实验条件的记录:包括温度、压力、溶剂种类和用量等。
这些条件对于实验结果的准确性有重要影响,应该始终保持实验条件的一致性。
2.观察结果的准确描述:对于观察到的现象或物质性质的描述应准确、详细。
比如,颜色的描述可以使用颜色比较法,或者使用对应的波长、吸收强度等数据来描述。
3.测量结果的精确度:应该对测量结果进行恰当的数据处理,包括对数据的重复测量、异常值的排除等。
常见的数据处理方法有均值、标准差、误差分析等。
数据处理是对实验数据进行整理、处理和分析的过程,目的是提取和总结数据中的有用信息。
常用的数据处理方法有:1.数据整理和清洗:对实验数据进行整理和筛选,去除重复数据和异常值,使得数据的质量更加可信。
2.数据转换和标准化:有时,需要将数据按照一定的标准进行转换,使得数据的分析更加方便。
如将温度从摄氏度转换为开氏度,将浓度单位换算为摩尔等。
3.数据统计和可视化:使用合适的统计方法对数据进行分析,比如计算均值、标准差、相关系数等。
同时,将数据可视化可以提供更直观的数据分析信息,如绘制柱状图、散点图等。
结果计算是根据实验数据和现有的模型、理论进行结果推导和计算的过程。
常见的结果计算方法有:1.摩尔计算:根据已知物质的摩尔质量和反应方程式,计算反应过程中各物质的物质的量。
2.溶解度计算:根据溶质在溶剂中的溶解度和溶解反应的平衡常数,计算溶质在溶剂中的溶解度。
3.吸收光谱计算:根据分子结构和吸收光谱数据,计算分子的吸收峰位置和吸收强度。
总之,分析化学数据处理及结果计算是进行化学研究和实验的重要环节。
在进行数据处理和结果计算时,应注重数据的准确性和全面性,并使用合适的方法对数据进行统计和分析,以获得准确、可靠的结果。
分析化学数据处理

分析化学数据处理首先,分析化学数据处理的第一步是数据的收集。
在实验室中,化学实验需要收集各种各样的数据,包括实验前的样品信息、实验过程中的各种测量数据、实验结果等。
这些数据通常通过实验仪器和技术设备进行测量和记录。
因此,准确地收集实验数据是确保实验结果可靠性和再现性的基础。
其次,分析化学数据处理的第二步是数据的整理。
在收集了大量的实验数据之后,需要对数据进行整理和归类,以便后续的分析和处理。
数据的整理可以包括数据的清洗、去除异常值、数据的统一格式等,以确保数据的一致性和准确性。
第三,分析化学数据处理的第三步是数据的分析。
在数据整理的基础上,可以使用各种统计方法和数据处理技术对数据进行分析和处理。
常用的统计方法包括均值、标准差、相关性分析、回归分析等,而数据处理技术包括数据的平滑、峰形分析、图谱处理等。
通过数据的分析,可以揭示数据内部的规律、趋势和相关性,从而得出科学结论。
第四,分析化学数据处理的第四步是数据的解释和报告。
在数据分析的基础上,需要对结果进行解释和报告。
这包括解释数据的实际意义、说明分析方法的有效性和可靠性、对结果做出解释和推论等。
数据的解释和报告需要准确、清晰地呈现,以便其他人员能够理解和使用。
最后,分析化学数据处理的最后一步是数据的存档和管理。
一旦数据分析和解释完成,需要将数据进行存档和管理。
这包括数据的备份、存储和维护等,以确保数据的长期保存和安全性。
总而言之,分析化学数据处理是一个全面而系统的过程,包括数据收集、整理、分析、解释和存档等多个步骤。
通过科学的数据处理方法,可以从数据中提取有价值的信息,并为实验结果提供准确性和可靠性的保证。
分析化学数据处理在化学研究中起到至关重要的作用,对于推动科学研究和实验实践具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
注意:
• 分析化学中,除用平行性来表示在完全相 同的条件下样品多次测定结果的精密度外; 还可用重复性和再现性来表示不同情况下 分析结果的精密度。 • 重现性:同一分析人员在同一条件下,不同 时间所得分析结果的精密度。 • 再现性:不同分析操作者或不同实验室之间, 在各自条件下所得分析结果的精密度。
表示 物质客观存在的数量特征。 特点:真实存在,但却未知。(?) 理论真值: 约定真值: 标准值(相对真值): 当作真值
将
作用: 检验分析结果的准确度。
1)理论真值:
由公认理论推导 如 或证明的某物理 H+与OH-反应的化学计量关系 量的数值。 即二者反应量的比值
水的组成常数或组成分数即为 理论真值
二、随机误差(random error): • 定义:由某些难以控制的、无法避免的、不 确定的偶然因素或在目前技术水平下尚未掌 握的原因造成的误差。 • 例:滴定管读数的不确定性、称量时温度及 湿度的波动和仪器性能的微小变化等造成的 误差。 • 特性:大小不等、正负不定、不可测性、不 可校正。 • 分布规律:多次测定的结果服从统计学规 律——正态分布(normal distribution):
0.24
s1
di
2
n 1
0.28
s2
di
2
n 1
0.33
→平均偏差和标准偏差的关系:
例:求下列三组数据的 d 和 s
I 10.02,10.02,9.98,9.98
平均值= 10.00
d = 0.02
s = 0.02
II 10.01,10.01,10.02,9.96
s = 0.027 d = 0.02 III 10.02, 10.02, 9.98, 9.98, 10.02, 10.02, 9.98, 9.98 平均值 = 10.00
d
d
i 1
n
i
0
d1 d 2 d n n
相对平均偏差: d
r
d x
100%
当n不大时,常用平均偏差表示精密度。
标准偏差和相对标准偏差——统计方法 • 标准偏差(s):xi与平均值的差方和均根(当 n较大时) 。 定义n-1为自由度f 。
s
( xi x )
例:甲乙丙丁4人 对同一样品进行 相同测定4次的结 果如图
甲:准确度与精密度均较高; 乙:精密度虽高,但准确度太低; 丙:准确度与精密度都很差; 丁:精密度太差,准确度碰巧较高,结果不可靠。
〄 准确度:决定于平均值的误差(包括随机误
差和系统误差)大小;
〄 精密度:决定于随机误差的大小; 〄 二者的关系:平均值的误差和随机误差的关
x 1 n ( x1 x2 ...... xn ) 1
x n
i 1
n
i
x1,x2,…,xn:为某一试样的n组of population) (μ):
无穷多次的测定值的算术平均值。 反映无穷多次测定结果的集中趋势。
lim
三、系统误差和随机误差的关系: ☃ 都在正常操作时出现,产生具有必然性; ☃ 分析结果既存在随机误差,还可能存在显 著的系统误差;
☃ 二者来源不同,其性质或分布规律和减免
方法也不同;
☃ 后者只能减小而无法避免;前者理论上虽
可避免,但实际上往往与后者并存,有时 也难以分清,二者还可相互转化。
过失:分析操作者由于疏忽或差错造成的差 异。 如:错用样品或标样、选错仪器、加错试剂、 器皿不清洁、试样损失或沾污、操作不规范、 忽视仪器故障、读数错误、计算错误等。 性质:是错误,不是误差。 避免方法:提高理论知识和个人实验素养。 错误的处理:含有过失错误的测量值表现为离 群值(?),要用统计检验方法决定取舍。确 知操作错误的数据必须舍弃。分析过程一旦出 现过失,应立即停止,及时纠正,重做实验。
按标准方法分析, 用统计方法确定的 相对准确的值。
标准方法对照 如 分析结果
权威专家反复分析确 国际原子量 定的相对准确的值。 如 和分子量
2. 平均值( x )
• 重复测定或一组平行测定的值具有集中趋势。 1) 样本平均值(sample mean):对某一分析对象总体
平行测定n次,或用相同方法在同一条件下重复测定 n次所得测定值的算术平均值。
d = 0.02
平均值 = 10.00
s = 0.021
♪ 可见: 标准偏差通过平方运算,能将较大 的偏差更显著地表示出来。因此能更好地 反映测定值的精密度。 极差或全距(R):一组测量数据中,最大值与 最小值之差。
R xmax xmin
特点:简单直观,便于运算;没有利用全 部测量数据。
n 1
2
di
2
n 1
• 描述各次测定值的平均分散度 • 避免各次测定的偏差相互抵消 • 突出大偏差
• 意义:更为恰当地衡量测定结果的分散程度、 随机误差和精密度;值越小,表示平行测定 结果的分散度越小、随机误差越小和精密度 越高。
相对标准偏差(RSD)/
变异系数(CV):
RSD
s x
14 . 75 %
E x xT 14.75% 14.78% 0.03%
Er 100% 0.03% 14.78% 100% 0.2%
2.偏差(d):测定结果与平均结果之间的差值。
di xi x
显然,偏差有正、负或零,则各 单次测定的偏差之和应为零: 平均偏差:
随机误差出现几率
0.4
☃ 大多数测量值集中在算术
0.3
n
平均值的附近;
☃ 小误差出现的几率大,大
0.2
0.1
误差出现的几率小,特大 误差出现的几率极小;
n3
☃ 绝对值相等的正、负误差
-4
-3
测定值的随机误差
-2
-1
0
1
2
3
4
出现的几率趋于相等。
★样本平均值是最佳测定值; ★总体平均值μ不存在随机误差:增加测定次数, 各测定结果的随机误差之和趋近于零。
E= x-xT= -0.06%
Er= -0.06/62.38= - 0.1%
B. Li2CO3试样中:xT=0.042%, x =0.044%
E = x -xT= 0.002%
Er=0.002/0.042= 5%
上述结论说明什么问题? 前者的绝对误差更大,后者的相对误差更大,
前者准确度更高。
例:测定BaCl2· 2O中结晶水的含量三次:14.73%, 2H 14.77%和14.75%。求测定结果的E和Er。
系统误差的分类及减免方法 p44
❤ 方法误差:由分析方法本身的缺陷引起。
减免:选择恰当的分析方法、测定其大小。
❤ 仪器误差:仪器本身不够精确引起。
减免:选择符合要求的仪器、设法测定其大 小、校正仪器。 ❤ 试剂误差:由试剂不纯净引起。
减免:空白试验或纯化试剂、提高水质、清 洁器皿等。
• 操作误差:分析人员掌握的操作不够正确 引起的误差。 • 主观误差(个人误差):由分析人员主观因 素引起的差异。有时又列入操作误差。 减免:加强训练、提高操作水平。
• 平均值的标准偏差 s x
❤
p59
1.0 0.8
n组平行测定结果的平均值的标准偏差; ❤ 反映平均值的精密度; ❤ 结论:若n组各平行测定n次,则平均值的标准偏 差与其中一组测定结果的s满足: s sx n
S
可由一组测定结果的s求得,
不必测定几组。 s x 随n增大而减小;当n>5时 变化很慢。 实际工作中n一般为3~6。
100%
能更好地比较不同情况下测定结果的精密度。
• 如以下两组分析数据各次的偏差为:
+0.3 -0.2 -0.4 +0.2 +0.1 +0.4 0.0 -0.3 +0.2 -0.3 0.0 +0.1 -0.7 +0.2 -0.1 -0.2 +0.5 -0.2 +0.3 +0.1
d d
n
i
X
0.6 0.4 0.2
n
0.0 0 2 4 6 8 10
3.1.2 准确度与精密度 p42
1. 准确度:分析结果和真值接近的程度。
误差——衡量准确度的高低。
误差越小,准确度越高。 2. 精密度:各次平行测定结果相互接近的程度。
偏差——衡量精密度的好坏。
偏差越小,精密度越好。
3. 准确度与精密度的关系:
3.1.3 随机误差和系统误差 p43
一、系统误差(systematic error)
• 定义:由确定的原因造成的误差。 • 特性:恒定性(一定条件下恒定不变,重复 测定重复出现,增加测定次数不能减免); 单向性(总偏高或总偏低); 可测性(大小可测,可以校正)。 • 大小衡量:总体平均值与真值之差(=μ-xT ) 。 • 意义:只影响分析结果的准确度,不影响精 密度。值越大,准确度越差。
n
1
x n
i 1
n
i
平均值的特点: • 最佳测定值,反映多次测定结果的集中趋势; • 比单次测定结果更接近真值。 ∴ 实际工作中总要平行测定或重复测定 多次,以求得平均值。
3. 中位数(xM):一组测量数据(n个)由小到大 排列, n为奇数时,排在正中间的那个数据; n为偶数时,中间相邻两个数据的平均值。 ♪ 特点:受离群值的影响较小;n很大时,其 计算简单。
2)约定真值:
计量组织学会或 管理部门等规定 如 并得到公认的计 光在真空中传播1/299792458 量单位的数值。
国际计量大会定义的长度、时间、 质量和物质的量等物理量的基本 单位
秒所经过的路径为1 m
