第八章 回归分析-SPSS
SPSS回归分析

SPSS回归分析SPSS(统计包统计软件,Statistical Package for the Social Sciences)是一种强大的统计分析软件,广泛应用于各个领域的数据分析。
在SPSS中,回归分析是最常用的方法之一,用于研究和预测变量之间的关系。
接下来,我将详细介绍SPSS回归分析的步骤和意义。
一、回归分析的定义和意义回归分析是一种对于因变量和自变量之间关系的统计方法,通过建立一个回归方程,可以对未来的数据进行预测和预估。
在实际应用中,回归分析广泛应用于经济学、社会科学、医学、市场营销等领域,帮助研究人员发现变量之间的关联、预测和解释未来的趋势。
二、SPSS回归分析的步骤1. 导入数据:首先,需要将需要进行回归分析的数据导入SPSS软件中。
数据可以以Excel、CSV等格式准备好,然后使用SPSS的数据导入功能将数据导入软件。
2. 变量选择:选择需要作为自变量和因变量的变量。
自变量是被用来预测或解释因变量的变量,而因变量是我们希望研究或预测的变量。
可以通过点击"Variable View"选项卡来定义变量的属性。
3. 回归分析:选择菜单栏中的"Analyze" -> "Regression" -> "Linear"。
然后将因变量和自变量添加到正确的框中。
4.回归模型选择:选择回归方法和模型。
SPSS提供了多种回归方法,通常使用最小二乘法进行回归分析。
然后,选择要放入回归模型的自变量。
可以进行逐步回归或者全模型回归。
6.残差分析:通过检查残差(因变量和回归方程预测值之间的差异)来评估回归模型的拟合程度。
可以使用SPSS的统计模块来生成残差,并进行残差分析。
7.结果解释:最后,对回归结果进行解释,并提出对于研究问题的结论。
要注意的是,回归分析只能描述变量之间的关系,不能说明因果关系。
因此,在解释回归结果时要慎重。
《SPSS回归分析》PPT课件

电子工业出版社
(1)确定性关系与非确定性关系
变量与变量之间的关系分为确定性关系和非确定性关系, 函数表达确定性关系。研究变量间的非确定性关系,构造变量 间经验公式的数理统计方法称为回归分析。
(2)回归分析基本概念
回归分析是指通过提供变量之间的数学表达式来定量描述 变量间相关关系的数学过程,这一数学表达式通常称为经验公 式。我们不仅可以利用概率统计知识,对这个经验公式的有效 性进行判定,同时还可以利用这个经验公式,根据自变量的取 值预测因变量的取值。如果是多个因素作为自变量的时候,还 可以通过因素分析,找出哪些自变量对因变量的影响是显著的 ,哪些是不显著的。
➢打开“统计量”对话框,选上“估计”和“模型拟合度”。
➢单击“绘制(T)…”按钮,打开“线性回归:图”对话框,选 用DEPENDENT作为y轴,*ZPRED为x轴作图。并且选择“直方图” 和“正态概率图”
➢作相应的保存选项设置,如预测值、残差和距离等。
h
10
10
SPSS 19(中文版)统计分析实用教程
可以看出两变量具有较强 的线性关系,可以用一元 线性回归来拟合两变量。
h
9
9
SPSS 19(中文版)统计分析实用教程
电子工业出版社
8.2 线性回归分析
第4步 一元线性回归分析设置:
➢选择菜单“分析→回归→线性”,打开“线性回归”对话框,将 变量“财政收入”作为因变量 ,“国内生产总值”作为自变量。
电子工业出版社
8.2线性回归分析
8.2.2 SPSS实例分析
【例8-1】现有1992年-2006年国家财政收入和国内生产总值的 数据如下表所示,请研究国家财政收入和国内生产总值之间的 线性关系。
年份
如何使用统计软件SPSS进行回归分析

如何使用统计软件SPSS进行回归分析如何使用统计软件SPSS进行回归分析引言:回归分析是一种广泛应用于统计学和数据分析领域的方法,用于研究变量之间的关系和预测未来的趋势。
SPSS作为一款功能强大的统计软件,在进行回归分析方面提供了很多便捷的工具和功能。
本文将介绍如何使用SPSS进行回归分析,包括数据准备、模型建立和结果解释等方面的内容。
一、数据准备在进行回归分析前,首先需要准备好需要分析的数据。
将数据保存为SPSS支持的格式(.sav),然后打开SPSS软件。
1. 导入数据:在SPSS软件中选择“文件”-“导入”-“数据”命令,找到数据文件并选择打开。
此时数据文件将被导入到SPSS的数据编辑器中。
2. 数据清洗:在进行回归分析之前,需要对数据进行清洗,包括处理缺失值、异常值和离群值等。
可以使用SPSS中的“转换”-“计算变量”功能来对数据进行处理。
3. 变量选择:根据回归分析的目的,选择合适的自变量和因变量。
可以使用SPSS的“变量视图”或“数据视图”来查看和选择变量。
二、模型建立在进行回归分析时,需要建立合适的模型来描述变量之间的关系。
1. 确定回归模型类型:根据研究目的和数据类型,选择适合的回归模型,如线性回归、多项式回归、对数回归等。
2. 自变量的选择:根据自变量与因变量的相关性和理论基础,选择合适的自变量。
可以使用SPSS的“逐步回归”功能来进行自动选择变量。
3. 建立回归模型:在SPSS软件中选择“回归”-“线性”命令,然后将因变量和自变量添加到相应的框中。
点击“确定”即可建立回归模型。
三、结果解释在进行回归分析后,需要对结果进行解释和验证。
1. 检验模型拟合度:可以使用SPSS的“模型拟合度”命令来检验模型的拟合度,包括R方值、调整R方值和显著性水平等指标。
2. 检验回归系数:回归系数表示自变量对因变量的影响程度。
通过检验回归系数的显著性,可以判断自变量是否对因变量有统计上显著的影响。
SPSS实验8-二项Logistic回归分析
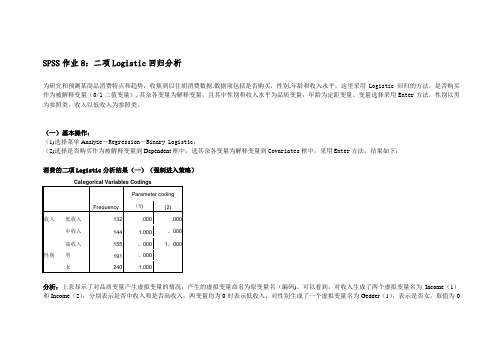
SPSS作业8:二项Logistic回归分析为研究和预测某商品消费特点和趋势,收集到以往胡消费数据.数据项包括是否购买,性别,年龄和收入水平。
这里采用Logistic回归的方法,是否购买作为被解释变量(0/1二值变量),其余各变量为解释变量,且其中性别和收入水平为品质变量,年龄为定距变量。
变量选择采用Enter方法,性别以男为参照类,收入以低收入为参照类。
(一)基本操作:(1)选择菜单Analyz e-Regression-Binary Logistic;(2)选择是否购买作为被解释变量到Dependent框中,选其余各变量为解释变量到Covariates框中,采用Enter方法,结果如下:消费的二项Logistic分析结果(一)(强制进入策略)Categorical Variables CodingsFrequency Parameter coding (1) (2)收入低收入132 .000 .000中收入144 1.000 。
000高收入155 。
000 1。
000性别男191 。
000女240 1.000分析:上表显示了对品质变量产生虚拟变量的情况,产生的虚拟变量命名为原变量名(编码)。
可以看到,对收入生成了两个虚拟变量名为Income(1)和Income(2),分别表示是否中收入和是否高收入,两变量均为0时表示低收入;对性别生成了一个虚拟变量名为Gedder(1),表示是否女,取值为0时表示为男。
消费的二项Logistic 分析结果(二)(强制进入策略)Block 0: Beginning BlockClassification Table a,bObserved Predicted是否购买 Percentage Correct不购买购买Step 0是否购买不购买 269 0 100。
购买162。
0 Overall Percentage62。
4a 。
Constant is included in the model 。
《SPSS数据分析与应用》第8章 逻辑回归分析

➢ TPR—在所有真实值为阳性的样本中,被正确地判断为阳性的样本所占的比例。
TPR=TP / TP FN
➢ FPR—在所有真实值为阴性的样本中,被正确地判断为阳性的样本所占的比例。
FPR=FP / FP TN
Part 8.2
逻辑回归分析模型 的实现与解读
定性变量 (3水平)
定量变量
定性变量
取值范围 1代表幸存 0代表死亡 1=男、2=女 [0.42,80]
1代表一等舱, 2代表二等舱, 3代表三等舱
[0, 512.3292]
C = 瑟堡港, Q =昆士敦,S = 南安普顿
定性变量
0代表无家庭成员,1代表成员为1~3人的中 型家庭,2代表成员为4人及以上的大型家庭
2.逻辑回归分析模型
逻辑回归分析模型
在经过Logit变换之后,就可以利用线性回归模型建立因 变量与自变量之间的分析模型,即
经过变换,有
Sigmoid函数 (S型生长曲线)
逻辑回归分析模型
Sigmoid函数
➢ Sigmoid函数,表示概率P和自变量之间 的非线性关系。通过这个函数,可以计 算出因变量取1或者取0的概率。
总计
混淆矩阵
预测值
Y=0(N)
Y=1(P)
TN
FP
FN
TP
总计 TN+FP FN+TP TP+FP+FN+TN
➢ TP:预测为1,预测正确,即实际1; ➢ FP:预测为1,预测错误,即实际0; ➢ FN:预测为0,预测错确,即实际1; ➢ TN:预测为0,预测正确即,实际0。
4.模型评价
➢ 准确率
SPSS-回归分析

SPSS-回归分析回归分析(⼀元线性回归分析、多元线性回归分析、⾮线性回归分析、曲线估计、时间序列的曲线估计、含虚拟⾃变量的回归分析以及逻辑回归分析)回归分析中,⼀般⾸先绘制⾃变量和因变量间的散点图,然后通过数据在散点图中的分布特点选择所要进⾏回归分析的类型,是使⽤线性回归分析还是某种⾮线性的回归分析。
回归分析与相关分析对⽐:在回归分析中,变量y称为因变量,处于被解释的特殊地位;;⽽在相关分析中,变量y与变量x处于平等的地位。
在回归分析中,因变量y是随机变量,⾃变量x可以是随机变量,也可以是⾮随机的确定变量;⽽在相关分析中,变量x和变量y都是随机变量。
相关分析是测定变量之间的关系密切程度,所使⽤的⼯具是相关系数;⽽回归分析则是侧重于考察变量之间的数量变化规律。
统计检验概念:为了确定从样本(sample)统计结果推论⾄总体时所犯错的概率。
F值和t值就是这些统计检定值,与它们相对应的概率分布,就是F分布和t分布。
统计显著性(sig)就是出现⽬前样本这结果的机率。
标准差表⽰数据的离散程度,标准误表⽰抽样误差的⼤⼩。
统计检验的分类:拟合优度检验:检验样本数据聚集在样本回归直线周围的密集程度,从⽽判断回归⽅程对样本数据的代表程度。
回归⽅程的拟合优度检验⼀般⽤判定系数R2实现。
回归⽅程的显著性检验(F检验):是对因变量与所有⾃变量之间的线性关系是否显著的⼀种假设检验。
回归⽅程的显著性检验⼀般采⽤F 检验。
回归系数的显著性检验(t检验): 根据样本估计的结果对总体回归系数的有关假设进⾏检验。
1.⼀元线性回归分析定义:在排除其他影响因素或假定其他影响因素确定的条件下,分析某⼀个因素(⾃变量)是如何影响另⼀事物(因变量)的过程。
SPSS操作2.多元线性回归分析定义:研究在线性相关条件下,两个或两个以上⾃变量对⼀个因变量的数量变化关系。
表现这⼀数量关系的数学公式,称为多元线性回归模型。
SPSS操作3.⾮线性回归分析定义:研究在⾮线性相关条件下,⾃变量对因变量的数量变化关系⾮线性回归问题⼤多数可以化为线性回归问题来求解,也就是通过对⾮线性回归模型进⾏适当的变量变换,使其化为线性模型来求解。
利用SPSS进行Logistic回归分析
6
研究生地理数学方法(实习)
Part 2 统计分析软件 SPSS
图 8-1-9 样品处理摘要
2. Dependent Variable Encoding(因变量编码)。这是很重要的信息,告诉我们对不同城 市化水平地区的分类编码结果(图 8-1-10)。我们开始根据全国各地区的平均结果 45.41 分 为两类:大于等于 45.41 的地区用 Yes 表示,否则用 No 表示。现在,图 8-1-10 显示,Yes 用 0 表示,No 用 1 表示。也就是说,在这次 SPSS 分析过程中,0 代表城市化水平高于平均 值的状态,1 代表城市化水平低于平均值的状态。记住这个分类。
§8.1 二值 logistic 回归
8.1.1 数据准备和选项设置
我们研究 2005 年影响中国各地区城市化水平的经济地理因素。城市化水平用城镇人口 比重表征,影响因素包括人均 GDP、第二产业产值比重、第三产业产值比重以及地理位置。 地理位置为名义变量,中国各地区被分别划分到三大地带:东部地带、中部地带和西部地带。 我们用各地区的地带分类代表地理位置。
Classification Tablea,b
Predicted
Observed
Step 0 城市化
Yes
No
Overall Percentage
a. Constant is included in the model.
b. The cut value is .500
城市化
Yes 0
No 11
0
20
3
研究生地理数学方法(实习)
Part 2 统计分析软件 SPSS
图 8-1-5 Logistic 回归分析的初步设置 接下来进行如下 4 项设置: ⒈ 设置 Categorical(分类)选项:定义分类变量(图 8-1-6)。 将中部调入 Categorical Covariates(分类协变量)列表框,其余选项取默认值即可。完 成后,点击 Continue 继续。
应用回归分析,第8章课后习题参考答案讲解

第8章 非线性回归思考与练习参考答案8.1 在非线性回归线性化时,对因变量作变换应注意什么问题?答:在对非线性回归模型线性化时,对因变量作变换时不仅要注意回归函数的形式, 还要注意误差项的形式。
如:(1) 乘性误差项,模型形式为e y AK L αβε=, (2) 加性误差项,模型形式为y AK L αβε=+对乘法误差项模型(1)可通过两边取对数转化成线性模型,(2)不能线性化。
一般总是假定非线性模型误差项的形式就是能够使回归模型线性化的形式,为了方便通常省去误差项,仅考虑回归函数的形式。
8.2为了研究生产率与废料率之间的关系,记录了如表8.15所示的数据,请画出散点图,根据散点图的趋势拟合适当的回归模型。
表8.15生产率x (单位/周) 1000 2000 3000 3500 4000 4500 5000 废品率y (%)5.26.56.88.110.2 10.3 13.0解:先画出散点图如下图:5000.004000.003000.002000.001000.00x12.0010.008.006.00y从散点图大致可以判断出x 和y 之间呈抛物线或指数曲线,由此采用二次方程式和指数函数进行曲线回归。
(1)二次曲线 SPSS 输出结果如下:Model Summ ary.981.962.942.651R R SquareAdjusted R SquareStd. E rror of the EstimateThe independent variable is x.ANOVA42.571221.28650.160.0011.6974.42444.2696Regression Residual TotalSum of Squares dfMean SquareF Sig.The independent variable is x.Coe fficients-.001.001-.449-.891.4234.47E -007.0001.4172.812.0485.843 1.3244.414.012x x ** 2(Constant)B Std. E rror Unstandardized Coefficients BetaStandardizedCoefficientstSig.从上表可以得到回归方程为:72ˆ 5.8430.087 4.4710yx x -=-+⨯ 由x 的系数检验P 值大于0.05,得到x 的系数未通过显著性检验。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章回归分析一、基本概念变量之间的联系可以分为两类:1.一类是确定性的关系确定型的关系是指某一个或某几个现象的变动必然会引起另一个现象确定的变动,它们之间的关系可以使用数学函数式确切地表达出来,即函数关系y=f(x)。
2.另一类是非确定关系称为统计关系或相关关系。
3.回归分析和相关分析的区别区别主要是模型的假设以及研究的目的有所不同。
在模型的假设方面,大致可分为两类:(1)第一类是两个变量一个是非随机变量,而另一个是随机变量。
(2)第二类是两个变量都是不能控制的随机变量,形成一个二维分布。
统计学中把前者的分析称为回归分析,把后者的分析称为相关分析。
概括地说,线性回归分析是处理两个或两个以上变量间线性依存关系的统计方法。
二、SPSS提供了丰富的回归分析,内容分为以下几种:Linear: 线性回归分析Curve Estimation: 曲线拟合估计Binary Logistic:二维logistic回归分析Multinomial Logistic:多维logistic回归分析Ordinal: Ordinal回归分析Probit:概率单位回归分析Nonline:非线性回归分析Weight Estimation:加权估测分析2-Stage least Squares:两阶最小二乘法分析本章主要介绍Linear Regression线性回归分析,它包括一元线性回归和多元线性回归,其他不做要求。
第一节一元线性回归一、一元线性回归模型及假设一元线性回归模型是两个变量之间的关系可以通过有关的参数直接用直线关系来表达,其模型是:Yi=a+bXi+εi式中:Yi表示变量Y在总体中的某一个具体的观察值;Xi表示在研究总体中相应的另一个变量的x的具体观察数值;a与b是参数,分别称为回归常数和回归系数;εi是一个随机变量,其均值为0,方差为σ2。
对一元线性回归模型做出以下的几点假设:1.Xi为一自变量,是预先确定的,因而是一个非随机变量。
2.当确定某一个Xi时,相应的Y就有许多Yi与之对应。
Yi是一个随机变量,这些Yi构成一个在X取值为Xi条件下的条件分布,并假设其服从正态分布。
3.所有的εi的均值和方差是相等的。
4.εi与εj之间是相互独立的。
简单概括起来,"线性"、"正态"、"独立"、"方差齐性"是线性回归的四个条件。
二、一元线性回归模型的检验确定了回归直线之后,需要评价直线回归方程是否有效地反映了这两个变量之间的关系。
检查和评价回归方程的方法可以从两方面入手。
1.残差图的评价(不作要求)残差图以方程的自变量为横坐标,以残差εi为纵坐标,将每一个自变量所对应的残差都画在平面上所形成的图形。
2.技术指标的检查(1)对样本回归系数a、b的检验检验的假设是:Ho:b=0。
(2) 方差分析(3) r2测定系数(Coefficient of Determination)如果各点愈接近回归直线,r2就趋近于1,说明配合好。
否则,如果r2不接近1,就说明配合不够令人满意。
(4) Durbin-Watson检验(不作要求)目的是检验"回归模型中的误差项是独立的"这一假设是否成立。
检验的参数为D,其取值范围为区间(0,4),表达意义为:D的数值在2附近,说明残差之间是独立的。
D<2,说明残差之间是正相关的。
D>2,说明残差之间是负相关的。
第二节多元线性回归一、多元回归模型及其假设多元回归模型的一般形式为:Yi=a+bX1i+X2i+εi应用多元回归模型必须满足以下假设1.Xi可以是任意确定的变量,也可以是有意选择的变量。
2.对于每一个i, εi都是正态独立的分布,其均值为0,方差为σ2。
3.每个因素之间是相互独立的。
4.因变量和自变量之间的关系是线性的。
二、多元线性回归模型的评价1.残差图的评价2.技术指标的检查(1)对样本回归系数a,b的检验假设是所有的系数为0,即Ho:bi=0。
若回归系数的效果显著,则回归函数有一定的合理性。
反之,如果结论是不能拒绝假设,即回归系数的效果不显著,可能是来源于两个原因:第一,自变量对因变量Y无显著性影响,此时应舍弃这个模型;第二,自变量对因变量Y有显著影响,但不能用线型关系来表述,此时可以考虑采用其他非线性回归分析。
(2)方差分析与一元线性回归模型的方差检验的原理相同。
(3)偏回归系数的显著性检验偏回归系数的显著性检验的目的是:探明是否每一个自变量对因变量都是重要的。
在偏回归系数的检验中,假设总体回归系数为0。
当回归检验表明某个自变量的系数不显著时,则相应的自变量被认为在回归方程中不起什么作用,应从回归方程中剔除,重新建立起更为简单的回归方程。
偏回归系数检验使用的统计量为t统计量。
(4)残差的正态型检验检验残差是否正态分布可以通过残差的直方图、累积概率图等来判断。
第三节在SPSS中建立回归方程一、建立数据文件,并利用散点图大致观察一下数据的分布。
(一)几种散点图状况:1,两个变量间的关系基本呈线性,可做回归分析;2,曲线关系;3,两个变量虽然呈线性关系,但有一个异常点,需先进行处理,再做回归分析;4,有异常点,容易错误地把它当作正常情况处理,应个别处理。
(二)一元线性回归方程举例1.下列10对数据是为确定某心理量与物理量之间的关系而做的实验结果,假设两者呈线性关系,试以这10对数据建立该心理量与物理量的回归方程。
A B C D E F G H I J心理量(y) 1 1 3 3 4 5 6 7 8 9物理量(x) 0 2 1 5 4 2 6 2 5 72.下列数据是20名工作人员的智商和某一次技术考试成绩,根据这个结果求出考试成绩队智商的回归方程。
如果另有一名工作人员智商为120,则估计一下若让他也参加技术考试,将会得多少分?工作人员 A B C D E F G H I J K L M N O P Q R S T智商(X) 89 97 126 87 119 101 130 115 108 105 84 121 97 101 92 110 128 111 99 120考试(Y) 55 74 87 60 71 54 90 73 67 70 53 82 58 60 67 80 85 73 71 90二、用SPSS建立回归模型的操作步骤1.操作步骤操作命令:Analyze→Regression→Linear→打开Linear Regression对话框。
在对话框中,可以具体设定要建立什么样的回归模型,需要输出哪些结果。
2.选择因变量进入右边Dependent框内,选出一个或多个变量进人Independent(s)框内作为自变量。
3.注意因变量和自变量必须都是数值型变量,不能是其他类型的变量。
4.采用不同的自变量、因变量和回归方法可建立不同的回归模型。
5. Method"栏。
选项有:Enter、Stepwise、Remove、Backward、Forward。
(1)Enter选项:系统的默认选项,表示让所有选择的自变量都进入回归模型。
(2)Stepwise选项:逐步进入法。
(3)Remove选项:消去法。
在建立回归模型时,根据设定的条件,删除部分自变量。
(4)Backward选项:向后剔除法。
首先让所有的自变量进入回归方程之中,然后逐一删除它们。
删除变量的判决标准是Options对话框中设定的F值。
(5)Forward选项:向前选择法。
这种变量选择方法恰好与"Backward"选项的方法相反,根据Options对话框中设定的判决标准F值,逐一地让自变量进入回归方程。
首先在所有的自变量中间,让和因变量之间有正最大或负最小相关系数的自变量进入回归方程,当然,这个自变量应满足进入标准。
然后使用同样的方法,逐一地让自变量进入回归方程,直到没有满足进入标准的自变量时为止。
6.选择Selection Variables对话框,在己有变量中选取满足某个条件的变量来分析。
(1)从左边的源变量对话框中,将变量选入右边Selection Variables框中。
(2)单击Rule按钮打开Set Rule对话框。
7.在左边的源变量对话框中,选择观测量标签。
8.单击WLS按钮,可以选择一个作为权重的变量进入WLS Weight框中。
9.单击"Statistics"按钮,打开Statistics对话框。
(1)Regression Coefficient栏,在此栏内选择回归系数。
A. Estimates默认复选项,输出回归系数估计值(B)及其标准误,标准化回归系数(Beta);B的t值及双侧显著性水平等相关测量。
B.Confident Interval复选项,输出回归系数的95%的置信区间。
C.Covariance复选项,输出协方差和相关矩阵。
(2)Model fit复选项,默认选项,列出进入或从模型中剔除的变量,输出复相关系数R,测定系数R2,调整R2,估计值的标准误,方差表。
(3)R squared change复选项,R2,F值的改变,以及方差分析P值的改变。
(4)Descriptive复选项,它显示了变量均值、标准差,单侧检验及相关系数矩阵。
(5)Part and partial correlation复选项,输出零阶相关系数(Zero-order, 即Pearson 相关)、偏相关系数,要求方程中至少有2个自变量。
(6)Co-linearity diagnostics复选项,共线性诊断。
(7)Residuals栏,分析残差的选择项。
A.Durbin-Watson复选项,用于残差分析。
B.Casewise diagnostics复选项,输出满足选择条件(条件设置在Outlier outside栏内) 的观测量诊断表。
C.Outlier outside栏:设置奇异值的判断条件,默认值n=3。
D.All cases选项,可输出所有关测量的残差值,标准化残差,实测值和预测值,残差。
10.单击Plots按钮,打开Plots对话框。
(1)在左上角上源变量框,ZPRED选项,标准化的预测值。
ZRESID选项,标准化的残差。
DRESID选项,删除的残差。
ADJPRED选项,修正后的预测值。
SRESID选项,用户化的残差。
SDRESID选项,用户化的删除的残差。
(2)在左下角的Standardize Residual Plots框内,有两个选项。
Histogram复选项,输出带有正态曲线的标准化残差的直方图。
Normal probability复选项,输出标准化残差的正态概率图。
通常用来检验残差的正态性。
(3)Produce all partial plots复选项,它对每一个自变量,会产生一个自变量与因变量残差的散点图。
