通分(二)
分式(二)之通分约分

分式(二) 通分约分授课对象授课教师授课题目 分 式 (二) 授课时间 课 型 新 授 课使用教具教学目标1. 使学生理解分式通分的意义,掌握分式通分的方法及步骤;2. 使学生理解分式约分的意义,掌握分式约分的方法及步骤;教学重点和难点 1. 通分时,最简公分母的寻找方法;2. 约分时,最大公因式的寻找方法;3. 因式分解在通分、约分中的应用;参考教材 人教版教学流程及授课详案一、 通分1. 从分数到分式2. 计算: 例1 求分式4322361,41,21xyy x z y x 的公分母。
(方法:找出系数的最小公倍数,找出字母的最高次幂)例2 求分式2241x x -与412-x 的最简公分母。
分数的通分:1. 把几个异分母分数化成与原来分数相等且分母相同的分数,叫做通分。
2. 通分方法:(1) 找出原来几个分数的分母的最小公倍数 (2) 根据分数基本性质,把原来分数化成以这个最小公倍数为分母的分数。
例1 4131和例2 607363和分式的通分:1. 将几个分式的分母利用分式基本性质化为相同分母的分式,叫通分。
2. 通分方法:(1) 找出原来几个分式的分母的最简公分母。
(2) 根据分式基本性质,把原来分式化成以这个最简公分母为分母的分式。
例1b a 223与cab b a 2-总结:1) 最简公分母的意义是,各分式分母中的系数是最小公倍数与所有的字母(或因式)的最高次幂的积,叫做最简公分母。
2) 概括求几个分式的最简公分母的步骤。
a) 取各分式的分母中系数最小公倍数;b) 各分式的分母中所有字母或因式都要取到; c) 相同字母(或因式)的幂取指数最大的d) 所得的系数的最小公倍数与各字母(或因式)的最高次幂的积(其中系数都取正数)即为最简公分母。
例3 通分:(1)xyy x x y 41,3,22; (2)22225,103,54ac b b a c c b a -例4 通分:(1)42,361,)42(222---x x x x x x (2)222231,)(1yxy x y x +-- 3. 计算 (1)bd c 2与243b ac (2)2)(2y x xy +与22yx x - (3)y x y x 22+-与2)(y x xy + (4)9422-m mn 与3232+-m m (5)y x 3与223yx(6)b a c 26与23ab c 二、 约分1. 从分数到分式分数约分: 1. 把一个分数化成和它相等,但分子分母比较小的分数叫做约分。
通分二(教学设计)

通分(二)
教学内容:教科书第95--96页练习十八4---9
教学目的:
1.掌握通分的方法,能比较熟练地进行通分。
2.使学生学会把三个分数通分的方法
教学重点和难点:
1.通分的一般方法。
2.确定公分母。
教具准备:投影.
教学过程:
一、复习
1.求下面每组数的最小公倍数.(教师出示口算卡片,指名学生口答.)
3和4 2和6 4和6 2、3和4 3、6和12
4和8 3和5 6和7 2、4和6 3、5和10 2.把下面每组中的两个分数通分.(教师出示题目,学生在练习本上做.)
和和和
二、探索
1.“我们已经学过两个分数的通分,今天我们学习三个分数的通分.”出示:把、和通分.
“在把两个分数通分时,需要先找出它们的公分母.三个分数的通分
也要先找出它们的公分母.怎样找它们的公分母呢?”指名学生回答.(要用3、4、8的最小公倍数24做公分母.)
“有了公分母,就可以根据不同情况,把每个分数分别化成用这个公分母做分母的分数.”
让学生完成这道题的通分.请一名学生在黑板上做.最后集体订正.2.巩固练习.
让学生在练习本上做第97页第6,8题.教师巡视,帮助有困难的学生.最后集体订正.
三、课堂练习
1、口答填空,并说明你是如何算出括号里应填的数的。
1/6和5/9通分:
7/12和11/30通分:
2、说出下面每组分数的公分母。
3、下面哪组分数的通分是对的?哪组不对?哪组不够简便?
4、下面题中的a,b,c各代表几?□里应填多少?(投影)
四、课堂总结。
青岛版(六三)数学五年级下册五关注环境—分数加减法(二)-1通分课件

温馨提示:
•通分时,选择最小公倍数作为公分 母比较简单。 •通分是把异分母分数变为同分母分 数。 •通分后,分数的大小不变。
练 习题
判断
1.把异分母分数分别化成同分母分数叫作通分。( X )
2.约分和通分都是根据分数的基本性质。 ( )
3.异分母分数通分后,分数单位是相同的。 ( )
4.约分时,分数越约越小,通分时每个分数的值越
二、合作探究 生活垃圾中塑料和菜叶果皮,哪类多?
怎样比较这两个分数的大小呢? 将它们化成小数来比较。 把它们化成分母相同的分数来比较。 把它们化成分子相同的分数来比较。
通分
异 分
1 8
=
1×5 8×5
=
5 40
同 分
母
分别化成和本来分数相等
母
分 数
2 5
=
2×8 5×8
=
16 40
分 数
<
<
像这样,把异分母分数分别化成与本来 分数相等的同分母分数的过程,叫作通分。
来越大。
( X)
5.约分是每个分数单独进行的,通分是在几个分数
中进行的。
()
把下面每组中的两个分数通分
5 6
和
7 8
5 6
=
5×4 6×4
=
20 24
7 8
=
7×3 8×3
=
21 24
3 7
和
2 9
3 7
=
3×9 7×9
=
27 63
2 9
=
2×7 9×7
=
14 63
4 9
和
7 18
4 9
=
4×2 9×2
=
《通分(2)》(教案)人教版五年级数学下册
1.学生已经掌握了哪些相关知识:在开始本节课之前,学生应该已经掌握了分数的基本概念,包括分数的表示方法、比较分数大小、分数的加减法等。他们应该能够理解分母和分子的含义,并能够进行简单的分数运算。此外,学生应该已经学习过通分的基本概念,并能够进行简单的通分运算。
2.学生的学习兴趣、能力和学习风格:五年级的学生通常对数学问题解决和逻辑推理感兴趣。他们具有较强的逻辑思维能力和问题解决能力,喜欢通过实际例子和问题来理解和应用数学知识。在学习风格上,他们通常喜欢互动和合作学习,通过与他人讨论和合作来加深对知识的理解。
核心素养目标
本节课的核心素养目标在于培养学生的数学抽象、逻辑推理和数学建模能力。通过学习通分的方法和技巧,学生能够理解分数的基本概念,掌握通分的原理,并能够运用通分解决实际问题。同时,通过小组合作和讨论,学生能够培养团队合作和沟通表达能力。通过自主探究和问题解决,学生能够培养批判性思维和问题解决能力。
提出问题,检查学生对旧知的掌握情况,为通分新课学习打下基础。
(三)新课呈现(预计用时:25分钟)
知识讲解:
清晰、准确地讲解通分的原理和方法,结合实例帮助学生理解。
突出通分的重点,强调通分的难点,通过对比、归纳等方法帮助学生加深记忆。
互动探究:
设计小组讨论环节,让学生围绕通分问题展开讨论,培养学生的合作精神和沟通能力。
One area that I felt needed improvement was the clarity of the explanation for reducing fractions. While I thought I had explained the concept thoroughly, some students still seemed confused. To address this, I plan to use more concrete examples and visual aids to illustrate the process of reducing fractions. This will help students visualize the steps involved and make the concept more accessible.
通分(二)

通分(二)教学课题:公倍数教学目标:1、在知道两数特殊关系的基础上,使学生学会用不同的方法求两个数的最小公倍数。
2、学会求三个数的最小公倍数。
教学重点:掌握求两个数的最小公倍数的方法。
教学难点:1、正确、熟练地求出特殊情况下两个数的最小公倍数。
2、能用短除法求三个数的最小公倍数。
教学准备:教学课时:2课时(本课时为第二课时)教学过程:一、创设情境:1、什么叫做两个数的公倍数?什么叫做两个数的最小公倍数?2、求8和12的最小公倍数。
3、说说下面每组中的两个数有什么关系?12和36 4和5二、探索研究:(一)我们已经学会求两个数的最小公倍数,这节课我们将继续学习求特殊情况下两个数的最小公倍数。
(板书课题:求两个数的最小公倍数)1、互质数求最小公倍数。
(1)投影出示下面几组数,求最小公倍数。
4和5 7和9 11和13 2和3(2)组织反馈,说说这几组数有什么特点。
猜想具有互质关系的两个数的最小公倍数怎样求?(3)举例验证。
2、倍数关系的数求最小公倍数。
(1)投影出示下面几组数,求最小公倍数。
6和12 7和49 3和15 21和42(2)组织反馈,说说这几组数有什么特点。
猜想具有倍数关系的两个数的最小公倍数怎样求?(3)举例验证。
3、小结。
(二)求三个数的最小公倍数1、出示例题:求8、12和30的最小公倍数。
2、把三个数分解质因数。
8=2×2×212=2×2×330=2×3×5组织反馈,在分解质因数的基础上标出要取的质因数。
3、归纳用短除怎样来算。
2 8 12 302 4 6 153 2 3 152 1 54、做一做,求6、9和12的最小公倍数。
5、与求两个数的最小公倍数进行比较。
(1)8和6 (2)8、6和18课堂练习课堂小结板书设计教学反思。
《通分》例1、例2

《通分》例1、例2一、任务目标通过本节课的学习,学生应达到以下目标:1. 理解分数的概念,能够将分数化为通分分数。
2. 能够通过实际情境和图形解决通分问题。
3. 掌握求分数通分的方法,能够自己解决通分问题。
4. 培养学生的分数运算意识和分析问题能力。
5. 提高学生的自学能力和合作能力。
二、学习重点1. 分数的通分和约分;2. 分数通分的基本方法,理解分数通分的含义;3. 运用实际情境和图形解决通分问题。
三、学习难点1. 分数通分的复杂问题;2. 改变习惯思维,从整数思维到分数思维;3. 分数通分的物理意义和代数方法的统一。
四、教学方法1. 创设情境教学法;2. 解释法;3. 讨论合作学习法;4. 图象法。
五、教学过程Step1:引入新课1. 学生们已经学习了分数,我们考虑一下下面的问题:老师:如果你们想在一份调味品里加1/2勺盐、1/3勺糖和1/4勺醋,你们会怎么做?请同学们说说自己的想法。
2. 接着,老师出示下面的图:老师:我们看这张图,这是5个相等的正方形,全部填满的为1,那么1/2是多少?请同学们思考一下。
(学生思考1-2分钟)老师:1/2代表的是这个正方形的一半,而这个正方形的面积是1,因此1/2代表的是这个正方形的1/2,也就是0.5。
3. 接下来,老师将继续给同学们介绍这个调味品的问题,并询问他们的解决方案。
老师:那么,在加入调味品的时候,应该如何计算1/2勺、1/3勺和1/4勺呢?请同学们思考一下。
Step2:分数的通分1. 用图象法让学生理解通分的含义:老师:其实,通分很简单,就是将两个或多个不同分母的分数化为相同的分母。
请同学们看以下的示意图,如果我们要将1/3和2/5通分,应该怎么做呢?(出示通分图示意图片)老师:从图中我们看到,将1/3化为分母为15的分数,就好像将第一个花瓶重新装起来,去除一些花瓶后,将剩余的满满的装在了一个大花瓶里。
同样的,将2/5化为以15为分母的分数,也就是将图中的第二个花瓶重新装起来,去除一些花瓶后,将剩余的满满拼在了第一个花瓶上。
通分(2)

第四课时:通分(二)教学内容:第94 页的内容及第95 页练习十八的第3、4、5、6 题 教学目标:1、通过教学,使学生理解通分的意义,掌握通分的方法,并能比较分子和分母都不相同的分数的大小。
2、渗透转化的数学思想。
3、培养学生认真审题的良好习惯和应用数学知识解决问题的意识。
教学重点:理解通分的意义,掌握通分的方法教学难点:理解通分的意义,掌握通分的方法教学过程:一、 复习。
(课件出示复习题)二、 故事创设情境,导入新课三、探究新知1、明确探究任务师:这种分子和分母都不相同的分数,同学们比较起来感到比较困难。
下面,就请同学们分小组讨论,找出比较43和65大小的方法来,把它写在答题纸上,行吗?(行。
)我们比一比,哪一组解决问题的策略最多?开始。
2、小组研究,师巡视指导。
3、小组汇报。
(1)、把43和65化成分母相同的分数,然后利用同分母分数相比较,分子大的分数就大。
(2)、把43和65化成分子相同的分数来比较:分母越小,分数越大。
(3)、把3和5分别化成小数来比较。
(4)、可以画图。
4、今天老师就带你们一起去研究把43和65化成同分母的分数的办法。
(板书课题:通分)5、教学例4,进一步理解通分过程和方法四、方法应用:1、2、(1)把几个分数化成分母相同的分数,叫做通分。
( )(2)通分与约分都是运用分数的基本性质 。
( )(3)34<45 ( ) (4)通分时用分母的最小公倍数作公分母比较简便。
( )1、大显身手我来填:(1).把异分母分数( )化成和( )相等的( )分数,叫做通分。
(2).通分时选用的公分母一般是原来几个分母( )(3).通分的方法先求出原来几个分母的( ),然后把各分数分别化成用这个( )作分母的分数(4).通分的依据( )。
(5).通分的目的是把( )分母的分数化成( )分母的分数。
五、做一做和练习十八3-6题。
请对照通分的意义想一想,下列计算,哪个是通分?哪个不是通分?37(1)275825(2)和和37========3×57×5153514352×75×72558272×47×45×38×31524828。
五年级数学下册约分和通分(二)一课一练人教版
(人教版)五年级数学下册约分和通分及答案(二)
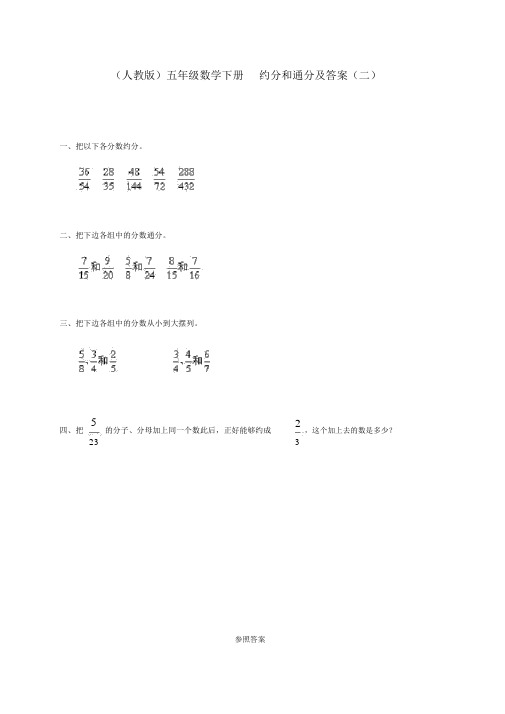
一、把以下各分数约分。
二、把下边各组中的分数通分。
三、把下边各组中的分数从小到大摆列。
四、把5
的分子、分母加上同一个数此后,正好能够约成
2
,这个加上去的数是多少?233
参照答案
一、把以下各分数约分。
二、把下边各组中的分数通分。
三、把下边各组中的分数从小到大摆列。
由于:16<25<30
404040
所以:2
<
5
<
3 584
由于:105 < 112< 120
140140140
所以: 3 < 4<
6
457
四、解:由于5的分子5 和分母 23 相差 18,加上同一个数此后,差不变。
约分后的分数2
233
分子分母相差1,所以需要扩大18 倍,变为36。
此时我们能够看出,分子分母同时加上了 31。
54。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
通分(二)
教学导航:
【教学内容】
用通分来比较分数的大小的方法(教材第74页例5、及75页练习十八的第2、3题)。
【教学目标】
1.理解和掌握通分的概念,掌握通分的方法,并能正确地把两个分数进行通分。
2.能运用通分的方法,比较异分母分数的大小。
3.经历探索活动,形成解决问题的一些基本策略。
【重点难点】
1.掌握通分的方法。
2.能很快地看出两个数的最小公倍数。
3.熟练灵活地掌握求两个数最小公倍数的方法。
教学过程:
【复习导入】
提问:1.3
10
的分数单位是(),它有()个这样的分数单位。
2.1 8与1
6
,哪个大,为什么?
教师:怎样比较它们的大小呢?今天,我们来探究一种新的方法,可以比较出它们的大小。
板书课题:通分。
【新课讲授】
1.出示教材第74页例5。
(1)提问:25和14
这两个分数有什么共同特点?
像这样分子和分母都不相同的分数,怎样比较大小?
学生思考并回答,可能出现以下两种思路:
一种是化成同分母分数比较,一种是化成同分子分数比较。
教师指出:这两种思路,都能把新问题转化成已学过的问题。
都是可以的,今天我们重点研究化成同分母分数的方法,我们把几个分数的相同分母叫做公分母。
(2)教师提问:用什么数做公分母?怎样把异分母分数化成与原来分数相等的同分母分数?
学生独立思考。
尝试解答,然后在小组内交流。
(3)请学生汇报解答过程。
先求出25和14的分母的最小公倍数是20,用20作公分母。
板书:2
24855420⨯==⨯ 115544520⨯==⨯ (4)教师提问:根据是什么?(分数的基本性质)
教师指出:异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
(板书课题:通分)
板书:异分母分数同分母分数
(5)教师提问:你能说一说怎样通分吗?(学生用自己的语言归纳) 小结:通分时,先求出原来分母的最小公倍数作分母,再看原来
分数的分母变成公分母要乘上几,分子也要乘上相同的数,提问:为什么用两个分母的最小公倍数作公分母,用其他较大的公倍数作公分母可以吗?
(6)在通分的基础上,比较25和14
的大小,让学生完整写出例5的比较过程。
224855420⨯==⨯ 115544520⨯==⨯ 2154> 2.巩固练习。
完成教材第74页“做一做”。
答案:①分母相同的分数,分子大的比较大,分子小的比较小;分子相同的分数,分母小的比较大,分母大的比较小;分子分母都不同的分数,先通分,再比较大小。
“< > > =”
【课堂作业】
完成教材第75页练习十八的第1~3题。
学生独立完成后集体订正。
答案:1.> < > <
2.> < > <
【课堂小结】
通过这节课的学习活动,你有什么收获?学生交流学习的收获。
【课后作业】
完成练习册中本课时练习。
教学板书:
通分(二)
例5:2
24855420⨯==⨯ 115544520⨯==⨯ 2154
> 把异分母分数化成和原来分数相等的同分母分数,叫做通分。
异分母分数
同分母分数
教学反思:
“通分”的教学目标是让学生理解通分的意义并掌握通分的方法,它用的是分数的基本性质。
通分是在学生已经掌握了分数的基本性质和求几个数的最小公倍数的基础上进行教学的,在教学中,关键是让学生理解为什么要通分和掌握通分的方法,为此教师将通分与比较异分母分数的大小联系起来,在比较归纳的基础上理解通分的目的。
