【2013年中考攻略】专题2.1.待定系数法在代数式变型中的应用
待定系数法的应用

数学知识点总结——待定系数法的运用待定系数法是初中数学非常重要的一种解题思想和方法,它的重要性不仅体现在某一类型题中,而是贯穿于整个初中阶段,各年级各题型的“杀手锏”,让原本复杂繁琐的难题巧妙进行巧妙地简化。
理解一种方法的运用,要远比做几十道题来得事半功倍。
下面我们就一起来探讨各年级中关于待定系数法的题目类型和特点。
1. 设K 法六年级:设K 法是六年级开始的一个重要工具,它可以将多个未知但相互有联系的未知量用一个和K 有关的式子表示出来。
变相地说,它起到了一个数学特别重要的“降维”作用,以一替多。
那什么时候该用设K 法呢?沈老师曾总结过:两类条件,肯定是暗示你去用设k 法的——条件含比例条件有连等式第一类是常常能判断出来的,便是条件中含有比例类型的题,让我们来看一个例题:例1: 自然数A B 、满足111182A B -=,且:7:13A B =,求A B +分析:AB 看似是两个未知数,但若通过比例式设k ,即能把两个未知数都用一个关于k 的式子表示出来,当你在对一个未知数进行求解时,代入条件往往是比较容易得出的,这就是所谓的利用设K 法“降维”。
解: 设7,13A k B k == 则有11111713182A B k k -=-=,进行通分 13761919191182k k k -== 求得12k =,故20240A B k +==如果说比例式用设k 法还算比较明显的话,那么连等式的技巧就没那么容易想到。
而越难想到的点就越能成为杀手锏:K ⎫⎬⎭设法例2: 已知,247x y z ==求: (1)::x y z(2)求x y x z ++的值 (3)若2358x y z ++=,求,,x y z 的值分析:根据沈老师的经验,初中阶段,凡是遇到连等式,90%都可以用设k 法快速求解。
解: 令247x y z k ===,则有2,4,7x k y k z k === (1)::2:4:7x y z k k k =即::2:4:7x y z =(2)24622793x y k k k x z k k k ++===++ (3)2344212958x y z k k k k ++=++==即2k =因而4,8,14x y z ===有没有发现设k 法在解决这类题时近乎可以说是“秒算”?除了六年级,七年级在实数板块,也会出现类似的“难题”!七年级:例3: 设333200620072008,a b c ==且0abc >= 求111a b c++分析:该题乍看之下并没有什么思路,而一旦陷入繁琐的计算,那么心情也会跟着一同浮躁。
初中数学重点梳理:待定系数法

待定系数法知识定位待定系数法是一种求未知数的方法。
将一个多项式表示成另一种含有待定系数的新的形式,这样就得到一个恒等式。
对于某些数学问题,如果已知所求结果具有某种确定的形式,则可引进一些尚待确定的系数来表示这种结果,通过已知条件建立起给定的算式和结果之间的恒等式,得到以待定系数为元的方程或方程组,解之即得待定的系数。
广泛应用于多项式的因式分解,求函数的解析式和曲线的方程等。
知识梳理知识梳理1:待定系数法在多项式除法中的应用多项式除多项式时,其结果的形式我们往往是可以判断出的,在这种情况下,我们可以先假设出最后的结果(当然也是含未知数的),转化为等式再进行计算。
知识梳理2:待定系数法在因式分解中的应用在因式分解时,一些多项式经过分析,可以断定它能分解成某几个因式,但这几个因式中的某些系数尚未确定,这时可以用一些字母来表示待定的系数.由于该多项式等于这几个因式的乘积,根据多项式恒等的性质,两边对应项系数应该相等,或取多项式中原有字母的几个特殊值,列出关于待定系数的方程(或方程组),解出待定字母系数的值,这种因式分解的方法叫作待定系数法.知识梳理3:待定系数法在解方程中的应用在解一些复杂方程时,如果能够判断出方程的部分根,或者有方程根的一些限制条件;在这种情况下,采用待定系数的方法去解方程,往往可以有意想不到的效果。
知识梳理3:待定系数法在代数式恒等变形中的应用 知识梳理4:待定系数法在求函数解析式中的应用例题精讲【试题来源】【题目】已知多项式56423+-+x x x ,除式为12+x ,求它们相除所得到的商式和余式。
【答案】【解析】【知识点】待定系数法 【适用场合】当堂例题 【难度系数】3【试题来源】【题目】已知r qx px x x ++++464234能被39323+++x x x 整除,求p,q,r 之值.【答案】【解析】【知识点】待定系数法 【适用场合】当堂例题 【难度系数】3【试题来源】【题目】把多项式x 3-x 2+2x+2表示为关于x -1的降幂排列形式. 【答案】x 3-x 2+2x+2=(x -1)3+2(x -1)2+3(x -1)+4. 【解析】用待定系数法:设x 3-x 2+2x+2=a(x -1)3+b(x -1)2+c(x -1)+d 把右边展开,合并同类项(把同类项对齐), 得 x 3-x 2+2x+2=ax 3-3ax 2+3ax -a +bx 2-2bx+b +cx -c +d 用恒等式的性质,比较同类项系数,得⎪⎪⎩⎪⎪⎨⎧=+-+-=+--=+-=2223131d c b a c b a b a a 解这个方程组,得⎪⎪⎩⎪⎪⎨⎧====4321d c b a∴x 3-x 2+2x+2=(x -1)3+2(x -1)2+3(x -1)+4. 本题也可用换元法: 设x -1=y, 那么x=y+1.把左边关于x 的多项式化为关于y 的多项式,最后再把y 换成x -1.【知识点】待定系数法 【适用场合】当堂例题 【难度系数】3【试题来源】【题目】已知:4310252323-+-++-x x x cbx x ax 的值是恒为常数求:a, b, c 的值.【答案】a = 1 b = 1.5 c = -2 【解析】【知识点】待定系数法 【适用场合】当堂练习题 【难度系数】3【试题来源】【题目】分解因式:.310434422-+---y x y xy x【答案】【解析】【知识点】待定系数法【适用场合】当堂练习题【难度系数】3【试题来源】【题目】m为何值时,6522-++-ymxyx能够分解因式,并分解之.【答案】【解析】【知识点】待定系数法 【适用场合】当堂例题 【难度系数】3【试题来源】【题目】已知:4x 4+ax 3+13x 2+bx+1是完全平方式.求: a 和b 的值.【答案】解得⎪⎩⎪⎨⎧==⎪⎩⎪⎨⎧-==⎩⎨⎧-=-=⎩⎨⎧==172174 172174612612b a b a b a b a -或或或.【解析】设4x 4+ax 3+13x 2+bx+1=(2x 2+mx±1)2(设待定的系数,要尽可能少.)右边展开,合并同类项,得4x 4+ax 3+13x 2+bx+1=4x 4+4mx 3+(m 2±4)x 2±2mx+1. 比较左右两边同类项系数,得方程组⎪⎩⎪⎨⎧==+=m b m m a 213442; 或⎪⎩⎪⎨⎧-==-=m b m ma 213442.解得⎪⎩⎪⎨⎧==⎪⎩⎪⎨⎧-==⎩⎨⎧-=-=⎩⎨⎧==172174 172174612612b a b a b a b a -或或或.【知识点】待定系数法 【适用场合】当堂例题 【难度系数】3【试题来源】【题目】推导一元三次方程根与系数的关系. 【答案】见解析【解析】设方程ax 3+bx 2+cx+d=0(a≠0)的三个根分别为x 1, x 2, x 3.原方程化为x 3+02=++adx a c x a b . ∵x 1, x 2, x 3是方程的三个根. ∴x 3+=++adx a c x a b 2(x -x 1) (x -x 2) (x -x 3). 把右边展开,合并同类项,得 x 3+=++adx a c x a b 2=x 3-( x 1+x 2+x 3)x 2+(x 1x 2+x 1x 3+x 2x 3)x -x 1x 2x 3. 比较左右同类项的系数,得 一元三次方程根与系数的关系是: x 1+x 2+x 3=-a b , x 1x 2+x 1x 3+x 2x 3=a c , x 1x 2x 3=-ad.【知识点】待定系数法 【适用场合】课后两周练习 【难度系数】3【试题来源】【题目】已知:x 3+px+q 能被(x -a )2整除.求证:4p 3+27q 2=0. 【答案】见解析 【解析】证明:设x 3+px+q =(x -a )2(x+b ). x 3+px+q=x 3+(b -2a)x 2+(a 2-2ab)x+a 2b.⎪⎩⎪⎨⎧==-=-③②①q b a p ab a a b 22202 由①得b=2a , 代入②和③得 ⎪⎩⎪⎨⎧=-=3223aq ap∴4p 3+27q 2=4(-3a 2)3+27(2a 3)2=4×(-27a 6)+27×(4a 6)=0. (证毕).【知识点】待定系数法 【适用场合】课后一个月练习 【难度系数】3【试题来源】【题目】已知:f (x)=x 2+bx+c 是g (x)=x 4 +6x 2+25的因式,也是q (x)=3x 4+4x 2+28x+5的因式.求:f (1)的值. 【答案】f (1)=4【解析】∵g (x),q (x)都能被f (x)整除,它们的和、差、倍也能被f (x)整除.为了消去四次项,设3g (x)-q (x)=kf (x), (k 为正整数). 即14x 2-28x+70=k (x 2+bx+c) 14(x 2-2x+5)=k (x 2+bx+c) ∴k=14, b=-2, c=5. 即f (x)=x 2-2x+5. ∴f (1)=4 . 【知识点】待定系数法 【适用场合】阶段测验 【难度系数】4【试题来源】【题目】已知:23)2)(3(22++-+=+-+-x Cx B x A x x x x x , 求:A ,B ,C 的值.【答案】A =-31. B =158. C =54. 【解析】去分母,得x 2-x+2=A(x -3)(x+2)+Bx(x+2)+Cx(x -3).根据恒等式定义(选择x 的适当值,可直接求出A ,B ,C 的值),当x=0时, 2=-6A. ∴A =-31. 当x=3时, 8=15B. ∴B =158.当x=-2时, 8=10C. ∴C =54.【知识点】待定系数法 【适用场合】随堂课后练习 【难度系数】3【试题来源】【题目】分解因式:x 2+3xy+2y 2+4x+5y+3.【答案】原式=(x+2y+3)(x+y+1).【解析】由于(x 2+3xy+2y 2)=(x+2y)(x+y),若原式可以分解因式,那么它的两个一次项一定是x+2y+m 和x +y +n 的形式,应用待定系数法即可求出m 和n ,使问题得到解决. 设x 2+3xy+2y 2+4x+5y+3 =(x+2y+m)(x+y+n)=x 2+3xy+2y 2+(m+n)x+(m+2n)y+mn , 比较两边对应项的系数,则有解之得m=3,n=1.所以原式=(x+2y+3)(x+y+1).【知识点】待定系数法【适用场合】当堂练习题【难度系数】3【试题来源】【题目】分解因式:x4-2x3-27x2-44x+7.【答案】原式=(x2-7x+1)(x2+5x+7)【解析】分析本题所给的是一元整系数多项式,根据前面讲过的求根法,若原式有有理根,则只可能是±1,±7(7的约数),经检验,它们都不是原式的根,所以,在有理数集内,原式没有一次因式.如果原式能分解,只能分解为(x2+ax+b)(x2+cx+d)的形式.解设原式=(x2+ax+b)(x2+cx+d)=x4+(a+c)x3+(b+d+ac)x2+(ad+bc)x+bd,所以有由bd=7,先考虑b=1,d=7有所以原式=(x2-7x+1)(x2+5x+7).说明由于因式分解的唯一性,所以对b=-1,d=-7等可以不加以考虑.本题如果b=1,d=7代入方程组后,无法确定a,c的值,就必须将bd=7的其他解代入方程组,直到求出待定系数为止.本题没有一次因式,因而无法运用求根法分解因式.但利用待定系数法,使我们找到了二次因式.由此可见,待定系数法在因式分解中也有用武之地.【知识点】待定系数法【适用场合】随堂课后练习【难度系数】4【试题来源】【题目】已知方程0412924=-+-x x x 有两根为1和2,解这个方程【答案】x 1 = 1 x 2 = 2【解析】【知识点】待定系数法【适用场合】当堂练习题【难度系数】3【试题来源】【题目】已知方程012823=+--x x x 有两个根相等,解这个方程. 【答案】【解析】【知识点】待定系数法【适用场合】当堂练习题【难度系数】3【试题来源】【题目】要使多项式))(2(2q x px x -++不含关于x 的二次项,则p 与q 的关系是()A 相等B 互为相反数C 互为倒数D 乘积等于1【答案】A【解析】【知识点】待定系数法【适用场合】随堂课后练习【难度系数】3【试题来源】【题目】已知多项式43261312x x x x m -+-+是一个完全平方式,试求常数m 的值。
初中数学专题复习运用待定系数法解题举例(含解答)

运用待定系数法解题举例待定系数法是一种最基本的数学方法,运用待定系数法解题的一般步骤是:先根据已知条件设出一个含有待定系数的恒等式,然后利用恒等式的性质列出几个方程,组成方程组,通过解方程组而求出各待定系数的值,或从方程组中消去这些待定系数,找出原来那些已知系数间存在的关系.现就用该法解题谈点粗浅的看法,供参考.一、用待定系数法分解因式运用待定系数法分解因式,往往是把多项式先设为含有待定系数的因式的积,再根据恒等的意义,运用比较系数法,求出待定系数,从而得出答案.例1.若χ+3是多项式χ2+m χ-15的一个因式,求m 的值,并将χ2+m χ-15分解因式.解:设χ2+m χ-15=(χ+3)(χ+n).∵ χ2+m χ-15=(χ+3)(χ+n)=χ2+n χ+3χ+3n=χ2+(n+3)χ+3n ,∴3153m n n =+⎧⎨-=⎩ 解之得25m n =-⎧⎨=-⎩∴ χ2+m χ-15= χ2-2χ-15=(χ+3)(χ-5).二、用待定系数法解异分母的分式的加减法对于异分母的分式相加减,课本上给出了运算的一般方法———先通分,变为同分母的分式,然后再加减.对于其中的一些问题,除了用一般方法求解外,还可用待定系数法求解.先看下面例子: 将962-x 化为部分分式. 解:因为χ2-9=(χ+3)(χ-3),故设962-x =3+x A +3-x B . ∵3+x A +3-x B =)3)(3()3()3(-+++-x x x B x A =)3)(3()33()(-++-++x x B A x B A , ∴962-x =)3)(3()33()(-++-++x x B A x B A . 比较两边分子对应项的系数,得0336A B A B +=⎧⎨-+=⎩ 解之得11A B =-⎧⎨=⎩ ∴962-x =-31+X +31-X . 下面请看正式例子:例2.计算962-m +m-31. 解:由上例知:962-m =-31+m +31-m , ∴原式=-31+m +31-m -31-m =-31+m . 例3.计算:2312++-x x x -262--x x -4102--x x . 解:设2312++-x x x =1+x A +2+x B =)2)(1()2()(+++++x x B A x B A . ∴121A B A B +=⎧⎨+=-⎩ 解之得23A B =-⎧⎨=⎩ ∴2312++-x x x =-12+x +23+x . 同理:262--x x =22-x -12+x ,4102--x x =23+x -22-x . ∴原式=-12+x +23+x -22-x +12+x -23+x +22-x =0.三、用待定系数法解分式方程某些分式方程,除了可用常规方法求解外,也可用待定系数法求解.例4.解方程:162-x +x-13=1. 解:设162-x =1+x A +1-x B =)1)(1()()(-++-++x x B A x B A ∴06A B A B +=⎧⎨-+=⎩ 解之得33A B =-⎧⎨=⎩∴原方程可化为: -13+x +13-x -13-x =1, 从而得 -13+x =1. 去分母,得 -3=χ+1. 解之得 χ=-4.经检验,χ=-4是原方程的解.∴原方程的解为χ=-4.[评注]:若用常规方法求解,去分母后,得到的是一个关于χ的一元二次方程,这有可能使未知数的取值范围扩大,从而产生增根.而采用待定系数法,能够避免产生增根.四、用待定系数法确定函数的解析式在运用待定系数法确定函数的解析式时,应根据题意,讲究技巧,合理假设,这会给解题带来很大方便.例5.已知一个二次函数的图象的顶点坐标为(1,3),且经过点(-1,-5),求它的解析式.解:因为这个二次函数的图象的顶点坐标为(1,3),故设它的解析式为y=a(χ-1)2+3.∵抛物线y=a(χ-1)2+3过点(-1,-5),∴-5=a(-1-1)2+3.解之得a=-2.∴这个二次函数的解析式为y=-2(χ-1)2+3或y=-2χ2+4χ+1.[评注]:此题若设这个二次函数的解析式为y=a χ2+b χ+c ,则得到的方程组是 2124345b a ac b aa b c ⎧-=⎪⎪-⎪=⎨⎪-+=-⎪⎪⎩求解这个方程组,运算量大,并且极易出错,而采用上述解法,则较为简便.。
待定系数法

【2013年中考攻略】专题2:待定系数法应用探讨锦元数学工作室 编辑在数学问题中,若得知所求结果具有某种确定的形式,则可设定一些尚待确定的系数(或参数)来表示这样的结果,这些待确定的系数(或参数),称作待定系数。
然后根据已知条件,选用恰当的方法,来确定这些系数,这种解决问题的方法叫待定系数法。
待定系数法是数学中的基本方法之一。
它渗透于初中数学教材的各个部分,在全国各地中考中有着广泛应用。
应用待定系数法解题以多项式的恒等知识为理论基础,通常有三种方法:比较系数法;代入特殊值法;消除待定系数法。
比较系数法通过比较等式两端项的系数而得到方程(组),从而使问题获解。
例如:“已知x 2-3=(1-A )·x 2+Bx +C ,求A ,B ,C 的值”,解答此题,并不困难,只需将右式与左式的多项式中对应项的系数加以比较后,就可得到A ,B ,C 的值。
这里的A ,B ,C 就是有待于确定的系数。
代入特殊值法通过代入特殊值而得到方程(组),从而使问题获解。
例如:“点(2,﹣3)在正比例函数图象上,求此正比例函数”,解答此题,只需设定正比例函数为y=kx ,将(2,﹣从而求得正比例函数解析式。
这里的k 就是有待于确定的系数。
代入所求,从而使问题获解。
b 2=k a 3=,则a=3k b=2k ,,;在初中阶段和中考中应用待定系数法解题常常使用在代数式变型、分式求值、因式分解、求函数解析式、求解规律性问题、几何问题等方面。
下面通过2011年和2012年全国各地中考的实例探讨其应用。
一. 待定系数法在代数式变型中的应用:在应用待定系数法解有关代数式变型的问题中,根据右式与左式多项式中对应项的系数相等的原理列出方程(组),解出方程(组)即可求得答案。
典型例题:例:(2011云南玉溪3分)若2x 6x k ++是完全平方式,则k =【 】A .9B .-9C .±9D .±3 【答案】A 。
中考数学专项讲解-待定系数法

待定系数法知识梳理对于某些数学问题,若得知所求结果具有某种确定的形式,则可研究和引入一些尚待确定的系数(或参数)来表示这样的结果.通过变形与比较.建立起含有待定字母系数(或参数)的方程(组),并求出相应字母系数(或参数)的值,进而使问题获解.这种方法称之为待定系数法.使用待定系数法解题的一般步骤是:(1)确定所求问题含待定系数的解析式;(2)根据恒等条件,列出一组含待定系数的方程;(3)解方程或消去待定系数,从而使问题得到解决.初中数学中,待定系数法主要用途如下:典型例题一、在求函数解析式中的运用这是待定系数法的一个主要用途,学生也是在这种运用过程中开始较深入的接触待定系数法.初中阶段主要有正比例函数、反比例函数、一次函数、二次函数这几类函数,前面三种分别可设y=kx ,k y x=,y=kx+b 的形式(其中k 、b 为待定系数,且k ≠0).而二次函数可以根据题目所给条件的不同,设成y=a x 2+bx+c(a 、b 、c 为待定系数),y=a (x -h) 2+k(a 、k 、h 为待定系数),y=a (x -x 1)(x -x 2)( a 、x 1、x 2为待定系数)三类形式.根据题意(可以是语句形式,也可以是图象形式),确定出h 、k 、a 、c 、b 、x 1、x 2等待定系数. 【例1】 (05上海)点A(2,4)在正比例函数的图象上,求这个正比例函数的解析式.【解】设这个正比例函数的解析式为y=kx(k ≠0),把A(2,4)代入得4=2k ,∴k=2,∴y=2x .【例2】 已知y 与x+1成反比例,且x=2时,y=4,求函数的解析式.【分析】 y 与x+1成反比例,把x+1看作一个整体,即可设为:1k y x =+ (k ≠0),然后把x=2,y=4代入,求出k 的值即得函数的解析式. 【解】 y 与x+1成反比例,∴可设1k y x =+(k ≠0) 将x=2,y=4代入1k y x =+(k ≠0),得421k =+,解得k=12 ∴所求的函数的解析式为121y x =+. 【解题反思】 本题中y 与x+1成反比例关系,但y 与x 不是反比例关系,所以当自变量为x 时,121y x =+不是反比例函数. 【例3】二次函数的图象经过A(1,0)、B(3,0)、C(2,-1)三点.(1)求这个函数的解析式.(2)求函数与直线y=-x+1的交点坐标.【解】 (1)设这个函数的解析式为y=a x 2+bx+c .依题意得:0093142a b c a b c a b c =++⎧⎪=++⎨⎪-=++⎩解这个方程组得143a b c =⎧⎪=-⎨⎪=⎩ ∴这个函数的解析式是:y=x 2-4x+3(2)2431y x x y x ⎧=-+⎨=-+⎩ 解这个方程组得:1110x y =⎧⎨=⎩,2221x y =⎧⎨=-⎩ ∴函数与直线的交点坐标是:(1,0)、(2,-1)【解题反思】 运用待定系数法,由已知建立方程(组),可求其系数的值,在把a 、b 、c 的值代入解析式时要注意符号.二、在确定方程或解方程时,某些时候使用待定系数法也可使问题得到简化. 例如:已知一元二次方程的两根为x 1、x 2,求二次项系数为1的一元二次方程时,可设该方程为x 2+mx+n=0,则有(x -x 1)(x -x 2)=0,即x 2-(x 1+x 2)x+x 1x 2=0,对应相同项的系数得m=-(x 1+x 2),n=x 1x 2,所以所求方程为:x 2-(x 1+x 2)x+x 1x 2=0.【例4】 已知三次方程x 3-6x 2+11x -6=0,有一根是另一根的2倍,解该方程.【解】设方程的三根分别为a 、2a 、b ,则有x 3-6x 2+11x -6=(x -a )(x -2a )(x -b),左右分别展开,并把相同项的系数作比较,可得:-3a -b=-6,2a 2+3a b=11,-2a 2b=-6.解得a =1,b=3,所以该方程的根分别为:x 1=1,x 2=2,x 3=3.三、待定系数法在分式展开化为部分分式中的应用.分式化为部分分式时,如果用待定系数法也会产生很好的效果.【例5】 把分式21172x x x-+-化为部分分式. 【解】设2117221x A B x x x x -+=+--,然后将右边进行通分,化成一个分式,由于左右两边分母相同,则只要分子相同,即:-11x+7=(A -B)x -B .由各项系数相同得:-11x=A -B ,7=-B ,解得A=3,B=-7.所以211737221x x x x x-+-=+-- 四、待定系数法在因式分解中的应用【例6】 分解因式:2x 2-xy -y 2+13x+8y -7【解】 因为2x 2-xy -y 2=(2x+y)(x -y),所以可设2x 2-xy -y 213x+8y -7=(2x+y+8)(x -y+b),展开比较相同项系数,可得:a =-1,b=7,所以2x 2-xy -y 2+13x+8y -7=(2x+y -1)(x -y+7).五、待定系数法在多项式除法中的应用【例7】 当a 、b 为何值时,2x 3-a x 2+bx+1能被2x -1整除?【解】 设2x 2-a x 2+bx+l=(2x -1)(x 2+mx -1),右边展开由x 的相同项的系数相同可得a 、b ,m 的方程组,解得:a =3,b=-3.m=-11.已知:一次函数的图象经过(-4,15)、(6,-5)两点,求此一次函数的解析式.2.(08镇江)二次函数的图象经过点A(0,-3),B(2,-3),C(-1,0).(1)求此二次函数的关系式;(2)求此二次函数图象的顶点坐标;(3)填空:把二次函数的图象沿坐标轴方向最少平移________个单位,使得该图象的顶点在原点.3.如图所示,已知抛物线的对称轴是直线x=3,它与x轴交于A、B两点,与y轴交于C点,点A、C的坐标分别是(8,0)、(0,4),求这个抛物线的解析式.4.(07枣庄)在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(-3,1)(1)求点B的坐标.(2)求过A,O,B三点的抛物线的解析式;(3)设点B关于抛物线的对称轴的对称点为B1,求△AB1B的面积.1.y=-2x+7 2.(1)设y=a x 2+bx -3,把点(2,-3),(-1,0)代入得4233300a b a b +-=-⎧⎨--=⎩,解方程组得12a b =⎧⎨=-⎩. ∴y=x 2-2x -3.(也可设y=a (x -1) 2+k). (2)y=x 2-2x -3=(x -1) 2-4,∴函数的顶点坐标为(1,-4). (3)53.解:观察图象可知,A 、C 两点的坐标分别是(8,0)、(0,4),对称轴是直线x=3.因为对称轴是直线x=3,所以B 点坐标为(-2,0).设所求二次函数为y=a (x -x 1)(x -x 2),由已知,这个图象经过点(8,0)、(-2,0),可以得到y=a (x -8)(x+2).又由于其图象过(0,4)点,将点代入,得所求二次函数的关系式是213442y x x =-++. 4.解:(1)作AC ⊥x 轴,BD ⊥x 轴,垂足分别为C ,D ,则∠ACO=∠ODB=90°. ∴∠AOC+∠OAC=90°.又∠AOB=90°,∴∠AOC+∠BOD=90°.∴∠OAC=∠BOD .又AO=BO ,∴△ACO ≌△ODB .∴OD=AC=1,DB=OC=3.∴点B 的坐标为(1,3).(2)抛物线过原点,可设所求抛物线的解析式为y=a x 2+bx .将A(-3,1),B(1,3)代入,解得56a =,136b =.故所求抛物线的解析式为251366y x x =+. (3)抛物线的对称轴的方程是1310x =-. 点B 关于抛物线的对称轴的对称点为11835B ⎛⎫-⎪⎝⎭,.在△AB 1B 中,底边B 1B=4.6,高为2.1 4.6S AB B ∴=。
待定系数法在初中数学解题中的应用1

初中数学题中的待定系数法摘要:本文阐释了待定系数法的定义,归纳了待定系数法解题的一般步骤,然后通过几种典型例题剖析,展现待定系数法在初中各种数学问题中的应用。
关键字:待定系数法,函数解析式,因式分解,解方程待定系数法广泛应用于中学数学解题中,是一种重要的解题方法,也是一种重要的数学思想.在初中数学中,待定系数法在初中阶段主要用于求函数的解析式,因式分解,解方程等。
1.待定系数法的定义待定系数法是对所给出的数学问题,根据已知条件和要求先设出问题的关系式(含待定的字母系数),然后利用已知条件列出以待定的字母系数为未知数的方程(组),再解方程(组)求出待定的字母系数,使问题获得解决的一种数学方法。
2.待定系数法解题的一般步骤待定系数法解题一般分三步:(1)根据数学问题的条件设出含有待定的字母系数的关系式;(2)根据已知条件列出以待定的字母为未知数的方程(组);(3)解方程(组),确定待定的字母系数的值。
3.几种常见案例(1)待定系数法求函数解析式初中数学主要有正比例函数(0)y kx k =≠,反比例函数()0k y k x=≠,一次函数y =kx +b,二次函数2(0)y ax bx c a =++≠212((),()())y a x h k y a x x x x =-+=--这几种函数,期中k ,a,b,c,h 都是待定系数,求函数的解析式问题大多通过将相关点的坐标代入相应的解析式构建方程(组),解方程求出待定系数使问题得于解决.例1.已知一次函数过点(3,5)和(-4,-9),求这个一次函数的解析式。
分析:一次函数的解析式为y =kx +b 关键就是求出k ,b 的值。
解:设一次函数的解析式为y =kx +b因为图像过点(3,5)和(-4,-9)354921k b k b x b +=⎧∴⎨-+=-⎩=⎧⎨=-⎩解得所以,这个一次函数的解析式为21y x =-.例2:二次函数的图象经过(1,15),(1,7),(0,7)A B C -三点,求这个函数的解析式.分析:利用待定系数法求解.先设出二次函数的一般形式2(0)y ax bx c a =++≠,由已知建立方程(组),可求其待定的系数。
【2013年中考攻略】专题2.6.待定系数法在几何问题中的应用
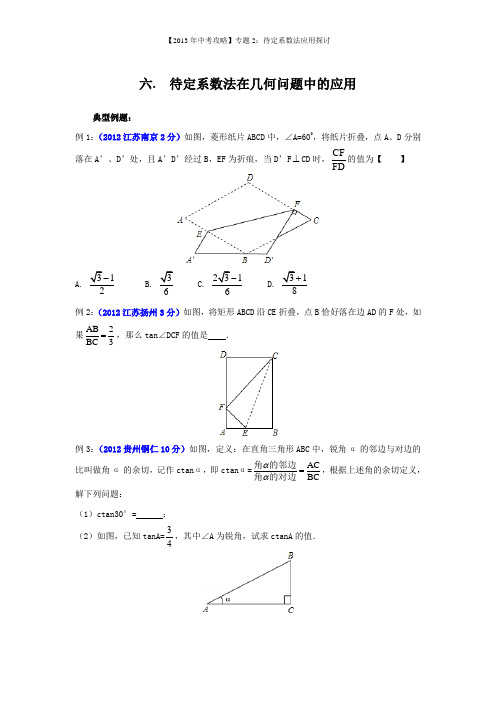
六. 待定系数法在几何问题中的应用典型例题:例1:(2012江苏南京2分)如图,菱形纸片ABCD 中,∠A=600,将纸片折叠,点A 、D 分别落在A’、D’处,且A’D’经过B ,EF 为折痕,当D’F ⊥CD 时,CFFD的值为【 】A.312- B.36C.2316- D.318+ 例2:(2012江苏扬州3分)如图,将矩形ABCD 沿CE 折叠,点B 恰好落在边AD 的F 处,如果AB 2BC 3=,那么tan∠DCF 的值是 .例3:(2012贵州铜仁10分)如图,定义:在直角三角形ABC 中,锐角α的邻边与对边的比叫做角α的余切,记作ctan α,即ctan α=ACBCαα=角的角的邻边对边,根据上述角的余切定义,解下列问题:(1)ctan30°= ; (2)如图,已知tanA=43,其中∠A 为锐角,试求ctanA 的值.例4:(2012江苏镇江11分)等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N (如图1)。
(1)求证:AM=AN;(2)设BP=x。
①若,BM=38,求x的值;②记四边形ADPE与△ABC重叠部分的面积为S,求S与x之间的函数关系式以及S的最小值;③连接DE,分别与边AB、AC交于点G、H(如图2),当x取何值时,∠BAD=150?并判断此时以DG、GH、HE这三条线段为边构成的三角形是什么特殊三角形,请说明理由。
练习题:1.(2012江苏连云港3分)小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是【】A.3+1 B.2+1 C.2.5 D.52.(2012广西河池3分)如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若△CDN的面积与△CMN的面积比为1︰4,则MNBM的值为【】A.2 B.4 C.25D.263.(2012广西柳州10分)如图,AB是⊙O的直径,AC是弦.(1)请你按下面步骤画图(画图或作辅助线时先使用铅笔画出,确定后必须使用黑色字迹的签字笔描黑);第一步,过点A作∠BAC的角平分线,交⊙O于点D;第二步,过点D作AC的垂线,交AC的延长线于点E.第三步,连接BD.(2)求证:AD2=AE•AB;(3)连接EO,交AD于点F,若5AC=3AB,求EOFO的值.4.(2012黑龙江哈尔滨10分)已知:在△ABC中,∠ACB=900,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN.(1)如图l,求证:PC=AN;(2)如图2,点E是MN上一点,连接EP并延长交BC于点K,点D是AB上一点,连接DK,∠DKE=∠ABC,EF⊥PM于点H,交BC延长线于点F,若NP=2,P C=3,CK:CF=2:3,求DQ 的长.5.(2012四川泸州9分)如图,△ABC内接于⊙O,AB是⊙O的直径,C是的弧AD中点,弦CE⊥AB于点H,连结AD,分别交CE、BC于点P、Q,连结BD。
中考专题:待定系数法应用

中考专题之:待定系数法在数学问题中,若得知所求结果具有某种确定的形式,则可设定一些尚待确定的系数(或参数)来表示这样的结果,这些待确定的系数(或参数),称作待定系数。
然后根据已知条件,选用恰当的方法,来确定这些系数,这种解决问题的方法叫待定系数法。
待定系数法是数学中的基本方法之一。
它渗透于初中数学教材的各个部分,在中考中有着广泛应用。
应用待定系数法解题以多项式的恒等知识为理论基础,通常有三种方法:比较系数法;代入特殊值法;消除待定系数法。
比较系数法通过比较等式两端项的系数而得到方程(组),从而使问题获解。
例如:“已知x2-3=(1-A)·x2+Bx+C,求A,B,C的值”,解答此题,并不困难,只需将右式与左式的多项式中对应项的系数加以比较后,就可得到A,B,C的值。
这里的A,B,C就是有待于确定的系数。
代入特殊值法通过代入特殊值而得到方程(组),从而使问题获解。
例如:“点(2,﹣3)在正比例函数图象上,求此正比例函数”,解答此题,只需设定正比例函数为y=kx,将(2,﹣3)代入即可得到k 的值,从而求得正比例函数解析式。
这里的k就是有待于确定的系数。
消除待定系数法通过设定待定参数,把相关变量用它表示,代入所求,从而使问题获解。
例如:“已知b2a3=,求a ba b-+的值”,解答此题,只需设定b2=ka3=,则a=3k b=2k,,代入a ba b-+即可求解。
这里的k就是消除的待定参数。
应用待定系数法解题的一般步骤是:(1)确定所求问题的待定系数,建立条件与结果含有待定的系数的恒等式;(2)根据恒等式列出含有待定的系数的方程(组);(3)解方程(组)或消去待定系数,从而使问题得到解决。
在初中阶段和中考中应用待定系数法解题常常使用在代数式变型、分式求值、因式分解、求函数解析式、求解规律性问题、几何问题等方面。
下面通过中考的实例探讨其应用。
一.待定系数法在代数式变型中的应用:在应用待定系数法解有关代数式变型的问题中,根据右式与左式多项式中对应项的系数相等的原理列出方程(组),解出方程(组)即可求得答案。
