DSP-第二章维纳滤波器
合集下载
维纳滤波器
w
* 1
m in
w
* 0
w
0
w
1
记 为 w w , w w
* T N 1
( w ) 若 使最 ( w )小 ， 须 0 w 即
( w ) ( w ) ( w ) ( w ) ， ,, 2 R w 2 p 0 w w w w 0 1 N 1
E dn () 2 w () n E d () n xn () N
2
T
期 望 响 应 的 平 均 功 率
2 d
( n ) 是 w 的 函 数 , 即 ( n ) ( w )
T w () n E xn () xn () w () n N N T
——维纳-霍甫夫(Wiener-Hopf)方程
它反映了相关函数与最佳单位脉冲响应之间的关系。
Wiener-Hopf方程的矩阵形式
R hR s x x x
自相关矩阵 故最佳单位脉冲响应 其中
s () n 与的 x () n互 相 关
h RR s x o p t
R 0, N1 R 1, N1 RN1,N1
xn 观察/测量数据
s n 真实信号
vn 加性噪声/干扰
ˆ s n x n h n h i x n i 线性估计问题 i
ˆ e n s n s n
2
估计误差
n E en m i n h n 最小均方误差(MMSE)估计
得到：
E [] e x 0 i 0 , 1 ,, N 1 i
或
N 1 E h x sx 0 i j j j 0
第2章 维纳滤波讲解
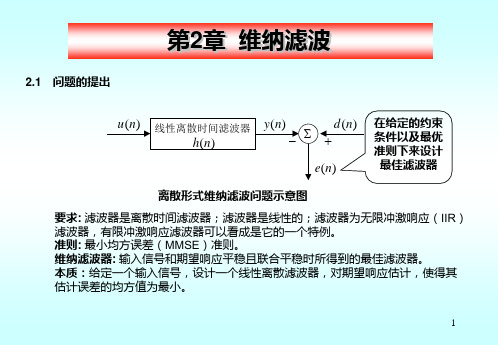
横向滤波器的二次误差性能曲面和等高 线
15
第2章 维纳滤波
相关矩阵R的特征分解与化为标准形
det[R I] 0
0 , 1 ,, M 1
0 0 Λ 0 0
Q q 0
q1 q M 1 R来自 QΛQT1 0
0 0 M 1
3
第2章 维纳滤波
得到维纳滤波器的另一个充要条件，即著名的维纳-霍夫（Wiener-Hopf）方程为
w
i 0
oi
r (i k ) p(k ) k 0,1,2,
2.3 离散形式维纳滤波器的性质 2.3.1 正交原理的几何解释
d (1 )
eo (1)
u (1 )
yo
u (0 )
p E[u(n)d (n)] [ p(0), p(1),, p(1 M )]T
则横向滤波器的维纳-霍夫方程式的矩阵表示形式为 Rwo p ，即维纳解为 w o R 1p 式中： w o [wo,0 , wo,1 ,, wo,M 1 ]T 是横向滤波器最优抽头权向量。
8
第2章 维纳滤波
2.4.2 横向滤波器的误差性能 一、误差性能曲面 M 1 输出： y(n) w u(n k ) u T (n)w(n) w T (n)u(n)
k 0
k
估计误差： 均方误差：
e(n) d (n) y(n) d (n) wT (n)u(n)
J E[e 2 (n)] E{[d (n) y (n)]2 } E{[d (n) wT (n)u(n)]2 } E[d 2 (n)] wT (n) E[u(n)uT (n)]w (n) 2wT (n) E[d (n)u(n)]
维纳滤波
m 0 N 1
e 2 (n) [ s(n) X (n) H ][ s(n) H T X (n)] s 2 ( n) 2 s ( n) X ( n) H H X (n) X (n)]H
E[e 2 n ] E[ s 2 n ] 2 E[ sn X T n ]H H T E[ X n X T n ]H
x(
我们已知
X ( z ) B( z )W ( z )
则信号功率谱为
2 Pxx ( z) B( z) B( z 1 )
如果已知信号的Pxx(z)，即可求得B(z) 。
非因果IIR维纳滤波器的求解
计算Hopt (z)：
1 B( z )
x( n )
w(n)
G(z)
ˆ( n ) y ( n) s
正交性原理：最优估计 误差正交于任一个进入 估计的输入信号或信号 空间。
由正交方程可得：
E[enxn m] E[{sn hmxn m}xn m]
E[snxn m] E[xn mxn p ]h p 0
m
m 0
k ≥ 0的约束使得上式不能直接转到Z域求解。如
能将其转化为非因果问题，则求解会大大简化。
如果滤波器的输入x(n)是方差为 w 的白噪声w(n)
2
因果维纳滤波器的维纳－霍夫方程变为：
2 2 xs m ws m h p w m p w hm m 0
代入可得： (h) s2 2P H H RH (二次型问题）
其解为：HOP R1P， 且
2 T H H 即 op s op P
结论：在所有N阶FIR滤波器中，最优滤波器的均 方误差值是最小的。其阶数越高，采用的已知信 息越多，最小均方误差越小，计算量也越大。
e 2 (n) [ s(n) X (n) H ][ s(n) H T X (n)] s 2 ( n) 2 s ( n) X ( n) H H X (n) X (n)]H
E[e 2 n ] E[ s 2 n ] 2 E[ sn X T n ]H H T E[ X n X T n ]H
x(
我们已知
X ( z ) B( z )W ( z )
则信号功率谱为
2 Pxx ( z) B( z) B( z 1 )
如果已知信号的Pxx(z)，即可求得B(z) 。
非因果IIR维纳滤波器的求解
计算Hopt (z)：
1 B( z )
x( n )
w(n)
G(z)
ˆ( n ) y ( n) s
正交性原理：最优估计 误差正交于任一个进入 估计的输入信号或信号 空间。
由正交方程可得：
E[enxn m] E[{sn hmxn m}xn m]
E[snxn m] E[xn mxn p ]h p 0
m
m 0
k ≥ 0的约束使得上式不能直接转到Z域求解。如
能将其转化为非因果问题，则求解会大大简化。
如果滤波器的输入x(n)是方差为 w 的白噪声w(n)
2
因果维纳滤波器的维纳－霍夫方程变为：
2 2 xs m ws m h p w m p w hm m 0
代入可得： (h) s2 2P H H RH (二次型问题）
其解为：HOP R1P， 且
2 T H H 即 op s op P
结论：在所有N阶FIR滤波器中，最优滤波器的均 方误差值是最小的。其阶数越高，采用的已知信 息越多，最小均方误差越小，计算量也越大。
维纳滤波器
z(n) Hw(z)
w(n) H2(z)
ˆ s ( n)
1 Hw(z) = + Gz (z)
维纳滤波器
+ H2 (z) = Gsw(z) =[Hw(z−1)Gsz (z)]+
1 Gsz (z) H(z) = + + −1 Gz (z) Gz (z )
+
维纳滤波器
Rsw (n1 , n2 ) = E {s (n1 ) w(n2 )} = E s (n1 )∑ z (n2 − k )hw (k ) k =0 = ∑ Rsz (n1 , n2 − k )hw (k )
维纳滤波器
维纳滤波器
波形估计 维纳滤波器频域解 维纳滤波器时域解
维纳滤波器
一、波形估计一般概念
z(n) = s(n) + v(n)
波形估计有三种类型 ：
n = n0, n0 +1 nf ,...,
(1)滤波： 根据当前和过去的观测值 滤波： 滤波 {z(k),k= n0, n0+1,...,n}对信号 对信号s(n)进行估计 对信号 进行估计 (2)预测 根据当前和过去的观测值 预测: 根据当前和过去的观测值{z(k),k= n0, n0+1,...,nf} 预测 对未来时刻n(n>nf)的信号 的信号s(n)进行估计，预测也称为外 进行估计， 对未来时刻 的信号 进行估计 推。
维纳滤波器 (3)内插 根据某一区间的观测数据 内插: 根据某一区间的观测数据{z(k),k= 内插 n0,n0+1,...,nf}对区间内的某一个时刻 0<n<nf)的信 对区间内的某一个时刻n(n 对区间内的某一个时刻 的信 号进行估计，内插也称为平滑。 号进行估计，内插也称为平滑。 波形估计的目的： 波形估计的目的： 选取线性滤波器的冲激响应函数或传输函数， 选取线性滤波器的冲激响应函数或传输函数， 使估计的均方误差达到最小。 使估计的均方误差达到最小。
维纳滤波概述
2 2
E[ x(t ) h(t ) y (t )d ]2
0
E[ x(t )]2 2 h( )( E[ y (t ) y ( )]d
0
h( )d h( ) E[ y (t ) y (t )]d
0 0
Rxx (0) 2 h( ) Ryx ( )d
E[e 2 (n)] lim
(2-25)
1 T 2T
T
T
(n) s (n)]2 dn [s
滤波器在n时刻复现信号s(n)显然是滤波问题。这是一种简单的过滤，滤除 噪声v(n)是唯一的目的。 但输出在时间上的简单的超前或者滞后，都不失为线性
(n a) ，这显然是一种超前的情况，输 滤波问题。在n时刻，滤波器输出如果为 s (n a) 是 s(n a) 的估计值，它比x(n)超前了 时间。这个时候滤波器所完成 出s
2 J1 2 J 2 0( 3 )
(2-15) 则将导致
J[ h h( t )] J [ o p t( t ) oh p t (t ) ]
(2-16) 这明显与最佳冲击响应将使均方误差最小的假设相矛盾。所以，我们只能取
J1 =0，即满足式(2-11)。由式(2-13)知，若使 J1 =0成立，则必须使式(2-13)中的方
第 2 章 维纳滤波理论
2.1 维纳滤波的概述
维纳 （Wiener） 滤波是用来解决从噪声中提取信号问题的一种过滤 （或滤波） 的方法。 实际上这种线性的滤波问题，可以看成是一种估计问题或是一种线性估 计问题。 维纳滤波器是一种基于最小均方误差准则下的估计滤波器。 滤波器的输入包 括有真实信号值x(t)和干扰噪声w(t)，信号值与噪声是统计独立的，则两者的合 成输入信号是
E[ x(t ) h(t ) y (t )d ]2
0
E[ x(t )]2 2 h( )( E[ y (t ) y ( )]d
0
h( )d h( ) E[ y (t ) y (t )]d
0 0
Rxx (0) 2 h( ) Ryx ( )d
E[e 2 (n)] lim
(2-25)
1 T 2T
T
T
(n) s (n)]2 dn [s
滤波器在n时刻复现信号s(n)显然是滤波问题。这是一种简单的过滤，滤除 噪声v(n)是唯一的目的。 但输出在时间上的简单的超前或者滞后，都不失为线性
(n a) ，这显然是一种超前的情况，输 滤波问题。在n时刻，滤波器输出如果为 s (n a) 是 s(n a) 的估计值，它比x(n)超前了 时间。这个时候滤波器所完成 出s
2 J1 2 J 2 0( 3 )
(2-15) 则将导致
J[ h h( t )] J [ o p t( t ) oh p t (t ) ]
(2-16) 这明显与最佳冲击响应将使均方误差最小的假设相矛盾。所以，我们只能取
J1 =0，即满足式(2-11)。由式(2-13)知，若使 J1 =0成立，则必须使式(2-13)中的方
第 2 章 维纳滤波理论
2.1 维纳滤波的概述
维纳 （Wiener） 滤波是用来解决从噪声中提取信号问题的一种过滤 （或滤波） 的方法。 实际上这种线性的滤波问题，可以看成是一种估计问题或是一种线性估 计问题。 维纳滤波器是一种基于最小均方误差准则下的估计滤波器。 滤波器的输入包 括有真实信号值x(t)和干扰噪声w(t)，信号值与噪声是统计独立的，则两者的合 成输入信号是
第二章维纳滤波2-3
2 -1
解 得 B ( z )。 因 B ( z ) 是 xx ( z ) 单 位 园 内 的 零 、 极 点 组 成 ， 所 以 B ( z )和 1 B(z) 都是物理可实现的因果系统。
G ( z )也 可 分 为 因 果 性 与 非 因 果 性 的 情 况 ， 但它是将激励信号白化后所得的白噪声， 使 求 解 G ( z )比 直 接 求 解 H
2 -1
又 因 为 x ( n ) s ( n ) ( n ), x ( n )的 信 号 模 型 为 ：
v(n)
w (n) A( z)
s(n)
x(n)
当 x ( n )的 功 率 谱 密 度 也 是 z的 有 理 式 时 ， 显 然 可 将 x (n )表 示 如 下 信 号 模 型 ：
2
1
2
ws (k )
2
ws ( z )=
xs
(z)
1
w k -
B(z
)
E e (n) m in =
2 -1 1 1 xs ( z ) xs ( z ) -1 c ss ( z ) - 2 B ( z -1 ) B ( z ) z d z 2 j w
x s (- m ) b ( m ) w s (- m )
x s ( m ) b (- m ) w s ( m )
(z) B(z xs
ws 1
)
1
ws
(z)
( z )=
xs
(z) )
B(z
H
opt
(z)
G (z) B(z)
xs 1
ˆ s ( n )的 均 方 误 差 ：
解 得 B ( z )。 因 B ( z ) 是 xx ( z ) 单 位 园 内 的 零 、 极 点 组 成 ， 所 以 B ( z )和 1 B(z) 都是物理可实现的因果系统。
G ( z )也 可 分 为 因 果 性 与 非 因 果 性 的 情 况 ， 但它是将激励信号白化后所得的白噪声， 使 求 解 G ( z )比 直 接 求 解 H
2 -1
又 因 为 x ( n ) s ( n ) ( n ), x ( n )的 信 号 模 型 为 ：
v(n)
w (n) A( z)
s(n)
x(n)
当 x ( n )的 功 率 谱 密 度 也 是 z的 有 理 式 时 ， 显 然 可 将 x (n )表 示 如 下 信 号 模 型 ：
2
1
2
ws (k )
2
ws ( z )=
xs
(z)
1
w k -
B(z
)
E e (n) m in =
2 -1 1 1 xs ( z ) xs ( z ) -1 c ss ( z ) - 2 B ( z -1 ) B ( z ) z d z 2 j w
x s (- m ) b ( m ) w s (- m )
x s ( m ) b (- m ) w s ( m )
(z) B(z xs
ws 1
)
1
ws
(z)
( z )=
xs
(z) )
B(z
H
opt
(z)
G (z) B(z)
xs 1
ˆ s ( n )的 均 方 误 差 ：
第二章维纳滤波2-4
{
}
{
}
（1）因果系统
取反变换：用b(n)表示B ( z )的逆变换。
E e2 (n + N )
∞ n=-∞
{
}
min ∞
2 2 = σ w ∑ b2 (n) - σ w ∑ b(n + N ) [b(n + N )u(n)] n=-∞
e2 (n + N ) 说明N 增大将导致E
N
Φ xyd ( z )
及 = 1
ˆ E [ s (n + N )-s (n + N ) ]
ss
{
c
2
}
min -1 -1
∫ Φ 2π j
( z ) - H opt ( z ) z Φ xs ( z ) z dz
-N
(2)物理可实现约束的(因果)维纳预测器
1 Φ xyd ( z ) H opt ( z ) = 2 -1 σ w B( z ) B( z ) + 1 Z Φ xs ( z ) = 2 -1 σ w B( z ) B( z ) +
因而，具有
2 Φ xx ( z) = Φss ( z) = Φ xs ( z) = σ w B( z) B( z -1 )
x(n) = s(n)
H ( z)
纯预测器
ˆ y (n) = s(n + N )
纯预测在工程上的意义： 当噪声小到一定程度以后可将该噪声忽略 或不再作更多考虑。 为此，可先用维纳滤波器等将噪声抑制到一定水准 之后再以纯预测方法作相应的预测处理。
φx y =∑hiφx x
j d
∞
i =1
j i
第二章—维纳滤波和卡尔曼滤波
H
c
(z)
2
1 B(
z)
[
Ssx (z) B(z 1 )
]
• 计算步骤如下：
•
(1)对
S xx
(z)
进行谱分解（因式分解）
S
x
x
(
z)
2
B(
z)
B(
z
1
)
• (2)对 Ssx (z)
进行因果和逆因果分解
B(z 1 )
Ssx (z) B(z 1 )
[
Ssx (z B(z 1
) )
]
[
Ssx (z B(z 1
N
• 称y(n) 是 sˆ(n)的估计值。 h(n) 为估计器。这种滤波器
称为最佳滤波器。
• 如果：s(n) 和 v(n) 的谱在频域上是分离的，容易设计一个
线性滤波器抑制噪声并提取信号。这是本科中经典数字信号 处理理论中详细讨论过的数字滤波器的设计问题。但是
• s(n) 和 v(n) 的谱有一部分相互重叠，则问题就要复杂的
E[e(n) x(n j)] 0
• 上式称为正交方程。（这是讲当用两个矢量正交时它们的 点乘等于零的关系，正交性原理可借用几何图形表示）
• 可见，满足正交性原理与满足最小均方误差的条件是等价
的。由图知，sˆ(n) 最满足最小均方误差的估计值。
• 正交方程表明，任何时刻的估计误差与用于估计的所有数 据（即滤波器的输入）正交。
• （2）
Ssx (z) B( z 1 )
[
Ssx (z B( z 1
) )
]
[
Ssx (z B( z 1
) )
]
0.36
(1 0.8z 1 )(1 0.8z)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章维纳滤波
其中：x(n)=s(n)+v(n)s(n)为真实有用信号v(n)为加性噪声
滤波的目的：在接收端得到s(n)的值，最好把v(n)全部给滤除掉
实际情况：不可能把噪声v(n)全部滤掉，只能让接收端接收的信号尽可能接近s(n),性能最好的这种线性滤波器就叫做维纳滤波器。
性能指标：最小均方误差MMSE（minimum mean square error）
滤波的目的：不断逼近S(n)
滤波的分类：
性能指标：最小均方误差MMSE（minimum mean square error）
◆维纳滤波器的设计（求解），实际上是找出一个滤波器，当输入x(n)=s(n)+v(n)时，滤
波器的输出最接近
s(n)。
◆确定一个滤波器：得到滤波器的单位冲击响应
h(n)
或者系统函数H(w)◆对于非因果的滤波器（Z域求解简单）：维纳滤波器时域求解
对于因果的滤波器：
维纳滤波器的Z域解（改进后的模型）
◆信号分解（通过白噪声获得色噪声）：
互逆操作◆白化滤波器（由色噪声得到白噪声）：
引入白化滤波器后的维纳滤波器滤波器的结构：
改进后的滤波器：
非因果维纳滤波器Z域求解（应用改进模型）
ΦXX z=σω2·B z·B(z−1)
最小均方误差：
因果维纳滤波器Z域求解（应用改进模型）
最小均方误差：
维纳预测器
◆维纳滤波器：
◆维纳预测器：
◆分类：
◆纯预测：x(n)中没有噪声，纯粹已知S(n),S(n-1)···对S(n + N)进行预测◆一般预测：带有噪声，已知x(n),x(n-1)···对S(n + N)进行预测
期望输出：y d(n)=S(n + N)
实际输出：y(n)=S(n+N)
◆非因果维纳预测器：
◆因果维纳预测器：
N步纯预测
一步纯线性预测时域求算
Yule-Walker方程：
自相关矩阵的的性质：
◆1.当x(n)为实数，自相关矩阵为对称阵Φxx=Φxx T
◆当x(n)为复数，自相关矩阵为厄米特阵Φxx=Φxx H
◆2.自相关矩阵为托普列兹阵，对角线上的元素相同。
◆3.自相关矩阵为正定阵。
习题。