最新七年级数学下册整式运算练习北师大版
七年级数学下册整式的乘除计算题练习(无答案)北师大版

1 整式的乘除计算
一:知识网络归纳
22
222
()(,,)()()()():()()()2m n m n
m n mn n n n
a a a a a m n a
b ab a b m a b ma mb
m n a b ma mb na nb
a b a b a b a b a ab b 特殊的=幂的运算法则为正整数,可为一个单项式或一个式项式单项式单项式
单项式多项式:多项式多项式:整式的乘法平方差公式 乘法公式完全平方公式:二:小试牛刀
专题一巧用乘法公式或幂的运算简化计算
方法 1 逆用幂的三条运算法则简化计算
例1 (1) 计算:19961996
31()(3)103。
(2) 已知3×9m ×27 m =321,求m 的值。
(3) 已知x 2n =4,求(3x 3n )2-4(x 2) 2n 的值。
2、已知:693273m m ,求m .
方法 2 巧用乘法公式简化计算。
例2 计算:24815111
11
(1)(1)(1)(1)22222.
思路分析:在进行多项式乘法运算时,应先观察给出的算式是否符合或可转化成某公式的形式,如果符合则应用公式计算,若不符合则运用多项式乘法法则计算。
观察本题容易发现缺少因式1(1)2,如果能通过恒等变形构造一个因式1
(1)2,则运用平方差公式就会迎刃而解。
方法 3 将条件或结论巧妙变形,运用公式分解因式化简计算。
整式
的乘法。
北师大版数学七年级下 第1章 整式的乘除 单元练习

第1章整式的乘除一.选择题(共10小题)1.长方形的面积是9a2﹣3ab+6a3,一边长是3a,则它的另一边长是()A.3a2﹣b+2a2B.b+3a+2a2C.2a2+3a﹣b D.3a2﹣b+2a2.如图,将边长为3a的正方形纸板沿虚线剪成两个正方形和两个长方形,若拿掉白色的大正方形后,将剩下的带阴影的三块拼成一个长方形,则这块长方形较长边的长为()A.3a﹣2b B.3a+2b C.3a+6b D.3a﹣6b3.如果x2+2mx+9是一个完全平方式,则m的值是()A.3B.±3C.6D.±64.若x+y=﹣2,x2+y2=10,则xy=()A.﹣3B.3C.﹣4D.45.如图1,从边长为a+4的正方形纸片中剪去一个边长为a+1的正方形(a>0),剩余部分沿虚线又剪拼成一个如图2所示的长方形ABCD(不重叠、无缝隙),则AD,AB的长分别是()A.3,2a+2B.5,2a+8C.5,2a+3D.3,2a+56.下列多项式相乘,不能用平方差公式计算的是()A.(2x﹣3y)(3y﹣2x)B.(﹣2x+3y)(﹣2x﹣3y)C.(x﹣2y)(2y+x)D.(x+3y)(x﹣3y)7.下列运算正确的是()A.a5•a3=a8B.3690000=3.69×107C.(﹣2a)3=﹣6a3D.20160=08.以下运算正确的是()A.(ab3)2=ab6B.(﹣3xy)3=﹣9x3y3C.x3•x4=x12D.(3x)2=9x29.计算:(8x5﹣6x3﹣4x2)÷(﹣2x)=()A.﹣4x4﹣3x2+2x B.﹣4x4+3x2+2xC.4x4+3x2﹣2x D.4x4﹣3x2﹣2x10.已知x+y=5,xy=6,则x2+y2的值是()A.1B.13C.17D.25二.填空题(共5小题)11.计算(2x3﹣3x2+4x﹣1)•(﹣2x)2=.12.计算(x+5)(3x﹣1)的结果中,一次项系数为.13.已知x2﹣2x=2,则(x﹣1)(3x+1)﹣(x+1)2﹣3的值为.14.新定义一种运算,其法则为=a2d2﹣bc,则=.15.已知a+b=4,ab=2,则a﹣b的值是.三.解答题(共5小题)16.计算:(1)(2)17.4(x+1)2﹣(2x+5)(2x﹣5)18.我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙的解决一些图形问题.(1)如图1所示,甲同学从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),求矩形的面积;(2)乙同学用如图2所示不同颜色的正方形与长方形纸片拼成了一个如图3所示的正方形.①用不同的代数式表示图中阴影部分的面积,你能得到怎样的等式,试用乘法公式说明这个等式成立;②根据①中的结论计算:已知(2016﹣m)(2018﹣m)=2009,求(2018﹣m)2+(m﹣2016)219.已知(x+7)2=11,求(x+6)(x+8)﹣5的值.20.某植物园现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米,B园区为正方形,边长为(x+2y)米(1)请用代数式表示A、B两园区的面积之和并化简;(2)现根据实际需要对A园区进行整改,长增加(4x﹣y)米,宽减少(x﹣2y)米,整改后A区的长比宽多190米,且整改后两园区的周长之和为660米①求x、y的值;②若A园区全部种植C种花,B园区全部种植D种花,且C、D两种花投入的费用与吸引游客的收益如表:C D投入(元/平方米)1612收益(元/平方米)2618求整改后A、B两园区旅游的净收益之和.(净利润=收益﹣投入)参考答案一.选择题(共10小题)1.C.2.B.3.B.4.A.5.D.6.A.7.A.8.D.9.B.10.B.二.填空题(共5小题)11.8x5﹣12x4+16x3﹣4x2.12.14.13.﹣1.14.2x6.15.±2.三.解答题(共5小题)16.解:(1)原式=4+1﹣(﹣0.125×8)2018×8=5﹣1×8=﹣3;(2)原式=﹣9×2+[﹣(1﹣)×9]=﹣18+[﹣6]=﹣24.17.解:原式=4x2+8x+4﹣4x2+25=8x+29.18.解:(1)矩形的面积=(a+4)2﹣(a+1)2=a2+8a+16﹣a2﹣2a﹣1=6a+15;(2)①如图2,阴影部分的面积=a2+b2,如图3,阴影部分的面积=(a+b)2﹣2ab,则得到等式a2+b2=(a+b)2﹣2ab,证明:(a+b)2﹣2ab=a2+2ab+b2﹣2ab=a2+b2;②(2018﹣m)2+(m﹣2016)2=(2018﹣m+m﹣2016)2﹣2×(m﹣2016)(2018﹣m)=4+2009×2=4022.19.解:∵(x+6)(x+8)﹣5=[(x+7)﹣1][(x+7)+1]﹣5=(x+7)2﹣1﹣5=(x+7)2﹣6.∵(x+7)2=11,∴原式=11﹣6=5.20.解:(1)(x+y)(x﹣y)+(x+2y)(x+2y)=x2﹣y2+x2+4xy+4y2=2x2+4xy+3y2(平方米)答:A、B两园区的面积之和为(2x2+4xy+3y2)平方米;(2)①(x+y)+(4x﹣y)=x+y+4x﹣y=5x(米),(x﹣y)﹣(x﹣2y)=x﹣y﹣x+2y=y(米),依题意有:,解得;②A园区面积为:5xy=2000(平方米),B园区面积为:(40+20)2=3600(平方米),(26﹣16)×2000+(18﹣12)×3600=41600(元).答:整改后A、B两园区旅游的净收益之和为41600元.。
北师大版七年级下册第一章整式的运算全章同步训练以及答案

北师大版七年级下册第一章整式的运算全章同步训练以及答案(总41页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除- 2 - 第一章 整式的运算同步练习1.1 整式一、精心选一选⒈ 下列说法正确的个数是 【 】① 单项式a 的系数为0,次数为0; ②21-ab 是单项式; ③ -xyz 的系数是-1,次数是1; ④ π是单项式,而2不是单项式.A .0个B .1个C .2个D .3个 ⒉若单项式1232--x n m 和c b a 245的次数相同,则代数式322+-x x 的值为【 】A .14B .20C .27D .35二、耐心填一填:⒈ 3a 2b 3c 系数是 次数是 ;πR 2系数是 次数是 . ⒉ n = 时,单项式231+n xy 的次数是6.三、用心做一做:⒈ 下列各代数式是不是单项式?如果是,请指出它们的系数和次数. ⑴ a 52 ⑵ b a 2- ⑶32b a - ⑷ 0.1532y x ⑸ 2x +1 ⑹ y ⑺ -m⒉ 小明认为既然单项式322y x 的次数是5,那么多项式322y x +的次数也是5.他的想法对吗为什么由此,你能谈谈单项式和多项式次数的确定有什么不同吗相信你能完成一、精心选一选⒈ 下列说法正确的个数是 【 】- 3 - ① 单项式是整式;② 单项式也是多项式;③ 单项式和多项式都是整式.A .0个B .1个C .2个D .3个⒉ 把3a 3-5和a 2b +ab 2+1按某种标准进行分类时属于同一类,则下列哪一个多项式也属于此类 【 】A .-a 5-b 5B .4x 2-7C .xyz -1D .a 2+2ab +b 2⒊ 若多项式(m +4)x 3+2x 2+x -1的次数是2,则m 2-m 的值为【 】A .10B .12C .16D .20二、耐心填一填⒈ 多项式x 3y +5xy -6-4xy 2是 的和.⒉ 5x 2+4x -3是 次 项式,其中常数项是 .⒊ 如图1-1-1则这个平面图形的面积是 。
整式的乘法练习题(含解析答案)

北师大版数学七年级下册第一章1.4整式的乘法课时练习一、选择题1.(-5a2b)·(-3a)等于()A.15a3b B.-15a2b C.-15a3b D.-8a2b答案:A解析:解答:(-5a2b)·(-3a)=15a3b,故A项正确.分析:由单项式乘单项式法则与同底数幂的乘法法则可完成此题.2.(2a)3·(-5b2)等于()A.10a3b B.-40a3b2C.-40a3b D.-40a2b答案:B解析:解答:(2a)3·(-5b2)=-40a3b2,故B项正确.分析:先由积的乘方法则得(2a)3=8a3,再由单项式乘单项式法则可完成此题.3.(2a3b)2·(-5ab2c)等于()A.-20a6b4c B.10a7b4c C.-20a7b4c D.20a7b4c答案:C解析:解答:(2a3b)2·(-5ab2c)=-20a7b4c,故C项正确.分析:先由积的乘方法则得(2a3b)2=-4a6b2,再由单项式乘单项式法则与同底数幂的乘法可完成此题.4.(2x3y)2·(5xy2)·x7 等于()A.-20x6y4B.10x y y4C.-20x7y4D.20x14y4答案:D解析:解答:(2x3y)2·(5xy2)·x7 =-20x14y4,故D项正确.分析:先由积的乘方法则得(2x3y)2=-4x6y2,再由单项式乘单项式法则与同底数幂的乘法法则可完成此题.5.2a3·(b2-5ac)等于()A.-20a6b2c B.10a5b2c C.2a3b2-10a4c D.a7b4c-10a4c答案:C解析:解答:2a3·(b2-5ac)=2a3b2-10a4c,故C项正确.分析:由单项式乘多项式法则与同底数幂的乘法法则可完成此题.6.x3y·(xy2+z)等于()A.x4y3+xyz B.xy3+x3yz C.z x14y4 D.x4y3+x3yz答案:D解析:解答:x3y·(xy2+z)=x4y3+x3yz,故D项正确.分析:由单项式乘单项式法则与同底数幂的乘法法则可完成此题.7.(-x7)2·(x3y+z)等于()A.x17y+x14z B.-xy3+x3yz C.-x17y+x14z D.x17y+x3yz答案:A解析:解答:(-x7)2·(x3y+z)=x17y+x14z,故A项正确.分析:先由幂的乘方法则得(-x7)2=x14,再由单项式乘多项式法则与同底数幂的乘法法则可完成此题.8.[(-6)3]4 .(b2-ac)等于()A.-612b2-b2c B.10a5-b2c C.612b2-612ac D.b4c-a4c答案:C解析:解答:[(-6)3]4 .(b2-ac)=612b2-612ac,故C项正确.分析:先由幂的乘方法则得[(-6)3]4=612,再由单项式乘多项式法则与同底数幂的乘法法则可完成此题.9.(2x)3.(x3y+z)等于()A.8x6y+x14z B.-8x6y+x3yz C.8x6y+8x3z D.8x6y+x3yz答案:C解析:解答:(2x)3.(x3y+z)=8x6y+8x3z,故C项正确.分析:先由积的乘方法则得(2x)3=8x3,再由单项式乘多项式法则与同底数幂的乘法法则可完成此题.10.(2x)2.[(-y2)2+z]等于()A.4xy4+xz B.-4x2y4+4x2z C.2x2y4+2x2z D.4x2y4+4x2z答案:D解析:解答:(2x)2.[(-y2)2+z]=4x2y4+4x2z,故D项正确.分析:先由积的乘方法则得(2x)2=4x2,由幂的乘方法则得(-y2)2=y4再由单项式乘多项式法则与同底数幂的乘法法则可完成此题.11.x2.x5.(y4+z)等于()A.x7y4+x7z B.-4x2y4+4x2z C.2x2y4+2x2z D.4x2y4+4x2z答案:A解析:解答:x2.x5.(y4+z)=x7y4+x7z,故A项正确.分析:先由同底数幂的乘法法则得x2.x5=x7,再由单项式乘多项式法则可完成此题. 12.x2·(x y2+z)等于()A.xy+xz B.-x2y4+x2z C.x3y2+x2z D.x2y4+x2z答案:C解析:解答:x2.(x y2+z)=x3y2+x2z,故C项正确.分析:由单项式乘多项式法则与同底数幂的乘法法则可完成此题.13.(a3+b2)·(-5ac)等于()A.-5a6b2-c B.5a5-b2c C.5a3b2-10a4c D.-5a4c-5ab2c答案:D解析:解答:(a3+b2)·(-5ac)=-5a4c-5ab2c,故D项正确.分析:由单项式乘多项式法则与同底数幂的乘法法则可完成此题.14.(x2+y5)·(y2+z)等于()A.x2y2+x2z+y7+y5z B.2x2y2+x2z+y5z C.x2y2+x2z+y5z D.x2y2+y7+y5z 答案:A解析:解答:(x2+y5).(y2+z)=x2y2+x2z+y7+y5z,故A项正确.分析:由多项式乘多项式法则与同底数幂的乘法法则可完成此题.15.2(a2+b5)·a2等于()A.a2c+b5c B.2a4+2b5a2C.a4+2b5a2D.2a4+ba2答案:B解析:解答:2(a2+b5)·a2=2a4+2b5a2,故B项正确.分析:由单项式乘多项式法则与同底数幂的乘法法则可完成此题.二、填空题16.5x2·(xy2+z)等于;答案:5x3y2+5x2z解析:解答:5x2·(xy2+z)=5x2·xy2+5x2·z=5x3y2+5x2z分析:由单项式乘多项式法则与同底数幂的乘法法则可完成此题17.2a2·(ab2+4c)等于;答案:2a3b2+8a2c解析:解答:2a2·(ab2+4c)=2a2·ab2+2a2·4c=2a3b2+8a2c分析:由单项式乘多项式法则与同底数幂的乘法法则可完成此题18.2a2·(3ab2+7c)等于;答案:6a3b2+14a2c解析:解答:2a2·(3ab2+7c=2a2·3ab2+2a2·7c=6a3b2+14a2c分析:由单项式乘多项式法则与同底数幂的乘法法则可完成此题19.(-2a2)·(3a+c)等于;答案:-6a3-2a2c解析:解答:-2a2·(3a+c)=(-2a2)·3a+(-2a2)·c=-6a3-6a2c分析:由单项式乘多项式法则与同底数幂的乘法法则可完成此题20.(-4x2)·(3x+1)等于;答案:-12x3-4x2解析:解答:(-4x2)·(3x+1)=(-4x2)·3x+(-4x2)·1=-12x3-4x2分析:由单项式乘多项式法则与同底数幂的乘法法则可完成此题三、计算题21.(-10x2y)·(2xy4z)答案:-20 x3 y5 z解析:解答:解:(-10x2y)·(2xy4z)= -20 x2+1·y4+1·z=-20 x3 y5 z分析:由单项式乘单项式法则与同底数幂的乘法法则可完成此题22.(-2 x y2)·(-3 x2y4)·(- x y)答案:-6 x4 y7解析:解答:解:(-2 x y2)·(-3 x2y4)·(- x y)= -6 x1+2+1·y2+4+1=-6 x4 y7分析:由单项式乘单项式法则与同底数幂的乘法法则可完成此题23.2a·(a+1)- a(3a-2)+2a2 (a2-1)答案:2a4 -3a2+4a解析:解答:解:2a·(a+1)- a(3a-2)+2a2(a2-1) =2a2+2a-3a2+2a+2a4-2a2=2a4-3a2+4a 分析:先由单项式乘多项式法则与同底数幂的乘法法则计算,再合并同类项可完成此题. 24.3ab·(a2b+ ab2-ab)答案:3a3b2+3 a2b3- 3 a2b2解析:解答:解:3ab·(a2b+ ab2-ab)=3ab·a2b+3ab·ab2- 3ab·ab=3a3b2+3 a2b3- 3 a2b2分析:由单项式乘多项式法则与同底数幂的乘法法则计算可完成题.25.(x-8y)·(x-y)答案:x2-9xy +8y2解析:解答:解:(x-8y)·(x-y)= x1+1-xy-8xy+8y1+1= x2-9xy +8y2分析:先由多项式乘多项式法则与同底数幂的乘法法则计算,再合并同类项可完成此题.。
整式的混合运算50题(综合练)-2023-2024学年七年级数学下册专项突破讲与练(北师大版)

专题1.26整式的混合运算50题(分层练习)(综合练))先化简,再求值:,其中,;3y,我们把3)定义的新运算“⊕”交换律是否还成立?请你写出你的探究过程.参考答案:【点拨】本题考查了整式的混合运算,能正确运用法则进行化简是解此题的关键.8.(1)y 12;(2)-8;9.【分析】(1)(2)根据幂的乘方和积的乘方以及同底数幂的乘法法则计算;解:(1)(y 2)3((y 3)2=y 6(y 6=y 12(2)(-0.125)9×(-8)10=(-0.125)9×(-8)9×(-8)=(0.125×8)9×(-8)=-8【点拨】本题考查了幂的乘方和积的乘方,同底数幂的乘法,以及整式的混合运算,解题的关键是掌握运算法则.9.(1)-1;(2)611a -;(3)86x +;(4)222a ac c -+-24b 【分析】(1)直接利用零指数幂,绝对值,负指数幂,乘方法则运算.(2)先利用幂的运算法则,再合并同类项.(3)利用整式的乘法法则进行运算.(4)利用平方差公式进行运算.解:(1)原式=1-3+2-1=-1(2)原式=68a -+6a -64a =611a -(3)原式=27x x +-()26x x --=27x x +26x x -++=86x +(4)原式=()2a c --()22b =222a ac c -+-24b 【点拨】本题主要考查了数的计算,整式的加减与乘法,解题的关键要对零指数幂,绝对值,负指数幂以及幂的运算和整式的乘法法则熟悉.10.(1)、-8a+12;16;(2)、;0解:(1)、原式=-4a--4a+12=-8a+12当a=-时,原式=-8×(-)+12=16.(2)、原式=-4-+4=当x=8,y=-8时原式=0考点:多项式的乘法计算【点拨】本题主要考查了整式乘法的公式运用,准确计算是解题的关键.(2)()()()()1614a a a a +----()226644a a a a a a =-+----+226644a a a a a a =-+--++-10=-.24.(1)6542126x x x --;(2)2419x -【分析】(1)根据幂的运算性质和单项式乘以多项式展开化简即可;(2)根据多项式乘以多项式化简即可;(1)解:原式()665486126x x x x =-++665486126x x x x =---6542126x x x =--(2)原式22284231015x x x x x x =-+-++--()()()22223810154x x x x x x =+++--+--2419x =-【点拨】本题主要考查了整式的乘法运算,掌握相关法则和公式是解题的关键.25.(1)12a -;(2)39a -;(3)4-;(4)4【分析】(1)先根据幂的乘方计算,然后再运用同底数幂相乘即可解答;(2)先根据幂的乘方、积的乘方计算,然后再运用四则混合运算求解即可;(3)先运用负整数次幂、零次幂化简,然后在根据有理数的四则混合运算计算即可;(3)先运用负整数次幂、零次幂、绝对值、乘方化简,然后在根据有理数的混合运算计算即可.(1)解:()()332·a a --,()66·a a =-,12a =-.(2)解:()()()23542a a a -+÷-,()5388a a a =-+÷-,338a a =--,39a =-.当=1x -,1y =时,原式()()224117111014171023=⨯-+⨯-⨯-⨯=--=-.【点拨】本题考查了整式的混合运算和求值的应用,熟练掌握整式的混合运算和求值是解题的关键.31.(1)28x x -,9;(2)42235x y x y +,42【分析】(1)先利用单项式乘以多项式的运算法则、合并同类项法则化简原式,再代入x 值计算即可;(2)先利用单项式乘以多项式的运算法则、合并同类项法则化简原式,再将23x y =整体代入求解即可.解:(1)3(1)(25)x x x x --+=223325x x x x---=28x x -,当x=﹣1时,原式=(﹣1)2﹣8×(﹣1)=9;(2)332(3)()xy x y x xy x y x ++-=42242226x y x y x y x y++-=42235x y x y +,当23x y =时,原式=3×32+5×3=42.【点拨】本题考查了整式的化简求值、单项式乘多项式的运算、合并同类项、有理数的混合运算,熟练掌握运算法则和运算顺序是解答的关键.32.(1)26x -;(2)67x -.【分析】(1)分别计算单项式乘多项式和多项式乘多项式,再合并同类项即可;(2)分别计算积的乘方和同底数幂相乘,再合并同类项即可.解:(1)原式=(1)(2)(3)x x x x -+-+=22326x x x x x -++--=26x -;(2)原式=668x x -+=67x -.【点拨】本题考查整式的混合运算,积的乘方公式和单项式乘单项式.掌握运算法则,能根据法则正确计算是解题关键.33.(1)8a ;(2)171.610⨯(3)322551x x x -++-;(4)31x -【分析】(1)根据整式乘法、同底数幂的乘法性质计算,即可得到答案;(2)根据整式乘法、幂的乘方的性质计算,即可得到答案;(3)根据整式乘法和加减法的性质计算,即可得到答案;【点拨】本题考查整式的计算、化简与求值,熟练掌握整式的运算法则和非负数和为abc,﹣【点拨】本题考查有理数的混合运算与整式的加减乘混合远算,掌握有理数的混合运算法则,整式加【点拨】本题考查整式的混合运算,涉及知识点:积的乘方、单项式乘以单项式、单项式乘以多项式、【分析】多项式乘以多项式,单项式乘以多项式展开,合并同类项对整式进行化简,然后再代值求解3=;(2)原式[262(2)261]3=-⨯-⨯--⨯+⊕(124121)3=-+-+⊕193=-⊕1932(19)231=-⨯-⨯--⨯+24=-;(3)成立,221a b ab a b ⊕=--+ ,221b a ab b a ⊕=--+,a b b a ∴⊕=⊕,∴定义的新运算“⊕”交换律还成立.【点拨】此题是定义新运算题型.直接把对应的数字代入所给的式子可求出所要的结果,理解题意是解题的关键.。
北师大版数学七下第一章《整式的乘除》计算题专项训练

北师大版数学七下第一章《整式的乘除》计算题专项训练1、4(a+b)+2(a+b)-5(a+b)化简得:(4+2-5)(a+b)=a+b答案为:a+b2、(3mn+1)(3mn-1)-8mn化简得:9m^2n^2-1-8mn=9m^2n^2-8mn-1答案为:9m^2n^2-8mn-13、-2-3×(1-(-1)÷2^2)×22÷7化简得:-2-3×(1-(-1)÷4)×2= -2-3×(1+0.25)×2=-16.5答案为:-16.54、[(xy-2)(xy+2)-2xy+4]÷(xy)化简得:(x^2y-4+2xy+4)÷xy=(x^2y+2xy)÷xy=x+2答案为:x+25、(2a-1)^2+(2a-1)(a+4),其中a=-2化简得:(2(-2)-1)^2+(2(-2)-1)(-2+4)=(-5)^2+(-10)(2)=45答案为:456、(1÷2ab)×(-2ab^2)^2÷4÷(1÷2x)^3化简得:-2a^2b^4×8x^3=-16a^2b^4x^3答案为:-16a^2b^4x^37、2(x^2+5xy)-6(2xy-x^2)化简得:2x^2+10xy-12xy+6x^2=8x^2-2xy答案为:8x^2-2xy8、(x+2)(x-3)-(x+1)(x-2)化简得:x^2-x-6-x^2+x+2x-2=x-4答案为:x-410、(x+2y)^2-(x+y)(x-y),其中x=-2,y=3化简得:(2(-2)+6)^2-(2(-2)+3)(2(-2)-3)=16-(-13)=29 答案为:2911、(-x-y)(x-y)+(x+y)^2化简得:-x^2+xy+xy-y^2+x^2+2xy+y^2=4xy答案为:4xy13、x^2-(x+2)(x-2)化简得:x^2-(x^2-4)=4答案为:414、(-3x^3)^2-(-2x^2)^3化简得:9x^6-8x^6=x^6答案为:x^615、(2a+b)^4÷(2a+b)^2化简得:(2a+b)^2=4a^2+4ab+b^2答案为:4a^2+4ab+b^216、123-124×122利用乘法公式计算124×122=化简得:123-=-答案为:-17、[(x+1)(x+2)-2]÷(-x)化简得:-(x^2+3x)=-(x(x+3))答案为:-(x(x+3))18、(2xy)·(-7xy)÷(14xy)化简得:-1/2答案为:-1/219、[(2x+y)^2+(2x+y)(2x-y)-4xy]÷(-2x),其中x=2,y=1化简得:[(2(2)+1)^2+(2(2)+1)(2(2)-1)-4(2)]÷(-2(2))=-15 答案为:-1520、-2a(3a-4b^2)÷5化简得:6a^2-8b^2÷5=-8/5(5-3a)(5+3a)答案为:-8/5(5-3a)(5+3a)21、(a+2b)(a-2b)化简得:a^2-4b^2答案为:a^2-4b^222、(x-1)(2x+3)化简得:2x^2+x-3答案为:2x^2+x-323、(a-3b)^2-9b^2-3.14化简得:a^2-6ab+9b^2-9b^2-3.14=a^2-6ab-3.14答案为:a^2-6ab-3.1424、3x^2y(-4xy^2)+5xy(-6xy)^2,其中x=2,y=3化简得:-36x^4y^3+5(-216x^3y^3)=-36x^4y^3-1080x^3y^3 答案为:-36x^4y^3-1080x^3y^325、3+0+(-2)+(892-890)化简得:3+0+(-2)+2=3答案为:326、(9abc)÷(2ab)·(-abc)化简得:-18c答案为:-18c27、(15xy-12xy-3x)÷(-3x)化简得:-1答案为:-128、(a+b)-4(2a-3b)+(3a-2b)化简得:a+b-8a+12b+3a-2b=-4a+11b答案为:-4a+11b30、(x+2)^2-(x-1)(x+1)化简得:x^2+4x+4-(x^2-1)=5x+5答案为:5x+531、3+0+(-2)+(892-890)化简得:3+0+(-2)+2=3答案为:332、(a-b)(a+ab+b)+b(a+b)化简得:a^2+ab^2+2ab+b^2答案为:a^2+ab^2+2ab+b^21.题目中的符号应该使用正确的数学符号,比如乘号用*代替,除号用/代替。
北师大版七年级数学下册整式运算练习题
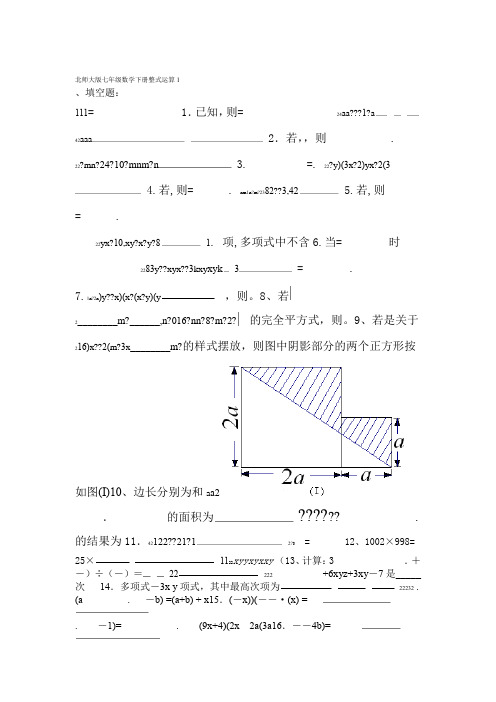
北师大版七年级数学下册整式运算1、填空题:111= 1.已知,则= 24aa???1?a2.若,,则 .42aaa3. =. 22?y)(3x?2)yx?2(322?mn?24?10?mnm?n4.若,则= . nm1n?m?2382??3,425.若,则= .. 项,多项式中不含6.当= 时22yx?10,xy?x?y?81= .2283y??xyx??3kxy xyk37.1n?2n)y??x)(x?(x?y)(y,则。
8、若的完全平方式,则。
9、若是关于2________m?______,n?016?nn?8?m?2?的样式摆放,则图中阴影部分的两个正方形按216)x??2(m?3x________m?如图(I)10、边长分别为和a a2.的面积为?????? .的结果为11.42122??21?12?0 = 12、1002×998= 25×1122xyyxyxxy(13、计算:3 .+-)÷(-)=22222+6xyz+3xy-7是_____次14.多项式-3x y项式,其中最高次项为22232 .(a . -b) =(a+b) + x15.(-x))(--·(x) =. -1)= . (9x+4)(2x 2a(3a16.--4b)=2222. y) =(x-(x+y) . -25y .17(3x+5y)·=9x-,则的一次项系数为--.18(x+2)(3xa)5a= .1北师大版七年级数学下册整式运算11232222;.19.?b))(5a?3a(??)2y)xy(?x(222;. 20.??2bcab(4?4)??b))(5x(2x?3x45532)=(3a b8a21 (-b c÷4ab. )·mn2m?n xy?aa?35?a. 22.若则4 ·,2 = ,则.若2x+y=3,2+x+m是一个完全平方式,则m= .若x . .23(a-b+2)(a-b-2)=222+ab+bc-ac=____________________. +b+c24如果a=-2002, b=2000, c=-2001, 则a222=_________.(用ab+y的代数式表示+z) ,则25.如果x+y+z=a,xy+yz+xz=bx m?1n?22n?12m53,则26若m+n=_______________.bb?aa?ab11111=______________ 计算:27.)1?)( (1?)(1?)((1?1?)222222349910022 , 那么a = - 9y 已知28. (x - ay) (x + ay ) = x.二、选择题:1下列等式中,计算正确的是()232693210 B、 D、 C A、、pq?pq)6?(3xx?xaa?x?a??x?x(3a?2b)(?3a?2b)?()、计算:2222222229a?6ab?bb?6ab?9a9a?4b4b?9a、、、A D C B、3毫米, 则其体积可表示为( )立方毫米. 3、一正方体的棱长为2×1090279.10 D. 6×10× C. 2×. A8×1010 B. 82222bb3?9b3b?9?m2m4a12?ab? ( )。
最新北师大版七年级数学下册整式运算练习题

、填空题:1.已知11=-a a ,则221aa += 441a a += 2.若10m n +=,24mn =,则22m n += . 3.-+2)23(y x =2)23(y x -. 4.若84,32==n m ,则1232-+n m = . 5.若10,8==-xy y x ,则22y x += .6.当k = 时,多项式8313322+---xy y kxy x 中不含xy 项. 7.)()()(12y x y x x y n n --⋅--= .8、若016822=+-+-n n m ,则______________,==n m 。
9、若16)3(22+-+m x 是关于x 的完全平方式,则________=m 。
10、边长分别为a 和a 2的两个正方形按如图(I)的样式摆放,则图中阴影部分的面积为 .11.()()()24212121+++的结果为 .12、1002×998= 20×52- = 13、计算:(3x 2y -xy 2+21xy )÷(-21xy )= . 14.多项式-3x 2y 2+6xyz+3xy 2-7是_____次 项式,其中最高次项为 15.(-x 2)(-x)2·(-x)3= . (a -b)2=(a+b)2+ . 16.-2a(3a -4b)= . (9x+4)(2x -1)= . 17.(3x+5y)· =9x 2-25y 2. (x+y)2- =(x -y)2. 18.(x+2)(3x -a)的一次项系数为-5,则a= .19.()()--=5323a b a ;()()-=1222222x y xy .20.52342x x x ()-+= ;()()422ab b bc --= . 21 (-8a 4b 5c÷4ab 5)·(3a 3b 2)= .22.若a m =3,a n =5,则a m n 2+= .若2x+y=3,则4x ·2y = .23.(a-b+2)(a-b-2)= .若x 2+x+m 是一个完全平方式,则m= . 24如果a=-2002, b=2000, c=-2001, 则a 2+b 2+c 2+ab+bc-ac=____________________. 25.如果x+y+z=a ,xy+yz+xz=b ,则x 2+y 2+z 2=_________.(用ab 的代数式表示) 26若3521221b a b a b a m n n m =⋅-++,则m+n=_______________. 27.计算:)10011)(9911()411)(311)(211(22222-----=______________ 28. 已知 (x - ay) (x + ay ) = x 2 - 9y 2 , 那么 a = .二、选择题:1下列等式中,计算正确的是( )A 、a a a =÷910B 、x x x =-23C 、pq pq 6)3(2=-D 、623x x x =⋅ 2、计算:)()23)(23(=---b a b aA 、2269b ab a --B 、 2296a ab b --C 、 2249b a -D 、 2294a b -3、一正方体的棱长为2×103毫米, 则其体积可表示为( )立方毫米. A .8×109 B. 8×100 C. 2×1027 D. 6×109.4、多项式的平方是m ab a +-1242,则=m ( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初一数学(整式的运算)单元测试题(二)
一、填空题:(每空2分,共28分)
1.把下列代数式的字母代号填人相应集合的括号内: A. xy+1 B. –2x 2
+y C.3
xy 2-
D.2
14
- E.x
1-
F.x 4
G.
x ax 2x 8
123
-- H.x+y+z
I.
3ab 2005
- J.)y x (3
1
+ K.c
3ab 2+
(1)单项式集合 { …} (2)多项式集合 { …} (3)三次多项式 { …} (4)整式集合 { …} 2.单项式bc a 7
92
-
的系数是 . 3.若单项式-2x 3y n-3是一个关于x 、y 的五次单项式,则n = . 4.(2x+y)2=4x 2+ +y 2. 5.计算:-2a 2(
2
1
ab+b 2)-5a(a 2b-ab 2) = . 6.3
22
43b a 21c b a 43⎪⎭
⎫
⎝⎛-÷⎪⎭⎫ ⎝⎛-= .
7.-x 2与2y 2的和为A ,2x 2与1-y 2的差为B , 则A -3B= . 8.()()()()()
=++++-884422y x y x y x y x y x .
9.有一名同学把一个整式减去多项式xy+5yz+3xz 误认为加上这个多项式,结果答案为 5yz-3xz+2xy ,则原题正确答案为 .
10.当a = ,b = 时,多项式a 2+b 2-4a+6b+18有最小值.
二、选择题(每题3分,共24分) 1.下列计算正确的是( )
(A )532x 2x x =+ (B )632x x x =⋅ (C )336x x x =÷ (D )623x x -=-)(
2.有一个长方形的水稻田,长是宽的2.8倍,宽为6.52
10⨯,则这块水稻田的面积是( ) (A )1.183710⨯ (B )510183.1⨯ (C )71083.11⨯ (D )610183.1⨯ 3.如果x 2-kx -ab = (x -a )(x +b ), 则k 应为( )
(A )a +b (B ) a -b (C ) b -a (D )-a -b 4.若(x -3)0 -2(3x -6)
-2
有意义,则x 的取值范围是( )
(A ) x >3 (B )x ≠3 且x ≠2 (C ) x ≠3或 x ≠2 (D )x < 2 5.计算:30
2
2
)2(21)x (4554---÷⎪⎭
⎫
⎝⎛--π-+⎪
⎭
⎫
⎝⎛-÷⎪⎭⎫ ⎝⎛得到的结果是( )
(A )8 (B )9 (C )10 (D )11 6.若a = -0.42
, b = -4-2
, c =2
41-⎪
⎭
⎫
⎝⎛-,d =0
41⎪⎭
⎫
⎝⎛-, 则 a 、b 、c 、d 的大小关系为( )
(A ) a<b<c<d (B )b<a<d<c (C ) a<d<c<b (D )c<a<d<b 7.下列语句中正确的是( ) (A )(x -3.14)0 没有意义 (B )任何数的零次幂都等于1
(C ) 一个不等于0的数的倒数的-p 次幂(p 是正整数)等于它的p 次幂 (D )在科学记数法a×10 n 中,n 一定是正整数 8.若k xy 30x 252++为一完全平方式,则k 为( )
(A ) 36y 2 (B ) 9y 2 (C ) 4y 2 (D )y 2
三、解答下列各题(每小题6分,共48分)
1.计算(1)(3xy -2x 2-3y 2)+(x 2-5xy +3y 2) (2)-51x 2(5x 2-2x +1) (3)(-3
5ab 3c)⋅103a 3
bc ⋅(-8abc)2
(4)
2005
20063
15155
321352125.0)()()()(-⨯+⨯- (5)〔21xy (x 2+y )(x 2-y )+23x 2y 7÷3xy 4〕÷(-8
1
x 4y ) (6)))((c b a c b a ---+
2.用简便方法计算:
欢迎来主页下载---精品文档
(1)7655.0469.27655.02345.12
2⨯++
(2)9999×10001-100002
3.化简求值:4(x 2+y )(x 2-y )-(2x 2-y )2 , 其中 x=2, y=-5 已知:2x -y =2, 求:〔(x 2+y 2)-(x -y )2+2y (x -y )〕÷4y
4.已知:a (a -1)-(a 2
-b )= -5 求: 代数式 2
b a 22+-ab 的值.
5.已知: a 2+b 2-2a +6b +10 = 0, 求:a 2005-b
1
的值.
6.已知多项式x 2+nx+3 与多项式 x 2-3x+m 的乘积中不含x 2和x 3项,求m 、n 的值.
7.请先阅读下面的解题过程,然后仿照做下面的题. 已知:01x x 2=-+,求:3x 2x 23++的值. 4
4004)1x x ()1x x (x 3
x x x x x 3
x 2x 2222323=++=+-++-+=+++-+=++ 若:0x x x 132=+++,求:200432x x x x ++++ 的值.
一、填空题:(每空2分,共28分)
1.把下列代数式的字母代号填人相应集合的括号内:
(1) C,D,F (2) A,B,G,H,J (3) G (4) A,B,C,D,F,G,H,J 2.7
9- 3.5 4.4xy
5.223b a 3b a 6+- 6.2
5c b 29-
7.3y x 722+-- 8.1616y x - 9.-5yz -9xz 10.2,-3
二、选择题(每题3分,共24分)
1.C 2.D 3.B 4.B 5.C 6.B 7.C 8.B
三、解答下列各题(每小题6分,共48分) 1.计算
(1)xy 2x 2
-- (2)234
x 5
1x 52x -+
- (3)466c b a 32- (4)13
5
1-
(5)-4x
(6)ac 2c b a 222-+-
2.用简便方法计算: (1)=(1.2345+0.7655)2
=4
(2)=(10000-1)(10000+1)-100002
= -1 3.
=22y 5y x 4- =-205 4. 5.12)b a (2
1
5b a 2=-=
=-原式 5.点评:由0)3b ()2a (22=++-得 3
1
1
3
b ,1a =-==原式 6.点评:
3n ,6m 03n 3m 0
3n m 3x )9mn (x )3n 3m ()3n (x x 234==∴=+-=-+-++-+-+=原式
7.
)x x x 1(x ...)x x x 1(x 32200132=++++++++=
附加题:
1.点评:2
122200320042200320042
1200320041200320042003200422
2
22
=-+⋅=
-++-=)()(原式
2.点评:设)7x 3)(6x 5x (42bx ax x 3233++-=+++ 比较系数得:⎩
⎨⎧-=-=17b 8
a。
