数学卷·2019届江苏省徐州一中(徐州市)高一下学期期末考试(2017.06)

合集下载

江苏省徐州市2019版高一下学期期末数学试卷(I)卷

江苏省徐州市2019版高一下学期期末数学试卷（I）卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题；共14分)1. （1分） (2017高二上·武清期中) 直线的斜率为k，若﹣1＜k＜，则直线的倾斜角的范围是________．2. （1分） (2019高一下·上高月考) 函数的最小正周期为________．3. （1分） (2016高一下·吉林期中) 圆柱的底面半径为3，侧面积为12π，则圆柱的体积为________．4. （1分）(2016高一下·衡水期末) 设数列{an}的通项为an=2n﹣7（n∈N*），则|a1|+|a2|+…+|a15|=________．5. （1分）(2017·三明模拟) 已知向量，满足 =（，1），| |=1，且=λ ，则实数λ=________．6. （1分） (2017高二上·武清期中) 棱长为2的四面体的体积为________．7. （1分）若角45°的终边上有一点（4，a），则a的值是________8. （1分） (2015高三上·江西期末) 设{an}是公比为q的等比数列，首项a1= ，对于n∈N* ， bn=an ，当且仅当n=4时，数列{bn}的前n项和取得最大值，则q的取值范围为________．9. （1分） (2016高二上·金华期中) 已知m，n是两条不同直线，α、β、γ是三个不同平面．下列命题中正确的是________．（1.）若α⊥γ，β⊥γ，则α∥β（2.）若m⊥α，n⊥α，则m∥n（3.）若m∥α，n∥α，则m∥n（4.）若m∥α，m∥β，则α∥β10. （1分） (2016高一下·苏州期末) =________．11. （1分） (2015高二上·济宁期末) 如图所示，已知四边形ABCD各边的长分别为AB=5，BC=5，CD=8，DA=3，且点A、B、C、D在同一个圆上，则对角线AC的长为________．12. （1分）已知点A（﹣1，2），B（﹣4，6），则|AB|等于________13. （1分）(2016·运城模拟) 已知非零向量，满足| |=2，且| + |=| ﹣ |，则向量﹣在向量方向上的投影是________．14. （1分） (2016高一下·张家港期中) 数列{an}的前n项和Sn=n2﹣4n+2，则|a1|+|a2|+…+|a10|=________．二、解答题 (共6题；共40分)15. （10分）已知函数的最小值为﹣3，且f（x）图象相邻的最高点与最低点的横坐标之差为2π，又f（x）的图象经过点；（1）求函数f（x）的解析式；（2）若方程f（x）﹣k=0在有且仅有两个零点x1，x2，求k的取值范围，并求出x1+x2的值．16. （10分） (2017高三上·连城开学考) 如图，己知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且=λ（0＜λ＜1）（1）求证：不论λ为何值，总有EF⊥平面ABC：（2）若λ= ，求三棱锥A﹣BEF的体积．17. （5分） (2016高二上·浦东期中) 已知| |=2，| |=3，且向量与的夹角为，求|3 ﹣2 |．18. （5分） (2016高二上·桃江期中) 如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求B点在AM上，D点在AN上，且对角线MN过点C，已知AB=3米，AD=2米．（Ⅰ）要使矩形AMPN的面积大于32平方米，则DN的长应在什么范围内？（Ⅱ）当DN的长度为多少时，矩形花坛AMPN的面积最小？并求出最小值．19. （5分） (2017高二上·荆门期末) 已知圆C：（x﹣3）2+（y﹣4）2=4．（Ⅰ）若直线l过点A（2，3）且被圆C截得的弦长为2 ，求直线l的方程；（Ⅱ）若直线l过点B（1，0）与圆C相交于P，Q两点，求△CPQ的面积的最大值，并求此时直线l的方程．20. （5分） (2016高一下·雅安期末) 等比数列{an}的前n项和为Sn ，若a1=3，S3=9，求数列{an}的公比与S10 ．参考答案一、填空题 (共14题；共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题；共40分)15-1、15-2、16-1、16-2、17-1、18-1、19-1、20-1、。

2016-2017学年江苏省徐州市高一(下)期末数学试卷

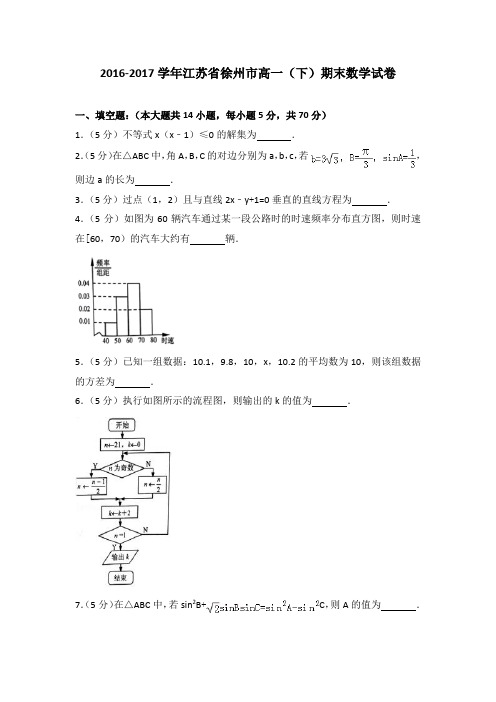
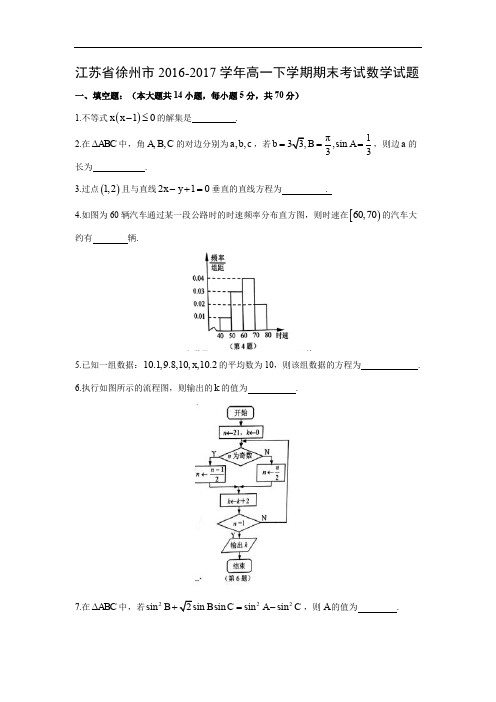
2016-2017学年江苏省徐州市高一（下）期末数学试卷一、填空题：（本大题共14小题，每小题5分，共70分）1．（5分）不等式x（x﹣1）≤0的解集为．2．（5分）在△ABC中，角A，B，C的对边分别为a，b，c，若，则边a的长为．3．（5分）过点（1，2）且与直线2x﹣y+1=0垂直的直线方程为．4．（5分）如图为60辆汽车通过某一段公路时的时速频率分布直方图，则时速在[60，70）的汽车大约有辆．5．（5分）已知一组数据：10.1，9.8，10，x，10.2的平均数为10，则该组数据的方差为．6．（5分）执行如图所示的流程图，则输出的k的值为．7．（5分）在△ABC中，若sin2B+C，则A的值为．8．（5分）若变量x，y满足约束条件，则z=2x+y的最大值为．9．（5分）已知sin，则cos2θ=．10．（5分）某数学兴趣小组有男生3人，女生2人，若从中任选两人去参加学校的数学竞赛，则至少选中一名女生的概率为．11．（5分）设S n是公差不为0的等差数列{a n}的前n项和，若a1，a2，a4成等比数列，则的值为．12．（5分）已知a＞1，b＞0，且a+2b=2，则的最小值为．13．（5分）已知函数f（x）=ax2+8x+b（a，b为互不相等的正整数），方程f（x）=0的两个实根为x1，x2（x1≠x2），且|x1|＜1，|x2|＜1，若f（1）+f（﹣1）的最大值与最小值分别为M，m，则M+m的值为．14．（5分）已知数列{a n}中，a1=3，n（a n+1﹣a n）=a n+1，n∈N*若对于任意的a∈[﹣1，1]，n∈N*，不等式﹣2at+1恒成立，则实数t的取值范围是．二、解答题：本大题共6小题，共90分.解答应写出必要的文字说明或推理、验算过程.15．（14分）已知直线l1：x﹣2y+3=0和l2：x+2y﹣9=0的交点为A．（1）求过点A，且与直线2x+3y﹣1=0平行的直线方程；（2）求过点A，且倾斜角为直线l1倾斜角2倍的直线方程．16．（14分）已知．（1）求cos（α﹣β）的值；（2）若，求sinα的值．17．（14分）已知△ABC的内角A，B，C的对边分别为a，b，c，且btanB=．（1）求角B的值；（2）若△ABC的面积为，a+c=8，求边b．18．（16分）设数列{a n}的前n项和为S n，且a n=2﹣2S n，数列{b n}为等差数列，且b5=14，b7=20．（1）求数列{a n}的通项公式；（2）若c n=a n•b n，n∈N*，求数列{c n}的前n项和T n．19．（16分）某单位拟建一个扇环形状的花坛（如图所示），按设计要求扇环的周长为30米，其中大圆弧所在圆的半径为10米．设小圆弧所在圆的半径为x 米，圆心角为θ（弧度）．（1）求θ关于x的函数关系式；（2）已知对花坛的边缘（实线部分）进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用之比为y，求y 关于x的函数关系式，并求出y的最大值．20．（16分）已知数列{a n}，{b n}分别满足a1=1，|a n+1﹣a n|=2，且|=2，其中n∈N*，设数列{a n}，{b n}的前n项和分别为S n，T n．（1）若数列{a n}，{b n}都是递增数列，求数列{a n}，{b n}的通项公式；，则称数列{c n}（2）若数列{c n}满足：存在唯一的正整数k（k≥2），使得c k＜c k﹣1为“k坠点数列”．①若数列{a n}为“5坠点数列”，求S n；②若数列{a n}为“p坠点数列”，数列{b n}为“q坠点数列”，是否存在正整数m使=T m？若存在，求出m的最大值；若不存在，请说明理由．得S m+12016-2017学年江苏省徐州市高一（下）期末数学试卷参考答案与试题解析一、填空题：（本大题共14小题，每小题5分，共70分）1．（5分）不等式x（x﹣1）≤0的解集为{x|0≤x≤1}．．【解答】解：解方程x（x﹣1）=0，得x1=0，x2=1，∴不等式x（x﹣1）≤0的解集是{x|0≤x≤1}．故答案为：{x|0≤x≤1}．2．（5分）在△ABC中，角A，B，C的对边分别为a，b，c，若，则边a的长为2．【解答】解：∵，∴由正弦定理可得：a===2．故答案为：2．3．（5分）过点（1，2）且与直线2x﹣y+1=0垂直的直线方程为x+2y﹣5=0．【解答】解：设与直线2x﹣y+1=0垂直的直线方程为x+2y+m=0，把点（1，2）代入可得：1+4+m=0，解得m=﹣5．可得要求的直线方程为：x+2y﹣5=0，故答案为：x+2y﹣5=0．4．（5分）如图为60辆汽车通过某一段公路时的时速频率分布直方图，则时速在[60，70）的汽车大约有24辆．【解答】解：由频率分布直方图得：60辆汽车通过某一段公路时的时速在[60，70）的汽车所占频率为：0.04×10=0.4，∴60辆汽车通过某一段公路时的时速在[60，70）的汽车大约有：60×0.4=24辆．故答案为：24．5．（5分）已知一组数据：10.1，9.8，10，x，10.2的平均数为10，则该组数据的方差为0.02．【解答】解：∵数据10.1，9.8，10，x，10.2的平均数为10，∴（10.1+9.8+10+x+10.2）=10，解得：a=9.8，故这组数据的方差是（0.04+0.01+0+0.01+0.04）=0.02，故答案为：0.02．6．（5分）执行如图所示的流程图，则输出的k的值为8．【解答】解：模拟程序的运行，可得：n=21，满足条件n为奇数，n=10，k=2，不满足条件n=1，执行循环体，不满足条件n为奇数，n=5，k=4，不满足条件n=1，执行循环体，满足条件n为奇数，n=2，k=6，不满足条件n=1，执行循环体，不满足条件n为奇数，n=1，k=8，满足条件n=1，退出循环，输出k的值为8．故答案为：8．7．（5分）在△ABC中，若sin2B+C，则A的值为．【解答】解：根据正弦定理=2R，化简已知的等式得：b2+bc=a2﹣c2，即b2+c2﹣a2=﹣bc，∴根据余弦定理得：cosA==﹣，又∵A∈（0，π），∴A=．故答案为：．8．（5分）若变量x，y满足约束条件，则z=2x+y的最大值为3．【解答】解：画出可行域如图阴影部分，由得A（1，1）目标函数z=2x+y可看做斜率为﹣2的动直线，其纵截距越大z越大，由图数形结合可得当动直线过点A时，z最大=2×1+1=3．故答案为：3．9．（5分）已知sin，则cos2θ=．【解答】解：∵sin，∴1+sinθ=，∴sinθ=﹣，∴cos2θ=1﹣2sin2θ=1﹣2×=．故答案为．10．（5分）某数学兴趣小组有男生3人，女生2人，若从中任选两人去参加学校的数学竞赛，则至少选中一名女生的概率为．【解答】解：某数学兴趣小组有男生3人，女生2人，从中任选两人去参加学校的数学竞赛，基本事件总数n=，至少选中一名女生的对立事件是选中两名男生，∴至少选中一名女生的概率为：p=1﹣=．故答案为：．11．（5分）设S n是公差不为0的等差数列{a n}的前n项和，若a1，a2，a4成等比数列，则的值为．【解答】解：设等差数列{a n}的公差d≠0，∵a1，a2，a4成等比数列，∴，可得=a1（a1+3d），d≠0．化为：d=a1≠0，∴==．故答案为：．12．（5分）已知a＞1，b＞0，且a+2b=2，则的最小值为4（+1）．【解答】解：∵a+2b=2，∴a﹣1=1﹣2b，∴+=+，设+=t，则2b+（2﹣2b）（1﹣2b）=tb（1﹣2b），故（4+2t）b2﹣（4+t）b+2=0，①4+2t=0时，t=﹣2，故（4﹣2）b+2=0，解得：b=1，a+2b=2，得a+2=2，故a=0，与a=1不符，故4+2t≠0；②4+2t≠0时，得t≠﹣2，由（4+2t）b2﹣（4+t）b+2=0，由△≥0，得（4+t）2﹣4（4+2t）﹣2≥0，故t2﹣8t﹣16≥0，解得：t≤4﹣4（舍）或t≥4+4，故的最小值为4（1+），故答案为：4（1+）．13．（5分）已知函数f（x）=ax2+8x+b（a，b为互不相等的正整数），方程f（x）=0的两个实根为x1，x2（x1≠x2），且|x1|＜1，|x2|＜1，若f（1）+f（﹣1）的最大值与最小值分别为M，m，则M+m的值为50．【解答】解：f（x）=ax2+8x+b，此函数的图象与x轴的两个交点在区间（﹣1，1），∴∴即有，∵a，b为互不相等的正整数，∴a，b可能的取值有（7，2）（8，1）（9，1）（10，1），（11，1），（12，1），（13，1），（14，1）（15，1）共9个．∴a+b的最小值是9，最大值为16．则f（1）+f（﹣1）=2（a+b）的最大值与最小值分别为M=32，m=18，可得M+m=50．故答案为：50．14．（5分）已知数列{a n}中，a1=3，n（a n+1﹣a n）=a n+1，n∈N*若对于任意的a∈[﹣1，1]，n∈N*，不等式﹣2at+1恒成立，则实数t的取值范围是（﹣∞，﹣3]∪[3，+∞）．﹣a n）=a n+1，【解答】解：∵n（a n+1∴﹣==．∴=++…++a1=++…++3=1﹣+3（n=1时也成立）．∴不等式﹣2at+1化为：4﹣＜t2﹣2at+1，∵对于任意的a∈[﹣1，1]，n∈N*，不等式﹣2at+1恒成立，∴t2﹣2at+1≥4，化为：t2﹣2at﹣3≥0，t≠0，t＞0时，a≤，可得1≤，化为t2﹣2t﹣3≥0，t＞0，解得t≥3．t＜0时，a≥，可得﹣1≥，化为t2+2t﹣3≥0，t＜0，解得t≤﹣3．则实数t的取值范围是（﹣∞，﹣3]∪[3，+∞）．故答案为：（﹣∞，﹣3]∪[3，+∞）．二、解答题：本大题共6小题，共90分.解答应写出必要的文字说明或推理、验算过程.15．（14分）已知直线l1：x﹣2y+3=0和l2：x+2y﹣9=0的交点为A．（1）求过点A，且与直线2x+3y﹣1=0平行的直线方程；（2）求过点A，且倾斜角为直线l1倾斜角2倍的直线方程．【解答】解：（1）由，解得：A（3，3）；设所求直线的方程是：2x+3y+c=0，将（3，3）代入，解得：c=﹣15，故所求直线方程是：2x+3y﹣15=0；（2）设直线的倾斜角是α，则tanα=，于是所求直线的斜率是tan2α==，故所求直线的方程为：y﹣3=（x﹣3），整理得：4x﹣3y﹣3=0．16．（14分）已知．（1）求cos（α﹣β）的值；（2）若，求sinα的值．【解答】解：（1）由，又sin2（α﹣β）+cos2（α﹣β）=1，解得或．∴cos（α﹣β）=；（2）∵0＜α＜，＜β＜0，∴0＜α﹣β＜π．又tan（α﹣β）=＞0，∴cos（α﹣β）=．∴sin（α﹣β）=．又sinβ=，∴cosβ=．∴sinα=sin[（α﹣β）+β]=sin（α﹣β）cosβ+cos（α﹣β）sinβ=．17．（14分）已知△ABC的内角A，B，C的对边分别为a，b，c，且btanB=．（1）求角B的值；（2）若△ABC的面积为，a+c=8，求边b．【解答】解：（1）∵△ABC的内角A，B，C的对边分别为a，b，c，且btanB=，∴由正弦定理得：sinBtanB=（sinAcosC+sinCcosA）=sin（A+C）=sinB，∵B∈（0，π），∴sinB≠0，∴tanB=，∵B∈（0，π），∴B=．（2）∵△ABC的面积为，∴=，∴，∵a+c=8，∴在△ABC中，由余弦定理得：b2=a2+c2﹣2accosB=（a+c）2﹣3ac=36，∴b=6．18．（16分）设数列{a n}的前n项和为S n，且a n=2﹣2S n，数列{b n}为等差数列，且b5=14，b7=20．（1）求数列{a n}的通项公式；（2）若c n=a n•b n，n∈N*，求数列{c n}的前n项和T n．【解答】解：（1）∵a n=2﹣2S n，当n=1时，a1=2﹣2a1，解得a1=；当n≥2时，a n=2﹣2S n﹣1，﹣1=2﹣2S n﹣（2﹣2S n﹣1）=﹣2a n，∴a n﹣a n﹣1化为3a n=a n﹣1，∴数列{a n}是等比数列，首项为，公比为，可得：a n=•（）n﹣1=2•（）n，n∈N*；（2）数列{b n}为等差数列，公差为d且b5=14，b7=20．可得b1+4d=14，b1+6d=20，解得b1=2，d=3，可得b n=b1+（n﹣1）d=2+3（n﹣1）=3n﹣1，n∈N*；c n=a n•b n=2（3n﹣1）•（）n．前n项和T n=2[2•（）+5•（）2+7•（）3+…+（3n﹣1）•（）n]，T n=2[2•（）2+5•（）3+7•（）4+…+（3n﹣1）•（）n+1]，相减可得T n=2[+2•（）2+2•（）3+…+2•（）n﹣（3n﹣1）•（）n+1]=2[+2•﹣（3n﹣1）•（）n+1]，化简可得T n=﹣．19．（16分）某单位拟建一个扇环形状的花坛（如图所示），按设计要求扇环的周长为30米，其中大圆弧所在圆的半径为10米．设小圆弧所在圆的半径为x 米，圆心角为θ（弧度）．（1）求θ关于x的函数关系式；（2）已知对花坛的边缘（实线部分）进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用之比为y，求y 关于x的函数关系式，并求出y的最大值．【解答】解：（1）由题可知30=θ（10+x）+2（10﹣x），所以θ=，x∈（0，10） (5)（2）花坛的面积为θ（102﹣x2）=（5+x）（10﹣x）=﹣x2+5x+50（0＜x＜10），装饰总费用为9θ（10+x）+8（10﹣x）=170+10x，所以花坛的面积与装饰总费用之比为y==﹣． (7)令t=17+x，t∈（17，27）则y=﹣（t+）≤﹣=，…（10分）当且仅当t=18时取等号，此时x=1，θ=．（若利用双勾函数单调性求最值的，则同等标准给分，但须说明单调性．）故当x=1时，花坛的面积与装饰总费用之比最大． (12)20．（16分）已知数列{a n}，{b n}分别满足a1=1，|a n+1﹣a n|=2，且|=2，其中n∈N*，设数列{a n}，{b n}的前n项和分别为S n，T n．（1）若数列{a n}，{b n}都是递增数列，求数列{a n}，{b n}的通项公式；（2）若数列{c n}满足：存在唯一的正整数k（k≥2），使得c k＜c k﹣1，则称数列{c n}为“k坠点数列”．①若数列{a n}为“5坠点数列”，求S n；②若数列{a n}为“p坠点数列”，数列{b n}为“q坠点数列”，是否存在正整数m使得S m+1=T m？若存在，求出m的最大值；若不存在，请说明理由．【解答】解：（1）∵数列{a n}，{b n}都为递增数列，∴由递推式可得a n+1﹣a n=2，b2=﹣2b1=2，b n+2=2b n+1，n∈N*，则数列{a n}为等差数列，数列{b n}从第二项起构成等比数列．∴a n=2n﹣1，b n=；（2）①∵数列{a n}满足：存在唯一的正整数k=5，使得a k＜a k﹣1，且|a n+1﹣a n|=2，∴数列{a n}必为1，3，5，7，5，7，9，11，…，即前4项为首项为1，公差为2的等差数列，从第5项开始为首项5，公差为2的等差数列，故S n=；②∵||=2，即b n+1=±2b n，∴|b n|=2n﹣1，而数列{b n}为“q坠点数列”且b1=﹣1，∴数列{b n}中有且只有两个负项．假设存在正整数m，使得S m+1=T m，显然m≠1，且T m为奇数，而{a n}中各项均为奇数，∴m必为偶数．≤1+3+…+（2m+1）=（m+1）2，由S m+1当q＞m时，T m=﹣1+2+4+…+2m﹣2+2m﹣1=2m﹣3，当m≥6时，2m﹣3＞（m+1）2，故不存在正整数m使得S m=T m；+1当q=m时，T m=﹣1+21+…+2m﹣2+（﹣2m﹣1）=﹣3＜0，=T m；显然不存在正整数m使得S m+1当q＜m时，∴（T m）min=﹣1+21+…+2m﹣3+（﹣2m﹣2）+2m﹣1=2m﹣1﹣3．=T m；当2m﹣1﹣3＜（m+1）2，才存在正整数m使得S m+1即m≤6．当m=6时，q＜6，构造：{a n}为1，3，1，3，5，7，9，…，{b n}为﹣1，2，4，8，﹣16，32，64，…此时p=3，q=5．∴m max=6，对应的p=3，q=5．。

江苏省徐州市2019版高一下学期数学期末考试试卷A卷

江苏省徐州市2019版高一下学期数学期末考试试卷A卷姓名:________ 班级:________ 成绩:________一、填空题 (共13题；共15分)1. （1分） (2019高一上·上海月考) 建平中学2019年的“庆国庆930”活动正如火如荼准备中，高一某班学生参加大舞台和风情秀两个节目情况如下：参加风情秀的人数占该班全体人数的八分之三；参加大舞台的人数比参加风情秀的人数多3人；两个节目都参加的人数比两个节目都不参加的学生人数7人，则此班的人数为________2. （1分） (2019高三上·衡阳月考) 交通部门对某路段公路上行驶的汽车速度实施监控，从速度在的汽车中抽取600辆进行分析，得到数据的频率分布直方图如图所示，则速度在以下的汽车________辆；3. （1分） (2019高二上·长沙月考) 若以连续掷两次骰子分别得到的点数作为的坐标，则点落在圆内的概率________.4. （1分） (2016高一上·荆门期末) 设向量，，则 =________5. （1分）某程序框图如图所示，则该程序运行后输出的S的值为________．6. （1分） (2016高一下·成都期中) 等差数列{an}的前n项和为Sn ，若S2=2，S4=8，则S6等于________．7. （2分） (2019高二下·浙江期中) 已知向量，的夹角为，则 ________，________．8. （1分）已知角终边经过点，则 ________．9. （1分） (2019高二上·蛟河期中) 在△ABC中，如果，那么等于________；10. （2分） (2018高一上·台州月考) 已知函数，则函数的图像关于点成中心对称________, ________.11. （1分）(2017·江苏) 某公司一年购买某种货物600吨，每次购买x吨，运费为6万元/次，一年的总存储费用为4x万元．要使一年的总运费与总存储费用之和最小，则x的值是________．12. （1分）已知等比数列{an}的前n项和Sn=t•2n﹣1+1，则t的值为________．13. （1分）(2019·温州模拟) 设函数 .若在上的最大值为2，则实数a 所有可能的取值组成的集合是________.二、解答题 (共6题；共60分)14. （10分） (2020高一下·大同月考)（1）计算；（2）已知，求的值.15. （5分）设等差数列{an}的前n项和为Sn ，且S4=4S2 ， a2n=2an+1．求数列{an}的通项公式.16. （10分）(2020·安徽模拟) 在中，内角的对边分别为，满足.（1）求；（2）若的面积为，，求的周长.17. （10分）在中，角的对边分别为，其面积为 .已知 . （1）求；（2）若，求的周长.18. （10分） (2020高一下·永济期中) 已知向量，， . （1）若，，求实数m的值；（2）记，若恒成立，求实数m的取值范围.19. （15分） (2017高一下·长春期末) 数列{an}的前n项和为Sn ，且Sn=n（n+1）（n∈N*）（1）求数列{an}的通项公式；（2）若数列{bn}满足：an= + + +…+ ，求数列{bn}的通项公式；（3）令cn= （n∈N*），求数列{cn}的前n项和Tn ．参考答案一、填空题 (共13题；共15分)1-1、2-1、3-1、答案：略4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、二、解答题 (共6题；共60分)14-1、14-2、15-1、16-1、16-2、17-1、17-2、18-1、18-2、19-1、19-2、19-3、。

江苏省徐州市2017-最新通用版学年高一下学期期末考试数学试题详解

2017~2018学年度第二学期期末抽测高一数学参考答案与评分标准一、填空题1．14 2．42 3．350 4．23 5．4 6．7 7．50 8．3109．52 10．2- 11．23π 12．9 13．(,1]-∞- 14．4033 二、解答题15．（1）直线l 的斜率为3tan 30︒=，…………………………………………………1分所以直线l 的方程为313)y x -=，即3y =．……………………4分（2）因为m l ⊥，所以直线m 的斜率为3- ……………………………………7分所以直线m 的方程为13(3)y x -=--340x y +-=．……………10分（3）因为n ∥l ，所以直线n 3， ………………………………………12分所以直线n 的方程为3323)3y x -=-，即330x +=．…………14分 16．（1）因为(,)2απ∈π，3sin 5α=，所以2234cos 1sin 1()55αα=-----，…2分所以sin()sin cos cos sin 44αααπππ+=+ 32422()55=-=． ………………………………6分（2）由（1）可知，3sin 35tan 4cos 45ααα===--， ……………………………………8分所以2232()2tan 244tan 231tan 71()4ααα⨯-===----， …………………………………11分所以241tan 2tan1774tan(2)244311tan 2tan 1()147αααπ-++π+===-π---⨯．……………………14分 17．（13sin sin 1sin C A A ==， …………………………………………2分即3tan C =，…………………………………………………………………4分因为(0,)C ∈π，所以6C π=．…………………………………………………6分（2）由余弦定理，2222cos c a b ab C =+-，即224323cos b b b π=+-，即210b b +-=， ……………………………10分解得51b -或51b --=， ………………………………………12分所以ABC △的面积1151153sin 3226S ab C -π-===．……14分 18．（1）当2a =-时，不等式()0f x >即2430x x ++<，即(1)(3)0x x ++<，所以31x -<<-，………………………………………3分故不等式()0f x >的解集为(3,1)--．…………………………………………4分（2）由题意知，24620ax ax a +--≤对任意的x ∈R 恒成立，所以20,164(62)0,a a a a <⎧⎨++⎩≤ …………………………………………………6分解得10a -<≤，故a 的取值范围为[1,0)-．…………………………………8分（3）由题意知，不等式2()54f x x x a >+-即2(1)(45)460a x a x a -+-+->，即[(1)23](2)0a x a x -+-+>的解集中恰含有两个小于2-的整数．…………10分若1a ≥，则解集中含有无数多个整数，不符合题意；所以1a <，则3201a a -<-，且3221a a -≠--． …………………………………12分所以不等式的解集为32(,2)1a a ---，其中所含的两个整数应为3-，4-，所以32541a a --<--≤，…………………………………………………………14分即32541a a --<--≤，解得1223a <≤．综上所述，a 的取值范围为12(,]23．……………………………………………16分 19．设ADF α∠=，BDF β∠=，则tan AF DF α=，tan BF DFβ=，tan tan()θαβ=-．（1）因为100a x ==，所以100tan 1100α==，501tan 1002β==，所以tan tan tan 1tan tan αβθαβ-=+111213112-==+⨯．…………………………………4分（2）因为100a =，所以100tan x α=，50tan xβ=，所以210050tan tan 50tan 100501tan tan 50001x x x x x xαβθαβ--===+++⋅………………………6分 5025000450002x x x x==+⋅ 当且仅当5000x x=，即50260x =>时，取“=”．答：当无人机离大楼的水平距离为502θ最大．…………………10分（3）因为200tan a x α-=，150tan a x β-=，所以2200150tan tan 501tan 2001501tan tan (200)(150)31a a x x x a a x a a x xαβθαβ----====--++--+⋅，即22150350200150x x a a -+=-+⨯．………………………………………12分因为50100a ≤≤，所以2500035020015015000a a -+⨯≤≤，所以2500015015000x x -+≤≤，解得50100x ≤≤， …………………14分又因为60x ≥，所以60100x ≤≤．答：无人机D 与大楼的水平距离x 的取值范围[60,100]．………………………16分20．（1）当1n =时，12112a a a S ==，又11a =，所以22a =； ………………………1分当2n ≥时，1112n n n n n n n a a a a a S S +---=-=，即112()n n n n a a a a +-=-．因为0n a >，所以112n n a a +--=，……………………………………………4分所以{}n a 的奇数项成以1为首项，2为公差的等差数列，偶数项成以2为首项，2为公差的等差数列．因此当21n k =-，*k ∈N 时，211(1)221k a k k -=+-⨯=-；当2n k =，*k ∈N 时，22(1)22k a k k =+-⨯=．即数列{}n a 的通项公式为n a n =．……………………………………………6分（2）由（1）知，n a n =，所以2n n b n =⋅．则1231222322n n T n =⨯+⨯+⨯++⋅L ，23121222(1)22n n n T n n +=⨯+⨯++-⨯+⋅L ，所以23122222n n n T n +-=++++-⋅L 12(12)212n n n +-=-⋅-…………………8分 1(1)22n n +=--，所以1(1)22n n T n +=-+．………………………………………………………10分（3）因为6n ≥时，1(1)()32n m m n -<+，所以111(1)32n n n m m m m n ==-<+∑∑，即121431()()()()33332n n n n n m m n n n n n n =++++++<++++∑L ．而23111(1)1111112211122222212n n m n n m =-=++++==-<-∑L ，所以(2)(1)43(3)(3)n a n n n n n n n n n a ++++++<+=+L ．所以当6n ≥时，34(2)(3)n a n n n n n a ++++=+L 无解．…………………14分当1n =时，34<；当2n =时，222345+=；3n =时，33333456++=；当4n =时，44443456+++为偶数，而47为奇数，不符合；当5n =时，5555534567++++为奇数，而58为偶数，不符合．综上可知，满足条件的n 的所有值为2，3．………………………………16分。

2019-2020学年江苏省徐州市高一下学期期末数学试卷 (解析版)

2019-2020学年江苏省徐州市高一第二学期期末数学试卷一、选择题（共8小题）.1．已知点M（1，6），N（7，3），则直线MN的斜率为（）A．﹣2B．﹣C．D．22．sin37°cos23°+cos37°sin23°的值为（）A．﹣B．﹣C．D．3．圆x2+y2﹣4x+6y﹣1＝0的圆心坐标为（）A．（﹣2，3）B．（2，﹣3）C．（﹣2，﹣3）D．（2，3）4．下列命题错误的是（）A．不在同一直线上的三点确定一个平面B．两两相交且不共点的三条直线确定一个平面C．如果两个平面垂直，那么其中一个平面内的直线一定垂直于另一个平面D．如果两个平面平行，那么其中一个平面内的直线一定平行于另一个平面5．下列叙述正确的是（）A．频率是稳定的，概率是随机的B．互斥事件一定不是对立事件，但是对立事件一定是互斥事件C．5张奖券中有1张有奖，甲先抽，乙后抽，那么乙比甲抽到有奖奖券的可能性小D．若事件A发生的概率为P（A），则0≤P（A）≤16．在△ABC中，已知∠B＝60°，边AB＝4，且△ABC的面积为2，则边AC的长为（）A．2B．2C．2D．47．某同学5次考试的数学成绩x与物理成绩y的统计数据如表，已知该同学的物理成绩y 与数学成绩x是线性相关的，根据数据可得回归方程的b的值为0.5，则当该生的物理成绩y达到90分时，可以估计他的数学成绩为（）数学x103137112128120物理y7188768481 A．140B．142C．145D．1488．阿基米德（Archimedes，公元前287年一公元前212年）是古希腊伟大的数学家、物理学家和天文学家．他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二，并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现，后人按照他生前的要求，在他的墓碑上刻着一个圆柱容器里放了一个球，如图，该球顶天立地，四周碰边，圆柱的底面直径与高都等于球的直径，若球的体积为36π，则圆柱的表面积为（）A．36πB．45πC．54πD．63π二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分．9．已知直线l1：x+my﹣1＝0，l2：（m﹣2）x+3y+3＝0，则下列说法正确的是（）A．若l1∥l2，则m＝﹣1或m＝3B．若l1∥l2，则m＝3C．若l1⊥l2，则D．若l1⊥l2，则10．已知△ABC的内角A，B，C所对的边分别为a，b，c，则下列说法正确的是（）A．若sin B＞sin C，则B＞CB．若a＝4，b＝2，A＝，则三角形有两解C．若b cos B﹣c cos C＝0，则△ABC一定为等腰直角三角形D．若b cos C﹣c cos B＝0，则△ABC一定为等腰三角形11．PM2.5是衡量空气质量的重要指标，如图是某地7月1日到10日的PM2.5日均值（单位：ug/m3）的折线图，则下列关于这10天中PM2.5日均值的说法正确的是（）A．众数为30B．中位数是31C．平均数小于中位数D．后4天的方差小于前4天的方差12．如图，在棱长为1的正方体中，下列结论正确的是（）A．异面直线AC与BC1所成的角为60°B．直线AB1与平面ABC1D1所成角为45°C．二面角A﹣B1C﹣B的正切值为D．四面体D1﹣AB1C的外接球的体积为三、填空题：本题共4小题，每小题5分，共20分．13．已知tanα＝2，tanβ＝﹣1，则tan（α﹣β）的值为．14．过圆x2+y2＝5上一点P（1，﹣2）的圆的切线的一般式方程为．15．在我国，每年的农历五月初五是端午节，民间有吃粽子的习惯，粽子又称粽粒，俗称“粽子”，古称“角黍”，传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原．如图，平行四边形形状的纸片是由六个边长为2的正三角形构成的，将它沿虚线折起来，可以得到如图所示粽子形状的六面体，则该六面体的体积为．16．如图，某数学学习兴趣小组的同学要测量学校地面上旗杆CD的高度（旗杆CD垂直于地面），设计如下的测量方案：先在地面选定距离为30米的A，B两点，然后在A处测得∠BAC＝30°，在B处测得∠ABC＝105°，∠DBC＝45°，由此可得旗杆CD的高度为米．∠CAD的正切值为．四、解答题：本题6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．已知A（3，2）和l：2x﹣y+1＝0．（1）求过点A且与直线l平行的直线方程；（2）求点A关于直线l的对称点B的坐标．18．已知．（1）求cosα的值；（2）求sin2α的值．19．已知△ABC的内角A，B，C所对的边分别为a，b，c，A＝，___且b＝，请从①b2+ac＝a2+c2，②a cos B＝b sin A，③sin B+cos B＝这三个条件中任选一个补充在横线上，求出此时△ABC的面积．20．手机支付也称为移动支付（MobilePayment），是当今社会比较流行的一种付款方式．某金融机构为了了解移动支付在大众中的熟知度，对15﹣65岁的人群作了问题为“你会使用移动支付吗？”的随机抽样调查，把回答“会”的100个人按照年龄分成5组，绘制成如图所示的频率分布表和频率分布直方图．组数第1组第2组第3组第4组第5组分组[15，25）[25，35）[35，45）[45，55）[55，65）频数x35y123（1）求x，a的值；（2）若从第1，3组中用分层抽样的方法抽取5人，求两组中分别抽取的人数；（3）在（2）抽取的5人中再随机抽取2人，求所抽取的2人来自同一个组的概率．21．如图，在三棱锥P﹣ABC中，PA⊥面ABC，PA＝2，CA＝CB＝AB＝2，D为棱AB 的中点，点E在棱PA上．（1）若AE＝EP，求证：PB∥平面CDE；（2）求证：平面PAB⊥平面CDE；（3）若二面角B﹣CD﹣E的大小为120°，求异面直线PC与DE所成角的余弦值．22．如图，在平面直角坐标系xOy中，已知圆M：x2+y2﹣4x﹣8y+12＝0，过点O及点A（﹣2，0）的圆N与圆M外切．（1）求圆N的标准方程；（2）若过点A的直线l被两圆截得的弦长相等，求直线l的方程；（3）直线MN上是否存在点B，使得过点B分别作圆M与圆N的切线，切点分别为P，Q（不重合），满足BQ＝2BP？若存在，求出点B的坐标，若不存在，请说明理由．参考答案一、单项选择题（共8小题）.1．已知点M（1，6），N（7，3），则直线MN的斜率为（）A．﹣2B．﹣C．D．2解：∵点M（1，6），N（7，3），则直线MN的斜率为＝﹣，故选：B．2．sin37°cos23°+cos37°sin23°的值为（）A．﹣B．﹣C．D．解：由两角和的正弦公式可得：sin37°cos23°+cos37°sin23°＝sin（37°+23°）＝sin60°＝故选：D．3．圆x2+y2﹣4x+6y﹣1＝0的圆心坐标为（）A．（﹣2，3）B．（2，﹣3）C．（﹣2，﹣3）D．（2，3）解：圆x2+y2﹣4x+6y﹣1＝0，即（x﹣2）2+（y+3）2＝14，故它的圆心坐标为（2，﹣3），故选：B．4．下列命题错误的是（）A．不在同一直线上的三点确定一个平面B．两两相交且不共点的三条直线确定一个平面C．如果两个平面垂直，那么其中一个平面内的直线一定垂直于另一个平面D．如果两个平面平行，那么其中一个平面内的直线一定平行于另一个平面解：由公理3可得，不在同一直线上的三点确定一个平面，故A正确；由公理3和公理1可得，两两相交且不共点的三条直线确定一个平面，故B正确；由面面垂直的性质定理可得，如果两个平面垂直，那么其中一个平面内的直线若与交线垂直，则垂直于另一个平面，故C错误；由面面平行的性质可得，如果两个平面平行，那么其中一个平面内的直线一定平行于另一个平面，故D正确．故选：C．5．下列叙述正确的是（）A．频率是稳定的，概率是随机的B．互斥事件一定不是对立事件，但是对立事件一定是互斥事件C．5张奖券中有1张有奖，甲先抽，乙后抽，那么乙比甲抽到有奖奖券的可能性小D．若事件A发生的概率为P（A），则0≤P（A）≤1解：对于A，频率是随机的，概率是稳定的，故A错误；对于B，互斥事件不一定是对立事件，但是对立事件一定是互斥事件，故B错误；对于C，5张奖券中有1张有奖，甲先抽，乙后抽，那么乙与甲抽到有奖奖券的可能性相同，故C错误；对于D，若事件A发生的概率为P（A），则由概率的定义得0≤P（A）≤1，故D正确．故选：D．6．在△ABC中，已知∠B＝60°，边AB＝4，且△ABC的面积为2，则边AC的长为（）A．2B．2C．2D．4解：由S△ABC＝AB•BC•sin∠B得，2＝×4×BC×，∴BC＝2，由余弦定理知，AC2＝AB2+BC2﹣2AB•BC•cos∠B＝16+4﹣2×4×2×＝12，∴AC＝．故选：C．7．某同学5次考试的数学成绩x与物理成绩y的统计数据如表，已知该同学的物理成绩y 与数学成绩x是线性相关的，根据数据可得回归方程的b的值为0.5，则当该生的物理成绩y达到90分时，可以估计他的数学成绩为（）数学x103137112128120物理y7188768481 A．140B．142C．145D．148解：计算平均数为＝×（103+137+112+128+120）＝120，＝×（71+88+76+84+81）＝80．代入回归方程中，得80＝0.5×120+，解得＝20，所以线性回归方程为＝0.5x+20，当该生的物理成绩y达到90分时，90＝0.5x+20．解得x＝140．故选：A．8．阿基米德（Archimedes，公元前287年一公元前212年）是古希腊伟大的数学家、物理学家和天文学家．他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二，并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现，后人按照他生前的要求，在他的墓碑上刻着一个圆柱容器里放了一个球，如图，该球顶天立地，四周碰边，圆柱的底面直径与高都等于球的直径，若球的体积为36π，则圆柱的表面积为（）A．36πB．45πC．54πD．63π解：设球的半径为R，由题意V球＝R3＝36π，所以R＝3，所以可得圆柱的底面半径为R＝3，高为h＝2R＝6，所以圆柱的表面积S＝2S底+S侧＝2π×32+2π×3×6＝54π，故选：C．二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分．9．已知直线l1：x+my﹣1＝0，l2：（m﹣2）x+3y+3＝0，则下列说法正确的是（）A．若l1∥l2，则m＝﹣1或m＝3B．若l1∥l2，则m＝3C．若l1⊥l2，则D．若l1⊥l2，则解：由直线l1：x+my﹣1＝0，l2：（m﹣2）x+3y+3＝0，得：若l1∥l2，则，解得m＝3，故A错误，B正确；若l1⊥l2，则1×（m﹣2）+m×3＝0，解得m＝，故C错误，D正确．故选：BD．10．已知△ABC的内角A，B，C所对的边分别为a，b，c，则下列说法正确的是（）A．若sin B＞sin C，则B＞CB．若a＝4，b＝2，A＝，则三角形有两解C．若b cos B﹣c cos C＝0，则△ABC一定为等腰直角三角形D．若b cos C﹣c cos B＝0，则△ABC一定为等腰三角形解：对于A，由正弦定理得sin B＞sin C⇔b＞c⇔B＞C，故A正确；对于B，由正弦定理得，则sin B＝＝＝，由b＞a，可知B＝或，故B正确；对于C，在△ABC中，若b cos B﹣c cos C＝0，则由正弦定理得：sin B cos B＝sin C cos C，即sin2B＝sin2C，∴2B＝2C或2B＝π﹣2C，∴B＝C或B+C＝，∴△ABC的形状为等腰三角形或直角三角形，故C错误；对于D，若b cos C﹣c cos B＝0，则由正弦定理得sin B cos C﹣sin C cos B＝sin（B﹣C）＝0，故B﹣C＝0，即B＝C，所以△ABC为等腰三角形，故D正确．故选：ABD．11．PM2.5是衡量空气质量的重要指标，如图是某地7月1日到10日的PM2.5日均值（单位：ug/m3）的折线图，则下列关于这10天中PM2.5日均值的说法正确的是（）A．众数为30B．中位数是31C．平均数小于中位数D．后4天的方差小于前4天的方差解：把折线图中的PM2.5日均值按照由小到大的顺序排列为：17，25，30，30，31，32，34，38，42，126．所以众数为30，选项A正确；最中间的两位数为31，32，所以中位数为，选项B错误；平均数为＝40.5＞31.5，选项C错误；后4天的PM2.5日均值更集中，所以方差更小，选项D正确．故选：AD．12．如图，在棱长为1的正方体中，下列结论正确的是（）A．异面直线AC与BC1所成的角为60°B．直线AB1与平面ABC1D1所成角为45°C．二面角A﹣B1C﹣B的正切值为D．四面体D1﹣AB1C的外接球的体积为解：对于A，连接A1C1，A1B，由题意可得AC∥A1C1，所以A1C1与BC1所成的角，即是异面直线AC与BC1所成的角，因为△A1C1B为等边三角形，所以∠A1C1B＝60°，所以A正确；对于B，以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，A（1，0，0），B1（1，1，1），B（1，1，0），D1（0，0，1），＝（0，1，1），＝（0，1，0），＝（﹣1，0，1），设平面ABC1D1的法向量＝（x，y，z），则，取x＝1，得＝（1，0，1），设直线AB1与平面ABC1D1所成角为θ，则sinθ＝＝＝，∴θ＝30°，∴直线AB1与平面ABC1D1所成角为30°，故B错误；对于C，平面BB1C的法向量＝（0，1，0），C（0，1，0），＝（0，1，1），＝（﹣1，1，0），设平面AB1C的法向量＝（a，b，c），则，取a＝1，得＝（1，1，﹣1），设二面角A﹣B1C﹣B的平面角为θ，则cosθ＝＝，sinθ＝＝，∴二面角A﹣B1C﹣B的正切值为tanθ＝＝，故C正确；对于D，平面AB1C的法向量＝（1，1，﹣1），＝（﹣1，0，1），点D1到平面AB1C的距离d＝＝，∵四面体D1﹣AB1C是棱长为的正四面体，设四面体D1﹣AB1C的外接球的半径为R，则R2＝[]2+（）2，解得R＝，∴四面体D1﹣AB1C的外接球的体积V＝＝，故D正确．故选：ACD．三、填空题：本题共4小题，每小题5分，共20分．13．已知tanα＝2，tanβ＝﹣1，则tan（α﹣β）的值为﹣3．解：已知tanα＝2，tanβ＝﹣1，所以＝．故答案为：﹣314．过圆x2+y2＝5上一点P（1，﹣2）的圆的切线的一般式方程为x﹣2y﹣5＝0．解：根据题意，设要求切线为l，点P（1，﹣2）在圆x2+y2＝5上，则k OP＝＝﹣2，则k l＝，则直线l的方程为y+2＝（x﹣1），变形可得x﹣2y﹣5＝0；故要求切线的方程为：x﹣2y﹣5＝0．故答案为：x﹣2y﹣5＝0．15．在我国，每年的农历五月初五是端午节，民间有吃粽子的习惯，粽子又称粽粒，俗称“粽子”，古称“角黍”，传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原．如图，平行四边形形状的纸片是由六个边长为2的正三角形构成的，将它沿虚线折起来，可以得到如图所示粽子形状的六面体，则该六面体的体积为．解：由图可知，该六面体是两个棱长为2的正四面体的组合体．在正四面体A﹣BCD中，设底面三角形BCD的外心为O，连接BO并延长，角CD于E，则，连接AO，则AO⊥平面BCD，且AO＝．∴＝．∴该六面体的体积为2×．故答案为：．16．如图，某数学学习兴趣小组的同学要测量学校地面上旗杆CD的高度（旗杆CD垂直于地面），设计如下的测量方案：先在地面选定距离为30米的A，B两点，然后在A处测得∠BAC＝30°，在B处测得∠ABC＝105°，∠DBC＝45°，由此可得旗杆CD的高度为米．∠CAD的正切值为．解：如图，在△ABC中，∠BAC＝30°，∠ABC＝105°，所以∠ACB＝45°，所以，所以，解得BC＝15．因为sin∠ABC＝sin105°＝sin（60°+45°）＝，所以，即，所以AC＝，在Rt△CBD中，∠DBC＝45°，，所以，所以．所以＝．四、解答题：本题6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．已知A（3，2）和l：2x﹣y+1＝0．（1）求过点A且与直线l平行的直线方程；（2）求点A关于直线l的对称点B的坐标．解：（1）设所求直线的方程为2x﹣y+C＝0，将点（3，2）代入，得C＝﹣4，故所求直线的方程为2x﹣y﹣4＝0．（2）设B（m，n），则由AB⊥l及线段AB的中点在直线l上，可得，解得m＝﹣1，n＝4，所以点B的坐标为（﹣1，4）．18．已知．（1）求cosα的值；（2）求sin2α的值．解：（1）因为，所以，，所以，．由，所以，，所以＝．（2）＝＝．19．已知△ABC的内角A，B，C所对的边分别为a，b，c，A＝，___且b＝，请从①b2+ac＝a2+c2，②a cos B＝b sin A，③sin B+cos B＝这三个条件中任选一个补充在横线上，求出此时△ABC的面积．解：情形一：若选择①，由余弦定理，因为B∈（0，π），所以；情形二：若选择②a cos B＝b sin A，则sin A cos B＝sin B sin A，因为sin A≠0，所以sin B＝cos B，因为B∈（0，π），所以；情形三：若选择③，则，所以，因为B∈（0，π），所以，所以，所以；由正弦定理，得，因为，，所以，所以，所以．故答案为：．20．手机支付也称为移动支付（MobilePayment），是当今社会比较流行的一种付款方式．某金融机构为了了解移动支付在大众中的熟知度，对15﹣65岁的人群作了问题为“你会使用移动支付吗？”的随机抽样调查，把回答“会”的100个人按照年龄分成5组，绘制成如图所示的频率分布表和频率分布直方图．组数第1组第2组第3组第4组第5组分组[15，25）[25，35）[35，45）[45，55）[55，65）频数x35y123（1）求x，a的值；（2）若从第1，3组中用分层抽样的方法抽取5人，求两组中分别抽取的人数；（3）在（2）抽取的5人中再随机抽取2人，求所抽取的2人来自同一个组的概率．解：（1）由题意可知，x＝0.02×10×100＝20，所以y＝100﹣（20+35+12+3）＝30，从而．（2）第1，3组共有50人，所以抽取的比例是，则从第1组抽取的人数为，从第3组抽取的人数为．（3）设第1组抽取的2人为A1，A2，第3组抽取的3人为B1，B2，B3，则从这5人中随机抽取2人有如下种情形：（A1，A2），（A1，B1），（A1，B2），（A1，B3），（A2，B1），（A2，B2），（A2，B3），（B1，B2），（B1，B3），（B2，B3）共有10个基本事件．其中符合“抽取的2人来自同一个组”的基本事件有：（A1，A2），（B1，B2），（B1，B3），（B2，B3）共4个基本事件，所以抽取的2人来自同一个组的概率．21．如图，在三棱锥P﹣ABC中，PA⊥面ABC，PA＝2，CA＝CB＝AB＝2，D为棱AB 的中点，点E在棱PA上．（1）若AE＝EP，求证：PB∥平面CDE；（2）求证：平面PAB⊥平面CDE；（3）若二面角B﹣CD﹣E的大小为120°，求异面直线PC与DE所成角的余弦值．【解答】（1）证明：由AE＝EP知，E为棱PA的中点，因为D为棱AB的中点，所以DE∥PB，因为PB⊄平面CDE，DE⊂平面CDE，所以PB∥平面CDE．（2）证明：因为PA⊥底面ABC，CD⊂平面ABC，所以PA⊥CD，在△ABC中，CA＝CB，D为AB的中点，所以AB⊥CD，又因为PA∩AB＝A，PA、AB⊂平面PAB，所以CD⊥平面PAB．因为CD⊂平面CDE，所以平面PAB⊥平面CDE．（3）解：因为二面角B﹣CD﹣E的大小为120°，所以二面角A﹣CD﹣E的大小为60°，由（2）可知，CD⊥平面PAB，因为DE⊂平面PAB，所以DE⊥CD，又AB⊥CD，所以∠ADE即为二面角A﹣CD﹣E的平面角，即∠ADE＝60°，因为PA⊥底面ABC，AB⊂平面ABC，所以PA⊥AB，在Rt△ADE中，，∠ADE＝60°，所以．因为，所以E为棱PA的中点，故DE∥PB，于是∠BPC即为异面直线PC与DE所成的角．因为PB＝PC＝＝＝4，BC＝2，所以在△PBC中，由余弦定理知，cos∠BPC＝＝＝，所以异面直线PC与DE所成角的余弦值为．22．如图，在平面直角坐标系xOy中，已知圆M：x2+y2﹣4x﹣8y+12＝0，过点O及点A（﹣2，0）的圆N与圆M外切．（1）求圆N的标准方程；（2）若过点A的直线l被两圆截得的弦长相等，求直线l的方程；（3）直线MN上是否存在点B，使得过点B分别作圆M与圆N的切线，切点分别为P，Q（不重合），满足BQ＝2BP？若存在，求出点B的坐标，若不存在，请说明理由．解：（1）由题意知，圆N的圆心N在直线x＝﹣1上，设N（﹣1，b），半径为r，因为圆N与圆M外切，且圆M的圆心M（2，4），半径为，所以，即①又，即1+b2＝r2②由①得，，代入②得，b2﹣8b+7＝0，解得b＝1或b＝7（舍），所以，故所求圆N的标准方程为（x+1）2+（y﹣1）2＝2；（2）当l的斜率不存在时，不符合题意．当l的斜率存在时，设l的方程为y＝k（x+2），因为l被两圆截得的弦长相等，所以，即3k2﹣10k+3＝0，解得k＝3或，故直线l的方程为3x﹣y+6＝0或x﹣3y+2＝0；（3）设B（x，y），由BQ＝2BP可知，BQ2＝4BP2，即BN2﹣2＝4（BM2﹣8），所以BN2＝4BM2﹣30，即（x+1）2+（y﹣1）2＝4[（x﹣2）2+（y﹣4）2]﹣30，整理得（x﹣3）2+（y﹣5）2＝18①，又直线MN的方程为x﹣y+2＝0②，由①②联立解得，x＝0，y＝2或x＝6，y＝8，由P，Q两点不重合，故x＝0，y＝2不合题意，舍去，故存在点B（6，8）符合题意．。

【数学】江苏省徐州市2016-2017学年高一下学期期末考试试题

江苏省徐州市2016-2017学年高一下学期期末考试数学试题一、填空题：（本大题共14小题，每小题5分，共70分） 1.不等式()10x x -≤的解集是 .2.在ABC ∆中，角,,A B C 的对边分别为,,a b c ，若π1,sin 33b B A ===，则边a 的长为 .3.过点()1,2且与直线210x y -+=垂直的直线方程为 .4.如图为60辆汽车通过某一段公路时的时速频率分布直方图，则时速在[)60,70的汽车大约有辆.5.已知一组数据：10.1,9.8,10,,10.2x 的平均数为10，则该组数据的方程为 .6.执行如图所示的流程图，则输出的k 的值为 .7.在ABC ∆中，若222sin sin sin sin B B C A C =-，则A 的值为 .8.若变量,x y 满足约束条件1325x y x x y ≥-⎧⎪≥⎨⎪+≤⎩，则2z x y =+的最大值是 .9.已知sincos223θθ+=，则cos2θ的值为 . 10.某数学兴趣小组有男生3人，女生2人，若从中任选两人去参加学校的数学竞赛，则至少选中一名女生的概率为 .11.设n S 是公差不为0的等差数列{}n a 的前n 项和，若124,,a a a 成等比数列，则42S S 的值为 .12.已知1,0a b >>，且22a b +=，则21aa b+-的最小值为 . 13.已知函数()28f x ax x b =++（,a b 为互不相等的正整数），方程()0f x =的两个实根为()1212,x x x x <，且121,1x x <<，若()()11f f +-的最大与最小值分别为M ,m ，则M m -的值为 .14.已知数列{}n a 中，()113,1,n n n a n a a a n N *+=-=+∈若对于任意的[]1,1,a n ∈-∈*N ，不等式21211n a t at n +<-++恒成立，则实数t 的取值范围是 . 二、解答题：本大题共6小题，共90分.解答应写出必要的文字说明或推理、验算过程. 15.（本题满分14分）已知直线1:230l x y -+=和2:290l x y +-=的交点为.A （1）求过点A ，且与直线2310x y +-=平行的直线方程；（2）求过点A ，且倾斜角为直线1l 倾斜角2倍的直线方程.16.（本题满分14分）已知()4tan .3αβ-=（1）求()cos αβ-的值；（2）若50,0,sin 2213ππαββ<<-<<=-，求sin α的值.17.（本题满分14分）已知ABC ∆的内角,,A B C 的对边分别为,,a b c ，且)tan cos cos .b B a C c A =+ （1）求角B 的值；（2）若ABC ∆的面积为,83a c +=，求边b .18.（本题满分16分）设数列{}n a 的前n 项和为n S ，且22n n a S =-，数列{}n b 为等差数列，且5714,20b b ==.（1）求数列{}n a 的通项公式；（2）若,n n n c a b n N *=⋅∈，求数列{}n c 的前n 项和n T .19.（本题满分16分）某广场拟建一个扇形的花坛（如图所示），按设计要求扇形的周长为30米，其中大圆弧所在圆的半径为10米.设小圆所在圆的半径为x 米，圆心角为θ（弧度）.（1）求θ关于x 的函数关系式；（2）现欲对花坛的边缘（实线部分）进行装饰，已知直线部分的装饰费用为4元/米，弧线部分的装饰费用为9元/米，设花坛的面积与装饰费用之比为y ，求y 关于x 的函数关系式，并求出y 的最大值.20.（本题满分16分）已知数列{}{},n n a b 分别满足111,2n n a a a +=-=，且111,2n nb b b +=-=，其中n ∈*N ，设数列{}{},n n a b 的前n 项和分别为,.n n S T（1）若数列{}{},n n a b 都是递增数列，求数列{}{},n n a b 的通项公式；（2）若数列{}n c 满足：存在唯一的正整数()2k k ≥，使得1k k c c -<，则称数列{}n c 为“k 坠点数列”.①若数列{}n a 为“5坠点数列”，求n S ；②若数列{}n a 为“p 坠点数列”，数列{}n b 为“q 坠点数列”，是否存在正整数m 使得1m m S T +=？若存在，求出m 的最大值；若不存在，请说明理由.。

江苏省徐州市高一下学期数学期末考试试卷

江苏省徐州市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）等于（）A . sin2－cos2B . cos2－sin2C . ±（sin2－cos2）D . sin2+cos22. （2分） (2020·随县模拟) 已知向量，满足，向量在向量方向上的投影为3，则向量与向量的夹角为（）A . 30°B . 45°C . 60°D . 90°3. （2分） (2016高二上·南阳期中) 在△ABC中，根据下列条件解三角形，则其中有两个解的是（）A . b=10，A=45°，B=60°B . a=60，c=48，B=120°C . a=7，b=5，A=75°D . a=14，b=16，A=45°4. （2分）(2018·广元模拟) 已知函数一个周期内的图象如图所示，，为图象上的最高点，则的值为（）A .B .C .D .5. （2分）若复数是纯虚数，则的值为（）A . -7B .C . 7D . 或6. （2分）(2017·辽宁模拟) 已知函数f（x）=asinx+bcosx（x∈R），若x=x0是函数f（x）的一条对称轴，且tanx0=3，则点（a，b）所在的直线为（）A . x﹣3y=0B . x+3y=0C . 3x﹣y=0D . 3x+y=07. （2分） (2016高一下·岳阳期中) 在△ABC中，D是BC的中点，| |=3，点P在AD上，且满足 =，则•（ + ）=（）A . 4B . 2C . ﹣2D . ﹣48. （2分） (2017高一下·株洲期中) 若先将函数y= sin（x﹣）+cos（x﹣）图象上各点的纵坐标不变，横坐标缩短到原来的倍，再将所得图象向左平移个单位，所得函数图象的一条对称轴的方程是（）A . x=B . x=C . x=D . x=9. （2分）在150米高的山顶上，测得山下一塔的塔顶与塔底的俯角分别为30°，60°x=0，则塔高为（）A . 50米B . 75米C . 100米D . 125米10. （2分）已知=(1-t,1-t,t),=(2,t,t)，则|-|的最小值是（）A .B .C .D .11. （2分）若sin（﹣θ）=，则cos（+2θ）的值为（）A .B . -C .D . -12. （2分） (2016高一上·绵阳期末) 一个半径是R的扇形，其周长为4R，则该扇形圆心角的弧度数为（）A . 1B . 2C . πD .二、填空题 (共4题；共4分)13. （1分）已知向量 =（3，4）， =（6，﹣3）， =（5﹣m，﹣3﹣m），若点A、B、C能构成三角形，则实数m应满足的条件是________．14. （1分） =________．15. （1分）(2018·肇庆模拟) 已知的角对边分别为，若，且的面积为，则的最小值为________.16. （1分）当a∈{﹣1，， 1，3}时，幂函数y=xa的图象不可能经过第________ 象限．三、解答题 (共6题；共60分)17. （10分） (2016高一下·重庆期中) 已知平面内三个向量 =（1，﹣1）， =（x，2）， =（2，1），满足∥（ + ）．（1）求实数x的值；（2）求在﹣上的投影．18. （10分） (2018高一下·河南月考) 已知 .（1）求的值；（2）求的值.19. （10分） (2018高一下·阿拉善左旗期末) 已知 ,计算:（1）（2） .20. （10分） (2018高二上·黑龙江期末) 已知的周长为，且 .（1）求边的长；（2）若的面积为，求角的度数.21. （10分） (2016高一下·惠来期末) 已知函数f（x）= sin（ωx+φ）（ω＞0，﹣≤φ＜），f（0）=﹣，且函数f（x）图象上的任意两条对称轴之间距离的最小值是．（1）求函数f（x）的解析式；（2）若f（）= （＜α＜），求cos（α+ ）的值．22. （10分） (2018高二上·西宁月考) 如图所示，B为△ACD所在平面外一点，M，N，G分别为△ABC，△ABD，△BCD的重心．（1）求证：平面MNG∥平面ACD；（2）求参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共60分)17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、。

江苏省徐州市高一下学期期末数学试卷

江苏省徐州市高一下学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分） (2017高一下·定西期中) 从编号为1～50的50枚最新研制的某种型号的导弹中随机抽取5枚来进行发射实验，若采用每部分选取的号码间隔一样的系统抽样方法，则所选取5枚导弹的编号可能是（）A . 5，10，15，20，25B . 3，13，23，33，43C . 1，2，3，4，5D . 2，4，8，16，322. （2分）在某项体育比赛中，七位裁判为一选手打出分数的茎叶图如图，去掉一个最高分和一个最低分后，该选手的平均分为（）A . 90B . 91C . 92D . 933. （2分） (2018高一下·枣庄期末) 某人在打靶中，连续射击次，至多有一次中靶的对立事件是（）A . 至少有一次中靶B . 两次都中靶C . 两次都不中靶D . 恰有一次中靶4. （2分） (2018高一下·枣庄期末) 若以连续掷两次骰子分别得到的点数、作为点的坐标，求点落在圆外部的概率是（）A .B .C .D .5. （2分）(2017·海淀模拟) 已知实数x，y满足则2x+y的最小值为（）A . 11B . 3C . 4D . 26. （2分） (2019高一下·吉林月考) 一船以的速度向东航行，船在处看到一个灯塔在北偏东方向上，行驶后，船到处，此时看到这个灯塔在北偏东方向上，这时船与灯塔的距离为（）A .B .C .D .7. （2分） (2016高一下·汕头期末) 如果执行如图所示的框图，输入N=5，则输出的数等于（）A .B .C .D .8. （2分）设a、b是非零实数，若a＜b，则下列不等式成立的是（）A .B .C .D .9. （2分） (2016高一上·德州期中) 某单位为了了解办公楼用电量y（度）与气温x（℃）之间的关系，随机统计了四个工作量与当天平均气温，并制作了对照表：气温（℃）1813 10﹣1用电量（度）243438 64由表中数据得到线性回归方程 =﹣2x+a，当气温为﹣4℃时，预测用电量均为（）A . 68度B . 52度C . 12度D . 28度10. （2分） (2018高二上·济宁月考) 设等差数列的前项和为 ,若则等于（）A . 3B . 4C . 5D . 6二、填空题 (共5题；共6分)11. （2分）将二进制数1011010（2）化为十进制结果为________；再将该数化为八进制数，结果为________．12. （1分） (2016高三上·江苏期中) 如图是一个算法的流程图，则输出x的值为________．13. （1分） (2019高一下·上海月考) 数列的通项公式为，其前n项和为，则________.14. （1分）把半径为2的圆分成相等的四段弧，再将四段弧围成星形放在半径为2的圆内，现在往该圆内任投一点，此点落在星形内的概率为________．15. （1分） (2016高一下·宿州期中) 若不等式（m2+4m﹣5）x2﹣4（m﹣1）x+3＞0一切实数x恒成立，则实数m的取值范围是________．三、解答题 (共5题；共30分)16. （5分）为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第2小组的频数为12．（1）求该校报考飞行员的总人数；（2）以这所学校的样本数据来估计全省的总体数据，若从全省报考飞行员的同学中（人数很多）任选二人，设X表示体重超过60公斤的学生人数，求X的分布列和数学期望．17. （5分） (2017高一下·怀仁期末) 如图，在中，，，点在边上，且，．（I）求；（II）求的长．18. （5分）(2018·南充模拟) 汽车行业是碳排放量比较大的行业之一，欧盟从2012年开始就对二氧化碳排放量超过的型汽车进行惩罚，某检测单位对甲、乙两类型品牌汽车各抽取5辆进行二氧化碳排放量检测，记录如下(单位： )：甲80110120140150乙100120100160经测算发现，乙类型品牌汽车二氧化碳排放量的平均值为 .（Ⅰ）从被检测的5辆甲类型品牌车中任取2辆，则至少有1辆二氧化碳排放量超过的概率是多少？(Ⅱ)求表中，并比较甲、乙两类型品牌汽车二氧化碳排放量的稳定性.，其中，表示的平均数，表示样本数量，表示个体，表示方差)19. （5分）(2017·厦门模拟) 设公比不为1的等比数列{an}的前n项和Sn ，已知a1a2a3=8，S2n=3（a1+a3+a5+…+a2n﹣1）（n∈N*）．（Ⅰ）求数列{an}的通项公式；（Ⅱ）设bn=（﹣1）nlog2an ，求数列{bn}的前2017项和T2017 ．20. （10分） (2016高一上·徐州期中) 设集合A={x|x2＜9}，B={x|（x﹣2）（x+4）＜0}．（1）求集合A∩B；（2）若不等式2x2+ax+b＜0的解集为A∪B，求a、b的值．参考答案一、选择题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共5题；共6分)11-1、12-1、13-1、14-1、15-1、三、解答题 (共5题；共30分)16-1、17-1、18-1、19-1、20-1、20-2、。

江苏省徐州市高一下学期数学期末考试试卷

江苏省徐州市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分） (2019高二上·南湖期中) 若直线经过两点，则直线的倾斜角为（）A .B .C .D .2. （2分）中角的对边分别为a,b,c，，,则a为（）A .B . 2C .D .3. （2分）以A(1，3)，B(-5，1)为端点的线段的垂直平分线方程是（）A . 3x-y+8=0B . 3x+y+4=0C . 3x-y+6=0D . 3x+y+2=04. （2分） (2018高一下·黑龙江期末) 正方体中，直线与所成的角为（）A . 30oB . 45oC . 60oD . 90o5. （2分）(2017·福州模拟) 在棱长为1的正方体ABCD﹣A'B'C'D'中，E是AA'的中点，P是三角形BDC'内的动点，EP⊥BC'，则P的轨迹长为（）A .B .C .D .6. （2分） (2016高三上·石家庄期中) 某班学生一次数学考试成绩频率分布直方图如图所示，数据分组依次为[70，90），[90，110），[110，130），[130，150]，若成绩大于等于90分的人数为36，则成绩在[110，130）的人数为（）A . 12B . 9C . 15D . 187. （2分） (2016高一下·老河口期中) 如图所示，为了测量某湖泊两侧A、B间的距离，李宁同学首先选定了与A、B不共线的一点C，然后给出了三种测量方案：（△ABC的角A、B、C所对的边分别记为a、b、c）：①测量A、C、b；②测量a、b、C；③测量A、B、a；则一定能确定A、B间距离的所有方案的序号为（）A . ①②B . ②③C . ①③D . ①②③8. （2分）圆锥SO的底面半径为，母线长2，A，B是底面圆周上两动点，过S，A，B作圆锥的截面，当△SAB的面积最大时，截面SAB与底面圆O所成的（不大于的）二面角等于（）A .B .C .D .9. （2分）已知正方体ABCD﹣A1B1C1D1的棱长为a，则棱A1B1所在直线与面对角线BC1所在直线间的距离是（）A .B . aC .D .10. （2分） (2018高一下·虎林期末) 若直线y=x+b 与曲线有公共点，则b的取值范围是（）A .B .C .D .二、填空题 (共6题；共6分)11. （1分） (2018高二下·泰州月考) 一组数据8 ,12 ,10,11,9的均值________．12. （1分） (2019高三上·双流期中) 已知中，，，，则该三角形的面积是________.13. （1分） (2016高一下·黄冈期末) 一个几何体的三视图如图所示，若其正视图、侧视图的轮廓都是边长为1的菱形，俯视图是边长为1的正方形，则该几何体的体积为________．14. （1分） (2019高二上·哈尔滨期中) 已知点在抛物线上，则 ________；点到抛物线的焦点的距离是________.15. （1分）如图所示，在四棱锥P﹣ABCD中，PA⊥底面ABCD，且底面各边都相等，M是PC上的一动点，请你补充一个条件________，使平面MBD⊥平面PCD．①DM⊥PC ②DM⊥BM③BM⊥PC ④PM=MC（填写你认为是正确的条件对应的序号）．16. （1分） (2019高二上·南宁月考) 已知x，y满足方程（x﹣2）2+y2＝1，则的最大值为________三、解答题 (共4题；共20分)17. （5分）(2018高一下·长阳期末) 在中，角所对的边分别为，且.（1）求边长；（2）若的面积为，求边长 .18. （5分） (2016高二上·徐水期中) 某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．（1）求图中a的值；（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；（3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求数学成绩在[50，90）之外的人数．分数段[50，60）[60，70）[70，80）[80，90）x：y1：12：13：44：519. （5分）(2018·榆社模拟) 如图，在各棱长均为2的正三棱柱中，，分别为棱与的中点，，为线段上的动点，其中，更靠近，且 .（1）证明：平面；（2）若与平面所成角的正弦值为，求异面直线与所成角的余弦值.20. （5分）(2018·长沙模拟) 已知椭圆 :（）的离心率为，，分别是它的左、右焦点，且存在直线，使，关于的对称点恰好是圆：（，）的一条直径的两个端点．（1）求椭圆的方程；（2）设直线与抛物线相交于、两点，射线、与椭圆分别相交于、．试探究：是否存在数集，当且仅当时，总存在，使点在以线段为直径的圆内？若存在，求出数集；若不存在，请说明理由．参考答案一、单选题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共6题；共6分)11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共4题；共20分) 17-1、17-2、18-1、18-2、18-3、19-1、19-2、20-1、20-2、。

江苏省徐州市2019年高一下学期数学期末考试试卷D卷

江苏省徐州市2019年高一下学期数学期末考试试卷D卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）设双曲线的离心率为2,是右焦点.若A,B为双曲线上关于原点对称的两点，且,则直线AB的斜率是（）A .B .C .D .2. （2分） (2019高一下·浙江期中) 己知a，b，c，d是四个互不相等的正实数，满足a+b>c+d，且la-b|＜lc-d|，则下列选项正确的是（）A . a2+b2>c2+d2B . |a2-b2|＜lc2-d2|C . <D . | |＜l |3. （2分）椭圆的左、右焦点分别为是上两点，，，则椭圆的离心率为（）A .B .C .D .4. （2分）已知sinθ＜0，cosθ＜0，则角θ的终边所在的象限是（）A . 第一象限B . 第二象限C . 第三象限D . 第四象限5. （2分） (2019高二上·哈尔滨月考) 已知是椭圆上的一点，是椭圆的两个焦点，且，则的面积是（）A . 1B .C .D .6. （2分） (2019高一上·利辛月考) 等差数列的前n项和为，且，，则（）A . 10B . 20C .D .7. （2分）若直线与直线互相垂直，那么a的值等于（）A . 1B .C .D . -28. （2分）(2018高二下·大名期末) 直线与相交于两点，，则的值为（）A .B .C .D .9. （2分） (2016高一上·金华期中) f（x）=（m﹣1）x2+2mx+3为偶函数，则f（x）在区间（2，5）上是（）A . 减函数B . 增函数C . 有增有减D . 增减性不确定10. （2分）(2016·商洛模拟) ⊙C：（x﹣4）2+（y﹣2）2=18上到直线l：x﹣y+2=0的距离为的点个数有（）个．A . 1B . 2C . 3D . 411. （2分）直线与椭圆交于两点，以线段为直径的圆过椭圆的右焦点，则椭圆的离心率为（）A .B .C .D .12. （2分）如果椭圆的弦被点（4，2）平分，则这条弦所在的直线方程是（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分） (2020高一下·河北期中) 在直角梯形中，点M为腰的中点，则________ ．14. （1分） (2020高二上·吉林期末) 已知变量满足约束条件，则的最大值为________.15. （1分）(2018·安徽模拟) 已知数列的前的前项和为，数列的的前项和为，则满足的最小的值为________．16. （1分）若圆x2+（y﹣2）2=1与椭圆 =1的三个交点构成等边三角形，则该椭圆的离心率的值为________三、解答题 (共6题；共50分)17. （10分） (2018高二上·遵化期中) 已知的三个顶点坐标分别为 .（1）求边的垂直平分线的方程；（2）求的面积.18. （5分） (2017高三上·涪城开学考) 已知向量 =（sin（A﹣B），， =（1，2sinB），且• =﹣sin2C，其中A、B、C分别为△ABC的三边a、b、c所对的角．（Ⅰ）求角C的大小；（Ⅱ）若，且S△ABC= ，求边c的长．19. （5分）为进行科学实验，观测小球A、B在两条相交成60°角的直线型轨道上运动的情况，如图所示，运动开始前，A和B分别距O点3m和1m，后来它们同时以每分钟4m的速度各沿轨道l1、l2按箭头的方向运动．问：（1）运动开始前，A、B的距离是多少米？（结果保留三位有效数字）．（2）几分钟后，两个小球的距离最小？20. （10分）设{an}是等差数列，{bn}是各项都为正数的等比数列，且a1=b1=1，a3+b5=21，a5+b3=13．（1）求{an}、{bn}的通项公式；（2）求数列的前n项和Sn ．21. （10分）(2018·榆林模拟) 已知过原点的动直线与圆：交于两点.（1）若，求直线的方程；（2）轴上是否存在定点，使得当变动时，总有直线的斜率之和为0？若存在，求出的值；若不存在，说明理由.22. （10分）(2012·湖北) 设A是单位圆x2+y2=1上的任意一点，l是过点A与x轴垂直的直线，D是直线l与x轴的交点，点M在直线l上，且满足丨DM丨=m丨DA丨（m＞0，且m≠1）．当点A在圆上运动时，记点M的轨迹为曲线C．（1）求曲线C的方程，判断曲线C为何种圆锥曲线，并求焦点坐标；（2）过原点且斜率为k的直线交曲线C于P、Q两点，其中P在第一象限，它在y轴上的射影为点N，直线QN交曲线C于另一点H，是否存在m，使得对任意的k＞0，都有PQ⊥PH？若存在，求m的值；若不存在，请说明理由．参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共50分)17-1、17-2、18-1、19-1、20-1、20-2、21-1、21-2、22-1、22-2、第11 页共11 页。

2019年江苏省徐州市高一下学期期末考试数学试卷

江苏省徐州市高一下学期期末考试数学试卷一、选择题（每小题5分,共60分）1.已知两点A （-6,6），B （-4,4），求线段AB 的长度（）． A.22 B.32 C.10 D. 52.已知两点P （1,-1），A （-2,2），且点P 是A 、B 两点中点，求点B 坐标（）A.（-1,1）B.（4,-4）C.（-5,5）D.（1,-1）3.求点P （3,-2）到直线3x-4y-2=0的距离是（）A.3B.4C.5D.6 4. 求直线12y-5x=2与直线5x-12y+15=0的距离为（）A.1B.2C.3D.45.在空间直角坐标系中，点（1 , 2 , 3 ）到（0 , -2 , 4 ）点的距离是（） A.18 B.16 C.32 D.426.已知点A （1,2），B （-3,4），C （5,5），求三角形ABC 的面积（）A.8B.9C.10D.117. 过点（1,-2）且与直线2x-y+3=0 平行的直线方程为（）A.2x-y-1=0B.2x-y-2=0C.2x-y-3=0D.2x-y-4=08. 已知点M （2,3），N （5,-2），若x 轴上存在一点P ，使∣PM+PN ∣最小，求P 点的坐标（）A.（10,0）B.（27,21） C.（12,0） D.（11,0） 9.9.在ABC △中，已知4,6a b ==，B=60°，则SinA 的值为( )A. 2B.2C.3D.310.求经过点（3，1）且与圆2x +2y -4=0相切的切线方程（） A.x-3y-4=0 B.x+3y-4=0 C.3x-3y-4=0 D.3x+y-4=011.把一个表面涂有黄漆的正方体木块平均分成64个小正方体，从中任意取一块，求这一块至少有2面涂有红漆的概率（）A.21B.32C.1613D.167 12.若从甲、乙、丙、丁、戊5位学生，选出3人参加端午节，则甲、乙都被选中的概率是（） A.21 B.31 C.103 D.52 二、填空题（每小题5分,共20分）13. 某学校学生男生1300人，女生1100人，现用分层抽样的方法从所有学生中抽取1个容量为n 的样本，已知从男生中抽取的人数为91人，那么n=_____14. 在锐角△ABC 中，AB ＝3，AC ＝4，S △ABC ＝23，则BC ＝________15.若K1、K2、K3、K4、K5的方差是13，则3K1-7、3K2-7、3K3-7、3K4-7、3K5-7的方差是 ____________16.在平面坐标系中，在直线x=2上有一点M ，在OM 延长线上，有一点P （x ，y ）,满足OM ·OP=12，则点p 的轨迹方程是 ____________________.三、解答题（共6个答题，满分80分）17. （本小题满分14分）已知点A （-3,2），B （1,4），直线L ：2x+y-10=0 .（1）求线段AB 的长度；（2）分别求点A 、点B 到直线L 的距离.18. （本小题满分14分）已知点ΔABC 的三个顶点坐标为（1,1），B （-3,4）， C （4,-1）.（1）求AB 长度及AB 边上的高.（2）求ΔABC 的面积.19.（本小题满分16分）河道上有一座圆拱桥，在正常水位时，拱圆最高点距水面9米，拱圆内水面宽22米。

江苏省徐州市高一下学期期末数学考试试卷

江苏省徐州市高一下学期期末数学考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分） (2017高一下·荔湾期末) 若a，b∈R，下列命题正确的是（）A . 若a＞|b|，则a2＞b2B . 若|a|＞b，则a2＞b2C . 若a≠|b|，则a2≠b2D . 若a＞b，则a﹣b＜02. （2分）已知向量 =（1，1）， =（﹣1，0），λ + 与﹣2 共线，则 =（）A .B .C . 2D . ﹣23. （2分）(2012·江西理) 在中，如果，则满足上述条件的三角形有（）A . 1个B . 2个C . 0个D . 无数个4. （2分）如图所示的几何体，关于其结构特征，下列说法不正确的是（）A . 该几何体是由两个同底的四棱锥组成的几何体B . 该几何体有12条棱、6个顶点C . 该几何体有8个面，并且各面均为三角形D . 该几何体有9个面，其中一个面是四边形，其余均为三角形5. （2分）一个几何体按比例绘制的三视图如图所示（单位：m）,则该几何体的体积为（）m3 ．A .B .C .D .6. （2分） (2018高一下·瓦房店期末) 已知函数，若函数在区间内没有零点，则的取值范围是（）A .B .C .D .7. （2分）已知各项不为0的等差数列满足，数列是等比数列，且，则=（）A . 2B . 4C . 8D . 168. （2分）已知△ABC的三边长a=3，b=5，c=6，则△ABC的面积为（）A .B . 2C .D . 29. （2分）关于的一元二次不等式的解集为，且，则a=（）A .B .C .D .10. （2分） (2016高二下·漯河期末) 已知等差数列{an}满足a6+a10=20，则下列选项错误的是（）A . S15=150B . a8=10C . a16=20D . a4+a12=2011. （2分） (2016高一上·揭阳期中) 函数f（x）=x2﹣2x+2在区间（0，4]的值域为（）A . （2，10]B . [1，10]C . （1，10]D . [2，10]12. （2分） (2018高二下·抚顺期末) “杨辉三角”又称“贾宪三角”，是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算，而杨辉在公元1261年所著的《详解九章算法》一书中，记录了贾宪三角形数表，并称之为“开方作法本源”图．下列数表的构造思路就源于“杨辉三角”．该表由若干行数字组成，从第二行起，每一行中的数字均等于其“肩上”两数之和，表中最后一行仅有一个数，则这个数是（）2017 2016 2015 2014……6 5 4 3 2 14033 4031 4029…………11 9 7 5 38064 8060………………20 16 12 816124……………………36 28 20………………………A .B .C .D .二、填空题 (共4题；共4分)13. （1分）已知不等式ax2﹣bx+2＜0的解集为{x|1＜x＜2}，则a+b=________．14. （1分） (2017高三上·安庆期末) 设实数x、y满足x+2xy﹣1=0，则x+y取值范围是________．15. （1分）设数列{an}的前n项和为Sn ，关于数列{an}有下列四个结论：①若数列{an}既是等差数列又是等比数列，则Sn=na1；②若Sn=2n﹣1 ，则数列{an}是等比数列；③若Sn=an2+bn（a，b∈R），则数列{an}是等差数列；④若Sn=an（a∈R），则数列{an}既是等差数列又是等比数列．其中正确结论的序号是________．16. （1分） (2016高一下·包头期中) 已知tan（α+β）= ，，那么tan（α+ ）的值是________．三、解答题 (共6题；共55分)17. （10分）(2013·湖南理) 过抛物线E：x2=2py（p＞0）的焦点F作斜率率分别为k1 ， k2的两条不同直线l1 ， l2 ，且k1+k2=2．l1与E交于点A，B，l2与E交于C，D，以AB，CD为直径的圆M，圆N（M，N为圆心）的公共弦所在直线记为l．（1）若k1＞0，k2＞0，证明：；（2）若点M到直线l的距离的最小值为，求抛物线E的方程．18. （10分）已知函数f（x）=2sin（2x﹣）+a，a为常数（1）求函数f（x）的最小正周期；（2）若x∈[0， ]时，f（x）的最小值为﹣2，求a的值．19. （10分） (2019高二上·石河子月考) 已知分别为△ 三个内角的对边，且满足．（1）求角的大小；（2）当时，求△ 面积的最大值．20. （10分） (2017高二上·宜昌期末) 已知等比数列{an}，a1=1，a6=32，Sn是等差数列{bn}的前n项和，b1=3，S5=35．（1）求数列{an}，{bn}的通项公式；（2）设cn=an+bn，求数列{cn}的前n项和Tn．21. （5分）东海水晶城大世界营业厅去年利润300万元，今年年初搬迁到新水晶城营业厅，扩大了经营范围．为了获取较大利润，需加大宣传力度．预计从今年起，利润以每年26%的增长率增长，同时在每年12月30日要支付x万元的广告费用．为了实现经过10年利润翻两翻的目标，试求每年用于广告费用x万元的最大值．（注：1.2610≈10．）22. （10分） (2019高一下·巴音郭楞月考) 已知：在数列中，，．（1）令，求证：数列是等差数列；（2）若为数列的前项的和，对任意恒成立，求实数的最小值．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共55分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、21-1、22-1、22-2、。

江苏省徐州市高一下学期数学期末考试试卷

江苏省徐州市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2019高二上·南宁月考) 已知集合，，则（）A .B .C .D .2. （2分） (2018高二下·黄陵期末) 方程（为参数）表示的曲线是（）A . 一条直线B . 两条射线C . 一条线段D . 抛物线的一部分3. （2分）设，则之间的关系是（）A .B .C .D .4. （2分）若函数是偶函数，则图象的对称轴是（）A .B .C .D .5. （2分） (2019高二下·吉林期末) 已知为定义在上的奇函数，当时，，则的值域为（）A .B .C .D .6. （2分） (2017高二下·黄山期末) 已知函数f（x）=x3+bx2+cx+d的图象如图，则函数的单调递减区间是（）A . （﹣∞，﹣2）B . （﹣∞，1）C . （﹣2，4）D . （1，+∞）7. （2分）若两个球的表面积之比为1：4，则这两个球的体积之比为（）A . 1：2,B . 1：4,C . 1：8,D . 1：16。

8. （2分） (2020高一下·潮州期中) 已知A，B，C，D是函数一个周期内的图象上的四个点，如图所示，，B为y轴上的点，C为图象上的最低点，E为该函数图象的一个对称中心，B与D关于点E对称，在x轴上的投影为，则ω，φ的值为（）A . ω＝2，φ＝B . ω＝2，φ＝C . ω＝，φ＝D . ω＝，φ＝9. （2分）点O为△ABC内一点，且满足++4=，设△OBC与△ABC的面积分别为S1、S2 ，则=（）A .B .C .D .10. （2分）如图A是单位圆与轴的交点，点在单位圆上，,,四边形的面积为,当取得最大值时的值和最大值分别为（）A . ，B . ， 1C . ，D . ，11. （2分） (2019高三上·深圳月考) 已知角的顶点在坐标原点，始边与轴的非负半轴重合，终边经过点，则的值为（）A .B .C .D .12. （2分）设a为实常数，y=f（x）是定义在R上的奇函数，当x＞0时，f（x）=4x++3，则对于y=f（x）在x＜0时，下列说法正确的是（）A . 有最大值7B . 有最大值﹣7C . 有最小值7D . 有最小值﹣7二、填空题 (共4题；共4分)13. （1分） (2019高二上·郑州月考) 在中，角，，的对边分别是，，，，，，则的面积为________．14. （1分） (2020高二上·舟山期末) 某简单几何体的三视图（俯视图为等边三角形）如图所示（单位：），则该几何体的体积（单位：）为________；表面积为________（单位：）.15. （1分）(2020·江苏模拟) 关于的不等式的解集为，则关于的不等式的解集为________.16. （1分） (2018高二上·浙江月考) 已知a，b都是正数，满足，则的最小值为________．三、解答题 (共6题；共70分)17. （10分） (2020高二下·嘉兴期末) 已知函数（）.（1）求的值；（2）求的最小正周期及单调递增区间.18. （15分） (2019高二上·拉萨月考) 已知函数 .（1）若，解不等式；（2）若对于任意实数，恒成立，求实数的取值范围.19. （10分） (2019高三上·株洲月考) 在中，内角，，所对的边分别为，，，已知（1）求角的大小；（2）已知，求的最大值.20. （10分）(2019·北京) 在△ABC中，a=3，b-c=2，cosB=- .（I）求b，c的值；（II）求sin（B-C）的值.21. （10分） (2018高三上·邹城期中) 山东省于2015年设立了水下考古研究中心，以此推动全省的水下考古、水下文化遗产保护等工作;水下考古研究中心工作站，分别设在位于刘公岛的中国甲午战争博物院和威海市博物馆。

徐州一中数学高一下期末经典测试(含答案解析)

一、选择题1．(0分)[ID ：12728]△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知5a =，2c =，2cos 3A =，则b= A ．2B ．3C ．2D ．32．(0分)[ID ：12717]设m ，n 为两条不同的直线，α，β为两个不同的平面，则（）A ．若//m α，//n α，则//m nB ．若//m α，//m β，则//αβC ．若//m n ，n α⊥，则m α⊥D ．若//m α，αβ⊥，则m β⊥3．(0分)[ID ：12716]已知集合{}220A x x x =-->，则A =RA ．{}12x x -<<B ．{}12x x -≤≤C ．}{}{|12x x x x <-⋃D ．}{}{|1|2x x x x ≤-⋃≥4．(0分)[ID ：12704]在ABC ∆中，2AB =，2AC =，E 是边BC 的中点.O 为ABC ∆所在平面内一点且满足222OA OB OC ==，则·AE AO 的值为（）A ．12B ．1C ．22D ．325．(0分)[ID ：12702]已知D ，E 是ABC 边BC 的三等分点，点P 在线段DE 上，若AP xAB yAC =+，则xy 的取值范围是( )A ．14,99⎡⎤⎢⎥⎣⎦B ．11,94⎡⎤⎢⎥⎣⎦C ．21,92⎡⎤⎢⎥⎣⎦D ．21,94⎡⎤⎢⎥⎣⎦6．(0分)[ID ：12701]在ABC 中，角A ，B ，C 所对的边为a ，b ，c ，且B 为锐角，若sin 5sin 2A c B b =，7sin 4B =，574ABC S =△，则b =（） A ．23B ．27C ．15D ．147．(0分)[ID ：12690]《九章算术》中，将底面是直角三角形的直三棱柱称为“堑堵”．某“堑堵”的三视图如图所示，则它的表面积为（）A ．2B ．422+C ．442+D ．642+8．(0分)[ID ：12687]C ∆AB 是边长为2的等边三角形，已知向量a ，b 满足2a AB =，C 2a b A =+，则下列结论正确的是（）A ．1b =B ．a b ⊥C ．1a b ⋅=D ．()4C a b +⊥B9．(0分)[ID ：12684]设样本数据1210,,,x x x 的均值和方差分别为1和4，若(i i y x a a =+为非零常数，1,2,,10)i =，则1210,,,y y y 的均值和方差分别为（）A ．1,4a +B ．1,4a a ++C ．1,4D ．1,4a +10．(0分)[ID ：12635]已知01a b <<<，则下列不等式不成立．．．的是 A ．11()()22ab>B ．ln ln a b >C ．11a b> D ．11ln ln a b> 11．(0分)[ID ：12633]阅读如图所示的程序框图，运行相应的程序，若输入N 的值为20，则输出T 的值为A ．1B ．2C ．3D ．412．(0分)[ID ：12671]函数223()2xx xf x e +=的大致图像是（）A ．B ．C ．D ．13．(0分)[ID ：12658]1()xf x e x=-的零点所在的区间是（） A ．1(0,)2B ．1(,1)2C ．3(1,)2D ．3(,2)214．(0分)[ID ：12647]与直线40x y --=和圆22220x y x y ++-=都相切的半径最小的圆的方程是A ．()()22112x y +++= B ．()()22114x y -++= C ．()()22112x y -++=D ．()()22114x y +++=15．(0分)[ID ：12648]已知()f x 是定义在R 上的奇函数，当0x >时，()32f x x =-，则不等式()0f x >的解集为（） A ．33,0,22⎛⎫⎛⎫-∞- ⎪⎪⎝⎭⎝⎭B ．33,,22⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭C ．33,22⎛⎫- ⎪⎝⎭D ．33,0,22⎛⎫⎛⎫-⋃+∞ ⎪ ⎪⎝⎭⎝⎭二、填空题16．(0分)[ID ：12825]在ABC △ 中，若223a b bc -= ，sin 23C B = ，则A 等于__________．17．(0分)[ID ：12815]()sin1013tan 70+=_____18．(0分)[ID ：12814]已知函数()sin 03y x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为π，若将该函数的图像向左平移()0m m >个单位后，所得图像关于原点对称，则m 的最小值为________.19．(0分)[ID ：12809]某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200,400,300,100件，为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取________ 件.20．(0分)[ID ：12800]若直线1x y -=与直线(3)80m x my ++-=平行，则m =______________．21．(0分)[ID ：12789]对于函数()f x ，()g x ，设(){}0m x f x ∈=，(){}0n x g x ∈=，若存在m ，n 使得1m n -<，则称()f x 与()g x 互为“近邻函数”.已知函数()()13log 2exf x x -=+-与()1422xx g x a +=⋅-+互为“近邻函数”，则实数a 的取值范围是______.（e 是自然对数的底数）22．(0分)[ID ：12778]设向量(12)(23)a b ==，，，，若向量a b λ+与向量(47)c =--，共线，则λ=23．(0分)[ID ：12776]若x ，y 满足约束条件10,{30,30,x y x y x -+≥+-≥-≤则z=x−2y 的最小值为__________.24．(0分)[ID ：12730]若1tan 46πα⎛⎫-= ⎪⎝⎭,则tan α=____________. 25．(0分)[ID ：12753]在直三棱柱111ABC A B C -中，90ACB ∠=，12AA =，1AC BC ==，则异面直线1A B 与1AC 所成角的余弦值是_____________．三、解答题26．(0分)[ID ：12911]在ABC ∆中，a 、b 、c 分别是角A 、B 、C 的对边，且()()3a b c a b c ab +++-=.（1）求角C 的值；（2）若2c =，且ABC ∆为锐角三角形，求+a b 的取值范围.27．(0分)[ID ：12896]某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益()f x 与投资额x 成正比，且投资1万元时的收益为18万元，投资股票等风险型产品的收益()g x 与投资额x 的算术平方根成正比，且投资1万元时的收益为0.5万元，（1）分别写出两种产品的收益与投资额的函数关系；（2）该家庭现有20万元资金，全部用于理财投资，问：怎样分配资金能使投资获得最大收益，其最大收益为多少万元？28．(0分)[ID ：12884]已知函数()()221+0g x ax ax b a =-+>在区间[2,3]上有最大值4和最小值1. (1)求a 、b 的值； (2)设()()2g x f x x =-，若不等式()0f x k ->在x ∈(]2,5上恒成立，求实数k 的取值范围．29．(0分)[ID ：12830]ABC ∆中，D 是BC 上的点，AD 平分∠BAC，ABD ∆面积是ADC ∆面积的2倍． (1)求sin sin BC；(2)若AD ＝1，DC ＝22，求BD 和AC 的长． 30．(0分)[ID ：12829]某校高一()1班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如图．(1)求分数在[)50,60的频数及全班人数；(2)求分数在[)80,90之间的频数，并计算频率分布直方图中[)80,90间矩形的高；(3)若要从分数在[)80,100之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份分数在[)90,100之间的概率．【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题 1．D 2．C 3．B 4．D 5．D 6．D7．D8．D9．A10．B11．B12．B13．B14．C15．A二、填空题16．【解析】由得所以即则又所以故答案为17．【解析】【分析】将写成切化弦后利用两角和差余弦公式可将原式化为利用二倍角公式可变为由可化简求得结果【详解】本题正确结果：【点睛】本题考查利用三角恒等变换公式进行化简求值的问题涉及到两角和差余弦公式二18．【解析】【分析】先利用周期公式求出再利用平移法则得到新的函数表达式依据函数为奇函数求出的表达式即可求出的最小值【详解】由得所以向左平移个单位后得到因为其图像关于原点对称所以函数为奇函数有则故的最小值19．18【解析】应从丙种型号的产品中抽取件故答案为18点睛:在分层抽样的过程中为了保证每个个体被抽到的可能性是相同的这就要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比即ni20．【解析】【分析】由题意得到关于m的方程解方程即可求得最终结果【详解】由题意结合直线平行的充分必要条件可得：解得：此时两直线方程分别为：两直线不重合据此可知：【点睛】本题主要考查直线平行的充分必要条件21．【解析】【分析】先求出的根利用等价转换的思想得到在有解并且使用分离参数方法可得结果【详解】由令所以又已知函数与互为近邻函数据题意可知：在有解则在有解即在有解令又令所以当时当时所以所以则故答案为：【点22．2【解析】【分析】由题意首先求得向量然后结合向量平行的充分必要条件可得的值【详解】=由向量共线的充分必要条件有：故答案为2【点睛】本题主要考查平面向量的坐标运算向量平行的充分必要条件等知识意在考查学23．【解析】【分析】【详解】试题分析：由得记为点；由得记为点；由得记为点分别将ABC的坐标代入得所以的最小值为【考点】简单的线性规划【名师点睛】利用线性规划求最值一般用图解法求解其步骤是：（1）在平面直24．【解析】故答案为25．【解析】【分析】先找出线面角运用余弦定理进行求解【详解】连接交于点取中点连接则连接为异面直线与所成角在中同理可得异面直线与所成角的余弦值是故答案为【点睛】本题主要考查了异面直线所成的角考查了空间想象三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1．D解析：D【解析】【分析】【详解】由余弦定理得，解得（舍去），故选D.【考点】余弦定理【名师点睛】本题属于基础题,考查内容单一,根据余弦定理整理出关于b 的一元二次方程,再通过解方程求b.运算失误是基础题失分的主要原因,请考生切记！2．C解析：C 【解析】【分析】根据空间线面关系、面面关系及其平行、垂直的性质定理进行判断．【详解】对于A 选项，若//m α，//n α，则m 与n 平行、相交、异面都可以，位置关系不确定；对于B 选项，若l αβ=，且//m l ，m α⊄，m β⊄，根据直线与平面平行的判定定理知，//m α，//m β，但α与β不平行；对于C 选项，若//m n ，n α⊥，在平面α内可找到两条相交直线a 、b 使得n a ⊥，n b ⊥，于是可得出m a ⊥，m b ⊥，根据直线与平面垂直的判定定理可得m α⊥；对于D 选项，若αβ⊥，在平面α内可找到一条直线a 与两平面的交线垂直，根据平面与平面垂直的性质定理得知a β⊥，只有当//m a 时，m 才与平面β垂直．故选C ．【点睛】本题考查空间线面关系以及面面关系有关命题的判断，判断时要根据空间线面、面面平行与垂直的判定与性质定理来进行，考查逻辑推理能力，属于中等题．3．B解析：B 【解析】分析：首先利用一元二次不等式的解法，求出220x x -->的解集，从而求得集合A ，之后根据集合补集中元素的特征，求得结果. 详解：解不等式220x x -->得12x x -或，所以{}|12A x x x =<->或，所以可以求得{}|12R C A x x =-≤≤，故选B.点睛：该题考查的是有关一元二次不等式的解法以及集合的补集的求解问题，在解题的过程中，需要明确一元二次不等式的解集的形式以及补集中元素的特征，从而求得结果.4．D解析：D 【解析】【分析】根据平面向量基本定理可知()12AE AB AC =+，将所求数量积化为1122AB AO AC AO ⋅+⋅；由模长的等量关系可知AOB ∆和AOC ∆为等腰三角形，根据三线合一的特点可将AB AO ⋅和AC AO ⋅化为212AB 和212AC ，代入可求得结果.【详解】E 为BC 中点 ()12AE AB AC ∴=+ ()111222AE AO AB AC AO AB AO AC AO ∴⋅=+⋅=⋅+⋅ 222OA OB OC == AOB ∴∆和AOC ∆为等腰三角形211cos 22AB AO AB AO OAB AB AB AB ∴⋅=∠=⋅=，同理可得：212AC AO AC ⋅=22111314422AE AO AB AC ∴⋅=+=+= 本题正确选项：D 【点睛】本题考查向量数量积的求解问题，关键是能够利用模长的等量关系得到等腰三角形，从而将含夹角的运算转化为已知模长的向量的运算.5．D解析：D 【解析】【分析】利用已知条件推出x +y ＝1，然后利用x ，y 的范围，利用基本不等式求解xy 的最值．【详解】解：D ，E 是ABC 边BC 的三等分点，点P 在线段DE 上，若AP xAB yAC =+，可得x y 1+=，x ，12y ,33⎡⎤∈⎢⎥⎣⎦，则2x y 1xy ()24+≤=，当且仅当1x y 2==时取等号，并且()2xy x 1x x x =-=-，函数的开口向下，对称轴为：1x 2=，当1x 3=或2x 3=时，取最小值，xy 的最小值为：29．则xy 的取值范围是：21,. 94⎡⎤⎢⎥⎣⎦故选D．【点睛】本题考查函数的最值的求法，基本不等式的应用，考查转化思想以及计算能力．6．D解析：D【解析】【分析】利用正弦定理化简sin5sin2A cB b=，再利用三角形面积公式，即可得到,a c，由sin B=，求得cos B，最后利用余弦定理即可得到答案．【详解】由于sin5sin2A cB b=，有正弦定理可得：52a cb b=，即52a c=由于在ABC中，sin B=，ABCS=△1sin2ABCS ac B==联立521sin2sina cac BB⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩，解得：5a=，2c=由于B为锐角，且sin B=，所以3cos4B==所以在ABC中，由余弦定理可得：2222cos14b ac ac B=+-=，故b=（负数舍去）故答案选D【点睛】本题考查正弦定理，余弦定理，以及面积公式在三角形求边长中的应用，属于中档题．7．D解析：D【解析】【分析】根据题意和三视图知几何体是一个放倒的直三棱柱，由三视图求出几何元素的长度，由面积公式求出几何体的表面积．【详解】根据题意和三视图知几何体是一个放倒的直三棱柱，底面是一个直角三角形，两条直角边,斜边是2，且侧棱与底面垂直，侧棱长是2，∴几何体的表面积12222262S =⨯+⨯⨯=+ 故选D ．【点睛】本题考查三视图求几何体的表面积，由三视图正确复原几何体是解题的关键，考查空间想象能力．8．D解析：D 【解析】试题分析：2,2AB a AC a b ==+,AC AB b ∴=+,b AC AB BC ∴=-=．由题意知12,cos1201212b a b a b ⎛⎫=⋅=⋅=⨯⨯-=- ⎪⎝⎭．()()2422a b BC AB BC BC AB BC BC∴+⋅=+⋅=⋅+212cos1202222402AB BC ⎛⎫=⋅+=⨯⨯⨯-+= ⎪⎝⎭．()4a b BC ∴+⊥．故D 正确．考点：1向量的加减法；2向量的数量积；3向量垂直．9．A解析：A 【解析】试题分析：因为样本数据1210,,,x x x 的平均数是1,所以1210,,...y y y 的平均数是121012101210 (1101010)y y y x a x a x a x x x a a ++++++++++++==+=+；根据i i y x a =+（a 为非零常数，1,2,,10i =），以及数据1210,,,x x x 的方差为4可知数据1210,,,y y y 的方差为2144⨯=，综上故选A.考点：样本数据的方差和平均数．10．B解析：B 【解析】【分析】根据指数函数、对数函数的单调性，以及不等式的性质，对选项逐一分析，由此得出不等式不成立的选项. 【详解】依题意01a b <<<，由于12xy ⎛⎫= ⎪⎝⎭为定义域上的减函数，故11()()22a b >，故A 选项不等式成立.由于ln y x =为定义域上的增函数，故ln ln 0a b <<，则11ln ln a b>，所以B 选项不等式不成立，D 选项不等式成立.由于01a b <<<，故11a b>，所以C 选项不等式成立.综上所述，本小题选B. 【点睛】本小题主要考查指数函数和对数函数的单调性，考查不等式的性质，属于基础题.11．B解析：B 【解析】分析：由题意结合流程图运行程序即可求得输出的数值. 详解：结合流程图运行程序如下：首先初始化数据：20,2,0N i T ===，20102N i ==，结果为整数，执行11T T =+=，13i i =+=，此时不满足5i ≥； 203N i =，结果不为整数，执行14i i =+=，此时不满足5i ≥； 2054N i ==，结果为整数，执行12T T =+=，15i i =+=，此时满足5i ≥；跳出循环，输出2T =. 本题选择B 选项.点睛：识别、运行程序框图和完善程序框图的思路： (1)要明确程序框图的顺序结构、条件结构和循环结构． (2)要识别、运行程序框图，理解框图所解决的实际问题． (3)按照题目的要求完成解答并验证．12．B解析：B 【解析】由()f x 的解析式知仅有两个零点32x =-与0x =，而A 中有三个零点，所以排除A ，又()2232xx x f x e-++'=，由()0f x '=知函数有两个极值点，排除C ，D ，故选B ． 13．B解析：B 【解析】函数f （x ）=e x ﹣1x 是（0，+∞）上的增函数，再根据f （12）2＜0，f （1）=e ﹣1＞0，可得f （12）f （1）＜0，∴函数f （x ）=e x ﹣1x 的零点所在的区间是（12，1），故选B ．点睛：判定函数的零点所在区间，只需计算区间端点处的函数值，并判断是否异号，只要异号，则区间内至少有一个零点存在.14．C解析：C 【解析】圆22220x y x y ++-=的圆心坐标为()1,1-，过圆心()1,1-与直线40x y --=垂直的直线方程为0x y +=，所求圆的圆心在此直线上，又圆心()1,1-到直线40x y --==，设所求圆的圆心为(),a b ，且圆心在直线40x y --==0a b +=，解得1,1a b ==-（3,3a b ==-不符合题意，舍去），故所求圆的方程为()()22112x y -++=.故选C ．【名师点睛】本题主要考查直线与圆的位置关系，考查了数形结合的思想，考查了计算能力，属于中档题．15．A解析：A 【解析】【分析】根据题意，结合函数的解析式以及奇偶性分析可得()f x 的图象，据此分析可得答案. 【详解】解：因为()f x 是定义在R 上的奇函数，所以它的图象关于原点对称，且()00f =，已知当0x >时，()32f x x =-，作出函数图象如图所示，从图象知：33022f f ⎛⎫⎛⎫=-=⎪ ⎪⎝⎭⎝⎭，则不等式()0f x >的解集为33,0,22⎛⎫⎛⎫-∞-⋃ ⎪ ⎪⎝⎭⎝⎭. 故选：A.【点睛】本题考查函数的奇偶性与单调性的综合应用，以及函数的解析式，考查数形结合思想.二、填空题16．【解析】由得所以即则又所以故答案为解析：6π【解析】由23sinC sinB = 得23c b =，所以2223323a b bc b -==，即227a b =，则22222223243b c a cosA bc b+-===，又0A π∈（，），所以6A π=．故答案为6π. 17．【解析】【分析】将写成切化弦后利用两角和差余弦公式可将原式化为利用二倍角公式可变为由可化简求得结果【详解】本题正确结果：【点睛】本题考查利用三角恒等变换公式进行化简求值的问题涉及到两角和差余弦公式二解析：1【解析】【分析】3tan 60，切化弦后，利用两角和差余弦公式可将原式化为sin10cos10cos 60cos 70，利用二倍角公式可变为1sin 202cos 60cos 70⋅，由sin 20cos70=可化简求得结果. 【详解】()()cos 60cos 7060sin 70sin1013tan70sin101tan 60tan70sin1s 0co i s 60o 7n c s 0+=++⋅=()cos 7060sin10cos101sin 201sin101cos60cos70cos60cos702cos60cos702cos60-=⋅==⋅==本题正确结果：1 【点睛】本题考查利用三角恒等变换公式进行化简求值的问题，涉及到两角和差余弦公式、二倍角18．【解析】【分析】先利用周期公式求出再利用平移法则得到新的函数表达式依据函数为奇函数求出的表达式即可求出的最小值【详解】由得所以向左平移个单位后得到因为其图像关于原点对称所以函数为奇函数有则故的最小值解析：3π【解析】【分析】先利用周期公式求出ω，再利用平移法则得到新的函数表达式，依据函数为奇函数，求出m 的表达式，即可求出m 的最小值．【详解】由2T ππω==得2ω=，所以sin 23y x π⎛⎫=+ ⎪⎝⎭，向左平移()0m m >个单位后，得到sin[2()]sin(22)33y x m x m ππ=++=++，因为其图像关于原点对称，所以函数为奇函数，有2,3m k k Z ππ+=∈，则62k m ππ=-+，故m 的最小值为3π．【点睛】本题主要考查三角函数的性质以及图像变换，以及sin()y A x ωϕ=+ 型的函数奇偶性判断条件．一般地sin()y A x ωϕ=+为奇函数，则k ϕπ=；为偶函数，则2k πϕπ=+；cos()y A x ωϕ=+为奇函数，则2k πϕπ=+；为偶函数，则k ϕπ=．19．18【解析】应从丙种型号的产品中抽取件故答案为18点睛:在分层抽样的过程中为了保证每个个体被抽到的可能性是相同的这就要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比即ni解析：18 【解析】应从丙种型号的产品中抽取30060181000⨯=件，故答案为18．点睛:在分层抽样的过程中，为了保证每个个体被抽到的可能性是相同的，这就要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比，即n i ∶N i ＝n ∶N ．20．【解析】【分析】由题意得到关于m 的方程解方程即可求得最终结果【详解】由题意结合直线平行的充分必要条件可得：解得：此时两直线方程分别为：两直线不重合据此可知：【点睛】本题主要考查直线平行的充分必要条件解析：32-【分析】由题意得到关于m 的方程，解方程即可求得最终结果. 【详解】由题意结合直线平行的充分必要条件可得：()()1130m m ⨯--⨯+=，解得：32m =-，此时两直线方程分别为：1x y -=，338022x y --=，两直线不重合，据此可知：32m =-. 【点睛】本题主要考查直线平行的充分必要条件，意在考查学生的转化能力和计算求解能力.21．【解析】【分析】先求出的根利用等价转换的思想得到在有解并且使用分离参数方法可得结果【详解】由令所以又已知函数与互为近邻函数据题意可知：在有解则在有解即在有解令又令所以当时当时所以所以则故答案为：【点解析：10,2⎛⎤ ⎥⎝⎦.【解析】【分析】先求出()0f x =的根，利用等价转换的思想，得到()0g x =在1m n -<有解，并且使用分离参数方法，可得结果【详解】由()()13log 2exf x x -=+-，令()0f x =所以1x =，又已知函数()()13log 2e xf x x -=+-与()1422xx g x a +=⋅-+互为“近邻函数”据题意可知：()0g x =在11x -<有解，则()0g x =在02x <<有解即1224x x a +-=在02x <<有解，令()1224x xh x +-=，又令2x t =，()1,4t ∈，11,14t ⎛⎫∈ ⎪⎝⎭所以2222111222t y t t -⎛⎫==--+ ⎪⎝⎭ 当112t =时max 12y =当11t=时0y = 所以10,2y ⎛⎤∈ ⎥⎝⎦所以()10,2h x ⎛⎤∈ ⎥⎝⎦，则10,2a ⎛⎤∈ ⎥⎝⎦故答案为：10,2⎛⎤⎥⎝⎦【点睛】本题考查对新定义的理解，以及分离参数方法的应用，属中档题.22．2【解析】【分析】由题意首先求得向量然后结合向量平行的充分必要条件可得的值【详解】=由向量共线的充分必要条件有：故答案为2【点睛】本题主要考查平面向量的坐标运算向量平行的充分必要条件等知识意在考查学解析：2 【解析】【分析】由题意首先求得向量a b λ+，然后结合向量平行的充分必要条件可得λ的值. 【详解】a b λ+=(,2(2,3)(2,23λλλλ+=++）），由向量共线的充分必要条件有：()()(2)7(23)42λλλ+⋅-=+⋅-⇒=. 故答案为2．【点睛】本题主要考查平面向量的坐标运算，向量平行的充分必要条件等知识，意在考查学生的转化能力和计算求解能力.23．【解析】【分析】【详解】试题分析：由得记为点；由得记为点；由得记为点分别将ABC 的坐标代入得所以的最小值为【考点】简单的线性规划【名师点睛】利用线性规划求最值一般用图解法求解其步骤是：（1）在平面直解析：5-【解析】【分析】【详解】试题分析：由10{30x y x y -+=+-=得12x y =⎧⎨=⎩，记为点()1,2A ；由10{30x y x -+=-=得34x y =⎧⎨=⎩，记为点()3,4Β；由30{30x x y -=+-=得3x y =⎧⎨=⎩，记为点()3,0C .分别将A ，B ，C 的坐标代入2z x y =-，得1223Αz =-⨯=-，3245Βz =-⨯=-，3203C z =-⨯=，所以2z x y =-的最小值为5-．【考点】简单的线性规划【名师点睛】利用线性规划求最值，一般用图解法求解，其步骤是：（1）在平面直角坐标系内作出可行域；（2）考虑目标函数的几何意义，将目标函数进行变形；（3）确定最优解：在可行域内平行移动目标函数变形后的直线，从而确定最优解；（4）求最值：将最优解代入目标函数即可求出最大值或最小值．24．【解析】故答案为解析：75【解析】1tan tan 17446tan tan 144511tan tan644ππαππααππα⎛⎫-++ ⎪⎡⎤⎛⎫⎝⎭=-+=== ⎪⎢⎥⎛⎫⎝⎭⎣⎦--- ⎪⎝⎭故答案为75.25．【解析】【分析】先找出线面角运用余弦定理进行求解【详解】连接交于点取中点连接则连接为异面直线与所成角在中同理可得异面直线与所成角的余弦值是故答案为【点睛】本题主要考查了异面直线所成的角考查了空间想象 30 【解析】【分析】先找出线面角，运用余弦定理进行求解【详解】连接1AB 交1A B 于点D ，取11B C 中点E ，连接DE ，则1DE AC ，连接1A E1A DE ∴∠为异面直线1A B 与1AC 所成角在111RtAC B 中，111AC =，1111122C E C B == 152A E ∴=, 同理可得16A D =5DE =222165530cos 10652A DE +-⎝⎭⎝⎭⎝⎭∠==⨯⨯, ∴异面直线1A B 与1AC 3030【点睛】本题主要考查了异面直线所成的角，考查了空间想象能力，运算能力和推理论证能力，属于基础题．三、解答题 26． (1) 3C π=.(2) (23,4].【解析】【分析】（1）根据题意，由余弦定理求得1cos 2C =，即可求解C 角的值；（2）由正弦定理和三角恒等变换的公式，化简得到4sin 6a b A π⎛⎫+=+ ⎪⎝⎭，再根据ABC ∆为锐角三角形，求得62A ππ<<，利用三角函数的图象与性质，即可求解.【详解】（1）由题意知()()3a b c a b c ab +++-=，∴222a b c ab +-=，由余弦定理可知，222cos 122a b c C ab +-==，又∵(0,)C π∈，∴3C π=.（2）由正弦定理可知，2sin sin sin 3a b A Bπ===，即,a A b B ==∴sin )a b A B +=+2sin sin 3A A π⎤⎛⎫=+- ⎪⎥⎝⎭⎦2cos A A =+4sin 6A π⎛⎫=+ ⎪⎝⎭，又∵ABC ∆为锐角三角形，∴022032A B A πππ⎧<<⎪⎪⎨⎪<=-<⎪⎩，即，则2363A πππ<+<，所以4sin 46A π⎛⎫<+≤ ⎪⎝⎭，综上+a b的取值范围为. 【点睛】本题主要考查了利用正弦定理和三角函数的恒等变换求解三角形问题，对于解三角形问题，通常利用正弦定理进行“边转角”寻求角的关系，利用“角转边”寻求边的关系，利用余弦定理借助三边关系求角，利用两角和差公式及二倍角公式求三角函数值. 利用正、余弦定理解三角形问题是高考高频考点，经常利用三角形内角和定理，三角形面积公式，结合正、余弦定理解题.27．（1）()1,()0)8f x x g x x ==≥；（2）投资债券等稳健型产品为16万元，投资股票等风险型产品为4万元，投资收益最大为3万元. 【解析】【分析】（1）投资债券等稳健型产品的收益()f x 与投资额x 成正比，投资股票等风险型产品的收益()g x 与投资额x 的算术平方根成正比，用待定系数法求这两种产品的收益和投资的函数关系；（2）由（1）的结论，设投资股票等风险型产品为x 万元，则投资债券等稳健型产品为20x -万元，这时可构造出一个关于收益y 的函数，然后利用求函数最大值的方法进行求解.【详解】（1）依题意设()1,()f x k x g x k ==，1211(1),(1)82f kg k ====， ()1,()0)8f x x g x x ==≥；（2）设投资股票等风险型产品为x 万元，则投资债券等稳健型产品为20x -万元，1(20)()(20)8y f x g x x =-+=-212)3,0208x =-+≤≤，2,4x ==万元时，收益最大max 3y =万元，20万元资金，投资债券等稳健型产品为16万元，投资股票等风险型产品为4万元，投资收益最大为3万元.【点睛】本题考查函数应用题，考查正比例函数、二次函数的最值、待定系数法等基础知识与基本方法，属于中档题.28．（1）1,0a b ==；（2）4k <.【解析】【分析】（1）函数()g x 的对称轴方程为1x =，开口向上，则在[]2,3上单调递增，则可根据最值列出方程，可解得,a b 的值.(2)由题意只需()min k f x <，则只需要求出()f x 在(]2,5上的最小值，然后运用基本不等式求最值即可.【详解】解：（1）()g x 开口方向向上，且对称轴方程为 1x =，()g x ∴在[]2,3上单调递增()()()()min max2441139614g x g a a b g x g a a b ⎧==-++=⎪∴⎨==-++=⎪⎩.解得1a =且0b =.（2）()0f x k ->在(]2,5x ∈上恒成立所以只需()min k f x <.有（1）知()()2211112222242222x x f x x x x x x x x -+==+=-++≥-⋅+=---- 当且仅当122x x -=-，即3x =时等号成立. 4k ∴<.【点睛】本题考查二次函数的最值的求法，注意讨论对称轴和区间的位置关系，考查不等式恒成立问题的解法，注意运用参数分离和基本不等式的应用，属于中档题. 29．（1）12；（2）1 【解析】试题分析：（1）借助题设条件运用三角形的面积公式求解；（2）借助题设余弦定理立方程组求解.试题解析：（1），1sin 2ACD S AC AD CAD ∆=⋅⋅∠， ∵2ABD ACD S S ∆∆=，BAD CAD ∠=∠，∴2AB AC =．由正弦定理可知sin 1sin 2B AC C AB ∠==∠. （2）∵::2:1ABD ACD BD DC S S ∆∆==，22DC =， ∴2BD =．设AC x =，则2AB x =，在△ABD 与△ACD 中，由余弦定理可知，2222cos 222AD BD AB ADB AD BD +-∠==⋅ 222232cos 22x AD CD AC ADC AD CD -+-∠==⋅ ∵ADB ADC π∠+∠=，∴cos cos ADB ADC ∠=-∠，2232222x -=1x =，即1AC =．考点：三角形的面积公式正弦定理余弦定理等有关知识的综合运用．30．（1）2，25；（2）0.012；（3）0.7.【解析】【分析】(1)先由频率分布直方图求出[)50,60的频率，结合茎叶图中得分在[)50,60的人数即可求得本次考试的总人数；(2)根据茎叶图的数据，利用(1)中的总人数减去[)50,80外的人数，即可得到[)50,80内的人数，从而可计算频率分布直方图中[)80,90间矩形的高；(3)用列举法列举出所有的基本事件，找出符合题意得基本事件个数，利用古典概型概率计算公式即可求出结果．【详解】(1)分数在[)50,60的频率为0.008100.08⨯=，由茎叶图知：分数在[)50,60之间的频数为2， ∴全班人数为2250.08=． (2)分数在[)80,90之间的频数为25223-=；频率分布直方图中[)80,90间的矩形的高为3100.01225÷=． (3)将[)80,90之间的3个分数编号为1a ，2a ，3a ，[)90,100之间的2个分数编号为1b ，2b ，在[)80,100之间的试卷中任取两份的基本事件为： ()12a ,a ，()13a ,a ，()11a ,b ，()12a ,b ，()23a ,a ，()21a ,b ，()22a ,b ，()31a ,b ，()32a ,b ，()12b ,b 共10个，其中，至少有一个在[)90,100之间的基本事件有7个，故至少有一份分数在[)90,100之间的概率是70.710=．【点睛】本题考查了茎叶图和频率分布直方图的性质，以及古典概型概率计算公式的应用，此题是基础题．对于古典概型，要求事件总数是可数的，满足条件的事件个数可数，使得满足条件的事件个数除以总的事件个数即可.。