站心坐标系
GNSS卫星三种站心极坐标的关系

, L
3
、,
、( ) +( ) /叫 。 /
. 0 一 J( { + ( { + ({ x) ) )
2 站 心 极 坐标 系 2 A2 2 2 ( , ,)
GN S卫 星 三 种 站 心 极 坐 标 的 关 系 S
刘 长 建 黄 献 波 . 洪 举 , 吴
( . 息 工 程 大 学 测 绘 学 院 , 南 郑 州 4 0 5 ;. 南 财经 政 法 大 学基 建处 , 南 郑 州 4 0 5 ) 1信 河 5022河 河 5 0 2
摘 要 : 全球 导航 卫 星 系统 ( GNS ) S 的应 用 中有 三种 常用 的站 心极 坐标 系, 天顶 方 向分 别 为参考 椭球 面外 法线 方向 、 垂 线上 方 向和地 心 向径 方 向 。传 统 大地 测 量 中给 出的部 分 极 坐 铅 标 关 系式是 高度 角很 小 时的近似 公 式 , 再适 用 于 GNS 不 S卫 星 , 外 , 另 实用 中还 有 混 淆或 近 似 使 用不 同站 心极 坐标 的情 况。 为此 , 出 了三种 站心 极 坐标 的严格 关 系式 , 给 分析 了它们 的差 异 规律 及量 级 , 为正确 使 用 它们提 供 了参 考 。
0 引 舌
全 球导航 卫 星系 统 ( GNS ) s 的应 用 中 , 一 类 有 坐 标系 常用 于描 述 GNS S卫 星 与 测 站 的相 对 位 置 关 系 , 为站 心坐 标 系[ j 有 时也 称为 站心 地平 坐 称 1, 标 系0 , 可具体 再分 为站 心直 角坐标 系和站 心极 坐 标 系 , 者一 一对应 , 容 易相互 转换 , 二 很 但前 者 常被 用作 求 取后 者的过 渡 。 站 心直角 坐 标 系通 常取 左 手 坐 标 系 。有 三 种 常用 的 站心 直角 坐标 系 , 根本 区别 在 于 z 指 向不 轴 同, 分别 为测 站参 考 椭 球 面外 法 线 方 向、 站 铅 垂 测
高空风的计算解剖

内插法定风向原理
量得风层间的风要素内插的假设前提是相关数据之间的变化是线性的, 而实际上两个量得风层间由于种种原因,在自然系统中的实际变化, 1 分钟之间的风向并不是线性化的
2020/10/16
2)增加量得风层的密度。现算法两个量得风层的间隔为 1 分钟,适当减小间隔时间,增加密度,既降低了误差又为 特殊情况下风向变化过程的判断提供依据。同时,更高的 计算密度可以反映出小尺度的变化,凸显风的垂直变化特 征精度,提高高空风观测垂直分辨率,并根据相关标准选 取风特性层。
2020/10/16
改进的方法:目前,先进的设备已经可以实现自动 跟踪,每秒采样一次球坐标数据,为提高高空风探 测提供大量、可信的数据。改变现行的高空风的算 法能够更充分地利用这些数据。
1)直接计算求取各规定层次风的数据。首先计算出标准等 压面或规定高度层等位置的时间,再根据此时间分辨率的 要求,以高度的时间为中心,直接计算求取各规定层次的 风向、风速值。此方法得出的规定层次风数据相对精确, 但在风的特性层选取等方面不能被应用.
Vi
Li 60(t i ti1)
注意:前提是不考虑气球的上升运动时,气球在空间的水平运动时沿
等位势面运动的。
三、地心坐标系与站心坐标系的坐标转换
地心转换站心:
X
' i
( X i
X0)cos
sin
(Yi
Y0 ) sin
sin
(Zi
Z0 ) cos
Yi' (Xi X0)sin (Yi Y0) cos
θi+1
Ci+1(Xi+1,Yi+1)
Li+1
y(E)
当气球采用升速W时,气球的水平距离可表示为:
测量学中的坐标系和他们之间相互转换
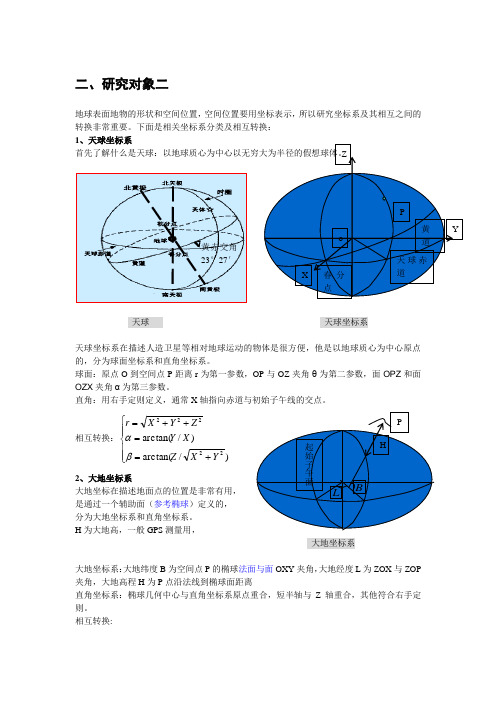
二、研究对象二地球表面地物的形状和空间位置,空间位置要用坐标表示,所以研究坐标系及其相互之间的转换非常重要。
下面是相关坐标系分类及相互转换: 1、天球坐标系首先了解什么是天球:以地球质心为中心以无穷大为半径的假想球体。
天球 天球坐标系天球坐标系在描述人造卫星等相对地球运动的物体是很方便,他是以地球质心为中心原点的,分为球面坐标系和直角坐标系。
球面:原点O 到空间点P 距离r 为第一参数,OP 与OZ 夹角θ为第二参数,面OPZ 和面OZX 夹角α为第三参数。
直角:用右手定则定义,通常X 轴指向赤道与初始子午线的交点。
相互转换:⎪⎪⎩⎪⎪⎨⎧+==++=)/arctan()/arctan(22222Y X Z X Y Z Y X r βα 2、大地坐标系大地坐标在描述地面点的位置是非常有用, 是通过一个辅助面(参考椭球)定义的, 分为大地坐标系和直角坐标系。
H 为大地高,一般GPS 测量用,大地坐标系大地坐标系:大地纬度B 为空间点P 的椭球法面与面OXY 夹角,大地经度L 为ZOX 与ZOP 夹角,大地高程H 为P 点沿法线到椭球面距离直角坐标系:椭球几何中心与直角坐标系原点重合,短半轴与Z 轴重合,其他符合右手定则。
相互转换:黄赤交角23°27′X YZ oP春分点黄道 天球赤道 起始子午面L B PH[]⎪⎩⎪⎨⎧+=+=-=+-=L B H N X L B H N Y B e a N B H e N Z cos cos )(sin cos )(e ,2sin 21/ sin )21(为第一扁率卯酉全曲率半径,其中3、惯性坐标系(CIS )与协议天球坐标系① 惯性坐标系(CIS ):在空间不动或做匀速直线运动的坐标系.② 协议天球坐标系:以某一约定时刻t0作为参考历元,把该时刻对应的瞬时自转轴经岁差和章动改正后作为Z 轴,以对应的春分点为X 轴的指向点,以XOZ 的垂直方向为Y 轴方向建立的天球坐标系。
地心地固坐标系(ECEF)与站心坐标系(ENU)的转换

地⼼地固坐标系(ECEF)与站⼼坐标系(ENU)的转换⽬录1. 概述我在这篇⽂章中已经论述了地⼼坐标系的概念。
我们知道,基于地⼼坐标系的坐标都是很⼤的值,这样的值是不太⽅便进⾏空间计算的,所以很多时候可以选取⼀个站⼼点,将这个很⼤的值变换成⼀个较⼩的值。
以图形学的观点来看,地⼼坐标可以看作是世界坐标,站⼼坐标可以看作局部坐标。
站⼼坐标系以⼀个站⼼点为坐标原点,当把坐标系定义为X轴指东、Y轴指北,Z轴指天,就是ENU(东北天)站⼼坐标系。
这样,从地⼼地固坐标系转换成的站⼼坐标系,就会成为⼀个符合常⼈对地理位置认知的局部坐标系。
同时,只要站⼼点位置选的合理(通常可选取地理表达区域的中⼼点),表达的地理坐标都会是很⼩的值,⾮常便于空间计算。
注意站⼼天向(法向量)与⾚道⾯相交不⼀定会经过球⼼2. 原理令选取的站⼼点为P,其⼤地经纬度坐标为(B_p,L_p,H_p),对应的地⼼地固坐标系为(X_p,Y_p,Z_p)。
地⼼地固坐标系简称为ECEF,站⼼坐标系简称为ENU。
2.1. 平移通过第⼀节的图可以看出,ENU要转换到ECEF,⼀个很明显的图形操作是平移变换,将站⼼移动到地⼼。
根据站⼼点P在地⼼坐标系下的坐标(X_p,Y_p,Z_p),可以很容易推出ENU转到ECEF的平移矩阵:T = \begin{bmatrix} 1&0&0&X_p\\ 0&1&0&Y_p\\ 0&0&1&Z_p\\ 0&0&0&1\\ \end{bmatrix}反推之,ECEF转换到ENU的平移矩阵就是T的逆矩阵:T^{-1} = \begin{bmatrix} 1&0&0&-X_p\\ 0&1&0&-Y_p\\ 0&0&1&-Z_p\\ 0&0&0&1\\ \end{bmatrix}2.2. 旋转另外⼀个需要进⾏的图形变换是旋转变换,其旋转变换矩阵根据P点所在的经度L和纬度B确定。
大地站心坐标系转换

cosBK cosLK x cosBK sin LK y
sin BK z
2.4.4 两个空间大地直角坐标系间的转换模型
4、卫星网与地面网之间的转换 卫星网精度高, 地面网平面坐标与高程点不重合。
2.4.5 大地坐标的微分公式
根据大地坐标与三维空间直角坐标间的微分公式:
dBi dLi dHi
上式同样可以简化为求解转换参数的形式如下:
X i X 0 X i 0 Yi Y0 Yi Zik Zi Z0 Zi YiK
ZiK 0
X iK
YiK X X iK X iK Y YiK
0 Z ZiK
其中,
X iK X i X K YiK Yi YK ZiK Zi ZK
Z Y X i X K X i X K
Yi Y0 YK Yi YK Z 0 X Yi YK Yi YK
Zi Z0 ZK Zi ZK Y X 0 Zi ZK Zi ZK
2.4.4 两个空间大地直角坐标系间的转换模型
(2). 绕y轴900+B;
(3). 绕z轴旋转-L。
xz
L
y
P0 B0 , L0
O
B
Y
KP
Q
X
2.4.3 站心地平坐标系及其应用
将站心系坐标轴变换到与三维空间 直角坐标轴指向一致时的旋转矩阵为:
Z
xz
1 0 0
R
R z
L0 R y
900
B0
0
1
0
0 0 1
sin B0 cosL0 sin B0 sin L0
(2). 绕站心系坐标轴的旋转向量有特殊意义
x
y
z 相当于平面控制网间的旋转角。
测绘各种坐标系

测绘各种坐标系1 大地坐标系:设P点的子午面NPS与起始子午面NGS所构成的二面角L,即P点的大地经度;P点的法线Pn与赤道的夹角B,即P点的大地纬度;从观测点沿椭球的法线方向大到椭球面的距离,即大地高H。
注意:内业的基准线是法线,基准面是参考椭球面;外业的基准线是铅垂线,基准面是大地水准面,此时高程为正高。
以似大地水准面为参照面的高程系统为正常高。
2 空间直角坐标系:空间任意点的坐标用(X,Y,Z)表示,坐标原点位于总地球质心或参考椭球中心,Z轴与地球平均自转轴相重合,即指向某一时刻的平均北极点,X轴指向平均自转轴与平均格林尼治天文台所决定的子午面与赤道面的交点Ge而Y轴与XOZ平面垂直,且指向东为正。
坐标参考系统:分为天球坐标系和地球坐标系。
天球坐标系用于研究天体和人造卫星的定位与运动。
地球坐标系用于研究地球上物体的定位与运动,是以旋转椭球为参照体建立的坐标系统,分为大地坐标系和空间直角坐标系。
即地固坐标系3 天球直角坐标系:原点位于地球质心O,z轴指向天球北极Pn,x轴指向春分点r,y轴垂直于xOz平面,从而建立起来的坐标系即为天球直角坐标系;天球直角坐标也可转化为赤经(a)、赤纬()、向径(d)构成的球面坐标。
春分点和天球赤道面,是建立天球坐标系的重要基准点和基准面。
4 惯性坐标系:是指在空间固定不动或做匀速直线运动的坐标系。
一般很难建立,通常约定建立近似的惯性坐标系,即协议惯性坐标系。
5 协议天球坐标系:由于地球的旋转轴是不断变化的,通常约定某一时刻t作为参考历元,把该时刻对应的瞬时自转轴经岁差和章动改正后的指向作为z轴,以对应的春分点为x 轴的指向点,以xoz的垂直方向为y轴建立的球坐标系协议天球坐标系与瞬时真天球坐标系的差异是由地球旋转轴的岁差和章动引起的,两者之间有其转换关系。
6 瞬时真天球坐标系:是一时刻t的瞬时北天极和真春分点为参考建立的天球坐标系。
它与瞬时平天球坐标系的差异主要是地球自转轴的章动造成的。
常用坐标系介绍及变换

➢ GPS定位采用坐标系: 在GPS定位测量中,采在空用间的两位类置和坐方标向应系保持,不变,
或仅作匀速直线运动。
即天球坐标系与地球坐标系,两坐标系的坐 标原点均在地球的质心,而坐标轴指向不 同。天球坐标系是一种惯性坐标系,其坐标 原点及各坐标轴指向在空间保持不变,用于 描述卫星运行位置和状态。地球坐标系随同 地球自转,可看作固定在地球上的坐标系, 用于描述地面观测站的位置。
长半轴: (m) 扁率: 1:298.3
BJ54可归结为: a.属参心大地坐标系; b.采用克拉索夫斯基椭球的两个几何参数; c. 大地原点在原苏联的普尔科沃; d.采用多点定位法进行椭球定位; e.高程基准为 1956年青岛验潮站求出的黄海平
均海水面。
f.高程异常以原苏联 1955年大地水准面重新平 差结果为起算数据。按我国天文水准路线推算而得 。
➢ 为什么选用空间直角坐标系? 任一点的空 间位置可由该点在三个坐标
面的投影(X,Y,Z)唯一地确定,通过坐 标平移、旋转和尺度转换,可以将一个点的 位置方便的从一个坐标系转换至另一个坐标 系。与某一空间直角坐标系所相应的大地坐 标系(B,L,H),只是坐标表现形式不 同,实质上是完全等价的,两者之间可相互 转化。
几何定义:
ZWGS84
原点—在地球质心
BIH定义的
Z轴—指向 BIH 1984.0 零子午圈
定义的协议地球 (1984.0)
P
N
CTP
赤道
平面
(CTP)方向。
X轴—指向BIH 1984.0
O
的零子午面和CTP 赤道的交点。 Y轴—与Z、X轴构成右
手坐标系。
E
YWGS8
4
XWGS84
坐标系转换
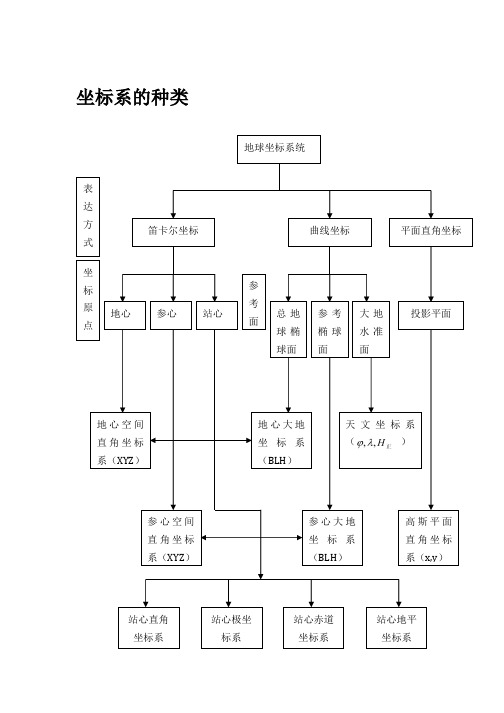
坐标系的种类坐标转换的意义不同的导航定位系统使用不同的空间坐标系,即通过它们的卫星星历和历书所提供的卫星轨道信息所默认采用的空间坐标系。
当利用单一GNSS的定位、定速结果自然也表达在此GNSS空间坐标系中。
但是在利用多个GNSS联合定位、定速应用中,我们原则上应该首先将所有不同的GNSS卫星的轨道信息都变换到统一空间坐标系中,然后所进行的实质性定位、定速解算才具有正确的物理意义。
一般而言,我们从伪距测量的得到的位置信息为三维坐标,但是为方便使用,我们通常将其转换为我们更为熟悉的大地坐标系,它通过给出一点的大地纬度、大地经度和大地高度,更加直观地告诉我们该点在地球中的位置。
各系统所使用坐标系1.GPSGPS采用了由美国国防部(DoD)下属的国防制图局(DMA)制定的世界大地坐标系(WGS), 经过多次的修改和完善,最终确定了将1984年版的大地坐标系(WGS-84)作为标准。
2.GalileoGalileo系统所采用的空间坐标系基于国际地球参考框架(ITRF)。
ITRF是由国际地球自转(及参考服务系统)服务(IERS)负责建立、维持的一个地心直角坐标系,也是国际公认的最为精确的全球参考框架。
而Galileo系统所采用的是2005版的国际地球参考框架。
3.GLONASSGLONASS原先采用前苏联的1985地心坐标系SGS-85,后再1994年改为SGS-90,前苏联解体之后SGS-90逐渐改名为PZ-90,和GPS的WGS-84一样,PZ-90也是一个自成一体的地心地固直角坐标系。
4.BeiDou我国的BeiDou卫星系统最先采用1954北京坐标系和1985高程基准的组合,但此坐标系统并不能满足导航卫星厘米级的定位精度,后来改为2000国家大地坐标系(CGCS2000)。
不同的定位系统坐标系不同,对于GPS 的WGS-84和Galileo 的ITRF ,他们的差异非常细微,在10cm 范围内,但是WGS-84与GLONASS 的PZ-90和BeiDou 的CGCS2000之间的差异却不能忽略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X
Zi Z0
Y X 1 Zi
2.4.4 两个空间大地直角坐标系间的转换模型
略去尺度参数和旋转参数的乘积项,上式可进一 步简化为:
X i X 0 X i 0 Z Y X i X i Yi Y0 Yi Z 0 X Yi Yi Zi Z0 Zi Y X 0 Zi Zi
3、空间直角坐标系与站心地平直角坐标系的旋转矢量 之间的关系
若x、y和z为空间坐标系的旋转矢量, x、 y和z为站心坐标系的旋转矢量。顾及旋转矢量是 平移不变量,旋转关系与坐标矢量相同。
X sin B0 cosL0 Y sin B0 sin L0 Z cosB0
sin L0 c os L0
sin B0 cosL0 sin B0 sin L0
cosB0
sin L0 c os L0
0
cosB0 cosL0 x cosB0 sin L0 y
sin B0 z
2.4.3 站心地平坐标系及其应用
由上式得,空间直角坐标系到站心系的变换公式为:
x
X X P0 sin B0 cos L0
X 0 X i 0 Zi Yi X X i Y0 Yi Zi 0 X i Y Yi
Z0 Zi Yi X i 0 Y Zi
上式第二式常用于转换参数未知时,利用同 名点在两个坐标系中的坐标计算转换参数。
2.4.4 两个空间大地直角坐标系间的转换模型
(2). 绕站心系坐标轴的旋转向量有特殊意义
x
y
z 相当于平面控制网间的旋转角。
2.4.3 站心地平坐标系及其应用
(4). 计算卫星的高度角和方位角 卫星Q的方位角和高度角可用其站心坐标xQ、yQ计算。
AQ
tan
1
yQ xQ
Q
tan
1
xQ
zQ cos AQ
yQ
sin
AQ
2.4.4 两个空间大地直角坐标系间的转换模型
(2). 绕y轴900+B;
(3). 绕z轴旋转-L。
xz
L
y
P0 B0 , L0
O
B
Y
KP
Q
X
2.4.3 站心地平坐标系及其应用
将站心系坐标轴变换到与三维空间 直角坐标轴指向一致时的旋转矩阵为:
Z
xz
1 0 0
R
R z
L0 R y
900
B0
0
1
0
0 0 1
sin B0 cosL0 sin B0 sin L0
x
cos
A
y
sin
Asin
Z
z
cos
Z
2.4.3 站心地平坐标系及其应用
也可以用以下公式计算:
A Z
tan
tan
1
1
x2
y
x
y2
z
D
x2 y2 z2
公式中的天顶距和方位角都归算到以法线为基准。测 量时以垂线为基准的,需要作垂线偏差改正。改正公式下 面将讲到。
2.4.3 站心地平坐标系及其应用
1、Bursa - Wolf 模型
转换参数包括三个平移参数、三个旋转参数与一
个尺度参数。
Z
Z
Xi Yi
X0 Y0
1
R
X
,
Y
,
Z
X i Yi
Zi Z0
Zi
O
Y
R为前面所述的旋转矩阵。当旋 X
转角为小角度时,上式可简化为:
O
Y
Xi Yi
X0 Y0
1
1
Z
Z
1
Y X i X Yi
X
0
Z
j
Zi
Z j
Zi
X j X i 0
Yj Yi Z j Zi
Z
j
Zi
Y j
Yi
Zj Zi
0
X j X i
Yj Yi X X j X i X j X i Y Yj Yi
0
cosB0 cosL0 x cosB0 sin L0 y
sin B0 z
2.4.3 站心地平坐标系及其应用
4、站心地平直角坐标系的应用 (1). 计算基线向量的大地方位角
A
tan1
y x
tan1
sin
B0
c os L0 Y
cosL0X
sin L0X
sin L0Y
cos
B0Z
其中,B0,L0为基线始端的纬度和经度。
定义:由站心系原点到点的空间距离、方位角和天顶距
为坐标变量确定三维点位,称为站心极坐标系。
x D sin Z cos A y D sin Z sin A z D cosZ
z
x
P
Z
D
由上式,得:
A
A Z
tan1y x tan1x cos A y sin A z
o
y
D
cosB0
sin L0 c os L0
0
cosB0 cosL0 cosB0 sin L0 X
sin B0
L
y
P0 B0 , L0
O
B
Y
KP
Q
顾及,站心系原点在空间坐标系中的坐标为:
X P0 YP0 Z P0
N0 N0
N0
H0 cos B0 H0 cos B0
1 e2 H0
cos L0 sin L0 sin B0
2.4.3 站心地平坐标系及其应用
则,站心系坐标到空间直角坐标系的变换公式为:
X Y Z
X P0 YP0 Z P0
R
x y z
N0 N0
N0
H0 cosB0 H0 cosB0
1 e2 H0
c os L0 sin L0 sin B0
上式应用于Pj,并与上式相减,得Pi与Pj两点 坐标差的坐标变换模型如下:
X j X i X j X i 0 Z Y X j X i X j X i
Yj Yi Yj Yi Z 0 X Yj Yi Yj Yi
Zj
Zi
Z jBiblioteka ZiY§2.4 空间大地直角坐标系及其转换模型
2.4.3 站心地平坐标系及其应用
1、站心地平直角坐标系与空间大地直角坐标系的转换关系
定义:站心点的法线为z轴,在地平面上以子午线方向为x轴,
y与x、z轴正交,指向东为正。
Z
将站心坐标轴 xyz 变 换成与空间坐标系的指向 一致,需要如下几步:
(1). z 坐标轴反向;
y RT z
Y YP0 Z Z P0
sin L0 cos B0 cos L0
sin B0 sin L0 cos L0
cos B0 sin L0
cos B0 X X P0
0 sin B0
Y YP0 Z Z P0
2.4.3 站心地平坐标系及其应用
2、站心极坐标系与站心地平直角坐标系的关系
