参心大地坐标与参心空间直角坐标转换参心大地坐标与参心空间直角坐标转换
测量中的常用坐标系及坐标转换概述

三、坐标转换
5、高斯投影的邻带换算
应用高斯投影正反算公式间接进行换带计算:实质是把椭球 面上的大地坐标作为过渡坐标,首先把某投影带(比如I带)内 有关点的平面坐标(x,y) I ,利用高斯投影反算公式换算成椭球 面上的大地坐标(B ,ι),进而得到L=L10+ ι,然后再由大地坐 标(B ,ι),利用投影正算公式换算成相邻带第Ⅱ带的平面坐标 (x,y) Ⅱ,在这一步计算中,要根据第Ⅱ带的中央子午线L20来 计算经差ι,此时ι=L- L20
大地高H:某点沿投影方向到基准面(参考椭球面)的距离。
在大地坐标系中,某点的位置用(B , L,H)来表示。
二、测量中的各种坐标系
2、空间直角坐标系
定义:以椭球体中心为原点,起始子午面与赤道面交线为X轴,在赤 道面上与X轴正交的方向为Y轴,椭球体的旋转轴为Z轴。
在空间直角坐标系中,某点的位置用(X,Y,Z)来表示。
二、测量中的各种坐标系
3、平面直角坐标系
在小区域进行测量工作若采用大地坐标来表示地面点位置是不方便的, 通常采用平面直角坐标系。 测量工作以x轴为纵轴,以y轴为横轴 投影坐标:为了建立各种比例尺地形图的控制及工程测量控制,一般应 将椭球面上各点的大地坐标按照一定的规律投影到平面上,并以相应的 平面直角坐标表示。
三、坐标转换
3、大地坐标同空间直角坐标的变换
X N cos B cos L Y N cos B sin L Z N (1 e 2 ) sin B
三、坐标转换
4、大地坐标与高斯平面坐标的变换
将大地坐标转换为高斯平面坐标,按照高斯投影正算公式 进行。
高斯投影正算公式:
x X 0 0.5 N sin B cos B l 2 y N cos B l 1 / 6 N cos3 B l 3 (1 t 2 2 )
坐标系之间的换算

XT
Z
P
Z
O X
X
Y Y
YT
R( ) R( Z )R(Y )R( X )
cosY cos Z cosY sin Z
sinY
cos X sin Z sin X sinY cos Z cos X cos Z sin X sinY sin Z
sin X cosY
sin X sin Z cos X sinY cos Z
Zi
T
Z0 Zi
Yi X i
0 Z Zi
(此即用于两空间直角坐标系相互变换的布尔莎七参数公式)
若上式中X=Y=0,Z≠0,则上式为五参数转换模型。若再有Z=0,则上式为 四参数转换模型。若尺度比参数亦为零,则得三参数转换模型
X i X0 X i
Yi Y0 Yi
A1C
da d
A1
X 0 Y0 Z0
A1dKB
A1QB
A1C
da d
上式中
X ( N H )cos B cos L
B Y ( N H )cos B sin L
Z [N (1 e2 ) H ]sin B
N a 1 e2 sin2 B
当根据多个公共点按最小二乘法求解转换参数时,对每个点有观测方程
X 0 Y0
XTi X i 1 0 0 X i
0
Zi
Yi
Z
0
YTi ZTi
Yi Zi
0 0
1 0
0 1
Yi Zi
Zi Yi
0 Xi
X i d K
0
X
设
Y Z
X0 Y0
XTi X i
VX BYˆ LX
测量学中的坐标系和他们之间相互转换
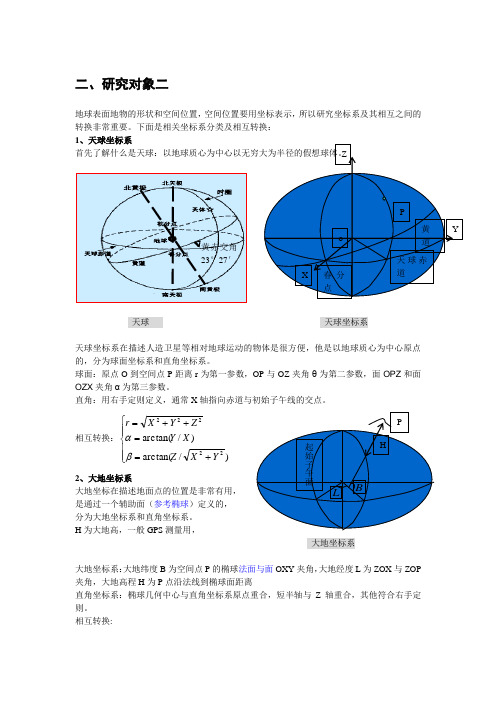
二、研究对象二地球表面地物的形状和空间位置,空间位置要用坐标表示,所以研究坐标系及其相互之间的转换非常重要。
下面是相关坐标系分类及相互转换: 1、天球坐标系首先了解什么是天球:以地球质心为中心以无穷大为半径的假想球体。
天球 天球坐标系天球坐标系在描述人造卫星等相对地球运动的物体是很方便,他是以地球质心为中心原点的,分为球面坐标系和直角坐标系。
球面:原点O 到空间点P 距离r 为第一参数,OP 与OZ 夹角θ为第二参数,面OPZ 和面OZX 夹角α为第三参数。
直角:用右手定则定义,通常X 轴指向赤道与初始子午线的交点。
相互转换:⎪⎪⎩⎪⎪⎨⎧+==++=)/arctan()/arctan(22222Y X Z X Y Z Y X r βα 2、大地坐标系大地坐标在描述地面点的位置是非常有用, 是通过一个辅助面(参考椭球)定义的, 分为大地坐标系和直角坐标系。
H 为大地高,一般GPS 测量用,大地坐标系大地坐标系:大地纬度B 为空间点P 的椭球法面与面OXY 夹角,大地经度L 为ZOX 与ZOP 夹角,大地高程H 为P 点沿法线到椭球面距离直角坐标系:椭球几何中心与直角坐标系原点重合,短半轴与Z 轴重合,其他符合右手定则。
相互转换:黄赤交角23°27′X YZ oP春分点黄道 天球赤道 起始子午面L B PH[]⎪⎩⎪⎨⎧+=+=-=+-=L B H N X L B H N Y B e a N B H e N Z cos cos )(sin cos )(e ,2sin 21/ sin )21(为第一扁率卯酉全曲率半径,其中3、惯性坐标系(CIS )与协议天球坐标系① 惯性坐标系(CIS ):在空间不动或做匀速直线运动的坐标系.② 协议天球坐标系:以某一约定时刻t0作为参考历元,把该时刻对应的瞬时自转轴经岁差和章动改正后作为Z 轴,以对应的春分点为X 轴的指向点,以XOZ 的垂直方向为Y 轴方向建立的天球坐标系。
空间直角坐标系与空间大地坐标系的相互转换及其C++源程序

空间直角坐标系与空间大地坐标系的相互转换1.空间直角坐标系/笛卡尔坐标系坐标轴相互正交的坐标系被称作笛卡尔坐标系。
三维笛卡尔坐标系也被称为空间直角坐标系。
在空间直角坐标系下,点的坐标可以用该点所对应的矢径在三个坐标轴上的投影长度来表示,只有确定了原地、三个坐标轴的指向和尺度,就定义了一个在三维空间描述点的位置的空间直角坐标系。
以椭球体中心O为原点,起始子午面与赤道面交线为X轴,在赤道面上与X轴正交的方向为Y轴,椭球体的旋转轴为Z轴构成右手坐标系O.XYZ,在该坐标系中,P点的位置用X,Y,Z表示。
在测量应用中,常将地球空间直角坐标系的坐标原点选在地球质心(地心坐标系)或参考椭球中心(参心坐标系),z轴指向地球北极,x轴指向起始子午面与地球赤道的交点,y轴垂直于XOZ面并构成右手坐标系。
空间直角坐标系2.空间大地坐标系由于空间直角坐标无法明确反映出点与地球之间的空间关系,为了解决这一问题,在测量中引入了大地基准,并据此定义了大地坐标系。
大地基准指的是用于定义地球参考椭球的一系列参数,包括如下常量:2.1椭球的大小和形状2.2椭球的短半轴的指向:通常与地球的平自转轴平息。
2.3椭球中心的位置:根据需要确定。
若为地心椭球,则其中心位于地球质心。
2.4本初子午线:通过固定平极和经度原点的天文子午线,通常为格林尼治子午线。
以大地基准为基础建立的坐标系被称为大地坐标系。
由于大地基准又以参考椭球为基准,因此,大地坐标系又被称为椭球坐标系。
大地坐标系是参心坐标系,其坐标原点位于参考椭球中心,以参考椭球面为基准面,用大地经度L、纬度B 和大地高H表示地面点位置。
过地面点P的子午面与起始子午面间的夹角叫P 点的大地经度。
由起始子午面起算,向东为正,叫东经(0°~180°),向西为负,叫西经(0°~-180°)。
过P点的椭球法线与赤道面的夹角叫P点的大地纬度。
由赤道面起算,向北为正,叫北纬(0°~90°),向南为负,叫南纬(0°~-90°)。
大地、地心空间直角和球面三种坐标的转换

第一章大地坐标第一节大地坐标系统科技名词定义中文名称:大地坐标系英文名称:geodetic coordinate system定义:以参考椭球中心为原点、起始子午面和赤道面为基准面的地球坐标系。
应用学科:测绘学(一级学科);大地测量学(二级学科)大地坐标系(geodetic coordinate system)是大地测量中以参考椭球面为基准面建立起来的坐标系。
地面点的位置用大地经度、大地纬度和大地高度表示。
大地坐标系的确立包括选择一个椭球、对椭球进行定位和确定大地起算数据。
一个形状、大小和定位、定向都已确定的地球椭球叫参考椭球。
参考椭球一旦确定,则标志着大地坐标系已经建立。
大地坐标系亦称为地理坐标系。
大地坐标系是用来表述地球上点的位置的一种地区坐标系统。
它采用一个十分近似于地球自然形状的参考椭球作为描述和推算地面点位置和相互关系的基准面。
一个大地坐标系统必须明确定义其三个坐标轴的方向和其中心的位置。
通常人们用旋转椭球的短轴与某一规定的起始子午面分别平行干地球某时刻的平均自转轴和相应的真起始子午面来确定坐标轴的方向。
若使参考椭球中心与地球平均质心重合,则定义和建立了地心大地坐标系。
它是航天与远程武器和空间科学中各种定位测控测轨的依据。
若椭球表面与一个或几个国家的局部大地水准面吻合最好,则建立了一个国家或区域的局部大地坐标系。
大地坐标系中点的位置是以其大地坐标表示的,大地坐标均以椭球面的法线来定义。
其中,过某点的椭球面法线与椭球赤道面的交角为大地纬度;包含该法线和大地子午面与起始大地子午面的二面角为该点的大地经度;沿法线至椭球面的距离为该点的大地高。
大地纬度、大地经度和大地高分别用大写英文字母B、L、H表示。
大地坐标系是以地球椭球赤道面和大地起始子午面为起算面并依地球椭球面为参考面而建立的地球椭球面坐标系。
它是大地测量的基本坐标系,其大地经度L、大地纬度B和大地高H为此坐标系的3个坐标分量。
它包括地心大地坐标系和参心大地坐标系。
坐标转换之计算公式+7参+四参模型

坐标转换之计算公式一、参心大地坐标与参心空间直角坐标转换1名词解释:A :参心空间直角坐标系:a) 以参心0为坐标原点;b) Z 轴与参考椭球的短轴(旋转轴)相重合;c) X 轴与起始子午面和赤道的交线重合;d) Y 轴在赤道面上与X 轴垂直,构成右手直角坐标系0-XYZ ;e) 地面点P 的点位用(X ,Y ,Z )表示;B :参心大地坐标系:a) 以参考椭球的中心为坐标原点,椭球的短轴与参考椭球旋转轴重合;b) 大地纬度B :以过地面点的椭球法线与椭球赤道面的夹角为大地纬度B ;c) 大地经度L :以过地面点的椭球子午面与起始子午面之间的夹角为大地经度L ;d) 大地高H :地面点沿椭球法线至椭球面的距离为大地高H ;e) 地面点的点位用(B ,L ,H )表示。
2 参心大地坐标转换为参心空间直角坐标:⎪⎭⎪⎬⎫+-=+=+=B H e N Z L B H N Y L B H N X sin *])1(*[sin *cos *)(cos *cos *)(2公式中,N 为椭球面卯酉圈的曲率半径,e 为椭球的第一偏心率,a 、b 椭球的长短半径,f 椭球扁率,W 为第一辅助系数ab a e 22-= 或 f f e 1*2-= W a N BW e =-=22sin *1(3 参心空间直角坐标转换参心大地坐标[]N BY X H H e N Y X H N Z B XY L -+=+-++==cos ))1(**)()(*arctan()arctan(22222 二 高斯投影及高斯直角坐标系1、高斯投影概述高斯-克吕格投影的条件:1. 是正形投影;2. 中央子午线不变形高斯投影的性质:1. 投影后角度不变;2. 长度比与点位有关,与方向无关;3. 离中央子午线越远变形越大为控制投影后的长度变形,采用分带投影的方法。
常用3度带或6度带分带,城市或工程控制网坐标可采用不按3度带中央子午线的任意带。
2、高斯投影正算公式:522242532236425442232)5814185(cos 120)1(cos 6cos )5861(cos sin 720 495(cos sin 24cos sin 2l t t t B N l t B N Bl N y l t t B B N l t B B N Bl B N X x ηηηηη-++-++-+=+-+++-++=)3、高斯投影反算公式:()()()⎥⎥⎦⎤⎪⎪⎭⎫ ⎝⎛+++⎪⎪⎭⎫ ⎝⎛⎢⎣⎡-++-⎪⎪⎭⎫ ⎝⎛-=⎥⎥⎥⎥⎦⎤⎪⎪⎭⎫ ⎝⎛+++++⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++-⎪⎪⎭⎫ ⎝⎛=442222224222422224590613601 9351211286242851201 )21(611cos 1f f f f f f f f f f f f f f f f f f f f f f f N y t t N y t t N y y M t B B N y t t t N y t N y B l ηηηηη四参数模型:。
【干货】两种七参数坐标转换方法

目前国内所用GNSS (Global Navigation Satellite System)即全球卫星导航系统,已经发展到多星,尤其随着北斗导航系统的逐步完善,正在向CGCS2000椭球过渡,但还是以WGS-84 坐标系统为主流,即仍以美国GPS为主,所发布的星历参数也是基于此坐标系统。
WGS-84 坐标系统(World Geodetic System-84,世界大地坐标系-84) 的坐标原点位于地球的质心,Z 轴指向BIH1984.0定义的协议地球极方向,X 轴指向BIH1984.0的启始子午面和赤道的交点,Y 轴与X轴和Z 轴构成右手系。
WGS-84 系所采用椭球参数为:长半轴6378137;扁率1:298.25 7223563。
而我国目前广泛采用的大地测量坐标系有3种:①北京1954 坐标系。
该坐标系采用的参考椭球是克拉索夫斯基椭球,该椭球的主要参数为:长半轴6378245;扁率1:298.3。
②1980 年国家大地坐标系。
该坐标系是参心坐标系,采用地球椭球基本参数为1975 年国际大地测量与地球物理联合会第十六届大会推荐的数据,大地原点设在我国中部的陕西省泾阳县永乐镇,也称西安80 坐标系。
长半轴6378140±5;扁率1:298.257。
③2000 中国大地坐标系。
该坐标系是地心坐标系,与WGS-84坐标类似。
原点在包括海洋和大气的整个地球的质量中心;定向在1984.0时与BIH(国际时间局)。
长半轴6378137.0;扁率1:298.257 222 101。
各坐标系之间的转换是工作中的经常遇到的问题,主要的转换方法有三参数、四参数和七参数法,而这三种方法中,七参数是一种空间直角坐标系的转换模型,是基于椭球间的三维转换,精度最高。
如果用七参数法来实现WGS84 坐标系与1980 年国家大地坐标系的转换,求解前必须确定控制网中各点对的距离。
如果两点间距离超过15 公里,必须考虑曲面因素即两种不同坐标系的椭球参数,避免因椭球的差异,导致转换后所得坐标残差过大,精度过低,为了保证精度必须采用七参数法。
弹道导弹常用坐标系及其转换

弹道导弹常用坐标系及其转换马清华, 王明海(第二炮兵工程学院, 陕西 西安 710025)摘 要: 将弹道导弹常用坐标及其相关转换分成几类, 给出了各种坐标转换算法, 分析了坐标选择及转换原则与思路, 并 利用 v i sua l c + + 等面向对象语言形成了坐标转换动态链接库, 实践表明该方式可大大缩短各种目的的科研开发周期。
关键词: 弹道导弹; 坐标转换; 方向余弦; DL LComm on Coord i na t e an d Con v er s i on of Ba ll ist i c M iss ileM A Q i n g 2h u a ,W A N G M i n g 2h a i(T h e S econd A r t i l l e r y E n g in ee r i n g C o l l eg e , X i ’an 710025, C h in a )A bstra c t : Comm o n coo rd i n a t e an d co n v e r s i o n o f b a l lis t i c m is s ile a re c l a s s i f i ed, coo rd i n a t e co n v e r s i o na r ithm e t i c a reb ro u g h t o u t , coo rd i n a t e se l ec t i o n and co n ve r s i o n p r i n c i p le an d tho u g h t a r e an a l yzed , co n v e r s i o n DL L a re g i ven b y v i su a l c+ +, sc i en c e re s ea rch a re sho r t en e d g r ea t l y i n p rac t i ce .Key word s : b a l lis t i c m iss ile , coo rd i n a t e co n v e r s i o n , d irec t i o n co s i n e , DL L年 地心坐标系统 (D X Z 78 或 1988 年的地心坐标系 (D X Z 88 ) , 另外还有非正式公布的地心坐标系 1995 年北京大地坐标系(B GS 1995) 和中国 2000 年大地坐标系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
参心大地坐标与参心空间直角坐标转换参心大地坐标与参心空间直角坐标转换参心大地坐标与参心空间直角坐标转换参心大地坐标与参心空间直角坐标转换1名词解释:A:参心空间直角坐标系:a) 以参心0为坐标原点;b) Z轴与参考椭球的短轴(旋转轴)相重合;
c) X轴与起始子午面和赤道的交线重合;d) Y轴在赤道面上与X轴垂直,构成右手直角坐标系0-XYZ;e) 地面点P的点位用(X,Y,Z)表示;B:参心大地坐标系:a) 以参考椭球的中心为坐标原点,椭球的短轴与参考椭球旋转轴重合;b) 大地纬度B:以过地面点的椭球法线与椭球赤道面的夹角为大地纬度B;c) 大地经度L:以过地面点的椭球子午面与起始子午面之间的夹角为大地经度L;d) 大地高H:地面点沿椭球法线至椭球面的距离为大地高H;e) 地面点的点位用(B,L,H)表示。
2 参心大地坐标转换为参心空间直角坐标:公式中,N为椭球面卯酉圈的曲率半径,e为椭球的第一偏心率,a、b 椭球的长短半径,f 椭球扁率,W为第一辅助系数 3 参心空间直角坐标转换参心大地坐标。
