七年级下册数学第三单元三角形测试题北师大版
北师大版七年级数学下册认识三角形专练
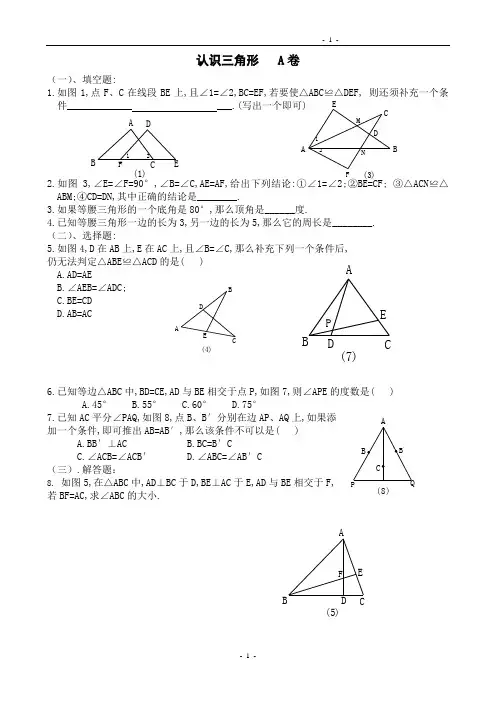
(8)(一)、填空题:1.如图1,点F 、C 在线段BE 上,且∠1=∠2,BC=EF,若要使△ABC ≌△DEF, 则还须补充一个条件_____________ ___.(写出一个即可)2.如图3,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF; ③△ACN ≌△ABM;④CD=DN,其中正确的结论是________.3.如果等腰三角形的一个底角是80°,那么顶角是______度.4.已知等腰三角形一边的长为3,另一边的长为5,那么它的周长是________. (二)、选择题:5.如图4,D 在AB 上,E 在AC 上,且∠B=∠C,那么补充下列一个条件后, 仍无法判定△ABE ≌△ACD 的是( )A.AD=AEB.∠AEB=∠ADC;C.BE=CDD.AB=AC6.已知等边△ABC 中,BD=CE,AD 与BE 相交于点P,如图7,则∠APE 的度数是( ) A.45° B.55° C.60° D.75°7.已知AC 平分∠PAQ,如图8,点B 、B ′分别在边AP 、AQ 上,如果添 加一个条件,即可推出AB=AB ′,那么该条件不可以是( ) A.BB ′⊥AC B.BC=B ′CC.∠ACB=∠ACB ′D.∠ABC=∠AB ′C(三).解答题:8. 如图5,在△ABC 中,AD ⊥BC 于D,BE ⊥AC 于E,AD 与BE 相交于F, 若BF=AC,求∠ABC 的大小.(1)12E D B A (3)12E DCB A N M F (4)EDB A(7)ED C B A P (5)E DCBAFBDB21DBAC (一)、选择题1.在ABC中,∠A=∠B=13∠C,则此三角形是()A.锐角三角形 B.直角三角形C.钝角三角形D.等腰三角形2.已知:如图,Rt ABC中,∠ACB=900,DE过点C,且DE//AB,若∠ACD=550,则∠B的度数为 ( )A.350 B.450 C.300 D.5503.下列判断:(1)一个三角形的三个内角中最多有1个直角;(2)一个三角形的三个内角中至少有两个锐角;(3)一个三角形中至少有1个钝角其中正确的有()A.0个B.1个 C.2个D.3个4.若一个三角形的三条高的交点恰是三角形的一个顶点,则此三角形是()A.锐角三角形 B.直角三角形C.钝角三角形D.等腰三角形5.下列长度的三条线段能组成三角形的是()A.1cm 2cm 3cm B.6cm 2cm 3cm C 4cm 6cm 8cm D.5cm 12cm 6cm6.如图,已知AB//CD, ∠1=1000, ∠ECD=600 , 则∠E等于()A.300B.400C.500D.6007.一个三角形的两个内角分别是550和650,则下列角度不可能是这个三角形外角的是()A.1350 B.1250 C.1200 D.1150(二)、填空题:8.如图所示:AB//CD,∠A=450,∠C=290,则∠E=_____ .9.P为ABC中BC边的延长线上一点,且∠A=400,∠B=700,则∠ACP=___ __10.如果一个三角形的两边长分别是2cm和7cm,且第三边为奇数,则三角形的周长是___cm. 11.如果将长度为 a—2,a+5和a+2的三条线段首尾顺次相接要以得到的一个三角形,那么a的取值范围是_____.12.在活动课上,小红有两根长为4cm、8cm的小木棒,现打算拼一个等腰三角形,则小红应取的第三根小木棒的长度是____cm.13.如右图,∠A=600,∠B=800,则.∠2+∠1=_____.(三).解答题:14. 如图2,CD平分∠ACB,AE∥DC交BC的延长线于点E,若∠ACE=80°,求∠CAE的度数。
北师大版七年级下数学《全等三角形》单元测试(含答案)

全等三角形章节测试一、心一(每小 3 分,共36 分)1. 以下法正确的选项是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( )A.周相等的两个三角形全等B. 面相等的两个三角形全等C. 三个角相等的两个三角形全等D.三条相等的两个三角形全等2. 以下各段能成三角形的是⋯⋯⋯⋯⋯⋯⋯⋯( )A.3cm , 3cm, 6cmB.7cm,4cm,5cmC.3cm,4cm,8cmD.4.2cm,2.8cm,7cm3. 以下形中,与已知形全等的是⋯⋯⋯⋯⋯⋯⋯⋯( )第3题图(A) (B) (C) (D)4. 如,已知△ ABC≌△ CDE,此中 AB=CD,那么以下中, A不正确的选项是⋯⋯⋯⋯⋯⋯⋯⋯⋯( )EA.AC=CEB. ∠ BAC=∠ CDEC. ∠ ACB=∠ ECDD. ∠B=∠ D BC D第 4 题5. 以下条件中,不可以判断三角形全等的是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( )A. 三条相等B. 两和一角相等C. 两角和此中一角的相等D. 两角和它的相等6. 如,把形沿BC折,点 A 和点 D 重合,那么中共有全等三角形⋯⋯⋯⋯⋯⋯⋯( )A.1B.2 AC.3D.4B EC7.在△ ABC 和△ A′ B′C′中,已知 AB= A′ B′,∠ B=∠ B′要保△ ABC≌△ A′B′ C′,可充的条D件是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( )A. ∠ B+∠A=900B.AC= A ′ C′C.BC=B ′ C′D.∠ A+∠ A′ =9008.已知在△ ABC和△ A′ B′ C′中,AB= A′ B′,∠ B=∠ B′,充下边一个条件,不可以明△ ABC≌△ A′B′ C′的是⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( )A. BC=B ′ C′B. AC= A ′ C′C.∠ C=∠ C′D. ∠A=∠ A′9. 如,已知 AE=CF,BE=DF要.△ ABE≌△ CDF,需增添的一个条件是⋯⋯⋯( )A. ∠ BAC=∠ ACDB. ∠ ABE=∠ CDFC. ∠ DAC=∠ BCAD. ∠ AEB=∠ CFDD C A ADEA OAFA B A B C第 9 题 A 第 11题第 10题10. 如图 AD是△ ABC的角均分线, DE是△ ABD的高, EF 是△ ACD的高,则 ( )A. ∠ B=∠CB. ∠ EDB=∠ FDCC. ∠ ADE=∠ ADFD. ∠ ADB=∠ADC11. 如图 AC与 BD订交于点 O,已知 AB=CD,AD=BC,则图中全等三角形有 ( )A.1 对B.2 对C.3 对D.4 对12. 如图 ,D 、 E 分别是 AB,AC 上一点,若∠ B=∠ C,则在以下条件中, B没法判断△ ABE≌△ ACD是( ) DA.AD=AEB.AB=ACC.BE=CDD. ∠ AEB=∠ ADC A E C第 12 题二、专心填一填:(每题 3 分,共 24 分)C F13.如图,△ ABC≌△ DEF,点 B 和点 E, 点 A 和点 D 是对应极点,则 AB=,CB=,∠C=,∠ CAB=.14.若已知两个三角形有两条边对应,则要视这两个三角形全等,还需增添的条件能够是或. A DB E15. 如图已知 AC与 BD订交于点 O, AO=CO,BO=DO,则 AB=CD请说明原因 .第 13题A B解:在△ AOB和△ COD中AO CO(已知)(对顶角相等OBO DO(已知)D C∴△ AOB≌△ COD()第 15题A ∴ AB=DC()16. 如图,已知 AO=OB,OC=OD,AD和 BC订交于点 E, C则图中全等三角形有对 .EO BD第 16题17. 在△ ABC和△ DEF中 ,AB=4, ∠ A=350, ∠ B=700,DE=4, ∠ D= , ∠ E=700, 依据判断△ ABC≌△ DEF. A DAB=DC(已知)18.如图,在△ ABC和△ DEF中BC=DA(已知)() B 第 18 题 C ∴△ ABC≌△ DEF( ) A D19. 如图∠ B=∠ DEF,AB=DE,要证明△ ABC≌△ DEF,(1) 若以“ ASA”为依照,需增添的条件是;B EC C第 19题(2) 若以“ SAS ”为依照,需增添的条件是 .A20. 如图,△ ABC 中, AB=AC=13cm , AB 的垂直均分线交 A B 于 D,交 AC 于 E, 若△ EBC 的周长为 21cm,则 BC= cm.DEBC6 小题,共 40第 20 题三、耐心答一答: (此题有 分)21.( 此题 4 分 ) 已知∠α、∠β和线段a, 如图,用直尺和圆规作△ABC ,使∠ A=∠α ,∠ B=∠β ,BC=a.22.( 此题 6 分 ) 已知 AD 均分∠ CAB,且 DC ⊥ AC, DB ⊥ AB ,那么 AB 和 AC 相等吗?请说明原因 .CDA23.( 此题 6 分 ) 如图,已知 BD=CD ,∠ 1=∠ 2.说出△ ABD ≌△ ACD 的原因 .AB1 2BD C24.( 此题 8 分) 如图,已知 AB=DC , AD=BC,说出以下判断建立的原因: (1)△ ABC ≌△ CDA (2)∠ B=∠DADBC25.( 此题 8 分 ) 如图,把大小为4× 4 的正方形方格图形分别切割成两个全等图形,比如图①,请在以下图中,沿着须先画出四种不一样的分法,把4× 4 的正方形切割成两个全等图形图①26.( 此题画法1画法28 分 ) 如图,△ ABC中, AD垂直均分 BC,H是画法AD上一点,3 画法 4连结 BH,CH.(1)AD 均分∠ BAC吗?为何?(2)你能找出几堆相等的角?请把他么写出来(不需写原因)AH一、仔细选一选:(每题 3 分,共 36 分)题号 1 2 3 4 5 6 7 8 9 10B11 12 CD答案 D B B C D C C B D C D D二、专心填一填(每题 3 分,共 24 分)13.DE,FE, ∠ F, ∠ FED. 14.3 第三边相等,这两边的夹角相等15. ∠ AOB=∠ COD,SAS,全等三角形的对应边相等16.4 17.35 0, AAS 18.AC,CA, 公共边, SSS19. ∠ A=∠ D 20.8三、耐心答一答(此题有六小题,共40 分)21. 图略 22.AB=AC 23. 略24. 略25.画法 1 画法 2 画法 3 画法 426.(1) 由△ ADB≌△ ADC(SAS)得∠ BAD=∠ CAD (4)4 对,∠ BHD=∠ CHD, ∠ ABD=∠ ACD,∠HBD=∠ HCD, ∠ BDA=∠CDA。
北师大版七年级下册数学第三章三角形单元测试(附答案)

北师大版七年级下册数学第三章三角形单元测试(附答案)学校:___________姓名:___________班级:___________考号:___________一、选择题1.如图,在△ABC中,△ADE的周长为8,DH为AB的中垂线,EF垂直平分AC,则BC的长为()A、4B、6C、8D、162.下列几组数不能作为直角三角形三边长的是().A.8、15、17 B.7、24、25C.30、40、50 D.32、60、803.下列条件中,不能判定△ABC≌△A′B′C′的是()A.∠A=∠A′,∠C=∠C′,AC=A′C′B.∠A=∠A′, BC=B′C′,AB=A′B′C.∠A=∠A′=80O,∠B=60O,∠C=40O,AB=A′B′D.∠C=∠C′=90O, BC=B′C′,AB=A′B′4.到三角形各顶点距离相等的点是三角形三条()A、中线的交点B、角平分线的交点C、高线的交点D、三边垂直平分线的交点5.到△ABC的三个顶点距离相等的点是 ( )A.三条中线的交点B.三条角平分线的交点C.三条高线的交点D.三条边的垂直平分线的交点6.已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为()A.20o B.120o C.20o或120o D.36o7.如图,两个高度相等的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P的距离是()A.2cm B.43cm C.6cm D.8cm8.下列说法正确的是( )A 、全等三角形是指周长和面积都一样的三角形;B 、全等三角形的周长和面积都一样 ;C 、全等三角形是指形状相同的两个三角形;D 、全等三角形的边都相等9.高为3,底边长为8的等腰三角形腰长为 ( ).(A )3 (B )4 (C )5 (D )610.如图,△ABC 中,∠ACB=90°,BA 的垂直平分线交CB 边于D ,若AB=10,AC=5,则图中等于60°的角的个数为( )A 、2B 、3C 、4D 、5二、填空题11.如图:∠B=∠C=90°,E 是BC 的中点,DE 平分∠ADC,∠CED=35°,则∠EAB =12.如图所示的正方形网格中,网格线的交点称为格点.已知A 、B 是两格点,如果C 也是图中的格点,且使得ABC 为等腰三角形.....,则点C 的个数是 .13.三角形三条中位线围成的三角形的周长为19,则原三角形的周长为 。
北师大版七年级数学下册《判定三角形全等的四种思路》专题试题(附答案)

北师大版七年级数学下册专题训练系列(附解析专训3判定三角形全等的四种思路名师点金:全等三角形是初中几何的重要内容之一,是几何入门最关键的一步,学习了判定三角形全等的几种方法之后,如何根据已知条件说明三角形全等,掌握说明全等的几种思路尤为重要.条件充足时直接用判定方法1.【中考·武汉】如图,AC和BD相交于点O,OA=OC,OB=OD,试说明:AB∥CD.(第1题)条件不足时添加条件用判定方法2.如图,点A,F,C,D在一条直线上,AF=DC,BC∥EF,请只补充一个条件,使得△ABC≌△DEF,并说明理由.(第2题)非三角形问题中构造全等三角形用判定方法3.如图是一个风筝模型的框架,由DE=DF,EH=FH,就能说明∠DEH=∠DFH.试用你所学的知识说明理由.(第3题)4.如图,要测量AB的长,因为无法过河接近点A,可以在AB所在直线外任取一点D,在AB的延长线上任取一点E,连接ED和BD,并且延长BD到点G,使DG=BD,延长ED到点F,使DF=ED,连接FG,并延长FG到点H,使H,D,A在一条直线上,则HG=AB,试说明理由.(第4题)答案1.解:在△AOB 和△COD 中,⎩⎪⎨⎪⎧OA =OC ,∠AOB =∠COD ,OB =OD ,所以△AOB ≌△COD.所以∠A =∠C.所以AB ∥CD.2.解:补充条件:EF =BC ,可使得△ABC ≌△DEF.理由如下:因为AF =DC ,点A ,F ,C ,D 在一条直线上, 所以AF +FC =DC +FC ,即AC =DF.因为BC ∥EF ,所以∠EFD =∠BCA.在△ABC 和△DEF 中,⎩⎪⎨⎪⎧BC =EF ,∠BCA =∠EFD ,AC =DF ,所以△ABC ≌△DEF(SAS).点拨:答案不唯一.(第3题)3.解:如图,连接DH.在△DEH 和△DFH 中,⎩⎪⎨⎪⎧DE =DF ,EH =FH ,DH =DH ,所以△DEH ≌△DFH(SSS).所以∠DEH =∠DFH(全等三角形的对应角相等).4.解:在△DEB 和△DFG 中,因为DB =DG ,∠BDE =∠GDF ,DE =DF , 所以△DEB ≌△DFG(SAS).所以∠E =∠F.所以AE ∥FH.所以∠DBA =∠DGH.又因为DB =DG ,∠ADB =∠HDG ,所以△ADB ≌△HDG(ASA).所以HG =AB.。
新北师大版七年级数学下册第三章全等三角形练习题

七年级数学周周清一、填空题1、若△ABC ≌△DEF ,△DEF 的周长为32 cm ,DE =9 cm ,EF =12 cm ,则AB =_____ cm ,BC =_____ cm,AC =_____ cm.2、若△ABC ≌△DEF ,AB =DE ,AC =DF ,∠A =80°,BC =9 cm,则∠D =_____,∠D 的对边是_____=_____ cm.3、已知如图1,在△ABF 和△DEC 中,∠A =∠D ,AB =DE ,若再添加条件_____=_____,则可根据边角边公理证得△ABF ≌△DEC .4、如图2,△ABC 中,∠C=90°,CD ⊥AB 于点D ,AE 是∠BAC 的平分线,点E 到AB 的距离等于3cm ,则CE=_____cm 。
图1图2 图35、如图3,△ABC ≌△ADE ,延长BC 交DA 于F ,交DE 于G ,∠D=25°,∠E=105°,∠DAC=16°,则∠DGB=____________。
6、为了使一扇旧木门不变形,木工师傅在木门的背面 加钉了一根木条,这样做的道理是 。
二、选择题1、有下列长度的三条线段,能组成三角形的是( )A 、 2cm ,3cm ,4cmB 、 1cm ,4cm ,2cmC 、1cm ,2cm ,3cmD 、 6cm ,2cm ,3cm 2、下列命题中正确的是( )①全等三角形对应边相等; ②三个角对应相等的两个三角形全等; ③三边对应相等的两三角形全等;④有两边对应相等的两三角形全等。
A .4个 B 、3个 C 、2个 D 、1个3、已知△ABC ≌△DEF ,∠A=70°,∠E=30°,则∠F 的度数为 ( )(A ) 80° (B ) 70° (C ) 30° (D ) 100°4、如图4,△ABD 和△ACE 都是等边三角形,那么△ADC ≌△ABE 的根据是( )图4A.SSSB.SASC.ASAD.AAS 5、如图所示,某同学把一块三角形玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )F EDC BAA.带①去B. 带②去C. 带③去D. 带①和②去 6、下列说法:①所有的等边三角形都全等 ②斜边相等的直角三角形全等③顶角和腰长对应相等的等腰三角形全等 ④有两个锐角相等的直角三角形全等其中正确的个数是( )A .1个B .2个C .3个D .4个第7题 第8题 第9题7、如图,AB 平分∠CAD ,E 为AB 上一点,若AC=AD ,则下列结论错误的是( )A.BC=BDB.CE=DEC.BA 平分∠CBDD.图中有两对全等三角形8、如图,D 在AB 上,E 在AC 上,且∠B=∠C ,则在下列条件中,无法判定△ABE ≌△ACD 的是( ) (A )AD=AE (B )AB=AC(C )BE=CD (D )∠AEB=∠ADC9、如图,AB=AC ,BE ⊥AC 于E ,CF ⊥AB 于F ,则①△ABE ≌△ACF ;②△BOF ≌△COE ;③点O 在∠BAC 的角平分线上,其中正确的结论有( ) A .3个 B .2个 C .1个 D .0个10、下列条件中能确定两个三角形全等的是( )A.一边及这条边上的高相等B.一边及这条边上的中线对应相等C.两角及第三个角平分线对应相等D.两条边及夹角的平分线对应相等11、下列各组图形中,一定全等的是( )A.各有一个角是45°的两个等腰三角形B.两个等边三角形C.各有一个角是40°,腰长都为3 cm 的两个等腰三角形D.腰和顶角对应相等的两个等腰三角形 三、解答题1、已知,如图,∠1=∠2,BD=CD,求证:AD 是∠BAC 的平分线.2、如图,点E 在△ABC 外部,点D 在BC 边上,DE 交AC 于点F ,若∠1=∠2=∠3,AC=AE ,求证:△ABC ≌△ADEA B C D EC B A E F O3、已知线段a 和∠1,作一个△ABC ,使得AB=a ,AC=2a ,∠A=∠ 1.4、如图,已知AB =DC ,AC =DB ,E 是BC 的中点,求证:AE =DE5、如图,在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB ,连结AD 、AG 。
北师大版七年级数学认识三角形练习题

北师大数学七年级下册课堂达标测试题一、填空(每空3分,共60分)1.三角形的三边关系:①三角形任意两边之和 第三边;②三角形任意两边之差 第三边.2.下列每组分别是三根小木棒的长度,用它们能摆成三角形吗(填“能”或“不能”):(1)3㎝,4㎝,5㎝( ) (2)8㎝,7㎝,15㎝ ( )(3)13㎝,12㎝,20㎝( ) (4)5㎝,5㎝,11㎝ ( )(5)6cm, 8cm, 10cm ( )(6)7cm, 7cm, 14cm ( ) 3.在△ABC 中,∠A =10°,∠B =30°,则∠C =.在△ABC 中,∠A =90°,∠B =∠C ,则∠B =_________.5.(1)一个等腰三角形的一边是2cm ,另一边是9cm ,则这个三角形的周长是 _____________cm.(2)一个等腰三角形的一边是5cm ,另一边是7cm ,则这个三角形的周长是_____________cm.…6.如果∠B +∠C =∠A ,那么△ABC 是 三角形. 7.在△ABC 中,AB =6 cm ,AC =8 cm 那么BC 长的取值范围是 .8.ABC ∆中,AD 是ABC ∆的中线,且cm BC 10=,则BD= cm. 9.在ABC ∆中,︒=∠80A ,AD 为A ∠的平分线,则BAD ∠=10.如果一个三角形两边上的高的交点,恰好是三角形的一个顶点,则此三角形是 _____________三角形.11.判断具备下面条件的三角形是直角三角形、锐角三角形还是钝角三角形:(1)如果4:3:1::=∠∠∠C B A ,那么ABC ∆是 三角形;(2)如果B A ∠=∠,︒=∠30C ,那么ABC ∆是 三角形;(3)如果C B A ∠=∠=∠51,那么ABC ∆是 三角形.二、选择(每题3分,共27 分)1.在△ABC 中,∠A 是锐角,那么△ABC 是( ) A 、锐角三角形 B 、直角三角形 C 、钝角三角形D 、不能确定2.△ABC 中,若∠A ∶∠B ∶∠C =1∶2∶3,则△ABC 的形状是( )¥A 、锐角三角形B 、直角三角形C 、钝角三角形D 、不确定3.以下是由四位同学描述三角形的三种不同的说法,正确的是( ) A 、由三个角组成的图形叫三角形 B 、由三条线段组成的图形叫三角形 C 、由三条直线组成的图形叫三角形 D 、由不在同一直线上的三条线段首尾顺次相接所组成的图形叫三角形 4.△AB C 中,已知a =8, b =5,则c 为( ) A 、c =3 B 、c =13C 、c 可以是任意正整数D 、c 可以是大于3小于13的任意数值5. 下面说法中正确的是:( )A 、三角形的角平分线,中线,高都在三角形内 B 、直角三角形的高只有一条C 、钝角三角形的三条高都在三角形外 D 、三角形至少有一条高在三角形内 6. 如果一个三角形的三条高线的交点恰好是三角形的一个顶点,那么这个三角形是( ) A 、直角三角形 B 、锐角三角形 C 、钝角三角形 D 、不能确定;7.在一个三角形,若︒=∠=∠40B A ,则ABC ∆是( )A 、直角三角形B 、锐角三角形C 、钝角三角形D 、以上都不对8.三角形的高线是 ( ) A 、线段 B 、垂线 C 、射线 D 、直线 9.在Rt △中,两个锐角关系是( )A 、互余 B 、互补 C 、相等 D 、以上都不对 三、解答题1.如图,在△ABC 中,∠BAC=60°,∠B=45°,AD 是△ABC 的一条角平分线求∠ADB 的度数. (7分)—2.在下列图中,分别画出三角形的三条高。
新版北师大版七年级下册数学第三章三角形作图、测距离、直角三角形判定经典练习
尺规作图、利用三角形全等测距离、直角三角形的判定 ——知识点对应典型练习【知识点一】作三角形1、已知三边,作出一个三角形?2、已知三角形的两个角分别等于∠a ,∠b ,这两角所夹的边等于a 如图,求作这个三角形3、如图,已知三角形的两边长分别等于a,b ,这两边的夹角等于∠a .求作这个三角形.4、已知线段a ,c (a <c ) , 和一个直角 ∠α,利用尺规作一个Rt △ABC ,使∠C=∠α, AB=c , CB=a . ;5. 已知△ABC, 用尺规作图, 作一个三角形,使得△DEF ≌△ABC.a cαC【知识点二】利用三角形全等测距离1.如图,A 、B 两个建筑分别位于两岸,要测得它们之间的距离,可以从B 出发沿河岸面一条射线BF,在BF 上截取BC=CF,过F 作FE ∥AB,使E 、C 、A 在同一条直线上, 则EF 的长就是A 、B 之间的距离,请你说明道理,B AEFC2、如图,公园里有一条“Z ”形的林荫小道ABCD ,其中AB ∥OD ,在AB 、BO 、OD 三段路旁各有一条石凳E 、G 、F ,且G 恰好为BC 的中点,E 、G 、F 三点在同一条直线上,点G 与F 之间有一座假山,而使得两处不能直接到达.你能想出测量G 、F 之间距离的方法吗?说明其中的道理.3.如图,有一池塘,要测池塘两端A 、B 的距离,可先在平地上取一个可以直接到达A 和B 的点C,连结AC 并延长到D,使CD=CA.连结BC 并延长到E,使EC=CB,连结DE,量出DE 的长,就是A 、B 的距离.写出你的证明.4.如图15,O 为码头,A ,B 两个灯塔与码头的距离相等,OA ,OB 为海岸线,一轮船从码头O 开出,计划沿∠AOB 的平分线航行,航行途中,测得轮船与灯塔A ,B 的距离相等,此时轮船有没有偏离航线?画出图形并说明你的理由.5.七年级(1)班同学到野外上数学活动课,为测量池塘两端A 、B 的距离,设计了如下方案: (I)如图(1),先在平地上取一个可直接到达A 、B 的点C ,连接AC 、BC ,并分别延长AC 至D ,BC 至E ,使DC=AC ,EC=BC ,最后测出DE 的距离即为AB 的长. (Ⅱ)如图(2),先过B 点作AB 的垂线BF ,再在BF 上取C 、D 两点使BC=CD ,接着过D 作BD 的垂线DE ,交AC 的延长线于E ,则测出DE 的长即为AB 的距离.阅读后回答下列问题:(1)方案(I)是否可行?请说明理由. (2)方案(Ⅱ)是否可行?请说明理由. (3)方案(Ⅱ)中作BF ⊥AB ,ED ⊥BF 的目的是_____________________;若仅满足∠ABD=∠BDE ≠90o ,方案(Ⅱ)是否成立?__________.【知识点三】探索直角三角形全等的条件 一.选择题1.已知在△ABC 和△DEF 中,∠A=∠D=90°,则下列条件中不能判定△ABC 和△DEF 全等的是( )A.AB=DE,AC=DFB.AC=EF,BC=DFC.AB=DE,BC=EFD.∠C=∠F,BC=EF2.如果两个直角三角形的两条直角边对应相等,那么两个直角三角形全等的依据是( ) A.AAS B.SAS C.HL D.SSS3、用12根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余、重叠和折断,则能摆出不同的三角形的个数是( ) A 、1 B 、2 C 、3 D 、4 4.如图17,某同学把一把三角形的玻璃打碎成了三块,现在要到玻璃店去配一块大小形状完全一样的玻璃,那么 最省事的办法是( )﹒(A )带①和②去 (B )带①去 (C )带②去 (D )带③去 5.有一专用三角形模具,损坏后,只剩下如图中的阴影部分,你对图中做哪些数据度量后,就可以重新制作一块与原模具完全一样的模具,并说明其中的道理.图15B ′C ′D ′O ′A ′O D CB A 6.已知:a 、b 、c 是△ABC 三边长,且M =(a +b +c)(a +b -c)(a -b -c),那么 ( ) A .M >0 B .M =0 C .M <0D .不能确定7.周长为P 的三角形中,最长边m 的取值范围是 ( )A .23P m P <≤ B .23P m P << C .23P m P ≤< D .23P m P ≤≤8.各边长均为整数且三边各不相等的三角形的周长小于13,这样的三角形个数共有( )A .5个B .4个C .3个D .2个图5 图69.如图5,已知∠1=∠2,请你添加一个条件使△ABC ≌△BAD ,你的添加条件是 (填一个即可)。
4.3探索三角形全等的条件(3)全等三角形的判定——SAS-2024学年北师大版数学七年级下册
所以∠B=∠C.
4.如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C,D,E三点
在同一直线上,连接BD,BE.以下四个结论:
①BD=CE;
②∠ACE+∠DBC=90°;
③BD⊥CE;
④∠BAE+∠DAC=180°.
①③④
其中正确的是____________.(把正确结论的序号填在横线上)
解:在△ABC与△DCB中,
= ,
∠ = ∠,
= ,
所以△ABC≌△DCB(SAS).
3.如图,已知线段BE,CD交于点O,点D在线段AB上,点E在线段
AC上,AB=AC,AD=AE.试说明∠B=∠C.
解:在△AEB和△ADC中,
= ,
∠ = ∠ ,
= ,
△AOD≌△COB.
= ,
解:在△AOD和△COB中, ∠ = ∠,
= ,
所以△AOD≌△COB(SAS).
如图,BA=BE,BC=BD,∠ABD=∠EBC.试说明△ABC≌
△EBD.
解:因为∠ABD=∠EBC,
所以∠ABD-∠CBD=∠EBC-∠CBD.
所以∠ABC=∠EBD.
是由它抽象出的几何图形,点B,C,E在同一条直线上,连接DC.请
找出图②中的全等三角形,并说明理由.(不再添加其他线段,不再
标注或使用其他字母)
△ABE≌△ACD
解:你找到的全等三角形是:_________________.
解:因为△ABC和△DAE是等腰直角三角形,
所以AB=AC,AE=AD,∠BAC=∠DAE=90°.
第四章
三角形
2020最新北师大版数学七下第三章《三角形》单元测试卷及答案(5套)
北师大版七年级数学下册第三章三角形单元测试卷(一)班级姓名学号得分一、选择题1.一定在△ABC内部的线段是()A.锐角三角形的三条高、三条角平分线、三条中线B.钝角三角形的三条高、三条中线、一条角平分线C.任意三角形的一条中线、二条角平分线、三条高D.直角三角形的三条高、三条角平分线、三条中线2.下列说法中,正确的是()A.一个钝角三角形一定不是等腰三角形,也不是等边三角形B.一个等腰三角形一定是锐角三角形,或直角三角形C.一个直角三角形一定不是等腰三角形,也不是等边三角形D.一个等边三角形一定不是钝角三角形,也不是直角三角形3.如图,在△ABC中,D、E分别为BC上两点,且BD=DE=EC,则图中面积相等的三角形有() A.4对 B.5对 C.6对 D.7对(注意考虑完全,不要漏掉某些情况)4.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定5.下列各题中给出的三条线段不能组成三角形的是()A.a+1,a+2,a+3(a>0) B.三条线段的比为4∶6∶10C.3cm,8cm,10cm D.3a,5a,2a+1(a>0)6.若等腰三角形的一边是7,另一边是4,则此等腰三角形的周长是()A.18 B.15 C.18或15 D.无法确定7.两根木棒分别为5cm和7cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒长为偶数,那么第三根木棒的取值情况有()种A.3 B.4 C.5 D.68.△ABC的三边a、b、c都是正整数,且满足a≤b≤c,如果b=4,那么这样的三角形共有()个 A.4 B.6 C.8 D.109.各边长均为整数的不等边三角形的周长小于13,这样的三角形有()A.1个 B.2个 C.3个 D.4个10.三角形所有外角的和是()A.180° B.360° C.720° D.540°11.锐角三角形中,最大角α的取值范围是()A.0°<α<90°; B.60°<α<180°; C.60°<α<90°; D.60°≤α<90°12.如果三角形的一个外角不大于和它相邻的内角,那么这个三角形为()A.锐角或直角三角形; B.钝角或锐角三角形;C.直角三角形; D.钝角或直角三角形13.已知△ABC中,∠ABC与∠ACB的平分线交于点O,则∠BOC一定()A .小于直角;B .等于直角;C .大于直角;D .大于或等于直角 二、填空题1.如图:(1)AD ⊥BC ,垂足为D ,则AD 是________的高,∠________=∠________=90°;(2)AE 平分∠BAC ,交BC 于点E ,则AE 叫________,∠________=∠________=21∠________,AH 叫________;(3)若AF =FC ,则△ABC 的中线是________;(4)若BG =GH =HF ,则AG 是________的中线,AH 是________的中线. 2.如图,∠ABC =∠ADC =∠FEC =90°. (1)在△ABC 中,BC 边上的高是________; (2)在△AEC 中,AE 边上的高是________; (3)在△FEC 中,EC 边上的高是________; (4)若AB =CD =3,AE =5,则△AEC 的面积为________. 3.在等腰△ABC 中,如果两边长分别为6cm 、10cm ,则这个等腰三角形的周长为________. 4.五段线段长分别为1cm 、2cm 、3cm 、4cm 、5cm ,以其中三条线段为边长共可以组成________个三角形. 5.已知三角形的两边长分别为3和10,周长恰好是6的倍数,那么第三边长为________. 6.一个等腰三角形的周长为5cm ,如果它的三边长都是整数,那么它的腰长为________cm . 7.在△ABC 中,若∠A ∶∠B ∶∠C =5∶2∶3,则∠A =______;∠B =______;∠C =______. 8.如图,△ABC 中,∠ABC 、∠ACB 的平分线相交于点I . (1)若∠ABC =70°,∠ACB =50°,则∠BIC =________; (2)若∠ABC +∠ACB =120°,则∠BIC =________; (3)若∠A =60°,则∠BIC =________; (4)若∠A =100°,则∠BIC =________; (5)若∠A =n °,则∠BIC =________. 三、解答题1.在△ABC 中,∠BAC 是钝角. 画出:(1)∠ABC 的平分线; (2)边AC 上的中线; (3)边AC 上的高.2.△ABC 的周长为16cm ,AB =AC ,BC 边上的中线AD 把△ABC 分成周长相等的两个三角形.若BD =3cm ,求AB 的长.3.如图,AB ∥CD ,BC ⊥AB ,若AB =4cm ,212cm =∆ABC S ,求△ABD 中AB 边上的高.4.学校有一块菜地,如下图.现计划从点D 表示的位置(BD ∶DC =2∶1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.有人说:如果D 是BC 的中点的话,由此点D 笔直地挖至点A 就可以了.现在D 不是BC 的中点,问题就无法解决了.但有人认为如果认真研究的话一定能办到.你认为上面两种意见哪一种正确,为什么?5.在直角△ABC 中,∠BAC =90°,如下图所示.作BC 边上的高,图中出现三个直角三角形(3=2×1+1);又作△ABD 中AB 边上的高1DD ,这时图中便出现五个不同的直角三角形(5=2×2+1);按照同样的方法作21D D 、32D D 、……、k k D D 1-.当作出k k D D 1-时,图中共有多少个不同的直角三角形?6.一块三角形优良品种试验田,现引进四个良种进行对比实验,需将这块土地分成面积相等的四块.请你制订出两种以上的划分方案.7.一个三角形的周长为36cm,三边之比为a∶b∶c=2∶3∶4,求a、b、c.8.已知△ABC的周长为48cm,最大边与最小边之差为14cm,另一边与最小边之和为25cm,求△ABC各边的长.9.已知三角形三边的长分别为:5、10、a-2,求a的取值范围.10.已知等腰三角形中,AB=AC,一腰上的中线BD把这个三角形的周长分成15cm和6cm 两部分,求这个等腰三角形的底边的长.11.如图,已知△ABC中,AB=AC,D在AC的延长线上.求证:BD-BC<AD-AB.12.如图,△ABC中,D是AB上一点.求证:(1)AB+BC+CA>2CD;(2)AB+2CD>AC+BC.13.如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,(1)完成下面的证明:∵ MG平分∠BMN(),1∠BMN(),∴∠GMN=21∠DNM.同理∠GNM=2∵ AB∥CD(),∴∠BMN+∠DNM=________().∴∠GMN+∠GNM=________.∵∠GMN+∠GNM+∠G=________(),∴∠G= ________.∴ MG与NG的位置关系是________.(2)把上面的题设和结论,用文字语言概括为一个命题:_______________________________________________________________.14.已知,如图D是△ABC中BC边延长线上一点,DF⊥AB交AB于F,交AC于E,∠A=46°,∠D=50°.求∠ACB的度数.15.已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC=60°,求∠BOC的度数.16.已知,如图△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线.求∠DAE的度数.17.已知,如图CE是△ABC的外角∠ACD的平分线,BE是∠ABC内任一射线,交CE于E.求证:∠EBC<∠ACE.18.画出图形,并完成证明:已知:AD 是△ABC 的外角∠EAC 的平分线,且AD ∥BC . 求证:∠B =∠C .单元测试卷(一)参考答案:一、1.A ; 2.D ; 3.A ; 4.C ;5.B ; 6.C ; 7.B ; 8.D ; 9.C (提示:边长分别为3、4、5;2、4、5;2、3、4.)10.C ; 11.D ; 12.D ; 13.C ; 二、1.(1)BC 边上,ADB ,ADC ;(2)∠BAC 的角平分线,BAE ,CAE ,BAC ,∠BAF 的角平分线; (3)BF ;(4)△ABH ,△AGF ; 2.(1)AB ; (2)CD ; (3)EF ; (4)7.5; 3.22cm 或26cm ; 4.3; 5.11; 6.2;7.90°,36°,54°;8.(1)120°; (2)120°; (3)120°; (4)140°; (5)290︒+︒n ;三、21.略;2.解法1:AB +BD +DA =DA +AC +CD ,∴ BD =CD ,∵ BD =3cm ,∴ CD =3cm ,BC =6cm ,∵ AB =AC ,∴ AB =5cm . 解法2:△ABD 与△ACD 的周长相等,而AB =AC ,∴ BD =CD , ∴ BC =2BD =6cm ,∴ AB =(16-6)÷2=5cm . 3.212cm =∆ABC S ,∴ 21AB ·BC =12,AB =4,∴ BC =6,∵ AB ∥CD ,∴ △ABD 中AB 边上的高=BC =6cm .4.后一种意见正确.5.不作垂线,一个直角三角形,即:1=2×0+1,作一条垂线,三个直角三角形,即:3=2×1+1,同理,5=2×2+1,找出相应的规律,当作出k k D D 1 时,图中共有2×k +1,即2k +1个直角三角形.6.第一种方案:在BC 上取E 、D 、F ,使BE =ED =DF =FC ,连结AE 、AD 、AF ,则△ABE 、△AED 、△ADF 、△AFC 面积相等;第二种方案:取AB 、BC 、CA 的中点D 、E 、F ,连结DE 、EF 、FD ,则△ADF 、△BDE 、△CEF 、△DEF 面积相等.7.设三边长a =2k ,b =3k ,c =4k ,∵ 三角形周长为36,∴ 2k +3k +4k =36,k =4, ∴ a =8cm ,b =12cm ,c =16cm .8.设三角形中最大边为a ,最小边为c ,由已知,a -c =14,b +c =25,a +b +c =48, ∴ a =23cm ,b =16cm ,c =9cm .9.10-5<a -2<10+5,∴ 7<a <17. 10.设AB =AC =2x ,则AD =CD =x ,(1)当AB +AD =15,BC +CD =6时,2x +x =15,∴ x =5,2x =10,∴ BC =6-5=1cm ;(2)当AB +AD =6,BC +CD =15时,2x +x =6,∴ x =2,2x =4,∴ BC =13cm ;经检验,第二种情况不符合三角形的条件,故舍去. 11.AD -AB =AC +CD -AB =CD ,∵ BD -BC <CD , ∴ BD -BC <AD -AB . 12.(1)AC +AD >CD ,BC +BD >CD , 两式相加:AB +BC +CA >2CD . (2)AD +CD >AC ,BD +CD >BC , 两式相加:AB +2CD >AC +BC . 13.(1)已知,角平分线定义,已知,180°,两直线平行同旁内角互补,90°,180°,三角形内角和定理,90°,互相垂直.(2)两平行直线被第三条直线所截,它们的同旁内角的角平分线互相垂直. 14.94°; 35.120°; 36.10°;17.∠EBC <∠DCE ,而∠DCE =∠ACE ,∴ ∠EBC <∠ACE . 18.略.北师大版七年级数学下册第三章三角形单元测试卷(二)班级姓名学号得分一、选择题1.一个三角形的两边长为2和6,第三边为偶数.则这个三角形的周长为 ( ) A.10 B.12 C.14 D.162.在△ABC中,AB=4a,BC=14,AC=3a.则a的取值范围是 ( )A.a>2 B.2<a<14 C.7<a<14 D.a<143.一个三角形的三个内角中,锐角的个数最少为 ( )[A.0 B.1 C.2 D.34.下面说法错误的是 ( )A.三角形的三条角平分线交于一点 B.三角形的三条中线交于一点C.三角形的三条高交于一点 D.三角形的三条高所在的直线交于一点5.能将一个三角形分成面积相等的两个三角形的一条线段是 ( )A.中线B.角平分线 C.高线D.三角形的角平分线6.如图5—12,已知∠ACB=90°,CD⊥AB,垂足是D,则图中与∠A相等的角是 ( )A.∠ 1 B.∠ 2 C.∠ B D.∠ 1、∠ 2和∠ B 7.点P是△ABC内任意一点,则∠APC与∠B的大小关系是( ) A.∠APC>∠B B.∠APC=∠B C.∠APC<∠B D.不能确定8.已知:a 、b 、c 是△ABC 三边长,且M =(a +b +c)(a +b -c)(a -b -c),那么 ( ) A .M >0 B . M =0 C .M <0 D .不能确定9.周长为P 的三角形中,最长边m 的取值范围是 ( )A .23P m P <≤B .23P m P <<C .23P m P ≤<D .23P m P ≤≤10.各边长均为整数且三边各不相等的三角形的周长小于13,这样的三角形个数共有( )A .5个B .4个C .3个D .2个 二、填空题1.五条线段的长分别为1,2,3,4,5,以其中任意三条线段为边长可以________个三角形.2.在△ABC 中,AB =6,AC =10,那么BC 边的取值范围是________,周长的取值范围是___________.3.一个三角形的三个内角的度数的比是2:2:1,这个三角形是_________三角形. 4.一个等腰三角形两边的长分别是15cm 和7cm 则它的周长是__________.5.在△ABC 中,三边长分别为正整数a 、b 、c ,且c ≥b ≥a >0,如果b =4,则这样的三角形共有_________个.6.直角三角形中,两个锐角的差为40°,则这两个锐角的度数分别为_________. 7.在△ABC 中,∠A -∠B =30°、∠C =4∠B ,则∠C =________.8.如图5—13,在△ABC 中,AD ⊥BC ,GC ⊥BC ,CF ⊥AB ,BE ⊥AC ,垂足分别为D 、C 、F 、E ,则_______是△ABC 中BC 边上的高,_________是△ABC 中AB 边上的高,_________是 △ABC 中AC 边上的高,CF 是△ABC 的高,也是△_______、△_______、△_______、△_________的高.[来9.如图5—14,△ABC 的两个外角的平分线相交于点D ,如果∠A =50°,那么∠D =_____. 10.如图5—15,△ABC 中,∠A =60°,∠ABC 、∠ACB 的平分线BD 、CD 交于点D ,则∠BDC =_____.11.如图5—16,该五角星中,∠A +∠B +∠C +∠D +∠E =________度. 12.等腰三角形的周长为24cm ,腰长为xcm ,则x 的取值范围是________. 三、解答题1.如图5—17,点B 、C 、D 、E 共线,试问图中A 、B 、C 、D 、E 五点可确定多少个三角形?说明理由.2.如图5—18,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗?说明理由.3.一个飞机零件的形状如图5—19所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,康师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗?4.如图5—20,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为11cm,求AC的长.5.如图5—21,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC 的平分线,求∠DAE的度数.6.如图5—22,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)△ABC的面积;(2)CD的长.7.已知:如图5—23,P是△ABC内任一点,求证:∠BPC>∠A.8.△ABC中,三个内角的度数均为整数,且∠A<∠B<∠C,4∠C=7∠A,求∠A的度数.9.已知:如图5—24,P 是△ABC 内任一点,求证:AB +AC >BP +PC .10.如图5—25,豫东有四个村庄A 、B 、C 、D .现在要建造一个水塔P .请回答水塔P 应建在何位置,才能使它到4村的距离之和最小,说明最节约材料的办法和理由.单元测试卷(二)参考答案:一、1.C 2.B 3.C 4.C 5.A 6.B 7.A 8.C 9.A 10.C 二、1.3; 2.32周长20,164<<<<BC ; 3.锐角(等腰锐角); 4.cm 37;5.10; 6.︒65和︒25; 7.︒100;8.GAC FAC FGC BFC BE CF AD ∆∆∆∆,,,,,,;9.︒65; 10.︒120; 11.︒180; 12.126<<x . 三、1.可以确定6个三角形.理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,所以图中可以确定6个三角形.2.错误.因为AD 虽然是线段,但不符合三角形角平分线定义,这里射线AD 是BAC ∠的平分线3.假设此零件合格,连接BD ,则︒=︒-︒=∠+∠37143180CBD CDB ;可知()︒=︒+︒-︒=∠+∠40203090CBD CDB .这与上面的结果不一致,从而知这个零件不合格.4.∵ AD 是BC 边上的中线,∴ D 为BC 的中点,BD CD =.∵ ADC ∆的周长-ABD ∆的周长=5cm ∴ cm AB AC 5=-. 又∵ cm AB AC 11=+, ∴ cm AC 8=.5.由三角形内角和定理,得︒=∠+∠+∠180BAC ACB B .∴ ︒=︒-︒-︒=∠4210434180BAC . 又∵ AE 平分∠BAC . ∴ ︒=︒⨯=∠=∠21422121BAC BAE .∴ ︒=︒+︒=∠+∠=∠552134BAE B AED . 又∵ ︒=∠+∠90DAE AED ,∴ ︒=︒-︒=∠-︒=∠35559090AED DAE . 6.(1)∵ 在△ABC 中,︒=∠90ACB ,cm AC 5=,cm BC 12=,().3012521212cm BCAC S ABC =⨯⨯=⋅=∴∆[ (2)∵ CD 是AB 边上的高, ∴ CD AB S ABC ⋅=∆21.即CD ⨯⨯=132130.∴ ()cm CD 1360=.7.如图,延长BP 交AC 于D ,∵ A PDC PDC BPC ∠>∠∠>∠,, ∴ A BPC ∠>∠ 8.∵ A C ∠=∠74,∴ C A ∠=∠74,∴ C B C ∠<∠<∠74.又∵ ︒=∠+∠+∠180C B A ,∴ ︒=∠+∠+∠18074C B C .∴ C B ∠-︒=∠711180,∵ C C C ∠<∠-︒<∠71118074,∴ ︒<∠<︒8470C .又∵ C A ∠=∠74为整数,∴ ∠C 的度数为7的倍数.∴ ︒=∠77C ,∴ ︒=∠=∠4474C A .9.如图,延长BP 交AC 于点D .在△BAD 中,BD AD AB >+, 即:PD BP AD AB +>+. 在△PDC 中,PC DC PD >+. ①+②得PC PD BP DC PD AD AB ++>+++, 即PC BP AC AB +>+10.如图,水塔P 应建在线段AC 和线段BD 的交点处.这样的设计将最节省材料.理由:我们不妨任意取一点P ',连结P A '、P B '、P C '、P D '、AB 、BC 、CD 、DA , ∵ 在C P A '∆中,CP AP AC P C P A +=>'+', ① 在D P B '∆中,DP BP BD P D P B +=>'+', ② ①+②得DP CP BP AP P D P C P B P A +++>'+'+'+'. ∵ 点P '是任意的,代表一般性,∴ 线段AC 和BD 的交点处P 到4个村的距离之和最小.北师大版七年级数学下册第三章 三角形 单元测试卷(三)班级 姓名 学号 得分一、选择题(每小题3分,共30分)1. 有下列长度的三条线段,能组成三角形的是( )A 2,3,4B 1,4,2C 1,2,3D 6,2,3 2. 在下列各组图形中,是全等的图形是( )3. 下列条件中,能判断两个直角三角形全等的是( )AB C DE图4图2 图 3 A 、一个锐角对应相等 B 、两个锐角对应相等C 、一条边对应相等D 、两条边对应相等4.已知:如图,CD ⊥AB ,BE ⊥AC ,垂足分别为D 、E ,BE 、CD 相交于O 点, ∠1=∠2.图中全等的三角形共有 ( ) A .4对 B ..3对 C 2对 D .1对5.如图所示,某同学把一块三角形玻璃打碎成了三块,现在要到玻店去配一块完全一样的玻璃,那么最省事的办法是( )A.带①去B. 带②去C. 带③去D. 带①和②去6.右图中三角形的个数是( )A .6 B .7 C .8 D .97.如果两个三角形全等,那么下列结论不正确的是( ) A .这两个三角形的对应边相等 B .这两个三角形都是锐角三角形C .这两个三角形的面积相等D .这两个三角形的周长相等8.在下列四组条件中,能判定△ABC ≌△A /B /C /的是( )A.AB=A /B /,BC= B /C /,∠A=∠A /B.∠A=∠A /,∠C=∠C /,AC= B /C /C.∠A=∠B /,∠B=∠C /,AB= B /C /D.AB=A /B /,BC= B /C /,△ABC 的周长等于△A /B /C /的周长9.下列图中,与左图中的图案完全一致的是( )10. 下列判断:①三角形的三个内角中最多有一个钝角,②三角形的三个内角中至少有两个锐角,③有两个内角为500和200的三角形一定是钝角三角形,④直角三角形中两锐角的和为900,其中判断正确的有( )A.1个B.2个C.3个D.4个 二、填空题:(每题4分共24分)11、为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是 。
七年级数学下册 3.1.1 三边关系试题(基础巩固提优+课外拓展提优+开放探究提优,pdf) (新版)北师大版
第三章㊀㊀㊀㊀㊀㊀㊀三 角 形1㊀认识三角形第1课时㊀三边关系㊀㊀1.认识三角形的概念及基本要素.2.掌握三角形三边之间的关系.1.若三角形两条边分别是2c m和7c m,则第三边c的范围是㊀㊀㊀㊀,当周长为偶数时,第三边长为㊀㊀㊀㊀,若周长为5的倍数时,第三边长为㊀㊀㊀㊀.2.若等腰三角形的腰长为6,则它的底边长a的取值范围是㊀㊀㊀㊀;若等腰三角形的底边长为4,则它的腰长b的取值范围是㊀㊀㊀㊀.3.一个木工师傅现有两根木条,它们的长分别为30c m和50c m,他要选择第三根木条,将它们钉成一个三角形木架,设第三根木条为x c m,则x的取值范围是㊀㊀㊀㊀,若第三根木条是整十数,则第三根木条可以有㊀㊀㊀㊀种选择.4.认识三角形后,勤于探索的贝贝和晶晶又用玩游戏的方式探索起来.贝贝:给出下列四组线段,请你找出能构成三角形的一组.晶晶略一思考,就正确地找了出来是(㊀㊀).A.2c m,4c m,6c mB.3c m,8c m,4c mC.7c m,7c m,3c mD.9c m,5c m,3c m5.若三角形的两边长分别为3和5,则其周长l的取值范围是(㊀㊀).A.6<l<15B.6<l<16C.10<l<16D.11<l<136.以长度为5,7,9,13中的三条线段为边,能组成一个三角形的情况有(㊀㊀).A.1种B.2种C.3种D.4种7.在下列各题中给出的三条线段不一定能组成三角形的是(㊀㊀).A.a+1,a+2,a+3(a>0)B.三条线段的比是4ʒ6ʒ8C.3c m,8c m,10c mD.3a,5a,2a-1(a>0)8.在周长为p的三角形中,最长边m的取值范围是(㊀㊀).A.p3ɤm<p2B.p3<m<p2C.p3<mɤp2D.p3ɤmɤp29.已知әA B C的周长为48c m,最大边与最小边之差为14c m,另一边与最小边之和为25c m,求әA B C各边的长.10.已知在әA B C中,A B=A C,点D在A C的延长线上.求证:B D-B C<A D-A B.(第10题)11.若三角形的三边长都是正整数,一边长为4,但它不是最短边,写出8种满足所有条件的三角形的三边长.12.如图,A C㊁B D相交于点O,试说明:A C+B D>12(A B+B C+C D+D A).(第12题)惟有真才能血性,须从本色见英雄. 黄㊀兴受人者,常畏人;与人者,常骄人.皇甫谧13.әA B C 的三边a ,b ,c 都是正整数,且满足a ɤb ɤc ,如果b =4,那么这样的三角形共有(㊀㊀).A.4个B .6个C .8个D.10个14.各边长均为整数且各边均不相等的三角形的周长小于13,这样的三角形有(㊀㊀).A.1个B .2个C .3个D.4个15.如果三角形的两边长分别为2和4,且第三边的长为奇数,试讨论三角形的第三边应为多少?若第三边为偶数,求这个三角形的周长.16.已知a ,b ,c 是三角形三条边的长,试判断代数式a 2-2a b-c 2+b2值的正负.17.已知a ,b ,c 是әA B C 的三边,化简:|a -b -c |+|a +b -c |-|b -c -a |+|c -a -b |.18.如图,草原上有4口油井,位于四边形A B C D 的4个顶点处,现在要建立一个维修站H ,试问维修站H 建在何处,才能使它到4口油井的距离之和HA +H B +H C +HD 为最小?说明理由.(第18题)19.(2012 广东)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是(㊀㊀).A.5B .6C .11D.1620.(2012 湖南长沙)现有3c m ,4c m ,7c m ,9c m 长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是(㊀㊀).A.1B .2C .3D.421.(2012 湖南郴州)以下列各组线段为边,能组成三角形的是(㊀㊀).A.1c m ,2c m ,4c m B .4c m ,6c m ,8c m C .5c m ,6c m ,12c m D.2c m ,3c m ,5c m22.(2012 浙江义乌)如果三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是(㊀㊀).A.2B .3C .4D.823.(2012 广东茂名)如图所示,建高楼时常需要用塔吊来吊建筑材料,而塔吊的上部都是三角形结构,这是应用了三角形的哪个性质?答:㊀.(第23题)48,则a =23c m ,b =16c m ,c =9c m .10.ȵ㊀A D -A B =A C +C D -A C =C D ,又㊀B D -B C <C D ,ʑ㊀B D -B C <A D -A B .11.如:1,4,4;2,4,4;2,3,4;2,4,5;3,3,4;3,4,4;3,4,5;3,4,6等12.在әA O D 中,A O +D O >A D ;在әA O B 中,A O +B O >A B ;在әB O C 中,B O +C O >B C ;在әC O D 中,C O +D O >C D .四个不等式两边分别相加,并化简,得2A C +2B D >A B +B C +C D +D A ,所以A C +B D >12(A B +B C +C D +D A ).13.D ㊀14.C15.设第三边为x ,根据三边关系,得4-2<x <4+2,所以2<x <6.所以第三边若为奇数,第三边长为3或5;若第三步为偶数,则第三边长为4,此时三角形的周长=2+4+4=10.16.㊀a 2-2a b -c 2+b2=(a -b )2-c2=(a -b -c )(a +c -b ).ȵ㊀a -b -c <0,a +c -b >0,ʑ㊀a 2-2a b -c 2+b 2<0.17.因为a ,b ,c 是әA B C 的三边,所以a -b -c <0,a +b -c >0,b -c -a <0,c -a -b <0,所以原式=-(a -b -c )+(a +b -c )+(b-c -a )-(c -a -b )=-a +b +c +a +b -c +b -c -a -c +a +b=4b -2c .18.维修站H 建在两条对角线A C ㊁B D 的交点处便符合要求,现不妨任取异于H 的一点H ᶄ,连接AH ᶄ㊁B H ᶄ㊁C H ᶄ㊁DH ᶄ,则AH ᶄ+C H ᶄ>A C =AH +C H ,①B H ᶄ+DH ᶄ>B D =B H +DH ,②①+②,得A H ᶄ+C H ᶄ+B H ᶄ+D H ᶄ>A H +C H +B H +D H .ʑ㊀对角线A C ㊁B D 的交点H 处到4口油井的距离之和为最小.(第18题)19.C ㊀20.A㊀21.B ㊀22.C ㊀23.稳定性第三章㊀三角形1㊀认识三角形第1课时㊀三边关系1.5c m<c <9c m㊀7c m㊀6c m 2.0<a <12㊀b >23.20<x <80㊀54.C ㊀5.C ㊀6.C ㊀7.D㊀8.B9.设三角形的三边长为a ,b ,c ,且a >b >c .由已知,可得a -c =14,b +c =25,a +b +c =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级下册数学第三单元三角形测试题(北师大版)以下是查字典数学网为您推荐的七年级下册数学第三单元三角形测试题(北师大版),希望本篇文章对您学习有所帮助。
七年级下册数学第三单元三角形测试题(北师大版)课堂练习:1.若一直角三角形两边长分别为12和5,则第三边长为( )A. 13B. 13或C. 13或15D. 152.直角三角形的周长为12,斜边长为5,则面积为( )A. 12B. 10C. 8D. 63.如果一个等腰直角三角形的面积是2,则斜边长的平方为( )A. 2B. 4C. 8D.4.若直角三角形两条直角边长分别为5㎝,12㎝,则斜边上的高为( )A. 6㎝B. ㎝C. 8㎝D. ㎝5.若等腰三角形两边长分别为4和6,则底边上的高等于( )A. 或B. 或C.D.6.△ABC中,若,则此三角形应是( )A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形7.一个直角三角形的两条直角边长为a、b,斜边上的高为h,页 1 第斜边长为c,则以c+h,a+b,h为边的三角形的形状是( )A. 直角三角形B. 锐角三角形C. 钝角三角形D.不能确定8.直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是( )A. ab=h2B. a2+b2=2h2C. + =D. + =9.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为()A.121B.120C.90D.不能确定10.如图是一个长方体盒子(尺寸如图所示),在长方体下底部的A点有一只蚂蚁,它想吃到上底面B点的食物(BC=3cm),需爬行的最短路程是多少?11.如图,公路MN和公路PQ在P点处交汇,点A处有一所中学,AP=160米,点A到公路MN的距离为80米,假使拖拉机行驶时,周围100米以内会受到噪音影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到影响,请说明理由;如果受到影响,已知拖拉机的速度是18千米/小时,那么学校受到影响的时间为多少?12.三角形ABC是等腰三角形AB=AC=13,BC=10,将AB向AC方向对折,再将CD折叠到CA边上,折痕CE,求三角形ACE的面积。
13.边长为8和4的矩形OABC的两边分别在直角坐标系的X页 2 第轴和Y轴上,若沿对角线AC折叠后,点B落在第四象限B1处,设B1C交X轴于点D,求:三角形ADC的面积14.已知:如图,△ABC是等腰直角三角形,BAC=90,EAF 与BC交于E、F两点,EAF=45,求证:。
15.如图,在中,相交于, 于,求证: .16.如图,在中,,D为斜边BC中点,,求证:17.如图,已知:,,于P. 求证: .18.折叠矩形纸片,先折出折痕对角线BD,在绕点D折叠,使点A落在BD的E处,折痕DG,若AB=2,BC=1,求AG的长.19.矩形ABCD中,AB=6,BC=8,先把它对折,折痕为EF,展开后再沿BG折叠,使A落在EF上的A1,求第二次折痕BG的长.20.矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长21.如图,长方形纸片ABCD中,AB=4cm,BC=3cm,现将A,C重合,使纸片折叠压平,设折痕为EF,试确定重叠部分三角形AEF的面积.22.圆柱形坡璃容器,高18cm,底面周长为60cm,在外侧距下底1cm点S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口页 3 第外侧距开口处1cm的点F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度。
23.如图所示,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DEDF,若BE=12,CF=5.求线段EF的长。
课堂小练05-直角三角形姓名:1.一根旗杆在离地面4.5米的地方折断,旗杆顶端落在离旗杆底部6米处,则旗杆折断前高( )A. 10.5米B. 7.5米C. 12米D. 8米2.等腰三角形底边长10,腰长为13,则此三角形的面积为()A. 40B. 50C. 60D. 703.三角形的三边长为,则这个三角形是( )A. 等边三角形B. 钝角三角形C. 直角三角形D. 锐角三角形4.已知直角三角形中30角所对的直角边长是cm,则另一条直角边的长是( )A. 4 cmB. cmC. 6 cmD. cm5.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )A.42B. 32C.42 或32D.37 或336.如图,在中, ,过顶点的直线的平分线分别交于点,若,则的长为( )页 4 第A.14B.16C.18D.207.若一个三角形的三边之比为3:4:5,且周长为60cm,则它的面积为、8.一个长方形的长为12cm,对角线长为13cm,则该长方形的周长为______9.在△ABC中,C=900,,BC=60cm,CA=80cm,一只蜗牛从C点出发,以每分20cm的速度沿CA-AB-BC的路径再回到C点,需要分的时间.10.在△ABC中,C=90,AC=2.1 cm,BC=2.8 cm.(1)求这个三角形的斜边AB的长和斜边上的高CD的长.(2)求斜边被分成的两部分AD和BD的长.11.如图,某购物中心在会十.一间准备将高5 m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?12.甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?13.如图所示,有一个圆柱形状的建筑物,底面直径为8 m,高为7 m.为方便工作人员从底部A点到达顶部的B点,要绕页 5 第建筑物修一螺旋状的梯子.试求梯子最短为多少米?14.已知:如图,D=90,A=60,AB=4,CD=2。
求:四边形ABCD的面积。
北师大版七年级数学(下)第三章检测题班级姓名:成绩:一、选择题(每小题3分,共24分)1. 有下列长度的三条线段,能组成三角形的是()A、2cm,3cm,4cmB、1cm,4cm,2cmC、1cm,2cm,3cmD、6cm,2cm,3cm2. 在下列各组图形中,是全等的图形是( )3. 下列条件中,能判断两个直角三角形全等的是( )A、一个锐角对应相等B、两个锐角对应相等C、一条边对应相等D、两条边对应相等4.已知:如图,CDAB,BEAC,垂足分别为D、E,BE、CD相交于O点,2.图中全等的三角形共有( )A.4对B..3对C 2对D.1对5.如图所示,某同学把一块三角形玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )A.带①去B. 带②去C. 带③去D. 带①和②去6.右图中三角形的个数是( )页 6 第A.6B.7C.8D.97.如果两个三角形全等,那么下列结论不正确的是( )A.这两个三角形的对应边相等B.这两个三角形都是锐角三角形C.这两个三角形的面积相等D.这两个三角形的周长相等8.下列图中,与左图中的图案完全一致的是( )二、填空题:(每题3分,共18分)9、为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是。
10、如图1所示:(1)在△ABC中,BC边上的高是;(2)在△AEC中,AE边上的高是;11、如图2,△ABC≌△AED,C=400,EAC=300,B=300,则D= ,12、如图3,已知2,请你添加一个条件使△ABC≌△BAD,你的添加条件是是(填一个即可)。
13、若一个等腰三角形两边长分别是3 cm和5 cm,则它周长是____ cm。
14、如图4,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF相等,若CBA=320,则FED= ,EFD= 。
页 7 第三、解答题(共58分)15、(6分)尺规作图:小明作业本上画的三角形被墨迹污染,他想画出一个与原来完全一样的三角形,请帮助小明想办法用尺规作图法画一个出来,并说明你的理由。
16、(6分)如图,两根钢绳一端固定在地面两个铁勾上,另一端固定在电线杆上(电线杆垂直于地面),已知两根钢绳的长度相等,则两个铁柱到电线杆底部的距离即BO与CO相等吗?为什么?17、(6分)如图AB、CD相交于点O,AO=BO,AC∥DB。
那么OC与OD相等吗?说明你的理由。
小明的解题过程如下,请你说明每一步的理由。
解:OC=OD,理由如下:∵AC∥DB ( )B D ( )在△AOC和△BOD中B ( 已证)D ( )AO=BO ( )△AOC≌△BOD ( )OC=OD ( )18、(6分)已知:AC和BD相交于点E,AB∥DC,AB=DC,试说明:BE=DE页 8 第19、(6分)如图,把大小为44的正方形方格分割成两个全等图形,例如图1,请在下图中,沿着虚线画出四种不同的分法,把44的正方形方格分割成两个全等图形.20、(7分)已知:AD∥BC,AD=CB,AE=CF,请问D吗?为什么?21(7分)有一座小山,现要在小山A、B的两端开一条隧道,施工队要知道A、B两端的距离,于是先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE 的长,就是A、B的距离,你能说说其中的道理吗?22、(7分)如图:已知AB=AE,BC=ED,E,AFCD,F为垂足, 求证:①AC=AD; ②CF=DF。
23、(7分)已知:如图,,。
求证:。
页 9 第。
