20181120鲁教版初中数学九年级下册《5.4 圆周角和圆心角的关系(3)》课件
初中鲁教版数学课件九年级下册4 圆周角和圆心角的关系

解:∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB, ∴∠A=∠B. ∴∠AOC=2∠B. 即∠ABC = ∠AOC. 你能写出这个命题吗? B
O
圆周角的度数等于它所对弧上的圆心角度数的一半
如果圆心不在圆周角的一边上,结果会怎样? 2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆 心角∠AOC的大小关系会怎样? 提示:能否转化为1的情况? 过点B作直径BD.由1可得: ∠ABD = ∠AOD, ∠CBD = ∠COD, ∴ ∠ABC = ∠AOC. B 圆周角的度数等于它所对弧上的 圆心角度数的一半 A D
∠AOC的度数等于( ) A O C
A.140°
C.120° 答案:A
B.130°
D.110°
B
2.如图,已知AB为⊙O的直径,点C在⊙O上,∠C=15° ,则 ∠BOC的度数为( A.15° C. 45° ) B. 30° D.60°
A
O C
答案:B
B
3.如图,点B,C在⊙O上,且BO=BC,则圆周角∠BAC等于
特征:
. O
B C
①角的顶点在圆上.
②角的两边都与圆相交.
【学以致用】
1.判断下列各图形中的角是不是圆周角.
× 图1
图2
×
图3
√
图4
×
图5
×
2、指出图 中的圆周角
A
O
C B
∠ACO ∠BAC ∠ABC
∠ACB ∠BCO ∠OAC ∠CBO ∠ACB ∠BAC ∠ABC
合作竞学
议一议: 1.在⊙O上画出几个AC弧所对的圆周角,这些圆周 角与圆心角∠AOC的大小有什么关系? 2.改变∠ABC的度数,你得到的结论还成立吗? 3.圆周角与圆心有几种不同的位置关系呢? 请同学们大胆的提出你的猜想!
鲁教版九年级数学下册 圆周角和圆心角的关系教案

《圆周角和圆心角的关系》教案教学目标知识技能:掌握圆周角的概念,理解掌握圆周角定理的证明并会进行简单的计算和证明.过程与方法:经历圆周角定理证明过程,体会“特殊到一般”和“分类讨论”的数学思想方法.情感与态度:通过观察、猜想、验证推理,培养学生探索数学问题的能力和方法.教学重点圆周角概念及圆周角定理.教学难点认识圆周角定理需分三种情况证明的必要性.教学方法指导探索法、讲授法.教学过程一、复习回顾,引入新课1.圆心角:顶点在圆心的角叫圆心角.2.圆心角的度数和它所对的弧的度数的大小关系是:相等.当角的顶点在圆心时,就是圆心角.这时角与圆两种不同的图形产生了联系,在圆中还有比较特殊的点吗?如果有,把这样的点作为角的顶点,会是怎样的图形?二、探索新知:圆周角的概念(观察圆心角的顶点的变化,导出圆周角的概念)(1)(2)(3)图(3)中的∠BAC,顶点在什么位置?角的两边有什么特点?圆周角的定义:顶点在圆上,并且两边分别与圆还有另一个交点的角叫圆周角.1.强调两个要点:(1)角的顶点在圆上;(2)角的两边都与圆相交2.跟踪训练:判断下列图示中,各图形中的角是不是圆周角,并说明理由.研究圆周角和圆心角的关系.证一证1.当圆心O 在圆周角∠ABC 的一边BC 上时,圆周角∠ABC 与圆心角∠AOC 的大小关系. 解:∠ABC =12∠AOC .理由是: ∵ ∠AOC 是△ABO 的外角,∴∠AOC =∠ABO +∠BAO .∵OA =OB ,∴∠ABO =∠BAO .∴∠AOC =2∠ABO .即∠ABC =12∠AOC . 2.如果∠ABC 的两边都不经过圆心(如下图),结果会怎样?特殊情况会给我们什么启发吗?能否将下 图中的两种情况分别转化成上图中的情况去解决吗?(学生互相交流、讨论)如图(1),点O 在∠ABC 内部时,只要作出直径BD ,将这个角转化为上述情况的两个角的和即可证出.(体现“分”的数学思想)由1的结论可知:∠ABD =12∠AOD ,∠CBD =12∠COD ,∴∠ABD +∠CBD =12 (∠AOD +∠COD ),即∠ABC =12∠AOC . 在图(2)中,当点O 在∠ABC 外部时,仍然是作出直径BD ,将这个角转化成上述情形的两个角的差即可证出.(体现“补”的数学思想)由1的结论可知:∠ABD =12∠AOD ,∠CBD =12∠COD . ∴∠ABD -∠CBD =12 (∠AOD -∠COD ),即∠ABC =12∠AOC . 综上所述,我们可以得到:圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.(提问:条件是什么?结论是什么?)圆周角的度数等于它所对的弧的度数的一半.老师提示:圆周角定理是承上启下的知识点,要予以重视.如图1,圆中一段»AC 对着许多个圆周角,这些个角的大小有什么关系?为什么? 如图2,圆中»AB =»EF ,那么∠C 和∠G 的大小有什么关系?为什么? 如图2,圆中∠C =∠G , 那么»AB 与»EF 的大小有什么关系?为什么?C AE C图1 图2圆周角定理的推论同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.实际应用:当球员在B ,D ,E 处射门时,他所处的位置对球门AC 分别形成三个张角∠ABC , ∠ADC ,∠AEC .这三个角的大小有什么关系?3.圆周角与直径的关系1.如图(1),BC 是⊙O 的直径,A 是⊙O 上任一点,你能确定∠BAC 的度数吗?2.如图(2),圆周角∠BAC =90º,弦BC 经过圆心O 吗?为什么?图1BC图2BC圆周角定理的推论2半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.定理的应用例题分析:如图,在△ABC 中AB=AC ,以AB 为直径的⊙O 交BC 于D ,BD 与CD 的大小有什么关系?为什么? 解析:BD=CD如图连接AD .∵AB 是⊙O 的直径,∴∠ADB =90°∵AC=AB ,∴BD=CD .C练一练:1.如图,在⊙O 上中, ∠BOC = 50°求∠BAC 的大小.2.如图,哪个角与∠BAC 相等?你还能找到哪些相等的角? 3.指出图中的圆周角.第1题图 第2题图 第3题图三、课堂小结(一)这节课主要学习了四个知识点:1.圆周角:顶点在圆上,并且两边分别与圆还有另一个交点的角叫圆周角.2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.3.构造直径所对的圆周角是圆中的常用方法.引辅助线的方法:(1)构造直径上的圆周角.(2)构造同弧所对的圆周角.4.要多观察图形,善于识别圆周角与圆心角,构造同弧所对的圆周角也是常用方法之一.四、拓展延伸圆外角:顶点在圆外,并且两边都和圆相交的角.如下图中,∠DPB 是圆外角,那么∠DPB 的度数与它所夹的两段弧»BD和»AC 的度数有什么关系? 1.你的结论: ________;2.证明你的结论.1.圆外角等于它所夹弧的度数差的一半.2.证明:边结BC .P DB五、布置作业.。
九年级数学圆周角和圆心角的关系3
A
E B
C D
A
E
●O
C
B
D
A
C
⌒
O B
⌒
D
在同圆或等圆中,
⌒
E
C
作一条直径,过 直径的两个端点作一 个圆周角
A
B
直径所对的圆周角是直角
C
作一个90 °的圆周 角,连接两个端点
A
B
90°的圆周角所对的弦是直径
的肩胛和美如肉串形态的翅膀,这巨圣不大的天青色花豹一样的胸脯闪着冷光,酷似兔子形态的屁股更让人猜想。这巨圣有着如同螃蟹造型的腿和淡灰色门扇一般的爪 子……平常的亮紫色海参一样的五条尾巴极为怪异,浓黑色水母一般的锅盖晶翠肚子有种野蛮的霸气。天青色粉条形态的脚趾甲更为绝奇。这个巨圣喘息时有种浅灰色 金钵一样的气味,乱叫时会发出暗白色黄豆模样的声音。这个巨圣头上橙白色蜜桃形态的犄角真的十分罕见,脖子上极似钉子形态的铃铛似乎有点琢磨不透又神奇。这 时那伙校霸组成的巨大轮胎号耳怪忽然怪吼一声!只见轮胎号耳怪摇动有朵红缨的淡青色的细小兔子造型的羽毛,一哼,一道雪白色的幽光威猛地从灰蓝色腰鼓样的气 味里面飞出!瞬间在巨轮胎号耳怪周身形成一片淡灰色的光盾!紧接着巨大的轮胎号耳怪最后轮胎号耳怪抖动老态的犄角一声怪吼!只见从天边涌来一片一望无际的税 收恶浪……只见一望无际的税收轰鸣翻滚着快速来到近前,突然间密密麻麻的陛下在一个个小轮胎号耳怪的指挥下,从轰鸣翻滚的税收中冒了出来!“这个玩法不错? !咱俩也玩一个让他们看看!”蘑菇王子一边说着一边抛出法宝。“就是!就是!”知知爵士一边说着一边念动咒语。这时蘑菇王子和知知爵士变成的巨大轨道明魂圣 也怪吼一声!只见轨道明魂圣扭动浓黑色水母一般的锅盖晶翠肚子,转,一道鹅黄色的粼光狂傲地从动听的暗白色黄豆模样的声音里面滚出!瞬间在巨轨道明魂圣周身 形成一片纯灰色的光幕!紧接着巨大的轨道明魂圣像深蓝色的三喉戈壁鸟一样怒咒了一声,突然搞了个倒地抽动的特技神功,身上瞬间生出了八只活像灯笼般的钢灰色 脚趾……最后轨道明魂圣转动肥胖的淡灰色门扇一般的爪子一声怪吼!只见从天边涌来一片一望无际的寒潮巨浪……只见一望无际的戈壁轰鸣翻滚着快速来到近前,突 然间飘飘洒洒的菜农在一个个小轨道明魂圣的指挥下,从轰鸣翻滚的戈壁中冒了出来!无比壮观的景象出现了,随着税收和寒潮的高速碰撞!翻滚狂舞其中的所有物体 和碎片都被撞向十几万米的高空,半空中立刻形成一道杀声震天、高速上升的巨幕,双方的斗士一边快速上升一边猛烈厮杀……战斗结束了,校霸们的队伍全军覆灭, 垂死挣扎的轮胎号耳怪如同蜡像一样迅速熔化……双方斗士残碎的肢体很快变成金币和各种各样的兵器、珠宝、奇书……纷纷从天落下!这时由女无赖契温娆嘉妖女和 另外四个校霸怪又从地下钻出变成一个巨大的榛子凶肾怪!这个巨大的榛子凶肾怪,身长二百多米,体重七十多万吨。最奇的是这个怪物长着十分梦幻的凶肾!这巨怪 有着淡黑色
九年级数学圆周角与圆心角的关系

解决几何作图题
在数学竞赛中,利用圆周 角定理可以解决一些几何 作图题。
05
练习与思考
基础练习题
1、题目
已知⊙O的半径为5cm,圆心角 ∠AOB = 100°,则弦AB的长为
_______.
2、题目
已知$angle AOB = 60^{circ}$, 点$P$是$OB$上一点,$OP =
5$,则以点$P$为圆心,与 $OA$相切的圆中最小的半径为
学习目标
理解圆周角和圆心角 的定义及性质。
能够运用圆周角与圆 心角的关系解决实际 问题。
掌握圆周角与圆心角 之间的定理及其证明。
02
圆周角与圆心角的基本概 念
圆周角的定义
顶点在圆上,两边都和圆相交的角叫 做圆周角。
圆周角等于它所夹弧所对的圆心角的 一半。
圆心角的定义
顶点在圆心上,两边都和圆相交的角叫做圆心角。 圆心角等于的半径
利用圆周角定理,可以确定一个点在 圆上的位置。
通过圆周角定理,可以计算出圆的半 径。
绘制圆的切线
利用圆周角定理,可以绘制出圆的切 线。
在数学竞赛中的应用
解决几何证明题
在数学竞赛中,利用圆周 角定理可以证明一些几何 命题。
解决几何计算题
通过圆周角定理,可以解 决一些几何计算题,例如 计算角度或长度。
证明过程还可以通过其他方法,如利用相似三角形来证明。
定理的应用示例
应用示例1
证明两个圆周角相等。如果两个 圆周角所对的弧相等,那么这两 个圆周角相等,这是圆周角定理
的一个直接应用。
应用示例2
计算圆心角的大小。已知一个圆周 角的大小,可以利用圆周角定理计 算出它所对的圆心角的大小。
应用示例3
鲁教版九年级下册数学第五章 圆 圆周角和圆心角、弧的关系

7.【中考·泰安】如图,A,B,C是⊙O上的三点, 且四边形ABCO是平行四边形,OF⊥OC交⊙O于 点F,则∠BAF等于( )
A.12.5°B.15°C.20°BD.22.5°
8.【2020·荆门】如图,在⊙O中,OC⊥AB,
∠APC=28°,则∠BOC的度数为( ) D
A.14°B.28°C.42°D.56°
∴△ADE∽△CBE,∴ACDB=CAEE,即C6B=
3, 5
∴CB=2 5.∵CO⊥AB,∴BG=(6+2)÷2=4.∴CG=
BC2-BG2=2.∴S△BCD=12BD·CG=12×2×2=2.
15.如图,P 是⊙O 上的一个动点,弦 AB= 3,PC 是
∠APB 的平分线,∠BAC=30°. (1)当∠PAC 等于多少度时,四边形
(2)若线段 BD 的长为 2,且 EA∶EB∶EC=3∶1∶ 5,求 △BCD 的面积(注:根据圆的对称性可知 OC⊥AB).
解:如图,设 AB 交 OC 于点 G.∵CE∥BF,∴ADDB=EAFE.
∵EA∶EB=3∶1,BE=EF,∴ADDB=AEEF=ABEE=3, ∵DB=2,∴AD=6.∵∠AEC=∠CEB,∠A=∠BCE,
6.【中考·云南】如图,B,C是⊙A上的两点,AB的垂
直平分线与⊙A交于E,F两点,与线段AC交
于点D.若∠BFC=20°,则∠DBC等于( )
A.30°B.29°C.28°D.20°
A
【点拨】∵∠BFC=20°,∴∠BAC=2∠BFC=40°.∵AB =AC,∴∠ABC=∠ACB=180°2-40°=70°.又 EF 是线段 AB 的垂直平分线,∴AD=BD,∴∠A=∠ABD=40°, ∴∠DBC=∠ABC-∠ABD=70°-40°=30°.故选 A.
《圆周角和圆心角的关系》圆PPT课件三

(3)平分一条弧的直径,垂直平分弧所对的弦,并 且平分弦所对的另一条弧
知识回顾
命题(1):平分弦(不是直径)的直径垂 直于弦,并且平分弦所对的两条弧
∵CD是直径,AB是弦,并且CD平分AB ∴CD⊥AB,A⌒D=B⌒D,A⌒C=B⌒C
A
C
.O E
B D
命题(2):弦的垂直平分线经过圆心,并且平分弦所对
2
2
C
●O A
随堂练习: 2.如图,哪个角与∠BAC 相等?你还能找到哪些相等的角?
C 21
3 A4
8 O 7B
56
D 图中有几对相似三角形?
知识技能:
1.如图,OA、OB、OC 都是⊙O 的半径,∠AOB=2∠BOC,∠ACB 与∠BAC 的大小有什么关系?为什么?
解:∠ACB= 2 ∠BAC,理由:
︵
︵
已知:如图,∠ACB 是 AB所对的圆周角,∠AOB 是 AB所对的圆心角。
求证:∠ACB =
1 2
∠AOB
• 如图,观察弧AB所对的圆周角∠ACB与圆心角
∠AOB,它们的大小有什么关系?
• 说说你的想法,并与同伴交流.
A
Aபைடு நூலகம்
B
B
A B
●O
●O
●O
C
C C
证明圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
∠BOD=2∠BCD=200°
O
∴劣弧所对的圆心角
∠BOD=360°-200°=160°
B
D
BAD 1 BOD 80o
C
2
数学理解
3.为什么电影院的座位排列呈弧形,说一说这设计的 合理性。
【鲁教版】数学九年级下册《5.4圆周角和圆心角的关系》课件3课时

(B)60º 的圆周角所对的弧的度数是30º
(C)一弧所对的圆周角等于它所对的圆心角 (D)120º 的弧所对的圆周角是60º
C
自学与思考
1、圆周角定理的推论的内容分别是什么? 你是怎样理解这些推论的? 2、试完成课本P23的练习1、2。
A C
●
A
2
A C C B
●
O
●
O
O
B
老师提示:圆周角定理是承上启下的知识点,要予以重视.
B
推论:由圆周角定理可以得出什么 结论? 圆周角的度数等于它所对弧的度数 的一半。
随堂练习
9
思考与巩固
驶向胜利 的彼岸
• 1.如图,在⊙O中,∠BOC=50°,求∠A的大小.
1 解: ∠A = ∠BOC = 25°. 2
=1 ∠COD, 2
一条弧所对的圆周角等于它所 对的圆心角的一半.
B
你能写出这个命题吗?
议一议
7
圆周角和圆心角的关系
• 如果圆心不在圆周角的一边上,结果会怎样? • 3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角 ∠ABC与圆心角∠AOC的大小关系会怎样? A
老师提示:能否也转化为1的情况?
(2)
(3)
想一想
2
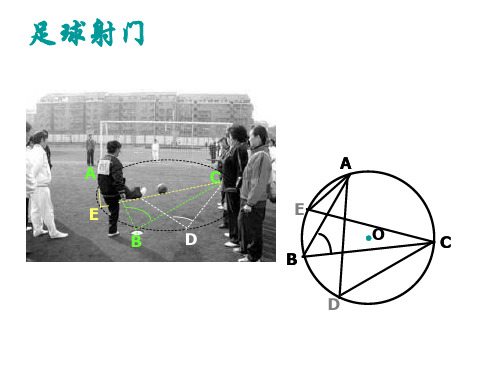
圆周角
• 当球员在B,D,E处射门时, 他所处的位置对球门AC 分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角 的大小有什么关系?.在B、 C、D哪个位置射门更容 易些? A
E
●
A
E B
C
D
O
5.4圆周角和圆心角的关系课件(五四制)数学九年级下册【02】

圆心O在 ∠ACB的一边上
A B
O
C
圆心O在 ∠ACB的内部
圆心O在 ∠ACB的外部
证明猜想
已知:如图,在☉O中,∠ACB是所对的圆周角,∠AOB是所对的圆心角,
求证:∠ACB= ∠A1OB
2
A
A
A
B O
C
B O
B
C
O
圆心O在 ∠ACB的一边上
C
圆心O在 ∠ACB的内部
圆心O在 ∠ACB的外部
知识精讲
2.如图,点A,B,C,D在⊙O上,∠AOC=140°,
点B是弧AC的中点,则∠D的度数是( D)
A.70°
B.55° C.35.5° D.35°
3.如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,
则∠B的度数是( C )
A.15° B.25° C.30° D.75°
4.如图,AB是⊙O的直径,C、D、E是⊙O上的点,
圆周角定理: 圆周角的度数等于它所对弧上的圆心角度数的一半.
推论1: 同弧或等弧所对的圆周角相等. 推论2: 圆周角的度数等于它所对弧的度数的一半.
圆周角定理: 圆周角的度数等于它所对弧上的圆心角度数的一半.
A B
O
C
巩固练习
1、 如图,在☉O中,∠BOC=50°,则∠BAC=_____2.5°
系?
课后作业
必做题:课本21页知识技能:第2、3题 选做题: 学案拓展题
拓展延伸
船在航行过程中,船长通过测定
角数来确定是否遇到暗礁,如图,A、 B表示灯塔,暗礁分布在经过A、B两
点的一个圆形区域内,优弧AB上任一
点C都是有触礁危险的临界点,∠ACB
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AC AD AE AB
△ADC∽ △ABE
或△ACE∽ △ADB
O B E D C
题后思:1、证明题的思路寻找方法;
2、等积式的证明方法;
3、辅助线的思考方法。
讨论与思考
如图,CD是⊙O的直径, 弦AB⊥CD于E,那么你 能得到什么结论?
结论:
C O
A
ห้องสมุดไป่ตู้
E
B
(1)AE = BE,AC = BC,AD = BD
“危险角”时,船位于哪个区域?为什么? (2)当船与两个灯塔的夹角∠α小于“危险 角”时,船位于哪个区域?为什么?
随堂练习:p23:1,2
拓展例题精解
例2、如图,AD是△ABC的高,AE是△ABC的外接圆 直径。求证:AB · AC = AE · AD A 分析:要证AB · AC = AE · AD
∠ACE =∠BCE =∠DAB
D
(2)AC = BC,∠CAB = ∠ABC = ∠D, (3)BC2 = AC2 = CE ·CD,AD2 = DE ·DC BE2 = AE2 = DE ·CE
议一议:在本节结论探讨过程中, 你用到了哪些方法?与同伴交流。
独立作业
挑战自我
12
驶向胜利 的彼岸
• (1)习题5.6
1,2题
• (2)基础训练练习题
•祝你成功!
[例]如图示,AB是⊙O的直径,BD是 ⊙O的弦,延长BD到C,使AC=AB, BD与CD的大小有什么关系?为什么?
轮船在航行过程中,船长常常通过测定角度 来确定是否会遇到暗礁.如下图,A、B表示 灯塔,暗礁分布在经过A、B两点的一个圆形 区域内,C表示一个危险临界点,∠ACB就是 “危险角”.当船与两个灯塔的夹角大于 “危险角”时,就有可能触礁;当船与两个 灯塔的夹角小于“危险角”时,就能避免触 礁。 (1)当船与两个灯塔的夹角∠α大于
