5以内数的分解组合练习题
5以内分解组成练习题

5以内分解组成练习题一、填空题(每题2分,共20分)1. 5可以分解成1和______。
2. 5可以分解成2和______。
3. 5可以分解成3和______。
4. 5可以分解成4和______。
5. 5可以分解成______和1。
6. 5可以分解成______和2。
7. 5可以分解成______和3。
8. 5可以分解成1和______。
9. 5可以分解成2和______。
10. 5可以分解成3和______。
二、选择题(每题2分,共20分)11. 下列哪组数字不能组成5?A. 1和4B. 2和3C. 3和2D. 4和112. 5可以分解成以下哪些组合?A. 1和4B. 2和2C. 3和1D. 4和013. 5分解成两个数的和,其中一个数是2,另一个数是______。
A. 1B. 3C. 4D. 214. 如果5分解成两个数,其中一个数是1,另一个数可能是以下哪个?A. 2B. 3C. 4D. 515. 5分解成两个数的和,其中一个数是3,另一个数是______。
A. 1B. 2C. 3D. 4三、判断题(每题1分,共10分)16. 5可以分解成1和1。
()17. 5可以分解成2和2。
()18. 5可以分解成3和3。
()19. 5可以分解成4和4。
()20. 5可以分解成5和0。
()四、连线题(每题2分,共20分)21. 将下列数字与它们对应的分解组合连线。
1 A. 1+42 B. 2+33 C. 3+24 D. 4+15 E. 5+0五、应用题(每题5分,共20分)22. 小明有5个苹果,他想平均分给2个朋友,每个朋友可以得到几个苹果?23. 小红有5支铅笔,她想分给3个朋友,每个朋友至少可以得到1支铅笔,问小红可以怎么分?24. 学校有5个篮球,需要分给5个班级,每个班级至少可以得到1个篮球,问学校可以怎么分?25. 一个班级有5个小组,老师想给每个小组分配一些书,如果每个小组至少得到1本书,问老师可以怎么分配?六、综合题(每题10分,共20分)26. 假设你有5个巧克力,你需要将它们分给5个不同的孩子,每个孩子至少得到1个巧克力。
小学数学分解组合练习题

小学数学分解组合练习题1. 一本书的页码用四个数字表示,其中不含有数字0,也不含有数字9。
问这本书最多有多少页?解析:由于不含有数字0和数字9,所以每一个数字都有8个选择(1, 2, 3, 4, 5, 6, 7, 8)。
设这本书的页数为abcd,那么a, b, c, d都有8个选择。
根据乘法原理,一共有8 * 8 * 8 * 8 = 8^4 = 4096 个可能。
因此,这本书最多有4096页。
2. 一家公司共有7个项目,现需要从中选择3个项目进行合作。
问有多少种选择方式?解析:由于需要选择3个项目,所以可以使用组合的方法进行计算。
C(7, 3)表示从7个项目中选择3个的组合数。
根据组合的计算公式,C(7, 3) = 7! / [(3!)(7-3)!] = (7 * 6 * 5) / (3 * 2 * 1) = 35。
因此,有35种选择方式。
3. 小明家有4种水果:苹果、香蕉、橙子和葡萄。
他每天从中选择2种水果搭配作为早餐水果。
问他一共有多少种早餐水果搭配方式?解析:小明每天从4种水果中选择2种水果,可以使用组合的方法进行计算。
C(4, 2)表示从4种水果中选择2种的组合数。
根据组合的计算公式,C(4, 2) = 4! / [(2!)(4-2)!] = (4 * 3) / (2 * 1) = 6。
因此,小明一共有6种早餐水果搭配方式。
4. 一个密码锁的密码为4位数,每一位数字从1-9中选择,且不允许重复。
问一共有多少种可能的密码?解析:由于每一位数字都有9个选择,且不允许重复,所以第一位有9种选择,第二位有8种选择,第三位有7种选择,第四位有6种选择。
根据乘法原理,一共有9 * 8 * 7 * 6 = 3024种可能的密码。
5. 一张纸被折叠3次,问一共有多少种不同的折叠方式?解析:每一次折叠都相当于在已有的折叠方式上新增一种可能性。
第一次折叠有1种方式,第二次折叠有2种方式,第三次折叠有4种方式。
15以内数的分解与组成练习

15以内数的分解与组成练习
概述
本文档旨在提供一些练,帮助学生们掌握15以内数的分解与组成。
分解15以内的数
1. 将15以内的数分解成两个数的组合。
例如:
- 7 = 3 + 4
- 9 = 2 + 7
2. 将15以内的数分解成三个数的组合。
例如:
- 10 = 4 + 3 + 3
- 13 = 4 + 4 + 5
3. 将15以内的数分解成更多个数的组合。
例如:
- 12 = 2 + 2 + 4 + 1 + 3
- 15 = 5 + 3 + 4 + 1 + 2
组成15以内的数
1. 根据题目中给定的数,组合成15以内的数。
例如:
- 如果题目中给定了数字2和3,可以组成5。
- 如果题目中给定了数字5、5、2和1,可以组成13。
2. 利用给定的运算符号(如加号、减号、乘号和除号),组成15以内的数。
例如:
- 如果题目中给定了+、-和×,可以用这些符号组合出不同的运算式,使结果等于15。
示例题目
1. 请将数字6分解成两个数的组合。
答案:6 = 2 + 4
2. 请将数字11分解成三个数的组合。
答案:11 = 3 + 3 + 5
3. 请用给定的数字5、2和符号×,组合出结果等于15的运算式。
答案:5 × 2 + 5 = 15
总结
通过这些练,学生们可以提高对15以内数的分解与组成能力,培养他们的数学思维和逻辑推理能力。
---
注:本文档提供的练习仅供参考,不保证涵盖全部情况,建议
学生根据自身情况进行适当的练习和总结。
小学数学一年级上册5以内数的分解练习题(共10套)
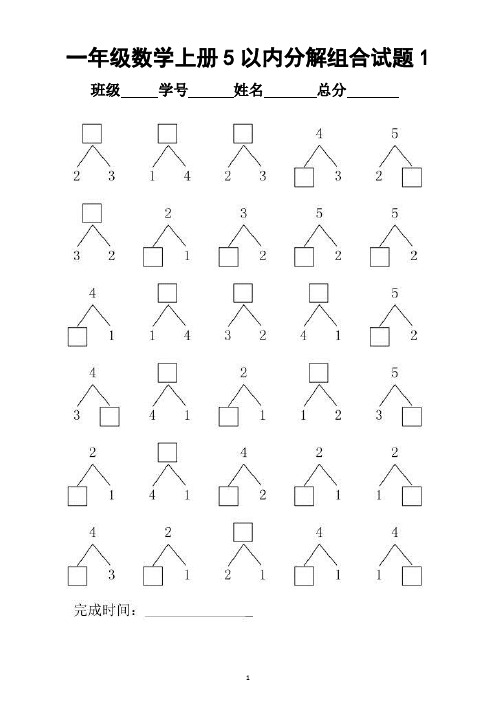
班级学号姓名总分
一年级数学上册5以内分解组合试题2
班级学号姓名总分
一年级数学上册5以内分解组合试题3
班级学号姓名总分
一年级数学上册5以内分解组合试题4
班级学号姓名总分
一年级数学上册5以内分解组合试题5
班级学号姓名总分
一年级数学上册合试题7
班级学号姓名总分
一年级数学上册5以内分解组合试题8
班级学号姓名总分
一年级数学上册5以内分解组合试题9
班级学号姓名总分
一年级数学上册5以内分解组合试题10
班级学号姓名总分
6以内数的分解与组合练习题(按规律)

6以内数的分解与组合练习题(按规律)本文档将给出一系列涉及6以内数的分解与组合的练题,旨在帮助学生巩固对这些数的认识和理解。
这些练题按照一定的规律组织,可以帮助学生更好地掌握数的分解与组合的技巧。
1. 分解练题练1:分解数6将数6分解成两个较小的数的和。
6 = __ + __练2:分解数5将数5分解成两个较小的数的和。
5 = __ + __练3:分解数4将数4分解成两个较小的数的和。
4 = __ + __练4:分解数3将数3分解成两个较小的数的和。
3 = __ + __练5:分解数2将数2分解成两个较小的数的和。
2 = __ + __练6:分解数1将数1分解成两个较小的数的和。
1 = __ + __2. 组合练题练7:两个数的组合将两个较小的数相加,得到一个数。
选择合适的数填入空格。
__ + __ = 6练8:三个数的组合将三个较小的数相加,得到一个数。
选择合适的数填入空格。
__ + __ + __ = 6练9:四个数的组合将四个较小的数相加,得到一个数。
选择合适的数填入空格。
__ + __ + __ + __ = 6练10:五个数的组合将五个较小的数相加,得到一个数。
选择合适的数填入空格。
__ + __ + __ + __ + __ = 6练11:六个数的组合将六个较小的数相加,得到一个数。
选择合适的数填入空格。
__ + __ + __ + __ + __ + __ = 6以上是一系列涉及6以内数的分解与组合的练习题,希望能够有效地帮助学生增强对这些数的数学理解和技巧。
通过这些练习,学生将能够更加灵活地处理数字,并在数学学习中取得更好的成绩。
祝学生们顺利完成练习!。
小学数学分解与组成练习题

小学数学分解与组成练习题1. 分解与组成整数题目1:将20分解为两个整数的和,使得一个整数是两位数,另一个整数是一位数。
题目2:将35分解为两个整数的和,使得一个整数是一位数,另一个整数是两位数。
题目3:将80分解为三个整数的和,使得每个整数都是两位数。
题目4:将77分解为三个整数的和,使得每个整数都是一位数。
题目5:将100分解为四个不同整数的和,使得每个整数都是两位数。
2. 分解与组成简单运算题目1:如果8 + y = 17,求y的值。
题目2:如果43 - x = 15,求x的值。
题目3:如果12 × m = 60,求m的值。
题目4:如果63 ÷ n = 7,求n的值。
题目5:如果a × b = 36,且a > b,求满足条件的a和b的值。
3. 数字的分解与组成题目1:将78拆分成两个数,使得个位数是3,十位数是7。
题目2:将56拆分成两个数,使得个位数比十位数小2。
题目3:将98拆分成两个数,使得个位数比十位数大3。
题目4:将24拆分成两个数,使得个位数是4,十位数是整数。
题目5:将62拆分成两个数,使得个位数和十位数的和为10。
4. 分解与组成的应用题目1:某班级共有30名学生,其中男生人数和女生人数的比例是2:3,分别使用x和y表示男生和女生的人数,请用x和y表示男生和女生的人数。
题目2:一个3位数的十位数比个位数多3,百位数比个位数多5,且三个数字的和是18,求这个3位数。
题目3:将25分解成3个数的和,使得第一个数比第二个数多2,第二个数比第三个数多3。
题目4:将72分解成两个数的和,这两个数的比是4:5。
题目5:某商店有一批相同的商品,总共有168件,已经售出了x 件,剩余的数量是总数量的4/7,请用x表示已售出数量。
结束语:以上是小学数学分解与组成的练习题。
通过这些题目的练习,可以帮助学生提升对数学分解与组成的理解和应用能力,同时加强他们的计算和逻辑思维能力。
2024大班数学《5的分解与组成》

01数的分解与组成基本概念Chapter分解与组成定义分解组成培养数感为加减法打基础解决实际问题030201数学中重要性及应用总数不变无论一个数如何分解,其总数始终保持不变。
例如,无论将5分解成哪两个数相加,其和始终是5。
分解方式多样5以内的数可以有多种分解方式,如5可以分解成2和3,也可以分解成1和4等。
组成数唯一虽然一个数可以有多种分解方式,但对于每一种分解方式,其组成数是唯一的。
例如,5分解成2和3后,2和3就是5的唯一的组成数。
分解与组成相互对应数的分解与组成是相互对应的,一个数的分解数就是其组成数,反之亦然。
例如,5的分解数2和3就是5的组成数。
5以内数分解与组成特点025的分解方法及实例演示Chapter按顺序逐步分解法01020304将5分解为1和4将5分解为2和3将5分解为3和2将5分解为4和1任意组合分解法不按特定顺序分解强调分解的多样性图形化表示方法使用实物或图形表示5的分解通过图形化表示加深理解实际生活应用举例分享场景组合场景购物场景035的组成方式及规律探究Chapter单一元素组成方式5个相同的元素相加例如5个1相加,即1+1+1+1+1=5。
单一元素重复5次例如一个元素重复5次,也可以表示成5。
1 2 3两个不同的元素组合三个不同的元素组合多于三个元素的组合多元素组合成5情况讨论规律性总结与发现奇偶性规律5是一个奇数,因此它不可能被分解成两个偶数相加。
分解方式有限性对于给定的一个数,其分解方式是有限的。
例如,5只能被分解成1和4、2和3等有限的几种方式。
分解与组成的可逆性如果一个数可以被分解成两个数相加,那么这两个数也可以组合成原来的数。
例如,5可以分解成2和3,那么2和3也可以组合成5。
创意性组合尝试数字与字母组合图形组合将数字与字母进行组合,例如用数字2和字母T过来的2,两者组合起来像生活中的实物组合04练习题巩固知识点掌握Chapter口头回答题目类型书面作业题目类型完成课本或练习册上的5的分解与组成相关练习题。
以内数的分解与组合练习题

以内数的分解与组合练习题2的分成:2可以分成0和2,也可以分成1和1.2的组成:2可以由0和2组成,也可以由1和1组成。
2的分成变式:2减去1等于1,2减去0等于2.2的组成变式:1加上1等于2,0加上2等于2.3的分成与组合:3可以分成0和3,1和2,2和1,3和0.也可以由1、2组成,2、1组成,3、0组成。
3的分成变式:3减去0等于3,3减去1等于2,3减去2等于1,3减去3等于0.3的组合变式:1加上2等于3,2加上1等于3,3加上0等于3.4的分成与组合:4可以分成0和4,1和3,2和2,3和1,4和0.也可以由1、3组成,2、2组成,3、1组成,4、0组成。
4的分成变式:4减去0等于4,4减去1等于3,4减去2等于2,4减去3等于1,4减去4等于0.4的组合变式:1加上3等于4,2加上2等于4,3加上1等于4,4加上0等于4.5的分成和组合:5可以分成0和5,1和4,2和3,3和2,4和1,5和0.也可以由1、4组成,2、3组成,3、2组成,4、1组成,5、0组成。
二、5的组合1+4=5.2+3=5.3+2=5.4+1=51.4.2.3.3.2.4.15.5.5.5三、5的分成变式0-5=5.1-4=3.2-3=2.3-2=1.5-1=4.5-2=3.5-3=2.5-4=1四、5的组合变式1+4=5.2+3=5.3+2=5.4+1=5六、6的分成和组合一、6的分成6.6.6.6.6.66.5.4.3.2.11.2.3.4.5.6二、6的组合1+5=6.2+4=6.3+3=6.4+2=6.5+1=61.5.2.4.3.3.3.3.4.2.5.10.1.2.3.4.5三、6的分成变式0-6=6.1-5=4.2-4=2.3-3=0.4-2=2.5-1=4四、6的组合变式1+5=6.2+4=6.3+3=6.4+2=6.5+1=6七、7的分成和组合一、7的分成1+7=8.2+6=8.3+5=8.4+4=8.5+3=8.6+2=8.7+1=8.这是8的组合变式。
