信号与系统实验2 线性系统时域分析
信号与系统实验总结1

实验总结班级:10电子班学号:1039035 姓名:田金龙这学期的实验都有:信号的时域分析、线性时不变系统的时域分析、连续时间信号系统的频域分析、连续时间在连续时间信号的频域LTI系统的复频域分析、连续时间LTI系统的频域分析。
在这学期的学习中学习了解到很多关于信号方面的处理方法加上硬件动手的实践能力,让我对课堂上所学到的知识有了更深层次的理解也加深了所学知识的印象。
下面则是对每次实验的分析和总结:实验一:信号的时域分析在第一次试验中进行信号的时域分析还有的就是学会使用MATLAB软件来利用它实现一些相关的运算并且绘制出相关的信号图。
在时域分析中掌握连续时间信号和离散时间信号的描述方法,并能够实现各种信号的时域变化和运算。
了解单位阶跃信号和单位冲激信号的拓展函数,以便于熟悉这两种函数在之后的程序中的应用。
在能够对简单信号的描述的前提下,通过一些简单的程序,实现信号的分析,时域反相,时域尺度变换和周期信号的描述。
clear,close alldt=0.01;t=-2:dt:2;x=u(t);plot(t,x)title('u signal u(t)')grid on连续时间信号的时域分析后,则是离散时间信号的仿真。
通过对连续时间信号的描述和对离散时间信号的描述,发现它们的不同之处在于对时间的定义和对函数的图形描述。
在离散时间信号的图形窗口描述时,使用的是stem(n,x)函数。
在硬件实验中,使用一些信号运算单元,加法器,减法器,倍乘器,反相器,积分器和微分器。
输入相应的简单信号,观察通过不同运算单元输出的信号。
实验二:线性时不变系统的时域分析在线性时不变系统的时域分析中主要研究的就是信号的卷积运算,学会进行信号的卷积运算和MATLAB对卷积运算的实现。
而系统则通常是由若干部件或单元组成的一个整体,根据系统所处理的信号不同,系统又有多种不同的分类。
而在学习总最常研究的则是线性时不变系统,而线性时不变系统则是形同同时满足齐次性和叠加性。
信号与系统实验
实验一信号与系统认知一、实验目的1、了解实验室的规章制度、强化安全教育、说明考核方法。
2、学习示波器、实验箱的使用、操作知识;3、学习常用连续周期信号的波形以及常用系统的作用。
二、实验仪器1、信号与系统实验箱(本次实验使用其自带的简易信号源,以及实验箱上的“信号通过系统”部分。
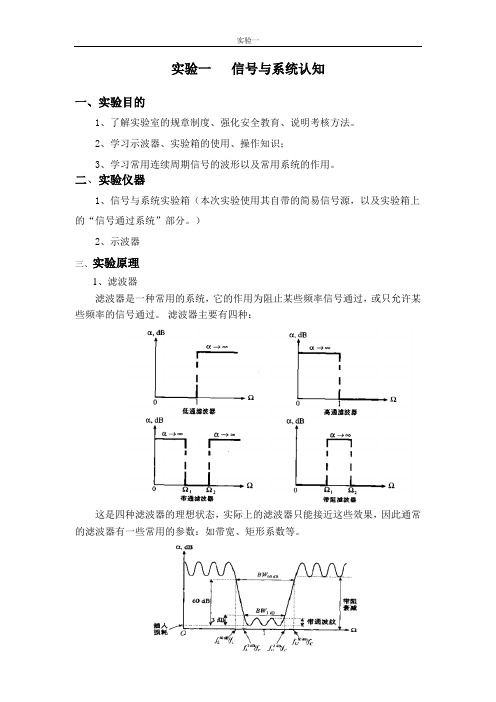
)2、示波器三、实验原理1、滤波器滤波器是一种常用的系统,它的作用为阻止某些频率信号通过,或只允许某些频率的信号通过。
滤波器主要有四种:这是四种滤波器的理想状态,实际上的滤波器只能接近这些效果,因此通常的滤波器有一些常用的参数:如带宽、矩形系数等。
通带范围:与滤波器最低衰减处比,衰减在3dB以下的频率范围。
2、线性系统线性系统是现实中广泛应用的一种系统,线性也是之后课程中默认为系统都具有的一种系统性质。
系统的线性表现在可加性与齐次性上。
齐次性:输入信号增加为原来的a倍时,输出信号也增加到原来的a倍。
四、预习要求1、复习安全操作的知识。
2、学习或复习示波器的使用方法。
3、复习典型周期信号的波形及其性质。
4、复习线性系统、滤波器的性质。
5、撰写预习报告。
五、实验内容及步骤1、讲授实验室的规章制度、强化安全教育、说明考核方法2、通过示波器,读出实验箱自带信号源各种信号的频率范围(1)测试信号源1的各种信号参数,并填入表1-1。
(2)测试信号源2的各种信号参数,并填入表1-2。
3、测量滤波器根据相应测量方法,用双踪示波器测出实验箱自带的滤波器在各频率点的输入输出幅度(先把双踪示波器两个接口都接到所测系统的输入端,调节到都可以读出输入幅度值,并把两侧幅度档位调为一致,记录下这个幅度值;之后,将示波器的一侧改接入所测系统的输出端,再调节用于输入的信号源,将信号频率其调至表1-3中标示的值,并使输入信号幅度保持原幅度值不变。
观察输出波形幅度的变化,并与原来的幅度作比较,记录变化后的幅度值。
),并将相应数据计入表1-3中。
4、测量线性系统(1)齐次性的验证自选一个输入信号,观察输出信号的波形并记录输入输出信号的参数,将输入信号的幅度增强为原信号的一定倍数后,再对输入输出输出参数进行记录,对比变化前后的输出。
第二章 信号与系统的时域分析

二 卷积积分(The convolution integral) 若 (t ) h(t ) 则 (t ) h(t ) = h (t )
x t x h t
x(t ) x( ) (t )d y(t ) x( )h (t )d
则 y(t ) ak yk (t )
k
4
信号与系统的时域分析:
一般的信号都可以表示为延迟冲激的线性组合。
结合系统的叠加性和时不变性,就能够用LTI的单位
冲激响应来完全表征任何一个LTI系统的特性。这样
一种表示在离散情况下称为卷积和;在连续时间情
况下称为卷积积分。
5
分析方法:
对信号分解可在时域进行,也可在频域或变换域 进行,相应地产生了对LTI系统的时域分析法、频 域分析法和变换域分析法。
h( n n kk n h ) uu (n k )k
1
1
k
0
...
0
k
n
12
运算过程:
k k) ,再随参变量 为 h(
点值累加,得到
将一个信号 xk 不动,另一个信号反转后成为
下,将 xk 与 hn k 对应点相乘,再把乘积的各
n
移位.在每个 n 值的情况
x( [ n] y x x[ (n n] )* [ (n) h2 (n n)] x ) y( n n) (h h1 ) 1 n h2 h (n ) h( n) h2 x(t ) 11 y(t ) x(t ) [h1 (t ) h2 (t )] h1 (t ) h2 (t )
0
16
对一般信号 x(t ) ,可以分成很多 宽度的区段, 用一个阶梯信号 x (t ) 近似表示 x(t ) .当 0 时,
信号与系统分析第二章 连续时间系统的时域分析

第二章 连续时间系统的时域分析
2.1.1
对系统进行分析时, 首先要建立系统的数学模型。 对于电的系统, 只要利用理想的电路元件, 根据基尔霍 夫定律, 就可以列出一个或一组描述电路特征的线性 微分方程。 现举例来说明微分方程的建立方法。
第二章 连续时间系统的时域分析
例2.1 图2.1所示为RLC串联电路, 求电路中电流i(t) 与激励e(t)之间的关系。
第二章 连续时间系统的时域分析
(3)
y(t) C 1 e t C 2 e 6 t5 2c 0 1o 2 t)s 5 3 (s0i2 n t) (
D(p)y(t)=N(p)f(t)
y(t) N(p) f (t) D(P)
式(2.15)中的 N ( p ) 定义为转移算子, 用H(p)表示,
D (P)
(2.14) (2.15)
H (p ) N D ( (P p ) ) b a m n p p m n a b n m 1 1 p p n m 1 1 a b 1 1 p p a b 0 0 (2.16)
t0
解 (1) 齐次解。 由例2.4 yh (t)=C1e-t+C2e-6t
第二章 连续时间系统的时域分析
(2) 特解。 查表2.2, yp(t)=B1cos (2t)+B2sin(2t)
-14B1+2B2-6=0 2B1+14B2=0
于是,
B15201,
B2530
yp(t)5 20 c 1o2ts) (530 si2 nt)(
第二章 连续时间系统的时域分析
3. 用算子符号表示微分方程, 不仅书写简便, 而且在建 立系统的数学模型时也很方便。 把电路中的基本元件R、 L、 C的伏安关系用微分算子形式来表示, 可以得到相应 的算子模型, 如表2.1所示。
实验二线性系统分析

实验二线性系统分析一、实验目的通过实验,掌握线性系统的特性和分析方法,了解系统的幅频特性和相频特性。
二、实验原理1.线性系统线性系统是指遵循叠加原理和比例原理的系统,可以表示为y(t)=h(t)⊗x(t),其中h(t)为系统的冲激响应,x(t)为输入信号,y(t)为输出信号,⊗为线性卷积操作。
2.系统的频域特性系统的频域特性可以通过离散傅里叶变换(Discrete Fourier Transform,简称DFT)来进行分析,DFT是将离散时间域信号变换到离散频域的方法。
3.系统的幅频特性系统的幅频特性描述了输出信号的幅度随频率变化的规律,可以通过对系统的单位冲激响应进行DFT来得到。
4.系统的相频特性系统的相频特性描述了输出信号的相位随频率变化的规律,可以通过对系统的单位冲激响应进行DFT来得到。
三、实验步骤1.准备工作:a.将信号发生器的频率设置为100Hz,幅度设置为5V。
b.将示波器的触发模式设置为自动,并调节水平位置使信号波形居中显示。
2.测量系统的幅频特性:a.将信号发生器的输出信号连接到线性系统的输入端口,将示波器的通道1连接到线性系统的输入端口,将示波器的通道2连接到线性系统的输出端口。
b.调节示波器的时间基准使波形显示在适当的范围内。
c.调节信号发生器的频率和示波器的触发模式,观察输入信号和输出信号的波形。
d.在示波器中进行幅度测量,并记录下输入信号和输出信号的幅值。
e.使用DFT算法对输入信号和输出信号进行频谱分析,得到幅频特性曲线。
f.绘制输入信号和输出信号的幅频特性曲线,并进行比较和分析。
3.测量系统的相频特性:a.调节信号发生器的频率和示波器的触发模式,观察输入信号和输出信号的相位差。
b.在示波器中进行相位测量,并记录下输入信号和输出信号的相位。
c.使用DFT算法对输入信号和输出信号进行频谱分析,得到相频特性曲线。
d.绘制输入信号和输出信号的相频特性曲线,并进行比较和分析。
线性系统的时域分析

《自动控制原理》实验报告实验一:线性系统的时域分析课程名称:自动控制原理目录1. 实验目的 (1)1.1一阶系统 (1)1.2二阶系统 (1)2. 实验内容 (2)2.1 观察比例环节的阶跃响应曲线 (2)2.2 观察惯性环节的阶跃响应曲线 (2)2.3 观察积分环节的阶跃响应曲线 (2)2.4 观察比例积分环节的阶跃响应曲线 (3)2.5 观察比例微分环节的阶跃响应曲线 (3)2.6 PID(比例积分微分)环节的响应曲线 (4)2.7 典型二阶系统的响应曲线 (4)3. 实验步骤 (5)3.1 比例环节的阶跃响应曲线 (5)3.2 惯性环节的阶跃响应曲线 (5)3.3 观察积分环节的阶跃响应曲线 (6)3.4 观察比例积分环节的阶跃响应曲线 (6)3.5 观察比例微分环节的阶跃响应曲线 (7)3.6 PID(比例积分微分)环节的响应曲线 (7)3.7 典型二阶系统的响应曲线 (8)4. 理论分析 (9)4.1 比例环节的阶跃响应曲线 (9)4.2 惯性环节的阶跃响应曲线 (9)4.3 积分环节的阶跃响应曲线 (9)4.4 比例积分环节的阶跃响应曲线 (10)4.5 比例微分环节的阶跃响应曲线 (10)4.6 PID环节的阶跃响应曲线 (11)4.7 二阶单位负反馈系统的阶跃响应曲线 (11)4.8 三阶单位负反馈系统的阶跃响应曲线 (12)5. MATLAB仿真 (14)5.1 比例环节的阶跃响应曲线 (14)5.2 惯性环节的阶跃相应曲线 (14)5.3 积分环节的阶跃相应曲线 (15)5.4 比例积分环节的阶跃相应曲线 (15)5.5 比例微分环节的阶跃相应曲线 (16)5.6 PID环节的阶跃相应曲线 (16)5.7 二阶单位负反馈系统的阶跃相应曲线 (16)5.8 三阶单位负反馈系统的阶跃相应曲线 (17)6. 实验结果 (19)6.1比例环节的阶跃响应曲线 (19)6.2惯性环节的阶跃响应曲线 (19)6.3 积分环节的阶跃响应曲线 (21)6.4比例积分环节的阶跃响应曲线 (22)6.5 比例微分环节的阶跃响应曲线 (24)6.6 (PID)比例积分微分环节的响应曲线 (24)6.7二阶系统的瞬态响应 (26)6.8 实验分析 (29)1. 实验目的1.1一阶系统1.了解和掌握各典型环节模拟电路的构成方法、传递函数表达式及输出时域函数表达式2.观察和分析各典型环节的阶跃响应曲线,了解各项电路参数对典型环节动态特性的影响1.2二阶系统1.了解和掌握典型二阶系统模拟电路的构成方法及Ⅰ型二阶闭环系统的传递函数标准式。
线性系统时域分析实验报告

竭诚为您提供优质文档/双击可除线性系统时域分析实验报告篇一:自动控制原理实验报告《线性控制系统时域分析》实验一线性控制系统时域分析1、设控制系统如图1所示,已知K=100,试绘制当h 分别取h=0.1,0.20.5,1,2,5,10时,系统的阶跃响应曲线。
讨论反馈强度对一阶系统性能有何影响?图1答:A、绘制系统曲线程序如下:s=tf(s);p1=(1/(0.1*s+1));p2=(1/(0.05*s+1));p3=(1/(0.02*s+1) );p4=(1/(0.01*s+1));p5=(1/(0.005*s+1));p6=(1/(0.002 *s+1));p7=(1/(0.001*s+1));step(p1);holdon;step(p2); holdon;step(p3);holdon;step(p5);holdon;step(p6);hol don;step(p7);holdon;b、绘制改变h系统阶跃响应图如下:stepResponse1.41.21Amplitude0.80.60.40.200.050.10.150.20.250.30.350.40.450.5Time(seconds)结论:h的值依次为0.1、0.2、0.5、1、2、5、10做响应曲线。
matlab曲线默认从第一条到第七条颜色依次为蓝、黄、紫、绿、红、青、黑,图中可知随着h值得增大系统上升时间减小,调整时间减小,有更高的快速性。
2?n?(s)?22,设已知s?2??ns??n2、二阶系统闭环传函的标准形式为?n=4,试绘制当阻尼比?分别取0.2,0.4,0.6,0.8,1,1.5,2,5等值时,系统的单位阶跃响应曲线。
求出?取值0.2,0.5,0.8时的超调量,并求出?取值0.2,0.5,0.8,1.5,5时的调节时间。
讨论阻尼比变化对系统性能的影响。
答:A、绘制系统曲线程序如下:s=tf(s);p1=16/(s^2+1.6*s+16);p2=16/(s^2+3.2*s+16);p3=16/(s^ 2+4.8*s+16);p4=16/(s^2+6.4*s+16);p5=16/(s^2+8*s+16) ;p6=16/(s^2+12*s+16);p7=16/(s^2+16*s+16);p8=16/(s^2 +40*s+16);step(p1);holdon;step(p2);holdon;step(p3); holdon;step(p4);holdon;step(p5);holdon;step(p6);hol don;step(p7);holdon;step(p8);holdon;b、绘制系统阶跃响应图如下:c、?取值为0.2、0.5、0.8、1.5、5时的参数值。
线性系统的时域分析实验报告

线性系统的时域分析实验报告线性系统的时域分析实验报告引言:线性系统是控制理论中的重要概念,它在工程领域中有广泛的应用。
时域分析是研究线性系统的一种方法,通过对系统输入和输出的时域信号进行观察和分析,可以得到系统的动态特性。
本实验旨在通过对线性系统进行时域分析,探究系统的稳定性、阶数和频率响应等特性。
实验一:稳定性分析稳定性是线性系统的基本性质之一,它描述了系统对于不同输入的响应是否趋于有界。
在本实验中,我们选取了一个简单的一阶系统进行稳定性分析。
首先,我们搭建了一个一阶系统,其传递函数为H(s) = 1/(s+1),其中s为复变量。
然后,我们输入了一个单位阶跃信号,观察系统的输出。
实验结果显示,系统的输出在输入信号发生变化后,经过一段时间后稳定在一个有限的值上,没有出现发散的情况。
因此,我们可以判断该系统是稳定的。
实验二:阶数分析阶数是线性系统的另一个重要特性,它描述了系统的动态响应所需的最小延迟时间。
在本实验中,我们选取了一个二阶系统进行阶数分析。
我们搭建了一个二阶系统,其传递函数为H(s) = 1/(s^2+2s+1)。
然后,我们输入了一个正弦信号,观察系统的输出。
实验结果显示,系统的输出在输入信号发生变化后,经过一段时间后才稳定下来。
通过进一步分析,我们发现系统的输出波形具有两个振荡周期,这表明系统是一个二阶系统。
实验三:频率响应分析频率响应是线性系统的另一个重要特性,它描述了系统对于不同频率输入信号的响应情况。
在本实验中,我们选取了一个低通滤波器进行频率响应分析。
我们搭建了一个低通滤波器,其传递函数为H(s) = 1/(s+1),其中s为复变量。
然后,我们输入了一系列不同频率的正弦信号,观察系统的输出。
实验结果显示,随着输入信号频率的增加,系统的输出幅值逐渐减小,表明系统对高频信号有较强的抑制作用。
这一结果与低通滤波器的特性相吻合。
结论:通过以上实验,我们对线性系统的时域分析方法有了更深入的了解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 线性系统时域分析一、目的(1)掌握求解连续时间信号时域卷积的方法 (2)掌握线性时不变系统时域分析方法二、连续时间信号卷积连续时间信号)(1t f 和)(2t f 的卷积运算可用信号的分段求和来实现,即:∑⎰∞-∞=→∆∞∞-∆⋅∆-∆=-==k k t f k f d t f f t f t f t f )()(lim )()()(*)()(2102121τττ 如果只求当为整数)(n n t ∆=时)(t f 的值)(∆n f ,则上式可得:∑∑∞-∞=∞-∞=∆-∆∆=∆⋅∆-∆∆=∆k k k n f k f k n f k f n f ])[()()()()(2121 (2-1)式(2-1)中的∑∞-∞=∆-∆k k n f k f ])[()(21实际上就是连续时间信号)(1t f 和)(2t f 经等时间间隔∆均匀抽样的离散序列)(1∆k f 和)(2∆k f 的卷积和。
当∆足够小时,)(∆n f 就是卷积积分的结果——连续时间信号)(t f 的较好数值近似。
因此,用MATLAB 实现连续信号)(1t f 和)(2t f 卷积的过程如下:1、将连续信号)(1t f 和)(2t f 以时间间隔∆进行取样,得到离散序列)(1∆k f 和)(2∆k f ;2、构造与)(1∆k f 和)(2∆k f 相应的时间向量1k 和2k (注意,1k 和2k 的元素不是整数,而是取样间隔∆的整数倍的时间间隔点);3、调用MATLAB 命令conv()函数计算积分)(t f 的近似向量)(∆n f ;4、构造)(∆n f 对应的时间向量k 。
下面是利用MATLAB 实现连续信号卷积的通用程序sconv(),该程序在计算出卷积积分的数值近似的同时,还绘制出)(t f 的时域波形图。
应注意,程序中是如何构造)(t f 的对应时间向量的?function [f,k]=sconv(f1,f2,k1,k2,p)%计算连续信号卷积积分f(t)=f1(t)*f2(t) % f: 卷积积分f(t)对应的非零样值向量 % k : f(t)的对应时间向量 % f1: f1(t)非零样值向量 % f2: f2(t)的非零样值向量 % k1: f1(t)的对应时间向量% k2: 序列f2(t)的对应时间向量 % p : 取样时间间隔 f=conv(f1,f2); %计算序列f1与f2的卷积和f f=f*p;k0=k1(1)+k2(1); %计算序列f 非零样值的起点位置 k3=length(f1)+length(f2)-2; %计算卷积和f 的非零样值的宽度 k=k0:p:(k3*p+k0); %确定卷积和f 非零样值的时间向量 subplot(2,2,1) plot(k1,f1) %在子图1绘f1(t)时域波形图 title('f1(t)') xlabel('t') ylabel('f1(t)')subplot(2,2,2) plot(k2,f2) %在子图2绘f2(t)时波形图 title('f2(t)') xlabel('t') ylabel('f2(t)') subplot(2,2,3) plot(k,f); %画卷积f(t)的时域波形 h=get(gca,'position'); h(3)=2.5*h(3);set(gca,'position',h) %将第三个子图的横坐标范围扩为原来的2.5倍 title('f(t)=f1(t)*f2(t)') xlabel('t') ylabel('f(t)')下面举例如何使用此程序:已知两信号波形图如下所示,用MATLAB 求解)(*)()(t f t f t f 。
实现卷积的命令如下: p=0.01;k1=0:p:2; f1=0.5*k1; k2=k1; f2=f1;[f,k]=sconv(f1,f2,k1,k2,p) 程序运行结果如下:图2-1 程序运行结果请同学们利用MATLAB 实现下述两个信号的卷积积分:要求:在实验报告中推导出这两个信号卷积积分运算表达式,并绘出图形;然后,利用MATLAB 进行求解验证。
计算验证:)3(]4)1[(25.0)1()1(25.0)5.1(]4)5.0[(25.0)5.0()5.0(25.0)]2()4(41)(41[*)]1()5.0([])2(5.0)(5.0[*)]1()5.0([})]2()([5.0{*)]1()5.0([)(*)()]2()([5.0)()1()5.0()(222222022121---+-----+-++=-----+=-⋅-⋅--+=----+=--=--+=⎰⎰⎰∞-t u t t u t t u t t u t t u t t u t t t t u d t u d t t d u u t t t f t f t u t u t t f t u t u t f tttδδττττδδττττδδ绘图:t = -0.5:0.01:3; y =0.25*(t+0.5).^2.*(0.5+0.5*sign(t+0.5))-0.25*((t+0.5).^2-4).*(0.5+0.5*sign(t-1.5))-0.25.*(t-1).^2.*(0.5+0.5*sign(t-1))+0.25.*((t-1).^2-4).*(0.5+0.5*sign(t-3)); plot(t,y)使用sconv 函数验证: p=0.01; k1=-0.5:p:1; f1= k1*0+1; k2=0:p:2; f2=0.5*k2;[f,k]=sconv(f1,f2,k1,k2,p);三、线性系统时域分析1、 连续系统的冲激响应、阶跃响应及MATLAB 实现LTI 系统当输入为冲激信号)(t δ时产生的零状态响应称为系统的冲激响应,用)(t h 表示。
若输入信号为单位阶跃信号)(t u 时系统产生的零状态响应则称为系统的阶跃响应,记为)(t g 。
对于LTI 连续系统,设其输入信号为)(t f ,冲激响应为)(t h ,零状态响应为)(t y ,则有:)(*)()(t h t f t y =即)(t h 包含了连续系统的固有特性,与系统的输入无关。
只要知道了系统的冲激响应,即可求得系统在不同输入时产生的输出。
因此,求解系统的冲激响应)(t h 对进行连续时间系统的分析具有非常重要的意义。
MATLAB 提供了专门用于求解连续系统冲激响应及阶跃响应,并绘制其时域波形的函数impulse 和step 。
在调用函数impulse()和step()时,需要用向量对连续系统进行表示。
设描述连续系统的微分方程为:∑∑===Mj j j Ni i it f b t ya 0)(0)()()(则可用向量a 和b 表示该系统,即],,,,[011a a a a a N N -= ],,,,[011b b b b b M M -=注意,在用向量表示微分方程描述的系统时,向量a 和b 的元素一定要以微分方程时间求导的降幂次序排列,且确项要用0补齐。
如微分方程)(*)()(t h t f t y =)()()(2)(3)(t f t f t y t y t y +''=+'+''则表示该系统的对应向量为a=[1 3 2]; b=[1 0 1];(1)impulse()函数函数impulse()将绘出由向量a 和b 表示的连续系统在指定时间范围内的冲激响应)(t h 的时域波形图,并能求出指定时间范围内冲激响应的数值解。
函数impulse()有如下几种调用格式: (a )impulse(b,a)该调用格式以默认方式绘出向量a 和b 定义的连续系统的冲激响应的时域波形。
如, 若描述某连续系统的微分方程为:)(2)(3)(6)(5)(t f t f t y t y t y +'=+'+''运行如下MATLAB 命令:a=[1 5 6]; b=[3 2]; impulse(b,a)绘出的冲激响应波形如下图所示:(b )impulse(b,a,t)该调用格式将绘出由向量a 和b 定义的连续系统在t~0时间范围内的冲激响应的时域波形。
对上例,如运行如下命令:impulse(b,a,10)则绘出系统在10~0秒范围内冲激响应的时域波形,如图2-3所示。
图2-2 LTI 系统的冲激响应1(c )impulse(b,a,t1:p:t2)该调用格式将绘出由向量a 和b 定义的连续系统在2~1t t 时间范围内,且以时间间隔p 均匀抽样的冲激响应的时域波形。
对上例,如运行impulse(b,a,1:0.1:2)则绘出系统在1~2秒范围内,并以时间间隔0.1秒取样的冲激响应的时域波形,如图2-4所示。
(d )y=impulse(b,a,t1:p:t2)该调用格式并不会出系统冲激响应的波形,而是求出向量a 和b 定义的连续系统在2~1t t 时间范围内以时间间隔p 均匀抽样的系统冲激响应数值解。
对上例,若运行命令:y=impulse(b,a,0:0.2:2) 则运行结果为: y =3.0000 1.1604图2-4 LTI 系统的冲激响应30.3110 -0.0477 -0.1726 -0.1928 -0.1716 -0.1383 -0.1054 -0.0777 -0.0559 (2)step()函数函数step()将绘制出由向量a 和b 表示的连续系统的阶跃响应)(t g 在指定时间范围内的波形图,并能求出其数值解。
和impulse()一样,step()函数也有以下四中调用格式:(a )step(b,a) (b )step(b,a,t)(c )step(b,a,t1:p:t2) (d )y=step(b,a,t1:p:t2)上述调用格式的功能与impulse()函数完全相同,所不同的是命令绘制的是系统的阶跃响应)(t g 的曲线而不是冲激响应)(t h 的曲线。
对上例,若执行命令:step(b,a)则绘制的系统阶跃响应时域波形如图2-5所示。
(3)实验内容求解如下LTI 系统的冲激响应、阶跃响应 要求:(a )求解出该系统的冲激响应、阶跃响应的数学表达式,画出波形; (b )利用MATLAB 进行求解验证。
求解:图2-5 LTI 系统的阶跃响应 )()(8)()(2t e t r t r t r =+'+'')(])473sin(1687)473cos(8181[)()473sin(2172)()()()473sin(2172]821[1)]([1)(821)(4141414122t u e t e t t u d e d h t g t u e t s s s H t h s s s H tt t t t ---∞----=⋅===++-=-=++=⎰⎰τττττL L 绘图:syms s t r; x = 0:0.01:25;h = ilaplace(1/(2*s^2+s+8),t); hd = subs(h, t, x); subplot(2,1,1); plot(x, hd); title('h(t)'); g = int(h,t,0,r); gd = subs(g, r, x); subplot(2,1,2); plot(x, gd); title('g(t)');Impulse 和step 函数验证: a=[2 1 8]; b=[1];impulse(b,a);step(b,a);2、LTI 连续系统的求解LTI 连续时间系统可用如下所示的线性常系数微分方程描述∑∑===Mj j j Ni i it f b t ya 0)(0)()()(如果系统的输入信号和初始状态已知,便可用微分方程的经典时域解法,求出系统的相应。
