三角形面积、等积变形测试题
五大模型(三角型等积变形、共角模型
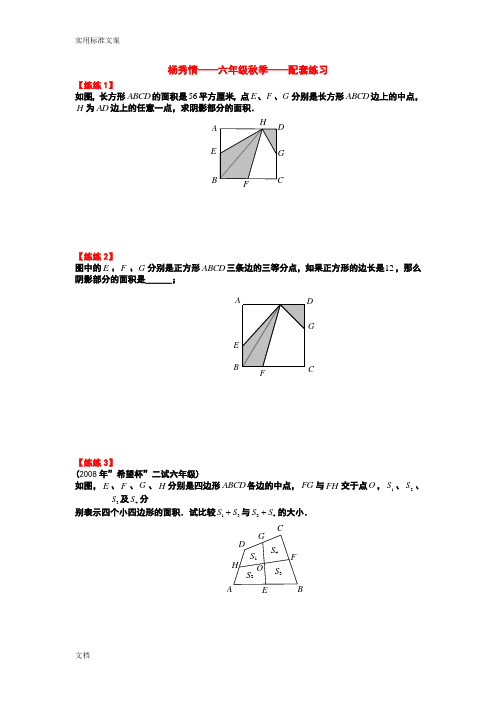
杨秀情——六年级秋季——配套练习【练练1】如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积.HGFE D CBA【练练2】图中的E 、F 、G 分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是______;E D GCFBA【练练3】(2008年”希望杯”二试六年级)如图,E 、F 、G 、H 分别是四边形ABCD 各边的中点,FG 与FH 交于点O ,1S 、2S 、3S 及4S 分 别表示四个小四边形的面积.试比较13S S +与24S S +的大小.OS 4S 3S 2S 1H GFEDC BA【练练4】如图,三角形ABC 中,2DC BD =,3CE AE =,三角形ADE 的面积是20平方厘米,三角形ABC 的面积是多少?EDCBA【练练5】(2008年第一届“学而思杯”综合素质测评六年级2试)如图,45BC =,21AC =,ABC ∆被分成9个面积相等的小三角形,那么DI FK += .KJIH GFE DC B A【练练6】如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米,那么图中阴影部分的面积是 平方厘米.A B CDE F【练练7】(2009年四中小升初入学测试题)如图所示,平行四边形的面积是50平方厘米,则阴影部分的面积是 平方厘米.【练练8】如下图,长方形AFEB 和长方形FDCE 拼成了长方形ABCD ,长方形ABCD 的长是20,宽是12,则它内部阴影部分的面积是 .F E DCBA【练练9】(第三届“华杯赛”初赛试题)一个长方形分成4个不同的三角形,绿色三角形面积占长方形面积的15%,黄色三角形面积是221cm .问:长方形的面积是多少平方厘米?红绿黄红【练练10】如图,正方形ABCD 的边长为6,AE =1.5,CF =2.长方形EFGH 的面积为 .HGF EDCBA【练练11】如图所示,四边形ABCD 与AEGF 都是平行四边形,请你证明它们的面积相等.GFEDCB A【练练12】2008年春蕾杯五年级决赛如图,长方形ABCD 的边上有两点E 、F ,线段AF 、BF 、CE 、BE 把长方形分成若干块,其中三个小木块的面积标注在图上,阴影部分面积是 平方米。
四年级下册数学试题-思维训练:三角形等积变形(下)(含答案)全国通用

正方形ABCD和正方形CEFG,且正方形ABCD边长为10厘米,则图中阴影面积为多少平方厘米?两个正方形如图排列,面积相差60,求阴影部分梯形面积。
如图所示,已知正方形ABCD的边长为10厘米,EC=2×BE,那么,图中阴影部分的面积是________平方厘米。
例3例2例1三角形等积变形(下)如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=2BC;延长CA至F,使AF=3AC,求三角形DEF的面积。
如图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米。
求三角形CDF的面积。
如图,在四边形ABCD中,对角线AC、BD交于E,且AF=CE,BG=DE,如果四边形ABCD 面积是1,求△EFG的面积?例6例5例4测试题1.如图,长方形ABCD的面积是1,M是AD边的中点,N在AB边上,且2AN BN。
那么,阴影部分的面积是多少?2.如图,梯形ABCD被它的一条对角线BD分成了两部分。
三角形BDC的面积比三角形ABD 的面积大10平方分米。
已知梯形的上底与下底的长度之和是15分米,它们的差是5分米。
求梯形ABCD的面积。
ADB C 3.图中两个正方形的边长分别是6厘米和4厘米,则图中阴影部分三角形的面积是()平方厘米。
4.正方形ABCD和正方形CEFG,且正方形ABCD边长为10厘米,则图中阴影面积为多少平方厘米?HGFEBA5.如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使2AF AC =,求三角形DEF 的面积。
答案1.A M连接BM ,因为M 是中点所以ABM ∆的面积为14又因为2AN BN =,所以ANM ∆的面积为1114312⨯=,又因为BDC ∆面积为12,所以阴影部分的面积为:115112212--= 2.bDCBA如右图,作AB 的平行线DE 。
小学数学《三角形的等积变形》练习题(含答案)

三角形ABC的面积=(12+4)×高÷2=8×高
三角形ADC的面积=4×高÷2=2×高
所以,三角形ABC的面积是三角形ABD面积的4/3倍;三角形ABD的面积是三角形ADC面积的3倍。
巩固理解结论:两个三角形等高时,面积的倍数=底的倍数
【例2】如右图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
而四边形CEFH是它们的公共部分,
所以三角形DHF的面积=三角形BCH的面积,
进而可得阴影面积=三角形BDF的面积=三角形BCD的面积= 10×10÷2=50(平方厘米)。
法2:连接CF,那么CF平行BD,
所以,阴影面积=三角形BDF的面积=三角形BCD的面积=50(平方厘米)。
附加题目
【附1】 如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.
巩固理解结论:两个三角形等底时,面积的倍数=高的倍数
【例3】用两种不同的方法,把任意一个三角形分成四个面积相等的三角形.
分析:法1:如图(1),将BC边四等分,连接各等分点,则△ABD、△ADE、△AEF、△AFC面积相等。
法2:如图(2),D是BC的二等分点,E、F是AC、AB的中点,从而得到四个等积三角形△ADF、△BDF、△DCE、△ADE.
【例7】图中△AOB的面积为15cm2,线段OB的长度为OD的3倍,求梯形ABCD的面积.
分析:
【例8】(北京市第一届“迎春杯”刊赛)如右图.将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F.如果三角形ABC的面积等于l,那么三角形DEF的面积是?
分析:连结AE、BF、CD(如右下图).由于三角形AEB与三角ABC的高相等,而底边EB=2BC,所以三角形AEB的面积是2.同理,三角形CBF的面积是3,三角形ACD的面积是1.
【小升初专项训练】04 等积变形

第5讲等积变形第一关三角形的等积变形【例1】如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为 平方厘米。
【答案】12.25【例2】如图,E、F分别是梯形ABCD两腰上的中点,已知阴影部分的面积是43c㎡,那么梯形ABCD 的面积是多少?【答案】172【例3】如图:三条直线互相平行,l1与l3之间的距离是7厘米,l2上AB=4厘米.求阴影部分三角形的面积是多少平方厘米? 【答案】14【例4】你能看出下面两个阴影部分A与B面积的大小关系吗?(两个长方形面积相等)【答案】A与B的面积相等【例5】如图,在斜边长为20cm的直角三角形ABC中去掉一个正方形EDFB,留下两个阴影部分直角三角形AED和DFC.若AD=8cm,CD=12cm,则阴影部分面积为多少?给出答案并说明你的计算依据.【答案】48【例6】如图,在直角三角形中有一个正方形,已知BD=10厘米,DC=7厘米,阴影部分的面积是多少?【答案】35平方厘米【例7】如图,梯形ABCD的面积是36,下底长是上底长的2倍,阴影三角形的面积是多少?【答案】16【例8】下图中阴影部分甲的面积与阴影部分乙的面积哪个大?【答案】图中甲乙的面积相等【例9】如图,在三角形ABC中,D是BC上靠近C的三等分点,E是AD中点,已知三角形ABC的面积为1,那么图中两个阴影三角形面积之和是多少?【答案】0.4【例10】已知△ABC面积为5,且BD=2DC,AE=ED,求阴影部分面积.要求写出关键的解题推理过程.【答案】2【例11】如图,将一个梯形分成四个三角形,其中两个三角形的面积分别为10与12.已知梯形的上底长度是下底的.请问:阴影部分的总面积是多少?【答案】23【例12】如图,已知梯形ABCD中,CD=10,梯形ABCD的高是4,那么阴影部分的面积是多少。
【答案】20【例13】(1)如图1,阴影部分的面积是多少?(2)如图2,一个长方形长4厘米,宽3厘米.A为长方形内的任意一点,阴影部分的面积是多少?【答案】(1)100;(2)6【例14】如图,在图中△ABE、ADF和四边形AECF面积相等.阴影部分的面积是多少?【答案】15【例15】如图,两个正方形(单位:厘米)中阴影部分的面积是多少平方厘米?【答案】8【例16】由面积为1,2,3,4的矩形拼成如图的长方形,图中阴影部分的面积为多少?【答案】【例17】如图所示,正方形ABCD的对角线BD长20厘米,BDFE是长方形.那么,五边形ABEFD的面积是多少平方厘米。
小学数学《三角形的等积变形》练习题(含答案)

内容概述
我们已经知道三角形面积的计算公式:三角形面积=底×高÷2
从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积.
如果三角形的底不变,高越大(小),三角形面积也就越大(小);
如果三角形的高不变,底越大(小),三角形面积也就越大(小);
这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1/3,则三角形面积与原来的一样。这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.
于是:三角形ABD的面积=12×高÷2=6×高
三角形ABC的面积=(12+4)×高÷2=8×高
三角形ADC的面积=4×高÷2=2×高
所以,三角形ABC的面积是三角形ABD面积的4/3倍;三角形ABD的面积是三角形ADC面积的3倍。
巩固理解结论:两个三角形等高时,面积的倍数=底的倍数
【例2】如右图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
【例6】如右图所示,在平行四边形ABCD中,E为AB的中点,AF=2CF,三角形AFE(图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?
【例7】图中△AOB的面积为15cm2,线段OB的长度为OD的3倍,求梯形ABCD的面积.
【例8】(北京市第一届“迎春杯”刊赛)如右图.将三角形ABC的BA边延长1倍到D,CB边延长2倍到E,AC边延长3倍到F.如果三角形ABC的面积等于l,那么三角形DEF的面积是?
例题精讲
三角形面积等积变形

三角形面积等积变形小学四年级阶段训练——三角形的等积变形一、填空:1.如图所示,已知矩形ABCD中,BE=1EC,则△ABE和△ABC的面积,则△2ABC的面积是△ABE的面积的()倍。
C(第1题)(第2题)2.如图所示,梯形ABCD中共有8个三角形,其中,面积相等的三角形有()对。
3.如图所示,已知平行四边形ABCD中,BC=3厘米,BC边的高AE是2厘米,则△ACD的面积是()平方厘米。
O(第3题)(第4题)4.如图所示,平行四边形MNOP中,Q是OP上任意一点,则S△MRQ( )S△NRO, S△MRN( )S△NRO,(填“>”“<”或“=”)5.如图所示,平行四边形ABCD中,E、F分别为AD,CD的中点,那么与△BFC面积相等的三角形有()个。
(第5题)(第6题)26.如图所示,△ABC中,D为BC中点,且DE=AD,则△ABC的面积等于5△CDE面积的()倍。
7.如图所示,在长方形ABCD中,阴影部分面积(>,<,=)空白部分面积表示()8.如图所示,△ABC与△BCD中,AE=ED,且AD⊥BC,把BC八等分,点F为第一个八等分点,E恰为第二个八等分点,则与△ABF面积相等的三角形有()个。
9.如图所示,已知BC长是5,其他数据如图所示,则画阴影线的两个三角形的面积之和是()(第7题)(第8题)(第9题)二.如图,已知在△ABC中,BE=3AE,AD=2CD,若△ADE的面积为2厘米。
求三角形ABC的面积。
三、如图,平行四边形ABCD中,直线DE交AB于F,若三角形ABE的面积是2平方厘米,求三角形CEF的面积。
四、如图所示,AD平行于BE,三角形ABC的面积是8平方厘米。
求四边形ACDE的面积。
小升初数学几何综合 (学生版)

习题课2之三角形面积、一半模型、等积变形一、面积公式长方形面积=长×宽(正方形面积=边长×边长=对角线2÷2)1.如图,有一块长方形田地被分成了五小块,分别栽种了茄子、黄瓜、豆角、莴笋和苦瓜.其中栽种茄子的面积是16平方米,栽种黄瓜的面积是28平方米,栽种豆角的面积是32平方米,栽种莴笋的面积是72平方米,而且左上角栽种茄子的田地恰好是一个正方形.请问:剩下的栽种苦瓜的田地面积是多少?2.如图,在正方形ABCD中,对角线AC的长度为8厘米,那么正方形的面积是多少平方厘米?平行四边形面积=底×高3.如图,小、中、大三个正方形从左到右依次紧挨着摆放,边长分别是3、7、9.图中两个阴影平行四边形的面积分别是多少?4.如图,两个边长10厘米的正方形相互错开3厘米,那么图中阴影平行四边形的面积是多少?5.如图,从梯形ABCD中分出两个平行四边形ABEF和CDFG.其中ABEF的面积等于60平方米,且AF的长度为10米,FD的长度为4米.平行四边形CDFG的面积等于多少平方米?三角形面积=底×高÷26.如图,把大、小两个正方形拼在一起,它们的边长分别是8厘米和6厘米,那么左图和右图中阴影部分的面积分别是多少平方厘米?7.如图,平行四边形ABCD中,AD的长度为20厘米,高CH的长度为9厘米;E是底边BC上的一点,且BE长6厘米,那么两个阴影三角形的面积之和是多少平方厘米?8.图中,平行四边形ABCD的面积是32平方厘米,三角形CED是一个直角三角形.已知AE=5厘米,CE=4厘米,那么阴影部分的面积是多少平方厘米?9.如图,在平行四边形ABCD中,三角形BCE的面积是42平方厘米,BC的长度为14厘米,AE的长度为9厘米,那么平行四边形ABCD的面积是多少平方厘米?三角形BCE的面积又是多少平方厘米?10.如图,小正方形ABCD放在大正方形EFGH的上面.已知小正方形的边长为4厘米,且梯形AEHD的面积是28平方厘米,那么梯形AFGD的面积多少平方厘米?二、几何变换和模型田字模型11.一块长方形的土地被分割成4个小长方形,其中三块的面积如图所示(单位:平方米),剩下一块的面积应该是多少平方米?12.如图8-11,有9个小长方形,其中的5个小长方形的面积分别为4、8、12、16、20平方米。
三角形等积变形

例5 如右图,已知在△ABC中,BE=3AE,CD=2AD.若△ADE 的面积为1平方厘米.求三角形ABC的面积.
解法1:连结BD,在△ABD 中 ∵ BE=3AE, ∴ S△ABD=4S△ADE=4 (平方厘米). 在△ABC中,∵CD=2AD, ∴ S△ABC=3S△ABD=3×4=12 (平方厘米).
上述结论,是我们研究三角形等积变形的 重要依据.
方法2:如右图,先将BC二等分,分点D、连结AD, 得到两个等积三角形,即△ABD与△ADC等 积.然后取AC、AB中点E、F,并连结DE、DF.以 而得到四个等积三角形,即△ADF、△BDF、 △DCE、△ADE等积.
例2 用三种不同的方法将任意一个三角形分成 三个小三角形,使它们的面积比为及 1∶3∶4.
三角形等积变形
我们已经掌握了三角形面积的计算公式: 三角形面积=底×高÷2
这个公式告诉我们:三角形面积的大小,取决 于三角形底和高的乘积.
①等底等高的两个三角形面积相等.
例如在右图中,若△ABD与 △AEC的底边相等 (BD=DE=EC=BC) ,它们所对的顶点同为A点, (也就是它们的高相等) 那么这两个三角形的面积 相等. 同时也可以知道△ABC 的面积是△ABD或 △AEC面积的3倍.
证明:∵△ABC与△DBC等 底等高, ∴S△ABC=S△DBC 又∵ S△AOB=S△ABC—S△BOC S△DOC=S△DBC— S△BOC ∴S△AOB=S△COD.
例4 如右图,把四边形ABCD改成一个等积的三角形
分析 本题有两点要求,一是把四边形改成一个三角形,二 是改成的三角形与原四边形面积相等.我们可以利用三角 形等积变形的方法,如右图, 把顶点A移到CB的延长线上的A′处, △A′BD与△ABD面积相等,从而 △A′DC面积与原四边形ABCD面积也 相等.这样就把四边形ABCD等积地 改成了三角形△A′DC.问题是A′位 置的选择是依据三角形等积变形原 则.过A作一条和DB平行的直线与 CB的延长线交于A′点. 解:①连结BD; ②过A作BD的平行线,与CB的 延长线交于A′. ③连结A′D,则△A′CD与四边形 ABCD等积.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形面积和等积变形测试题 姓名 得分 1. 右图中,四边形ABCD 的面积是320平方厘米,四边形ABED
是个正方形,已知BC 等于CE 的3倍,求三角形ECD 的面积。
2.已知三角形ABC 中,BC =3.5cm,AD =2cm,AC =2.8cm 求BE 的长度。
3.已知三角形ABC 中,DC =BD,阴影部分的
面积是36平方厘米,求:三角形的面积。
4. 如下左图,D 、E 、F 分别是BC 、AD 、BE 的三等分点,
已知S △ABC=27平方厘米,求S △DEF 。
5.求下面阴影部分的面积:
6.如图,由两个边长分别是4cm 和3cm
的正方形组成,求阴影部分的面积。
A B C
D E A
B C D E
A
B
C D
7.求右图中阴影部分的面积 。
(单位:dm)
8.长方形ABCD 中,三角形ABE 、ADF,四边形AECF 的面积都相等,求三角形AEF 的面积。
9.如下左图,在平行四边形ABCD 中,E 、F 分别
是AC 、BC 的三等分点,且SABCD=54平方厘米,求S △BEF 。
10.如图,已知△ABC 的面积为12,M 为AB 边的中点。
MD 与EC 平行。
求△EBD 的面积。
★★
一块长方形的菜地,长为15米,宽为12米,请用经过A 点的两条直线把这个长方形分成面积 相等的三部分。
说明怎样划分。
7 3 5 E A
F B 12dm 9dm A B C
15 12。
