中考数学锐角三角函数的综合题试题及答案
九年级中考数学专题练习锐角三角函数的增减性(含解析)

九年级中考数学专题练习锐角三角函数的增减性(含解析)中考数学专题练习-锐角三角函数的增减性(含解析)一、单选题1.已知sinα<0.5,那么锐角α的取值范围是()A. 60°<α<90°B. 30°<α<90°C. 0°<α<60°D. 0°<α<30°2.如图,是半径为1的半圆弧,△AOC为等边三角形,D是上的一动点,则△COD的面积S 的最大值是()A. s=B. s=()A. <cosα<B. <cosα< C.<cosα<D. <cosα<6.梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是()A. sinA的值越大,梯子越陡B. co sA的值越大,梯子越陡C. tanA的值越小,梯子越陡D. 陡缓程度与∠A的函数值无关7.若0<α<30°,则sinα,cosα,tanα的大小关系是()A. sinα<cosα<tanα B. sinα<tanα<cosα C. tanα<sinα<cosα D. tanα<cosα<sinα8.已知甲、乙两坡的坡角分别为α、β,若甲坡比乙坡更陡些,则下列结论正确的是()A. tanα<t anβB. sinα<sinβC. cosα<cosβD. cosα>cosβ9.α是锐角,且cosα=,则()A. 0°<α<30°B. 30°<α<45°C. 45°<α<60°D. 60°<α<90°10.如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是()A. sinA的值越小,梯子越陡B. co sA的值越小,梯子越陡C. tanA的值越小,梯子越陡D. 陡缓程度与∠A的函数值无关11.在Rt△ABC中,∠C=90°,下列结论:(1)sinA<1;(2)若A>60°,则cosA>;(3)若A>45°,则sinA>cosA.其中正确的有()A. 0个B. 1个C. 2个D. 3个12.三角函数sin30°、cos16°、cos43°之间的大小关系是()A. cos43°>cos16°>sin30°B.cos16°>sin30°>cos43°C. cos16°>cos43°>sin30°D.cos43°>sin30°>cos16°13.在Rt△ABC中,各边的长度都扩大2倍,那么锐角A的正切值()A. 都扩大2倍B. 都扩大4倍C. 没有变化D. 都缩小一半14.如图,△ABC是锐角三角形,sinC= ,则sinA的取值范围是()A.0B.C.D.15.α是锐角,且sinα>,则α()A. 小于30°B. 大于30°C. 小于60°D. 大于60°二、填空题16.比较大小:sin44°________cos44°(填>、<或=).17.若∠A是锐角,cosA>,则∠A的取值范围是________ .18.若α是锐角,且sinα=1﹣3m,则m的取值范围是________ ;将cos21°,cos37°,sin41°,cos46°的值,按由小到大的顺序排列是________ .19.若∠A是锐角,cosA>,则∠A应满足________ .三、解答题20.用“<”符号连接下列各三角函数cos15°、cos30°、cos45°、cos60°、cos75°.21.已知:在Rt△ABC中,∠C=90°,sinA、sinB 是方程x2+px+q=0的两个根.(1)求实数p、q应满足的条件(2)若p、q满足(1)的条件,方程x2+px+q=0的两个根是否等于Rt△ABC中两锐角A、B的正弦?22.设a、b、c是直角三角形的三边,c为斜边,n为正整数,试判断a n+b n与c n的关系,并证明你的结论.四、综合题23.如图①②,锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化.试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.(1)根据你探索到的规律,试比较18°,34°,50°,62°,88°这些锐角的正弦值的大小和余弦值的大小.(2)比较大小(在横线上填写“<”“>”或“=”):若α=45°,则sin α________cos α;若α<45°,则sin α________cos α;若α>45°,则sin α________cos α.(3)利用互为余角的两个角的正弦和余弦的关系,试比较下列正弦值和余弦值的大小:sin 10°,cos 30°,sin 50°,cos 70°.24.如图(1)如图中①、②,锐角的正弦值和余弦值都是随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值及余弦值的变化规律;(2)根据你探索到的规律,试分别比较18°、34°、50°、62°、88°这些锐角的正弦值的大小和余弦值的大小.答案解析部分一、单选题1.已知sinα<0.5,那么锐角α的取值范围是()A. 60°<α<90°B. 30°<α<90°C. 0°<α<60°D. 0°<α<30°【答案】D【考点】锐角三角函数的增减性【解析】【解答】解:由sinα=0.5,得α=30°,由锐角函数的正弦值随锐角的增大而增大,得0°<α<30°,故选:D.【分析】根据锐角函数的正弦值随锐角的增大而增大,可得答案.2.如图,是半径为1的半圆弧,△AOC为等边三角形,D是上的一动点,则△COD的面积S 的最大值是()A. s=B. s=C. s=D. s=【答案】D【考点】锐角三角函数的增减性【解析】【解答】解:S=CO•ODsin∠COD,△COD∵CO=OD=1,=sin∠COD,∴S△COD∵△AOC为等边三角形,∴∠COB=120°,∴0°<∠COD<120°,∴当∠COD=90°时,sin∠COD最大,最大值是1,∴△COD的面积S的最大值是.故选D.=【分析】根据三角形的面积公式S△COD CO•ODsin∠COD,因为ab都是圆的半径1,所以sin∠COD的值越大,面积越大进行解答.3.若sinA=,则A的取值范围是()A. 0°<∠A<30° B. 30°<∠A<45° C. 45°<∠A<60° D. 60°<∠A<90°【答案】B【考点】锐角三角函数的增减性【解析】【解答】解:∵sin30°=,sin45°=.又<<,正弦值随着角的增大而增大,∴30°<∠A<45.故选B.【分析】首先明确sin30°=,sin45°=;再根据正弦值随着角的增大而增大,进行分析.4.如果把一个锐角三角形三边的长都扩大为原来的两倍,那么锐角A的余切值()A. 扩大为原来的两倍B. 缩小为原来的C. 不变D. 不能确定【答案】C【考点】锐角三角函数的增减性【解析】【解答】因为△ABC三边的长度都扩大为原来的2倍所得的三角形与原三角形相似,所以锐角A的大小没改变,所以锐角A的余切值也不变.故答案为:C.【分析】根据相似三角形的性质可知三角形的边长扩大,角度不会发生改变,即锐角A的大小没改变,所以锐角A的余切值也不变.5.已知30°<α<60°,下列各式正确的是()A. <cosα<B. <cosα< C.<cosα<D. <cosα<【答案】C【考点】锐角三角函数的增减性【解析】【解答】解:∵cos30°=,cos60°=,余弦函数是减函数,∴<cosα<.故选C.【分析】根据特殊角的三角函数值及余弦函数随角增大而减小解答.6.梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是()A. sinA的值越大,梯子越陡B. co sA的值越大,梯子越陡C. tanA的值越小,梯子越陡D. 陡缓程度与∠A的函数值无关【答案】A【考点】锐角三角函数的增减性【解析】【解答】解:根据锐角三角函数值的变化规律,知sinA的值越大,∠A越大,梯子越陡.故选A.【分析】锐角三角函数值的变化规律:正弦值和正切值都是随着角的增大而增大,余弦值和余切值都是随着角的增大而减小.7.若0<α<30°,则sinα,cosα,tanα的大小关系是()A. sinα<cosα<tanα B. sinα<tanα<cosα C. tanα<sinα<cosα D. tanα<cosα<sinα【答案】B【考点】锐角三角函数的增减性【解析】【解答】解:∵0<α<30°,∴0<sinα<, 0<tanα<,<cosα<1,∴sinα<cosα,tanα<cosα,又∵<cosα<1,∴tanα=,∴sinα<tanα<cosα.故选:B.【分析】首先根据0<α<30°,可得0<sinα<, 0<tanα<,<cosα<1,据此判断出sinα<cosα,tanα<cosα;然后判断出sinα<tanα,即可判断出sinα,cosα,tanα的大小关系.8.已知甲、乙两坡的坡角分别为α、β,若甲坡比乙坡更陡些,则下列结论正确的是()A. tanα<tanβB. sinα<sinβC. cosα<cosβD. cosα>cosβ【答案】C【考点】锐角三角函数的增减性【解析】解:根据题意,得α>β.根据锐角三角函数的变化规律,只有C正确.故选C.【分析】若甲坡比乙坡更陡些,则α>β;再根据锐角三角函数的变化规律解答:正弦和正切都是随着角的增大而增大,余弦和余切都是随着角的增大而减小.9.α是锐角,且cosα=,则()A. 0°<α<30°B. 30°<α<45°C. 45°<α<60°D. 60°<α<90°【答案】B【考点】锐角三角函数的增减性【解析】【解答】解:∵在锐角三角函数中,余切值都是随着角的增大而减小,又知cos30°=,cos45°=,故30°<α<45°,故选B.【分析】在锐角三角函数中,余切值都是随着角的增大而减小.cos30°=,cos45°=,故知α的范围.10.如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是()A. sinA的值越小,梯子越陡B. co sA的值越小,梯子越陡C. tanA的值越小,梯子越陡D. 陡缓程度与∠A的函数值无关【答案】B【考点】锐角三角函数的增减性【解析】【解答】解:sinA的值越小,∠A越小,梯子越平缓;cosA的值越小,∠A就越大,梯子越陡;tanA的值越小,∠A越小,梯子越平缓,所以B正确.故答案为:B.【分析】根据锐角三角函数的增减性可判断正误。
2023年中考数学高频考点训练——锐角三角函数(有答案)

2023年中考数学高频考点训练——锐角三角函数一、综合题1.如图, AB 是O 的直径,点C 、G 为圆上的两点,当点C 是弧 BG 的中点时, CD 垂直直线AG ,垂足为D ,直线 DC 与 AB 的延长线相交于点P ,弦 CE 平分 ACB ∠ ,交 AB 于点F ,连接BE .(1)求证: DC 与 O 相切;(2)求证: PC PF = ; (3)若 1tan 3E =, 5BE =,求线段 PF 的长. 2.如图,AB 是⊙O 的直径,AC 交⊙O 于点D ,点E 时弧AD 的中点,BE 交AC 于点F ,BC =FC.(1)求证:BC 是⊙O 的切线; (2)若BF =3EF ,求tan⊙ACE 的值.3.如图,ABC 内接于,O D 是O 的直径 AB 的延长线上一点, DCB OAC ∠=∠ .过圆心 O作 BC 的平行线交 DC 的延长线于点 E .(1)求证: CD 是 O 的切线;(2)若 4,6CD CE == ,求O 的半径及 tan OCB ∠ 的值;4.如图,四边形ABCD 内接于⊙O ,AB 是⊙O 的直径,点D 是AC 的中点,连接OD ,交AC 于点E ,作BFCD ,交DO 的延长线于点F.(1)求证:四边形BCDF 是平行四边形. (2)若AC=8,连接BD ,tan⊙DBF=34,求直径AB 的长及四边形ABCD 的周长. 5.如图,已知 AB 是O 的直径,弦 CD AB ⊥ 于点 E , 42AC =, 2BC = .(1)求 sin ABC ∠ ; (2)求CD 的长.6.如图,点 O 在 ABC ∆ 的 BC 边上,O 经过点 A 、 C ,且与 BC 相交于点 D .点 E 是下半圆弧的中点,连接 AE 交 BC 于点 F ,已知 AB BF = .(1)求证: AB 是O 的切线;(2)若 3OC = , 1OF = ,求 cos B 的值.7.如图,在Rt ΔABC 中,9068C AC BC ∠=︒==,,,AD平分ABC 的外角BAM ∠,AD BD ⊥于点D ,过D 点作DE 平行BC 交AM 于点E.点P 在线段AB 上,点Q 在直线AC 上,且22CQ BP t ==,连接PQ ,作P 点关于直线DE 的对称点P ',连接PP P Q '',.(1)当P 在AB 中点时,t = ;连接DP ,则此时DP 与EC 位置关系为 (2)①求线段AD 的长:②将线段AD 绕着平面上某个点旋转180︒后,使AD 的两个对应点A '、D '落在Rt ABC 的边上,求点A 到对应点A '的距离;(3)如图,当PP Q '的一边与ABD 的AD 或BD 边平行时,求所有满足条件的t 的值.8.如图,在平面直角坐标系中,抛物线y =ax 2+bx ﹣3过点A(﹣3,0),B(1,0),与y 轴交于点C ,顶点为点D ,连接AC ,BC.(1)求抛物线的解析式;(2)在直线CD 上是否存在点P ,使⊙PBC =⊙BCO ?若存在,求出点P 的坐标;若不存在,请说明理由;(3)若点M 为抛物线对称轴l 上一点,点N 为抛物线上一点,当直线AC 垂直平分线段MN 时,请直接写出点M 和点N 的坐标.9.如图,点F 是正方形ABCD 边AB 上一点,过F 作FG⊙BC ,交CD 于G ,连接FC ,H 是FC 的中点,过H 作EH⊙FC 交BD 于点E .(1)连接EF ,EA ,求证:EF =AE .(2)若BFk BA= , ①若CD =2, 13k = ,求HE 的长;②连接CE ,求tan⊙DCE 的值.(用含k 的代数式表示)10.如图,在 Rt ABC 中, 90,6,8ACB BC AC ∠=︒== ,D 是边AB 的中点,动点P 在线段BA 上且不与点A ,B ,D 重合,以PD 为边构造 Rt PDQ ,使 PDQ A ∠=∠ , 90DPQ ∠=︒ ,且点Q 与点C 在直线AB 同侧,设 BP x = ,PDQ 与 ABC 重叠部分图形的面积为S .(1)当点Q 在边BC 上时,求BP 的长; (2)当 7x ≤ 时,求S 关于x 的函数关系式.11.如图,在⊙ABC中,⊙ABC =90°,过点B 作BD⊙AC 于点D .(1)尺规作图,作边BC 的垂直平分线,交边AC 于点E . (2)若AD :BD =3:4,求sinC 的值.(3)已知BC =10,BD =6.若点P 为平面内任意一动点,且保持⊙BPC =90°,求线段AP 的最大值.12.【学习概念】有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.(1)【理解运用】如图1,对余四边形中,AB = 5,BC = 6,CD = 4,连接AC ,若AC = AB ,则cos⊙ABC= , sin⊙CAD= .(2)如图2,凸四边形中,AD = BD ,AD⊙BD ,当2CD 2 + CB 2 = CA 2时,判断四边形ABCD 是否为对余四边形,证明你的结论.(3)【拓展提升】在平面直角坐标中,A (-1,0),B (3,0),C (1,2),四边形ABCD 是对余四边形,点E 在对余线BD 上,且位于⊙ABC 内部,⊙AEC = 90° + ⊙ABC.设AEBE= u ,点D 的纵坐标为t ,请在下方横线上直接写出u 与t 的函数表达,并注明t 的取值范围 .13.如图,在梯形ABCD 中,AD⊙BC ,BC =18,DB =DC =15,点E 、F 分别在线段BD 、CD 上,DE =DF=5.AE 的延长线交边BC 于点G ,AF 交BD 于点N 、其延长线交BC 的延长线于点H .(1)求证:BG =CH ;(2)设AD =x ,⊙ADN 的面积为y ,求y 关于x 的函数解析式,并写出它的定义域;(3)联结FG ,当⊙HFG 与⊙ADN 相似时,求AD 的长.14.(1)【问题提出】如图1,在四边形ABCD 中,60A ∠=︒,90ABC ADC ∠=∠=︒,点E 为AB 延长线上一点,连接EC 并延长,交AD 的延长线于点F ,则BCE DCF ∠+∠的度数为 °;(2)【问题探究】如图2,在Rt⊙ABC 中,90ABC ∠=︒,点D 、E 在直线BC 上,连接AD 、AE ,若60DAE ∠=︒,6AB =,求⊙ADE 面积的最小值;(3)【问题解决】近日,教育部印发了《义务教育课程方案和课程标准(2022年版)》,此次修订中增加的跨学科主题学习活动,突破学科边界,鼓励教师开展跨学科教研,设计出主题鲜明、问题真实的跨学科学习活动.为此,某校欲将校园内一片三角形空地ABC (如图3所示)进行扩建后作为跨学科主题学习活动中心,在AB 的延长线上取一点D ,连接DC 并延长到点E ,连接AE ,已知AE BC ,40AB BC ==米,90ABC ∠=︒,为节约修建成本,需使修建后⊙ADE 的面积尽可能小,问⊙ADE 的面积是否存在最小值?若存在,求出其最小面积;若不存在,请说明理由.15.抛物线y =﹣x 2+bx+c 与x 轴交于A 、B 两点,与y 轴交于点C ,且B (﹣1,0),C (0,3).(1)求抛物线的解析式;(2) 如图1,点P 是抛物线上位于直线AC 上方的一点,BP 与AC 相交于点E ,求点P 的坐标;(3)如图2,点D 是抛物线的顶点,将抛物线沿CD 方向平移,且DD'=2CD ,点M 是平移后所得抛物线上位于D'左侧的一点,连结CN.当5D'N+CN 的值最小时16.在 Rt ABC 中, 90ACB ∠=︒ , 3AC = , 4BC = .将 Rt ABC 绕点B 顺时针旋转()060αα︒<<︒ 得到 Rt DEB ,直线DE , AC 交于点P.(1)如图1,当 BD BC ⊥ 时,连接BP. ①求BDP 的面积;②求 tan CBP ∠ 的值;(2)如图2,连接AD ,若F 为AD 中点,求证;C ,E ,F 三点共线.17.如图,抛物线与x 轴交于A (5,0),B ( 1- ,0),与y 轴的正半轴交于点C ,连接BC ,AC ,已知2sin 2BAC ∠=.(1)求抛物线的解析式;(2)直线 y kx = ( 0k > )交线段AC 于点M ,当以A 、O 、M 为顶点的三角形与⊙ABC 相似时,求k 的值,并求出此时点M 的坐标;(3)P 为第一象限内抛物线上一点,连接BP 交AC 于点Q ,请判断: PQQB是否有最大值,如有请求出这个最大值,如没有请说明理由.18.如图1,已知 Rt ABC ∆ 中, 90ACB ∠= , 2AC = , 23BC = ,它在平面直角坐标系中位置如图所示,点 ,A C 在 x 轴的负半轴上(点 C 在点 A 的右侧),顶点 B 在第二象限,将 ABC ∆ 沿AB 所在的直线翻折,点 C 落在点 D 位置(1)若点 C 坐标为 ()1,0- 时,求点 D 的坐标;(2)若点 B 和点 D 在同一个反比例函数的图象上,求点 C 坐标;(3)如图2,将四边形 BCAD 向左平移,平移后的四边形记作四边形 1111B C A D ,过点 1D 的反比例函数 (0)ky k x=≠ 的图象与 CB 的延长线交于点 E ,则在平移过程中,是否存在这样的 k ,使得以点 1,,E B D 为顶点的三角形是直角三角形且点 11,,D BE 在同一条直线上?若存在,求出 k 的值;若不存在,请说明理由答案解析部分1.【答案】(1)证明:CD AD ⊥,90D ∴∠=︒ ,∴⊙DAC+⊙DCA=90°, 点c 是弧 BG 的中点, ∴CG BC =DAC BAC ∴∠=∠ , OA OC = , OCA BAC ∴∠=∠ , OCA DAC ∴∠=∠ , //AD OC ∴ ,∴⊙D=⊙OCP=90°,OC 是圆O 的半径, DC ∴ 与O 相切,(2)证明:AB 是O 的直径,90ACB ∴∠=︒ ,90PCB ACD ∴∠+∠=︒ ,由(1)得: 90DAC DCA ∠+∠=︒ ,PCB DAC ∴∠=∠ , DAC BAC ∠=∠ , PCB BAC ∴∠=∠ , CE 平分 ACB ∠ , ACF BCF ∴∠=∠ ,∵⊙PFC=⊙BAC+⊙ACF ,⊙PCF=⊙PCB+⊙BCF ,PFC PCF ∴∠=∠ , PC PF ∴= ;(3)解:连接 AE ,CE 平分 ACB ∠ ,∴ AE BE = ,AE BE ∴= , AB 是O 的直径,90AEB ∴∠=︒ ,AEB ∴∆ 为等腰直角三角形,∵AB=210BE = ,∴OB=OC= 10∵1tan 3E =∴1tan 3BC CAB AC ∠== , ∵⊙PCB=⊙BAC ,⊙P=⊙P , ∴⊙PCB⊙⊙PAC , ∴13BC PB AC PC == , ∴ 设 PB x = , 3PC x = ,在 Rt OCP ∆ 中, 222OC PC OP += , ∴2221010(3))22x x +=+ , ∴10x =或x=0(舍去), ∴PC=310,∴PF=310.2.【答案】(1)证明:连接AE ,如图,∵AB 是⊙O 的直径, ∴⊙AEB =90°.∴⊙EAF+⊙AFE =⊙EAB+⊙ABE =90°. ∵点E 是弧AD 的中点, ∴AE DE = . ∴⊙EAD =⊙ABE. ∴⊙AFE+⊙ABE =90°. ∵⊙AFE =⊙BFC ,∴⊙ABE+⊙CFB =90°. ∵BC =FC , ∴⊙CFB =⊙CBF. ∴⊙CBF+⊙ABE =90°. ∴⊙ABC =90°, ∵AB 是⊙O 的直径, ∴BC 是⊙O 的切线. (2)解:连接OE ,BD ,∵点E 是弧AD 的中点,∴OH⊙AD ,AH =HD = 12AD . ∵AB 是⊙O 的直径, ∴BD⊙AD.∴BD⊙OE. ∴EH EFBD BF = . ∵BF =3EF ,∴13EH BD = . 设EH =2a ,则BD =6a. ∵OE⊙BD ,OA =OB , ∴OF =12BD =3a. ∴OA =OE =OH+HE =5a. ∴AB =2OA =10a. ∴AD =228AB BD a -= .∴HD =12AD =4a. ∵⊙ABC =90°,BD⊙AC , ∴⊙ABD⊙⊙BCD. ∴AD BDBD CD= . ∴CD = 292BD a AD = .∴CH =HD+CD =172a . 在Rt⊙EHC 中,tan⊙ACE = 2417172EH a CH a ==.3.【答案】(1)证明:如图,,OA OC =OAC OCA ∴∠=∠ ,DCB OAC ∠=∠ , OCA DCB ∴∠=∠ ,AB 是O 的直径,90ACB ∴∠=︒ ,90OCA OCB ∴∠+∠=︒ ,90DCB OCB ∴∠+∠=︒ ,即 90OCD ∠=︒ , OC DC ∴⊥ ,又OC 是 O 的半径,CD ∴ 是O 的切线.(2)解:,BC OEBD CD OB CE ∴= ,即 4263BD OB == , ∴设 2BD x = ,则 3,5OB OC x OD OB BD x ===+= ,,OC DC ⊥222OC CD OD ∴+=222(3)4(5)x x ∴+= ,解得, 1x = ,33OC x ∴== .即O 的半径为3,,BC OEOCB EOC ∴∠=∠ ,在 Rt OCE 中, 6tan 23EC EOC OC ∠=== , tan tan 2OCB EOC ∴∠=∠=4.【答案】(1)证明:∵AB 是⊙O 的直径,∴⊙C=90°,∵点D 是AC 的中点,∴DO 垂直平分AC ,且AD=DC , ∴CA⊙DF ,AE=EC , ∴⊙AEO=90°,∴BC DF , ∵BF CD ,∴四边形BCDE 是平行四边形; (2)∵BC DF , ∴⊙DBF=⊙CDB ,又∵根据圆周角定理有⊙CDB=⊙BAC , ∴⊙DBF=⊙BAC , 即tan⊙BAC=34, ∵AC=8, ∴CB=6,则在Rt⊙ACB 中,利用勾股定理可得AB=10,即AO=5=OD , ∵AE=EC=12AC , ∴AE=EC=4,在Rt⊙AEO 中,利用勾股定理得OE=3,∴DE=OD-OE=5-3=2,在Rt⊙AED 中,利用勾股定理,得55 ∴四边形ABCD 的周长5555.【答案】(1)解:∵AB 是O 的直径, 42AC =, 2BC = ,∴90ACB ∠=︒ , 22236AB AC BC =+= , ∴6AB = , 2sin 3ABC ∠=(2)解:∵CD AB ⊥ ,∴CE DE = , 由三角形的面积公式得:1122AC BC AB CE ⨯⨯=⨯⨯ , ∴423CE =, ∴822CD CE ==. 6.【答案】(1)证明:连接 OA 、 OE ,∵点 E 是下半圆弧的中点, OE 过 O , ∴OE DC ⊥ , ∴90FOE ∠=︒ , ∴90E OFE ∠+∠=︒ , ∵OA OE = , AB BF = ,∴BAF BFA ∠=∠ , E OAE ∠=∠ , ∵AFB OFE ∠=∠ , ∴90OAE BAF ∠+∠=︒ , 即 OA AB ⊥ , ∵OA 为半径, ∴AB 是O 的切线(2)解:设 AB x = ,则 BF x = , 1OB x =+ , ∵3OA OC == ,由勾股定理得: 222OB AB OA =+ , ∴()22213x x +=+ , 解得: 4x = ,∴4cos 5AB B OB == 7.【答案】(1)5;平行(2)解:①P 在AB 中点时,连接DP 并延长交BC 于点F ,由(1):DP CE ,∴1BF BPFC AP==, ∴142BF FC BC ===,∴132PF AC ==,11822DF DP PF AB AC =+=+=,∵90DEA BCE PDE ∠=∠=∠=︒, ∴四边形DECF 是矩形, ∴84CE DF DE CF ====,, ∴2AE CE AC =-=, ∴22222425AD AE DE =+=+=②将线段AD 绕着平面上某个点旋转180︒后,使AD 的两个对应点A '、D '落在Rt ABC 的边上, ∴AA '与DD '垂直平分,两条线段的交点O 即为旋转中心,如图所示:则:OD AB ⊥,∵902510ADB AD AB ∠=︒==,,, ∴()2222102545BD AB AD =-=-=∵1122ABD S AD BD AB DO ∆=⋅=⋅, ∴254510DO =, ∴4OD =, ∴222AO AD OD =-=,∴24AA OA '==;(3)解:当P Q AD '时;如图:延长P P '交BC 于点G ,过点P P ',分别作PH AC P T CQ '⊥⊥,,垂足为:H T ,,则:四边形CGP T '为矩形,∵3455AC BC sin ABC cos ABC AB AB ∠==∠==,, ∴3455PG BP sin ABC t BG BP cos ABC t =⋅∠==⋅∠=,,∴34855CH PG t P T CG BC BG t ====-=-',,∴385HE CE CH t =-=-,∵P ,P '关于直线DE 对称 ∴385ET EH t ==-,∴3138821655t QT CT CQ CE ET CQ t t =-=+-=+--=-,∵P Q AD ', ∴P QT DAE ∠=∠',∴2DEtan P QT tan DAE AE∠='∠==, ∴2P T TQ '=,即:413821655t t ⎛⎫-=- ⎪⎝⎭, 解得:6011t =; 当PQ BD 时,延长BD 交CQ 于点K ,∵PQ BD ,∴APQ ABD AQP AKB ∠=∠∠=∠,,∵90ADB ADK DAB KAD ∠=∠=︒∠=∠,(角平分线), ∴ABD AKB ∠=∠, ∴APQ AQP ∠=∠, ∴AP AQ =,∵1026AP AB BP t AQ CQ AC t =-=-=-=-,, ∴1026t t -=-, 解得:163t =; 当P Q BD '时,如图:延长P P '交BC 于点G ,过点P P ',分别作PO AC P R CQ '⊥⊥,,垂足为:OR,,延长BD ,交CM 于点S ,则:四边形CNP R '为矩形,∵3455AC BC sin ABC cos ABC AB AB ∠==∠==,, ∴3455PN BP sin ABC t BN BP cos ABC t =⋅∠==⋅∠=,,∴34855CO PN t P R CN BC BN t ====-=-',,∴385OE CE CO t =-=-,∵P ,P '关于直线DE 对称 ∴385ER OE t ==-,∴3132881655t QR CQ CR CQ CE ER t t =-=-+=--+=-; ∵AD BD ⊥,90AED ∠=︒,∴90ADE EDS ADE DAE ∠+∠=∠+∠=︒ ∴EDS DAE ∠=∠, ∵P Q BD ',∴QP R EDS DAE ∠=∠=∠', ∴2DEtan QP R tan DAE AE∠='∠==, ∴2QR P R =', 即:413281655t t ⎛⎫-=- ⎪⎝⎭,解得:8011t =; 综上:当PP Q '的一边与ABD 的AD 或BD 边平行时,6011t =或163t =或8011t =. 8.【答案】(1)解:根据二次函数交点式为 ()()()120y a x x x x a =--≠ ,抛物线过A(﹣3,0),B(1,0)两点,∴设 ()()2331y ax bx a x x =+-=+- ,∵x=0时,y =ax 2+bx ﹣3=-3,∴将 ()0,3- 代入 ()()31y a x x =+- ∴﹣3a =﹣3, ∴a =1,故抛物线的表达式为:y =x 2+2x ﹣3.(2)解:由抛物线的表达式知,点C 、D 的坐标分别为(0,﹣3)、(﹣1,﹣4), 由点C 、D 的坐标知,直线CD 的表达式为:y =x ﹣3①,1tan 3BCO ∠= ,则 cos 10BCO ∠= ,当点P (P′)在点C 的右侧时,如图所示:∵⊙P'BC =⊙BCO ,故P′B⊙y 轴,则点P′(1,﹣2), 当点P 在点C 的左侧时,设直线PB 交y 轴于点H ,过点H 作HN⊙BC 于点N , ∵⊙P'BC =⊙BCO , ∴⊙BCH 为等腰三角形,则 222cos 23110BC CH BCO CH =⋅∠=⨯=+, 解得: 53CH =,则 433OH CH =-= ,故点 4(0,)3H = , 由点B 、H 的坐标得,直线BH的表达式为: 4433y x =-②,联立①②并解得:58xy=-⎧⎨=-⎩,故点P的坐标为(﹣5,﹣8),综上所述,满足条件的点P坐标为(1,﹣2)或(﹣5,﹣8).(3)M(﹣1,2﹣2),N(﹣1﹣2,﹣2)或M'(﹣1,﹣2﹣2),N'(﹣1+ 2,﹣2) 9.【答案】(1)证明:如图,连接EF,EA,EC,∵ EH⊙FC,H是FC的中点,∴EF=EC,∵AD=CD,⊙ADE=⊙CDE=45°,DE=DE,∴⊙ADE⊙⊙CDE,∴AE=EC,∴EF=AE;(2)解:如图,①∵CD=2,13 BFBA=,∴BF=23,AF=43,∴FC=22210 3BC BF+=,过点E作EM⊙AB于点M,∵EF=AE,∴EM垂直平分FA,∴FM=AM=23,∴BM=ME=43,∴2253FM ME+=,∵H是FC的中点,∴10,∴2210EF FH-=②设AB=2a,∵BFkBA=,∴BF=2ak,∴FM=MA=a-ka,BM=a+ak=ME,∵⊙ADE⊙⊙CDE,∴⊙DCE=⊙DAE=⊙FEM,∴tan⊙DCE=tan⊙FEM=11FM kME k-=+. 10.【答案】(1)解:在Rt ABC中,90,6,8 ACB BC AC∠=︒==,22226810 AB AC BC∴+=+=.4tan3ACBBC==,3tan4BCAAC==, ∵D是边AB的中点,∴5BD=如图,当点Q落在BC上时,BP x = ,4tan 3PQ BP B x ==, ∵PDQ A ∠=∠ , 90DPQ ∠=︒ ,16tan 9QP PD x A == , 5BD PD BP =+= ,1659xx += , 解得, 95x = ,95BP ∴= ;(2)解:如图,当 905x < 时,设PQ 、DQ 与BC 交于点M 、N ,∵D 是边AB 的中点,∴5BD = , 4ND = , 3BN = ,4tan 3PM BP B x == , 211423462233BNDPBMS SSx x x =-=⨯⨯-⨯=- ; 当955x << 时, 5PD x =- , 3tan (5)4PQ DP A x ==- , 21331575(5)(5)24848PDQS Sx x x x ==⨯--=-+ ; 当 57x <≤ 时, 5PD x =- , 3tan (5)4PQ DP A x ==- , 21331575(5)(5)24848PDQS Sx x x x ==⨯--=-+ ; 故 PDQ 与 ABC 重叠部分图形的面积关系式为: 2222960353157595848531575(57)848x x S x x x x x x ⎧⎛⎫-< ⎪⎪⎝⎭⎪⎪⎛⎫=-+<<⎨ ⎪⎝⎭⎪⎪-+<⎪⎩ . 11.【答案】(1)解:作图如下:(2)解:∵⊙ABC=⊙BDC=90°, ∴⊙ABD +⊙CBD=90°,⊙CBD +⊙C=90°,∴⊙ABD=⊙C ,在Rt⊙ABD 中,AD :BD =3:4, ∴AB⊙AD=3⊙5,∴sinC=sin⊙ABD=35AD AB =. (3)解:如图,点P 在BC 为直径的圆上,O 为圆心,当A 、P 、O 三点共线时,AP 最大,∵BC =10,BD =6,∴CD=8,∵⊙ABD⊙⊙BCD ,∴2BD AD CD =⋅,26=8AD ,解得9=2AD , 在Rt⊙ABD 中,AB=152,∵BC=10, ∴BO=OP=5, 在Rt⊙ABO 中,22513AO AB OB =+=, ∴AP=AO +513, 故答案为:5132.. 12.【答案】(1)35;1225(2)解:如图②中,结论:四边形ABCD 是对余四边形.理由:过点D 作DM⊙DC ,使得DM =DC ,连接CM. ∵四边形ABCD 中,AD =BD ,AD⊙BD ,∴⊙DAB =⊙DBA =45°, ∵⊙DCM =⊙DMC =45°, ∴⊙CDM =⊙ADB =90°, ∴⊙ADC =⊙BDM , ∵AD =DB ,CD =DM , ∴⊙ADC⊙⊙BDM (SAS ), ∴AC =BM ,∵2CD 2+CB 2=CA 2,CM 2=DM 2+CD 2=2CD 2,∴CM 2+CB 2=BM 2, ∴⊙BCM =90°,∴⊙DCB =45°, ∴⊙DAB+⊙DCB =90°, ∴四边形ABCD 是对余四边形. (3)4)2tu t =<< 13.【答案】(1)解:∵AD⊙BC ,∴AD DE BG EB = , AD DFCH FC= . ∵DB =DC =15,DE =DF =5,∴12DE DF EB FC == , ∴AD ADBG CH= . ∴BG =CH .(2)解:过点D 作DP⊙BC ,过点N 作NQ⊙AD ,垂足分别为点P 、Q .∵DB =DC =15,BC =18,∴BP =CP =9,DP =12.∵12AD DE BG EB == , ∴BG =CH =2x , ∴BH =18+2x . ∵AD⊙BC ,∴AD DNBH NB = , ∴182x DNx NB=+ , ∴18215xDN DNx x NB DN ==+++ ,∴56xDNx=+.∵AD⊙BC,∴⊙ADN=⊙DBC,∴sin⊙ADN=sin⊙DBC,∴NQ PD DN BD=,∴46xNQx=+.∴211422266x xy AD NQ xx x=⋅=⋅=++(0<x≤9).(3)解:∵AD⊙BC,∴⊙DAN=⊙FHG.(i)当⊙ADN=⊙FGH时,∵⊙ADN=⊙DBC,∴⊙DBC=⊙FGH,∴BD⊙FG,∴BG DF BC DC=,∴5 1815 BG=,∴BG=6,∴AD=3.(ii)当⊙ADN=⊙GFH时,∵⊙ADN=⊙DBC=⊙DCB,又∵⊙AND=⊙FGH,∴⊙ADN⊙⊙FCG.∴AD FC DN CG=,∴5(182)106xx xx⋅-=⨯+,整理得x2﹣3x﹣29=0,解得3552x+=,或3552x-=(舍去).综上所述,当⊙HFG与⊙ADN相似时,AD的长为3或3552x+=.14.【答案】(1)60(2)解:S⊙ADE=12DE·AB=3DE,∴当DE取最小值时,⊙ADE面积取最小值.作⊙ADE的外接圆,圆心为O,连接OD、OE、OA,过O作OH⊙DE于H,则⊙DOE=2⊙DAE=120°,由OD=OE知,⊙ODH=30°,∴OD=2OH,∵OA+OH≥AB,∴OA+12OA≥6,即OA≥4,OH≥2,由垂径定理得:3OH≥3此时,A、O、H共线,AD=AE,∴⊙ADE面积的最小值为:3×433(3)解:过C作CH⊙AE于H,如图所示,设BD=x,EF=y,∵⊙ABC=90°,AE⊙BC,∴四边形ABCF 为矩形, ∵AB=BC=40∴四边形ABCF 为正方形, 由tan⊙E=tan⊙BCD 知,CF BDEF BC=, 即4040x y =, ∴y=1600x, 即xy=1600, ∵22220x x y y x y-+=≥,∴2x y xy +≥,当x=y 时取等号,即x+y 的最小值为80,又⊙ADE 的面积=正方形ABCF 面积+三角形BCD 面积+三角形CEF 面积, 即⊙ADE 的面积=1600+20(x+y )≥1600+20×80=3200, 综上所述,⊙ADE 的面积的最小值为3200 m 2.15.【答案】(1)解:∵y =﹣x 2+bx+c 经过B (﹣1,6),3),∴340c b c =⎧⎨-++=⎩ , 解得 25b c =⎧⎨=⎩, ∴抛物线的解析式为y =﹣x 2+2x+7(2)解:如图1中,过点B 作BT⊙y 轴交AC 于T.设P(m ,﹣m 2+2m+3),对于抛物线y =﹣x 2+5x+3,令y =0,∴A(2,0), ∵C(0,8),∴直线AC 的解析式为y =﹣x+3, ∵B(﹣1,2), ∴T(﹣1,4), ∴BT =3, ∵PQ⊙OC , ∴Q(m ,﹣m+3),∴PQ =﹣m 2+2m+3﹣(﹣m+3)=﹣m 3+3m , ∵PQ⊙BT , ∴PQ BT = PE BC = 15, ∴﹣m 2+3m =4,解得m =1或2,∴P(4,4)或2.(3)解:如图8中,连接AD ,过点C 作CT⊙AD 于T.∵抛物线y=﹣x2+2x+6=﹣(x﹣1)2+3,∴顶点D(1,4),∵C(8,3),∴直线CD的解析式为y=x+3,CD=7,∵DD′=2CD,∵DD′=2 4,CD′=3 2,∴D′(4,6),∵A(3,2),∴AD′⊙x轴,∴OD′=22OA D A+'=2256+=3 5,∴sin⊙OD′A=OAOD'=45,∵CT⊙AD′,∴CT=3,∵NJ⊙AD′,∴NJ=ND′•sin⊙OD′A=7D′N,5D'N+CN=CN+NJ,∵CN+NJ≥CT,∴55D'N+CN≥7,5D'N+CN的最小值为8.16.【答案】(1)解:①过点P作PH BD⊥于H.BD BC⊥,PH BD⊥,90CBH PHB C∴∠=∠=∠=︒,∴四边形BCPH 是矩形,4PH BC∴==,在Rt ACB中,2222345AB AC BC++=,由旋转的旋转可知,5BD BA==,11541022PBDS BD PH∆∴=⋅⋅=⨯⨯=.②由旋转的性质可知,4BE BC==,12PBDS PD BE∆=⋅⋅,2054PD∴==,90PHD∠=︒,2222543DH PD PH∴=-=-=,2PC BH∴==,90C∠=︒,21tan42PCPBCBC∴∠===.(2)证明:如图2中,连接BF,取BD的中点T,连接FT,ET.BC BE = , BA BD = ,BCE BEC ∴∠=∠ , BAD BDA ∠=∠ ,BDE ∆ 是由 BAC ∆ 旋转得到, BCE ABD ∴∠=∠ , BEC ADB ∴∠=∠ ,BA BD = , AF DF = , BF AD ∴⊥ , 90AFD ∴∠=︒ ,90BED AFD ∠=∠=︒ , DT TB = ,12ET BD ∴=, 12FT BD = , ET FT DT TB ∴=== , E ∴ ,F ,D ,B 四点共圆, 1DBF ∴∠=∠ ,90DBF BDF ∠+∠=︒ , 190BEC ∴∠+∠=︒ ,1180BEC BED ∴∠+∠+∠=︒ , C ∴ 、E 、F 三点共线.17.【答案】(1)解:由 ()50A ,可知 5OA = , 在Rt⊙AOC 中, 2sin 2BAC ∠= , ∴45BAC ∠=︒ ,∴5OA OC == ,即点C (0,5),由题意可设 ()()51y a x x =-+ ,把点C 代入得: 55a -= , 解得: 1a =- ,∴抛物线解析式为 ()()25145y x x x x =--+=-++ ;(2)解:由(1)可得:C (0,5), ()50A ,,设直线AC 的解析式为 1y k x b =+ ,把点A 、C 坐标代入得:{b =55k 1+b =0 ,解得: {b =5k 1=−1, ∴直线AC 的解析式为 5y x =-+ ,∵直线 y kx = ( 0k > )交线段AC 于点M ,则设 ()5M m m -+,, ∴5m k m-+=, 由(1)可知 5OA OC == , 1OB = , ∴()()22055052AC =-+-=, 6AB = ,由题意可分:①当 AOM ABC ∽ 时,∴56AO AM AB AC == , ∴525266AM AC ==, ∴由两点距离公式可得: ()()226255518m m -+-= , 解得: 1255566m m ==, , ∵05m ≤≤ , ∴56m =, ∴55525655666M k -+⎛⎫== ⎪⎝⎭,, ; ②当 AOM ACB ∽ 时,∴2252AO AM AC AB ===,∴232AM AB ==,∴由两点距离公式可得: ()()225518m m -+-= , 解得: 1228m m ==, (不符合题意,舍去),∴()2532322M k -+==,, ; (3)解:过点B 作BF⊙x 轴,交AC 的延长线于点F ,过点P 作PD⊙x 轴于点D ,交AC 于点H ,如图所示:∴BF⊙PH ,∴BQF PQH ∽ ,∴PQ PHBQ BF= , 由(2)知,直线AC 的解析式为 5y x =-+ ,点 ()10B -, , ∴点 ()16F -, ,即 6BF = , 设点 ()245P a a a -++,,则有 ()5H a a -+, , ∴()224555PH a a a a a =-++--+=-+ ,∴225152566224PQ a a a BQ -+⎛⎫==--+⎪⎝⎭ , ∵106-< , ∴当 52a =时, PQ BQ 的值最大,最大值为 2524.18.【答案】(1)解:如图,过点 D 作 DM x ⊥ 轴于点 M∵90ACB ∠=︒ , ∴3tan 32BC CAB AC ∠===∴60CAB ∠=由题意可知 2DA AC == , 60DAB CAB ∠=∠=︒ . ∴180180606060DAM DAB CAB ∠=︒-∠-∠=︒-︒-︒=︒ . ∴906030ADM ∠=︒-︒=︒ 在 Rt ADM ∆ 中, 2DA = , ∴1AM = , 3DM =.∵点 C 坐标为 (10)-,, ∴1214OM OC AC AM =++=++= . ∴点 D 的坐标是 (3)-(2)解:设点 C 坐标为 (,0)a ( 0a < ),则点 B 的坐标是 (,3)a , 由(1)可知:点 D 的坐标是 (3)a - ∵点 B 和点 D 在同一个反比例函数的图象上, ∴33(3)a a =- .解得 3a =- . ∴点 C 坐标为 (3,0)-(3)解:存在这样的 k ,使得以点 E, 1B , D 为顶点的三角形是直角三角形①当 190EDB ∠= 时.如图所示,连接 ED , 1B B , 1B D , 1B B 与 ED 相交于点 N .则 190EBN NDB ∠=∠=︒ , 1BNE DNB ∠=∠ , 130DBN NB E ∠=∠= .∴BNE ∆ ⊙ 1DNB ∆∴1BN ENDN B N= ∴1BN DNEN B N= 又∵1BND ENB ∠=∠ , ∴BND ∆ ⊙ 1ENB ∆ .∴130NEB NBD ∠=∠= , 130NDB NB E ∠=∠= , ∴30BED BDE ∠=∠=︒ . ∴23BE BD == , 16tan 30BEBB ==设 (43)E m , ( 0m < ),则 1(3)D m - , ∵E , 1D 在同一反比例函数图象上, ∴433(9)m m =- .解得: 3m =- . ∴(343)E -,∴343123k =-⨯=-②当 190EB D ∠= 时.如图所示,连接 ED , 1B B , 1B D ,∵1//BD ED ,∴1118090BDB EB D ∠=︒-∠=︒ .在 1Rt BDB ∆ 中,∵130DBB ∠=︒ , 3BD =, ∴14cos30BDBB == .在 1Rt EBB ∆ 中, ∵130BB E ∠=︒ ,∴143tan 30EB BB =︒=. ∴1033EC BC EB =+=设 3(,)3E m ( 0m < ),则 1(13)D m - ∵E , 1D 在同一反比例函数图象上,1033(7)m=-.解得:3m=-,∴103 (3,3 E-∴3333k=-⨯=-21/ 21。
中考数学真题精选之《锐角三角函数》综合解答题

中考数学真题精选之《锐角三角函数》综合解答题1.如图所示是消防员攀爬云梯到小明家的场景.已知AE⊥BE,BC⊥BE,CD∥BE,AC=10.4m,BC=1.26m,点A关于点C的仰角为70°,则楼AE的高度为多少m?(结果保留整数.参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)2.贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚A为起点,沿途修建AB、CD两段长度相等的观光索道,最终到达山顶D处,中途设计了一段与AF平行的观光平台BC为50m.索道AB与AF的夹角为15°,CD与水平线夹角为45°,A、B两处的水平距离AE为576m,DF⊥AF,垂足为点F.(图中所有点都在同一平面内,点A、E、F在同一水平线上)(1)求索道AB的长(结果精确到1m);(2)求水平距离AF的长(结果精确到1m).(参考数据:sin15°≈0.25,cos15°≈0.96,tan15°≈0.26,√2≈1.41)3.徐州电视塔为我市的标志性建筑之一,如图,为了测量其高度,小明在云龙公园的点C 处,用测角仪测得塔顶A的仰角∠AFE=36°,他在平地上沿正对电视塔的方向后退至点D处,测得塔顶A的仰角∠AGE=30°.若测角仪距地面的高度FC=GD=1.6m,CD =70m,求电视塔的高度AB(精确到0.1m).(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin30°≈0.50,cos30°≈0.87,tan30°≈0.58)4.问题情境:筒车是我国古代发明的一种水利灌溉工具,既经济又环保.明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理(如图①).假定在水流量稳定的情况下,筒车上的每一个盛水筒都按逆时针做匀速圆周运动,每旋转一周用时120秒.问题设置:把筒车抽象为一个半径为r的⊙O.如图②,OM始终垂直于水平面,设筒车半径为2米.当t=0时,某盛水筒恰好位于水面A处,此时∠AOM=30°,经过95秒后该盛水筒运动到点B处.问题解决:(1)求该盛水筒从A处逆时针旋转到B处时,∠BOM的度数;(2)求该盛水筒旋转至B处时,它到水面的距离.(结果精确到0.1米)(参考数据√2≈1.414,√3≈1.732)5.今年“五一”长假期间,小陈、小余同学和家长去沙滩公园游玩,坐在如图的椅子上休息时,小陈感觉很舒服,激发了她对这把椅子的好奇心,就想出个问题考考同学小余,小陈同学先测量,根据测量结果画出了图1的示意图(图2).在图2中,已知四边形ABCD 是平行四边形,座板CD与地面MN平行,△EBC是等腰三角形且BC=CE,∠FBA=114.2°,靠背FC=57cm,支架AN=43cm,扶手的一部分BE=16.4cm.这时她问小余同学,你能算出靠背顶端F点距地面(MN)的高度是多少吗?请你帮小余同学算出结果(最后结果保留一位小数).(参考数据:sin65.8°=0.91,cos65.8°=0.41,tan65.8°=2.23)6.暑假期间,小明与小亮相约到某旅游风景区登山.需要登顶600m高的山峰,由山底A 处先步行300m到达B处,再由B处乘坐登山缆车到达山顶D处.已知点A,B,D,E,F在同一平面内,山坡AB的坡角为30°,缆车行驶路线BD与水平面的夹角为53°(换乘登山缆车的时间忽略不计).(1)求登山缆车上升的高度DE;(2)若步行速度为30m/min,登山缆车的速度为60m/min,求从山底A处到达山顶D处大约需要多少分钟(结果精确到0.1min).(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)7.如图,一艘海轮位于灯塔P的北偏东72°方向,距离灯塔100nmile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东40°方向上的B处.这时,B处距离灯塔P有多远(结果取整数)?(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)8.为了增强学生体质、锤炼学生意志,某校组织一次定向越野拉练活动.如图,A点为出发点,途中设置两个检查点,分别为B点和C点,行进路线为A→B→C→A.B点在A 点的南偏东25°方向3√2km处,C点在A点的北偏东80°方向,行进路线AB和BC所在直线的夹角∠ABC为45°.(1)求行进路线BC和CA所在直线的夹角∠BCA的度数;(2)求检查点B和C之间的距离(结果保留根号).9.为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形ABCD,斜面坡度i=3:4是指坡面的铅直高度AF与水平宽度BF的比.已知斜坡CD长度为20米,∠C=18°,求斜坡AB的长.(结果精确到0.1米)(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)10.2023年5月30日9点31分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面O处发射,当飞船到达A点时,从位于地面C处的雷达站测得AC 的距离是8km,仰角为30°;10s后飞船到达B处,此时测得仰角为45°.(1)求点A离地面的高度AO;(2)求飞船从A处到B处的平均速度.(结果精确到0.1km/s,参考数据:√3≈1.73)11.“游张家界山水,逛七十二奇楼”成为今年旅游新特色.某数学兴趣小组用无人机测量奇楼AB的高度,测量方案如图:先将无人机垂直上升至距水平地面225m的P点,测得奇楼顶端A的俯角为15°,再将无人机沿水平方向飞行200m到达点Q,测得奇楼底端B的俯角为45°,求奇楼AB的高度.(结果精确到1m,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)12.无人机在实际生活中的应用越来越广泛.如图所示,某人利用无人机测量大楼的高度BC,无人机在空中点P处,测得点P距地面上A点80米,点A处的俯角为60°,楼顶C点处的俯角为30°,已知点A与大楼的距离AB为70米(点A,B,C,P在同一平面内),求大楼的高度BC(结果保留根号).13.图1是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图2,摄像头A的仰角、俯角均为15°,摄像头高度OA=160cm,识别的最远水平距离OB=150cm.(1)身高208cm的小杜,头部高度为26cm,他站在离摄像头水平距离130cm的点C处,请问小杜最少需要下蹲多少厘米才能被识别?(2)身高120cm的小若,头部高度为15cm,踮起脚尖可以增高3cm,但仍无法被识别,社区及时将摄像头的仰角、俯角都调整为20°(如图3),此时小若能被识别吗?请计算说明.(精确到0.1cm,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)14.鄂州市莲花山是国家4A级风景区,元明塔造型独特,是莲花山风景区的核心景点,深受全国各地旅游爱好者的青睐.今年端午节,景区将举行大型包粽子等节日庆祝活动.如图2,景区工作人员小明准备从元明塔的点G处挂一条大型竖直条幅到点E处,挂好后,小明进行实地测量,从元明塔底部F点沿水平方向步行30米到达自动扶梯底端A点,在A点用仪器测得条幅下端E的仰角为30°;接着他沿自动扶梯AD到达扶梯顶端D点,测得点A和点D的水平距离为15米,且tan∠DAB=43;然后他从D点又沿水平方向行走了45米到达C点,在C点测得条幅上端G的仰角为45°.(图上各点均在同一个平面内,且G,C,B共线,F,A,B共线,G、E、F共线,CD∥AB,GF⊥FB).(1)求自动扶梯AD的长度;(2)求大型条幅GE的长度.(结果保留根号)15.综合实践活动中,某小组用木板自制了一个测高仪测量树高,测高仪ABCD为正方形,AB=30cm,顶点A处挂了一个铅锤M.如图是测量树高的示意图,测高仪上的点D,A 与树顶E在一条直线上,铅垂线AM交BC于点H.经测量,点A距地面1.8m,到树EG 的距离AF=11m,BH=20cm.求树EG的高度(结果精确到0.1m).16.如图,直线MN和EF为河的两岸,且MN∥EF,为了测量河两岸之间的距离,某同学在河岸FE的B点测得∠CBE=30°,从B点沿河岸FE的方向走40米到达D点,测得∠CDE=45°.(1)求河两岸之间的距离是多少米?(结果保留根号)(2)若从D点继续沿DE的方向走(12√3+12)米到达P点.求tan∠CPE的值.17.如图1是我国第一个以“龙”为主题的主题公园——“兰州龙源”、“兰州龙源”的“龙”字主题雕塑以紫铜铸造,如巨龙腾空,气势如虹,屹立在黄河北岸、某数学兴趣小组开展了测量“龙”字雕塑CD高度的实践活动,具体过程如下,如图2,“龙”字雕塑CD 位于垂直地面的基座BC上,在平行于水平地面的A处测得∠BAC=38°,∠BAD=53°,AB=18m.求“龙”字雕塑CD的高度,(B,C,D三点共线,BD⊥AB,结果精确到0.1m)(参考数据:sin38°=0.62,cos38°=0.79,tan38°=0.78,sin53°=080,cos53°=0.60,tan53°=1.33)18.2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站.如图中的照片展示了中国空间站上机械臂的一种工作状态.当两臂AC=BC=10m,两臂夹角∠ACB=100°时,求A,B两点间的距离.(结果精确到0.1m,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)19.东昌湖西岸的明珠大剧院,隔湖与远处的角楼、城门楼、龙堤、南关桥等景观遥相呼应.如图所示,城门楼B在角楼A的正东方向520m处,南关桥C在城门楼B的正南方向1200m 处.在明珠大剧院P测得角楼A在北偏东68.2°方向,南关桥C在南偏东56.31°方向(点A,B,C,P四点在同一平面内),求明珠大剧院到龙堤BC的距离(结果精确到1m)(参考数据:sin68,2°≈0.928,cos68.2°≈0.371,tan68.2°≈2.50,sin56.31°≈0.832,cos56.31°≈0.555,tan56.31°≈1.50)20.某次军事演习中,一艘船以40km/h的速度向正东航行,在出发地A测得小岛C在它的北偏东60°方向,2小时后到达B处,浏得小岛C在它的北偏西45°方向,求该船在航行过程中与小岛C的最近距离(参考数据:√2≈1.41,√3≈1.73.结果精确到0.1km).21.我国航天事业捷报频传,2023年5月30日,被誉为“神箭”的长征二号F运载火箭托举神舟十六号载人飞船跃入苍穹,中国空间站应用与发展阶段首次载人发射任务取得圆满成功.如图,有一枚运载火箭从地面O处发射,当火箭到达P处时,地面A处的雷达站测得AP距离是5000m,仰角为23°,9s后,火箭直线到达Q处,此时地面A处雷达站测得Q处的仰角为45°,求火箭从P到Q处的平均速度(结果精确到1m/s).(参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.42)22.根据背景素材,探索解决问题.测算发射塔的高度背景素材某兴趣小组在一幢楼房窗口测算远处小山坡上发射塔的高度MN(如图1),他们通过自制的测倾仪(如图2)在A,B,C三个位置观测,测倾仪上的示数如图3所示.经讨论,只需选择其中两个合适的位置,通过测量、换算就能计算发射塔的高度问题解决任务1分析规划选择两个观测位置:点和点.获取数据写出所选位置观测角的正切值,并量出观测点之间的图上距离.任务2推理计算计算发射塔的图上高度MN.任务3换算高度楼房实际宽度DE为12米,请通过测量换算发射塔的实际高度.注:测量时,以答题纸上的图上距离为准,并精确到1mm.23.“一缕清风银叶转”,某市20台风机依次矗立在云遮雾绕的山脊之上,风叶转动,风能就能转换成电能,造福千家万户.某中学初三数学兴趣小组,为测量风叶的长度进行了实地测量.如图,三片风叶两两所成的角为120°,当其中一片风叶OB与塔干OD叠合时,在与塔底D水平距离为60米的E处,测得塔顶部O的仰角∠OED=45°,风叶OA 的视角∠OEA=30°.(1)已知α,β两角和的余弦公式为:cos(α+β)=cosαcosβ﹣sinαsinβ,请利用公式计算cos75°;(2)求风叶OA的长度.24.图1是某款篮球架,图2是其示意图,立柱OA垂直地面OB,支架CD与OA交于点A,支架CG⊥CD交OA于点G,支架DE平行地面OB,篮筐EF与支架DE在同一直线上,OA=2.5米,AD=0.8米.∠AGC=32°.(1)求∠GAC的度数;(2)某运动员准备给篮筐挂上篮网,如果他站在凳子上,最高可以把篮网挂到离地面3米处,那么他能挂上篮网吗?请通过计算说明理由.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)25.某校学生开展综合实践活动,测量某建筑物的高度AB,在建筑物附近有一斜坡,坡长CD=10米,坡角α=30°,小华在C处测得建筑物顶端A的仰角为60°,在D处测得建筑物顶端A的仰角为30°.(已知点A,B,C,D在同一平面内,B,C在同一水平线上)(1)求点D到地面BC的距离;(2)求该建筑物的高度AB.。
备战中考数学综合题专题复习【锐角三角函数】专题解析附答案解析

一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).【答案】.【解析】试题分析:作AD⊥BC于D,于是有∠ABD=45°,得到AD=BD=,求出∠C=60°,根据正切的定义求出CD的长,得到答案.试题解析:作AD⊥BC于D,∵∠EAB=30°,AE∥BF,∴∠FBA=30°,又∠FBC=75°,∴∠ABD=45°,又AB=60,∴AD=BD=,∵∠BAC=∠BAE+∠CAE=75°,∠ABC=45°,∴∠C=60°,在Rt△ACD中,∠C=60°,AD=,则tanC=,∴CD==,∴BC=.故该船与B港口之间的距离CB的长为海里.考点:解直角三角形的应用-方向角问题.2.如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.(1)求证:直线CP是⊙O的切线.(2)若BC=2,sin∠BCP=,求点B到AC的距离.(3)在第(2)的条件下,求△ACP的周长.【答案】(1)证明见解析(2)4(3)20【解析】试题分析:(1)利用直径所对的圆周角为直角,2∠CAN=∠CAB,∠CAB=2∠BCP判断出∠ACP=90°即可;(2)利用锐角三角函数,即勾股定理即可.试题解析:(1)∵∠ABC=∠ACB,∴AB=AC,∵AC为⊙O的直径,∴∠ANC=90°,∴∠CAN+∠ACN=90°,2∠BAN=2∠CAN=∠CAB,∵∠CAB=2∠BCP,∴∠BCP=∠CAN,∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°,∵点D在⊙O上,∴直线CP是⊙O的切线;(2)如图,作BF⊥AC∵AB=AC,∠ANC=90°,∴CN=CB=,∵∠BCP=∠CAN,sin∠BCP=,∴sin∠CAN=,∴∴AC=5,∴AB=AC=5,设AF=x,则CF=5﹣x,在Rt△ABF中,BF2=AB2﹣AF2=25﹣x2,在Rt△CBF中,BF2=BC2﹣CF2=2O﹣(5﹣x)2,∴25﹣x2=2O﹣(5﹣x)2,∴x=3,∴BF2=25﹣32=16,∴BF=4,即点B到AC的距离为4.考点:切线的判定3.如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.(1)求证:△ABC∽△BCD;(2)求x的值;(3)求cos36°-cos72°的值.【答案】(1)证明见解析;(215-+;(3758+【解析】试题分析:(1)由等腰三角形ABC中,顶角的度数求出两底角度数,再由BD为角平分线求出∠DBC的度数,得到∠DBC=∠A,再由∠C为公共角,利用两对角相等的三角形相似得到三角形ABC与三角形BCD相似;(2)根据(1)结论得到AD=BD=BC,根据AD+DC表示出AC,由(1)两三角形相似得比例求出x的值即可;(3)过B作BE垂直于AC,交AC于点E,在直角三角形ABE和直角三角形BCE中,利用锐角三角函数定义求出cos36°与cos72°的值,代入原式计算即可得到结果.试题解析:(1)∵等腰△ABC中,AB=AC,∠BAC=36°,∴∠ABC=∠C=72°,∵BD平分∠ABC,∴∠ABD=∠CBD=36°, ∵∠CBD=∠A=36°,∠C=∠C , ∴△ABC ∽△BCD ; (2)∵∠A=∠ABD=36°, ∴AD=BD , ∵BD=BC , ∴AD=BD=CD=1,设CD=x ,则有AB=AC=x+1, ∵△ABC ∽△BCD ,∴AB BC BD CD =,即111x x +=, 整理得:x 2+x-1=0,解得:x 1=15-+,x 2=15--(负值,舍去),则x=15-+; (3)过B 作BE ⊥AC ,交AC 于点E ,∵BD=CD ,∴E 为CD 中点,即DE=CE=154-+, 在Rt △ABE 中,cosA=cos36°=151514151AE AB -+++==-++ 在Rt △BCE 中,cosC=cos72°=1515414EC BC -+-+==, 则cos36°-cos72°=51+=15-+=12. 【考点】1.相似三角形的判定与性质;2.等腰三角形的性质;3.黄金分割;4.解直角三角形.4.如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO.并延长AO交☉O于点E,与PB的延长线交于点D.(1)求证:PA是☉O的切线;(2)若=,且OC=4,求PA的长和tan D的值.【答案】(1)证明见解析;(2)PA =3,tan D=.【解析】试题分析: (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;(2)连接BE,由,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.试题解析:(1)连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB,在△PAO和△PBO中,∵,∴△PAO≌△PBO(SSS)∴∠PBO=∠PAO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;(2)连接BE,∵,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:AO=,∴AE=2OA=4,OB=OA=2,在Rt△APO中,∵AC⊥OP,∴AC2=OC PC,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP==3.易证,所以,解得,则,在中,.考点:1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.5.如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F 点.若AB=6cm.(1)AE的长为 cm;(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;(3)求点D′到BC的距离.【答案】(1);(2)12cm;(3)cm.【解析】试题分析:(1)首先利用勾股定理得出AC的长,进而求出CD的长,利用直角三角形斜边上的中线等于斜边的一半进而得出答案:∵∠BAC=45°,∠B=90°,∴AB=BC=6cm,∴AC=12cm.∵∠ACD=30°,∠DAC=90°,AC=12cm,∴(cm).∵点E为CD边上的中点,∴AE=DC=cm.(2)首先得出△ADE为等边三角形,进而求出点E,D′关于直线AC对称,连接DD′交AC 于点P,根据轴对称的性质,此时DP+EP值为最小,进而得出答案.(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,进而得出△ABD′≌△CBD′(SSS),则∠D′BG=45°,D′G=GB,进而利用勾股定理求出点D′到BC边的距离.试题解析:解:(1).(2)∵Rt△ADC中,∠ACD=30°,∴∠ADC=60°,∵E为CD边上的中点,∴DE=AE.∴△ADE为等边三角形.∵将△ADE沿AE所在直线翻折得△AD′E,∴△AD′E为等边三角形,∠AED′=60°.∵∠EAC=∠DAC﹣∠EAD=30°,∴∠EFA=90°,即AC所在的直线垂直平分线段ED′.∴点E,D′关于直线AC对称.如答图1,连接DD′交AC于点P,∴此时DP+EP值为最小,且DP+EP=DD′.∵△ADE是等边三角形,AD=AE=,∴,即DP+EP最小值为12cm.(3)如答图2,连接CD′,BD′,过点D′作D′G⊥BC于点G,∵AC垂直平分线ED′,∴AE=AD′,CE=CD′,∵AE=EC,∴AD′=CD′=.在△ABD′和△CBD′中,∵,∴△ABD′≌△CBD′(SSS).∴∠D′BG=∠D′BC=45°.∴D′G=GB.设D′G长为xcm,则CG长为cm,在Rt△GD′C中,由勾股定理得,解得:(不合题意舍去).∴点D′到BC边的距离为cm.考点:1.翻折和单动点问题;2.勾股定理;3.直角三角形斜边上的中线性质;4.等边三角形三角形的判定和性质;5.轴对称的应用(最短线路问题);6.全等三角形的判定和性质;7.方程思想的应用.6.在正方形ABCD中,AC是一条对角线,点E是边BC上的一点(不与点C重合),连接AE,将△ABE沿BC方向平移,使点B与点C重合,得到△DCF,过点E作EG⊥AC于点G,连接DG,FG.(1)如图,①依题意补全图;②判断线段FG与DG之间的数量关系与位置关系,并证明;(2)已知正方形的边长为6,当∠AGD=60°时,求BE的长.BE【答案】(1)①见解析,②FG=DG,FG⊥DG,见解析;(2)3【解析】【分析】(1)①补全图形即可,②连接BG,由SAS证明△BEG≌△GCF得出BG=GF,由正方形的对称性质得出BG=DG,得出FG=DG,在证出∠DGF=90°,得出FG⊥DG即可,(2)过点D作DH⊥AC,交AC于点H.由等腰直角三角形的性质得出DH=AH=2FG=DG=2GH=6,得出DF2DG=3Rt△DCF中,由勾股定理得出CF=3得出结果.【详解】解:(1)①补全图形如图1所示,②FG=DG,FG⊥DG,理由如下,连接BG,如图2所示,∵四边形ABCD是正方形,∴∠ACB=45°,∵EG⊥AC,∴∠EGC =90°,∴△CEG 是等腰直角三角形,EG =GC , ∴∠GEC =∠GCE =45°, ∴∠BEG =∠GCF =135°, 由平移的性质得:BE =CF ,在△BEG 和△GCF 中,BE CF BEG GCF EG CG =⎧⎪∠=∠⎨⎪=⎩,∴△BEG ≌△GCF (SAS ), ∴BG =GF ,∵G 在正方形ABCD 对角线上, ∴BG =DG , ∴FG =DG ,∵∠CGF =∠BGE ,∠BGE+∠AGB =90°, ∴∠CGF+∠AGB =90°, ∴∠AGD+∠CGF =90°, ∴∠DGF =90°, ∴FG ⊥DG.(2)过点D 作DH ⊥AC ,交AC 于点H .如图3所示, 在Rt △ADG 中, ∵∠DAC =45°, ∴DH =AH =2在Rt △DHG 中,∵∠AGD =60°, ∴GH 33236,∴DG =2GH =6, ∴DF 2DG =3 在Rt △DCF 中,CF ()22436-3∴BE =CF =3.【点睛】本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质、勾股定理、解直角三角形的应用等知识;本题综合性强,证明三角形全等是解题的关键.7.在Rt△ABC中,∠ACB=90°,AB=7,AC=2,过点B作直线m∥AC,将△ABC绕点C 顺时针旋转得到△A′B′C(点A,B的对应点分别为A',B′),射线CA′,CB′分別交直线m于点P,Q.(1)如图1,当P与A′重合时,求∠ACA′的度数;(2)如图2,设A′B′与BC的交点为M,当M为A′B′的中点时,求线段PQ的长;(3)在旋转过程中,当点P,Q分别在C A′,CB′的延长线上时,试探究四边形PA'B′Q的面积是否存在最小值.若存在,求出四边形PA′B′Q的最小面积;若不存在,请说明理由.【答案】(1)60°;(2)PQ=72;(3)存在,S四边形PA'B′Q=33【解析】【分析】(1)由旋转可得:AC=A'C=2,进而得到BC3=∠A'BC=90°,可得cos∠A'CB3'BCA C==∠A'CB=30°,∠ACA'=60°;(2)根据M为A'B'的中点,即可得出∠A=∠A'CM,进而得到PB3=32=,依据tan∠Q=tan∠A32=BQ=BC3=2,进而得出PQ=PB+BQ72=;(3)依据S四边形PA'B'Q=S△PCQ﹣S△A'CB'=S△PCQ3-S四边形PA'B'Q最小,即S△PCQ最小,而S△PCQ12=PQ×BC3=,利用几何法即可得到S△PCQ的最小值=3,即可得到结论.【详解】(1)由旋转可得:AC =A 'C =2.∵∠ACB =90°,AB 7=,AC =2,∴BC 3=. ∵∠ACB =90°,m ∥AC ,∴∠A 'BC =90°,∴cos ∠A 'CB 3'BC A C ==,∴∠A 'CB =30°,∴∠ACA '=60°;(2)∵M 为A 'B '的中点,∴∠A 'CM =∠MA 'C ,由旋转可得:∠MA 'C =∠A ,∴∠A =∠A 'CM ,∴tan ∠PCB =tan ∠A 3=,∴PB 3=BC 32=. ∵∠BQC =∠BCP =∠A ,∴tan ∠BQC =tan ∠A 3=,∴BQ =BC 3⨯=2,∴PQ =PB +BQ 72=; (3)∵S 四边形PA 'B 'Q =S △PCQ ﹣S △A 'CB '=S △PCQ 3-,∴S 四边形PA 'B 'Q 最小,即S △PCQ 最小,∴S △PCQ 12=PQ ×BC 3=PQ , 取PQ 的中点G . ∵∠PCQ =90°,∴CG 12=PQ ,即PQ =2CG ,当CG 最小时,PQ 最小,∴CG ⊥PQ ,即CG 与CB 重合时,CG 最小,∴CG min 3=,PQ min =23,∴S △PCQ 的最小值=3,S 四边形PA 'B 'Q =33-;【点睛】本题属于几何变换综合题,主要考查了旋转的性质,解直角三角形以及直角三角形的性质的综合运用,解题时注意:旋转变换中,对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.8.在Rt △ABC 中,∠ACB =90°,CD 是AB 边的中线,DE ⊥BC 于E ,连结CD ,点P 在射线CB 上(与B ,C 不重合)(1)如果∠A =30°,①如图1,∠DCB 等于多少度;②如图2,点P 在线段CB 上,连结DP ,将线段DP 绕点D 逆时针旋转60°,得到线段DF ,连结BF ,补全图2猜想CP 、BF 之间的数量关系,并证明你的结论;(2)如图3,若点P 在线段CB 的延长线上,且∠A =α(0°<α<90°),连结DP ,将线段DP绕点逆时针旋转2α得到线段DF,连结BF,请直接写出DE、BF、BP三者的数量关系(不需证明)【答案】(1)①∠DCB=60°.②结论:CP=BF.理由见解析;(2)结论:BF﹣BP=2DE•tanα.理由见解析.【解析】【分析】(1)①根据直角三角形斜边中线的性质,结合∠A=30°,只要证明△CDB是等边三角形即可;②根据全等三角形的判定推出△DCP≌△DBF,根据全等的性质得出CP=BF,(2)求出DC=DB=AD,DE∥AC,求出∠FDB=∠CDP=2α+∠PDB,DP=DF,根据全等三角形的判定得出△DCP≌△DBF,求出CP=BF,推出BF﹣BP=BC,解直角三角形求出CE=DEtanα即可.【详解】(1)①∵∠A=30°,∠ACB=90°,∴∠B=60°,∵AD=DB,∴CD=AD=DB,∴△CDB是等边三角形,∴∠DCB=60°.②如图1,结论:CP=BF.理由如下:∵∠ACB=90°,D是AB的中点,DE⊥BC,∠DCB=60°,∴△CDB为等边三角形.∴∠CDB=60°∵线段DP绕点D逆时针旋转60°得到线段DF,∵∠PDF=60°,DP=DF,∴∠FDB=∠CDP,在△DCP和△DBF中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,∴△DCP ≌△DBF ,∴CP =BF.(2)结论:BF ﹣BP =2DEtanα.理由:∵∠ACB =90°,D 是AB 的中点,DE ⊥BC ,∠A =α,∴DC =DB =AD ,DE ∥AC ,∴∠A =∠ACD =α,∠EDB =∠A =α,BC =2CE ,∴∠BDC =∠A+∠ACD =2α,∵∠PDF =2α,∴∠FDB =∠CDP =2α+∠PDB ,∵线段DP 绕点D 逆时针旋转2α得到线段DF ,∴DP =DF ,在△DCP 和△DBF 中DC DB CDP BDF DP DF =⎧⎪∠=∠⎨⎪=⎩,∴△DCP ≌△DBF ,∴CP =BF ,而 CP =BC+BP ,∴BF ﹣BP =BC ,在Rt △CDE 中,∠DEC =90°,∴tan ∠CDE =CE DE, ∴CE =DEtanα, ∴BC =2CE =2DEtanα,即BF ﹣BP =2DEtanα.【点睛】本题考查了三角形外角性质,等边三角形的判定和性质,全等三角形的性质和判定,直角三角形的性质,旋转的性质的应用,能推出△DCP ≌△DBF 是解此题的关键,综合性比较强,证明过程类似.9.如图,正方形ABCD+1,对角线AC 、BD 相交于点O ,AE 平分∠BAC 分别交BC 、BD 于E 、F ,(1)求证:△ABF ∽△ACE ;(2)求tan ∠BAE 的值;(3)在线段AC 上找一点P ,使得PE+PF 最小,求出最小值.【答案】(1)证明见解析;(2)tan∠EAB=2﹣1;(3)PE+PF的最小值为 .22【解析】【分析】(1)根据两角对应相等的两个三角形相似判断即可;(2)如图1中,作EH⊥AC于H.首先证明BE=EH=HC,设BE=EH=HC=x,构建方程求出x 即可解决问题;(3)如图2中,作点F关于直线AC的对称点H,连接EH交AC于点P,连接PF,此时PF+PE的值最小,最小值为线段EH的长;【详解】(1)证明:∵四边形ABCD是正方形,∴∠ACE=∠ABF=∠CAB=45°,∵AE平分∠CAB,∴∠EAC=∠BAF=22.5°,∴△ABF∽△ACE.(2)解:如图1中,作EH⊥AC于H.∵EA平分∠CAB,EH⊥AC,EB⊥AB,∴BE=EB,∵∠HCE=45°,∠CHE=90°,∴∠HCE=∠HEC=45°,∴HC=EH,∴BE=EH=HC,设BE=HE=HC=x,则EC2,∵BC2+1,∴x+x2+1,∴x=1,在Rt△ABE中,∵∠ABE=90°,∴tan ∠EAB =1221BE AB ==+﹣1. (3)如图2中,作点F 关于直线AC 的对称点H ,连接EH 交AC 于点P ,连接PF ,此时PF+PE 的值最小.作EM ⊥BD 于M .BM =EM =22, ∵AC =22AB BC +=2+2,∴OA =OC =OB =12AC =22+ , ∴OH =OF =OA•tan ∠OAF =OA•tan ∠EAB =222+ •(2﹣1)=22, ∴HM =OH+OM =222+, 在Rt △EHM 中,EH =2222222EM HM 22⎛⎫⎛⎫+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭= =22+.. ∴PE+PF 的最小值为22+..【点睛】本题考查正方形的性质,相似三角形的判定,勾股定理,最短问题等知识,解题的关键是学会添加常用辅助线,学会利用轴对称解决最短问题,属于中考常考题型.10.小明坐于堤边垂钓,如图①,河堤AC 的坡角为30°,AC 长米,钓竿AO 的倾斜角是60°,其长为3米,若AO 与钓鱼线OB 的夹角为60°,求浮漂B 与河堤下端C 之间的距离(如图②).【答案】1.5米.【解析】试题分析:延长OA交BC于点D.先由倾斜角定义及三角形内角和定理求出在Rt△ACD中,米,CD=2AD=3米,再证明△BOD是等边三角形,得到米,然后根据BC=BD−CD即可求出浮漂B与河堤下端C之间的距离.试题解析:延长OA交BC于点D.∵AO的倾斜角是,∴∵在Rt△ACD中, (米),∴CD=2AD=3米,又∴△BOD是等边三角形,∴(米),∴BC=BD−CD=4.5−3=1.5(米).答:浮漂B与河堤下端C之间的距离为1.5米.。
中考数学锐角三角函数综合经典题含答案

中考数学锐角三角函数综合经典题含答案一、锐角三角函数1.图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG =FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米.【答案】553【解析】【分析】如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J.解直角三角形求出MQ,AQ即可求出AM,再分别求出BE,B′E′即可.【详解】解:如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J.∵AM⊥CD,∴∠QMP=∠MPO=∠OQM=90°,∴四边形OQMP是矩形,∴QM=OP,∵OC=OD=10,∠COD=60°,∴△COD是等边三角形,∵OP⊥CD,∠COD=30°,∴∠COP=12∴QM=OP=OC•cos30°=3∵∠AOC=∠QOP=90°,∴∠AOQ=∠COP=30°,∴AQ=1OA=5(分米),2∴AM=AQ+MQ=5+3∵OB∥CD,∴∠BOD=∠ODC=60°在Rt△OFK中,KO=OF•cos60°=2(分米),FK=OF•sin60°=23(分米),在Rt△PKE中,EK=22-=26(分米),EF FK∴BE=10−2−26=(8−26)(分米),在Rt△OFJ中,OJ=OF•cos60°=2(分米),FJ=23(分米),在Rt△FJE′中,E′J=22-(2)=26,63∴B′E′=10−(26−2)=12−26,∴B′E′−BE=4.故答案为:5+53,4.【点睛】本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.2.(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).【答案】.【解析】试题分析:作AD⊥BC于D,于是有∠ABD=45°,得到AD=BD=,求出∠C=60°,根据正切的定义求出CD的长,得到答案.试题解析:作AD⊥BC于D,∵∠EAB=30°,AE∥BF,∴∠FBA=30°,又∠FBC=75°,∴∠ABD=45°,又AB=60,∴AD=BD=,∵∠BAC=∠BAE+∠CAE=75°,∠ABC=45°,∴∠C=60°,在Rt △ACD 中,∠C=60°,AD=,则tanC=,∴CD==,∴BC=.故该船与B 港口之间的距离CB 的长为海里.考点:解直角三角形的应用-方向角问题.3.如图(9)所示(左图为实景侧视图,右图为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB 和CD (均与水平面垂直),再将集热板安装在AD 上.为使集热板吸热率更高,公司规定:AD 与水平面夹角为1θ,且在水平线上的射影AF 为1.4m .现已测量出屋顶斜面与水平面夹角为2θ,并已知1tan 1.082θ=,2tan 0.412θ=.如果安装工人确定支架AB 高为25cm ,求支架CD 的高(结果精确到1cm )?【答案】【解析】过A 作AF CD ⊥于F ,根据锐角三角函数的定义用θ1、θ2表示出DF 、EF 的值,又可证四边形ABCE为平行四边形,故有EC=AB=25cm,再再根据DC=DE+EC进行解答即可.4.如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.(1)求证:直线CP是⊙O的切线.(2)若BC=2,sin∠BCP=,求点B到AC的距离.(3)在第(2)的条件下,求△ACP的周长.【答案】(1)证明见解析(2)4(3)20【解析】试题分析:(1)利用直径所对的圆周角为直角,2∠CAN=∠CAB,∠CAB=2∠BCP判断出∠ACP=90°即可;(2)利用锐角三角函数,即勾股定理即可.试题解析:(1)∵∠ABC=∠ACB,∴AB=AC,∵AC为⊙O的直径,∴∠ANC=90°,∴∠CAN+∠ACN=90°,2∠BAN=2∠CAN=∠CAB,∵∠CAB=2∠BCP,∴∠BCP=∠CAN,∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°,∵点D在⊙O上,∴直线CP是⊙O的切线;(2)如图,作BF⊥AC∵AB=AC,∠ANC=90°,∴CN=CB=,∵∠BCP=∠CAN,sin∠BCP=,∴sin∠CAN=,∴∴AC=5,∴AB=AC=5,设AF=x,则CF=5﹣x,在Rt△ABF中,BF2=AB2﹣AF2=25﹣x2,在Rt△CBF中,BF2=BC2﹣CF2=2O﹣(5﹣x)2,∴25﹣x2=2O﹣(5﹣x)2,∴x=3,∴BF2=25﹣32=16,∴BF=4,即点B到AC的距离为4.考点:切线的判定5.如图,在⊙O的内接三角形ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.(1)求证:△PAC∽△PDF;(2)若AB=5,,求PD的长;(3)在点P运动过程中,设=x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)【答案】(1)证明见解析;(2);(3).【解析】试题分析:(1)应用圆周角定理证明∠APD=∠FPC,得到∠APC=∠FPD,又由∠PAC=∠PDC,即可证明结论.(2)由AC=2BC,设,应用勾股定理即可求得BC,AC的长,则由AC=2BC得,由△ACE∽△ABC可求得AE,CE的长,由可知△APB是等腰直角三角形,从而可求得PA的长,由△AEF是等腰直角三角形求得EF=AE=4,从而求得DF的长,由(1)△PAC∽△PDF得,即可求得PD的长.(3)连接BP,BD,AD,根据圆的对称性,可得,由角的转换可得,由△AGP∽△DGB可得,由△AGD∽△PGB可得,两式相乘可得结果.试题解析:(1)由APCB内接于圆O,得∠FPC=∠B,又∵∠B=∠ACE=90°-∠BCE,∠ACE=∠APD,∴∠APD=∠FPC.∴∠APD+∠DPC=∠FPC+∠DPC,即∠APC=∠FPD.又∵∠PAC=∠PDC,∴△PAC∽△PDF.(2)连接BP,设,∵∠ACB=90°,AB=5,∴.∴.∵△ACE∽△ABC,∴,即. ∴.∵AB⊥CD,∴.如图,连接BP,∵,∴△APB是等腰直角三角形. ∴∠PAB=45°,.∴△AEF是等腰直角三角形. ∴EF=AE=4. ∴DF=6.由(1)△PAC∽△PDF得,即.∴PD的长为.(3)如图,连接BP,BD,AD,∵AC=2BC,∴根据圆的对称性,得AD=2DB,即.∵AB⊥CD,BP⊥AE,∴∠ABP=∠AFD.∵,∴.∵△AGP∽△DGB,∴.∵△AGD∽△PGB,∴.∴,即.∵,∴.∴与之间的函数关系式为.考点:1.单动点问题;2.圆周角定理;3.相似三角形的判定和性质;4.勾股定理;5.等腰直角三角形的判定和性质;6.垂径定理;7.锐角三角函数定义;8.由实际问题列函数关系式.6.如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.(1)求tan∠DBC的值;(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.【答案】(1)tan∠DBC=;(2)P(﹣,).【解析】试题分析:(1)连接CD,过点D作DE⊥BC于点E.利用抛物线解析式可以求得点A、B、C、D的坐标,则可得CD//AB,OB=OC,所以∠BCO=∠BCD=∠ABC=45°.由直角三角形的性质、勾股定理和图中相关线段间的关系可得BC=4,BE=BC﹣DE=.由此可知tan∠DBC=;(2)过点P作PF⊥x轴于点F.由∠DBP=45°及∠ABC=45°可得∠PBF=∠DBC,利用(1)中的结果得到:tan∠PBF=.设P(x,﹣x2+3x+4),则利用锐角三角函数定义推知=,通过解方程求得点P的坐标为(﹣,).试题解析:(1)令y=0,则﹣x2+3x+4=﹣(x+1)(x﹣4)=0,解得 x1=﹣1,x2=4.∴A(﹣1,0),B(4,0).当x=3时,y=﹣32+3×3+4=4,∴D(3,4).如图,连接CD,过点D作DE⊥BC于点E.∵C(0,4),∴CD//AB,∴∠BCD=∠ABC=45°.在直角△OBC中,∵OC=OB=4,∴BC=4.在直角△CDE中,CD=3.∴CE=ED=,∴BE=BC﹣DE=.∴tan∠DBC=;(2)过点P作PF⊥x轴于点F.∵∠CBF=∠DBP=45°,∴∠PBF=∠DBC,∴tan∠PBF=.设P(x,﹣x2+3x+4),则=,解得 x1=﹣,x2=4(舍去),∴P(﹣,).考点:1、二次函数;2、勾股定理;3、三角函数7.如图,已知点从出发,以1个单位长度/秒的速度沿轴向正方向运动,以为顶点作菱形,使点在第一象限内,且;以为圆心,为半径作圆.设点运动了秒,求:(1)点的坐标(用含的代数式表示);(2)当点在运动过程中,所有使与菱形的边所在直线相切的的值.【答案】解:(1)过作轴于,,,,,点的坐标为.(2)①当与相切时(如图1),切点为,此时,,,.②当与,即与轴相切时(如图2),则切点为,,过作于,则,,.③当与所在直线相切时(如图3),设切点为,交于,则,,.过作轴于,则,,化简,得,解得,,.所求的值是,和.【解析】(1)过作轴于,利用三角函数求得OD、DC的长,从而求得点的坐标⊙P 与菱形OABC 的边所在直线相切,则可与OC 相切;或与OA 相切;或与AB 相切,应分三种情况探讨:①当圆P 与OC 相切时,如图1所示,由切线的性质得到PC 垂直于OC ,再由OA=+t ,根据菱形的边长相等得到OC=1+t ,由∠AOC 的度数求出∠POC 为30°,在直角三角形POC 中,利用锐角三角函数定义表示出cos30°=oc/op ,表示出OC ,等于1+t 列出关于t 的方程,求出方程的解即可得到t 的值;②当圆P 与OA ,即与x 轴相切时,过P 作PE 垂直于OC ,又PC=PO ,利用三线合一得到E 为OC 的中点,OE 为OC 的一半,而OE=OPcos30°,列出关于t 的方程,求出方程的解即可得到t 的值;③当圆P 与AB 所在的直线相切时,设切点为F ,PF 与OC 交于点G ,由切线的性质得到PF 垂直于AB ,则PF 垂直于OC ,由CD=FG ,在直角三角形OCD 中,利用锐角三角函数定义由OC 表示出CD ,即为FG ,在直角三角形OPG 中,利用OP 表示出PG ,用PG+GF 表示出PF ,根据PF=PC ,表示出PC ,过C 作CH 垂直于y 轴,在直角三角形PHC 中,利用勾股定理列出关于t 的方程,求出方程的解即可得到t 的值,综上,得到所有满足题意的t 的值.8.在平面直角坐标系中,四边形OABC 是矩形,点()0,0O ,点()3,0A ,点()0,4C ,连接OB ,以点A 为中心,顺时针旋转矩形AOCB ,旋转角为()0360αα︒<<︒,得到矩形ADEF ,点,,O C B 的对应点分别为,,D E F .(Ⅰ)如图,当点D 落在对角线OB 上时,求点D 的坐标;(Ⅱ)在(Ⅰ)的情况下,AB 与DE 交于点H .①求证BDE DBA ∆≅∆;②求点H 的坐标.(Ⅲ)α为何值时,FB FA =.(直接写出结果即可).【答案】(Ⅰ)点D 的坐标为5472(,)2525;(Ⅱ)①证明见解析;②点H 的坐标为(3,258);(Ⅲ)60α=︒或300︒.【解析】【分析】 (Ⅰ) 过A D 、分别作,AM OB DN OA ⊥⊥,根据点A 、点C 的坐标可得出OA 、OC 的长,根据矩形的性质可得AB 、OB 的长,在Rt △OAM 中,利用∠BOA 的余弦求出OM 的长,由旋转的性质可得OA=AD ,利用等腰三角形的性质可得OD=2OM ,在Rt △ODN 中,利用∠BOA 的正弦和余弦可求出DN 和ON 的长,即可得答案;(Ⅱ)①由等腰三角形性质可得∠DOA=∠ODA ,根据锐角互余的关系可得ABD BDE ∠∠=,利用SAS 即可证明△DBA ≌△BDE ;②根据△DBA ≌△BDE 可得∠BEH=∠DAH ,BE=AD ,即可证明△BHE ≌△DHA ,可得DH=BH ,设AH=x ,在Rt △ADH 中,利用勾股定理求出x 的值即可得答案;(Ⅲ)如图,过F 作FO ⊥AB ,由性质性质可得∠BAF=α,分别讨论0<α≤180°时和180°<α<360°时两种情况,根据FB=FA 可得OA=OB ,利用勾股定理求出FO 的长,由余弦的定义即可求出∠BAF 的度数.【详解】(Ⅰ)∵点()30A ,,点()04C ,, ∴3,4OA OC ==.∵四边形OABC 是矩形,∴AB=OC=4,∵矩形DAFE 是由矩形AOBC 旋转得到的∴3AD AO ==.在Rt OAB ∆中,225OB OA AB =+=, 过A D 、分别作B,DN OA AM O ⊥⊥在Rt ΔOAM 中,OM OA 3cos BOA OA OB 5∠===, ∴9OM 5= ∵AD=OA ,AM ⊥OB , ∴18OD 2OM 5==. 在Rt ΔODN 中:DN 4sin BOA OD 5∠==,cos ∠BOA=ON OD =35, ∴72DN 25=,54ON 25=. ∴点D 的坐标为5472,2525⎛⎫⎪⎝⎭.(Ⅱ)①∵矩形DAFE 是由矩形AOBC 旋转得到的,∴OA AD 3,ADE 90,DE AB 4∠===︒==.∴OD AD =.∴DOA ODA ∠∠=.又∵DOA OBA 90∠∠+=︒,BDH ADO 90∠∠+=︒∴ABD BDE ∠∠=. 又∵BD BD =,∴ΔBDE ΔDBA ≅.②由ΔBDE ΔDBA ≅,得BEH DAH ∠∠=,BE AD 3==,又∵BHE DHA ∠∠=,∴ΔBHE ΔDHA ≅.∴DH=BH ,设AH x =,则DH BH 4x ==-,在Rt ΔADH 中,222AH AD DH =+,即()222x 34x =+-,得25x 8=, ∴25AH 8=. ∴点H 的坐标为253,8⎛⎫ ⎪⎝⎭. (Ⅲ)如图,过F 作FO ⊥AB ,当0<α≤180°时,∵点B 与点F 是对应点,A 为旋转中心,∴∠BAF 为旋转角,即∠BAF=α,AB=AF=4,∵FA=FB ,FO ⊥AB ,∴OA=12AB=2, ∴cos ∠BAF=OA AF =12, ∴∠BAF=60°,即α=60°,当180°<α<360°时, 同理解得:∠BAF′=60°,∴旋转角α=360°-60°=300°.综上所述:α60=︒或300︒.【点睛】本题考查矩形的性质、旋转变换、全等三角形的判定与性质、锐角三角函数的定义等知识,正确找出对应边与旋转角并熟记特殊角的三角函数值是解题关键.9.如图,在⊙O 的内接三角形ABC 中,∠ACB =90°,AC =2BC ,过C 作AB 的垂线l 交⊙O 于另一点D ,垂足为E .设P 是»AC 上异于A ,C 的一个动点,射线AP 交l 于点F ,连接PC 与PD ,PD 交AB 于点G .(1)求证:△PAC ∽△PDF ;(2)若AB =5,¼¼AP BP=,求PD 的长.【答案】(1)证明见解析;(2310 【解析】【分析】 (1)根据AB ⊥CD ,AB 是⊙O 的直径,得到¶¶ADAC =,∠ACD =∠B ,由∠FPC =∠B ,得到∠ACD =∠FPC ,可得结论;(2)连接OP ,由¶¶APBP =,得到OP ⊥AB ,∠OPG =∠PDC ,根据AB 是⊙O 的直径,得到∠ACB =90°,由于AC =2BC ,于是得到tan ∠CAB =tan ∠DCB =BC AC ,得到12CE BE AE CE ==,求得AE =4BE ,通过△OPG ∽△EDG ,得到OG OP GE ED=,然后根据勾股定理即可得到结果.【详解】(1)证明:连接AD,∵AB⊥CD,AB是⊙O的直径,∴¶¶AD AC=,∴∠ACD=∠B=∠ADC,∵∠FPC=∠B,∴∠ACD=∠FPC,∴∠APC=∠ACF,∵∠FAC=∠CAF,∴△PAC∽△CAF;(2)连接OP,则OA=OB=OP=15 22 AB=,∵¶¶AP BP=,∴OP⊥AB,∠OPG=∠PDC,∵AB是⊙O的直径,∴∠ACB=90°,∵AC=2BC,∴tan∠CAB=tan∠DCB=BCAC,∴12 CE BEAE CE==,∴AE=4BE,∵AE+BE=AB=5,∴AE=4,BE=1,CE=2,∴OE=OB﹣BE=2.5﹣1=1.5,∵∠OPG=∠PDC,∠OGP=∠DGE,∴△OPG∽△EDG,∴OG OP GE ED=,∴2.52 OE GE OPGE CE-==,∴GE=23,OG=56,∴PG5 6 =,GD23 =,∴PD=PG+GD【点睛】本题考查了相似三角形的判定和性质,垂径定理,勾股定理,圆周角定理,证得△OPG ∽△EDG 是解题的关键.10.阅读下面材料:观察与思考:阅读下列材料,并解决后面的问题.在锐角△ABC 中,∠A 、∠B 、∠C 的对边分别是a 、b 、c ,过A 作AD ⊥BC 于D (如图),则sin B =AD c ,sin C =AD b ,即AD =c sin B ,AD =b sin C ,于是c sin B =b sin C ,即sin sin b c B C = .同理有:sin sin c a C A =,sin sin a b A B=,所以sin sin sin a b c A B C ==. 即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.(1)如图,△ABC 中,∠B =75°,∠C =45°,BC =60,则AB = ;(2)如图,一货轮在C 处测得灯塔A 在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B 处,此时又测得灯塔A 在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A 的距离AB .(3)在(2)的条件下,试求75°的正弦值.(结果保留根号)【答案】(1)6;(2)6海里;(36+2 【解析】【分析】(1)根据材料:在一个三角形中,各边和它所对角的正弦的比相等,写出比例关系,代入数值即可求得AB的值.(2)此题可先由速度和时间求出BC的距离,再由各方向角得出∠A的角度,过B作BM⊥AC于M,求出∠MBC=30°,求出MC,由勾股定理求出BM,求出AM、BM的长,由勾股定理求出AB即可;(3)在三角形ABC中,∠A=45,∠ABC=75,∠ACB=60,过点C作AC的垂线BD,构造直角三角形ABD,BCD,在直角三角形ABD中可求出AD的长,进而可求出sin75°的值.【详解】解:(1)在△ABC中,∠B=75°,∠C=45°,BC=60,则∠A=60°,∵ABsinC =sinBCA,∴45ABsin o=60sin60o,即2 =3,解得:AB=206.(2)如图,依题意:BC=60×0.5=30(海里)∵CD∥BE,∴∠DCB+∠CBE=180°∵∠DCB=30°,∴∠CBE=150°∵∠ABE=75°.∴∠ABC=75°,∴∠A=45°,在△ABC中,sin AB ACB∠=BCsin A∠即60?ABsin=3045?sin,解之得:AB=156.答:货轮距灯塔的距离AB=156海里.(3)过点B作AC的垂线BM,垂足为M.在直角三角形ABM中,∠A=45°,6,所以3BDC中,∠BCM=60°,BC=30°,可求得CM=15,所以3,15315+156sin75°6+2.【点睛】本题考查方向角的含义,三角形的内角和定理,含30度角的直角三角形,等腰三角形的性质和判定等知识点,解题关键是熟练掌握解直角三角形方法.11.如图,A(0,2),B(6,2),C(0,c)(c>0),以A为圆心AB长为半径的¶BD 交y轴正半轴于点D,¶BD与BC有交点时,交点为E,P为¶BD上一点.(1)若c=3,①BC=,¶DE的长为;②当CP=2时,判断CP与⊙A的位置关系,井加以证明;(2)若c=10,求点P与BC距离的最大值;(3)分别直接写出当c=1,c=6,c=9,c=11时,点P与BC的最大距离(结果无需化简)【答案】(1)①12,π;②详见解析;(2)①65;②65(3)答案见详解 【解析】【分析】 (1)①先求出AB ,AC ,进而求出BC 和∠ABC ,最后用弧长公式即可得出结论;②判断出△APC 是直角三角形,即可得出结论;(2)分两种情况,利用三角形的面积或锐角三角函数即可得出结论;(3)画图图形,同(2)的方法即可得出结论.【详解】 (1)①如图1,∵c =3+2,∴OC =3,∴AC =3﹣2=3∵AB =6,在Rt △BAC 中,根据勾股定理得,BC =12,tan ∠ABC =AC AB3 ∴∠ABC =60°,∵AE =AB ,∴△ABE 是等边三角形,∴∠BAE =60°,∴∠DAE =30°, ∴»DE的长为306180π⨯=π, 故答案为12,π;②CP 与⊙A 相切.证明:∵AP =AB =6,AC =OC ﹣OA =63, ∴AP 2+CP 2=108,又AC 2=(63)2=108,∴AP 2+PC 2=AC 2.∴∠APC =90°,即:CP ⊥AP .而AP 是半径,∴CP 与⊙A 相切.(2)若c =10,即AC =10﹣2=8,则BC =10.①若点P 在»BE上,AP ⊥BE 时,点P 与BC 的距离最大,设垂足为F , 则PF 的长就是最大距离,如图2,S △ABC =12AB ×AC =12BC ×AF , ∴AF =AB AC BC ⋅=245, ∴PF =AP ﹣AF =65; ②如图3,若点P 在»DE 上,作PG ⊥BC 于点G ,当点P 与点D 重合时,PG 最大.此时,sin ∠ACB =PG AB CP BC =, 即PG =AB CP BC ⋅=65∴若c =10,点P 与BC 距离的最大值是65; (3)当c =1时,如图4,过点P 作PM ⊥BC ,sin ∠BCP =AB PMBC CD= ∴PM =67423737AB CD BC ⋅⨯===423737; 当c =6时,如图5,同c =10的①情况,PF =6﹣1213=1213613-,当c =9时,如图6,同c =10的①情况,PF =4285685-,当c =11时,如图7,点P 和点D 重合时,点P 到BC 的距离最大,同c =10时②情况,DG 18117. 【点睛】此题是圆的综合题,主要考查了弧长公式,勾股定理和逆定理,三角形的面积公式,锐角三角函数,熟练掌握锐角三角函数是解本题的关键.12.如图,AB 为O e 的直径,C 、D 为O e 上异于A 、B 的两点,连接CD ,过点C作CE DB ⊥,交CD 的延长线于点E ,垂足为点E ,直径AB 与CE 的延长线相交于点F .(1)连接AC 、AD ,求证:180DAC ACF ∠+∠=︒. (2)若2ABD BDC ∠=∠. ①求证:CF 是O e 的切线. ②当6BD =,3tan 4F =时,求CF 的长. 【答案】(1)详见解析;(2)①详见解析;② 203CF =. 【解析】 【分析】(1)根据圆周角定理证得∠ADB=90°,即AD ⊥BD ,由CE ⊥DB 证得AD ∥CF ,根据平行线的性质即可证得结论;(2)①连接OC .先根据等边对等角及三角形外角的性质得出∠3=2∠1,由已知∠4=2∠1,得到∠4=∠3,则OC ∥DB ,再由CE ⊥DB ,得到OC ⊥CF ,根据切线的判定即可证明CF 为⊙O 的切线;②由CF ∥AD ,证出∠BAD=∠F ,得出tan ∠BAD=tan ∠F=BD AD =34,求出AD=43BD=8,利用勾股定理求得AB=10,得出OB=OC=,5,再由tanF=OC CF =34,即可求出CF . 【详解】解:(1)AB 是O e 的直径,且D 为O e 上一点,90ADB ∴∠=︒, CE DB ⊥Q , 90DEC ∴∠=︒, //CF AD ∴,180DAC ACF ∴∠+∠=︒. (2)①如图,连接OC . OA OC =Q ,12∴∠=∠. 312∠=∠+∠Q , 321∴∠=∠.42BDC Q ∠=∠,1BDC ∠=∠, 421∴∠=∠, 43∴∠=∠,//OC DB ∴. CE DB ⊥Q , OC CF ∴⊥.又OC Q 为O e 的半径, CF ∴为O e 的切线.②由(1)知//CF AD ,BAD F ∴∠=∠,3tan tan 4BAD F ∴∠==, 34BD AD ∴=. 6BD =Q483AD BD ∴==, 226810AB ∴=+=,5OB OC ==. OC CF Q ⊥, 90OCF ∴∠=︒,3tan 4OC F CF ∴==,解得203CF =. 【点睛】本题考查了切线的判定、解直角三角形、圆周角定理等知识;本题综合性强,有一定难度,特别是(2)中,需要运用三角函数、勾股定理和由平行线得出比例式才能得出结果.13.如图,在平面直角坐标系xOy 中,抛物线y =﹣14x 2+bx +c 与直线y =12x ﹣3分别交x 轴、y 轴上的B 、C 两点,设该抛物线与x 轴的另一个交点为点A ,顶点为点D ,连接CD 交x 轴于点E .(1)求该抛物线的表达式及点D 的坐标; (2)求∠DCB 的正切值;(3)如果点F 在y 轴上,且∠FBC =∠DBA +∠DCB ,求点F 的坐标.【答案】(1)21y 234x x =-+-,D (4,1);(2)13;(3)点F 坐标为(0,1)或(0,﹣18). 【解析】 【分析】 (1)y =12x ﹣3,令y =0,则x =6,令x =0,则y =﹣3,求出点B 、C 的坐标,将点B 、C 坐标代入抛物线y =﹣14x 2+bx+c ,即可求解; (2)求出则点E (3,0),EH =EB•sin ∠OBC =5,CE =32,则CH =5,即可求解;(3)分点F 在y 轴负半轴和在y 轴正半轴两种情况,分别求解即可. 【详解】 (1)y =12x ﹣3,令y =0,则x =6,令x =0,则y =﹣3, 则点B 、C 的坐标分别为(6,0)、(0,﹣3),则c =﹣3, 将点B 坐标代入抛物线y =﹣14x 2+bx ﹣3得:0=﹣14×36+6b ﹣3,解得:b =2, 故抛物线的表达式为:y =﹣14x 2+2x ﹣3,令y =0,则x =6或2, 即点A (2,0),则点D (4,1); (2)过点E 作EH ⊥BC 交于点H ,C 、D 的坐标分别为:(0,﹣3)、(4,1), 直线CD 的表达式为:y =x ﹣3,则点E (3,0), tan ∠OBC =3162OC OB ==,则sin ∠OBC 5,则EH=EB•sin∠OBC=5,CE=32,则CH=5,则tan∠DCB=13 EHCH=;(3)点A、B、C、D、E的坐标分别为(2,0)、(6,0)、(0,﹣3)、(4,1)、(3,0),则BC=35,∵OE=OC,∴∠AEC=45°,tan∠DBE=164-=12,故:∠DBE=∠OBC,则∠FBC=∠DBA+∠DCB=∠AEC=45°,①当点F在y轴负半轴时,过点F作FG⊥BG交BC的延长线与点G,则∠GFC=∠OBC=α,设:GF=2m,则CG=GFtanα=m,∵∠CBF=45°,∴BG=GF,即:5=2m,解得:m=5CF22GF CG+5=15,故点F(0,﹣18);②当点F在y轴正半轴时,同理可得:点F(0,1);故:点F坐标为(0,1)或(0,﹣18).【点睛】本题考查的是二次函数综合运用,涉及到一次函数、解直角三角形等相关知识,其中(3),确定∠FBC =∠DBA+∠DCB =∠AEC =45°,是本题的突破口.14.如图,在ABC △中,10AC BC ==,3cos5C =,点P 是BC 边上一动点(不与点,A C 重合),以PA 长为半径的P e 与边AB 的另一个交点为D ,过点D 作DE CB ⊥于点E .()1当P e 与边BC 相切时,求P e 的半径;()2联结BP 交DE 于点F ,设AP 的长为x ,PF 的长为y ,求y 关于x 的函数解析式,并直接写出x 的取值范围;()3在()2的条件下,当以PE 长为直径的Q e 与P e 相交于AC 边上的点G 时,求相交所得的公共弦的长.【答案】(1)409;(2))25880010x x x y x -+=<<;(3)105- 【解析】 【分析】(1)设⊙P 与边BC 相切的切点为H ,圆的半径为R ,连接HP ,则HP ⊥BC ,cosC=35,则sinC=45,sinC=HP CP =R 10R -=45,即可求解; (2)PD ∥BE ,则EB PD =BFPF,即:2248805x x x y xy--+=,即可求解;(3)证明四边形PDBE 为平行四边形,则AG=GP=BD ,即:5求解. 【详解】(1)设⊙P 与边BC 相切的切点为H ,圆的半径为R ,连接HP ,则HP ⊥BC ,cosC=35,则sinC=35, sinC=HP CP =R 10R -=45,解得:R=409; (2)在△ABC 中,AC=BC=10,cosC=35, 设AP=PD=x ,∠A=∠ABC=β,过点B 作BH ⊥AC ,则BH=ACsinC=8, 同理可得:CH=6,HA=4,AB=45,则:tan ∠CAB=2BP=()2284x +-=2880x x -+, DA=25x ,则BD=45-25x ,如下图所示,PA=PD ,∴∠PAD=∠CAB=∠CBA=β,tanβ=2,则cosβ=5,sinβ=5,EB=BDcosβ=(45-25x)×5=4-25x,∴PD∥BE,∴EBPD=BFPF,即:2248805x x x yx y--+-=,整理得:y=()25x x8x800x10-+<<;(3)以EP为直径作圆Q如下图所示,两个圆交于点G,则PG=PQ,即两个圆的半径相等,则两圆另外一个交点为D,GD为相交所得的公共弦,∵点Q时弧GD的中点,∴DG⊥EP,∵AG是圆P的直径,∴∠GDA=90°,∴EP∥BD,由(2)知,PD∥BC,∴四边形PDBE为平行四边形,∴AG=EP=BD,∴5设圆的半径为r,在△ADG中,55AG=2r,5551+,则:55相交所得的公共弦的长为5【点睛】本题考查的是圆知识的综合运用,涉及到解直角三角形、勾股定理等知识,其中(3),要关键是根据题意正确画图,此题用大量的解直角三角形的内容,综合难度很大.15.已知AB 是⊙O 的直径,弦CD ⊥AB 于H ,过CD 延长线上一点E 作⊙O 的切线交AB 的延长线于F ,切点为G ,连接AG 交CD 于K . (1)如图1,求证:KE =GE ; (2)如图2,连接CABG ,若∠FGB =12∠ACH ,求证:CA ∥FE ; (3)如图3,在(2)的条件下,连接CG 交AB 于点N ,若sin E =35,AK =10,求CN 的长.【答案】(1)证明见解析;(2)△EAD 是等腰三角形.证明见解析;(3201013【解析】 试题分析:(1)连接OG ,则由已知易得∠OGE=∠AHK=90°,由OG=OA 可得∠AGO=∠OAG ,从而可得∠KGE=∠AKH=∠EKG ,这样即可得到KE=GE ;(2)设∠FGB=α,由AB 是直径可得∠AGB=90°,从而可得∠KGE=90°-α,结合GE=KE 可得∠EKG=90°-α,这样在△GKE 中可得∠E=2α,由∠FGB=12∠ACH 可得∠ACH=2α,这样可得∠E=∠ACH ,由此即可得到CA ∥EF ; (3)如下图2,作NP ⊥AC 于P ,由(2)可知∠ACH=∠E ,由此可得sinE=sin ∠ACH=35AH AC =,设AH=3a ,可得AC=5a ,CH=4a ,则tan ∠CAH=43CH AH =,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC ,从而可得CK=AC=5a ,由此可得HK=a ,tan ∠AKH=3AHHK=,10a ,结合10可得a=1,则AC=5;在四边形BGKH 中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG 可得∠ACG=∠AKH , 在Rt △APN 中,由tan ∠CAH=43PN AP=,可设PN=12b ,AP=9b ,由tan ∠ACG=PN CP =tan ∠AKH=3可得CP=4b ,由此可得AC=AP+CP=13b =5,则可得b=513,由此即可在Rt △CPN 中由勾股定理解出CN 的长. 试题解析:(1)如图1,连接OG .∵EF 切⊙O 于G , ∴OG ⊥EF ,∴∠AGO+∠AGE=90°, ∵CD ⊥AB 于H , ∴∠AHD=90°, ∴∠OAG=∠AKH=90°, ∵OA=OG , ∴∠AGO=∠OAG , ∴∠AGE=∠AKH , ∵∠EKG=∠AKH , ∴∠EKG=∠AGE , ∴KE=GE . (2)设∠FGB=α, ∵AB 是直径, ∴∠AGB=90°,∴∠AGE =∠EKG=90°﹣α, ∴∠E=180°﹣∠AGE ﹣∠EKG=2α,∵∠FGB=12∠ACH , ∴∠ACH=2α, ∴∠ACH=∠E , ∴CA ∥FE .(3)作NP ⊥AC 于P . ∵∠ACH=∠E , ∴sin ∠E=sin ∠ACH=35AH AC =,设AH=3a ,AC=5a , 则224AC CH a -=,tan ∠CAH=43CH AH =, ∵CA ∥FE ,∴∠CAK=∠AGE,∵∠AGE=∠AKH,∴∠CAK=∠AKH,∴AC=CK=5a,HK=CK﹣CH=4a,tan∠AKH=AHHK =3,AK=2210AH HK a+=,∵AK=10,∴1010a=,∴a=1.AC=5,∵∠BHD=∠AGB=90°,∴∠BHD+∠AGB=180°,在四边形BGKH中,∠BHD+∠HKG+∠AGB+∠ABG=360°,∴∠ABG+∠HKG=180°,∵∠AKH+∠HKG=180°,∴∠AKH=∠ABG,∵∠ACN=∠ABG,∴∠AKH=∠ACN,∴tan∠AKH=tan∠ACN=3,∵NP⊥AC于P,∴∠APN=∠CPN=90°,在Rt△APN中,tan∠CAH=43PNAP=,设PN=12b,则AP=9b,在Rt△CPN中,tan∠ACN=PNCP=3,∴CP=4b,∴AC=AP+CP=13b,∵AC=5,∴13b=5,∴b=513,∴CN=22PN CP+=410b⋅=2010 13.。
初中数学中考复习:25锐角三角函数综合复习(含答案)

中考总复习:锐角三角函数综合复习—巩固练习(提高)【巩固练习】一、选择题1. 在△ABC中,∠C=90°,cosA=,则tan A等于( )A.B.C.D.2.在Rt△ABC中,∠C=90°,把∠A的邻边与对边的比叫做∠A的余切,记作cotA=.则下列关系式中不成立的是( )A.tanA•cotA=1 B.sinA=tanA•cosA C.cosA=cotA•sinA D.tan2A+cot2A=1第2题第3题3.如图,在四边形ABCD中,E、F分別是AB、AD的中点,若EF=2,BC=5,CD=3,则tanC等于( )A.B.C.D.4.如图所示,直角三角形纸片的两直角边长分别为6、8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是( )A.B.C.D.5.如图所示,已知∠α的终边OP⊥AB,直线AB的方程为y=-x+,则cosα等于( )A.B.C.D.第5题第6题6.如图所示,在数轴上点A所表示的数x的范围是( )A. B.C. D.;二、填空题7.设θ为锐角,且x2+3x+2sinθ=0的两根之差为.则θ=.8.如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为.9.已知△ABC的外接圆O的半径为3,AC=4,则sinB= .第8题第9题第11题10.当0°<α<90°时,求的值为.11.如图,点E(0,4),O(0,0),C(5,0)在⊙A上,BE是⊙A上的一条弦.则tan∠OBE=.12.已知:正方形ABCD的边长为2,点P是直线CD上一点,若DP=1,则tan∠BPC的值是 .三、解答题13.如图所示,某拦河坝截面的原设计方案为AH∥BC,坡角∠ABC=74°,坝顶到坝脚的距离AB=6m 为了提高拦河坝的安全性,现将坡角改为55°,由此,点A需向右平移至点D,请你计算AD的长.(精确到0.1m)14. 为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,如图所示.按规定,地下停车库坡道1:3上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE(精确到0.1 m)(sin18°≈0.3090,cos18°≈0.9511,tan18°≈0.3249)15.如图所示,某中学九年级一班数学课外活动小组利用周末开展课外实践活动,他们要在某公园人工湖旁的小山AB上,测量湖中两个小岛C、D间的距离.从山顶A处测得湖中小岛C的俯角为60°,测得湖中小岛D的俯角为45°.已知小山AB的高为180米,求小岛C、D间的距离.(计算过程和结果均不取近似值)16. 在△ABC中,AB=AC,CG⊥BA,交BA的延长线于点G.一等腰直角三角尺按如图①所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.(1)在图①中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;(2)当三角尺沿AC方向平移到图②所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系;然后证明你的猜想;(3)当三角尺在②的基础上沿AC方向继续平移到图③所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)【答案与解析】一、选择题1.【答案】D;【解析】在Rt△ABC中,设AC=3k,AB=5k,则BC=4k,由定义可知tan A=.故选D.2.【答案】D;【解析】根据锐角三角函数的定义,得A、tanA•cotA==1,关系式成立;B、sinA=,tanA•cosA=,关系式成立;C、cosA=,cotA•sinA=,关系式成立;D、tan2A+cot2A=()2+()2≠1,关系式不成立.故选D.3.【答案】B;【解析】连接BD.∵E、F分別是AB、AD的中点.∴BD=2EF=4∵BC=5,CD=3∴△BCD是直角三角形.∴tanC=故选B.4.【答案】C;【解析】设CE=x,则AE=8-x.由折叠性质知AE=BE=8-x.在Rt△CBE中,由勾股定理得BE2=CE2+BC2,即(8-x)2=x2+62,解得,∴tan∠CBE.5.【答案】A;【解析】∵y=-x+,∴当x=0时,y=,当y=0时,x=1,∴A(1,0),B,∴OB=,OA=1,∴AB==,∴cos∠OBA=.∴OP⊥AB,∴∠α+∠OAB=90°,又∵∠OBA+∠OAB=90°,∴∠α=∠OBA.∴cosα=cos∠OBA=.故选A.6.【答案】D;【解析】由数轴上A点的位置可知,<A<2.A、由sin30°<x<sin60°可知,×<x<,即<x<,故本选项错误;B、由cos30°<x<cos45°可知,<x<×,即<x<,故本选项错误;C、由tan30°<x<tan45°可知,×<x<1,即<x<1,故本选项错误;D、由cot45°<x<cot30°可知,×1<x<,即<x<,故本选项正确.故选D.二、填空题7.【答案】30°;【解析】x1·x2=2sinθ,x1+x2=-3,则(x1-x2)2=(x1+x2)2-4x1x2=9-8sinθ=()2,∴sinθ=,∴θ=30°.8.【答案】;【解析】∵四边形ABCD是矩形,∴∠A=∠B=∠D=90°,CD=AB=4,AD=BC=5,由题意得:∠EFC=∠B=90°,CF=BC=5,∴∠AFE+∠DFC=90°,∠DFC+∠FCD=90°,∴∠DCF=∠AFE,∵在Rt△DCF中,CF=5,CD=4,∴DF=3,∴tan∠AFE=tan∠DCF==.9.【答案】;【解析】连接AO并延长交圆于E,连CE.∴∠ACE=90°(直径所对的圆周角是直角);在直角三角形ACE中,AC=4,AE=6,∴sin∠E=;又∵∠B=∠E(同弧所对的的圆周角相等),∴sinB=.10.【答案】1;【解析】由sin2α+cos2α=1,可得1-sin2α=cos2α∵sin2α+cos2α=1,∴cos2α=1-sin2α.∴.∵0°<α<90°,∴cosα>0.∴原式==1.11.【答案】;【解析】连接EC.根据圆周角定理∠ECO=∠OBE.在Rt△EOC中,OE=4,OC=5,则tan∠ECO=.故tan∠OBE=.12.【答案】2或;【解析】此题有两种可能:(1)当点P在线段CD上时,∵BC=2,DP=1,CP=1,∠C=90°,∴tan∠BPC==2;(2)当点P在CD延长线上时,∵DP=1,DC=2,∴PC=3,又∵BC=2,∠C=90°,∴tan∠BPC=.故答案为:2或.三、解答题13.【答案与解析】解:如图所示,过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.在Rt△ABE中,,∴AE=ABsin∠ABE=6sin 74°≈5.77(cm);,∴BE=ABcos∠ABE=6cos 74°≈1.65(m).∵AH∥BC,∴DF=AE≈5.77m.在Rt△BDF中,,∴(m).∴AD=EF=BF-BE=4.04-1.65≈2.4(m).14.【答案与解析】解:在Rt△ABD中,∠ABD=90°,∠BAD=18°,∴,BD=tan∠BAD·AB=tan 18°×9,∴CD=tan 18°×9-0.5.在Rt△DCE中,∠DEC=90°,∠CDE=72°,∴,=sin 72°×(tan 18°×9-0.5)≈2.3(m).即该图中CE的长约为2.3m.15.【答案与解析】解:如图所示,由已知可得∠ACB=60°,∠ADB=45°.∴在Rt△ABD中,BD=AB.又在Rt△ABC中,∵,∴,即.∵BD=BC+CD,∴.∴CD=AB-AB=180-180×=(180-60)米.答:小岛C、D间的距离为(180-)米.16.【答案与解析】解:(1)BF=CG.证明:在△ABF和△ACG中,∵∠F=∠G=90°,∠FAB=∠GAC,AB=AC,∴△ABF≌△ACG(AAS),∴BF=CG.(2)DE+DF=CG.证明:过点D作DH⊥CG于点H(如图所示).∵DE⊥BA于点E,∠G=90°,DH⊥CG,∴四边形EDHG为矩形,∴DE=HG.DH∥BG.∴∠GBC=∠HDC∴AB=AC.∴∠FCD=∠GBC=∠HDC.又∵∠F=∠DHC=90°,CD=DC,∴△FDC≌△HCD(AAS),∴DF=CH.∴GH+CH=DE+DF=CG,即DE+DF=CG.(3)仍然成立.(注:本题还可以利用面积来进行证明,比如(2)中连结AD)。
2023年九年级中考数学一轮复习:锐角三角函数(含答案)
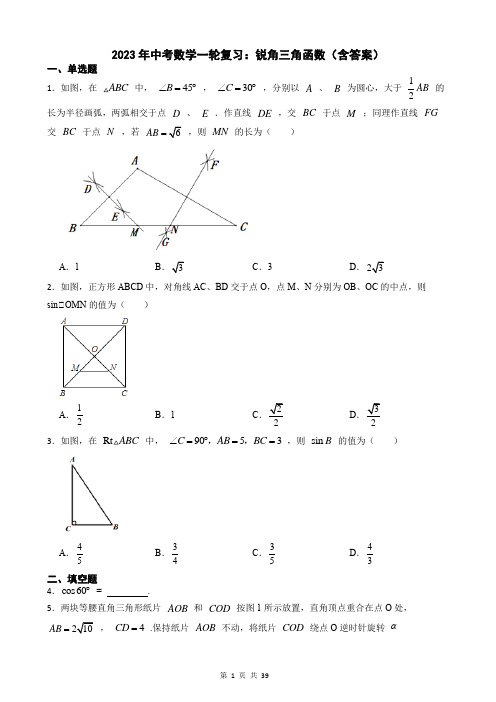
2023年中考数学一轮复习:锐角三角函数(含答案)一、单选题1.如图,在ABC 中, 45B ∠=︒ , 30C ∠=︒ ,分别以 A 、 B 为圆心,大于12AB 的长为半径画弧,两弧相交于点 D 、 E .作直线 DE ,交 BC 于点 M ;同理作直线 FG 交 BC 于点 N ,若 6AB = ,则 MN 的长为( )A .1B 3C .3D .232.如图,正方形ABCD 中,对角线AC 、BD 交于点O ,点M 、N 分别为OB 、OC 的中点,则sin∠OMN 的值为( )A .12B .1C .2 D 33.如图,在 Rt ABC 中, 9053C AB BC ∠=︒==,, ,则 sin B 的值为( )A .45B .34C .35D .43二、填空题4.cos60︒ = .5.两块等腰直角三角形纸片 AOB 和 COD 按图1所示放置,直角顶点重合在点O 处,210AB = , 4CD = .保持纸片 AOB 不动,将纸片 COD 绕点O 逆时针旋转 α()090α<<︒ .当BD 与 CD 在同一直线上(如图2)时, α 的正切值等于 .6.在 ABC ∆ 中, 903016ACB A AB ︒︒∠=∠==,, ,点 P 是斜边 AB 上一点,过点 P 作PQ AB ⊥ ,垂足为 P ,交边 AC (或边 CB )于点 Q ,设 AP x = ,当 APQ ∆ 的面积为 3时, x 的值为 .三、综合题7.如图,在直角三角形ABC 中,∠C =90°,∠A =30°,AC =4,将∠ABC 绕点A 逆时针旋转60°,使点B 落在点E 处,点C 落在点D 处.P 、Q 分别为线段AC 、AD 上的两个动点,且AQ =2PC ,连接PQ 交线段AE 于点M .(1)AQ = ,∠APQ 为等边三角形;(2)是否存在点Q ,使得∠AQM 、∠APQ 和∠APM 这三个三角形中一定有两个三角形相似?若存在请求出AQ 的长;若不存在请说明理由; (3)AQ = ,B 、P 、Q 三点共线.8.(1)计算:3tan30°-(cos60°)-1+8 cos45°+()1tan 60-︒(2)先化简,再求代数式 221(1)122x x x --÷++ 的值,其中x=4cos30°-tan45° 9.如图,AB 是∠O 的直径,点P 在∠O 上,且PA =PB ,点M 是∠O 外一点,MB 与∠O 相切于点B ,连接OM ,过点A 作AC OM 交∠O 于点C ,连接BC 交OM 于点D .(1)求证:MC是∠O的切线;(2)若152OB=,12BC=,连接PC,求PC的长.10.如图,在∠ABC中,过点C作CD//AB,E是AC的中点,连接DE并延长,交AB于点F,连接AD,CF.(1)求证:四边形AFCD是平行四边形;(2)若AB=6,∠BAC=60°,∠DCB=135°,求AC的长.11.如图,∠ABC内接于∠O,AB是∠O的直径,∠O的切线AP与OC的延长线相交于点P,∠P=∠BCO.(1)求证:AC=PC;(2)若AB=6 3,求AP的长.12.(12744 sin603233-︒-(2)先化简,再求值:342111xxx x-⎛⎫+-÷⎪--⎝⎭,其中22x=.13.如图,以AB为直径作O,过点A作O的切线AC,连接BC,交O于点D,点E是BC边的中点,连结AE.(1)求证: 2AEB C ∠=∠ ; (2)若 5AB = , 3cos 5B =,求 DE 的长. 14.(1)计算: 2cos 45sin 30tan 45︒︒︒+⋅ . (2)求二次函数 21212y x x =++ 图象的顶点坐标. 15. 如图,直线y =-x +b 与反比例函数 3y x=-的图象相交于点A (a ,3),且与x 轴相交于点B .(1) 求a 、b 的值;(2) 若点P 在x 轴上,且∠AOP 的面积是∠AOB 的面积的12,求点P 的坐标. 16.如图, PA 、 PB 为O 的切线,A 、B 为切点,点C 为半圆弧的中点,连 AC 交 PO于E 点.(1)求证: PB PE = ; (2)若 3tan 5CPO ∠=,求 sin PAC ∠ 的值. 17.(120313213(202248)64---⨯--().(2)先化简,再求值:2243()22ab a ba b a b b a a b---⨯÷+-+,代入你喜欢的a ,b 值求结果. 18.矩形AOBC 中,OB =4,OA =3,分别以OB ,OA 所在直线为x 轴,y 轴,建立如图所示的平面直角坐标系,F 是BC 边上一个动点(不与B ,C 重合),过点F 的反比例函数 ky x= (k >0)的图象与边AC 交于点E.(1)当点F 为边BC 的中点时,求点E 的坐标; (2)连接EF ,求∠EFC 的正切值.19.如图1,已知矩形ABCD 中,AB=6,BC=8,O 是对角线AC 的中点,点E 从A 点沿AB 向点B运动,运动过程中连接OE ,过O 作OF∠OE 交BC 于F ,连接EF ,(1)当点E 与点A 重合时,如图2,求 tan OEF ∠ 的值;(2)运动过程中, tan OEF ∠ 的值是否与(1)中所求的值保持不变,并说明理由; (3)当EF 平分∠OEB 时,求AE 的长.20.如图1,已知二次函数()20y ax bx c a =++>的图象与x 轴交于点()10A -,、()20B ,,与y 轴交于点C ,且2tan OAC ∠=.(1)求二次函数的解析式;(2)如图2,过点C 作CD x 轴交二次函数图象于点D ,P 是二次函数图象上异于点D 的一个动点,连接PB 、PC ,若PBCBCDSS=,求点P 的坐标;(3)如图3,若点P 是二次函数图象上位于BC 下方的一个动点,连接OP 交BC 于点Q.设点P 的横坐标为t ,试用含t 的代数式表示PQ OQ 的值,并求PQOQ的最大值. 21.如图1,四边形 ABCD 内接于O , BD 为直径, AD 上存在点E ,满足AE CD = ,连结 BE 并延长交 CD 的延长线于点F , BE 与 AD 交于点G.(1)若 DBC α∠= ,请用含 α 的代数式表列 AGB ∠ . (2)如图2,连结 ,CE CE BG = .求证; EF DG = . (3)如图3,在(2)的条件下,连结 CG , 2AG = . ①若 3tan 2ADB ∠=,求 FGD 的周长. ②求 CG 的最小值.22.如图,直线364y x =+分别与x 轴、y 轴交于点A 、B ,点C 为线段AB 上一动点(不与A 、B 重合),以C 为顶点作OCD OAB ∠=∠,射线CD 交线段OB 于点D ,将射线OC 绕点O 顺时针旋转90︒交射线CD 于点E ,连接BE .(1)证明:CD ODDB DE=;(用图1) (2)当BDE 为直角三角形时,求DE 的长度;(用图2) (3)点A 关于射线OC 的对称点为F ,求BF 的最小值.(用图3)23.如图,在二次函数 2221y x mx m =-+++ (m 是常数,且 0m > )的图象与x 轴交于A ,B两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为D.其对称轴与线段BC 交于点E ,与x 轴交于点F.连接AC ,BD.(1)求A ,B ,C 三点的坐标(用数字或含m 的式子表示),并求 OBC ∠ 的度数; (2)若 ACO CBD ∠=∠ ,求m 的值;(3)若在第四象限内二次函数 2221y x mx m =-+++ (m 是常数,且 0m > )的图象上,始终存在一点P ,使得 75ACP ∠=︒ ,请结合函数的图象,直接写出m 的取值范围.24.如图,已知 AB 是O 的直径,点 E 是O 上异于 A , B 的点,点 F 是 EB 的中点,连接 AE , AF , BF ,过点 F 作 FC AE ⊥ 交 AE 的延长线于点 C ,交 AB 的延长线于点 D , ADC ∠ 的平分线 DG 交 AF 于点 G ,交 FB 于点 H .(1)求证: CD 是 O 的切线;(2)求 sin FHG ∠ 的值; (3)若 GH 42=, HB 2= ,求 O 的直径.25.如图,在平面直角坐标系中,二次函数 ()240y ax bx a =++≠ 的图象经过 ()3,0A - ,()4,0B 两点,且与 y 轴交于点 C .点 D 为 x 轴负半轴上一点,且 BC BD = ,点 P ,Q 分别在线段 AB 和 CA 上.(1)求这个二次函数的表达式.(2)若线段 PQ 被 CD 垂直平分,求 AP 的长. (3)在第一象限的这个二次函数的图象上取一点 G ,使得 GCBGCASS= ,再在这个二次函数的图象上取一点 E (不与点 A , B , C 重合),使得 45GBE ∠=︒ ,求点 E 的坐标.参考答案1.【答案】A【解析】【解答】如解图,连接AM、AN,由作法可知,DE、FG分别为线段AB、AC的垂直平分线,∴AM=BM,AN=CN.∵∠B=45°,∠C=30°,∴∠BAM=45°,∠CAN=30°.∴∠AMB=∠AMC=90°.∴∠MAN=90°−∠C−∠CAN=30°.∵AB= 6,∴AM= 3,∴MN=AM·tan30°=1,故答案为:A.【分析】利用线段垂直平分线的性质得到AM=BM,AN=CN,∠BAM=45°,∠CAN=30°.求得∠MAN=90°−∠C−∠CAN=30°,利用特殊角的三角函数值即可求解。
人教中考数学专题训练---锐角三角函数的综合题分类含答案

一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.某地是国家AAAA 级旅游景区,以“奇山奇水奇石景,古賨古洞古部落”享誉巴渠,被誉为 “小九寨”.端坐在观音崖旁的一块奇石似一只“啸天犬”,昂首向天,望穿古今.一个周末,某数学兴趣小组的几名同学想测出“啸天犬”上嘴尖与头顶的距离.他们把蹲着的“啸天犬”抽象成四边形ABCD ,想法测出了尾部C 看头顶B 的仰角为40,从前脚落地点D 看上嘴尖A 的仰角刚好60,5CB m =, 2.7CD m =.景区管理员告诉同学们,上嘴尖到地面的距离是3m .于是,他们很快就算出了AB 的长.你也算算?(结果精确到0.1m .参考数据:400.64400.77400.84sin cos tan ︒≈︒≈︒≈,,.2 1.41,3 1.73≈≈)【答案】AB 的长约为0.6m . 【解析】 【分析】作BF CE ⊥于F ,根据正弦的定义求出BF ,利用余弦的定义求出CF ,利用正切的定义求出DE ,结合图形计算即可. 【详解】解:作BF CE ⊥于F ,在Rt BFC ∆中, 3.20BF BC sin BCF ⋅∠≈=,3.85CF BC cos BCF ⋅∠≈=,在Rt ADE ∆E 中,3 1.73tan 3AB DE ADE ===≈∠, 0.200.58BH BF HF AH EF CD DE CF ∴+=﹣=,==﹣=由勾股定理得,22BH AH 0.6(m)AB =+≈, 答:AB 的长约为0.6m .【点睛】考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.2.在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE=12∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.(1)当点P与点C重合时(如图1).求证:△BOG≌△POE;(2)通过观察、测量、猜想:BFPE=,并结合图2证明你的猜想;(3)把正方形ABCD改为菱形,其他条件不变(如图3),若∠ACB=α,求BF PE的值.(用含α的式子表示)【答案】(1)证明见解析(2)12BFPE=(3)1tan2BFPEα=【解析】解:(1)证明:∵四边形ABCD是正方形,P与C重合,∴OB="OP" ,∠BOC=∠BOG=90°.∵PF⊥BG ,∠PFB=90°,∴∠GBO=90°—∠BGO,∠EPO=90°—∠BGO.∴∠GBO=∠EPO .∴△BOG≌△POE(AAS).(2)BF1PE2=.证明如下:如图,过P作PM//AC交BG于M,交BO于N,∴∠PNE=∠BOC=900,∠BPN=∠OCB.∵∠OBC=∠OCB =450,∴∠NBP=∠NPB.∴NB=NP.∵∠MBN=900—∠BMN , ∠NPE=900—∠BMN ,∴∠MBN=∠NPE . ∴△BMN ≌△PEN (ASA ).∴BM=PE .∵∠BPE=12∠ACB ,∠BPN=∠ACB ,∴∠BPF=∠MPF . ∵PF ⊥BM ,∴∠BFP=∠MFP=900.又∵PF=PF , ∴△BPF ≌△MPF (ASA ).∴BF="MF" ,即BF=12BM . ∴BF=12PE , 即BF 1PE 2=. (3)如图,过P 作PM//AC 交BG 于点M ,交BO 于点N ,∴∠BPN=∠ACB=α,∠PNE=∠BOC=900.由(2)同理可得BF=12BM , ∠MBN=∠EPN . ∵∠BNM=∠PNE=900,∴△BMN ∽△PEN .∴BM BNPE PN=. 在Rt △BNP 中,BN tan =PN α, ∴BM =tan PE α,即2BF=tan PEα. ∴BF 1=tan PE 2α. (1)由正方形的性质可由AAS 证得△BOG ≌△POE .(2)过P 作PM//AC 交BG 于M ,交BO 于N ,通过ASA 证明△BMN ≌△PEN 得到BM=PE ,通过ASA 证明△BPF ≌△MPF 得到BF=MF ,即可得出BF 1PE 2=的结论. (3)过P 作PM//AC 交BG 于点M ,交BO 于点N ,同(2)证得BF=12BM , ∠MBN=∠EPN ,从而可证得△BMN ∽△PEN ,由BM BN PE PN =和Rt △BNP 中BNtan =PNα即可求得BF 1=tan PE 2α.3.已知Rt △ABC 中,AB 是⊙O 的弦,斜边AC 交⊙O 于点D ,且AD=DC ,延长CB 交⊙O 于点E .(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)【答案】(1)AE=CE;(2)①;②.【解析】试题分析:(1)连接AE、DE,如图1,根据圆周角定理可得∠ADE=∠ABE=90°,由于AD=DC,根据垂直平分线的性质可得AE=CE;(2)连接AE、ED,如图2,由∠ABE=90°可得AE是⊙O的直径,根据切线的性质可得∠AEF=90°,从而可证到△ADE∽△AEF,然后运用相似三角形的性质可得=AD•AF.①当CF=CD时,可得,从而有EC=AE=CD,在Rt△DEC中运用三角函数可得sin∠CED=,根据圆周角定理可得∠CAB=∠DEC,即可求出sin∠CAB的值;②当CF=aCD(a>0)时,同①即可解决问题.试题解析:(1)AE=CE.理由:连接AE、DE,如图1,∵∠ABC=90°,∴∠ABE=90,∴∠ADE=∠ABE=90°,∵AD=DC,∴AE=CE;(2)连接AE、ED,如图2,∵∠ABE=90°,∴AE是⊙O的直径,∵EF是⊙OO的切线,∴∠AEF=90°,∴∠ADE=∠AEF=90°,又∵∠DAE=∠EAF,∴△ADE∽△AEF,∴,∴=AD•AF.①当CF=CD时,AD=DC=CF,AF=3DC,∴=DC•3DC=,∴AE=DC,∵EC=AE,∴EC=DC,∴sin∠CAB=sin∠CED===;②当CF=aCD(a>0)时,sin∠CAB=.∵CF=aCD,AD=DC,∴AF=AD+DC+CF=(a+2)CD,∴=DC•(a+2)DC=(a+2),∴AE=DC,∵EC=AE,∴EC=DC,∴sin∠CAB=sin∠CED==.考点:1.圆的综合题;2.探究型;3.存在型.4.如图,抛物线C1:y=(x+m)2(m为常数,m>0),平移抛物线y=﹣x2,使其顶点D 在抛物线C1位于y轴右侧的图象上,得到抛物线C2.抛物线C2交x轴于A,B两点(点A 在点B的左侧),交y轴于点C,设点D的横坐标为a.(1)如图1,若m=.①当OC=2时,求抛物线C2的解析式;②是否存在a,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;(2)如图2,当OB=2﹣m(0<m<)时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).【答案】(1) ①y=﹣x2+x+2.②.(2)P1(﹣m,1),P2(﹣m,﹣3),P3(﹣﹣m,3),P4(3﹣m,3).【解析】试题分析:(1)①首先写出平移后抛物线C2的解析式(含有未知数a),然后利用点C (0,2)在C2上,求出抛物线C2的解析式;②认真审题,题中条件“AP=BP”意味着点P在对称轴上,“点B与点C到直线OP的距离之和最大”意味着OP⊥BC.画出图形,如图1所示,利用三角函数(或相似),求出a的值;(2)解题要点有3个:i)判定△ABD为等边三角形;ii)理论依据是角平分线的性质,即角平分线上的点到角两边的距离相等;iii)满足条件的点有4个,即△ABD形内1个(内心),形外3个.不要漏解.试题解析:(1)当m=时,抛物线C1:y=(x+)2.∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,∴D(a,(a+)2).∴抛物线C2:y=﹣(x﹣a)2+(a+)2(I).①∵OC=2,∴C(0,2).∵点C在抛物线C2上,∴﹣(0﹣a)2+(a+)2=2,解得:a=,代入(I)式,得抛物线C2的解析式为:y=﹣x2+x+2.②在(I)式中,令y=0,即:﹣(x﹣a)2+(a+)2=0,解得x=2a+或x=﹣,∴B(2a+,0);令x=0,得:y=a+,∴C(0,a+).设直线BC的解析式为y=kx+b,则有:,解得,∴直线BC的解析式为:y=﹣x+(a+).假设存在满足条件的a值.∵AP=BP,∴点P在AB的垂直平分线上,即点P在C2的对称轴上;∵点B与点C到直线OP的距离之和≤BC,只有OP⊥BC时等号成立,∴OP⊥BC.如图1所示,设C2对称轴x=a(a>0)与BC交于点P,与x轴交于点E,则OP⊥BC,OE=a.∵点P在直线BC上,∴P(a,a+),PE=a+.∵tan∠EOP=tan∠BCO=,∴,解得:a=.∴存在a=,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP="BP"(3)∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,∴D(a,(a+m)2).∴抛物线C2:y=﹣(x﹣a)2+(a+m)2.令y=0,即﹣(x﹣a)2+(a+m)2=0,解得:x1=2a+m,x2=﹣m,∴B(2a+m,0).∵OB=2﹣m,∴2a+m=2﹣m,∴a=﹣m.∴D(﹣m,3).AB=OB+OA=2﹣m+m=2.如图2所示,设对称轴与x轴交于点E,则DE=3,BE=AB=,OE=OB﹣BE=﹣m.∵tan∠ABD=,∴∠ABD=60°.又∵AD=BD,∴△ABD为等边三角形.作∠ABD的平分线,交DE于点P1,则P1E=BE•tan30°=×=1,∴P1(﹣m,1);在△ABD形外,依次作各个外角的平分线,它们相交于点P2、P3、P4.在Rt△BEP2中,P2E=BE•tan60°=•=3,∴P2(﹣m,﹣3);易知△ADP3、△BDP4均为等边三角形,∴DP3=DP4=AB=2,且P3P4∥x轴.∴P3(﹣﹣m,3)、P4(3﹣m,3).综上所述,到△ABD的三边所在直线的距离相等的所有点有4个,其坐标为:P1(﹣m,1),P2(﹣m,﹣3),P3(﹣﹣m,3),P4(3﹣m,3).【考点】二次函数综合题.5.如图(1),已知正方形ABCD在直线MN的上方BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2)连接FC,观察并直接写出∠FCN的度数(不要写出解答过程)(3)如图(2),将图中正方形ABCD改为矩形ABCD,AB=6,BC=8,E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请求出tan∠FCN的值.若∠FCN的大小发生改变,请举例说明.【答案】(1)见解析;(2)∠FCN =45°,理由见解析;(3)当点E 由B 向C 运动时,∠FCN 的大小总保持不变,tan ∠FCN =43.理由见解析. 【解析】 【分析】(1)根据三角形判定方法进行证明即可.(2)作FH ⊥MN 于H .先证△ABE ≌△EHF ,得到对应边相等,从而推出△CHF 是等腰直角三角形,∠FCH 的度数就可以求得了.(3)解法同(2),结合(1)(2)得:△EFH ≌△GAD ,△EFH ∽△ABE ,得出EH=AD=BC=8,由三角函数定义即可得出结论. 【详解】(1)证明:∵四边形ABCD 和四边形AEFG 是正方形, ∴AB =AD ,AE =AG =EF ,∠BAD =∠EAG =∠ADC =90°, ∴∠BAE +∠EAD =∠DAG +∠EAD ,∠ADG =90°=∠ABE , ∴∠BAE =∠DAG , 在△ADG 和△ABE 中,ADG ABE DAG BAE AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ADG ≌△ABE (AAS ). (2)解:∠FCN =45°,理由如下: 作FH ⊥MN 于H ,如图1所示:则∠EHF =90°=∠ABE , ∵∠AEF =∠ABE =90°,∴∠BAE +∠AEB =90°,∠FEH +∠AEB =90°, ∴∠FEH =∠BAE ,在△EFH 和△ABE 中,EHF ABE FEH BAE AE EF ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△EFH ≌△ABE (AAS ), ∴FH =BE ,EH =AB =BC , ∴CH =BE =FH , ∵∠FHC =90°, ∴∠FCN =45°.(3)当点E 由B 向C 运动时,∠FCN 的大小总保持不变,理由如下: 作FH ⊥MN 于H ,如图2所示:由已知可得∠EAG =∠BAD =∠AEF =90°,结合(1)(2)得:△EFH ≌△GAD ,△EFH ∽△ABE , ∴EH =AD =BC =8, ∴CH =BE , ∴EH FH FHAB BE CH==; 在Rt △FEH 中,tan ∠FCN =8463FH EH CH AB ===, ∴当点E 由B 向C 运动时,∠FCN 的大小总保持不变,tan ∠FCN =43. 【点睛】本题是四边形综合题目,考查了正方形,矩形的判定及全等三角形的判定方法等知识点的综合运用,其重点是通过证三角形全等或相似来得出线段的相等或成比例.6.如图,在平面直角坐标系xOy 中,抛物线y =﹣14x 2+bx +c 与直线y =12x ﹣3分别交x 轴、y 轴上的B 、C 两点,设该抛物线与x 轴的另一个交点为点A ,顶点为点D ,连接CD 交x 轴于点E .(1)求该抛物线的表达式及点D 的坐标; (2)求∠DCB 的正切值;(3)如果点F 在y 轴上,且∠FBC =∠DBA +∠DCB ,求点F 的坐标.【答案】(1)21y 234x x =-+-,D (4,1);(2)13;(3)点F 坐标为(0,1)或(0,﹣18). 【解析】 【分析】 (1)y =12x ﹣3,令y =0,则x =6,令x =0,则y =﹣3,求出点B 、C 的坐标,将点B 、C 坐标代入抛物线y =﹣14x 2+bx+c ,即可求解; (2)求出则点E (3,0),EH =EB•sin ∠OBC =5,CE =32,则CH =5,即可求解;(3)分点F 在y 轴负半轴和在y 轴正半轴两种情况,分别求解即可. 【详解】 (1)y =12x ﹣3,令y =0,则x =6,令x =0,则y =﹣3, 则点B 、C 的坐标分别为(6,0)、(0,﹣3),则c =﹣3, 将点B 坐标代入抛物线y =﹣14x 2+bx ﹣3得:0=﹣14×36+6b ﹣3,解得:b =2, 故抛物线的表达式为:y =﹣14x 2+2x ﹣3,令y =0,则x =6或2, 即点A (2,0),则点D (4,1); (2)过点E 作EH ⊥BC 交于点H ,C 、D 的坐标分别为:(0,﹣3)、(4,1), 直线CD 的表达式为:y =x ﹣3,则点E (3,0), tan ∠OBC =3162OC OB ==,则sin ∠OBC 5,则EH =EB•sin ∠OBC 5CE=32,则CH=5,则tan∠DCB=13 EHCH=;(3)点A、B、C、D、E的坐标分别为(2,0)、(6,0)、(0,﹣3)、(4,1)、(3,0),则BC=35,∵OE=OC,∴∠AEC=45°,tan∠DBE=164-=12,故:∠DBE=∠OBC,则∠FBC=∠DBA+∠DCB=∠AEC=45°,①当点F在y轴负半轴时,过点F作FG⊥BG交BC的延长线与点G,则∠GFC=∠OBC=α,设:GF=2m,则CG=GFtanα=m,∵∠CBF=45°,∴BG=GF,即:5=2m,解得:m=5CF22GF CG+5=15,故点F(0,﹣18);②当点F在y轴正半轴时,同理可得:点F(0,1);故:点F坐标为(0,1)或(0,﹣18).【点睛】本题考查的是二次函数综合运用,涉及到一次函数、解直角三角形等相关知识,其中(3),确定∠FBC =∠DBA+∠DCB =∠AEC =45°,是本题的突破口.7.已知AB 是⊙O 的直径,弦CD ⊥AB 于H ,过CD 延长线上一点E 作⊙O 的切线交AB 的延长线于F ,切点为G ,连接AG 交CD 于K . (1)如图1,求证:KE =GE ; (2)如图2,连接CABG ,若∠FGB =12∠ACH ,求证:CA ∥FE ; (3)如图3,在(2)的条件下,连接CG 交AB 于点N ,若sin E =35,AK =10,求CN 的长.【答案】(1)证明见解析;(2)△EAD 是等腰三角形.证明见解析;(3201013【解析】 试题分析:(1)连接OG ,则由已知易得∠OGE=∠AHK=90°,由OG=OA 可得∠AGO=∠OAG ,从而可得∠KGE=∠AKH=∠EKG ,这样即可得到KE=GE ;(2)设∠FGB=α,由AB 是直径可得∠AGB=90°,从而可得∠KGE=90°-α,结合GE=KE 可得∠EKG=90°-α,这样在△GKE 中可得∠E=2α,由∠FGB=12∠ACH 可得∠ACH=2α,这样可得∠E=∠ACH ,由此即可得到CA ∥EF ; (3)如下图2,作NP ⊥AC 于P ,由(2)可知∠ACH=∠E ,由此可得sinE=sin ∠ACH=35AH AC =,设AH=3a ,可得AC=5a ,CH=4a ,则tan ∠CAH=43CH AH =,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC ,从而可得CK=AC=5a ,由此可得HK=a ,tan ∠AKH=3AHHK=,10a ,结合10可得a=1,则AC=5;在四边形BGKH 中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG 可得∠ACG=∠AKH , 在Rt △APN 中,由tan ∠CAH=43PN AP=,可设PN=12b ,AP=9b ,由tan ∠ACG=PN CP =tan ∠AKH=3可得CP=4b ,由此可得AC=AP+CP=13b =5,则可得b=513,由此即可在Rt △CPN 中由勾股定理解出CN 的长. 试题解析:(1)如图1,连接OG .∵EF 切⊙O 于G , ∴OG ⊥EF ,∴∠AGO+∠AGE=90°, ∵CD ⊥AB 于H , ∴∠AHD=90°, ∴∠OAG=∠AKH=90°, ∵OA=OG , ∴∠AGO=∠OAG , ∴∠AGE=∠AKH , ∵∠EKG=∠AKH , ∴∠EKG=∠AGE , ∴KE=GE . (2)设∠FGB=α, ∵AB 是直径, ∴∠AGB=90°,∴∠AGE =∠EKG=90°﹣α, ∴∠E=180°﹣∠AGE ﹣∠EKG=2α,∵∠FGB=12∠ACH , ∴∠ACH=2α, ∴∠ACH=∠E , ∴CA ∥FE .(3)作NP ⊥AC 于P . ∵∠ACH=∠E , ∴sin ∠E=sin ∠ACH=35AH AC =,设AH=3a ,AC=5a , 则224AC CH a -=,tan ∠CAH=43CH AH =, ∵CA ∥FE , ∴∠CAK=∠AGE , ∵∠AGE=∠AKH ,∴∠CAK=∠AKH,∴AC=CK=5a,HK=CK﹣CH=4a,tan∠AKH=AHHK =3,AK=2210AH HK a+=,∵AK=10,∴1010a=,∴a=1.AC=5,∵∠BHD=∠AGB=90°,∴∠BHD+∠AGB=180°,在四边形BGKH中,∠BHD+∠HKG+∠AGB+∠ABG=360°,∴∠ABG+∠HKG=180°,∵∠AKH+∠HKG=180°,∴∠AKH=∠ABG,∵∠ACN=∠ABG,∴∠AKH=∠ACN,∴tan∠AKH=tan∠ACN=3,∵NP⊥AC于P,∴∠APN=∠CPN=90°,在Rt△APN中,tan∠CAH=43PNAP=,设PN=12b,则AP=9b,在Rt△CPN中,tan∠ACN=PNCP=3,∴CP=4b,∴AC=AP+CP=13b,∵AC=5,∴13b=5,∴b=513,∴CN=22PN CP+=410b⋅=2010 13.8.如图,AB为⊙O的直径,P是BA延长线上一点,CG是⊙O的弦∠PCA=∠ABC,CG⊥AB,垂足为D(1)求证:PC是⊙O的切线;(2)求证:PA AD PC CD;(3)过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若sin∠P=35,CF=5,求BE的长.【答案】(1)见解析;(2)BE=12.【解析】【分析】(1)连接OC,由PC切⊙O于点C,得到OC⊥PC,于是得到∠PCA+∠OCA=90°,由AB为⊙O的直径,得到∠ABC+∠OAC=90°,由于OC=OA,证得∠OCA=∠OAC,于是得到结论;(2)由AE∥PC,得到∠PCA=∠CAF根据垂径定理得到弧AC=弧AG,于是得到∠ACF=∠ABC,由于∠PCA=∠ABC,推出∠ACF=∠CAF,根据等腰三角形的性质得到CF=AF,在R t△AFD中,AF=5,sin∠FAD=35,求得FD=3,AD=4,CD=8,在R t△OCD中,设OC=r,根据勾股定理得到方程r2=(r-4)2+82,解得r=10,得到AB=2r=20,由于AB为⊙O的直径,得到∠AEB=90°,在R t△ABE中,由sin∠EAD=35,得到BEAB=35,于是求得结论.【详解】(1)证明:连接OC,∵PC切⊙O于点C,∴OC⊥PC,∴∠PCO=90°,∴∠PCA+∠OCA=90°,∵AB为⊙O的直径,∴∠ACB=90°,∴∠ABC+∠OAC=90°,∵OC=OA,∴∠OCA=∠OAC,∴∠PCA=∠ABC;(2)解:∵AE∥PC,∴∠PCA=∠CAF,∵AB⊥CG,∴弧AC=弧AG,∴∠ACF=∠ABC,∵∠PCA=∠ABC,∴∠ACF=∠CAF,∴CF=AF,∵CF=5,∴AF=5,∵AE∥PC,∴∠FAD=∠P,∵sin∠P=35,∴sin∠FAD=35,在R t△AFD中,AF=5,sin∠FAD=35,∴FD=3,AD=4,∴CD=8,在R t△OCD中,设OC=r,∴r2=(r﹣4)2+82,∴r=10,∴AB=2r=20,∵AB为⊙O的直径,∴∠AEB=90°,在R t△ABE中,∵sin∠EAD=35,∴35BEAB,∵AB=20,∴BE=12.【点睛】本题考查切线的性质,锐角三角函数,圆周角定理,等腰三角形的性质,解题关键是连接OC构造直角三角形.9.我市在创建全国文明城市的过程中,某社区在甲楼的A处与E处之间悬挂了一副宣传条幅,在乙楼顶部C点测得条幅顶端A点的仰角为45°,条幅底端E点的俯角为30°,若甲、乙两楼之间的水平距离BD为12米,求条幅AE的长度.(结果保留根号)【答案】AE 的长为(123)+ 【解析】 【分析】在Rt ACF 中求AF 的长, 在Rt CEF 中求EF 的长,即可求解. 【详解】过点C 作CF AB ⊥于点F 由题知:四边形CDBF 为矩形12CF DB ∴==在Rt ACF 中,45ACF ∠=︒tan 1AFACF CF∴∠== 12AF ∴=在Rt CEF 中,30ECF ∠=︒ tan EFECF CF∴∠= 3123EF ∴=43EF ∴=1243AE AF EF ∴=+=+∴求得AE 的长为(1243+【点睛】本题考查了三角函数的实际应用,中等难度,作辅助线构造直角三角形是解题关键.10.已知:如图,在Rt △ABO 中,∠B =90°,∠OAB =30°,OA =3.以点O 为原点,斜边OA 所在直线为x 轴,建立平面直角坐标系,以点P (4,0)为圆心,PA 长为半径画圆,⊙P 与x 轴的另一交点为N ,点M 在⊙P 上,且满足∠MPN =60°.⊙P 以每秒1个单位长度的速度沿x 轴向左运动,设运动时间为ts ,解答下列问题: (发现)(1)MN 的长度为多少;(2)当t =2s 时,求扇形MPN (阴影部分)与Rt △ABO 重叠部分的面积.(探究)当⊙P 和△ABO 的边所在的直线相切时,求点P 的坐标.(拓展)当MN 与Rt △ABO 的边有两个交点时,请你直接写出t 的取值范围.【答案】【发现】(1)MN 的长度为π3;(23P 的坐标为10(,);或230)或230();【拓展】t 的取值范围是23t ≤<或45t ≤<,理由见解析.【解析】 【分析】发现:(1)先确定出扇形半径,进而用弧长公式即可得出结论; (2)先求出PA =1,进而求出PQ ,即可用面积公式得出结论; 探究:分圆和直线AB 和直线OB 相切,利用三角函数即可得出结论;拓展:先找出MN 和直角三角形的两边有两个交点时的分界点,即可得出结论. 【详解】 [发现](1)∵P (4,0),∴OP =4. ∵OA =3,∴AP =1,∴MN 的长度为6011803ππ⨯=. 故答案为3π; (2)设⊙P 半径为r ,则有r =4﹣3=1,当t =2时,如图1,点N 与点A 重合,∴PA =r =1,设MP 与AB 相交于点Q .在Rt △ABO 中,∵∠OAB =30°,∠MPN =60°. ∵∠PQA =90°,∴PQ 12=PA 12=,∴AQ =AP ×cos30°3=∴S 重叠部分=S △APQ 12=PQ ×AQ 3= 即重叠部分的面积为38. [探究]①如图2,当⊙P 与直线AB 相切于点C 时,连接PC ,则有PC ⊥AB ,PC =r =1. ∵∠OAB =30°,∴AP =2,∴OP =OA ﹣AP =3﹣2=1; ∴点P 的坐标为(1,0);②如图3,当⊙P 与直线OB 相切于点D 时,连接PD ,则有PD ⊥OB ,PD =r =1,∴PD ∥AB ,∴∠OPD =∠OAB =30°,∴cos ∠OPD PD OP =,∴OP 123303cos ==︒,∴点P 的坐标为(233,0); ③如图4,当⊙P 与直线OB 相切于点E 时,连接PE ,则有PE ⊥OB ,同②可得:OP 233=; ∴点P 的坐标为(233-,0);[拓展]t 的取值范围是2<t ≤3,4≤t <5,理由:如图5,当点N 运动到与点A 重合时,MN 与Rt △ABO 的边有一个公共点,此时t =2; 当t >2,直到⊙P 运动到与AB 相切时,由探究①得:OP =1,∴t 411-==3,MN 与Rt △ABO 的边有两个公共点,∴2<t ≤3.如图6,当⊙P 运动到PM 与OB 重合时,MN 与Rt △ABO 的边有两个公共点,此时t =4; 直到⊙P 运动到点N 与点O 重合时,MN 与Rt △ABO 的边有一个公共点,此时t =5; ∴4≤t <5,即:t 的取值范围是2<t ≤3,4≤t <5.【点睛】本题是圆的综合题,主要考查了弧长公式,切线的性质,锐角三角函数,三角形面积公式,作出图形是解答本题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学锐角三角函数的综合题试题及答案一、锐角三角函数1.在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.(1)如图1,请直接写出线段OE与OF的数量关系;(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由(3)若|CF﹣AE|=2,EF=23,当△POF为等腰三角形时,请直接写出线段OP的长.【答案】(1)OF =OE;(2)OF⊥EK,OF=OE,理由见解析;(3)OP的长为62或23.【解析】【分析】(1)如图1中,延长EO交CF于K,证明△AOE≌△COK,从而可得OE=OK,再根据直角三角形斜边中线等于斜边一半即可得OF=OE;(2)如图2中,延长EO交CF于K,由已知证明△ABE≌△BCF,△AOE≌△COK,继而可证得△EFK是等腰直角三角形,由等腰直角三角形的性质即可得OF⊥EK,OF=OE;(3)分点P在AO上与CO上两种情况分别画图进行解答即可得.【详解】(1)如图1中,延长EO交CF于K,∵AE⊥BE,CF⊥BE,∴AE∥CK,∴∠EAO=∠KCO,∵OA=OC,∠AOE=∠COK,∴△AOE≌△COK,∴OE=OK,∵△EFK是直角三角形,∴OF=12EK=OE;(2)如图2中,延长EO交CF于K,∵∠ABC=∠AEB=∠CFB=90°,∴∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,∴∠BAE=∠CBF,∵AB=BC,∴△ABE≌△BCF,∴BE=CF,AE=BF,∵△AOE≌△COK,∴AE=CK,OE=OK,∴FK=EF,∴△EFK是等腰直角三角形,∴OF⊥EK,OF=OE;(3)如图3中,点P在线段AO上,延长EO交CF于K,作PH⊥OF于H,∵|CF﹣AE|=2,3AE=CK,∴FK=2,在Rt△EFK中,tan∠3∴∠FEK=30°,∠EKF=60°,∴EK=2FK=4,OF=12EK=2,∵△OPF是等腰三角形,观察图形可知,只有OF=FP=2,在Rt△PHF中,PH=12PF=1,3OH=23∴()2212362+-=如图4中,点P 在线段OC 上,当PO=PF 时,∠POF=∠PFO=30°, ∴∠BOP=90°, ∴OP=33OE=233, 综上所述:OP 的长为62 或233. 【点睛】本题考查了全等三角形的判定与性质、直角三角形斜边中线等于斜边一半、等腰直角三角形的判定与性质、解直角三角形等,综合性较强,正确添加辅助线是解题的关键.2.如图,在平行四边形ABCD 中,平分,交于点,平分,交于点,与交于点,连接,.(1)求证:四边形是菱形; (2)若,,,求的值.【答案】(1)证明见解析 (2)【解析】试题分析:(1)根据AE 平分∠BAD 、BF 平分∠ABC 及平行四边形的性质可得AF=AB=BE ,从而可知ABEF 为平行四边形,又邻边相等,可知为菱形(2)由菱形的性质可知AP 的长及∠PAF=60°,过点P 作PH ⊥AD 于H ,即可得到PH 、DH 的长,从而可求tan ∠ADP试题解析:(1)∵AE 平分∠BAD BF 平分∠ABC ∴∠BAE=∠EAF ∠ABF=∠EBF ∵AD//BC∴∠EAF=∠AEB ∠AFB=∠EBF ∴∠BAE=∠AEB ∠AFB=∠ABF ∴AB=BE AB=AF∴AF=AB=BE∵AD//BC∴ABEF为平行四边形又AB=BE∴ABEF为菱形(2)作PH⊥AD于H由∠ABC=60°而已(1)可知∠PAF=60°,PA=2,则有PH=,AH=1,∴DH=AD-AH=5∴tan∠ADP=考点:1、平行四边形;2、菱形;3、直角三角形;4、三角函数3.如图,在△ABC中,AB=7.5,AC=9,S△ABC=814.动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM (P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.(1)求cosA的值;(2)当△PQM与△QCN的面积满足S△PQM=95S△QCN时,求t的值;(3)当t为何值时,△PQM的某个顶点(Q点除外)落在△QCN的边上.【答案】(1)coaA=45;(2)当t=35时,满足S△PQM=95S△QCN;(3)当2733-或2733+时,△PQM的某个顶点(Q点除外)落在△QCN的边上.【解析】分析:(1)如图1中,作BE⊥AC于E.利用三角形的面积公式求出BE,利用勾股定理求出AE 即可解决问题;(2)如图2中,作PH ⊥AC 于H .利用S △PQM =95S △QCN 构建方程即可解决问题; (3)分两种情形①如图3中,当点M 落在QN 上时,作PH ⊥AC 于H .②如图4中,当点M 在CQ 上时,作PH ⊥AC 于H .分别构建方程求解即可; 详解:(1)如图1中,作BE ⊥AC 于E .∵S △ABC =12•AC•BE=814,∴BE=92, 在Rt △ABE 中,AE=22=6AB BE -,∴coaA=647.55AE AB ==. (2)如图2中,作PH ⊥AC 于H .∵PA=5t ,PH=3t ,AH=4t ,HQ=AC-AH-CQ=9-9t , ∴PQ 2=PH 2+HQ 2=9t 2+(9-9t )2, ∵S △PQM =95S △QCN , ∴34•PQ 2=9354⨯•CQ 2, ∴9t 2+(9-9t )2=95×(5t )2, 整理得:5t 2-18t+9=0,解得t=3(舍弃)或35.∴当t=35时,满足S△PQM=95S△QCN.(3)①如图3中,当点M落在QN上时,作PH⊥AC于H.易知:PM∥AC,∴∠MPQ=∠PQH=60°,∴PH=3HQ,∴3t=3(9-9t),∴t=2733-.②如图4中,当点M在CQ上时,作PH⊥AC于H.同法可得3,∴39t-9),∴27+33综上所述,当2733-s27+33时,△PQM的某个顶点(Q点除外)落在△QCN 的边上.点睛:本题考查三角形综合题、等边三角形的性质、勾股定理锐角三角函数、解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考常考题型.4.已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O 于点E.(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)【答案】(1)AE=CE;(2)①;②.【解析】试题分析:(1)连接AE、DE,如图1,根据圆周角定理可得∠ADE=∠ABE=90°,由于AD=DC,根据垂直平分线的性质可得AE=CE;(2)连接AE、ED,如图2,由∠ABE=90°可得AE是⊙O的直径,根据切线的性质可得∠AEF=90°,从而可证到△ADE∽△AEF,然后运用相似三角形的性质可得=AD•AF.①当CF=CD时,可得,从而有EC=AE=CD,在Rt△DEC中运用三角函数可得sin∠CED=,根据圆周角定理可得∠CAB=∠DEC,即可求出sin∠CAB的值;②当CF=aCD(a>0)时,同①即可解决问题.试题解析:(1)AE=CE.理由:连接AE、DE,如图1,∵∠ABC=90°,∴∠ABE=90,∴∠ADE=∠ABE=90°,∵AD=DC,∴AE=CE;(2)连接AE、ED,如图2,∵∠ABE=90°,∴AE是⊙O的直径,∵EF是⊙OO的切线,∴∠AEF=90°,∴∠ADE=∠AEF=90°,又∵∠DAE=∠EAF,∴△ADE∽△AEF,∴,∴=AD•AF.①当CF=CD时,AD=DC=CF,AF=3DC,∴=DC•3DC=,∴AE=DC,∵EC=AE,∴EC=DC,∴sin∠CAB=sin∠CED===;②当CF=aCD(a>0)时,sin∠CAB=.∵CF=aCD,AD=DC,∴AF=AD+DC+CF=(a+2)CD,∴=DC•(a+2)DC=(a+2),∴AE=DC,∵EC=AE,∴EC=DC,∴sin∠CAB=sin∠CED==.考点:1.圆的综合题;2.探究型;3.存在型.5.已知Rt△ABC中,∠ACB=90°,点D、E分别在BC、AC边上,连结BE、AD交于点P,设AC=kBD,CD=kAE,k为常数,试探究∠APE的度数:(1)如图1,若k=1,则∠APE的度数为;(2)如图2,若k=3,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出∠APE的度数.(3)如图3,若k=3,且D、E分别在CB、CA的延长线上,(2)中的结论是否成立,请说明理由.【答案】(1)45°;(2)(1)中结论不成立,理由见解析;(3)(2)中结论成立,理由见解析.【解析】分析:(1)先判断出四边形ADBF是平行四边形,得出BD=AF,BF=AD,进而判断出△FAE≌△ACD,得出EF=AD=BF,再判断出∠EFB=90°,即可得出结论;(2)先判断出四边形ADBF是平行四边形,得出BD=AF,BF=AD,进而判断出△FAE∽△ACD,再判断出∠EFB=90°,即可得出结论;(3)先判断出四边形ADBF是平行四边形,得出BD=AF,BF=AD,进而判断出△ACD∽△HEA,再判断出∠EFB=90°,即可得出结论;详解:(1)如图1,过点A作AF∥CB,过点B作BF∥AD相交于F,连接EF,∴∠FBE=∠APE,∠FAC=∠C=90°,四边形ADBF是平行四边形,∴BD=AF,BF=AD.∵AC=BD,CD=AE,∴AF=AC.∵∠FAC=∠C=90°,∴△FAE≌△ACD,∴EF=AD=BF,∠FEA=∠ADC.∵∠ADC+∠CAD=90°,∴∠FEA+∠CAD=90°=∠EHD.∵AD∥BF,∴∠EFB=90°.∵EF=BF,∴∠FBE=45°,∴∠APE=45°.(2)(1)中结论不成立,理由如下:如图2,过点A作AF∥CB,过点B作BF∥AD相交于F,连接EF,∴∠FBE=∠APE,∠FAC=∠C=90°,四边形ADBF是平行四边形,∴BD=AF,BF=AD.∵3BD,3AE,∴3AC CDBD AE ==. ∵BD=AF ,∴3AC CDAF AE==. ∵∠FAC=∠C=90°, ∴△FAE ∽△ACD ,∴3AC AD BFAF EF EF ===,∠FEA=∠ADC . ∵∠ADC+∠CAD=90°,∴∠FEA+∠CAD=90°=∠EMD . ∵AD ∥BF , ∴∠EFB=90°.在Rt △EFB 中,tan ∠FBE=3EF BF =, ∴∠FBE=30°, ∴∠APE=30°,(3)(2)中结论成立,如图3,作EH ∥CD ,DH ∥BE ,EH ,DH 相交于H ,连接AH ,∴∠APE=∠ADH ,∠HEC=∠C=90°,四边形EBDH 是平行四边形, ∴BE=DH ,EH=BD . ∵3BD ,3AE ,∴3AC CDBD AE==. ∵∠HEA=∠C=90°, ∴△ACD ∽△HEA ,∴3AD ACAH EH==∠ADC=∠HAE . ∵∠CAD+∠ADC=90°, ∴∠HAE+∠CAD=90°, ∴∠HAD=90°.在Rt △DAH 中,tan ∠ADH=3AHAD=∴∠ADH=30°,∴∠APE=30°.点睛:此题是三角形综合题,主要考查了全等三角形的判定和性质,相似三角形的判定和性质,平行四边形的判定和性质,构造全等三角形和相似三角形的判定和性质.6.如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB 的延长线于切点为G,连接AG交CD于K.(1)求证:KE=GE;(2)若KG2=KD•GE,试判断AC与EF的位置关系,并说明理由;(3)在(2)的条件下,若sinE=,AK=,求FG的长.【答案】(1)证明见解析;(2)AC∥EF,证明见解析;(3)FG= .【解析】试题分析:(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;(2)AC与EF平行,理由为:如图2所示,连接GD,由∠KGE=∠GKE,及KG2=KD•GE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;(3)如图3所示,连接OG,OC,先求出KE=GE,再求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.试题解析:(1)如图1,连接OG.∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又∵OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.(2)AC∥EF,理由为连接GD,如图2所示.∵KG2=KD•GE,即,∴,又∵∠KGE=∠GKE,∴△GKD∽△EGK,∴∠E=∠AGD,又∵∠C=∠AGD,∴∠E=∠C,∴AC∥EF;(3)连接OG,OC,如图3所示,∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又∵OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.∵sinE=sin∠ACH=,设AH=3t,则AC=5t,CH=4t,∵KE=GE,AC∥EF,∴CK=AC=5t,∴HK=CK-CH=t.在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即(3t)2+t2=(2)2,解得t=.设⊙O半径为r,在Rt△OCH中,OC=r,OH=r-3t,CH=4t,由勾股定理得:OH2+CH2=OC2,即(r-3t)2+(4t)2=r2,解得r= t=.∵EF为切线,∴△OGF为直角三角形,在Rt△OGF中,OG=r=,tan∠OFG=tan∠CAH=,∴FG=【点睛】此题考查了切线的性质,相似三角形的判定与性质,垂径定理,勾股定理,锐角三角函数定义,圆周角定理,平行线的判定,以及等腰三角形的判定,熟练掌握定理及性质是解本题的关键.7.在Rt△ACB和△AEF中,∠ACB=∠AEF=90°,若点P是BF的中点,连接PC,PE.特殊发现:如图1,若点E、F分别落在边AB,AC上,则结论:PC=PE成立(不要求证明).问题探究:把图1中的△AEF绕点A顺时针旋转.(1)如图2,若点E落在边CA的延长线上,则上述结论是否成立?若成立,请给予证明;若不成立,请说明理由;(2)如图3,若点F落在边AB上,则上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)记ACBC=k,当k为何值时,△CPE总是等边三角形?(请直接写出后的值,不必说)【答案】()1 PC PE =成立 ()2 ,PC PE =成立 ()3当k 为33时,CPE V 总是等边三角形 【解析】 【分析】(1)过点P 作PM ⊥CE 于点M ,由EF ⊥AE ,BC ⊥AC ,得到EF ∥MP ∥CB ,从而有EM FPMC PB=,再根据点P 是BF 的中点,可得EM=MC ,据此得到PC=PE . (2)过点F 作FD ⊥AC 于点D ,过点P 作PM ⊥AC 于点M ,连接PD ,先证△DAF ≌△EAF ,即可得出AD=AE ;再证△DAP ≌△EAP ,即可得出PD=PE ;最后根据FD ⊥AC ,BC ⊥AC ,PM ⊥AC ,可得FD ∥BC ∥PM ,再根据点P 是BF 的中点,推得PC=PD ,再根据PD=PE ,即可得到结论.(3)因为△CPE 总是等边三角形,可得∠CEP=60°,∠CAB=60°;由∠ACB=90°,求出∠CBA=30°;最后根据AC k BC =,ACBC=tan30°,求出当△CPE 总是等边三角形时,k 的值是多少即可. 【详解】解:(1)PC=PE 成立,理由如下:如图2,过点P 作PM ⊥CE 于点M ,∵EF ⊥AE ,BC ⊥AC ,∴EF ∥MP ∥CB ,∴EM FPMC PB=,∵点P 是BF 的中点,∴EM=MC ,又∵PM ⊥CE ,∴PC=PE ;(2)PC=PE 成立,理由如下:如图3,过点F 作FD ⊥AC 于点D ,过点P 作PM ⊥AC 于点M ,连接PD ,∵∠DAF=∠EAF ,∠FDA=∠FEA=90°,在△DAF 和△EAF 中,∵∠DAF=∠EAF ,∠FDA=∠FEA ,AF=AF , ∴△DAF ≌△EAF (AAS ), ∴AD=AE ,在△DAP 和△EAP 中, ∵AD=AE ,∠DAP=∠EAP ,AP=AP , ∴△DAP ≌△EAP (SAS ), ∴PD=PE ,∵FD ⊥AC ,BC ⊥AC ,PM ⊥AC , ∴FD ∥BC ∥PM , ∴DM FPMC PB=, ∵点P 是BF 的中点, ∴DM=MC ,又∵PM ⊥AC , ∴PC=PD ,又∵PD=PE , ∴PC=PE ;(3)如图4,∵△CPE 总是等边三角形, ∴∠CEP=60°, ∴∠CAB=60°, ∵∠ACB=90°,∴∠CBA=90°﹣∠ACB=90°﹣60°=30°, ∵AC k BC =,ACBC=tan30°, ∴k=tan30°=3∴当k 为33时,△CPE 总是等边三角形.【点睛】考点:1.几何变换综合题;2.探究型;3.压轴题;4.三角形综合题;5.全等三角形的判定与性质;6.平行线分线段成比例.8.如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO.并延长AO交☉O于点E,与PB的延长线交于点D.(1)求证:PA是☉O的切线;(2)若=,且OC=4,求PA的长和tan D的值.【答案】(1)证明见解析;(2)PA =3,tan D=.【解析】试题分析: (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;(2)连接BE,由,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.试题解析:(1)连接OB,则OA=OB,∵OP⊥AB,∴AC=BC,∴OP是AB的垂直平分线,∴PA=PB,在△PAO和△PBO中,∵,∴△PAO≌△PBO(SSS)∴∠PBO=∠PAO,PB=PA,∵PB为⊙O的切线,B为切点,∴∠PBO=90°,∴∠PAO=90°,即PA⊥OA,∴PA是⊙O的切线;(2)连接BE,∵,且OC=4,∴AC=6,∴AB=12,在Rt△ACO中,由勾股定理得:AO=,∴AE=2OA=4,OB=OA=2,在Rt△APO中,∵AC⊥OP,∴AC2=OC PC,解得:PC=9,∴OP=PC+OC=13,在Rt△APO中,由勾股定理得:AP==3.易证,所以,解得,则,在中,.考点:1.切线的判定与性质;2.相似三角形的判定与性质;3.解直角三角形.9.如图,某公园内有一座古塔AB,在塔的北面有一栋建筑物,某日上午9时太阳光线与水平面的夹角为32°,此时塔在建筑物的墙上留下了高3米的影子CD.中午12时太阳光线与地面的夹角为45°,此时塔尖A在地面上的影子E与墙角C的距离为15米(B、E、C在一条直线上),求塔AB的高度.(结果精确到0.01米)参考数据:sin32°≈0.5299,cos32°≈0.8480,tan32°≈0.6249,2 1.4142.【答案】塔高AB 约为32.99米. 【解析】 【分析】过点D 作DH ⊥AB ,垂足为点H ,设AB =x ,则 AH =x ﹣3,解直角三角形即可得到结论. 【详解】解:过点D 作DH ⊥AB ,垂足为点H .由题意,得 HB = CD = 3,EC = 15,HD = BC ,∠ABC =∠AHD = 90°, ∠ADH = 32°.设AB = x ,则 AH = x – 3.在Rt △ABE 中,由 ∠AEB = 45°,得 tan tan451ABAEB EB∠=︒==. ∴ EB = AB = x .∴ HD = BC = BE + EC = x + 15. 在Rt △AHD 中,由 ∠AHD = 90°,得 tan AHADH HD∠=. 即得 3tan3215x x -︒=+. 解得 15tan32332.991tan32x ⋅︒+=≈-︒.∴ 塔高AB 约为32.99米. 【点睛】本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.10.水库大坝截面的迎水坡坡比(DE 与AE 的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.【答案】故大坝的截面的周长是(345)米,面积是1470平方米. 【解析】试题分析:先根据两个坡比求出AE 和BF 的长,然后利用勾股定理求出AD 和BC ,再由大坝的截面的周长=DC+AD+AE+EF+BF+BC ,梯形的面积公式可得出答案.试题解析:∵迎水坡坡比(DE与AE的长度之比)为1:0.6,DE=30m,∴AE=18米,在RT△ADE中,AD=22DE AE+=634米∵背水坡坡比为1:2,∴BF=60米,在RT△BCF中,BC=22CF BF+=305米,∴周长=DC+AD+AE+EF+BF+BC=634+10+305+88=(634+305+98)米,面积=(10+18+10+60)×30÷2=1470(平方米).故大坝的截面的周长是(634+305+98)米,面积是1470平方米.11.在△ABC中,∠B=45°,∠C=30°,点D是边BC上一点,连接AD,将线段AD绕点A 逆时针旋转90°,得到线段AE,连接DE.(1)如图①,当点E落在边BA的延长线上时,∠EDC=度(直接填空);(2)如图②,当点E落在边AC上时,求证:BD=12 EC;(3)当AB=22,且点E到AC的距离等于3﹣1时,直接写出tan∠CAE的值.【答案】(1)90;(2)详见解析;(3)633 tan EAC-∠=【解析】【分析】(1)利用三角形的外角的性质即可解决问题;(2)如图2中,作PA⊥AB交BC于P,连接PE.只要证明△BAD≌△PAE(SAS),提出BD=PE,再证明EC=2PE即可;(3)如图3,作EF⊥AC于F,延长FE交BC于H,作AG⊥BC于G,PA⊥AB交BC于P,连接PE.设PH=x,在Rt△EPH中,可得EP3,EH=2PH=2x,由此FH=31,CF=33,由△BAD≌△PAE,得BD=EP3x,AE=AD,在Rt△ABG中, AG=GB=2,在Rt△AGC中,AC=2AG=4,故AE2=AD2=AF2+EF2,由勾股定理得AF=3tan∠EAF=23tan∠EAC=6-33.11【详解】(1)如图1中,∵∠EDC=∠B+∠BED,∠B=∠BED=45°,∴∠EDC=90°,故答案为90;(2)如图2中,作PA⊥AB交BC于P,连接PE.∵∠DAE=∠BAP=90°,∴∠BAD=∠PAE,∵∠B=45°,∴∠B=∠APB=45°,∴AB=AP,∵AD=AE,∴△BAD≌△PAE(SAS),∴BD=PE,∠APE=∠B=45°,∴∠EPD=∠EPC=90°,∵∠C=30°,∴EC=2PE=2BD;(3)如图3,作EF⊥AC于F,延长FE交BC于H,作AG⊥BC于G,PA⊥AB交BC于P,连接PE.设PH=x,在Rt△EPH中,∵∠EPH=90°,∠EHP=60°,∴EP3,EH=2PH=2x,∴FH=31,CF3FH=33∵△BAD≌△PAE,∴BD=EP3,AE=AD,在Rt△ABG中,∵AB=2∴AG=GB=2,在Rt△AGC中,AC=2AG=4,∵AE2=AD2=AF2+EF2,∴22+(23)231)2+(4﹣3﹣32,整理得:9x2﹣12x=0,解得x=43(舍弃)或0∴PH=0,此时E,P,H共点,∴AF=3∴tan∠EAF=EFAF 331+=23根据对称性可知当点E在AC的上方时,同法可得tan∠EAC 6-33.【点睛】本题属于几何变换综合题,考查了等腰直角三角形的判定和性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.12.如图,正方形OABC的顶点O与原点重合,点A,C分别在x轴与y轴的正半轴上,点A的坐标为(4,0),点D在边AB上,且tan∠AOD=12,点E是射线OB上一动点,EF⊥x轴于点F,交射线OD于点G,过点G作GH∥x轴交AE于点H.(1)求B,D两点的坐标;(2)当点E在线段OB上运动时,求∠HDA的大小;(3)以点G为圆心,GH的长为半径画⊙G.是否存在点E使⊙G与正方形OABC的对角线所在的直线相切?若不存在,请说明理由;若存在,请求出所有符合条件的点E的坐标.【答案】(1)B(4,4),D(4,2);(2)45°;(3)存在,符合条件的点为(8﹣2,8﹣2)或(2,2)或42164216,77⎛⎫⎪ ⎪⎝⎭或16421642--⎝⎭,理由见解析【解析】【分析】(1)由正方形性质知AB=OA=4,∠OAB=90°,据此得B(4,4),再由tan∠AOD= 12得AD=12OA=2,据此可得点D坐标;(2)由1tan2GFGOFOF∠==知GF=12OF,再由∠AOB=∠ABO=45°知OF=EF,即GF=12EF,根据GH∥x轴知H为AE的中点,结合D为AB的中点知DH是△ABE的中位线,即HD∥BE,据此可得答案;(3)分⊙G与对角线OB和对角线AC相切两种情况,设PG=x,结合题意建立关于x的方程求解可得.【详解】解:(1)∵A(4,0),∴OA=4,∵四边形OABC为正方形,∴AB=OA=4,∠OAB=90°,∴B(4,4),在Rt△OAD中,∠OAD=90°,∵tan∠AOD=12,∴AD=12OA=12×4=2,∴D(4,2);(2)如图1,在Rt△OFG中,∠OFG=90°∴tan∠GOF=GFOF =12,即GF=12OF,∵四边形OABC为正方形,∴∠AOB=∠ABO=45°,∴OF=EF,∴GF=12EF,∴G为EF的中点,∵GH∥x轴交AE于H,∴H为AE的中点,∵B(4,4),D(4,2),∴D为AB的中点,∴DH是△ABE的中位线,∴HD∥BE,∴∠HDA=∠ABO=45°.(3)①若⊙G与对角线OB相切,如图2,当点E在线段OB上时,过点G作GP⊥OB于点P,设PG=x,可得PE=x,EG=FG2x,OF=EF=2x,∵OA=4,∴AF=4﹣22x,∵G为EF的中点,H为AE的中点,∴GH为△AFE的中位线,∴GH=12AF=12×(4﹣22x)=2﹣2x,则x=2﹣2x,解得:x=22﹣2,∴E(8﹣42,8﹣42),如图3,当点E在线段OB的延长线上时,x=2x﹣2,解得:x=2+2,∴E(8+42,8+42);②若⊙G与对角线AC相切,如图4,当点E在线段BM上时,对角线AC,OB相交于点M,过点G作GP⊥OB于点P,设PG=x,可得PE=x,EG=FG2,OF=EF=2x,∵OA=4,∴AF=4﹣2,∵G为EF的中点,H为AE的中点,∴GH 为△AFE 的中位线, ∴GH =12AF =12×(4﹣22x )=2﹣2x , 过点G 作GQ ⊥AC 于点Q ,则GQ =PM =3x ﹣22, ∴3x ﹣22=2﹣2x , ∴4227x +=, ∴42164216,77E ⎛⎫++ ⎪⎪⎝⎭; 如图5,当点E 在线段OM 上时,GQ =PM =22﹣3x ,则22﹣3x =2﹣2x , 解得4227x -=, ∴16421642,77E ⎛⎫-- ⎪ ⎪⎝⎭; 如图6,当点E 在线段OB 的延长线上时,3x ﹣22x ﹣2, 解得:422x -=(舍去); 综上所述,符合条件的点为(8﹣2,8﹣2)或(2,2)或42164216,⎛⎫++ ⎪ ⎪⎝⎭或16421642,⎛⎫-- ⎪ ⎪⎝⎭. 【点睛】本题是圆的综合问题,解题的关键是掌握正方形和直角三角形的性质、正切函数的定义、三角形中位线定理及分类讨论思想的运用.13.如图①,在菱形ABCD 中,60B ︒∠= ,4AB =.点P 从点A 出发以每秒2个单位的速度沿边AD 向终点D 运动,过点P 作PQ AC ⊥交边AB 于点Q ,过点P 向上作//PN AC ,且32PN PQ =,以PN 、PQ 为边作矩形PQMN .设点P 的运动时间为t (秒),矩形PQMN 与菱形ABCD 重叠部分图形的面积为S . (1)用含t 的代数式表示线段PQ 的长. (2)当点M 落在边BC 上时,求t 的值. (3)当0t 1<<时,求S 与t 之间的函数关系式,(4)如图②,若点O 是AC 的中点,作直线OM .当直线OM 将矩形PQMN 分成两部分图形的面积比为12:时,直接写出t 的值【答案】(1)23PQ t =;(2)45;(3)2193403163t t -+-;(4) 23t = 或87t = . 【解析】 【分析】(1)由菱形性质得∠D=∠B=60°,AD=AB=CD=4,△ACD 是等边三角形,证出△APQ 是等腰三角形,得出PF=QF ,3,即可得出结果;(2)当点M 落在边BC 上时,由题意得:△PDN 是等边三角形,得出PD=PN ,由已知得3,得出PD=3t ,由题意得出方程,解方程即可; (3)当0<t≤45时,3t ,3,S=矩形PQMN 的面积=PQ×PN ,即可得出结果;当45<t <1时,△PDN 是等边三角形,得出PE=PD=AD-PA=4-2t ,∠FEN=∠PED=60°,得出NE=PN-PE=5t-4,FN=3NE=3(5t-4),S=矩形PQMN的面积-2△EFN的面积,即可得出结果;(4)分两种情况:当0<t≤45时,△ACD是等边三角形,AC=AD=4,得出OA=2,OG是△MNH的中位线,得出OG=4t-2,NH=2OG=8t-4,由面积关系得出方程,解方程即可;当45<t≤2时,由平行线得出△OEF∽△MEQ,得出EF OFEQ MQ=,即233ttEF t-=+,解得EF=243232t tt--,得出EQ=2332234t ttt--+,由三角形面积关系得出方程,解方程即可.【详解】(1)∵在菱形ABCD中,∠B=60°,∴∠D=∠B=60°,AD=AB=CD=4,△ACD是等边三角形,∴∠CAD=60°,∵PQ⊥AC,∴△APQ是等腰三角形,∴PF=QF,PF=PA•sin60°=2t×3=3t,∴PQ=23t;(2)当点M落在边BC上时,如图2所示:由题意得:△PDN是等边三角形,∴PD=PN,∵PN=32PQ=323t=3t,∴PD=3t,∵PA+PD=AD,即2t+3t=4,解得:t=45.(3)当0<t≤45时,如图1所示:PQ=23t,PN=32PQ=32×23t=3t,S=矩形PQMN的面积=PQ×PN=23t×3t=63t2;当45<t<1时,如图3所示:∵△PDN是等边三角形,∴PE=PD=AD-PA=4-2t,∠FEN=∠PED=60°,∴NE=PN-PE=3t-(4-2t)=5t-4,∴FN=3NE=3(5t-4),∴S=矩形PQMN的面积-2△EFN的面积=63t2-2×12×3(5t-4)2=-19t2+403t-163,即S=-19t2+403t-163;(4)分两种情况:当0<t≤45时,如图4所示:∵△ACD是等边三角形,∴AC=AD=4,∵O是AC的中点,∴OA=2,OG是△MNH的中位线,∴OG=3t-(2-t)=4t-2,NH=2OG=8t-4,∴△MNH 的面积=12MN×NH=12×23t×(8t-4)=13×63t 2, 解得:t=23; 当45<t≤2时,如图5所示:∵AC ∥QM , ∴△OEF ∽△MEQ ,∴EF OF EQ MQ =233tt EF t -=+, 解得:2332t t -,∴233234t t t t --+,∴△MEQ 的面积=12×3t×2332234t t t t -+)=1332,解得:t=87; 综上所述,当直线OM 将矩形PQMN 分成两部分图形的面积比为1:2时,t 的值为23或87. 【点睛】本题是四边形综合题目,考查了菱形的性质、矩形的性质、等边三角形的判定与性质、勾股定理、相似三角形的判定与性质、三角形中位线定理等知识;本题综合性强,难度较大,熟练掌握菱形和矩形的性质,综合运用知识,进行分类讨论是解题的关键.14.已知AB 是⊙O 的直径,弦CD ⊥AB 于H ,过CD 延长线上一点E 作⊙O 的切线交AB 的延长线于F ,切点为G ,连接AG 交CD 于K . (1)如图1,求证:KE =GE ; (2)如图2,连接CABG ,若∠FGB =12∠ACH ,求证:CA ∥FE ;(3)如图3,在(2)的条件下,连接CG 交AB 于点N ,若sin E =35,AK =10,求CN 的长.【答案】(1)证明见解析;(2)△EAD 是等腰三角形.证明见解析;(3201013【解析】 试题分析:(1)连接OG ,则由已知易得∠OGE=∠AHK=90°,由OG=OA 可得∠AGO=∠OAG ,从而可得∠KGE=∠AKH=∠EKG ,这样即可得到KE=GE ;(2)设∠FGB=α,由AB 是直径可得∠AGB=90°,从而可得∠KGE=90°-α,结合GE=KE 可得∠EKG=90°-α,这样在△GKE 中可得∠E=2α,由∠FGB=12∠ACH 可得∠ACH=2α,这样可得∠E=∠ACH ,由此即可得到CA ∥EF ; (3)如下图2,作NP ⊥AC 于P ,由(2)可知∠ACH=∠E ,由此可得sinE=sin ∠ACH=35AH AC =,设AH=3a ,可得AC=5a ,CH=4a ,则tan ∠CAH=43CH AH =,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC ,从而可得CK=AC=5a ,由此可得HK=a ,tan ∠AKH=3AHHK=,10a ,结合10可得a=1,则AC=5;在四边形BGKH 中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG 可得∠ACG=∠AKH , 在Rt △APN 中,由tan ∠CAH=43PN AP=,可设PN=12b ,AP=9b ,由tan ∠ACG=PN CP =tan ∠AKH=3可得CP=4b ,由此可得AC=AP+CP=13b =5,则可得b=513,由此即可在Rt △CPN 中由勾股定理解出CN 的长. 试题解析:(1)如图1,连接OG .∵EF 切⊙O 于G , ∴OG ⊥EF ,∴∠AGO+∠AGE=90°, ∵CD ⊥AB 于H , ∴∠AHD=90°, ∴∠OAG=∠AKH=90°, ∵OA=OG , ∴∠AGO=∠OAG , ∴∠AGE=∠AKH , ∵∠EKG=∠AKH , ∴∠EKG=∠AGE , ∴KE=GE . (2)设∠FGB=α, ∵AB 是直径, ∴∠AGB=90°,∴∠AGE =∠EKG=90°﹣α, ∴∠E=180°﹣∠AGE ﹣∠EKG=2α,∵∠FGB=12∠ACH , ∴∠ACH=2α, ∴∠ACH=∠E , ∴CA ∥FE .(3)作NP ⊥AC 于P . ∵∠ACH=∠E , ∴sin ∠E=sin ∠ACH=35AH AC =,设AH=3a ,AC=5a , 则224AC CH a -=,tan ∠CAH=43CH AH =, ∵CA ∥FE , ∴∠CAK=∠AGE , ∵∠AGE=∠AKH , ∴∠CAK=∠AKH ,∴AC=CK=5a ,HK=CK ﹣CH=4a ,tan ∠AKH=AHHK=3,2210AH HK a +=,∵AK=10,∴1010a=,∴a=1.AC=5,∵∠BHD=∠AGB=90°,∴∠BHD+∠AGB=180°,在四边形BGKH中,∠BHD+∠HKG+∠AGB+∠ABG=360°,∴∠ABG+∠HKG=180°,∵∠AKH+∠HKG=180°,∴∠AKH=∠ABG,∵∠ACN=∠ABG,∴∠AKH=∠ACN,∴tan∠AKH=tan∠ACN=3,∵NP⊥AC于P,∴∠APN=∠CPN=90°,在Rt△APN中,tan∠CAH=43PNAP=,设PN=12b,则AP=9b,在Rt△CPN中,tan∠ACN=PNCP=3,∴CP=4b,∴AC=AP+CP=13b,∵AC=5,∴13b=5,∴b=513,∴CN=22PN CP+=410b⋅=2010 13.15.如图,直线与轴交于点,与轴交于点,抛物线经过点,.点为轴上一动点,过点且垂直于轴的直线分别交直线及抛物线于点,.(1)填空:点的坐标为,抛物线的解析式为;(2)当点在线段上运动时(不与点,重合),①当为何值时,线段最大值,并求出的最大值;②求出使为直角三角形时的值;(3)若抛物线上有且只有三个点到直线的距离是,请直接写出此时由点,,,构成的四边形的面积.【答案】(1),;(2)①当时,有最大值是3;②使为直角三角形时的值为3或;(3)点,,,构成的四边形的面积为:6或或.【解析】【分析】(1)把点A坐标代入直线表达式y=,求出a=−3,把点A、B的坐标代入二次函数表达式,即可求解;(2)①设:点P(m,),N(m,)求出PN值的表达式,即可求解;②分∠BNP=90°、∠NBP=90°、∠BPN=90°三种情况,求解即可;(3)若抛物线上有且只有三个点N到直线AB的距离是h,则只能出现:在AB直线下方抛物线与过点N的直线与抛物线有一个交点N,在直线AB上方的交点有两个,分别求解即可.【详解】解:(1)把点坐标代入直线表达式,解得:,则:直线表达式为:,令,则:,则点坐标为,将点的坐标代入二次函数表达式得:,把点的坐标代入二次函数表达式得:,解得:,故:抛物线的解析式为:,故:答案为:,;(2)①∵在线段上,且轴,∴点,,∴,∵,∴抛物线开口向下,∴当时,有最大值是3,②当时,点的纵坐标为-3,把代入抛物线的表达式得:,解得:或0(舍去),∴;当时,∵,两直线垂直,其值相乘为-1,设:直线的表达式为:,把点的坐标代入上式,解得:,则:直线的表达式为:,将上式与抛物线的表达式联立并解得:或0(舍去),当时,不合题意舍去,故:使为直角三角形时的值为3或;(3)∵,,在中,,则:,,∵轴,∴,若抛物线上有且只有三个点到直线的距离是,则只能出现:在直线下方抛物线与过点的直线与抛物线有一个交点,在直线上方的交点有两个.当过点的直线与抛物线有一个交点,点的坐标为,设:点坐标为:,则:,过点作的平行线,则点所在的直线表达式为:,将点坐标代入,解得:过点直线表达式为:,将拋物线的表达式与上式联立并整理得:,,将代入上式并整理得:,解得:,则点的坐标为,则:点坐标为,则:,∵,,∴四边形为平行四边形,则点到直线的距离等于点到直线的距离,即:过点与平行的直线与抛物线的交点为另外两个点,即:、,直线的表达式为:,将该表达式与二次函数表达式联立并整理得:,解得:,则点、的横坐标分别为,,作交直线于点,则,作轴,交轴于点,则:,,,则:,同理:,故:点,,,构成的四边形的面积为:6或或.【点睛】本题考查的是二次函数知识的综合运用,涉及到一次函数、解直角三角形等相关知识,其中(3)中确定点N的位置是本题的难点,核心是通过△=0,确定图中N点的坐标.。
