考试试题试卷选择题
2023年广东中考数学试题试卷及答案

2023年广东中考数学试题试卷及答案满分120分,考试用时90分钟.一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 负数的概念最早出现在我国古代著名的数学专著《九章算术》中,如果把收入5元记作元,那么支5+出5元记作( )A. 元B. 0元C. 元D. 元5-5+10+2. 下列出版社的商标图案中,是轴对称图形的为( ) A. B. C. D.3. 2023年5月28日,我国自主研发的C919国产大飞机商业首航取得圆满成功,C919可储存约186000升燃油,将数据186000用科学记数法表示为( )A. B. C. D.50.18610⨯51.8610⨯418.610⨯318610⨯4. 如图,街道与平行,拐角,则拐角( )AB CD 137ABC ∠=︒BCD ∠=A.B. C. D. 43︒53︒107︒137︒5. 计算的结果为( ) 32a a+A. B. C. D.1a 26a 5a 6a 6. 我国著名数学家华罗庚曾为普及优选法作出重要贡献,优选法中有一种0.618法应用了( )A. 黄金分割数B. 平均数C. 众数D. 中位数7. 某学校开设了劳动教育课程.小明从感兴趣的“种植”“烹饪”“陶艺”“木工”4门课程中随机选择一门学习,每门课程被选中的可能性相等,小明恰好选中“烹饪”的概率为( )A. B. C. D. 181614128. 一元一次不等式组的解集为( ) 214x x ->⎧⎨<⎩A. B. C. D.14x -<<4x <3x <34x <<9. 如图,是的直径,,则( )AB O A 50BAC ∠=︒D ∠=A. B. C. D.20︒40︒50︒80︒10. 如图,抛物线经过正方形的三个顶点A ,B ,C ,点B 在轴上,则的值为2y ax c =+OABC y ac ( )A. B. C. D.1-2-3-4-二、填空题:本大题共5小题,每小题3分,共15分.11. 因式分解:______.21x -=12. 计算_________.312⨯=13. 某蓄电池的电压为,使用此蓄电池时,电流(单位:)与电阻(单位:)的函数表达式为48V I A R Ω,当时,的值为_______. 48I R=12R =ΩI A 14. 某商品进价4元,标价5元出售,商家准备打折销售,但其利润率不能少于,则最多可打10%_______折.15. 边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为_______.三、解答题(一):本大题共3小题,第16题10分,第17、18题各7分,共24分.16. (1)计算:;202338|5|(1)+-+-(2)已知一次函数的图象经过点与点,求该一次函数的表达式.y kx b =+(0,1)(2,5)17. 某学校开展了社会实践活动,活动地点距离学校,甲、乙两同学骑自行车同时从学校出发,甲12km 的速度是乙的倍,结果甲比乙早到,求乙同学骑自行车的速度.1.210min 18. 2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站,如图中的照片展示了中国空间站上机械臂的一种工作状态,当两臂,两臂夹角10m AC BC ==100ACB ∠=︒时,求A ,B 两点间的距离.(结果精确到,参考数据,,0.1m sin500.766︒≈cos500.643︒≈)tan50 1.192︒≈四、解答题(二):本大题共3小题,每小题9分,共27分.19. 如图,在中,. ABCD Y 30DAB ∠=︒(1)实践与操作:用尺规作图法过点作边上的高;(保留作图痕迹,不要求写作法)D AB DE (2)应用与计算:在(1)的条件下,,,求的长.4=AD 6AB =BE 20. 综合与实践主题:制作无盖正方体形纸盒素材:一张正方形纸板.步骤1:如图1,将正方形纸板的边长三等分,画出九个相同的小正方形,并剪去四个角上的小正方形; 步骤2:如图2,把剪好的纸板折成无盖正方体形纸盒. 猜想与证明:(1)直接写出纸板上与纸盒上的大小关系;ABC ∠111A B C ∠(2)证明(1)中你发现的结论.21. 小红家到学校有两条公共汽车线路,为了解两条线路的乘车所用时间,小红做了试验,第一周(5个工作日)选择A 线路,第二周(5个工作日)选择B 线路,每天在固定时间段内乘车2次并分别记录所用时间,数据统计如下:(单位:min)数据统计表 试验序号 1 2 3 4 5 6 7 8 9 10A 线路所用时间 15 32 15 16 34 18 21 14 35 20B 线路所用时间 25 29 23 25 27 26 31 28 30 24数据折线统计图根据以上信息解答下列问题:平均数 中位数 众数 方差A 线路所用时间 22a 15 63.2 B 线路所用时间 b26.5 c 6.36 (1)填空:__________;___________;___________;=a b =c =(2)应用你所学的统计知识,帮助小红分析如何选择乘车线路.五、解答题(三):本大题共2小题,每小题12分,共24分.22. 综合探究如图1,在矩形中,对角线相交于点,点关于的对称点为,连接ABCD ()AB AD >AC BD ,O A BD A '交于点,连接.AA 'BD E CA '(1)求证:;AA CA '⊥'(2)以点为圆心,为半径作圆.O OE ①如图2,与相切,求证:;O A CD 3AA CA '='②如图3,与相切,,求的面积.O A CA '1AD =O A 23. 综合运用如图1,在平面直角坐标系中,正方形的顶点A 在轴的正半轴上,如图2,将正方形绕点OABC x OABC 逆时针旋转,旋转角为,交直线于点,交轴于点.O ()045αα︒<<︒AB y x =E BC y F(1)当旋转角为多少度时,;(直接写出结果,不要求写解答过程)COF ∠OE OF =(2)若点,求的长;(4,3)A FC (3)如图3,对角线交轴于点,交直线于点,连接,将与的面积AC y M y x =N FN OFN △OCF △分别记为与,设,,求关于的函数表达式.1S 2S 12S S S =-AN n =S n 参考答案一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.【1题答案】【答案】A【2题答案】【答案】A【3题答案】【答案】B【4题答案】【答案】D【5题答案】【答案】C【6题答案】【答案】A【7题答案】【答案】C【8题答案】【答案】D【9题答案】【答案】B【10题答案】【答案】B二、填空题:本大题共5小题,每小题3分,共15分.【11题答案】【答案】()()11x x +-【12题答案】【答案】6【13题答案】【答案】4【14题答案】【答案】9.2【15题答案】【答案】15三、解答题(一):本大题共3小题,第16题10分,第17、18题各7分,共24分.【16题答案】【答案】(1);(2)621y x =+【17题答案】【答案】乙同学骑自行车的速度为千米/分钟.0.2【18题答案】【答案】15.3m 四、解答题(二):本大题共3小题,每小题9分,共27分.【19题答案】【答案】(1)见解析 (2)623-【20题答案】【答案】(1)111ABC A B C ∠=∠(2)证明见解析.【21题答案】【答案】(1)19,26.8,25(2)见解析五、解答题(三):本大题共2小题,每小题12分,共24分.【22题答案】【答案】(1)见解析 (2)①见解析;②224π+【23题答案】【答案】(1)22.5︒(2) 154FC =(3) 212S n =。
英语考试试卷试题库及参考答案

一、单项选择题1.下列哪个单词的划线部分发音与其他三个不同?A. bagB. catC. dadD. egg答案:B2. — Could you please _______ the radio? I'm studying.— Sure, I'll turn it down right now.A. turn onB. turn offC. turn downD. turn up答案:C3. My mother _______ me to buy some fruits in the market.A. tellsB. toldC. is tellingD. has told答案:B4. There are many _______ in the sky. They are flying kites.A. birdB. birdsC. childD. children答案:B5. — What's your favorite subject, Lily?— _______A. EnglishB. ScienceC. MathD. Music答案:A二、完形填空Once upon a time, there was a _______ (1) named Paddy. He was a very kind and helpful person. One day, Paddy was walking in the forest when he saw a fox. The fox's leg was_______ (2) in a trap (陷阱). Paddy felt sorry for the fox and wanted to help it. He carefully opened the trap and_______ (3) the fox's leg out. The fox was very happy and thanked Paddy _______ (4).A few days later, Paddy was _______ (5) in the forest again. This time, he was caught some hunters. They wanted to _______ (6) him. Just then, the fox Paddy had helped _______ (7) along. It saw Paddy in trouble and _______ (8) a plan to save him. The fox made some _______ (9) like a ba crying. The hunters heard the _______ (10) and thought there was a ba in the forest. They left Paddy and went to find the ba. The fox had saved Paddy's life.(1) A. boy B. girl C. man D. woman答案:C(2) A. hurt B. hurting C. hurtes D. hurted答案:A(3) A. put B. took C. got D. picked答案:B(4) A. very much B. very well C. very good D. very nice答案:A(5) A. walking B. running C. playing D. jumping答案:A(6) A. catch B. kill C. hit D. hurt答案:B(7) A. came B. goes C. gone D. going答案:A(8) A. thought B. thought of C. think D. think of答案:B(9) A. voice B. noises C. sound D. music答案:B(10) A. voice B. noises C. sound D. music答案:B三、阅读理解Tom was born in a small town. He liked to draw pictures when he was a child. His parents wanted him to be a great artist, so they sent him to an art school. However, Tomdidn't like the art school. He thought the teachers and students there were too serious. They only focused on drawing and didn't have any fun.1. Why did Tom's parents send him to an art school?A. Because they wanted him to be a great artist.B. Because they wanted him to make friends.C. Because they wanted him to have fun.D. Because they wanted him to learn more about art.答案:A2. Why didn't Tom like the art school?A. Because the teachers were too serious.B. Because the students were too serious.C. Because they only focused on drawing.D. Both A and C.答案:DA. He drew pictures for advertisements.B. He wrote articles for advertisements.C. He took photos for advertisements.D. He designed advertisements.答案:AA. Because he could draw whatever he wanted.B. Because he could make a lot of money.C. Because he could meet many people.D. Because he could travel to different places.答案:A5. What was special about Tom's drawings?A. They were funny and creative.B. They were serious and traditional.C. They were beautiful and colorful.D.四、词语运用根据句意,选择合适的词语填空。
国家开放大学考试试卷真题

国家开放大学考试试卷真题一、选择题(每题2分,共20分)1. 国家开放大学成立于哪一年?A. 1978年B. 1980年C. 1990年D. 2000年2. 下列哪项不是国家开放大学的主要教学方式?A. 远程教育B. 面授课程C. 自学D. 实验操作3. 国家开放大学的教学资源主要来源于哪里?A. 网络资源B. 学校图书馆C. 教师自编教材D. 所有上述选项4. 国家开放大学的学生需要参加哪些形式的考试?A. 期中考试B. 期末考试C. 开卷考试D. 闭卷考试5. 国家开放大学的学生可以申请哪些类型的学位?A. 学士学位B. 硕士学位C. 博士学位D. 所有上述选项...(此处省略其他选择题)二、填空题(每空1分,共10分)1. 国家开放大学的办学理念是________。
2. 国家开放大学的教学模式强调________和________的结合。
3. 学生在国家开放大学学习期间,需要完成________学分才能毕业。
4. 国家开放大学提供________和________两种学位类型。
5. 国家开放大学的学生可以通过________平台进行在线学习。
三、简答题(每题10分,共20分)1. 简述国家开放大学远程教育的特点。
2. 描述国家开放大学如何保证远程教育的教学质量。
四、论述题(每题15分,共30分)1. 论述国家开放大学在终身教育体系中的作用和意义。
2. 分析国家开放大学如何利用现代信息技术提高教学效果。
五、案例分析题(每题15分,共15分)某国家开放大学的学生小李,因为工作原因无法按时参加期末考试,他应该怎么办?请结合国家开放大学的相关规定,给出建议。
六、作文题(15分)请以“我与国家开放大学的相遇”为题,写一篇不少于800字的作文,描述你选择国家开放大学的原因,以及在国家开放大学学习过程中的体验和收获。
【注】本试卷为模拟试题,具体考试内容以国家开放大学官方发布的考试大纲为准。
(完)。
2024年高考数学真题试卷(天津卷)附详细解答
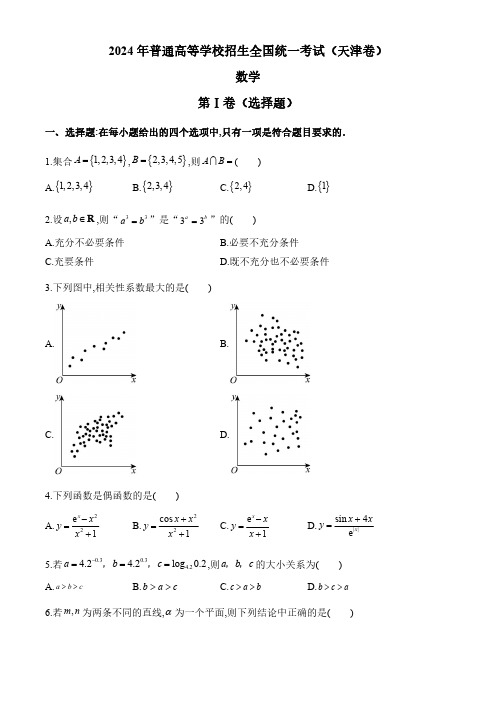
2024年普通高等学校招生全国统一考试(天津卷)数学第Ⅰ卷(选择题)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}1,2,3,4A =,{}2,3,4,5B =,则A B = ()A.{}1,2,3,4 B.{}2,3,4 C.{}2,4 D.{}12.设,a b ∈R ,则“33a b =”是“33a b =”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件3.下列图中,相关性系数最大的是()A. B.C. D.4.下列函数是偶函数的是()A.22e 1x x y x -=+ B.22cos 1x x y x +=+ C.e 1x x y x -=+ D.||sin 4e x x x y +=5.若0.30.3 4.24.2 4.2log 0.2a b c -===,,,则a b c ,,的大小关系为()A.a b c>> B.b a c>> C.c a b>> D.b c a>>6.若,m n 为两条不同的直线,α为一个平面,则下列结论中正确的是()A.若//m α,n ⊂α,则//m nB.若//,//m n αα,则//m nC.若//,αα⊥m n ,则m n⊥ D.若//,αα⊥m n ,则m 与n 相交7.已知函数()()πsin303f x x ωω⎛⎫=+> ⎪⎝⎭的最小正周期为π.则函数在ππ,126⎡⎤-⎢⎥⎣⎦的最小值是()A.32-B.32-C.0D.328.双曲线22221()00a x y a bb >-=>,的左、右焦点分别为12.F F P 、是双曲线右支上一点,且直线2PF 的斜率为2.12PF F △是面积为8的直角三角形,则双曲线的方程为()9.一个五面体ABC DEF -.已知AD BE CF ∥∥,且两两之间距离为1.并已知123AD BE CF ===,,.则该五面体的体积为()A.6B.33142+ C.32D.33142-第Ⅱ卷二、填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分.10.已知i 是虚数单位,复数))i 2i ⋅=______.11.在63333x x⎛⎫+ ⎪⎝⎭的展开式中,常数项为______.12.22(1)25-+=x y 的圆心与抛物线22(0)y px p =>的焦点F 重合,A 为两曲线的交点,则原点到直线AF 的距离为______.13.,,,,A B C D E 五种活动,甲、乙都要选择三个活动参加.(1)甲选到A 的概率为______;已知乙选了A 活动,他再选择B 活动的概率为______.14.在边长为1的正方形ABCD 中,点E 为线段CD 的三等分点,1,2CE DE BE BA BC ==+uur uur uuu r λμ,则λμ+=______;若F 为线段BE 上的动点,G 为AF 中点,则AF DG ⋅的最小值为______.15.若函数()21f x ax =--+有唯一零点,则a 的取值范围为______.三、解答题:本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤.16.在ABC 中,92cos 5163a Bbc ===,,.(1)求a ;(2)求sin A ;(3)求()cos 2B A -.17.已知四棱柱1111ABCD A B C D -中,底面ABCD 为梯形,//AB CD ,1A A ⊥平面ABCD ,AD AB ⊥,其中12,1AB AA AD DC ====.N 是11B C 的中点,M 是1DD 的中点.(1)求证1//D N 平面1CB M ;(2)求平面1CB M 与平面11BB CC 的夹角余弦值;(3)求点B 到平面1CB M 的距离.18.已知椭圆22221(0)x y a b a b+=>>椭圆的离心率12e =.左顶点为A ,下顶点为B C ,是线段OB 的中点,其中ABC S =△.(1)求椭圆方程.(2)过点30,2⎛⎫- ⎪⎝⎭的动直线与椭圆有两个交点P Q ,.在y 轴上是否存在点T 使得0TP TQ ⋅≤ 恒成立.若存在求出这个T 点纵坐标的取值范围,若不存在请说明理由.19.已知数列{}n a 是公比大于0的等比数列.其前n 项和为n S .若1231,1a S a ==-.(1)求数列{}n a 前n 项和n S ;(2)设11,2,kn n k k k n a b b k a n a -+=⎧=⎨+<<⎩,11b =,其中k 是大于1的正整数.(ⅰ)当1k n a +=时,求证:1n k n b a b -≥⋅;(ⅱ)求1nS i i b =∑.20.设函数()ln f x x x =.(1)求()f x 图象上点()()1,1f 处的切线方程;(2)若()(f x a x ≥-在()0,x ∞∈+时恒成立,求a 的取值范围;(3)若()12,0,1x x ∈,证明()()121212f x f x x x -≤-.2024年普通高等学校招生全国统一考试(天津卷)数学答案解析一、选择题.1.【答案】B【解析】因为集合{}1,2,3,4A =,{}2,3,4,5B =所以{}2,3,4A B = 故选:B 2.【答案】C【解析】根据立方的性质和指数函数的性质,33a b =和33a b =都当且仅当a b =,所以二者互为充要条件.故选:C.3.【答案】A【解析】观察4幅图可知,A 图散点分布比较集中,且大体接近某一条直线,线性回归模型拟合效果比较好,呈现明显的正相关,r 值相比于其他3图更接近1.故选:A 4.【答案】B【解析】对A,设()22e 1x x f x x -=+,函数定义域为R ,但()112e 1f ---=,()112e f -=,则()()11f f -≠,故A 错误;对B,设()22cos 1x x g x x +=+,函数定义域为R 且()()()()()2222cos cos 11x x x x g x g x x x -+-+-===+-+,则()g x 为偶函数,故B 正确;对C,设()e 1x xh x x -=+,函数定义域为{}|1x x ≠-,不关于原点对称,则()h x 不是偶函数,故C 错误;对D,设()||sin 4e x x x x ϕ+=,函数定义域为R,因为()sin141e ϕ+=,()sin141eϕ---=则()()11ϕϕ≠-,则()x ϕ不是偶函数,故D 错误.故选:B.5.【答案】B【解析】因为 4.2x y =在R 上递增,且0.300.3-<<所以0.300.30 4.2 4.2 4.2-<<<所以0.30.30 4.21 4.2-<<<,即01a b <<<因为 4.2log y x =在(0,)+∞上递增,且00.21<<所以 4.2 4.2log 0.2log 10<=,即0c <所以b a c >>故选:B 6.【答案】C【解析】对于A,若//m α,n ⊂α,则,m n 平行或异面,故A 错误.对于B,若//,//m n αα,则,m n 平行或异面或相交,故B 错误.对于C,//,αα⊥m n ,过m 作平面β,使得s βα= 因为m β⊂,故//m s ,而s α⊂,故n s ⊥,故m n ⊥,故C 正确.对于D,若//,αα⊥m n ,则m 与n 相交或异面,故D 错误.故选:C.7.【答案】A【解析】()()πsin3sin 3πsin 33f x x x x ωωω⎛⎫=+=+=- ⎪⎝⎭,由2ππ3T ω==得23ω=即()sin2f x x =-,当,126⎡⎤∈-⎢⎣⎦ππx 时,ππ2,63x ⎡⎤∈-⎢⎥⎣⎦画出()sin2f x x =-图象,如下图由图可知,()sin2f x x =-在ππ,126⎡⎤-⎢⎥⎣⎦上递减所以,当π6x =时,()min πsin 32f x =-=-故选:A 8.【答案】C【解析】如下图:由题可知,点P 必落在第四象限,1290F PF ∠=︒,设2PF m=211122,PF F PF F θθ∠=∠=,由21tan 2PF k θ==,求得12sin 5θ=因为1290F PF ∠=︒,所以121PF PF k k ⋅=-,求得112PF k =-,即21tan 2θ=21sin 5θ=由正弦定理可得:121212::sin :sin :sin 902:1:5PF PF F F θθ=︒=则由2PF m =得1122,25PF m F F c m ===由1212112822PF F S PF PF m m =⋅=⋅= 得2m =则21122,2,210,10PF PF F F c c =====由双曲线第一定义可得:1222PF PF a -==222,8a b c a ==-=所以双曲线的方程为22128x y -=.故选:C 9.【答案】C【解析】用一个完全相同的五面体HIJ LMN -(顶点与五面体ABC DEF -一一对应)与该五面体相嵌,使得,D N ;,E M ;,F L 重合因为AD BE CF ∥∥,且两两之间距离为1.1,2,3AD BE CF ===则形成的新组合体为一个三棱柱该三棱柱的直截面(与侧棱垂直的截面)为边长为1的等边三角形,侧棱长为1322314+=+=+=2132211311422ABC DEF ABC HIJ V V --==⨯⨯⨯⨯=.故选:C.第Ⅱ卷二、填空题.10.【答案】7【解析】))i 2i 527+⋅=+-+=-.故答案为:7.11.【答案】20【解析】因为63333x x ⎛⎫+ ⎪⎝⎭的展开式的通项为()63636216633C 3C ,0,1,,63rr r r r r r x T x r x ---+⎛⎫⎛⎫===⋅⋅⋅ ⎪ ⎪⎝⎭⎝⎭令()630r -=,可得3r =所以常数项为0363C 20=.故答案为:20.12.【答案】45【解析】圆22(1)25-+=x y 的圆心为()1,0F ,故12p =即2p =由()2221254x y y x⎧-+=⎪⎨=⎪⎩可得22240x x +-=,故4x =或6x =-(舍)故()4,4A ±,故直线()4:13AF y x =±-即4340x y --=或4340x y +-=故原点到直线AF 的距离为4455d ==故答案为:4513.【答案】①.35②.12【解析】设甲、乙选到A 为事件M ,乙选到B 为事件N则甲选到A 的概率为()2435C 3C 5P M ==;乙选了A 活动,他再选择B 活动的概率为()()()133524351C 2C C P MN C P N M P M ===故答案为:35;1214.【答案】①.43②.518-【解析】因为12CE DE =,即23CE BA =uur uur ,则13BE BC CE BA BC =+=+uuu r uur u uu ur r uuu r 可得1,13λμ==,所以43λμ+=;由题意可知:1,0BC BA BA BC ==⋅= 因为F 为线段BE 上的动点,设[]1,0,13BF k BE k BA k BC k ==+∈ 则113AF AB BF AB k BE k BA k BC ⎛⎫=+=+=-+ ⎪⎝⎭又因为G 为AF 中点,则1111112232DG DA AG BC AF k BA k BC ⎛⎫⎛⎫=+=-+=-+- ⎪ ⎪⎝⎭⎝⎭可得11111113232AF DG k BA k BC k BA BC ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⋅=-+⋅-+- ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ 22111563112329510k k k k ⎛⎫⎛⎫⎛⎫=-+-=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭又因为[]0,1k ∈,可知:当1k =时,AF DG ⋅ 取到最小值518-;15.【答案】()(1- 【解析】令()0f x =,即21ax =--由题可得20x ax -≥当0a =时,x ∈R ,有211=--=,则2x =±,不符合要求,舍去;当0a >时,则23,2121,ax x a ax ax x a ⎧-≥⎪⎪=--=⎨⎪-<⎪⎩即函数()g x =与函数()23,21,ax x a h x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩有唯一交点由20x ax -≥,可得x a ≥或0x ≤当0x ≤时,则20ax -<,则211ax ax=--=-即()22441x ax ax -=-,整理得)()()2242121210a x ax a x a x ⎡⎤⎡⎤---=++--=⎣⎦⎣⎦当2a =时,即410x +=,即14x =-当()0,2a ∈,12x a =-+或102x a =>-(正值舍去)当()2,a ∈+∞时,102x a =-<+或102x a=<-,有两解,舍去即当(]0,2a ∈时,210ax -+=在0x ≤时有唯一解则当(]0,2a ∈时,210ax -+=在x a ≥时需无解当(]0,2a ∈,且x a ≥时由函数()23,21,ax x a h x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩关于2x a =对称,令()0h x =,可得1x a =或3x a =且函数()h x 在12,a a ⎛⎫ ⎪⎝⎭上单调递减,在23,a a ⎛⎫ ⎪⎝⎭上单调递增令()g x y ==,即2222142a x y a a⎛⎫- ⎪-⎭=⎝故x a ≥时,()g x 图象为双曲线()222214y x a a-=右支的x 轴上方部分向右平移2a 所得由()222214y x a a -=的渐近线方程为22a y x xa =±=±即()g x 部分的渐近线方程为22a y x ⎛⎫=- ⎪⎝⎭,其斜率为2又(]0,2a ∈,即()23,21,ax x a h x ax x a⎧-≥⎪⎪=⎨⎪-<⎪⎩在2x a ≥时的斜率(]0,2a ∈令()0g x ==,可得x a =或0x =(舍去)且函数()g x 在(),a +∞上单调递增故有13aaaa ⎧<⎪⎪⎨⎪>⎪⎩,解得1a <<,故1a <<符合要求;当a<0时,则23,2121,ax x aax ax x a⎧-≤⎪⎪=--=⎨⎪->⎪⎩即函数()g x =与函数()23,21,ax x a h x ax x a⎧-≤⎪⎪=⎨⎪->⎪⎩有唯一交点由20x ax -≥,可得0x ≥或x a ≤当0x ≥时,则20ax -<,则211ax ax=--=-即()22441x ax ax -=-,整理得()()()2242121210a x ax a x a x ⎡⎤⎡⎤---=++--=⎣⎦⎣⎦当2a =-时,即410x -=,即14x =当()2,0a ∈-,102x a =-<+(负值舍去)或102x a =-当(),2a ∈-∞时,102x a =->+或102x a =>-,有两解,舍去即当[)2,0a ∈-时,210ax --+=在0x ≥时有唯一解则当[)2,0a ∈-时,210ax --+=在x a ≤时需无解当[)2,0a ∈-,且x a ≤时由函数()23,21,ax x a h x ax x a ⎧-≤⎪⎪=⎨⎪->⎪⎩关于2x a =对称,令()0h x =,可得1x a =或3x a =且函数()h x 在21,a a ⎛⎫ ⎪⎝⎭上单调递减,在32,a a ⎛⎫ ⎪⎝⎭上单调递增同理可得:x a ≤时,()g x 图象为双曲线()222214y x a a -=左支的x 轴上方部分向左平移2a 所得()g x 部分的渐近线方程为22a y x ⎛⎫=-+ ⎪⎝⎭,其斜率为2-又[)2,0a ∈-,即()23,21,ax x a h x ax x a ⎧-≥⎪⎪=⎨⎪-<⎪⎩在2x a <时的斜率[)2,0a ∈-令()0g x ==,可得x a =或0x =(舍去)且函数()g x 在(),a -∞上单调递减故有13a a a a⎧>⎪⎪⎨⎪<⎪⎩,解得1a <<-,故1a <<-符合要求;综上所述,()(11,a ∈- .故答案为:()(1-⋃.三、解答题.16.【答案】(1)4(2)74(3)5764【小问1详解】设2,3a t c t ==,0t >,则根据余弦定理得2222cos b a c ac B=+-即229254922316t t t t =+-⨯⨯⨯,解得2t =(负舍);则4,6a c ==.【小问2详解】因为B 为三角形内角,所以57sin 16B ===再根据正弦定理得sin sin a b A B =,即4sin 5716A =,解得7sin 4A =【小问3详解】因为9cos 016B =>,且()0,πB ∈,所以π0,2B ⎛⎫∈ ⎪⎝⎭由(2)法一知57sin 16B =因为a b <,则A B <,所以3cos 4A ==则7337sin 22sin cos 2448A A A ==⨯⨯=,2231cos 22cos 12148A A ⎛⎫=-=⨯-= ⎪⎝⎭()19573757cos 2cos cos 2sin sin 281616864B A B A B A -=+=⨯+⨯=.17.【答案】(1)证明见解析(2)22211(3)21111【小问1详解】取1CB 中点P ,连接NP ,MP由N 是11B C 的中点,故1//NP CC ,且112NP CC =由M 是1DD 的中点,故1111122D M DD CC ==,且11//D M CC 则有1//D M NP 、1D M NP=故四边形1D MPN 是平行四边形,故1//D N MP又MP ⊂平面1CB M ,1D N ⊄平面1CB M故1//D N 平面1CB M ;【小问2详解】以A为原点建立如图所示空间直角坐标系有()0,0,0A 、()2,0,0B 、()12,0,2B 、()0,1,1M 、()1,1,0C 、()11,1,2C 则有()11,1,2CB =- 、()1,0,1CM =- 、()10,0,2BB = 设平面1CB M 与平面11BB CC 的法向量分别为()111,,m x y z = 、()222,,n x y z = 则有111111200m CB x y z m CM x z ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩ ,1222122020n CB x y z n BB z ⎧⋅=-+=⎪⎨⋅==⎪⎩ 分别取121x x ==,则有13y =、11z =、21y =,20z =即()1,3,1m = 、()1,1,0n =则cos ,11m n m n m n ⋅===⋅ 故平面1CB M 与平面11BB CC 的夹角余弦值为22211;【小问3详解】由()10,0,2BB = ,平面1CB M 的法向量为()1,3,1m =则有111BB m m ⋅== 即点B 到平面1CB M 的距离为21111.18.【答案】(1)221129x y +=(2)存在()30,32T t t ⎛⎫-≤≤ ⎪⎝⎭,使得0TP TQ ⋅≤ 恒成立.【小问1详解】因为椭圆的离心率为12e =,故2a c =,b =,其中c 为半焦距所以()()32,0,0,,0,2A c B C ⎛⎫-- ⎪ ⎪⎝⎭,故13332222ABC S c c =⨯⨯=△故c =所以a =,3b =,故椭圆方程为:221129x y +=.【小问2详解】若过点30,2⎛⎫- ⎪⎝⎭的动直线的斜率存在,则可设该直线方程为:32y kx =-设()()()1122,,,,0,P x y Q x y T t 由22343632x y y kx ⎧+=⎪⎨=-⎪⎩可得()223412270k x kx +--=故()222Δ144108343245760k k k =++=+>且1212221227,,3434k x x x x k k+==-++而()()1122,,,TP x y t TQ x y t =-=- 故()()121212123322TP TQ x x y t y t x x kx t kx t ⎛⎫⎛⎫⋅=+--=+---- ⎪⎪⎝⎭⎝⎭ ()()22121233122k x x k t x x t ⎛⎫⎛⎫=+-++++ ⎪ ⎪⎝⎭⎝⎭()22222731231342342k k k t t k k ⎛⎫⎛⎫⎛⎫=+⨯--+⨯++ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭()2222222327271812332234k k k t t t k k ⎛⎫----++++ ⎪⎝⎭=+()22223321245327234t t k t k ⎛⎫⎡⎤+--++- ⎪⎣⎦⎝⎭=+因为0TP TQ ⋅≤ 恒成立,故()223212450332702t t t ⎧+--≤⎪⎨⎛⎫+-≤⎪ ⎪⎝⎭⎩,解得332t -≤≤.若过点30,2⎛⎫- ⎪⎝⎭的动直线的斜率不存在,则()()0,3,0,3P Q -或()()0,3,0,3P Q -此时需33t -≤≤,两者结合可得332t ≤≤.综上,存在()30,32T t t ⎛⎫-≤≤ ⎪⎝⎭,使得0TP TQ ⋅≤ 恒成立.19.【答案】(1)21n n S =-(2)①证明见详解;②()131419n n S i i n b =-+=∑【小问1详解】设等比数列{}n a 的公比为0q >因为1231,1a S a ==-,即1231a a a +=-可得211q q +=-,整理得220q q --=,解得2q =或1q =-(舍去)所以122112nn n S -==--.【小问2详解】(i )由(1)可知12n n a -=,且N*,2k k ∈≥当124k k n a +=≥=时,则111221111k k k k k a n n a a -++⎧=<-=-⎨-=-<⎩,即11k k a n a +<-<可知12,1k k n a b k -==+()()()1111222121k k k n a k k b b a a k k k k --+=+--⋅=+-=-可得()()()()1112112122120k n k n k k k k k k k k b k a b ---=--+=--≥--=-⋅≥-当且仅当2k =时,等号成立所以1n k n b a b -≥⋅;(ii )由(1)可知:1211n n n S a +=-=-若1n =,则111,1S b ==;若2n ≥,则112k k k a a -+-=当1221k k i -<≤-时,12i i b b k --=可知{}i b 为等差数列可得()()()111211112221122431434429k k k k k k k k i i b k k k k k -------=-⎡⎤=⋅+=⋅=---⎣⎦∑所以()()()232113141115424845431434499n n S n n i i n b n n -=-+⎡⎤=+⨯-⨯+⨯-⨯+⋅⋅⋅+---=⎣⎦∑且1n =,符合上式,综上所述:()131419n n S i i n b =-+=∑.20.【答案】(1)1y x =-(2){}2(3)证明过程见解析【小问1详解】由于()ln f x x x =,故()ln 1f x x ='+.所以()10f =,()11f '=,所以所求的切线经过()1,0,且斜率为1,故其方程为1y x =-.【小问2详解】设()1ln h t t t =--,则()111t h t t t'-=-=,从而当01t <<时()0h t '<,当1t >时()0h t '>.所以()h t 在(]0,1上递减,在[)1,+∞上递增,这就说明()()1h t h ≥,即1ln t t -≥,且等号成立当且仅当1t =.设()()12ln g t a t t =--,则()((ln 12ln f x a x x x a x x a x g ⎛⎫-=-=-=⋅ ⎪⎭⎝.当()0,x ∞∈+时的取值范围是()0,∞+,所以命题等价于对任意()0,t ∞∈+,都有()0g t ≥.一方面,若对任意()0,t ∞∈+,都有()0g t ≥,则对()0,t ∞∈+有()()()()112012ln 12ln 1212g t a t t a t a t at a t t t ⎛⎫≤=--=-+≤-+-=+-- ⎪⎝⎭取2t =,得01a ≤-,故10a ≥>.再取t =,得2022a a a ≤--=--=-,所以2a =.另一方面,若2a =,则对任意()0,t ∞∈+都有()()()212ln 20g t t t h t =--=≥,满足条件.综合以上两个方面,知a 的取值范围是{}2.【小问3详解】先证明一个结论:对0a b <<,有()()ln 1ln 1f b f a a b b a -+<<+-.证明:前面已经证明不等式1ln t t -≥,故ln ln ln ln ln ln ln 1ln 1b b b a a a b a a a b b b b b a b a a--=+=+<+---且1lnln ln ln ln ln ln ln 1ln 11a a b b a a b b b a b b a a a a a a b a b a b b ⎛⎫--- ⎪--⎝⎭=+=+>=+----所以ln ln ln 1ln 1b b a a a b b a -+<<+-,即()()ln 1ln 1f b f a a b b a-+<<+-.由()ln 1f x x ='+,可知当10e x <<时()0f x '<,当1ex >时()0f x '>.所以()f x 在10,e ⎛⎤ ⎥⎝⎦上递减,在1e ,⎡⎫+∞⎪⎢⎣⎭上递增.不妨设12x x ≤,下面分三种情况(其中有重合部分)证明本题结论.情况一:当1211e x x ≤≤<时,有()()()()()()122122121ln 1f x f x f x f x x x x x x -=-<+-<-<结论成立;情况二:当1210ex x <≤≤时,有()()()()12121122ln ln f x f x f x f x x x x x -=-=-.对任意的10,e c ⎛⎤∈ ⎥⎝⎦,设()ln ln x x x c c ϕ=--则()ln 1x x ϕ=++'由于()x ϕ'单调递增,且有1111111ln 1ln 11102e 2e e c c ϕ⎛⎫ ⎪=++<+=-= ⎪⎝⎭'且当2124ln 1x c c ≥-⎛⎫- ⎪⎝⎭,2c x >时,2ln 1c ≥-可知()2ln 1ln ln 102c x x c ϕ⎛⎫=++>++=-≥ ⎪⎝⎭'.所以()x ϕ'在()0,c 上存在零点0x ,再结合()x ϕ'单调递增,即知00x x <<时()0x ϕ'<,0x x c <<时()0x ϕ'>.故()x ϕ在(]00,x 上递减,在[]0,x c 上递增.①当0x x c ≤≤时,有()()0x c ϕϕ≤=;②当00x x <<时,112221e e f f c ⎛⎫=-≤-=< ⎪⎝⎭,故我们可以取1,1q c ⎫∈⎪⎭.从而当201c x q <<-时,>可得()1ln ln ln ln 0x x x c c c c c c q c ϕ⎫=--<--<--=-<⎪⎭.再根据()x ϕ在(]00,x 上递减,即知对00x x <<都有()0x ϕ<;综合①②可知对任意0x c <≤,都有()0x ϕ≤,即()ln ln 0x x x c c ϕ=--.根据10,e c ⎛⎤∈ ⎥⎝⎦和0x c <≤的任意性,取2c x =,1x x =,就得到1122ln ln 0x x x x --≤.所以()()()()12121122ln ln f x f x f x f x x x x x -=-=-≤.情况三:当12101ex x <≤≤<时,根据情况一和情况二的讨论,可得()11e f x f ⎛⎫-≤≤ ⎪⎝⎭,()21e f f x ⎛⎫-≤≤ ⎪⎝⎭而根据()f x 的单调性,知()()()1211e f x f x f x f ⎛⎫-≤- ⎪⎝⎭或()()()1221e f x f x f f x ⎛⎫-≤- ⎪⎝⎭.故一定有()()12f x f x -≤成立.综上,结论成立.。
“反三违”培训考试试题考试试卷及答案

“反三违”培训考试试题考试试卷(时间:45分钟满分:100分)一、选择题(每题3分,共计45分)1、“三违”是指()。
A、违章指挥违规作业违反纪律B、违反指挥违规作业违反纪律C、违章作业违反指挥违反劳动纪律D、违章指挥违章作业违反劳动纪律2、请问下列属于违章指挥的是()。
A、无特种作业操作证从事特种作业B、指挥员工在不具备安全条件的情况下冒险作业C、不按检查表要求检查D、物品存放不当3、请问下列属于违反劳动纪律的是()。
A、未组织开车前安全检查就安排开车B、酒后上岗、班中饮酒。
C、用手替代工具操作。
D、未进行动火安全分析或分析结果不合格进行作业。
4、未对新员工进行三级安全教育就安排其工作,属于()。
A、违章指挥B、违规作业C、违反劳动纪律5、强令使用公司超期未校验的安全阀属于()。
A、违章指挥B、违规作业C、违反劳动纪律6、串岗、脱岗、睡岗,在岗期间从事与岗位工作无关的事属于()。
A、违章指挥B、违规作业C、违反劳动纪律7、高处()米以上作业,必须系好安全带。
A、2.5B、3C、28、新入职员工必须接受()安全培训教育,经考核合格后方可上岗操作。
A、公司、车间B、公司、车间、班组C、车间、班组9、煤矿、非煤矿山、危险化学品、烟花爆竹、金属冶炼等生产经营单位新上岗的从业人员安全培训时间不得少于()学时,每年再培训的时间不得少于()学时。
( )A、72、20B、72、30C、72、2410、《安全生产法》规定企业最基本的安全生产管理制度是()。
A、安全生产责任制B、安全生产奖惩制度C、安全培训教育制度11、对()人员进行紧急救护时不能进行人工呼吸。
A、有毒气体中毒B、触电假死C、溺水12、根据《化学品生产单位特殊作业安全规范》(GB30871)规定,()(含)级风以上天气,原则上禁止露天动火作业。
因生产确需动火,动火作业应升级管理。
A、四B、五C、六13、I级高处作业为()。
A、2 m≤ h≤5 mB、5m<h≤15 mC、l5 m<h ≤30 mD、h > 30 m14、生产经营单位的()对本单位的安全生产工作全面负责。
黑龙江省绥化市第二中学2024-2025学年高二上学期期中考试生物学试题(含答案)

绥化市第二中学2024—2025学年度高二学年上学期期中考试生物本试卷满分100分,考试时间75分钟。
一、选择题(本题共15小题,每题2分,共30分。
在每小题给出的四个选项中,只有一项符合题目要求。
)1.如图表示人体体液各成分之间的相互关系,下列相关叙述错误的是()A.a与b、c、d相比,含有较多的蛋白质和Na+B.b到d的组成成分,与d到b的组成成分不同C.d中含有糖类、脂质、蛋白质、尿素等化学成分D.甲状腺激素可以存在于b中2.细胞是生命活动的基本单位,并与其生活的环境之间不断进行着物质和能量的交换。
下列相关叙述正确的是()A.单细胞生物都只能生活在水中,并从水中获取营养物质和氧气B.组织液是绝大多数细胞直接生活的环境,血浆是血细胞直接生活的环境C.细胞内液和细胞外液都属于体液,其中细胞外液约占体液的2/3D.抽搐、镰状细胞贫血都是内环境成分发生明显变化而引起的病症3.如图表示某人从初进高原到完全适应,其体内血液中乳酸浓度的变化曲线,下列对AB段和BC段变化原因的分析,正确的是()A.AB段上升是因为人初进高原,呼吸频率加快造成的B.由于产生大量乳酸,因此血浆的PH将由碱性变为酸性C.AB段产生的乳酸,在BC段与NaHCO3反应D.AB段上升过程中人体主要进行无氧呼吸,BC段下降过程中主要进行有氧呼吸4.下列关于内环境稳态的叙述,错误的是()A.实现内环境稳态的基础是人体各器官、系统协调一致地正常运行B.内环境稳态是进行正常生命活动的必要条件C.内环境稳态指的是各种化学成分和理化性质保持不变D.内环境稳态失调会引发疾病5.正确地运用机械刺激如抚拍、拉追踪绳等,能使警犬对所训练科目的口令快速产生条件反射。
下列相关叙述错误的是()A.反射活动产生的兴奋可以在低级中枢与高级中枢内传导B.条件反射一定需要中枢神经系统参与,非条件反射则不一定需要中枢神经系统参与C.反复仅给口令不给予机械刺激,该条件反射会消退,需大脑皮层参与D.条件反射建立前口令称为无关刺激,条件反射建立后口令称为条件刺激6.如图所示,当神经冲动在轴突上传导时,下列叙述错误的是甲()A.甲区域与丙区域可能刚恢复为静息电位B.乙区域与丁区域间膜内局部电流的方向是从乙到丁C.丁区是静息电位,因此没有离子的移动D.图示神经冲动的传导方向有可能是从左到右或从右到左7.神经递质作为信号分子,发挥完作用后其去向主要有两种,如图所示。
电工考试试题试卷及答案

电工考试试题试卷及答案一、单项选择题(每题2分,共20分)1. 电流通过电阻时,电阻两端的电压与电流的比值称为电阻的()。
A. 电阻率B. 电导C. 电阻D. 电势差答案:C2. 交流电路中,电流的有效值是指()。
A. 最大值B. 平均值C. 瞬时值D. 有效值答案:D3. 电路中的功率因数是指()。
A. 电压与电流的相位差B. 电压与电流的比值C. 电压与电流的有效值的比值D. 电压与电流的瞬时值的比值答案:C4. 星形连接的三相电路中,线电压与相电压的关系是()。
A. 相电压是线电压的√3倍B. 线电压是相电压的√3倍C. 相电压等于线电压D. 线电压等于相电压答案:B5. 并联电路中,各支路电流之和等于()。
A. 总电流B. 总电压C. 总电阻D. 总电导答案:A6. 电路中,欧姆定律的数学表达式是()。
A. V = IRB. I = V/RC. R = V/ID. V = I * R答案:A7. 电容器的单位是()。
A. 欧姆B. 法拉C. 亨利D. 西门子答案:B8. 电感器的单位是()。
A. 欧姆B. 亨利C. 法拉D. 西门子答案:B9. 交流电路中,电感的感抗与频率的关系是()。
A. 与频率成正比B. 与频率成反比C. 与频率无关D. 与频率的平方成正比答案:A10. 交流电路中,电容的容抗与频率的关系是()。
A. 与频率成正比B. 与频率成反比C. 与频率无关D. 与频率的平方成反比答案:B二、多项选择题(每题3分,共15分)1. 以下哪些属于电路的基本组成部分?()A. 电源B. 负载C. 开关D. 导线答案:A, B, C, D2. 电路中,哪些因素会影响电路的总电阻?()A. 电阻的数量B. 电阻的阻值C. 电阻的连接方式D. 电源的电压答案:A, B, C3. 以下哪些是电路中常用的保护元件?()A. 保险丝B. 断路器C. 过载保护器D. 变压器答案:A, B, C4. 以下哪些属于电磁感应现象的应用?()A. 变压器B. 发电机C. 电动机D. 电感器答案:A, B5. 以下哪些属于电路中的储能元件?()A. 电容器B. 电感器C. 电阻器D. 二极管答案:A, B三、判断题(每题2分,共10分)1. 电路中的电流总是从高电位流向低电位。
(完整版)微生物考试试题(附答案)

试卷一一.选择题(每个2分,共20分)1、组成病毒粒子衣壳的化学物质是()A、糖类B、蛋白质C、核酸D、脂肪2、属于细菌细胞特殊结构的为()A、荚膜B、细胞壁C、细胞膜D、核质体3、噬菌体属于病毒类别中的()A、微生物病毒B、昆虫病毒C、植物病毒D、动物病毒4、半固体培养基中,琼脂使用浓度为()。
A、0B、0.3—0.5%C、1.5—2.0%D、5%6.下述那个时期细菌群体倍增时间最快 ( )A 稳定期B 衰亡期C 对数期D 延滞期7.下面关于连续培养的说法中,叙述不正确的是()A.恒化连续培养的控制对象是菌体密度B.恒浊连续培养中微生物菌体以最高生长速率生长C.恒化连续培养的产物是不同生长速率的菌体D.恒浊连续培养无生长限制因子8. 下列叙述中正确的说法是()A.产生抗逆性强的芽孢是产芽孢细菌在不良环境条件下的一种生殖方式。
B.厌氧的微生物需要较低的氧化还原电位。
C.一种细菌的学名是Staphylococcus aureus,其中aureus属名,Staphyloccus是种名D.类病毒是有侵染性的蛋白颗粒。
9.下述诱变剂中常引起移码突变的是:()A 亚硝酸B 烷化剂C 碱基类似物D 丫啶类染料10.下述那个最可能产生一个重组细胞:()A F+ x F-B Hfr x F+C Hfr x F-D F+ xF-二、写出下列名词解释的中文翻译及作出解释(每个2分,共12分)1.Gram positive bacteria2.parasporal crystal3 ,colony4, life cycle5,capsule6,endospore三、判断改错题(每个2分,共10分)1.大肠杆菌和枯草芽孢杆菌属于单细胞生物,唾液链球菌和金黄色葡萄球菌属于多细胞生物()2.遗传型相同的个体在不同环境条件下会有不同的表现型。
()3.低剂量照射紫外线,对微生物几乎没有影响,但以超过某一阈值剂量的紫外线照射,则会导致微生物的基因突变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
综合素质试题一1、教师专业情意发展成熟的标志是教师的()。
A专业理想B专业情操C专业性向D.专业自我2、人本位儿童观认为()。
A. 儿童是家族繁衍的工具B. 儿童是父母的私有财产C. 儿童是国家的财富D. 儿童享有生存权、发展权、教育权3、实现了几何和代数结合的是()。
A. 笛卡尔创立解析几何学B. 牛顿建立微积分学C.莱布尼茨建立微积分学D. 哥白尼创立太阳中心说4、中国历史上最大的一部百科全书是()。
A. 《资治通鉴》B. 《永乐大典》C. 《古今图书集成》D. 《四库全书》5、下列关于多媒体的叙述,错误的是()。
A. 多媒体是指信息表示和传播的载体,它向人们传递各种信息B. 多媒体计算机系统就是有声卡的计算机系统C. 多媒体技术是指计算机技术把多媒体综合一体化,并进行加工处理的技术D. 多媒体技术要求各种媒体都必须数字化6、利用搜索引擎检索教学资源时,通常用加号“+”或空格表示的逻辑关系是()。
A.逻辑“或”B. 逻辑“与”C. 逻辑“非”D. 字符串7、最早提出教师要做“人类灵魂的工程师”的是前苏联的()。
A.加里宁B.列宁C.凯洛夫D.赞可夫8、可用来为教育实践活动提供行动规范、价值观的教育定义属于()。
A.约定性定义B.描述性定义C.纲领性定义D.操作性定义9、测验题目对预测的内容或行为范围取样的适宜性程度,被称为()。
A.效标关联效度B.预测效度C.构想效度D.内容效度10、下列关于美育的说法,哪个是不正确的()。
A.美育就是“育美”B.美育又叫美学教育或审美教育C.美育就是对学生进行艺术教育D.美育是全面发展教育的升华,为全面发展提供审美保证11、“孟母三迁”体现了()对个体成长的影响。
A.环境B.家庭C.社会D.学校12、《论语》有言:“天何言哉?四时行焉,百物生焉。
天何言哉?”这体现在教育中即()。
A.行不言之教B.因材施教C.情境陶冶D.身体力行13、将教育者与受教育者连接起来的媒介是()。
A.教育内容B.教育环境C.教育影响D.教育目标14、CAI指的是()。
A.计算机辅助设计软件B.自动办公系统C.计算机辅助教学D.系统软件15、素质教育的核心和灵魂是()。
A.德育B.创新教育C.智育D.全面发展教育16、教师和学生在社会道德上是()的关系。
A.上下级B.平等C.授受D.相互促进17、我国《教育法》规定公民“依法享有平等的受教育的机会”。
这体现了素质教育的()。
A.全体性B.基础性C.发展性D.全面性18、()提出了教师成长公式:经验+反思=成长。
A.布鲁纳B.波斯纳C.布鲁巴奇D.科顿19、可用来为教育实践活动提供行动规范、价值观的教育定义属于()。
A. 约定性定义B. 描述性定义C. 纲领性定义D. 操作性定义20、最早提出教师要做“人类灵魂的工程师”的是前苏联的()。
A. 加里宁B. 列宁C. 凯洛夫D. 赞可夫21、教师素质的核心是()。
A. 教师的人格素养B. 教师的知识水平C. 教师的专业能力D. 教师的科学素养22、“建安七子”中,文学成就最高的是()。
A. 陈琳B. 曹植C. 曹丕D. 王粲23、建设有中国特色社会主义文化的根本任务是()。
A. 促进人的全面发展B. 提高人的道德素质C. 提高全民族的科学文化水平D. 在全社会形成共同的理想和精神支柱24、实际意义取决于特定的语言环境,人们要在特定的语言环境中才能理解的是()。
A. 约定性定义B. 描述性定义C. 纲领性定义D. 操作性定义25、我国教育家()在《师说》中说:“师者,所以传道、授业、解惑也。
”A.孔子B.荀子C.孟子D.韩愈26、学校进行全面发展教育的基本途径是()。
A.教育与生产劳动相结合B.思想政治教育C.课外活动D.教学27、不属于对中小学教师的职业道德要求的是()。
A.依法执教B.爱岗敬业C.热爱学生D.严谨治学28、现代教育与传统教育的根本区别在于()。
A.重视实践能力的培养B.重视创新能力的培养C.重视高尚品德的培养D.重视劳动品质的培养29、在古代社会,“才高八斗”和“学富五车”体现的是教师的()。
A.道德形象B.人格形象C.财富形象D.文化形象30、义务教育法对义务教育阶段学校收费的规定是()。
A.收学费,不收杂费B.不收学费、杂费C.不收书本费、杂费D.收学费,不收杂费31、下列哪句说法是错误的?()A.素质教育是指以促进知识深刻内化为目标B.以全面传授更有价值的知识为基础C.以激活每一位受教育者的个性潜能发展为核心32、构建素质教育目标,必须遵循青少年儿童身心素质发展的(),才能保证目标的科学性、可行性。
A.顺序B.客观规律C.特征D.重点33、()中关于教师素质的规定是制定和执行教师素质要求的根本依据。
A.《教师法》B.《高等教育法》C.《义务教育法》D.《教育法》34、按测验的目的分类可分为诊断性测验、终结性测验和()。
A.形成性测验B.个别测验C.人格测验D.常模参照测验35、我国《教师法》的颁布实施是在()年。
A.1993B.1995C.1998D.198536、按测验的功用分类可分为学绩测验、能力测验、()。
A.人格测验B.个别测验C.团体测验D.常模参照测验37、《义务教育法》规定,实施义务教育的公办学校实行()。
1 / 6A.党支部领导下的校长分工负责制B.校长负责制C.教职工代表大会负责制不D.校务委员会负责制38、按测验的功用分类可分为学绩测验、能力测验、()。
A.人格测验B.个别测验C.团体测验D.常模参照测验39、金某(15周岁)在课间因小事与同学沈某发生争执,金某一拳击中沈某头部,致使沈某倒地,送医院不洽死亡,问金某应当负什么责任?()A.应负相对刑事责任B.不应负刑事责任C.应负完全刑事责任D.应负刑事责任40、我国实行的是九年义务教育制度。
新修订的《中华人民共和国义务教育法》共有()章六十三条。
A.八B.七C.六D.九41、在我国教育管理体制上,《教育法》规定我国教育实行()原则A.统一管理B.分级管理C.分工负责D.分级管理.分工负责42、下列关于义务教育均衡发展的说法,哪种是错误的()。
A.县级以上人民政府及其教育行政部门不得将学校分为重点学校和非重点学校B.县级以上人民政府及其教育行政部门不得以任何名义改变或者变相改变公办学校的性质C.学校不得分重点班与非重点班D.县级人民政府编制预算应当均衡安排义务教育经费,不得向任何学校倾斜。
43、人民法院审判未成年人犯罪的刑事案件,应当由熟悉未成年人身心特点的审判员或者审判员和人民陪审员依法组成少年法庭进行。
对于()未成年人犯罪的案件,一律不公开审理。
A.已满14周岁不满16周岁B.已满16周岁不满18周岁C.已满15周岁不满17周岁D.已满18周岁不满20周岁44、班主任工作量按当地教师标准课时工作量的()计入教师基本工作量。
A.全部B.四分之三C.一半D.三分之一45.根据《中华人民共和国教育法》的规定,中等及中等以下教育在国务院领导下,由()管理。
A.教育部门B.学校自己C.地方人民政府D.国务院行政部门46、教师的平均工资水平应当()当地公务员的平均工资水平。
A.高于B.等同于C.低于D.不低于47、目前通行的《中华人民共和国教育法》是自()开始施行的。
A.2006年12月29日B.2006年6月29日C.1995年9月1日D.1994年1月1日48、县级人民政府教育行政部门应当均衡配置本行政区域内学校师资力量,组织校长教师的(),加强对薄弱学校的建设。
A.学习和培训B.沟通和合作C.培训和流动D.交流和互访49、基础教育管理权属于()。
A.学校B.地方C.中央D.家庭50、外籍教师的聘任办法由()规定。
A.国务院B.国家教育部C.国务院教育行政部门D.学校自行51、教师在未经学生同意的情况下,私自拆阅或者毁坏学生的日记、信件,这侵犯了学生()的权利。
A.安全B.受教育C.受尊重D.人身自由52、我国首次以法律形式明确规定“国家实行教师资格制度”的法规是()。
A.《中华人民共和国教师资格条例》B.《中华人民共和国教师法》C.《中华人民共和国义务教育法》D.《中华人民共和国教育法》53、地方人民政府对违反《教师法》规定,拖欠教师工资或者侵犯教师其他合法权益的,应当()。
A.责令其限期改正B.给予行政处分C.依法追究刑事责任D.对其处以罚款并责令改正54、希望广大教师爱岗敬业、关爱学生,刻苦钻研、严谨笃学。
勇于创新、奋发进取,淡泊名利、志存高远,这些话是()提出来的。
A.邓小平B.胡锦涛C.江泽民D.温家宝55、第一次提出“国家实行教师资格制度”的国家法律文件是()。
A.《教师资格条例》B.《教师资格认定的过渡办法》C.《(教师资格条例)实施办法》D.《中华人民共和国教师法》56、“青少年、儿童是社会未来,人类的希望,有着独立的社会地位,是行使权利的主体。
”这是()。
A.《儿童权利公约》的核心精神B.《全面推进素质教育的决定》的核心精神C.《义务教育法》的核心精神D.《未成年人保护法》的核心精神57、1995年颁布的是()。
A.《中华人民共和国义务教育法》B.《中华人民共和国教师法》C.《中华人民共和国教育法》D.《中华人民共和国职业教育法》58、1986年,我国颁布了()。
A.《中华人民共和国学位条例》B.《中华人民共和国高等教育法》C.《中华人民共和国义务教育法》D.《中华人民共和国教育法》59、教师的任用方式一般有三种,它们是派用制、聘用制和()。
A.代用制B.自用制C.长用制D.暂用制60、()把教育和科技列为经济建设的三大战略重点之一。
A.十二大B.十三大C.十四大,D.十五大61、我国的《教师法》颁布于()。
A.1991年B.1992年C.1993年D.1994年62、党的十六大报告指出,教育是发展科学技术和培养人才的基础,在现代化建设中具有()的作用。
A.基础性B.前瞻性C.先导性、全局性D.普及性63、教师职业道德在全社会道德体系中处于()和主干地位。
A.重要B.首要C.核心D.完全64、“你怎么这么懒?还不快去做作业!”属于()。
A.沟通本意是“想了解学生的心理反应”却变成了“斥责”B.沟通本意是“指导”却变成了“命令”C.沟通本意是“提醒”却变成了“批评”D.沟通本意是“想了解学生的状态”却变成了“催促”65、中小学教师职业道德建设在教师对待教育事业的较高道德目标是()。
A.献身于人民的教育事业B.忠于职守,为人师表,积极进取C.热爱教育事业D.为教育事业奋斗终身66、课堂教学要紧密联系学生的(),从学生的经验和已有知识出发,创设有助于学生自主学习,合作交流的情境。
A.生活环境B.社会环境C.实际问题D.现实问题67、现行的《中小学教师职业道德规范》共()。
