DES算法实现过程分析
DES算法实现过程分析

DES算法实现过程分析【摘要】DES算法是一种经典的对称加密算法,本文对其实现过程进行了深入分析。
首先介绍了DES算法的基本概念,包括密钥长度、明文长度等。
然后详细描述了密钥生成过程以及初始置换过程,为后续的Feistel网络结构和轮函数打下基础。
Feistel网络结构是DES算法的核心,是一种将明文分成两部分并交替进行加密的结构。
轮函数则是Feistel网络中的关键部分,负责将一个子密钥应用到数据块上。
文章对DES算法实现过程进行了总结,并对其安全性进行评估。
未来发展方向包括对更高级的加密算法的研究和应用。
DES算法实现过程的深入分析可以帮助读者更好地理解和应用该算法。
【关键词】DES算法、实现过程、分析、基本概念、密钥生成过程、初始置换、Feistel网络结构、轮函数、总结、安全性评估、未来发展方向1. 引言1.1 DES算法实现过程分析DES算法是一种对称密码算法,广泛应用于数据加密领域。
其实现过程涉及到一系列复杂的步骤,包括密钥生成、初始置换、Feistel 网络结构以及轮函数。
本文将对DES算法的实现过程进行深入分析,以便读者更好地理解其工作原理。
在DES算法中,密钥生成过程是非常重要的一环,它决定了加密过程中所使用的密钥。
密钥生成过程通过将原始密钥进行置换和轮转操作,生成出多个子密钥,用于不同轮次的加密运算。
初始置换阶段将输入的64位数据按照一定规则重新排列,以便后续Feistel网络结构的处理。
Feistel网络结构是DES算法的核心部分,采用了多轮迭代加密的方式,每轮中都会使用不同的子密钥进行加密和解密操作。
轮函数通过一系列的代换和置换操作,将输入的数据与子密钥进行混合,得到加密后的输出。
经过多轮的轮函数处理,最终得到加密后的密文。
2. 正文2.1 基本概念DES算法是一种对称密钥加密算法,其全称为Data Encryption Standard,由IBM公司在1975年设计并发布。
三轮DES差分分析实验报告-刘杰
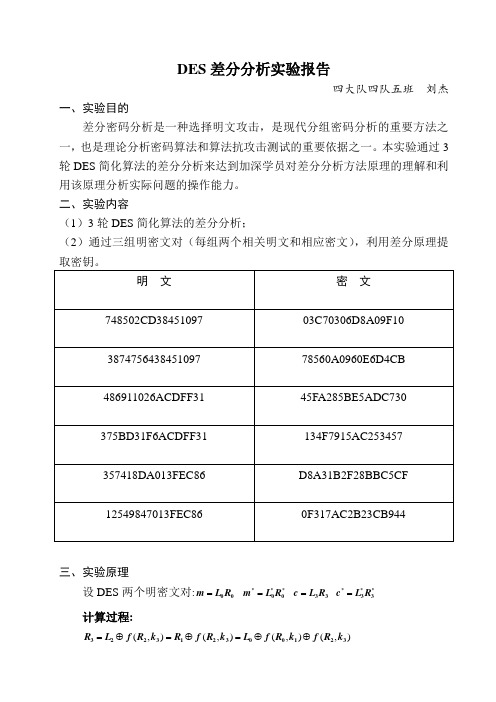
DES 差分分析实验报告四大队四队五班 刘杰一、实验目的差分密码分析是一种选择明文攻击,是现代分组密码分析的重要方法之一,也是理论分析密码算法和算法抗攻击测试的重要依据之一。
本实验通过3轮DES 简化算法的差分分析来达到加深学员对差分分析方法原理的理解和利用该原理分析实际问题的操作能力。
二、实验内容(1)3轮DES 简化算法的差分分析;(2)通过三组明密文对(每组两个相关明文和相应密文),利用差分原理提三、实验原理设DES 两个明密文对:=00m L R ***=00m L R =33c L R ***=33c L R计算过程:(,)(,)(,)(,)=⊕=⊕=⊕⊕322312300123R L f R k R f R k L f R k f R k(,)(,)****=⊕⊕300123R L f R k f R k令:*'=⊕000L L L (,)(,)(,)(,)***''=⊕=⊕⊕⊕⊕333001012323R R R L f R k f R k f R k f R k 观察得:在本次实验原始数据中,明文对*=00R R ,即*'=⊕=00000000000R R R 则(,)(,)**''=⊕=⊕⊕33302323R R R L f R k f R k 同时有:=00m L R ***=00m L R =23R L **=23R L则可计算出:*'=⊕000L L L *'=⊕333R R R (,)(,)*''⊕=⊕232330f R k f R k R L则可得出:S 盒输入差:(())(())()()**⊕⊕⊕=⊕232333E R k E R k E L E LS 盒输出差:()*-''⊕=⊕130D D P R L分析过程:令:()()*⊕=3312345678E L E L B B B B B B B B()-''⊕=13012345678P R L C C C C C C C C ()=312345678E L A A A A A A A A =312345678k J J J J J J J J()⊕=3312345678E L k X X X X X X X X *()⊕=3312345678E L k Y Y Y Y Y Y Y Y基本思路:(分别计算12345678J J J J J J J J ){|,()()}∈=⊕⊕=⊕=i i i i i i i J Test x A x y B S x S y C ,,,,,,,=12345678i对于本次实验的3个具有明文差(*,0)的明密文对,则可构造上面的3个Test 集合,显然 ()()()∈12i i i i J Test Test Test t ,,,,,,,=12345678i一种确定Ji 的直接方法:1.建立26=64长度的数组J[64]={0};2.对Testi(r),r = 1,2,…,t ,若a ∈Testi(r),则 J[a] = J[a] + 1。
【精品】DES算法实验报告

【精品】DES算法实验报告一、理论部分DES算法是一种对称加密算法,也是目前广泛应用的加密算法之一。
DES算法使用的是分组加密的思想,将明文数据分成一定长度的数据块,按照一定的算法进行加密,得到密文数据。
DES算法中的关键是密钥,只有持有正确密钥的人才能解密。
DES算法的密钥长度为64位,但由于存在弱密钥的问题,使用时需要特别注意。
DES算法的加密过程包括以下几个步骤:1、密钥的生成和处理:DES算法的密钥长度为64位,但由于存在弱密钥的问题,使用时需要使用程序进行特殊处理,以确保生成的密钥不为弱密钥。
2、初始置换(IP):将明文数据按照一定的规则进行置换,得到置换后的数据。
3、分组:将置换后的明文数据分成左半部分和右半部分。
4、轮函数(f函数):将右半部分进行扩展置换、异或运算、S盒代替、置换等操作,得到一个新的右半部分。
5、轮秘钥生成:生成本轮加密所需要的秘钥。
6、异或运算:将左半部分和右半部分进行异或运算,得到一个新的左半部分。
7、左右交换:将左右部分进行交换。
以上步骤循环执行16次,直到得到最终的密文数据。
二、实验部分本次实验使用C语言实现了DES算法的加密和解密过程。
具体实现过程包括以下几个部分:1、密钥的生成:使用DES算法生成64位密钥,其中包括了对弱密钥的处理。
2、置换:使用DES算法中的IP置换和IP逆置换进行数据置换。
3、轮函数:使用DES算法中的f函数进行一轮加密操作。
5、加密:循环执行16轮加密操作,得到密文数据。
以上实现过程全部基于DES算法的规范。
三、结果分析1、速度慢:由于DES算法采用的是分组加密的思想,需要执行多次操作才能得到最终结果。
因此本次实验的加密和解密速度相对较慢。
2、代码简单:本次实验的代码相对简单,只需要用到一些基本数据结构和算法即可实现DES算法的加密和解密过程。
但需要注意的是,由于DES算法本身的复杂性,代码实现中需要注意细节和边界问题。
四、总结本次实验使用C语言实现了DES算法的加密和解密过程,通过实验得到了一些结果。
DES算法及其工作模式分析

DES算法及其工作模式分析褚慧丽中南财经政法大学信息管理与信息系统专业2009级[摘要] 现代密码学的发展经过了一个漫长而复杂的过程,在这过程中出现了一系列经典而高效的加密体制。
DES作为分组密码的典型代表,对密码学的发展做出了重要的贡献。
本文主要介绍了DES的概况,并对它的算法进行描述,找出它的设计思想和特点,分析它的安全性。
在此基础上,进一步介绍了DES的工作模式。
[关键词] 分组密码信息安全 DES 演化密码对称密码1.概况1.1DES简介DES算法是由IBM公司在20世纪70年代发展起来的,于1976年11月被美国政府采用,随后被美国国家标准局和美国国家标准协会承认,同时也成为全球范围内事实上的工业标准。
DES算法作为分组密码的代表,已成为金融界及其他各种行业广泛应用的对称密钥密码系统。
它以feistel网络结构理论为基础,采用迭代分组形式,在提高算法的运行速度,改善了密码的实用性的同时,也大大的提高了密码的安全性,对于我们研究密码学以及展望密码学的发展方向有重要意义。
1.2算法描述DES使用56位密钥对64位的数据块进行加密,并对64位的数据块进行16轮编码。
在每轮编码中,一个48位的密钥值由56位的“种子”密钥得出来。
DES算法把64位的明文输入快变成64位的密文输出块,整个算法的变换过程如图1.1所示。
图1.1 DES算法框图图中描述的是DES的加密过程。
而解密和加密过程大致相同,不同之处仅在于右边的16个子密钥的使用顺序不同,加密的子密钥的顺序为K1,K2,…,K16,而解密的子密钥的使用顺序则为K16,K15,…,K1。
IP即初始换位的功能是把输入的64位明文数据块按位重新组合,并把输出分为L0,R0两部分,每部分各长32位。
其置换规则如表1.1所示。
表1.1 DES算法初始换位规则表即将输入的64位数据的第58位换到第1位,第50位换到第2位......依此类推。
设置换前的输入值为D1D2...D64,则经过初始换位后的结果为:L0=D58D50...D8,R0=D57D49 (7)经过初始换位后,将R0与密钥发生器产生的密钥K1进行计算,其结果记为f(R0,K1)再与L0进行异或运算得到L0⊕f(R0,K1),把R0记为L1放在左边,把L0⊕f(R0,K1)记为R1放在右边,从而完成了第一次迭代运算。
SM4算法、AES算法、DES算法三种分组密码的基础分析

SM4算法、AES算法、DES算法三种分组密码的基础分析 分组密码当中代表性的SM4算法、AES算法、DES算法在计算机和通信系统中起着重要的实际作用,每一种的算法都会有其独有的一份结构,讲解起来其实每一种都有很大的一个篇幅。
在这里主要是把这几种密码算法放在一起做一个简单的分析,也可以通过了解每一种算法来比较一下三者之间的差别。
那么,我们就通过了解SM4算法、AES算法、DES算法这几种有代表性的近代分组密码来讨论一下分组密码的基本理论及其在计算机和通信系统中的实际应用。
1、SM4算法 SM4密码算法是一个分组算法,其算法设计简沽,结构有特点,安全高效。
数据分组长度为128比特,密钥长度为128比特。
加密算法与密钥扩展算法均采取32轮迭代结构。
SM4密码算法以字节8位和字节32位作为单位进行数据处理。
SM4密码算法是对合运算,因此解密算法与加密算法的结构相同,只是轮密钥的使用顺序相反,解密轮密钥是加密轮密钥的逆序。
SM4密码算法结构 SM4算法的基本内容有以下几方面: 基本运算:SM4密码算法使用模2加和循环移位作为基本运算。
基本密码部件:SM4密码算法使用了S盒、非线性变换τ、线性变换部件L、合成变换T基本密码部件。
轮函数:SM4密码算法采用对基本轮函数进行迭代的结构。
利用上述基本密码部件,便可构成轮函数。
SM4密码算法的轮函数是一种以字为处理单位的密码函数。
加密算法:SM4密码算法是一个分组算法。
数据分组长度为128比特,密钥长度为128比特。
加密算法采用32轮迭代结构,每轮使用一个轮密钥。
解密算法:SM4密码算法是对合运算,因此解密算法与加密算法的结构相同,只是轮密铝的使用顺序相反,解密轮密钥是加密轮密钥的逆序。
密钥扩展算法:SM4密码算法使用128位的加密密钥,并采用32轮法代加密结构,每一轮加密使用一个32位的轮密钥,共使用32个轮密钥。
因此需要使用密钥扩展算法,从加密密钥产生出32个轮密钥。
DES算法的详细分析

DES算法的详细分析DES(Data Encryption Standard)是一种对称加密算法,是美国联邦政府使用的加密标准。
它采用了分组密码的方式对数据进行加密和解密处理。
本文将对DES算法进行详细分析,涵盖算法原理、加密过程、密钥生成、弱点以及DES的安全性评估等方面。
1.算法原理:-将明文数据分成64位的分组,使用64位密钥进行加密。
-密钥通过密钥生成算法进行处理,生成16个48位的子密钥。
-明文分为左右两半部分,每轮加密时,右半部分与子密钥进行逻辑运算,并与左半部分进行异或操作。
-运算结果作为下一轮的右半部分,左半部分不变。
循环16轮后得到密文。
2.加密过程:-初始置换(IP):将64位明文按照预定的规则进行位重排。
-分为左右两半部分L0,R0。
-通过16轮的迭代过程,每轮使用不同的48位子密钥对右半部分进行扩展置换(E盒扩展),与子密钥进行异或操作,再通过S盒代换和P 盒置换输出。
-将经过迭代的左右两半部分进行交换。
-最后经过逆初始置换(IP^-1)后输出64位密文。
3.密钥生成:-密钥生成算法从初始64位密钥中减小奇偶校验位,然后使用置换选择1(PC-1)表对密钥进行位重排,得到56位密钥。
-将56位密钥分为两部分,每部分28位,并进行循环左移操作,得到16个48位的子密钥。
4.弱点:-DES算法的密钥长度较短,只有56位有效位,容易受到穷举攻击。
-由于DES算法设计时的数据量较小,运算速度较快,使得密码破解更加容易。
-DES算法对明文的局部统计特性没有进行充分的打乱,可能导致部分明文模式的加密结果不够随机。
5.DES的安全性评估:-DES算法的弱点导致了它在现代密码学中的安全性问题,已经不再适用于高强度加密要求的场景。
- 美国国家标准与技术研究所(NIST)发布了Advanced Encryption Standard(AES)来替代DES作为加密标准。
-DES算法可以用于低安全性需求的领域,或作为加密算法的组成部分。
DES算法实验报告

DES算法实验报告DES (Data Encryption Standard)算法是一种对称密钥加密算法,由IBM于1970s年代开发。
它是加密领域的经典算法之一,被广泛应用于安全通信和数据保护领域。
本实验报告将介绍DES算法的原理、实现和安全性分析。
一、DES算法原理1.初始置换(IP置换):将输入的64位明文进行初始置换,得到一个新的64位数据块。
2.加密轮函数:DES算法共有16轮加密,每轮加密包括3个步骤:扩展置换、密钥混合、S盒置换。
扩展置换:将32位数据扩展为48位,并与轮密钥进行异或运算。
密钥混合:将异或运算结果分为8组,每组6位,并根据S盒表进行置换。
S盒置换:将6位数据分为两部分,分别代表行和列,通过查表得到一个4位结果,并合并为32位数据。
3. Feistel网络:DES算法采用了Feistel网络结构,将32位数据块分为左右两部分,并对右半部分进行加密处理。
4.置换:将加密后的左右两部分置换位置。
5.逆初始置换:将置换后的数据进行逆初始置换,得到加密后的64位密文。
二、DES算法实现本实验使用Python编程语言实现了DES算法的加密和解密功能。
以下是加密和解密的具体实现过程:加密过程:1.初始化密钥:使用一个64位的密钥,通过PC-1表进行置换,生成56位的初始密钥。
2.生成子密钥:根据初始密钥,通过16次的循环左移和PC-2表进行置换,生成16个48位的子密钥。
3.初始置换:对输入的明文进行初始置换,生成64位的数据块。
4.加密轮函数:对初始置换的数据块进行16轮的加密操作,包括扩展置换、密钥混合和S盒置换。
5.逆初始置换:对加密后的数据块进行逆初始置换,生成加密后的64位密文。
解密过程:1.初始化密钥:使用相同的密钥,通过PC-1表进行置换,生成56位的初始密钥。
2.生成子密钥:根据初始密钥,通过16次的循环左移和PC-2表进行置换,生成16个48位的子密钥。
3.初始置换:对输入的密文进行初始置换,生成64位的数据块。
ctf中des的题

ctf中des的题DES是一种对称加密算法,它在CTF竞赛中常常被用作题目的一部分。
下面将介绍一些关于CTF中DES题目的基本知识以及解题思路。
## DES简介DES(Data Encryption Standard)是一种对称密钥加密算法,它是美国国家标准局(NIST)于1977年发布的算法。
DES的密钥长度为56位,明文长度为64位。
DES算法由一系列置换、替代和变换操作组成,可以实现高强度的数据加密。
在CTF中,DES题目通常以加密算法的参数和密文给出,要求我们还原出明文或找到加密算法中的弱点。
解题的关键在于理解DES的工作原理和算法流程。
## DES算法流程DES算法的加密过程主要分为以下几个步骤:1. 初始置换:将输入的64位明文按照指定的置换表进行置换,生成置换后的数据块。
2. 迭代运算:将置换后的数据块分为左右两半,迭代运算一共进行16轮。
每轮的运算过程包括:对右半部分进行扩展置换、与轮密钥进行异或、通过S盒替换、进行P盒置换和左右半部分的交换。
3. 逆初始置换:将16轮迭代运算后的数据块再次按照指定的逆置换表进行置换,得到最终的加密结果。
解密过程与加密过程类似,只是在迭代运算中使用的密钥顺序相反。
## DES的弱点尽管DES在发布时被认为是非常安全的加密算法,但随着计算机技术的发展,其密钥长度逐渐显得不够安全。
DES的密钥长度只有56位,尽管每轮迭代中使用的轮密钥是由56位密钥生成的,但由于密钥空间的限制,理论上存在暴力破解攻击的可能。
另外,DES的其他一些弱点包括:1. 已知明文攻击:攻击者拥有一些已知明文和对应的密文对,利用这些信息可以在不知道密钥的情况下推导出其他密文的密钥。
2. 密钥编排:DES加密算法中使用的轮密钥是通过56位密钥进行生成的,如果密钥在生成过程中存在弱点,那么整个加密过程就会受到影响。
3. 无法抵抗差分分析攻击:差分分析攻击是一种利用DES算法的性质和特点进行破解的攻击方法,DES算法对差分分析攻击并不具备足够的抵抗能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
DES算法实现过程分析来源:中国论文下载中心 [ 03-03-18 14:30:00 ] 作者:本站会员编辑:丢oO丢oO1. 处理密钥:1.1 从用户处获得64位密钥.(每第8位为校验位,为使密钥有正确的奇偶校验,每个密钥要有奇数个”1”位.(本文如未特指,均指二进制位)1.2 具体过程:1.2.1 对密钥实施变换,使得变换以后的密钥的各个位与原密钥位对应关系如下表所示:表一为忽略校验位以后情况1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 2857 49 41 33 25 17 9 1 58 50 42 34 26 18 10 2 59 51 43 35 27 19 11 3 60 52 44 3629 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 5663 55 47 39 31 23 15 7 62 54 46 38 30 22 14 6 61 53 45 37 29 21 13 5 28 20 12 41.2.2 把变换后的密钥等分成两部分,前28位记为C[0], 后28位记为D[0].1.2.3 计算子密钥(共16个),从i=1开始。
1.2.3.1 分别对C[i-1],D[i-1]作循环左移来生成C[i],D[i].(共16次)。
每次循环左移位数如下表所示:循环次数1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16左移位数1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 11.2.3.2 串联C[i],D[i],得到一个56位数,然后对此数作如下变换以产生48位子密钥K[i]。
变换过程如下:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 2414 17 11 24 1 5 3 28 15 6 21 10 23 19 12 4 26 8 16 7 27 20 13 225 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 4841 52 31 37 47 55 30 40 51 45 33 48 44 49 39 56 34 53 46 42 50 36 29 321.2.3.3 按以上方法计算出16个子密钥。
2.对64位数据块的处理:2.1 把数据分成64位的数据块,不够64位的以适当的方式填补。
2.2对数据块作变换。
bit goes to bit bit goes to bit58 1 57 3350 2 49 3442 3 41 3534 4 33 3626 5 25 3718 6 17 3810 7 9 392 8 1 4060 9 59 4152 10 51 4244 11 43 4336 12 35 4428 13 27 4520 14 19 4612 15 11 474 16 3 4862 17 61 4954 18 53 5046 19 45 5138 20 37 5230 21 29 5322 22 21 5414 23 13 556 24 5 5664 25 63 5756 26 55 5848 27 47 5940 28 39 6032 29 31 6124 30 23 6216 31 15 638 32 7 642.3 将变换后的数据块等分成前后两部分,前32位记为L[0],后32位记为R[0]。
2.4 用16个子密钥对数据加密。
2.4.1 根据下面的扩冲函数E,扩展32位的成48位bit goes to bit bit goes to bit bit goes to bit bit goes to bit32 1 8 13 16 25 24 371 2 9 14 17 26 25 382 3 10 15 18 27 26 393 4 11 16 19 28 27 404 5 12 17 20 29 28 415 6 13 18 21 30 29 424 7 12 19 20 31 28 435 8 13 20 21 32 29 446 9 14 21 22 33 30 457 10 15 22 23 34 31 468 11 16 23 24 35 32 479 12 17 24 25 36 1 482.4.2 用E{R[i-1]}与K[i]作异或运算。
2.4.3 把所得的48位数分成8个6位数。
1-6位为B[1],7-12位为B[2],……43-48位为B[8]。
2.4.4 用S密箱里的值替换B[j]。
从j=1开始。
S密箱里的值为4位数,共8个S密箱2.4.4.1 取出B[j]的第1和第6位串联起来成一个2位数,记为m.。
m即是S密箱里用来替换B[j]的数所在的列数。
2.4.4.2 取出B[j]的第2至第5位串联起来成一个4位数,记为n。
n即是S密箱里用来替换B[j]的数所在的行数。
2.4.4.3 用S密箱里的值S[j][ m][ n]替换B[j]。
8个S密箱如下所示:--------S-BOXES1Binary d1d6 => 00 01 10 11\/ d2..d5 \/ Dec 0 1 2 30000 0 14 0 4 150001 1 4 15 1 120010 2 13 7 14 80011 3 1 4 8 20100 4 2 14 13 40101 5 15 2 6 90110 6 11 13 2 10111 7 8 1 11 71000 8 3 10 15 51001 9 10 6 12 111010 10 6 12 9 31011 11 12 11 7 141100 12 5 9 3 101101 13 9 5 10 01110 14 0 3 5 61111 15 7 8 0 13--------S-BOXES2binary d1d6 => 00 01 10 110000 0 15 3 0 130001 1 1 13 14 80010 2 8 4 7 100011 3 14 7 11 10100 4 6 15 10 30101 5 11 2 4 150110 6 3 8 13 40111 7 4 14 1 21000 8 9 12 5 111001 9 7 0 8 61010 10 2 1 12 71011 11 13 10 6 121100 12 12 6 9 01101 13 0 9 3 51110 14 5 11 2 141111 15 10 5 15 9--------S-BOXES3binary d1d6 => 00 01 10 11 \/ d2..d5 \/ dec 0 1 2 3 0000 0 10 13 13 10001 1 0 7 6 100010 2 9 0 4 130011 3 14 9 9 00100 4 6 3 8 60101 5 3 4 15 90110 6 15 6 3 80111 7 5 10 0 71000 8 1 2 11 41001 9 13 8 1 151010 10 12 5 2 141011 11 7 14 12 31100 12 11 12 5 111101 13 4 11 10 51110 14 2 15 14 21111 15 8 1 7 12--------S-BOXES4binary d1d6 => 00 01 10 110000 0 7 13 10 30001 1 13 8 6 150010 2 14 11 9 00011 3 3 5 0 60100 4 0 6 12 100101 5 6 15 11 10110 6 9 0 7 130111 7 10 3 13 81000 8 1 4 15 91001 9 2 7 1 41010 10 8 2 3 51011 11 5 12 14 111100 12 11 1 5 121101 13 12 10 2 71110 14 4 14 8 21111 15 15 9 4 14--------S-BOXES5binary d1d6 => 00 01 10 11 \/ d2..d5 \/ dec 0 1 2 3 0000 0 2 14 4 110001 1 12 11 2 80010 2 4 2 1 120011 3 1 12 11 70100 4 7 4 10 10101 5 10 7 13 140110 6 11 13 7 20111 7 6 1 8 131000 8 8 5 15 61001 9 5 0 9 151010 10 3 15 12 01011 11 15 10 5 91100 12 13 3 6 101101 13 0 9 3 41110 14 14 8 0 51111 15 9 6 14 3--------S-BOXES6binary d1d6 => 00 01 10 110000 0 12 10 9 4 0001 1 1 15 14 3 0010 2 10 4 15 2 0011 3 15 2 5 12 0100 4 9 7 2 9 0101 5 2 12 8 5 0110 6 6 9 12 15 0111 7 8 5 3 10 1000 8 0 6 7 11 1001 9 13 1 0 14 1010 10 3 13 4 1。
