电路理论基础 (卢元元 王晖 著) 西安电子科技课后答案
电路分析基础第四版课后答案 (2)
电路分析基础第四版课后答案第一章电路基本概念和定律1.1 电路基本概念1.什么是电路？2.什么是电流？3.什么是电压？4.什么是电阻？5.什么是电导？1.2 电路定律1.请简述欧姆定律的表达式及其在电路分析中的应用。
2.请简述基尔霍夫电流定律的表达式及其在电路分析中的应用。
3.请简述基尔霍夫电压定律的表达式及其在电路分析中的应用。
第二章电路分析方法2.1 参考方向和参考极性1.请简述参考方向在电路分析中的作用。
2.请说明电流方向和电压极性的确定方法。
2.2 串联与并联电路1.什么是串联电路？2.什么是并联电路？3.串联和并联电路的特点有哪些？2.3 电压分流和电流合并定律1.请简述电压分流定律的表达式及其在电路分析中的应用。
2.请简述电流合并定律的表达式及其在电路分析中的应用。
2.4 电阻网络简化1.什么是电阻网络简化？2.列举电阻网络简化的方法。
第三章基本电路3.1 电压源与电流源1.请简述理想电压源的特性及其在电路分析中的应用。
2.请简述理想电流源的特性及其在电路分析中的应用。
3.2 集总元件与非集总元件1.什么是集总元件？2.什么是非集总元件？3.请举例说明集总元件和非集总元件的特点。
3.3 电阻的平均功率和瞬时功率1.请简述电阻的平均功率和瞬时功率的计算方法。
3.4 等效电路和戴维南定理1.什么是等效电路？2.请简述戴维南定理及其在电路分析中的应用。
第四章变流电路4.1 正弦波电压和正弦波电流1.什么是正弦波电压？2.什么是正弦波电流？3.请简述正弦波电压和正弦波电流的特点。
4.2 交流电路中的电阻、电感和电容1.请简述交流电路中电阻、电感和电容的特性及其在电路分析中的应用。
4.3 相量法和复数法分析交流电路1.请简述相量法分析交流电路的基本原理。
2.请简述复数法分析交流电路的基本原理。
4.4 等效电路和史密斯图分析交流电路1.什么是等效电路？2.请简述史密斯图分析交流电路的基本原理。
第五章电流电压分析基础5.1 直流稳态分析1.什么是直流稳态？2.请简述直流稳态分析的基本步骤。
电路基础课后习题答案[1]
![电路基础课后习题答案[1]](https://img.taocdn.com/s3/m/4901aec5d0d233d4b14e69e7.png)
第1章 章后习题解析一只“100Ω、100 W ”的电阻与120 V 电源相串联，至少要串入多大的电阻 R 才能使该电阻正常工作？电阻R 上消耗的功率又为多少？解：电阻允许通过的最大电流为1100100'===R P I A 所以应有 1120100=+R ，由此可解得：Ω=-=201001120R电阻R 上消耗的功率为 P =12×20=20W图（a ）、（b ）电路中，若让I =0.6A ，R =？ 图（c ）、（d ）电路中，若让U =，R =？ 解：(a)图电路中，3Ω电阻中通过的电流为 I ˊ=2－=1.4AR 与3Ω电阻相并联，端电压相同且为 U =×3= 所以 R =÷=7Ω(b)图电路中，3Ω电阻中通过的电流为 I ˊ=3÷3=1A R 与3Ω电阻相并联，端电压相同，因此 R =3÷=5Ω (c)图电路中，R 与3Ω电阻相串联，通过的电流相同，因此R =÷2=Ω(d)图电路中，3Ω电阻两端的电压为 U ˊ=3－= R 与3Ω电阻相串联，通过的电流相同且为 I =÷3=0.8A 所以 R =÷=Ω两个额定值分别是“110V ，40W ”“110V ，100W ”的灯泡，能否串联后接到220V 的电源上使用？如果两只灯泡的额定功率相同时又如何？解：两个额定电压值相同、额定功率不等的灯泡，其灯丝电阻是不同的，“110V ，40W ”灯泡的灯丝电阻为： Ω===5.302401102240P U R ;“110V ，100W ”灯泡的灯丝电阻为：Ω===12110011022100P U R ，若串联后接在220V 的电源上时，其通过两灯泡的电流相同，且为：52.01215.302220≈+=I A ，因此40W 灯泡两端实际所加电压为：3.1575.30252.040=⨯=U V ，显然这个电压超过了灯泡的额定值，而100 W 灯泡两端实际所加电压为：U 100=×121=，其实际电压低于额定值而不能正常工作，因此，这两个功率不相等的灯泡是不能串联后接到220V 电源上使用的。
电路理论基础第四版第2章习题答案详解
答案2.3解：电路等效如图(b)所示。
20k Ω1U +-20k Ω(b)+_U图中等效电阻(13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得：220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯= 再对图(a)使用分压公式得：13==30V 1+3U U ⨯ 答案2.4解：设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1)由已知条件得如下联立方程：32113130.05(2) 40k (3)eqR U U R R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω 再将3R 代入(1)式得210k 3R =Ω 答案2.5解：由并联电路分流公式，得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=- 答案2.6解：首先将电路化简成图(b)。
图 题2.5120Ω(a)(b)图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦ 由并联电路分流公式得211210A 6A R I R R =⨯=+及21104A I I =-=再由图(a)得321201A 360120I I =⨯=+由KVL 得，3131200100400V U U U I I =-=-=- 答案2.7xRx(a-1)图2.6解：（a ）设R 和r 为1级，则图题2.6(a)为2级再加x R 。
将22'-端x R 用始端11'-x R 替代，则变为4级再加x R ，如此替代下去，则变为无穷级。
从始端11'-看等效电阻为x R ,从33'-端看为1-∞级，也为x R , 则图(a)等效为图(a-1)。
电子线路分析基础_西安电子科技大学中国大学mooc课后章节答案期末考试题库2023年
电子线路分析基础_西安电子科技大学中国大学mooc课后章节答案期末考试题库2023年1.电路如图所示，已知【图片】>>1，【图片】=0.7V，要求【图片】=1mA，则【图片】为（）【图片】。
【图片】参考答案:4.3k2.若想增大输入电阻，且保持放大器稳定，放大器应引入（）反馈。
参考答案:串联负3.放大器输入单一频率的信号时，不会出现线性失真。
参考答案:正确4.图示电路，若想实现输出电压稳定，则应该在（）引入反馈支路。
【图片】参考答案:①和③之间5.图示电路中，【图片】和【图片】特性完全相同，则输出电阻约为【图片】。
【图片】参考答案:正确6.图示电路是一个两级放大器。
【图片】参考答案:错误7.图示电路为三级放大器电路。
【图片】参考答案:错误8.图示电路中，【图片】和【图片】特性完全相同，下列叙述正确的是（）。
【图片】参考答案:为CE组态放大器、为CB组态放大器。
9.无外加电压时，PN结中没有载流子的运动。
参考答案:错误10.在OCL乙类功放电路中，若最大输出功率为12W，则电路中功放管的集电极最大功耗约为（）W。
参考答案:2.411.放大器的非线性失真与输入信号频率大小有关。
参考答案:错误12.电路如图所示，已知【图片】=4mS，【图片】=【图片】。
电路的输出电阻为（）【图片】。
【图片】参考答案:20k13.某放大器的交直流负载线如图所示，忽略晶体管的饱和压降，则最大不失真输出电压振幅值为（）V。
【图片】参考答案:314.某放大电路的幅频特性渐进线波特图如图所示，由此可知中频电压放大倍数为（）dB。
【图片】参考答案:4015.电路如图所示，深度负反馈条件下的电压放大倍数为（）。
【图片】参考答案:5116.若想减少输出电阻，且保持放大器稳定，放大器应引入（）反馈。
参考答案:电压负17.负反馈可以改善放大器的性能，相应的代价是使得放大倍数下降。
参考答案:正确18.直接耦合的放大器，带宽为无穷大。
电路理论基础第四章习题解答西安电子科技大学出版社
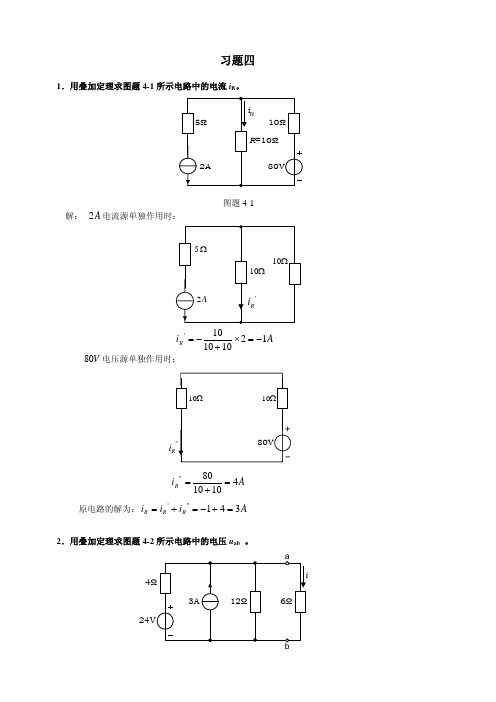
习题四1．用叠加定理求图题4-1所示电路中的电流i R 。
图题4-1解： A 2电流源单独作用时：A i R 12101010'−=×+−=V 80电压源单独作用时：i A i R 4101080''=+=原电路的解为：A i i i R R R 341'''=+−=+=2．用叠加定理求图题4-2所示电路中的电压u ab 。
4图题4-2解：V 24电压源单独作用时：Ω6Ω=+×==46126126//121RV R R u ab 1224411'=×+=A 3电流源单独作用时：Ω4Ω6''A i 13623611214161''=×=×++=V i u ab 6616''''=×=×= 原电路的解为：V u u u ab ab ab 18612'''=+=+=3．用叠加定理求图题4-3所示电路中的电流i 。
6A图题4-3解： A 6电流源单独作用时：ΩΩ6A i 4612612'−=×+−= V 36电压源单独作用时：Ω6Ω6ΩΩA i 261236''−=+−=原电路的解为：()()A i i i 624'''−=−+−=+=4．图题4-4所示电路中，R =6Ω，求R 消耗的功率。
图题4-4解： 将R 支路以外的部分看作一个二端电路。
可采用叠加原理求oc u ：12⎟⎠⎞⎜⎝⎛++××+×+=26363212636oc u V 1688=+=求其等效电阻：eqRΩ=++×=426363eq R 原电路简化为：Ri=eq R u oc =RA R R u i eq oc R 6.14616=+=+=W R i P R R 36.1566.122=×=×=5．图题4-5所示电路中， R 1=1.5Ω R 2=2Ω，求（a ）从a、b 端看进去的等效电阻；（b ）i 1与i s 的函数关系。
电子电路基础课后习题答案【整理版】
第一章 思考题与习题
1.1. 半导体材料都有哪些特性？为什么电子有源器件都是由半导体材料制成 的？
1.2. 为什么二极管具有单向导电特性？如何用万用表判断二极管的好坏？
1.3. 为什么不能将两个二极管背靠背地连接起来构成一个三极管？
1.4. 二极管的交、直流等效电阻有何区别？它们与通常电阻有什么不同？
(b) uo
t
(a)
(c)
图 P2-3
2.13 设如图 P2-4(a)所示的放大电路，Rb=200k，RC=2k，UD=0.7V，β＝100， VCC=12V，VBB=2.7V，各电容值足够大，输入、输出特性曲线分别如图 P2-4(c)、 (d)所示，试 1. 计算印静态工作点，画出负载线 2. 画出中频交流等效电路 3. 设输入电压 ui 如图 P2-4(b)所示，试用图解法画出输出 uo 的波形 4. 输出主要产生何种失真，如何改善
(b) 1. D1、D2 均反向导通，Uo = UZ2＋UZ1 ＝ 9.6 V 2. 反向不导通，Uo = 6V
3. Uo = 3V
(c) 1. D1、D2 均正向导通，Uo = UD＋UD ＝ 1.4 V
2. Uo = UD＋UD ＝ 1.4 V
3. Uo = UD＋UD ＝ 1.4 V
(d) 1. D2 反向导通，D1 不导通， Uo = 3.3 V
D1
u1
u1
5V
0
u2
＋
t
D2 R uo
u2
5V
0
t
图 P1-4(a)
图 P1-4(b)
解： u0
4.7V
0
t
1.13.如图 P1-5 所示电路，设二极管为理 想二极管(导通电压 UD=0，击穿电压 UBR=∞ )，试画出输出 uo 的波形。
西安电子科技大学数字电路基础参考答案
习题4 4－3解：该电路的输入为3x 2x 1x 0x ，输出为3Y 2Y 1Y 0Y 。
真值表如下：由此可得：1M =当时，33232121010Y x Y x x Y x x Y x x =⎧⎪=⊕⎪⎨=⊕⎪⎪=⊕⎩ 完成二进制至格雷码的转换。
0M =当时，332321321210321010Y x Y x x Y x x x Y x Y x x x x Y x =⎧⎪=⊕⎪⎨=⊕⊕=⊕⎪⎪=⊕⊕⊕=⊕⎩ 完成格雷码至二进制的转换。
4－9 设计一个全加（减）器，其输入为A,B,C 和X(当X ＝0时，实现加法运算；当X ＝1时，实现减法运算)，输出为S(表示和或差)，P （表示进位或借位）。
列出真值表，试用3个异或门和3个与非门实现该电路，画出逻辑电路图。
解：根据全加器和全减器的原理，我们可以作出如下的真值表：由真值表可以画出卡诺图，由卡诺图得出逻辑表达式，并画出逻辑电路图：A B C XP4－10 设计一个交通灯故障检测电路，要求红，黄，绿三个灯仅有一个灯亮时，输出F ＝0；若无灯亮或有两个以上的灯亮，则均为故障，输出F ＝1。
试用最少的非门和与非门实现该电路。
要求列出真值表，化简逻辑函数，并指出所有74系列器件的型号。
解：根据题意，我们可以列出真值表如下：对上述的真值表可以作出卡诺图，由卡诺图我们可以得出以下的逻辑函数：F AB AC BC ABC AB AC BC ABC =+++=∙∙∙逻辑电路图如下所示：A F4－13 试用一片3－8译码器和少量逻辑门设计下列多地址输入的译码电路。
（1） 有8根地址输入线7A ~1A ,要求当地址码为A8H,A9H ,…,AFH 时，译码器输出为0Y ~7Y 分别被译中，且地电平有效。
（2） 有10根地址输入线9A ～0A ，要求当地址码为2E0H,2E1H, …,2E7H 时，译码器输出0Y ~7Y 分别被译中，且地电平有效。
解：（1）当122100A BE E E =,即75364210111,00,A A A A A A A A ==从000～111变化时07~Y Y 分别被译中，电路如下图所示：Y Y （2）当122100A B E E E =，即97538432101111,000,A A A A A A A A A A ==从000～111变化时，07~Y Y 分别被译中。
电路理论基础课后答案第12章
图示电路，设i Lf 1(小)，i R方程:列出状态方q i f i (q i )/R 3 f 2(q 2)/R 3 i sf 2(u R )。
以q 及小为状态变量列出状态方程，并讨论所得方程是图题12.1解：分别对节点①和右边回路列KCL 与KVLi C q C i R i LU L U C q/C将各元件方程代入上式得非线性状态方程：qf i ( ) f 2(q/C)方程中不明显含有时间变量 t,因此是自治的 题 图示电路，设 u 1 f 1(q 1), u 2f 2(q 2)，解：分别对节点①、②列 KCL 方程： 节点①：11 q i i s (u i U 2)/ R 3节点②：12 q 2 (u 1 u 2)/R 3 u 2 / R 4将u i f i (q i ), U 2 f 2(q 2)代入上述方程，整理得状态方程:q 2f i (q i )/R 3 f 2 (q 2)(R 3 &)但"解得i 2 i 3 i 4 i 2U3R 3u 3 u i c ———^ 0 R 4U3将(U i R 4i 2)R 3/(R 3R 4) [f i (q i ) R 4f 2( 2)]R 3/(R 3 R 4)f i (q i) ' i2 f2 (寸 2)及U 3代入式(i)、(2)整理得：U iq if i (q i )/(R 3 R 4) f 2( 2旧/(艮 R 4) 2f i (q i )R 3/(R 3 R 4)f 2(2)g(& RJ U S图示电路，设i a 3...小,u Ssin( t)，试分别写出用前向欧拉法、后向欧拉法和梯形法计算响U L — Ri U S dt(3 ) sin( t)k i kh[ R (3k) sin( t k )]在图示电路中电容的电荷与电压关系为 u 1f 〔(q 〔)，电感的磁链电流关系为i 2 f 2 (小2)。
电路理论基础 (卢元元 王晖 著) 西安电子科技课后答案
p = ui = 6 sin 2t ⋅ 4 sin 2t = 24 sin 2 2t (mW ) w[0, t ] = ∫ pdt = ∫ 24 sin 2 2tdt = ∫ 24 ×
t t t 0 0 0
1 − cos 4t dt 2
= 12t − 3 sin 4t mJ
，求： （a）在 2 小时内电池被供 8．电流 i=2A 从 u=6V 的电池正极流入（电池正在被充电） 给的能量； （b）在 2 小时内通过电池的电荷（注意单位的一致性，1V=1J/C） 。 解: (1)
t1 t2
(
)
= 2t 3 − t 2
(
)
t2 t1
从 t=1s 到 t=3s,由该端流入的电荷量为
3 q[1, 3] = (2t 3 − t 2 ) 1 = 2 × 3 3 − 3 2 − 2 × 1 + 1 = 44(C )
3．一个二端元件的端电压恒为 6V，如果有 3A 的恒定电流从该元件的高电位流向低电位， 求（a）元件吸收的功率； （b）在 2s 到 4s 时间内元件吸收的能量。 解: (1) 元件吸收功率 p = 6 × 3 = 18W
2Ω 电阻上的电流为 I 2 = 6 − 4 = 2 A 方向向右
则 i = 2 + 1 = 3A
U ab = −3 × 3 − 2 × 2 + 4 × 5 + 12
= 19V
13．根据图题 1-13 中给定的电流，尽可能多地确定图中其他各元件中的未知电流。
3A 2A 4A
-10A 6A
图题 1-13 解: 图中虚线部分是一个闭合面
（a）求电压ux ； （b）若图中电压源的给定电压为Us，求出ux关 18．电路如图题 1-18 所示， 于Us的函数。
西安电子科技大学数字电路基础答案
习题4 4－3解：该电路的输入为3x 2x 1x 0x ，输出为3Y 2Y 1Y 0Y 。
真值表如下：由此可得：1M =当时，33232121010Y x Y x x Y x x Y x x =⎧⎪=⊕⎪⎨=⊕⎪⎪=⊕⎩ 完成二进制至格雷码的转换。
0M =当时，332321321210321010Y x Y x x Y x x x Y x Y x x x x Y x =⎧⎪=⊕⎪⎨=⊕⊕=⊕⎪⎪=⊕⊕⊕=⊕⎩ 完成格雷码至二进制的转换。
4－9 设计一个全加（减）器，其输入为A,B,C 和X （当X ＝0时，实现加法运算；当X ＝1时,实现减法运算),输出为S(表示和或差），P(表示进位或借位）。
列出真值表，试用3个异或门和3个与非门实现该电路，画出逻辑电路图。
解：根据全加器和全减器的原理,我们可以作出如下的真值表:由真值表可以画出卡诺图，由卡诺图得出逻辑表达式，并画出逻辑电路图:A B C XP4－10 设计一个交通灯故障检测电路，要求红，黄，绿三个灯仅有一个灯亮时,输出F ＝0；若无灯亮或有两个以上的灯亮，则均为故障，输出F ＝1。
试用最少的非门和与非门实现该电路。
要求列出真值表，化简逻辑函数，并指出所有74系列器件的型号. 解:根据题意，我们可以列出真值表如下：对上述的真值表可以作出卡诺图，由卡诺图我们可以得出以下的逻辑函数：F AB AC BC ABC AB AC BC ABC =+++=•••逻辑电路图如下所示：A F4－13 试用一片3－8译码器和少量逻辑门设计下列多地址输入的译码电路.（1） 有8根地址输入线7A ~1A ,要求当地址码为A8H,A9H ，…,AFH 时，译码器输出为0Y ～7Y 分别被译中，且地电平有效。
（2） 有10根地址输入线9A ～0A ，要求当地址码为2E0H,2E1H, …,2E7H 时，译码器输出0Y ~7Y 分别被译中，且地电平有效.解：(1）当122100A B E E E =，即75364210111,00,A A A A A A A A ==从000～111变化时07~Y Y 分别被译中，电路如下图所示：Y Y (2）当122100A B E E E =，即97538432101111,000,A A A A A A A A A A ==从000～111变化时，07~Y Y 分别被译中。
电路基础课后练习答案分析(专业教材).doc
电路基础课后练习答案分析(专业教材)1.1“100ω，100瓦”电阻与120伏电源串联。
使电阻器正常工作的最小电阻是多少？电阻r的功耗是多少？解决方案:允许通过电阻器的最大电流是A，因此它应该是，因此它可以被获得:电阻R的功耗为p=12×20=20W 2 a3ωri(a)3ωri(b)2 a3ωR u-(c)3v-3ωR u-(d)3v-图1.27练习1.2电路图1.2图1.27(a)和(b)电路，如果I=0.6A，R=？如果U=0.6V，R=？解决方案:(a)在图形电路中，流经3ω电阻的电流为I \u=2-0.6=1.4ar，与3ω电阻并联，端电压相同，u=1.4x3=4.2v，因此在图形电路中，R=4.2 \u 0.6=7ω(b)，流经3ω电阻的电流为I \u=3 \u 3=1，与3ω电阻并联，端电压相同。
因此，在图形电路中，R=3 \u 0.6=5ω(c)，R与3ω电阻串联，通过它的电流是相同的。
因此，在R=0.6 \u 2=0.3ω(d)的电路中，3ω电阻两端的电压为u \u=3-0.6=220伏，R与3ω电阻串联，流过它的电流相同，I=2.4÷ 3=0.8A，因此R=0.6÷ 0.8=0.75Ω 1.3两个灯泡的额定值为“110伏，40瓦”和“110伏，100瓦”-usris (a) -usris (b)图1.28练习1.4电路图ABA解决方案:两个额定电压相同、额定功率不同的灯泡的灯丝电阻不同，“110伏、40瓦”灯泡的灯丝电阻如下:；“110伏，100瓦”灯泡的灯丝电阻为:如果串联连接并连接到220伏电源，通过两个灯泡的电流是相同的，并且是:答:因此，40W灯泡上实际施加的电压为:显然，该电压超过了灯泡的额定值，而100瓦灯泡上实际施加的电压为:U100=0.52×121=62.92伏，实际电压低于额定值，不能正常工作。
因此，这两个功率不相等的灯泡不能串联后再连接到220伏电源上使用。
电路理论基础课后习题解析 第一章
+
3U1 U2
解： 利用KCL可得 3U1-10-2U1=0 U1=10V
3U1电流源提供的电功率为 P3U1= -U2×3U1= -(-2 × 3U1+U1 ) ×3U1 =1500W 2U1电流源提供的电功率为 P2U1= U3×2U1= (5+U1) ×2U1 = 300W
例1-10 图示电路为某电路中的一部分，已知i1 = 4A， i2 =cos2t，uc=15sin2t，求iL和ubd。
练习1-2 求U4 、 U6 、 U8。
U2=-2V U7=1V U6 U5=4V U3=6V
电路理论基础
U1=10V
U8
U4
(U4=10V 、 U6 =-13V、 U8 =7V)
练习1-3 图示电路含有理想运算放大器，求电流ix、 电压uo及60K W电阻消耗的电功率。
u1
i1 ∞ u2 i2
解:
0 t 1 1 t 3 3 t 4 t4
10 mA 10 mA i(t ) 10 mA 10 mA
0 t 1 1 t 3 3 t 4 t4
3、基尔霍夫定律的应用
电路理论基础
4A
例1-4 计算图示电路中的U和I，你能确定元件A可 能是什么元件吗？ 解： 应用KCL，对节点a有 I1 4W I= 3-4 = -1A 2A c d 对节点d有， I1= 4-3-2 = -1A 2W 6V 3A
4W I
12V
2U0
VCVS
4W
12V
I
2U0 4V
6W
+U0 -
4V
Байду номын сангаас
+U0 -
电路基础学习知识原理课后习题集规范标准答案
第五版《电路原理》课后作业第一章“电路模型和电路定律”练习题1-1说明题1-1图（a）、（b）中：（1）u、i的参考方向是否关联？（2）ui乘积表示什么功率？（3）如果在图（a）中u>0、i<0；图（b）中u>0、i>0，元件实际发出还是吸收功率？（a）（b）题1-1图解（1）u、i的参考方向是否关联？答：(a) 关联——同一元件上的电压、电流的参考方向一致，称为关联参考方向；(b) 非关联——同一元件上的电压、电流的参考方向相反，称为非关联参考方向。
（2）ui乘积表示什么功率？答：(a) 吸收功率——关联方向下，乘积p = ui > 0表示吸收功率；(b) 发出功率——非关联方向，调换电流i的参考方向之后，乘积p = ui < 0，表示元件发出功率。
（3）如果在图(a) 中u>0，i<0，元件实际发出还是吸收功率？答：(a) 发出功率——关联方向下，u > 0，i < 0，功率p为负值下，元件实际发出功率；(b) 吸收功率——非关联方向下，调换电流i的参考方向之后，u > 0，i > 0，功率p为正值下，元件实际吸收功率；1-4 在指定的电压u和电流i的参考方向下，写出题1-4图所示各元件的u和i的约束方程（即VCR）。
（a）（b）（c）（d）（e）（f）题1-4图解（a）电阻元件，u、i为关联参考方向。
由欧姆定律u = R i = 104 i（b）电阻元件，u、i为非关联参考方向由欧姆定律u = - R i = -10 i（c）理想电压源与外部电路无关，故u = 10V（d）理想电压源与外部电路无关，故u = -5V(e) 理想电流源与外部电路无关，故 i=10×10-3A=10-2A （f ）理想电流源与外部电路无关，故i=-10×10-3A=-10-2A1-5 试求题1-5图中各电路中电压源、电流源及电阻的功率（须说明是吸收还是发出）。
电路理论基础习题答案
电路理论基础习题答案第一章1-1. (a)、(b)吸收10W ；(c)、(d)发出10W. 1-2. –1A; –10V; –1A; – 4mW.1-3. –0.5A; –6V; –15e –t V; 1.75cos2t A; 3Ω; 1.8cos 22t W.1-4. u =104 i ; u = -104 i ; u =2000i ; u = -104 i ; 1-5.1-6. 0.1A. 1-7.1-8. 2F; 4C; 0; 4J. 1-9. 9.6V,0.192W, 1.152mJ; 16V , 0, 3.2mJ.1-10. 1– e -106t A , t >0 取s .1-11. 3H, 6(1– t )2 J; 3mH, 6(1–1000 t ) 2 mJ;1-12. 0.4F, 0 .1-13. 供12W; 吸40W;吸2W; (2V)供26W, (5A)吸10W. 1-14. –40V , –1mA; –50V, –1mA; 50V , 1mA. 1-15. 0.5A,1W; 2A,4W; –1A, –2W; 1A,2W. 1-16. 10V ,50W;50V ,250W;–3V ,–15W;2V ,10W. 1-17. (a)2V;R 耗4/3W;U S : –2/3W, I S : 2W; (b) –3V; R 耗3W; U S : –2W, I S :5W; (c)2V ,–3V; R 耗4W;3W;U S :2W, I S :5W; 1-18. 24V , 发72W; 3A, 吸15W;24V 电压源; 3A ↓电流源或5/3Ω电阻. 1-19. 0,U S /R L ,U S ;U S /R 1 ,U S /R 1 , –U S R f /R 1 . 1-20. 6A, 4A, 2A, 1A, 4A; 8V, –10V , 18V . 1-21. K 打开：(a)0, 0, 0; (b)10V , 0, 10V; (c)10V,10V ,0; K 闭合: (a)10V ,4V ,6V; (b)4V ,4V ,0; (c)4V,0,4V; 1-22. 2V; 7V; 3.25V; 2V. 1-23. 10Ω.1-24. 14V .1-25. –2.333V , 1.333A; 0.4V , 0.8A.1-26. 12V , 2A, –48W; –6V , 3A, –54W . ※第二章2-1. 2.5Ω; 1.6R ; 8/3Ω; 0.5R ; 4Ω; 1.448Ω; . R /8; 1.5Ω; 1.269Ω; 40Ω; 14Ω. 2-2. 11.11Ω; 8Ω; 12.5Ω. 2-3. 1.618Ω.2-4. 400V;363.6V;I A =.5A, 电流表及滑线电阻损坏. 2-6. 5k Ω. 2-7. 0.75Ω.2-8. 10/3A,1.2Ω;–5V ,3Ω; 8V ,4Ω; 0.5A,30/11Ω. 2-9. 1A,2Ω; 5V,2Ω; 2A; 2A; 2A,6Ω. 2-10. –75mA; –0.5A.2-11. 6Ω; 7.5Ω; 0; 2.1Ω. 2-12. 4Ω; 1.5Ω; 2k Ω. 2-13. 5.333A; 4.286A. 2-14. (a) –1 A ↓; (b) –2 A ↓, 吸20W. 2-16. 3A. 2-17. 7.33V . 2-18. 86.76W. 2-19. 1V , 4W. 2-20. 64W.2-21. 15A, 11A, 17A. 2-23. 7V , 3A; 8V ,1A. 2-24. 4V , 2.5V, 2V. 2-26. 60V . 2-27. 4.5V. 2-28. –18V .2-29. 原构成无解的矛盾方程组; (改后)4V ,10V . 2-30. 3.33 k , 50 k . 2-31. R 3 (R 1 +R 2 ) i S /R 1 .2-32. 可证明 I L =－u S /R 3 . 2-33. –2 ; 4 .2-34. (u S1 + u S2 + u S3 )/3 . ※第三章3-1. –1+9=8V; 6+9=15V; sin t +0.2 e – t V. 3-2. 155V . 3-3. 190mA.i A0 s 1 12 3 1-e -t t 0 t ms i mA 410 0 t ms p mW 4 100 2 25i , A 0.4 .75 t 0 .25 1.25 ms -0.4 (d) u , V 80 0 10-20 t , ms(f ) u , V 1000 10 t , ms (e)p (W) 100 1 2 t (s) -103-4. 1.8倍.3-5. 左供52W, 右供78W. 3-6. 1; 1A; 0.75A.3-7. 3A; 1.33mA; 1.5mA; 2/3A; 2A. 3-8. 20V , –75.38V.3-9. –1A; 2A; –17.3mA. 3-10. 5V , 20; –2V, 4. 3-12. 4.6. 3-13. 2V; 0.5A. 3-14. 10V , 5k .3-15. 4/3, 75W; 4/3, 4.69W. 3-16. 1, 2.25W. 3-18. 50. 3-19. 0.2A. 3-20. 1A. 3-21. 1.6V . 3-22. 4A; –2A.3-23. 23.6V; 5A,10V . 3-24. 52V . ※第四章4-1. 141.1V , 100V , 50Hz, 0.02s,0o , –120o ; 120 o.4-2. 7.07/0 o A, 1/–45 o A, 18.75/–40.9 oA. 4-3. 3mU , 7.75mA .4-4. 10/53.13o A, 10/126.87o A, 10/–126.87oA,10/–53.13oA ；各瞬时表达式略。
电子电路答案
答：在求解电路参数时，对于稍微复杂的电路，必须列方程求解，列出方程又必须知 道电流、电压的方向，为此，引入电流、电压参考方向，根据参考方向列出电路方程，利用 方程求出电路参数，若结果为负，表明实际的方向与参考方向相反，若结果为正，表明参考 方向就是实际方向。
1-16 电压如题图 1-7(a)所示，施加于电容 C 如题图 1-7(b)所示，试求 i(t)，并绘出波形 图。
u(V) 1
i i(A)
1
+
u
C=2F
–
0
2
4 t(s)
0
2
4
t(s)
(a)
(b)
-1 (c)
题图 1-7 习题 1-16 图
解：为求 i(t)，先由图(a)列出 u(t)的函数关系为：
a
4Ω b
c
4V 2Ω
(a)
I 1Ω
2Ω c
8V
3V a
5Ω b
(b)
题图 1-1 习题 1-6 电路图
解：（1）图(a)，由 a 到 b 的电压降 Uab=Uac+Ucb，假定电流方向如图所示，沿 a—电池 —c—a 回路逆时针方向绕行一周，电压方程式为：
-6+4I+2I=0
即得：I=1A
则 Uac=2(-I)=-2V
– U11 + 11
+ U8 –
8
d
e
+ U9 –
9 f
知电流之外，还需求解 6 个未知电流。 在图中标出节点 a、b、c、d、e、f。
对 f 节点：-I9-I10-I4=0 代入数据
电路理论基础第三章习题解答 西安电子科技大学出版社
3u n1 − u n 2 = −12 ⎫ ⎬ − 3u n1 + 5u n 2 = 84⎭
解得：
u n 2 = u 2 = 18V ⎫ ⎬ u n1 = u1 = 2V ⎭
5．用节点分析法求图题 3-5 所示电路中的i1和i2。
i2 4Ω 3A 24V 12Ω 6Ω
i1
（1）
（2）
辅助方程： u n 2 − u n1 = 8V （3） （1） （2） （3）联立得：
u n1 = 2V ⎫ ⎬ u n 2 = 10V ⎭
∴ u = u n 2 = 10V
i= u n1 = 1A 2
11．用节点分析法求图题 3-11 所示电路中的uo。
1
ix
10Ω
0.2u1 2 3
2Ω
40V
il3
10Ω
4Ω
8Ω
iR
il2
R = 80Ω
10Ω
il1
20V
il3
图题 3-16 解：选择如图所示三个回路电流，列出回路方程如下
il1 (10 + 4 + 10) − 4il 2 + 10il 3 = −20
（1） （2） （3）
得：
3u 2 − u 3 = −32 ⎫ ⎬ − u 2 + 2u 3 = 44⎭ u 2 = −4V ⎫ ⎪ u 3 = 20V ⎬ u1 = 24V ⎪ ⎭
解得：
7．图 3-7 所示电路中如果元件 x 是一个上端为正极的 4V 独立电压源，用节点分析法求电压 u。
ix
3Ω
24V
2
1
6Ω
i
x
- u +
电路基础、电子技术与元器件习题答案
部分习题参考答案第1章1．略2．略3．略4．480度5．0.45瓦6．0.32A 不能，因为电流超过了电阻允许通过的最大电流。
7．588米8．通路时 1.7A 6.8V短路时 5A 0V开路时 0A 10V9．接3Ω的负载时，输出最大功率，且为48W。
10．(1) 60kΩ (2) 0.2mA (3) V1=2V V2=10V11．(1) 11Ω (2) 0.5A (3) 内阻上压降 0.5V V1=3V V2=1V V3=1.5V 12．120Ω13．(1) 13.3Ω (2) 2.2A (3) 内阻上压降 6.6V 路端电压 29.4V 14．(a)图5条支路、4个节点、6个回路(b)图5条支路、4个节点、6个回路15．R3= 4Ω16．I3=0.2A I1=1A I2=0.8A17．S断开I3=0.3A S接通I3=0.6A18．Va= 0V Vab=－10VVb=10V Vbc=3.3VVc=6.7V Vcd=14VVd=－7.3V Vde=－14VVe=6.7V Vac=－6.7V第2章1．略2．略3．3.96×10-2库仑4．不能，耐压值不够5．略6．1.5×10-3秒7．略8．（a）2μF (b) 0.625μF9．16V10．逆时针方向11．线圈内垂直纸面朝里，标“×”线圈外垂直纸面朝外，标“·”12．左正右负13．线圈左端为S极，右端为N极。
14．朝上受力朝下受力电流垂直纸面朝里，标“×”导体不会受力，图中所标的受力箭头不正确。
15．5×10-3Wb16．先产生顺时针方向感生电流，然后电流为零，再产生逆时针方向感生电流，最后电流为零；产生大小、方向随时间变化的感生电流；不产生感生电流。
17．（1）Ｌ２：感生电动势左正右负；感生电流从左向右流过电阻；Ｌ１：感生电动势左正右负；感生电流与实际电流方向相反；（2）Ｌ２：感生电动势左负右正；感生电流从右向左流过电阻；Ｌ１：情况与Ｌ２同；（3）情况与（1）同；（4）均无感生电动势，感生电流。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(
)
= 2t 3 − t 2
(
)
t2 t1
从 t=1s 到 t=3s,由该端流入的电荷量为
3 q[1, 3] = (2t 3 − t 2 ) 1 = 2 × 3 3 − 3 2 − 2 × 1 + 1 = 44(C )
3．一个二端元件的端电压恒为 6V，如果有 3A 的恒定电流从该元件的高电位流向低电位， 求（a）元件吸收的功率； （b）在 2s 到 4s 时间内元件吸收的能量。 解: (1) 元件吸收功率 p = 6 × 3 = 18W
P 24 = = 6V I 4 Q 并联的电阻 R 上的电流为 6 − 4 = 2 A U 6 R = = = 3Ω 根据欧姆定律, 2 2
Q P = UI
∴U =
17．求出图题 1-17 所示电路中 5Ω电阻消耗的功率。
2Ω 20A 6Ω 10Ω 8Ω
5Ω
图题 1-17 解:
Q 右边支路电阻为 2 + 8 + 5 = 15Ω
t =0
= − 12mA
t =3 = 3 × 12 − 12
= 24mA
由某元件一端流入该元件的电流为 i=6 t 2－2 t A， 求从t=1s到t=3s由该端点流入该元件的 2． 电荷量。 解:
Q i (t ) =
dq dt
t2 t1
∴ q[t1 , t 2 ] = ∫ i (t )dt = ∫ 6t 2 − 2t dt
中间支路与右边支路并联后的阻值为
10 × 15 150 = = 6Ω 10 + 15 25
2Ω
20A
I1
I2
6Ω
10Ω I 3
8Ω
5Ω
根据分流公式 根据分流公式
I 1 = I 2 + I 3 = 10 A I3 =
5Ω 电阻消耗的功率为
10 × 10 = 4 A 10 + 15
P = I 32 × 5 = 16 × 5 = 80W
10×60 0
600
(1)
w[0,10 × 60] = ∫
pdt
=∫
0
1 ⎞ ⎛ ⎜ 6 + t ⎟ × 2dt 50 ⎠ ⎝
2 1 2 600 × t 0 50 2 1 = 12 × 600 + × 600 2 50 = 14400 J = 12 × 600 +
(2)
Qi =
dq dt
t2 t1
∴ q[t1 , t 2 ] = ∫ idt
∴ q[0,10 × 60] = ∫
600 0
2dt = 1200 C
10．一个 5kΩ电阻吸收的瞬时功率为 2 sin2 377t W。求u和i。 解:
QP =
u2 R
∴U = P ⋅ R
= 5000 × 2 sin 2 377t = 100 sin 377t (V)
又Q p = i R
2
∴i = =
3A 2A 4A
I1
I2
-10A 6A
根据基尔霍夫电流定律
I 1 = 3 + 4 − 6 = 1A
对节点 1 用基尔霍夫电流定律
I 2 = 2 + 1 − (− 10 ) = 13 A
14．求图题 1-14 中的i1，i2和u。
2A 1A
8Ω 4A
i1 6Ω
i2
3Ω
4Ω 3A u
图题 1-14
解:
7200
0
2dt = 14400 C
9．如果上题中，在 t 从 0 到 10 分钟时间内，电压 u 随 t 从 6V 到 18V 线性变化，i=2A，求 这段时间内： （a）电池被供给的能量； （b）通过电池的电荷。 解: 根据题意: u = 6 +
18 − 6 t (V) 10 × 60 1 = 6 + t (V) 50
第一章
1．由某元件一端流入该元件的电荷量为q =（6 t 2－12 t）mC，求在t=0 和t=3s时由该端流入 该元件的电流i。 解:
Q i (t ) =
dq dt
=
d 6t 2 − 12t dt
(
) (mA)
= 12t − 12 (mA)
∴ t = 0 s时, ∴ t = 3s时,
i (t ) i (t )
令电源电流为 I
30 × 15 = 10Ω 30 + 15
I=
20 20 = = 2A Rab 10
电源发生的功率 P = 20 × I = 20 × 2 = 40W (产生) 20．电路如图题 1-20 所示，求： （1） 开关K打开时，图a、b中的电压uab； （2） 开关 K 闭合时，图 a、b 开关中的电流；
∴ pis = 3 × 30 = 90W (吸收功率)
12．求图题 1-12 中的i和uab。
a 1A + 12V b
图题 1-12 根据欧姆定律: 4Ω 电阻上的电流为
5Ω 4Ω
6A 2Ω
3Ω
i
1A
解:
12 = 3 A 方向向下 4
根据节点定律: 5Ω 电阻上的电流为 I 5 = 3 + 1 = 4 A 方向向左
且 i = 0.1 cos1000 πt A ，求在 t=1ms 和 t=4ms 时元件上的电压。
w (mJ) 13 10
0
2
图题 1-4
8 t (ms)
解:
Qp=
dw dt
又 Q p t
w = 5t (mJ )
在 t = 0 − 2(ms ) 时
∴u =
∴u
5 5 dw (V ) i= = dt i 0.1cos1000πt
t =4
=
5 = 5(V ) cos 1000π × 4 × 10 −3
(
)
5．求图题 1-5 中各电源所提供的功率。
3A + 12V 10V 2A
4A 6V 5A (b) (c) (d) -9V
(a)
解:
a ) u , i 非关联参考方向 电源提供的功率为
p = ui = 12 × 3 = 36W
(2) 在 2s 到 4s 时间内元件吸收的能量 dw(t ) Qp=
dt
∴ w[t1 , t 2 ] = ∫ p(t )dt
t2 t1
w[2, 4] = ∫ 18dt = 18(4 − 2 ) = 36 J
4 2
如果该元件的电流和电压为关联参考方向， 4． 一个二端元件吸收的电能 w 如图题 1-4 所示。
p = R
2 sin 2 377t 5000
sin 377t = 2 × 10 − 2 sin 377t (A) 50
11．求图题 1-11 中各含源支路中的未知量。图（d）中的pis表示电流源吸收的功率。
- 2A 16V 8V R=?
3A 10Ω u=? 20V
i=? 10Ω -10V 6V is=3A 5Ω 45V pis=? (d)
(
)
7．一个电压源的端口电压为 u=6 sin 2t V，如果从其电压参考极性的正端流出的电荷 q=-2 cos 2t mC，求在任意时刻 t，电压源提供的功率，及电压源在 0 到 t 秒内提供的能量。 解: 从电压参考极性正端流出,应是非关联参考方向. p = ui 是产生功率
Qi =
dq dt
∴ i = 4 sin 2t mA
b ) p = 2 × 10 = 20W c ) p = −4 × 6 = −24W d ) p = −9 × 5 = −45W
6．按图题 1-6 中所示的参考方向以及给定的值，计算各元件的功率，并说明元件是吸收功 率还是发出功率。
2A + 6V (a)
3cos ωt A
-
+
10cos ωt V (b)
2Ω 电阻上的电流为 I 2 = 6 − 4 = 2 A 方向向右
则 i = 2 + 1 = 3A
U ab = −3 × 3 − 2 × 2 + 4 × 5 + 12
= 19V
13．根据图题 1-13 中给定的电流，尽可能多地确定图中其他各元件中的未知电流。
3A 2A 4A
-10A 6A
图题 1-13 解: 图中虚线部分是一个闭合面
p = ui = 6 sin 2t ⋅ 4 sin 2t = 24 sin 2 2t (mW ) w[0, t ] = ∫ pdt = ∫ 24 sin 2 2tdt = ∫ 24 ×
t t t 0 0 0
1 − cos 4t dt 2
= 12t − 3 sin 4t mJ
，求： （a）在 2 小时内电池被供 8．电流 i=2A 从 u=6V 的电池正极流入（电池正在被充电） 给的能量； （b）在 2 小时内通过电池的电荷（注意单位的一致性，1V=1J/C） 。 解: (1)
(a)
(b)
图题 1-11
(c)
解:
a ) Q 8v = 16 − 2 R
∴ R = 4Ω
b ) Q u = 20 + 3 × 10 ∴ u = 50V c ) Q i × 10 − 6 = −10 ∴ i = −0.4 A d ) Q pis = i s × u 3 A
u 3 A = 45 − 5 × 3 = 30v
（a）求电压ux ； （b）若图中电压源的给定电压为Us，求出ux关 18．电路如图题 1-18 所示， 于Us的函数。
5kΩ 30V
60kΩ
- ux +
1kΩ 15kΩ
图题 1-18 解:
(1) 根据分压公式及两点间电压求法
15 1 × 30 − × 30 60 + 15 5 +1 = 6 − 5 = 1V 15 1 ux = ×U S − ×U S 60 + 15 5 +1 1 1 1 = US − US = US 5 6 30