图及其应用
统计图及应用

统计图及应用统计图是一个可视化的工具,用于呈现和展示数据的不同方面和关系。
统计图的应用范围广泛,适用于各个领域,包括商业、科学、社会科学等。
在下面的文章中,我将介绍几种常见的统计图及其应用。
1. 条形图:条形图是一种以长方形的长度为基础的图表,用于比较不同类别间的数据。
条形图可以明确地展示不同类别的数值大小,便于直观地比较数据的差异。
条形图常用于展示销售额、人口统计、学生成绩等信息。
举个例子,一家公司可以用条形图来比较不同地区的销售额,以便于了解各个地区的销售情况。
2. 折线图:折线图通过连接不同的数据点来展示数据的变化趋势。
折线图可以很好地展示数据的变化关系,特别适用于表达时间序列数据。
折线图通常用于展示股票走势、气温变化等信息。
例如,一个气象学家可以通过折线图来显示一年中每个月份的平均气温,以便于分析季节性变化。
3. 饼图:饼图通过将一个圆形区域划分为不同的扇形,用于表达数据在整体中的比例关系。
饼图常用于展示组成部分的比例,例如市场份额、人口结构等信息。
举个例子,一家公司可以使用饼图来显示不同产品的市场份额,以便于了解产品在市场上的竞争情况。
4. 散点图:散点图以笛卡尔坐标系为基础,通过在坐标平面上绘制离散的数据点来展示数据的分布情况。
散点图可以显示变量之间的相关性和趋势,特别适用于观察两个变量之间的关系。
散点图通常用于研究变量之间的相关性,例如考察身高和体重之间的关系。
5. 柱状图:柱状图和条形图类似,但是柱状图的长方形是竖直方向的。
柱状图常用于展示不同类别间的数据比较,和条形图一样,它可以很好地比较不同类别的数值大小。
柱状图通常用于展示经济数据、人口统计等信息。
举个例子,一个城市可以使用柱状图来比较不同年份的人口增长情况。
统计图在现实生活中有很多应用。
在商业领域,统计图可以帮助企业了解市场需求、销售趋势和客户满意度。
在科学领域,统计图可以帮助研究人员可视化和分析实验结果。
在社会科学领域,统计图可以用来展示人口统计、民意调查等数据。
图论及其应用

图和子图 图和简单图图 G = (V, E), 其中 V = {νv v v ,......,,21} V ---顶点集, ν---顶点数E = {e e e 12,,......,ε}E ---边集, ε---边数例。
左图中, V={a, b,......,f}, E={p,q, ae, af,......,ce, cf} 注意, 左图仅仅是图G 的几何实现(代表), 它们有无穷多个。
真正的 图G 是上面所给出式子,它与顶点的位置、边的形状等无关。
不过今后对两者将经常不加以区别。
称 边 ad 与顶点 a (及d) 相关联。
也称 顶点 b(及 f) 与边 bf 相关联。
称顶点a 与e 相邻。
称有公共端点的一些边彼此相邻,例如p 与af 。
环(loop ,selfloop ):如边 l 。
棱(link ):如边ae 。
重边:如边p 及边q 。
简单图:(simple graph )无环,无重边 平凡图:仅有一个顶点的图(可有多条环)。
一条边的端点:它的两个顶点。
记号:νε()(),()().G V G G E G ==。
习题1.1.1 若G 为简单图,则εν≤⎛⎝ ⎫⎭⎪2 。
1.1.2 n ( ≥ 4 )个人中,若每4人中一定有一人认识其他3人,则一定有一 人认识其他n-1人。
同构在下图中, 图G 恒等于图H , 记为 G = H ⇔ V (G)=V(H), E(G)=E(H)。
图G 同构于图F ⇔ V(G)与V(F), E(G)与E(F)之间各存在一一对应关系,且这二对应关系保持关联关系。
记为 G ≅F 。
注 往往将同构慨念引伸到非标号图中,以表达两个图在结构上是否相同。
de f G = (V, E)y z w cG =(V , E )w cyz H =(V ’, E ’)’a ’c ’y ’e ’z ’F =(V ’’, E ’’)注 判定两个图是否同构是NP-hard 问题。
完全图(complete graph) Kn空图(empty g.) ⇔ E = ∅ 。
图论及其应用

顶点染色
定理:对于任何一个图χ(G)≤ω(G)。 ω(G)为图G的团数,用来描述χ(G)的下 界,其中ω(G)=max{k|Kk属于G}。
顶点染色
给定图G=(V,E)的一个k-点染色。用Vi表示G中染以 第i色的顶点集合(i=1,2,…,k),则每个Vi都是G 的独立集。因而G的每一个K-点染色对应V(G)的一个划 分[V1,V2,…,Vk],其中每一个Vi是一个独立集。反之 ,给出V(G)的这样一个划分(V1,V2,…,Vk),其中每 一个Vi均是独立集(1≤i≤k),则相应得到G的一个k点染色,称V(G)的这样一个划分为G的一个色划分,每 一个Vi称为色类。因此,G的色数χ(G)就是使这种划 分成为可能最小自然数k。
推论:若G是p(G) 3且g(G) 3的平图,则 q(G) g(G) ( p(G) 2)。 g(G) 2
平面图的性质
推论:任何一个简单平面图G,有 q(G)≤3p(G)-6
推论:设G是简单平面图,则δ(G)≥6.
定理:仅存在5种正多面体,即正四面体、正 方体、正八面体、正十二面体和正二十面体。
定理:每一个平面的色数不超过5
边染色
定义:无环图G的一个正常染色k-边染色(简 称k-边染色)是指一个映射φ:E(G)→{1,2, …,k},使对G中任意两条相邻的边e1和e2,有 φ(e1)≠φ(e2)。若G有一个正常k-边染色,则 称G是k-边染色的。G的边色数是指G为k-边染 色的最小整数k的值,记为
χ'(G)。若χ'(G)=k,则称G是k-边可色的。
边染色
设G有一个正常k-边染色,置Ei为G中所有染 以第i种颜色的边的全体,则E1,E2,…,Ek 是G的k个边不相交的对集,并且
地形图及其应用(12)
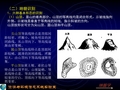
(4)山谷。指两山脊间的低凹部分。
山谷等高线的特点与山脊正好相反,是一 组向高处突出且两侧对称的曲线。山谷按 形状可分为尖形谷(V形)、圆形谷(U形) 和槽形谷三种。 V形谷等高线过谷底处呈V字形转折, 谷坡上均匀密集。 U形谷等高线特点是在谷底处呈U字 形转折,在谷坡上比较密集,且由谷缘向 谷底等高线逐渐变稀。 槽形谷等高线特点是过谷底是在其两 侧呈近于直角形,谷坡谷底转化明显。 表示山谷各等高线凸出部分的顶点的 连线叫集水线。
(二)地貌识别
1、六种基本形态的识别 (1)山顶。是山的最高部分。山顶的等高线均是闭合形式。示坡线指向 外侧。示坡线是垂直于等高线的短线,指示斜坡的方向。 山顶按形状可分为尖山顶、圆山顶和平山顶。 尖山顶等高线特点是顶部间 距较密,环圈小,棱角明显的封 闭曲线,从山顶向下,等高线逐 渐由密变稀。 圆山顶等高线特点是顶部间 距较稀,圆滑的封闭曲线,环圈 较大,由山顶向下等高线逐渐密 集。 平山顶如黄土塬、桌状山等 特点是山顶平坦,山坡陡峭,等 高线特点是,等高线环圈大,呈 较宽的空白,顶部向下等高线骤 然变密。
(三)后方交会法
当站立点附近没有明显地形点时,可采用本法。
(1)标定地图。 (2)在远方找到两个以上实地和图上都有的明显地形点。 (3) 用直尺分别切于两个以上明显地形符号的主点上。并转动直尺另一端, 瞄准实地地物,不得破坏地形图定向,瞄准后沿直尺向后划方向线,两个或 两个以上方向线的交点为站立点在图上位置。
四、圈定汇水界线
当修建水库或研究水文状 况时,要知道有多大范围的降 水向谷底汇集,这可以用等高 线地形图确定。 为了确定汇水区,就要划 出谷底周围的分水线,这条线 往往是谷地周围相邻山顶鞍部 山脊等的连线,而又必定是闭 合的线,它和等高线直交,常 与山脊线一致,只有到了山顶 才会突然改变方向。勾绘时, 要注意他的这些特性。 从河口或河道指定的断面 开始,将相邻的山脊线和作为 分水线的鞍部的界线,汇水界 线包围的范围叫汇水区。
图论及其应用PPT课件

图论及其应用第一章
1.2 图的同构
由前已知,同一个图有不同形状的图示。反过来, 两个不同的图也可以有形状相同的图示。比如:
u2
u3
可见 G1 和 G2 的顶点及边之间都一一对应,且连
接关系完全相同,只是顶点和边的名称不同而已。这
样的两个图称为是同构的(isomorphic)。
-29-
图论及其应用第一章
v1
(i=1,2,3,4,5,6)下是同构的。
x1
y1
v6
y3
x2
v2
x3
y2
v4
v3
-31-v5
图论及其应用第一章 画出所有的阶数不大于4,大小为3的所有非同构 简单图:
-32-
图论及其应用第一章 画出阶数为5大小为3的所有非同构简单图
G1
G2
G3
G4
-33-
图论及其应用第一章
无标号的图 注:判断两个图是否同构目前没有好算法。
图论起源于18世纪的一个游戏----俄罗斯的哥尼斯堡七桥问 题。
(1736年 瑞士数学家欧拉——图论之父)
-2-
图论及其应用第一章
七桥问题
C
A
D
B
包含两个要素:对象(陆 地)及对象间的二元关系 (是否有桥连接)
转化
Euler 1736年
C
A
D
B 图论中讨论的图
问题:是否能从A,B,C,D 转化 中的任一个开始走,通过每 座桥恰好一次再回到起点?
从数学上看,同构的两个图,其顶点间可建立一 一对应,边之间也能建立一一对应,且若一图的两点 间有边,则在另一图中对应的两点间有对应的边。严 格的数学定义如下。
定义: 两个图G = (V (G), E(G)) 与H = (V (H), E(H)) , 如果存在两个一一映射:
图论及其应用(25)

u
N (u ) k 1
u
N (u)
12
设п 是G的k着色方案,因为 u N (u ) k 1 ,所以, 在п 下,至少有一种颜色u及其邻域均没有用到,设该色 为m,改变u的颜色为m,其余点的着色不变,这样得到G的k 着色方案п 1.显然,п 与п 1导出的G的顶点划分不同,这 与G是唯一可着色图矛盾。 (2) 若不然,则存在G的k着色方案п 和G的两个色组C1 与C2,使得H=G[C1∪C2]不连通。设H1与H2是H的两个分支。 因为G是唯一可着色图,所以,对任意点u和其邻域 N(u), 它们在п 下,必然用完了k种颜色,否则,由(1)的 证明,得到G是非唯一可着色图。 这样,H1与H2中同时含有C1和C2中的顶点。
由于 H 也是某偶图的补,所以只需要证明 (G) cl (G)
25
证明:在 G 的正常着色方案下,每个色组对应G的一 (G ) 应该是G的最小点覆盖中包含 个顶点或者K2。这样, 的点数和边数。由补充定理:它等于G中最大独立集包含 的顶点数,即等于 G 的团数。所以有:
10
(2) 对于G2来说,G2的任意3正常着色方案导出的顶点 划分均是{{v1}, {v2,v4}{v3,v5}},所以,G2是 唯一3可着色图;例如:
v1 v2 v3 G2 v5 v2 v3 G2 v1 v5 v2 v3 v1 v5
v4
v4
v4
G2
(3) 对于G3来说,G3不是唯一3可着色图;因为:
设Hi=G[Vi∪{v}], (1≦i≦r)。则Hi是k-1可正常点着色 的,现对每个Hi进行k-1正常点着色,且v都分配同一种颜色, 那么,将着色后的Hi合在一起,得到G的k-1正常点着色方 案,这与G是k色图矛盾。所以临界图没有割点。
图论及其应用习题答案

图论及其应用习题答案图论及其应用习题答案图论是数学的一个分支,研究的是图的性质和图之间的关系。
图是由节点和边组成的,节点表示对象,边表示对象之间的关系。
图论在计算机科学、电子工程、物理学等领域有着广泛的应用。
下面是一些图论习题的解答,希望对读者有所帮助。
1. 问题:给定一个无向图G,求图中的最大连通子图的节点数。
解答:最大连通子图的节点数等于图中的连通分量个数。
连通分量是指在图中,任意两个节点之间存在路径相连。
我们可以使用深度优先搜索(DFS)或广度优先搜索(BFS)来遍历图,统计连通分量的个数。
2. 问题:给定一个有向图G,判断是否存在从节点A到节点B的路径。
解答:我们可以使用深度优先搜索(DFS)或广度优先搜索(BFS)来遍历图,查找从节点A到节点B的路径。
如果能够找到一条路径,则存在从节点A到节点B的路径;否则,不存在。
3. 问题:给定一个有向图G,判断是否存在环。
解答:我们可以使用深度优先搜索(DFS)或广度优先搜索(BFS)来遍历图,同时记录遍历过程中的访问状态。
如果在搜索过程中遇到已经访问过的节点,则存在环;否则,不存在。
4. 问题:给定一个加权无向图G,求图中的最小生成树。
解答:最小生成树是指在无向图中,选择一部分边,使得这些边连接了图中的所有节点,并且总权重最小。
我们可以使用Prim算法或Kruskal算法来求解最小生成树。
5. 问题:给定一个有向图G,求图中的拓扑排序。
解答:拓扑排序是指将有向图中的节点线性排序,使得对于任意一条有向边(u, v),节点u在排序中出现在节点v之前。
我们可以使用深度优先搜索(DFS)或广度优先搜索(BFS)来遍历图,同时记录节点的访问顺序,得到拓扑排序。
6. 问题:给定一个加权有向图G和两个节点A、B,求从节点A到节点B的最短路径。
解答:我们可以使用Dijkstra算法或Bellman-Ford算法来求解从节点A到节点B的最短路径。
这些算法会根据边的权重来计算最短路径。
第3章地形图及其应用2

三、百分比尺和坡度尺
百分比尺使用
• (一)百分比尺 是地图缩小旳比率,(图上某线段与实地相应 水平距离之比)。百分比尺分三种:数字百分比尺、直线百分比 尺(图解百分比尺)、文字百分比尺(阐明百分比尺)。例“十 万分之一”、“图上1cm代表实地1km”
• 侧视符号:按地物旳侧面形状设计。符号与地物侧视 形状相像。
• 象征符号:有些地物既不宜用正形符号表达又不宜用 侧视符号表达,而用一种象征地物含意旳图形表达旳。
按地物符号旳图形特征分类
2.符号与地物旳百分比关系分 类
• 依百分比符号:又叫轮廓符号或面状符号,即实地上面积较大旳地物,依百 分比尺缩小后,仍能保持与实地形状相同、图形清楚旳符号叫依百分比符号, 如居民地、森林、大旳河流湖泊等,外部轮廓是依百分比旳,周界以实线或 虚线表达,地物旳意义、性质、数量、质量等特征采用轮廓线内加绘排列或 散列旳填充符号和阐明注记表达。
2.符号与地物旳百分比关系分 类
3.按符号旳定位情况分类
• 定位符号:指图上有拟定旳位置,一般不能任意移动旳符 号,图上符号大部分属于这一类,他们都能够根据符号旳 位置,拟定其所代表旳地物及实地位置。
• 阐明符号:指为了阐明事物旳质量和数量特征而附加旳一 类符号,它一般依附定位符号而存在,如森林树种旳符号、 果园符号等,他们在图上配置于地类界范围内,呈规则或 不规则排列,但无定位意义。
• (二)坡度尺 用来在图上量测地面沿某一方向旳倾斜角。
利用坡度尺量取地面坡度
四、三北方向线
• (一)三种基本方向线 • 真北 过地面上任意一点,指向
北极旳方向,叫真北。其方向 线叫真北方向线或真子午线。 地图上东西内图廓就是真子午 线。 • 磁北 过地面上任意一点,磁针 所指旳北方,叫磁北。其方向 线叫磁方向线或磁子午线。地 图上P、P′点或磁北、磁南点旳 连线叫磁子午线。 • 坐标纵线北 地图上坐标纵线所 指旳北方,叫坐标纵线北。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
}
}
}
4.主函数的描述如下:
void main()
{
int v,i;
Start_Screen();
if(t!=1)
{
printf("\t\t\t\a请先建立图的邻接表!\n");
Start_Screen();
}
while(1)
{
switch(t)
{
case 1:GreateGraph();//建立图的邻接表算法
printf("* 5.退出系统*\t\n");
printf("\t* *\t\n");
printf("\t* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *\t\n");
printf("\t*请输入您的选择选择: "); scanf("%d",&t);
int count,t,c[MAXSIZE];
typedef struct node//定义表结构体类型
{
int adjvex,info;
struct node *next;//指向下一个结点的指针
}nodetype;
typedef struct frontnode//定义表头结点类型
{
char data;
front=(front+1)%MAXSIZE;
q[front]=v;
}
p=p->next;
}
}
for(i=1;i<=count;i++)
if(c[i]==0)
{
c[i]=1;
printf("%c",adjlist[i].data);
q[++front]=i;
while(front>rear)
{
rear=(rear+1)%MAXSIZE;
四、实验内容:
利用邻接表存储结构,设计一种图(有向或无向),并能够对其进行如下操作:
1.建立图的邻接表算法
函数名:GreateGraph()
操作结果:采用邻接表存储结构,构造图G;
2.确定图的顶点数和弧数算法
函数名:var_adjcount()
操作结果:确定图G的结点数和弧(有向或无向)数;
3.邻接表表示的图的递归深度优先遍历的算法
break;
case 2:var_adjcount();//确定图的顶点数和弧数算法
break;
case 3:printf("请输入您要进行深度优先遍历的开始顶点序号:");
scanf("%d",&v);
for(i=1;i<=count;i++)c[i]=0;
DFSTraverse(v);//邻接表表示的图的递归深度优先遍历的算法
本次实验使自己加深了对图的理解,能够掌握图的基本运算,加深了对编程的浓厚兴趣,能够根据错误或警告找出问题的所在并修改,进一步熟练的掌握调试技术。
九、对本实验过程及方法、手段的改进建议:
在这次实验中没有深入对图的运算进行操作,如删除图的结点,用广度优先搜索或深度优先搜索方法找出从一顶点到另一顶点边数最少的路径等。因此还有待于对图的其他操作进行应用。
{
i=p->adjvex;
if(c[i]==0)
{
printf(" -> ");
DFSTraverse(i);
}
}
printf("\n");
for(i=1;i<=count;i++)
if(c[i]==0)DFSTraverse(i);
printf("\n\n\n\n\n");
}
//邻接表表示的图的广度优先遍历的算法
Start_Screen();
}
Start_Screen();
}
}
七、实验结果:
1.有向图G1测试:
(a)有向图G1 G1的邻接矩阵
G1的邻接表
(1)图的顶点数和弧数
顶点数:6弧数:8
(2)图的递归深度优先遍历
输入:A (从A结点开始的深度优先遍历)
预期输出:A-﹥B-﹥E-﹥C-﹥D-﹥F
(3)图的非递归广度优先遍历
p->next=NULL;
adjlist[i].next=p;
printf("请输入第%d个顶点的邻接点域,数据域,以‘-1,-1’结束(注意数与数以空格隔开):\n",i);
scanf("%d,%d",&adj,&we);
while(adj!=-1)
{
q=(nodetype *)malloc(sizeof(nodetype));
输入:C (从C结点开始的广度优先遍历)
预期输出:C-﹥D-﹥F-﹥E-﹥A-﹥B
实验结果:
输入图G1的所有顶点:
输入各个顶点的邻接结点:
输出图的顶点数和弧数:
从A结点开始的深度优先遍历:
从C结点开始的广度优先遍历:
退出系统:
2.无向图G2测试:
(b)无向图G2邻接矩阵
邻接表
(1)图的顶点数和弧数
顶点数:5弧数:8
v=q[rear];
p=adjlist[i].next;
while(p!=NULL)
{
v=p->adjvex;
if(c[v]==0)
{
c[v]=1;
printf(" -> %c",adjlist[v].data);
front=(front+1)%MAXSIZE;
q[front]=v;
}
p=p->next;
报告评分:
指导教师签字:批阅日期:
注意:
实验报告以纸质文档形式上交。实验报告将记入平时成绩;
每次实验开始时,交上一次的实验报告,否则将扣除此次实验成绩。
printf("\t* *\t\n");
printf("\t* 2.输出图的顶点数和弧数*\t\n");
printf("\t* *\t\n");
printf("\t* 3.深度优先遍历图*\t\n");
printf("\t* *\t\n");
printf("\t* 4.广度优先遍历图*\t\n");
printf("\t* *\t\n");
printf("\t* *\t\n");
printf("\t* ***** Welcome to图的应用***** *\t\n");
printf("\t* *\t\n");
printf("\t* *\t\n");
printf("\t* *\t\n");
printf("\t* 1.建立图的邻接表*\t\n");
q->adjvex=adj;
q->info=we;
q->next=NULL;
p->next=q;
p=p->next;
scanf("%d,%d",&adj,&we);
}
p=adjlist[i].next;
adjlist[i].next=p->next;
free(p);
}
}
//确定图的顶点数和弧数算法
void var_adjcount()
printf("\n");
}
3.编写图的基本操作函数描述如下:
//建立图的邻接表算法
void GreateGraph()
{
nodetype *p,*q;
char ch;
int i=1,adj,we;
printf("请输入该图的所有顶点,以‘#’结束:\n");
scanf("\n%c",&ch);
while(ch!='#')
{
nodetype *p,*q;
int i,v,e=0;
for(i=1;i<=count;i++)
{
p=adjlist[i].next;
while(p!=NULL)
{
e++;
p=p->next;
}
}
p=adjlist[1].next;
v=p->adjvex;
q=adjlist[v].next;
if(adjlist[q->adjvex].data==adjlist[1].data)e=e/2;
printf("该图的顶点数为%d,弧数为%d",count,e);
}
//邻接表表示的图的递归深度优先遍历的算法
void DFSTraverse(int v)
{
int i;//标志数组初始化
nodetype *p;
c[v]=1;
printf("%c",adjlist[v].data);
for(p=adjlist[v].next;p!=NULL;p=p->next)//从v的第一个邻接顶点开始
六、实验步骤及操作:
1.用一维数组存储顶点信息,用链接矩阵存储顶点间关系信息的图或网的形
式描述下:
#include<stdio.h>
