自动控制原理 实验三SIMULINK环境下典型环节阶跃响应仿真及分析
自控实验报告-典型环节

自动控制原理实验报告课程名称 自动控制原理实验 成绩评定 实验项目名称 典型环节 指导教师实验项目编号 0806105701 实验项目类型 设计 实验地点学院 电气工程学院 系 专业 电气工程及其自动化 实验时间 2020年 5 月 18 日 下午 一、实验目的1.熟悉Matlab/simulink 各典型模块;2.测量各典型环节的阶跃响应曲线,并了解参数变化对其动态特性的影响。
二、实验环境Matlab/simulink 仿真平台 三、实验报告要求1.画出各环节的模块连接图,并注明参数。
2.写出各典型环节的传递函数。
3.根据测得的典型环节单位阶跃响应曲线,分析参数变化对动态特性的影响。
四、实验内容及分析1.观测三阶系统的 ()(0.11)(0.51)KW s S S S =++开环增益K 为不同数值时的阶跃响应曲线(1) 0<K <12; (2) K =12;(3) K >12。
(1)K=1K=5K=10(2)K=12(3)K=15K=50K=100分析图象曲线可知:0<k<12时 ,系统是稳定系统,随着开环增益K 的增大,系统调节时间增大,超调量增大K=12,系统是临界稳定系统k>12,系统发散不稳定,随着开环增益K 的增大,系统震荡越明显2.比例积分(PI)环节1()I W s K T S=+设U i (S )为一单位阶跃信号,记录PI 的输出 (1) 若比例系数K =2、积分时间常数T I =0.1S ; (2)若比例系数K =1.1、积分时间常数T I =1S 。
(1)(2)由图像曲线可得:时间常数越小,积分时间越小,响应过程的快速性也越好。
四、实验小结由实验一得,随着开环增益K的增大,此三阶系统的动态稳定性变差,由实验二可知,比例环节的时间常数越小,积分时间越小,响应过程的快速性也越好。
自动控制原理实验指导典型环节及其阶跃响应

%100%max ⨯-=∞∞Y Y Y σ实验一 典型环节及其阶跃响应一、实验目的1. 掌握控制模拟实验的基本原理和一般方法。
2. 掌握控制系统时域性能指标的测量方法。
二、实验仪器1. EL-AT-III 型自动控制系统实验箱一台 2. 计算机一台 三、实验原理1.模拟实验的基本原理:控制系统模拟实验采用复合网络法来模拟各种典型环节,即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节,然后按照给定系统的结构图将这些模拟环节连接起来,便得到了相应的模拟系统。
再将输入信号加到模拟系统的输入端,并利用计算机等测量仪器,测量系统的输出,便可得到系统的动态响应曲线及性能指标。
若改变系统的参数,还可进一步分析研究参数对系统性能的影响。
2. 时域性能指标的测量方法: 超调量Ó %:1) 启动计算机,在桌面双击图标 [自动控制实验系统] 运行软件。
2) 检查USB 线是否连接好,在实验项目下拉框中选中任实验,点击按钮,出现参数设置对话框设置好参数按确定按钮,此时如无警告对话框出现表示通信 正常,如出现警告表示通信不正常,找出原因使通信正常后才可以继续进行实验。
3) 连接被测量典型环节的模拟电路。
电路的输入U1接A/D 、D/A 卡的DA1 输出,电路的输出U2接A/D 、D/A 卡的AD1输入。
检查无误后接通电源。
4) 在实验项目的下拉列表中选择实验一[典型环节及其阶跃响应] 。
5) 鼠标单击按钮,弹出实验课题参数设置对话框。
在参数设置对话框中设置相应的实验参数后鼠标单击确认等待屏幕的显示区显示实验结果。
6) 用软件上的游标测量响应曲线上的最大值和稳态值,代入下式算出超调量: T P 与T S :利用软件的游标测量水平方向上从零到达最大值与从零到达95%稳态值所需的时间值,便可得到T P 与T S 。
四、实验内容构成下述典型一阶系统的模拟电路,并测量其阶跃响应: 1. 比例环节的模拟电路及其传递函数如图1-1。
实验三-三阶系统的阶跃响应及稳定性分析实验
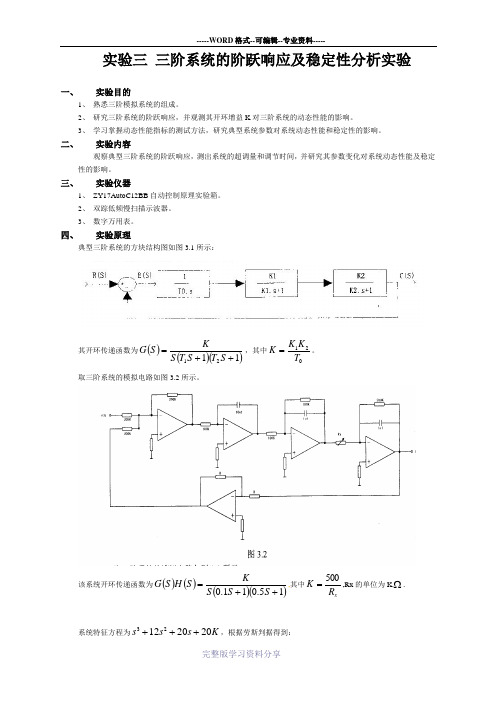
实验三 三阶系统的阶跃响应及稳定性分析实验一、 实验目的1、 熟悉三阶模拟系统的组成。
2、 研究三阶系统的阶跃响应,并观测其开环增益K 对三阶系统的动态性能的影响。
3、 学习掌握动态性能指标的测试方法,研究典型系统参数对系统动态性能和稳定性的影响。
二、 实验内容观察典型三阶系统的阶跃响应,测出系统的超调量和调节时间,并研究其参数变化对系统动态性能及稳定性的影响。
三、 实验仪器1、 ZY17AutoC12BB 自动控制原理实验箱。
2、 双踪低频慢扫描示波器。
3、 数字万用表。
四、 实验原理典型三阶系统的方块结构图如图3.1所示:其开环传递函数为()()()1121++=S T S T S K S G ,其中021T K K K =。
取三阶系统的模拟电路如图3.2所示。
该系统开环传递函数为()()()()15.011.0++=S S S K S H S G,其中x R K 500=,Rx 的单位为K Ω.系统特征方程为K s s s 20201223+++,根据劳斯判据得到:系统稳定0<K<12系统临时稳定K=12系统不稳定K>12根据K可求取Rx,改变Rx即可实现三种典型的实验。
该系统的阶跃响应图如所示,图3.3.1,图3.3.2和图3.3.3分别对应于系统处于稳定,临界稳定和不稳定的三种情况。
五、实验步骤1、利用实验仪器,按照实验原理设计并连接由一个积分环节和两个惯性环节组成的三阶闭环系统的模拟电路。
此实验可使用运放单元(一)、(二)、(三)、(五)、(六)及元器件单元中的电容和可调电阻。
(1)同时按下电源单元中的按键开关S001,S002,再按下S003,调节可调电位器W001,使T006(-12V-----+12V)输出电压为+1V,形成单位阶跃信号电路,然后将S001,S002再次按下关闭电源。
(2)按照图3.2连接好电路,按下电路中所用到的运放单元的按键开关。
(3)用导线将连接好的模拟电路的输入端与T006相连接,电路的输出端与示波器相连接。
实验3 典型闭环系统的阶跃响应的仿真

实验3 典型闭环系统的阶跃响应的仿真一、实验目的1. 了解MATLAB 在仿真中的具体应用2. 熟悉MATLAB 语言环境3. 掌握M 文件的应用二、实验步骤1. 对控制系统的典型结构形式二次模型化,经一定方式把数学模型转化为便于在计算机上运行的表达形式。
2. 讨论采用数值积分法求解系统响应的仿真程序实现,绘制仿真框图。
x 0t ft jk 11,++k k y x ft t =图3-1 典型闭环系统的仿真程序框图3.编写MATLAB程序语句,实现对典型闭环系统的阶跃响应的仿真Filename:sa.m1)输入数据a=[a0,a1,…,an]; %% n+1维分母系数向量b=[b0,b1,…,bm]; %% m+1维分子系数向量X0=[x0,x1,…,xn]; %% 状态向量初值V=V0; %% 反馈系数n=n0; %% 系统阶次T0=t0; %% 起始时间Tf=tf; %% 终止时间h=h0; %% 计算步长R=r; %% 阶跃输入函数的幅值2)形成开、闭环系数阵b=b/a(1);a=a/a(1);A=a(2:n+1); %% 首一化处理A=[rot90(rot90(eye(n-1,n)));-fliplr(A)]; %%形成能控标准型A阵B=[zeros(1,n-1),1]'; %%形成输入阵Bm1=length(b); %%分子向量维数M+1C=[fliplr(b),zeros(1,n-m1)]; %%形成输出阵CAb=A-B*C*V; %%形成闭环系数阵X=X0';y=0;t=T0; %%设初值,准备开始递推运算3)运算求解N=round(Tf-T0)/h; %%确定输出点数for i=1:N %%四阶龙格-库塔法K1=Ab*X+B*R;K2=Ab*(X+h*K1/2)+B*R;K3=Ab*(X+h*K2/2)+B*R;K4=Ab*(X+h*K3)+B*R; %%求各次斜率KX=X+h*(K1+2*K2+2*K3+K4)/6; %%求状态y=[y,C*X]; %%求输出并以向量形式保存t=[t,t(i)+h];end4) 输出结果[t',y'] %% 输出数据形式的结果plot(t,y,'g:') %%输出曲线形式的结果具体应用:根据以上所述,求图5-2所示系统的阶跃响应y(t)的数值解。
实验三 SIMULINK环境下典型环节阶跃响应仿真及分析

(7)设仿真过程参数:SIMULATION 菜单\PARAMETERS 菜单项。 其中: Start Time 为仿真开始时间, Stop time 为仿真终止时间, Mix Step Size 为仿真最小步长。 Max Step Size 为仿真最大步长。, Tolerance 为仿真精度。 仿真开始前应对 Stop Time 进行修改,如改为 10 秒,50 秒或 200 秒,再根据实际情况进行 调整。
012??ssg积分环节ssg11?微分环节ssg?1比例微分环节pd21??ssg和12??ssg比例积分环节pissg111??和ssg2112??2对典型二阶系统4442???szssg进行仿真分别取00205071观察p?和ts的变化情况
实验三 SIMULINK 环境下典型环节阶跃响应仿真及分析
3.实验总结 初步了解 MATLAB 中 SIMULINK 的使用方法,了解 SIMULINK 下实现典型环节阶跃响应 方法。定性了解各参数变化对典型环节动态特性的影响,实现了实验目的。
S
s2 ,则令 2 s 3s 4
2
为[1];
Denominator 为[1,0]; 例 3-3:要将传递函数变为振荡环节: Denominator 为[1,1,1]; (在此传函中阻尼系数ζ为 0.5) 例 3-4:要将传递函数变为实际微分环节:
1 ,则令 Numerator 为[1]; s s 1
2
s ,则令 Numerator 为[1,0]; s 1
Denominator 为[1,1];
实际微分环节的传递函数为:
K d Td s 1 Td s
分子分母同除以 Td,则为
Kd s s 1 / Td
因此,上式中分子 s 的系数即为 Kd 值,分母中常数项为 Td 的倒数. (6)用鼠标将 step、transfer fcn 及 scope 模块连接。如下图所示:
实验三 控制系统的Simulink仿真

-
1 s
信号 2
10 s5
信号 3
ห้องสมุดไป่ตู้
输出 6 s 2 5s 6
0.7
K 。 s( s 2)
2、 已知单位负反馈系统的开环传递函数为 G ( s)
①利用 Simulink 仿真模型求 K=2 时系统的单位阶跃响应曲线。 ②将上述系统创建为子系统,并进行子系统封装,设置子系统的模块参数 K。 ③编制 MATLAB 程序绘制系统的开环 Bode 图,同时显示系统的幅值裕量和相 位裕量,确定系统的稳定性。 ④编制程序绘制系统的单位阶跃响应和单位脉冲响应,时间范围[0,10]。
实验三 控制系统的 Simulink 仿真
实验目的: 学会利用 Simulink 进行系统仿真;了解子系统的创建方法和简单应用;运用 Simulink 实现经典控制系统的仿真。
实验内容: 1、 如图所示控制系统。 ①利用 Siumulink 仿真模型,观察单位阶跃输入时(阶跃时间:2 s)的信 号 1、信号 2、信号 3 和输出信号波形(仿真时间 20 s) 。分析系统稳定性。 ②改变信号波形的显示方式,利用信号通路模块库将所有输入信号、中间信 号和输出信号在一个示波器上混合显示。 ③利用信号通路模块库将所有输入信号、中间信号和输出信号在一个示波器 上分别显示。 ④编写 Matlab 程序求取系统的闭环传递函数,并求系统的闭环特征根,分 析系统的稳定性,并与①比较。
《自动控制原理》仿真实验报告

中国地质大学江城学院《自动控制原理》仿真实验报告姓名吴丽芳班级数控(2)班学号2520110228指导教师祁锋2013年12月9 日目录实验一 MATLAB软件的安装与认知实验二使用软件进行数值运算和绘图实验三采用SIMULINK仿真模块进行系统性能分析实验一 MATLAB软件的认识一、实验目的MATLAB软件是具有数值分析、矩阵运算、复杂的信息处理和完美的图形显示等多种功能的软件包,它具有许多专门用途的工具箱,进一步扩展了MATLAB 的应用领域,使其在自动控制系统的分析和设计方面获得广泛的应用。
1、熟悉启动和退出MATLAB软件的方法;2、熟悉MATLAB软件的运行环境;3、熟悉MATLAB软件的基本操作;4、掌握建立矩阵的方法;5、掌握熟悉MATLAB软件各种表达式的书写规则以及常用函数的使用;6、能够进行基本的数组、矩阵运算。
二、实验内容熟悉MATLAB软件的各个工具箱、指令及常用工具,掌握数值的表示方法、运算符的使用规则及运算表达式的写法。
三、分析讨论题1、MATLAB软件有哪些常用指令?有哪些专用工具箱?help elfun %列出所有基本函数。
lookfor image 查找有关图像的函数和命令。
几个常用的通用命令。
quit 关闭MATLABexit 关闭MATLABclc 清除MATLAB命令窗口中的所有显示内容clear 清除工作空间中保存的所有变量Matlab Main Toolbox——matlab主工具箱Control System Toolbox——控制系统工具箱Communication Toolbox——通讯工具箱Financial Toolbox——财政金融工具箱System Identification Toolbox——系统辨识工具箱Fuzzy Logic Toolbox——模糊逻辑工具箱Neural Network Toolbox——神经网络工具箱Optimization Toolbox——优化工具箱Partial Differential Toolbox——偏微分方程工具箱Robust Control Toolbox——鲁棒控制工具箱Signal Processing Toolbox——信号处理工具箱Spline Toolbox——样条工具箱Statistics Toolbox——统计工具箱Symbolic Math Toolbox——符号数学工具箱Simulink Toolbox——动态仿真工具箱Wavele Toolbox——小波工具箱2、用举例的方法说明数值的表示方法是怎样的?MATLAB的数值采用十进制,可以带小数点或负号。
自动控制原理MATLAB实验报告

实验一典型环节的 MATLAB 仿真一、实验目的1.熟悉 MATLAB 桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验原理1.比例环节的传递函数为Z 2R22 R1 100K , R2200KG( s)R1Z1其对应的模拟电路及 SIMULINK图形如图 1 所示。
图 1 比例环节的模拟电路及SIMULINK图形2.惯性环节的传递函数为R2Z2R12 G ( s)R2C1 1R1 100K , R2 200K , C1 1ufZ10.2s 1其对应的模拟电路及SIMULINK图形如图 2 所示。
图 2 惯性环节的模拟电路及SIMULINK图形3.积分环节 (I) 的传递函数为Z211 G(s)R1C1s R1 100K ,C1 1ufZ10.1s其对应的模拟电路及SIMULINK图形如图3所示。
图 3积分环节的模拟电路及及SIMULINK图形4.微分环节 (D) 的传递函数为G( s)Z 2R1C1 s s R1 100K, C110uf C2C1 0.01uf Z1其对应的模拟电路及 SIMULINK图形如图 4所示。
图 4 微分环节的模拟电路及及SIMULINK 图形5.比例 +微分环节( PD)的传递函数为G( s)Z 2R2(R1C1 s1)(0.1s1)Z1R1R1 R2100K , C110uf C2C10.01uf 其对应的模拟电路及 SIMULINK图形如图 5 所示。
实验报告6.比例 +积分环节( PI)的传递函数为R21(1 1)R1 R2 100K , C1 10ufG( s)Z2C1sZ1R1s其对应的模拟电路及SIMULINK图形如图 6 所示。
图 6 比例 +积分环节的模拟电路及SIMULINK图形曲三、实验内容按下列各典型环节的传递函数,建立相应的 SIMULINK 仿真模型,观察并记录其单位阶跃响应波形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程名称自动控制原理
实验序号实验三
实验项目SIMULINK环境下典型环节阶跃响应仿真及分析实验地点
实验学时实验类型操作性
指导教师实验员
专业 _______ 班级
学号姓名
年月日
教
师
评
语
一、实验目的及要求
1、初步了解MATLAB中SIMULINK的使用方法;
2、了解SIMULINK下实现典型环节阶跃响应方法;
3、定性了解各参数变化对典型环节动态特性的影响。
二、实验原理与内容
三、实验软硬件环境
装有MATLA软件的电脑
四、实验过程(实验步骤、记录、数据、分析)
1、按下列各典型环节的传递函数,建立相应的SIMULINK仿真模型,观察并记录其单位阶跃响应波形。
(1)比例环节G1(s)=1和G2(s)=2;
比例环节G1(s)=1的实验结果:
比例环节G2(s)=2的实验结果:
结果分析:由以上阶跃响应波形图知,比例环节的输出量与输入量成正比,比例系数越大,输出量越大。
(2) 惯性环节G1(s)=1/(s+1)和G2(s)=1/(0.5s+1)
惯性环节G1(s)=1/(s+1)的实验结果:
惯性环节G1(s)=1/(0.5s+1)的实验结果:
结果分析:由以上单位阶跃响应波形图知,惯性环节使输出波形在开始的时候以指数曲线上升,上升速度与时间常数有关,时间常数越小响应越快。
(3)积分环节G(s)=1/s
(4)微分环节G(s)=s
(5)比例+微分(PD)G1(s)=s+2和G2(s)=s+1
G1(s)=s+2的实验结果:
G2(s)=s+1的实验结果:
结果分析:由以上单位阶跃响应波形图知,比例作用与微分作用一起构成导前环节,输出反映了输
入信号的变化趋势,波形也与时间常数有关。
(6)比例+积分(PD)G1(s)=1+1/s和G2(s)=1+1/2s
G1(s)=1+1/s的实验结果:
G2(s)=1+1/2s的实验结果:
结果分析:由以上单位阶跃响应波形图知,积分环节的输出量反映了输入量随时间的积累,时间常数越大,积累速度越快。
实验结果:
结果分析:由以上单位阶跃波形知,当ξ=0时,系统的单位阶跃响应为不衰减;随着阻尼ξ的减小,其振荡特性表现的愈加强烈,当ξ的值在0.2-0.7之间时,过渡过程时间较短,振荡不太严重;当ξ=1时,响应慢。
